Методика оценки времени выполнения программ, оптимизированных под конкретную архитектуру процессора, по тексту программ на языке высокого уровня. Балашов В. В.,Капитонова А. П., Костенко В. А., Смелянский Р. Л., Ющенко Н. В

Вид материала

Содержание

2.Методика оценки времени выполнения оптимизированных программ.
3.Апробация методики для процессора DSP96002 в классе методов цифровой обработки сигналов.
3.2.Результаты измерений.

Подобный материал:

МЕТОДИКА ОЦЕНКИ ВРЕМЕНИ ВЫПОЛНЕНИЯ ПРОГРАММ, ОПТИМИЗИРОВАННЫХ ПОД КОНКРЕТНУЮ АРХИТЕКТУРУ ПРОЦЕССОРА, ПО ТЕКСТУ ПРОГРАММ НА ЯЗЫКЕ ВЫСОКОГО УРОВНЯ.

Балашов В.В.,Капитонова А.П., Костенко В.А., Смелянский Р.Л., Ющенко Н.В.

119899, Москва, ГСП-3, Воробьевы горы, МГУ, 2-й учебный корпус, ф-т ВМиК,

тел.: (095) 939-46-71, факс: (095) 939-25-96, е-mail: kost@cs.msu.su

Реферат: В работе ?????????вается методика оценки времени выполнения прикладных программ, для которых проведена оптимизация под конкретный процессор, по данным о времени выполнения эквивалентных программ, записанных на языке высокого уровня. Методика основана на выделении множества базовых операций, для которых известны (могут быть получены предварительно) коэффициенты, корректирующие время выполнения операций при оптимизации. Методика позволяет получать оценки с ??????руемой погрешностью. Приводятся результаты применения методики для процессора DSP 96002 в классе задач цифровой обработки сигналов.

1.????????.

Задача прогнозирования времени выполнения программ на заданном вычислительном комплексе хорошо осознана на сегодня [1,2] и, можно сказать, стала классической в области проектирования и разработки вычислительных систем. Постановка этой задачи варьируется в зависимости от прикладной области. В этой статье мы рассмотрим эту задачу применительно к системам реального времени, ??? эта задача имеет следующую специфику. Программы в системах реального времени подвергаются значительной оптимизации, которая зачастую выполняется вручную. Штатные компиляторы, поставляемые с кристаллами процессоров, как правило, не эффективны. Например, как показано в этой работе штатный компилятор Motorola g96k для процессора DSP96002 на программах цифровой обработки сигналов (ЦОС) дает замедление в 13 раз по сравнению с той же программой, оптимизированной вручную и записанной на ассемблере.

Такая чувствительность к качеству кода существенно усложняют задачу прогнозирования времени выполнения программы. В особенности это относится к тем случаям когда надо подобрать процессор для системы, либо когда надо выбрать конфигурацию системы (например, число процессоров), ??? ???????, ??? качественный компилятор недоступен, ? приложения ??? системы представлены на языке программирования высокого уровня

В данной работе предложена методика прогнозирования времени выполнения оптимизированных программ по их тексту, заданном на языке программирования высокого уровня ??? ??????? ?????????? ??????????????? ???????????. Существенными достоинствами предлагаемой методики являются контролируемая точность и простота.

2.Методика оценки времени выполнения оптимизированных программ.

Идея предлагаемой методики состоит в следующем. Для заданной прикладной области, в данном случае ЦОС, выделяется набор базовых операций {b_i} , к которым в задачах данной области сводится большая часть вычислительной нагрузки. Каждая базовая операция реализуется экспертом как на языке программирования высокого уровня, так и на ассемблере. Обе реализации выполняются на процессоре или его эмуляторе. В случае реализации на языке программирования естественно используется штатный компилятор процессора. В обоих прогонах замеряется время исполнения на различных наборах исходных данных и вычисляется отношение времени исполнения реализации на языке высокого уровня к времени исполнения ассемблерной реализации. Это отношение будем в дальнейшем называть корректирующим коэффициентом k_i операции b_i.

Сначала в программе выделяются все имеющиеся базовые операции из множества {b_i}. Части кода программы, не относящиеся к выделенным базовым операциям, назовем неструктурированными операциями {u_j}.

После выделения базовых операций программа запускается на модели процессора [3,4]. При этом измеряются следующие следующие величины:

времена T(b_i) и кратности r(b_i) выполнения базовых операций из множества {b_i},
суммарное время выполнения базовых операций – T_B,
суммарное время выполнения неструктурированных операций – T_U.

Для этого запуска используется штатный компилятор. Времена T_B и T_U соответствуют неоптимизированной программе.

Пусть в оптимизированном варианте программы эти времена равны соответственно Tў_B и Tў_U. Предположим для определенности, что базовые и неструктурированные операции оптимизируются независимо, т.е. время выполнения оптимизированной программы равно Tў=Tў_B+Tў_U.

Так как для базовых операций нам известны корректирующие коэффициенты, мы можем вычислить Tў_B:

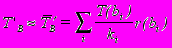
Время Tў_U нам неизвестно. Будем оценивать его по формуле

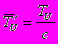, где c – параметр.

Время работы всей оптимизированной программы оценивается по формуле

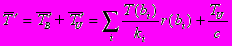(1)

Введем коэффициенты: ?=T_U/T_B – доля времени выполнения неоптимизированной программы, потраченная на неструктурированные операции, K_B=T_B/Tў_B, K_U=T_U/Tў_U – средние коэффициенты ускорения базовых и неструктурированных операций соответственно. Заметим, что величины ? и K_B нам известны, а K_U – нет.

Для оценки погрешности формулы (1) предположим, что

m ??K_U/K_B??M

Значение констант m и M можно оценить, зная дополнительную информацию о применяемых оптимизациях. Так, разумно взять M=1: архитектура процессоров обычно расчитана на максимально эффективное выполнение стандартных (в нашем случае базовых операций), и едва ли неструктурированных операции будут оптимизированы лучше базовых.

Теорема. Оптимальное значение параметра c в формуле (1) равно c_opt=MK_B. При этом относительная погрешность оценки не превосходит значения

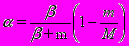(2)

Доказательство.

Найдем, чему равна погрешность:

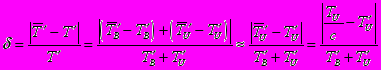
Учтем, что T_U=K_UTў_U и Tў_B=T_B/K_B=T_U???K_B)=Tў_UK_U???K_B), получим:

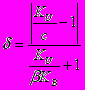
Обозначая x=K_U/K_B , получим окончательно

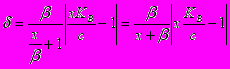
Мы хотим оценить сверху эту погрешность, т.е. найти минимальное ? , при котором существует такое c , что при ?x?[m,M] выполняется неравенство

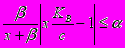
Для решения этой задачи следует рассмотреть три области по c :

1. c?mK_B .

В этой области модуль раскрывается со знаком “+”. Функция, стоящая в левой части неравенства, монотонно возрастает при x?[m,M]. Поэтому для выполнения неравенства при всех x необходимо и достаточно выполнение его при x=M. Получаем:

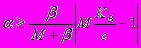
Видно, что минимальное ? тем меньше, чем больше c. Поэтому на данной области c_opt1=mK_B и

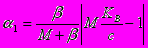
2. mK_B?c?MK_B

В этой области модуль нужно раскрывать два раза с разными знаками. В итоге получим тот же результат: c_opt2=c_opt1, ?₂=?₁ .

3. c?MK_B

Раскрывая модуль и проводя аналогичные рассуждения, получаем c_opt3=MK_B и

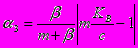
Объединяя результаты рассмотренных случаев и принимая во внимание неравенство

,

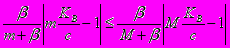получаем утверждение теоремы.

Следствие. При любых значениях T_U, T_B , K_B точность формулы (1), где c=c_opt, не ниже точности оценки

, в которой влияние неструктурированных операций не учитывается.

Это следует из того, что

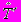является частным случаем (1), где c=?, и, следовательно, дает точность не выше оптимальной.

Из формулы (2) можно также получить максимально допустимое значение ?_max(?), при котором может быть достигнyта требуемая (наперед заданная) точность:

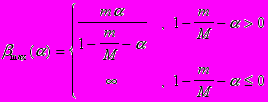
Если окажется, что ?=T_U/T_B>?_max(?), то для достижения требуемой точности ? нужно расширить набор базовых операций {b_i}.

3.Апробация методики для процессора DSP96002 в классе методов цифровой обработки сигналов.

3.1.Выделение базового набора операций.

Набор базовых операций в классе методов цифровой обработки сигналов (ЦОС) ??? выделен при анализе следующих методов[5-18]:

Традиционные методы, основанные на преобразованиях Фурье;
Адаптивные методы:

основанные на непосредственном обращении взамно-спектральных/корреляционных матриц (ВСМ);
максимума энтропии и авторегресси;
градиентные методы;

3.Методы с высокой разрешающей способностью, основанные на использовании собственных значений и векторов ВСМ и сингулярном разложении ВСМ.

К полученному набору базовых операций сводится в среднем до 96% вычислительной нагрузки методов ЦОС [19-21]. Базовый набор включает следующие группы макропераций (24 операции):

векторно-матричная арифметика;
задачи линейной алгебры;
специализированные операции ЦОС, например, свертка, БПФ и т.п.;
операции сравнения/поиска в массивах.

Для апробации методики, набор базовых операций ??? ???????? до ?????????? набора ???????? :

Скалярное произведение векторов для действительных (R) и комплексных (C) операндов.
Умножение вектора на скаляр для действительных и комплексных операндов.
Поэлементное сложение/умножение векторов для действительных и комплексных операндов.
Внешнее произведение векторов для действительных и комплексных операндов.
Перемножение матриц для действительных и комплексных операндов.
Транспонирование матриц для действительных и комплексных операндов.
Сравнение элементов массива с заданной константой для действительных операндов.

Эти операции были реализованы на языке Си и на ассемблере процессора DSP96002 с учетом его архитектурных особенностей [22]. Поскольку ??????????? ??????? ?????????? ??????, ??? используемый способ размещения данных в памяти оказывает сильное влияние на время выполнения программы, то рассматрились два варианта ?????????? ??????:

все данные, используемые программой, расположены в накристальной памяти или входные данные для программы поступают из порта A, выходные данные выдаются в порт B или входные массивы берутся из разных портов;
входные и выходные данные передаются через один и тот же порт.

3.2.Результаты измерений.

В таблице приведены корректирующие коэффициэнты для набора эталонных программ. Время работы соотвествующей программы на Си было получено ??? на созданной модели процессора DSP96002, ??? и на ??? эмуляторе.

В колонках “N=16”, “N=32”, “N=64”, “N=128”, ??? N ????????? ????? ??????????????? ??????? ??????, первое число показывает время работы программы в тактах процессора, когда ????????? ???? ???????? при помощи компилятора g96k (исходная программа на Си), второе — время работы функционал??? ??????????? ?????????, ?? написанной программистом на ассемблере, третье — отношение первых двух. Поскольку значения времен работы программы на Си, полученные при помощи модели [4] и при использовании эмулятора, совпали для всех операций, ?? в таблице приведено только одно значение (первое число каждой колонки). Последняя колонка таблицы показывает отношение времен работы при N®Ґ .

Выполнить на эмуляторе перемножение матриц при N=128 за разумное время ????????? не возможным, поэтому соответствующие графы таблицы не заполнены.

	Задачи	N=16	N=32	N=64	N=128	N ®Ґ
1.	Скалярное произведение векторов (R, в одном порту)	174 98 1.775	302 162 1.864	558 290 1.924	1070 546 1.960	2.0
2.	Скалярное произведение векторов (R, в разных портах)	174 64 2.719	302 96 3.146	558 160 3.486	1070 288 3.715	4.0
3.	Скалярное произведение векторов (C, в одном порту)	1402 166 8.446	2682 294 9.122	5242 550 9.531	10362 1062 9.757	10.0
4.	Скалярное произведение векторов (C, в разных портах)	1402 164 8.549	2682 292 9.185	5242 548 9.566	10362 1060 9.775	10.0
5.	Умножение вектора на скаляр (R, исходный вектор и результат в одном порту)	134 94 1.425	230 158 1.456	422 286 1.475	806 542 1.487	1.5
6.	Умножение вектора на скаляр (R, исходный вектор и результат в разных портах)	134 62 2.161	230 94 2.447	422 158 2.671	806 286 2.818	3.0
7.	Умножение вектора на скаляр (C, исходный вектор и результат в одном порту)	1322 164 8.061	2570 292 8.801	5066 548 9.245	10058 1060 9.489	9.5
8.	Умножение вектора на скаляр (C, исходный вектор и результат в разных портах)	1322 164 8.061	2570 292 8.801	5066 548 9.245	10058 1060 9.489	9.5
9.	Поэлементное сложение/умножение векторов (R, исходные векторы и результат в одном порту)	174 128 1.359	302 224 1.348	558 416 1.341	1070 800 1.337	1.33
10.	Поэлементное сложение/умножение векторов (R, исходные векторы в одном порту, результат в другом)	174 96 1.813	302 160 1.888	558 288 1.938	1070 544 1.967	2.0
11.	Поэлементное сложение векторов (C, исходные векторы и результат в одном порту)	872 224 3.893	1672 416 4.019	3272 800 4.090	6472 1568 4.181	4.17
12.	Поэлементное сложение векторов (C, исходные векторы в одном порту, результат в другом)	872 160 5.450	1672 288 5.806	3272 544 6.015	6472 1056 6.129	6.25
13.	Поэлементное умножение векторов (C, исходные векторы и результат в одном порту)	1268 230 5.513	2452 422 5.810	4820 806 5.980	9556 1574 6.071	6.17
14.	Поэлементное умножение векторов (C, исходные векторы в одном порту, результат в другом)	1268 166 7.639	2452 294 8.340	4820 550 8.764	9556 1062 8.998	9.25
15.	Внешнее произведение векторов (R, исходные векторы и результат в одном порту)	5996 1188 5.047	23180 4388 5.283	91340 16932 5.395	362828 66596 5.448	5.5
16.	Внешнее произведение векторов (R, исходные векторы в одном порту, результат в другом)	5996 676 8.870	23180 2340 9.906	91340 8740 10.451	362828 33828 10.726	11.0
17.	Внешнее произведение векторов (C, исходные векторы и результат в одном порту)	20386 2248 9.069	80610 8552 9.426	320866 33448 9.593	1280610 132392 9.673	9.75
18.	Внешнее произведение векторов (C, исходные векторы в одном порту, результат в другом)	20386 2184 9.334	80610 8424 9.570	320866 33192 9.667	1280610 131880 9.710	9.75
19.	Перемножение матриц (R, исходные матрицы в одном порту)	116502 21190 5.498	891318 149862 5.948	6972150 1122982 6.209	-	6.5
20.	Перемножение матриц (R, исходные матрицы в разных портах)	116502 11554 10.083	891318 82214 10.841	6972150 590374 11.810	-	13.0
21.	Перемножение матриц (C, исходные матрицы в одном порту)	425548 39622 10.740	3339276 289126 11.550	26462092 2204326 12.001	-	12.5
22.	Перемножение матриц (C, исходные матрицы в разных портах)	425548 38054 11.183	3339276 282918 11.803	26462092 2179622 12.141	-	12.5
23.	Транспонирование матрицы (R, исходная матрица и результат в одном порту)	4976 1210 4.112	19120 4442 4.304	75056 17050 4.402	297520 66842 4.451	4.5
24.	Транспонирование матрицы (R, исходная матрица и результат в разных портах)	4976 698 7.129	19120 2394 7.987	75056 8858 8.473	297520 34074 8.732	9.0
25.	Транспонирование матрицы (C, исходная матрица и результат в одном порту)	10622 2266 4.688	41662 8602 4.843	165182 33562 4.922	657982 132634 4.961	5.0
26.	Транспонирование матрицы (C, исходная матрица и результат в разных портах)	10622 1242 8.552	41662 4506 9.246	165182 17178 9.616	657982 67098 9.806	10.0

Коэффициенты для операции “сравнение элементов вещественного массива с заданной константой” зависят от данных, поэтому в таблицу не включены. Значения коэффициент? ??? ???? ???????? меняется в интервале [2 ё 3.5].

Корректирующие коэффициенты с ростом размера обрабатываемых массивов сходятся к предельному значению (N®Ґ) и в самом худшем случае уже при N=128 (см. табл.) отклонение не превышает 2,5%.

4.Заключение.

Выполненная работа показала высокую эффективность использования предложенной методики и инструментальных средств, в частности статико-динамического подхода к прогнозированию времени выполнения программ из класса алгоритмов ЦОС на процессоре цифровой обработки сигналов DSP96002. Без погрешности оценивается в среднем 96% вычислительной нагрузки, создаваемой алгоритмами ЦОС. На всем наборе эталонных программ достигнута 100% точность оценки времени выполнения программ на Си (не оптимизированных программ) и время работы модели в среднем на три порядка меньше времени работы эмулятора.

Библиография.

Головкин Б.А. Расчет характеристик и планирование параллельных вычислительных процессов. - М.: Радио и связь, 1983. - 272с.
Смелянский Р.Л. Об инварианте поведения программ//Вестник МГУ, сер.15, Вычисл. матем. и киберн., 1990. - N 4 - С.54-60.

?.?.???????????, ?.?.??????????, ?.?.??????. ?????? ? ???????? ??????????????? ??????? ?????????? ???????????????? ????????.//?????? ??????????????? ?????????????. ???, 1997., N 2.
?????????? ?.?.,???????? ?.?., ?????????? ?.?., ?????? ?.?., ??????? ?.?. ?????????? ??????? ??????????? ???????? ????????? ???????? ?? ?????? ???????-????????????? ???????//? ?????? ????????.
???????????? ???????????? ????? ? ??????????? ????????? ????????/ ??? ???.?.???? - ?.: ????? ? ????? , 1989.
?.?.???????. ?????????? ??????? ????????????? ?????????? ??????? ??????????? ??????? ????????? ?????????? ?????????//?????, 1982., ?.70, N 9, ?.126-139.
Kay S.M. and S.L.Marple Jr." Spektrum Analysis - A Modern -Perspective " Proc.IEEE, vol.69, N 11, Nov.1981, pp.1380-1418.
?.???????, ?.?????. ?????? ? ?????????? ???????? ????????? ????????. - ?.: ???, 1978. - 848?.
???????? ?.?. ??????????? ???????????? ????????? ?????????? ? ???????? ???????? ??????? ??????? ???????????????// ????????????, 1995., N 3, ?.32-36.
??????? ?.,?????? ?. ?????????? ????????? ????????. - ?.: ????? ? ?????, 1989. - 440?.
?.????? ,?.?.??????. ???????????????? ?????? ? ????????? ??????????? ???????? ? ??????? ?????????? ???????//?????, 1987., ?.75, N 11, ???.21-37.
??????. ???????????????-????????? ???????????? ?????? ? ??????? ???????????//?????, 1969., ?.57, N 8, ???.69-79.
?.?.????????. ???????????? ?????? ? ?????? ??????????????? ? ?????????????? ?????????? ???????// ?????,1980, ?.68, N 6, ?.19-32.
G.Beinvenu and L.Kopp. "Source Power Estimation Method -Associated with High Resolution Bearing Estimation," Proc. -ICASSP81, Atlanta, Ga., Mar. 1981, pp. 153-156.
???????? ?.?.,?????? ?.?. ?????????? ???????? ???????. - ?.: ????? ? ?????, 1986. - 448?.
A.M.Vural "Effects of Perturbation on the Perfomance of Optimum/Adaptive Arrays." IEEE Trans., Aerosp. Electron. Syst. Vol. AEC-15. N 1 January 1979. pp.76-87.
W.S.Liget, "Passive Sonar: Fitting Models to Multiple Time Series," Proc. NATO ASI Signal Process., Academic Press, Loughborough, U.K., 1972, pp.327-345.
N.L.Owsley and J.F.Law, "Dominant Mode Power Spectrum Estimation," Proc.ICASSP82, Paris, May 3-5, 1982, pp.775-778.
???????? ?.?. ?????????? ?????????????? ?????????? ???????? ????????? ???????? ? ?????????? ??????????? “???????? ??????”//?????????? ? ????????????, 1994., N12, C.151-162.
???????? ?.?. ????????????? ??????????? ? ??????? ????????? ????????//????????????????, 1997., N 2, ?.67-75.
???????? ?.?. ???????? ?????????? ??????????? ?????????????? ??????, ??????????????? ? ?????? ????? ???????? ????????? ???????? ? ???????? ???????? ???????, ?? ?????? ????????????? ? ?????????? ???????????//??????? ?????????? ?????????????? ??????????, 1993., N8, ?.12-19.
????????? ????????? ???????? Motorola DSP96002. ??????????? ????????????.

Blog

Содержание