Линия тождественных преобразований Практическое занятие №1 Тождественные преобразования алгебраических выражений
| Вид материала | Документы |
СодержаниеВопросы для повторения Практическое занятие №2 Вопросы для повторения Задания для подготовки к занятиям |
- «упаковать», 279.17kb.
- Законы алгебры логики. Преобразование логических выражений, 28.19kb.
- Методические материалы к практическому занятию №2 Практическое занятие в форме дискуссии, 27.01kb.
- Календарно-тематический план (балльно-рейтинговая система, 1 семестр), 58.92kb.
- Лекция Преобразования типов Преобразования типов. Преобразования внутри арифметического, 236.75kb.
- Задача решается за, 14.24kb.
- Правила преобразования элементов и расчетные соотношения для основных видов преобразований., 201.09kb.
- Практикум по Excel Занятие 1 Решение задач прикладной информатики в менеджменте. Практическое, 136.8kb.
- Ерофеев А. Н. 12. 09 практическое занятие, 396.65kb.
- Рабочая программа по математике в 7 классе, 276.85kb.
Линия тождественных преобразований
Практическое занятие №1
Тождественные преобразования алгебраических выражений
Основные цели работы: познакомиться с содержанием линии «Тождественные преобразования алгебраических выражений» в школьном курсе математики и основами методики изучения содержания темы «Тождественные преобразования рациональных выражений»»; рассмотреть пример организации самостоятельной учебно-познавательной деятельности на уроках математики.
Вопросы для повторения:
Блок А (вопросы для контроля и самоконтроля содержательного характера)
1. Какое понятие более общее по отношению к понятию «тождество»?
2. Вычислите без калькулятора: а) 173· 227; б) 592; в)
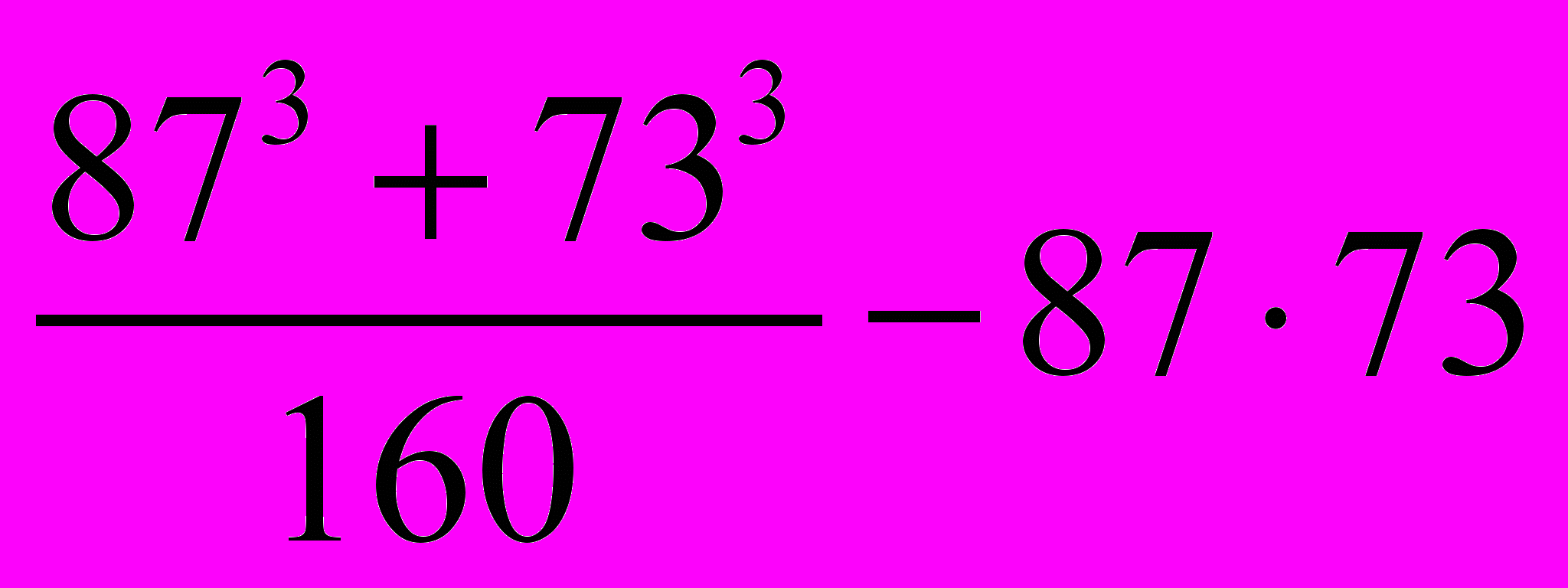 .
. 3. Зная, что
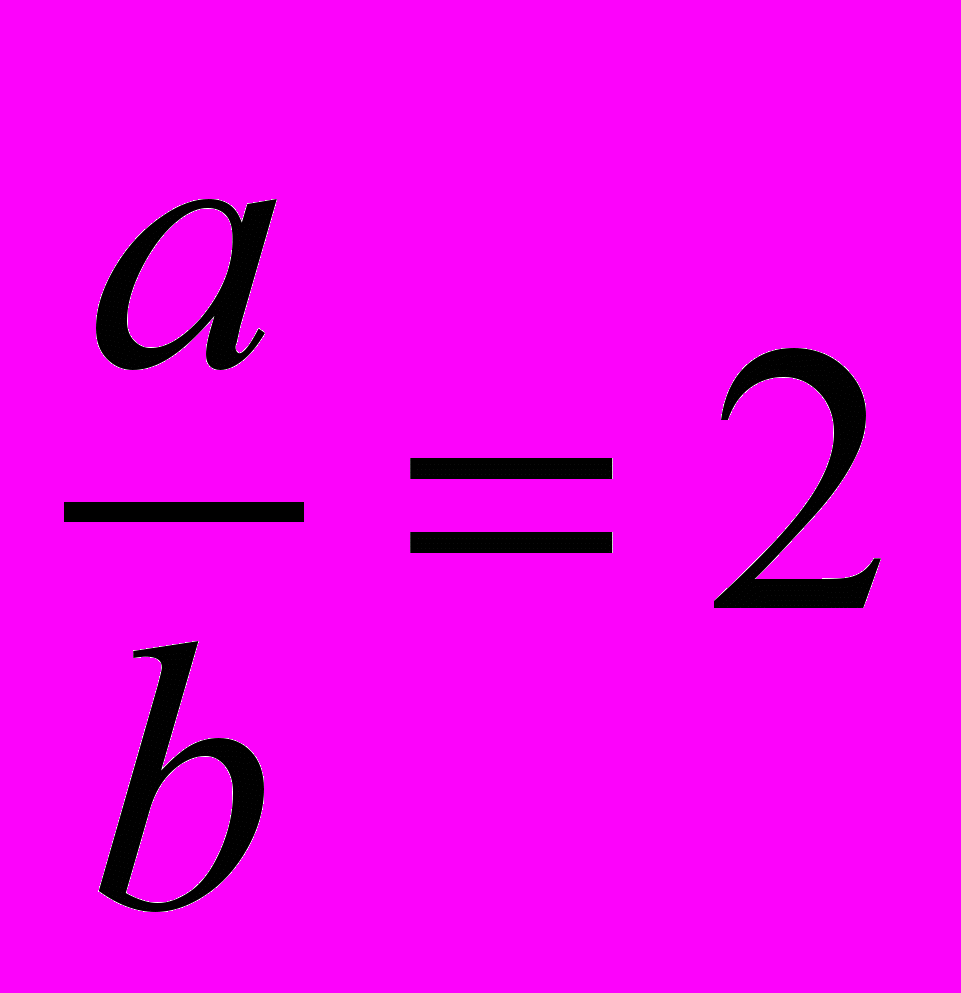 , найдите значение выражения
, найдите значение выражения 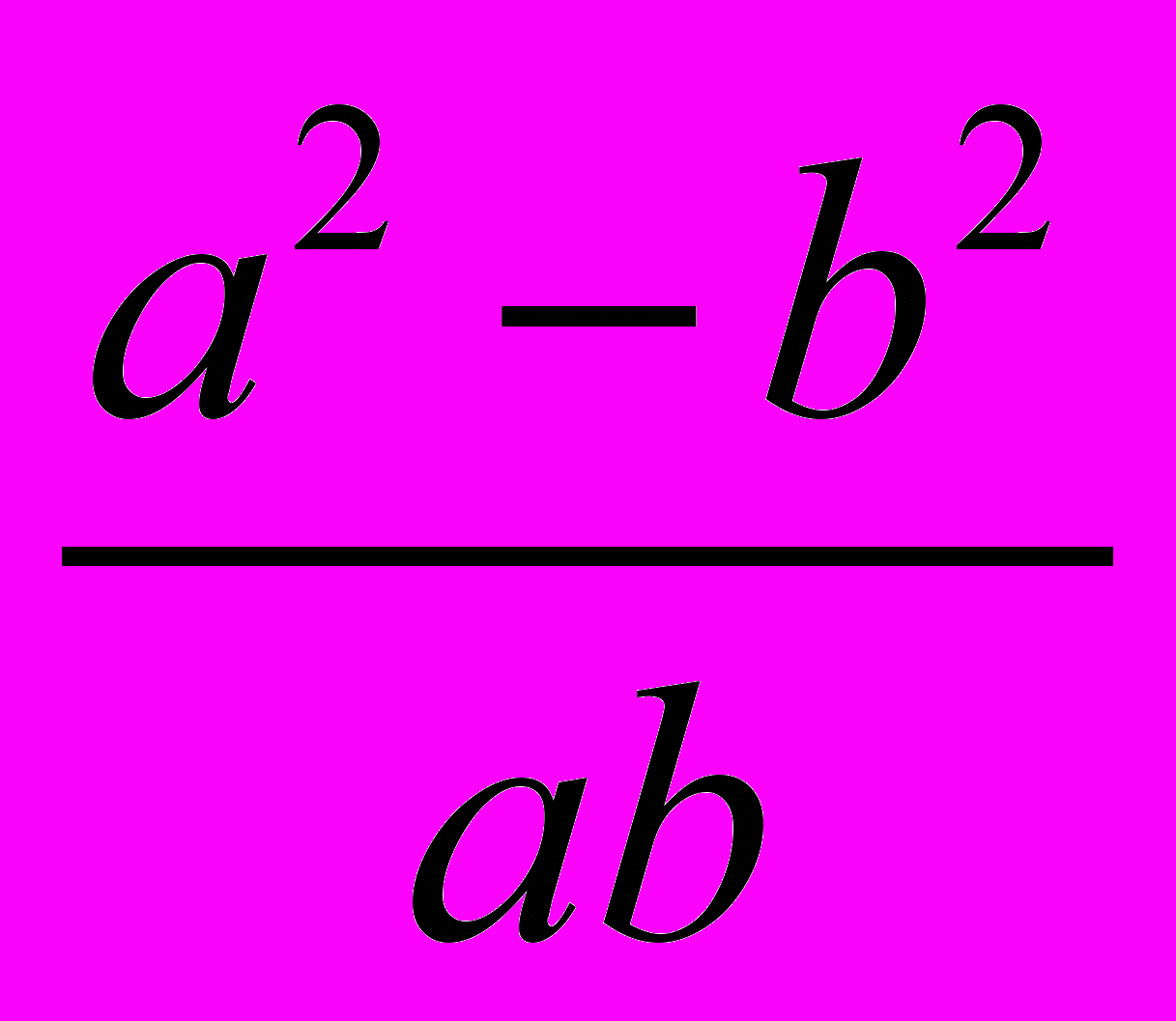 .
.4. Упростите:
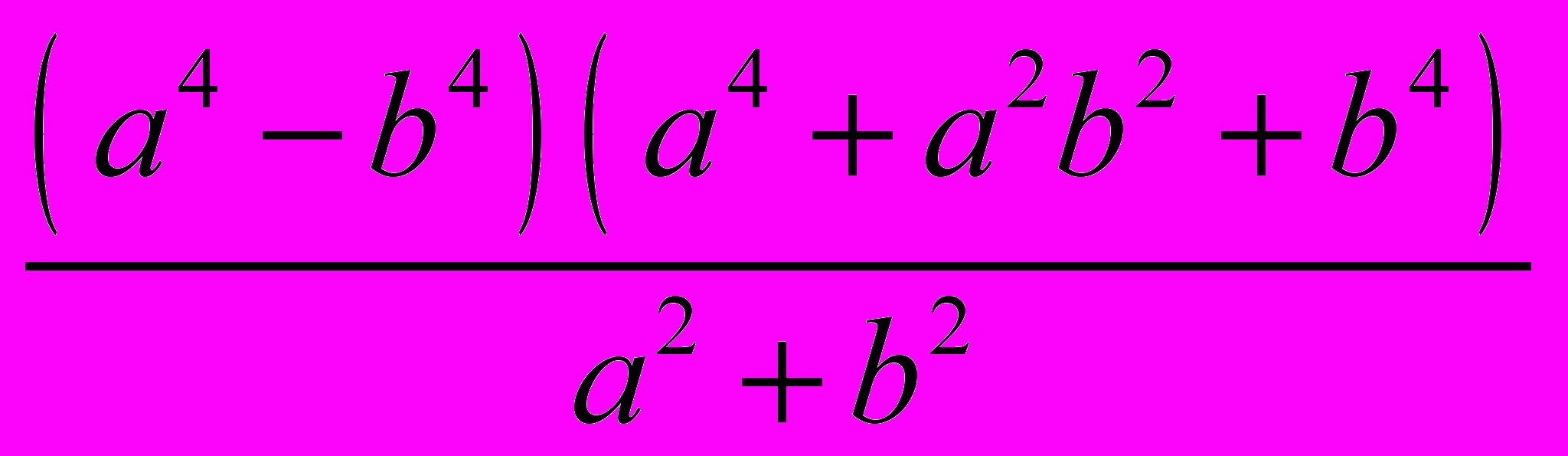 .
. 5. Найдите значения а и
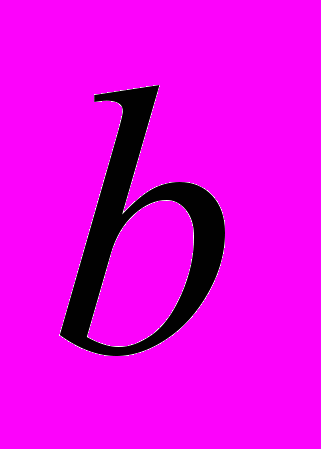 , при которых выполняется равенство:
, при которых выполняется равенство: 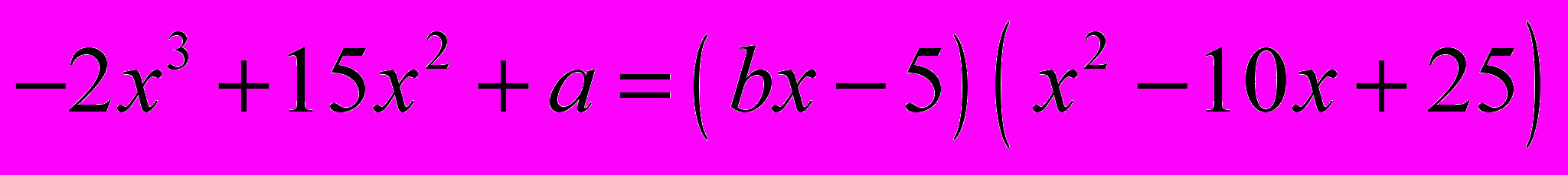 . В ответ запишите сумму а и
. В ответ запишите сумму а и 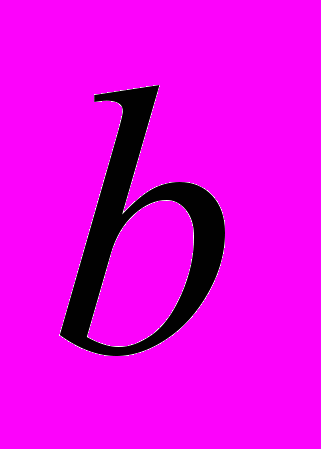 .
. 6. Найдите значение выражения
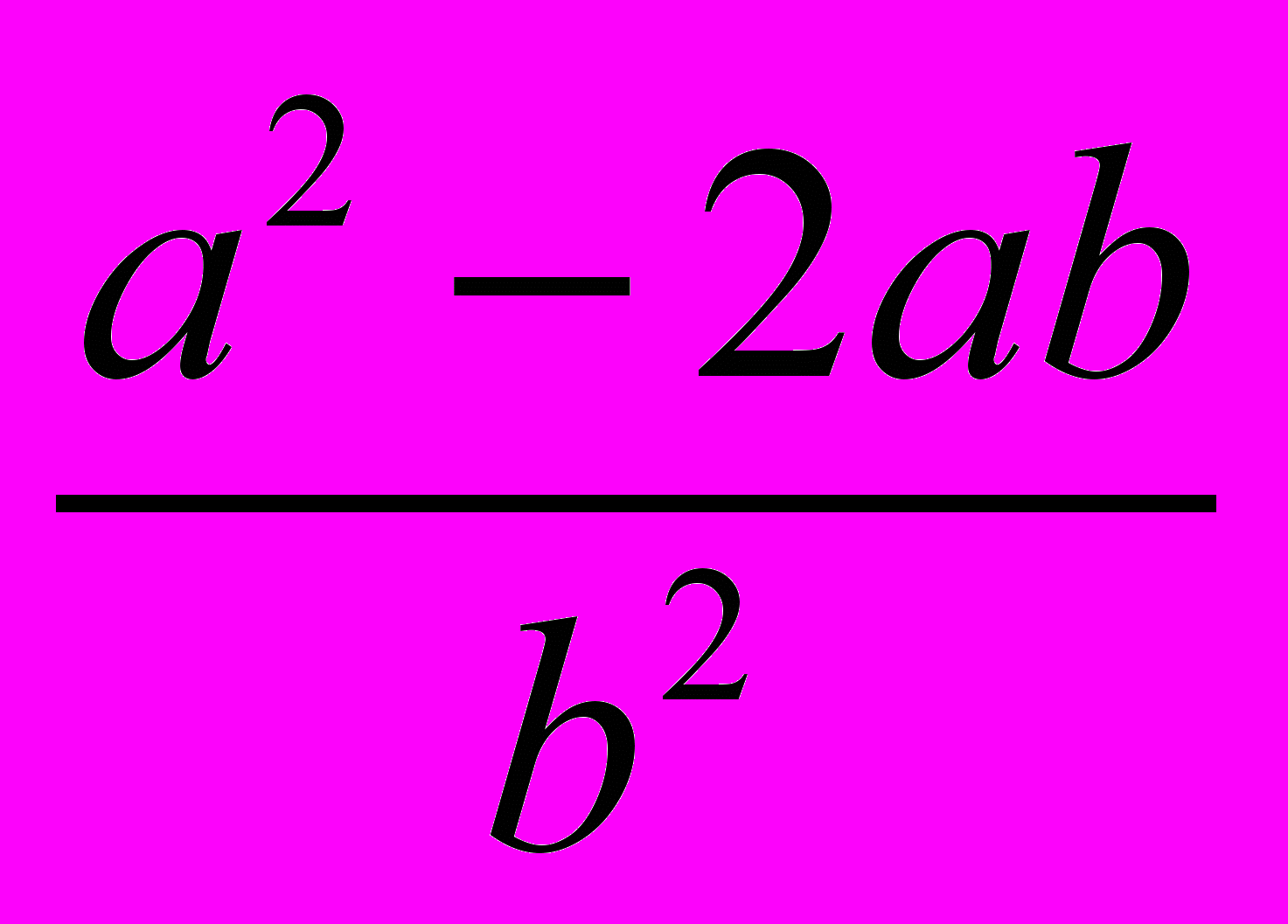 , если известно, что
, если известно, что 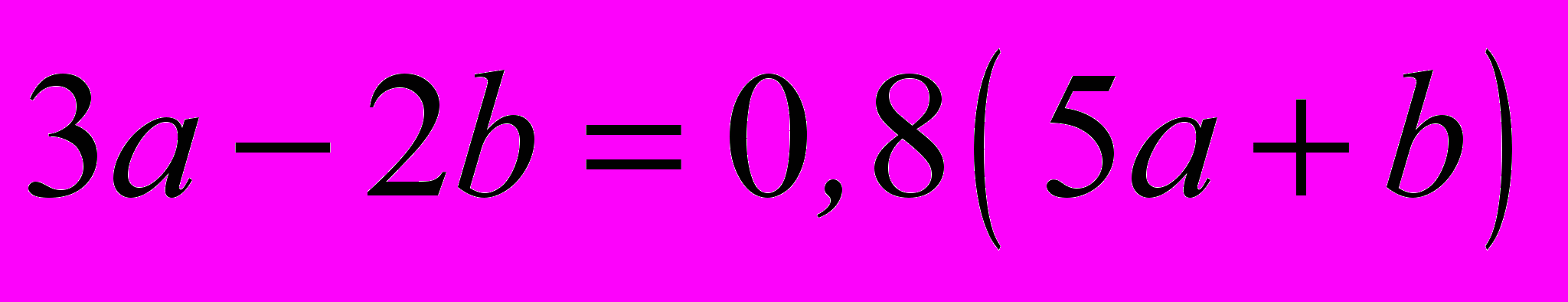 .
.Блок В (вопросы для контроля и самоконтроля методического характера)
1. Имеют ли место взаимосвязи линии тождественных преобразований с другими основными содержательными линиями школьного курса математики? Если да, то с какими? Приведите примеры связей.
2. Перечислите возможные цели обучения линии «Тождественные преобразования».
3. Является ли тождеством равенство
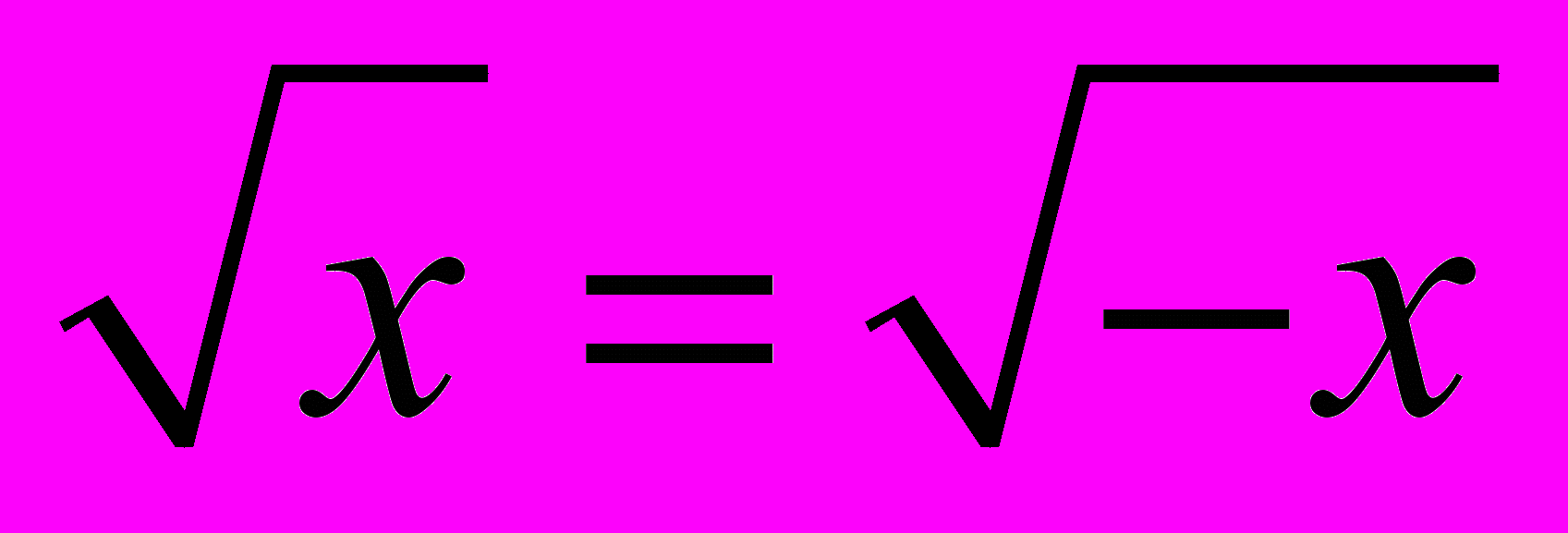 в соответствии с определением в учебнике:
в соответствии с определением в учебнике: а) «Алгебра - 8» Ш.А. Алимова и др.; б) «Алгебра – 9» Ш.А. Алимова и др.?
4. Выполняя задание на упрощение выражения, ученик оформил его так:
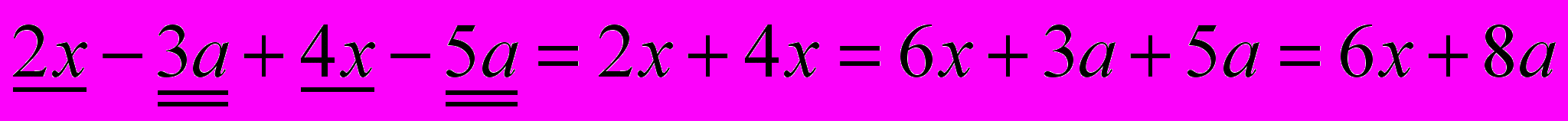 . Какие ошибки допущены? Дайте версию причин их появления.
. Какие ошибки допущены? Дайте версию причин их появления.5. Выделите элементы теории тождественных преобразований, используемые при устном нахождении значения выражения
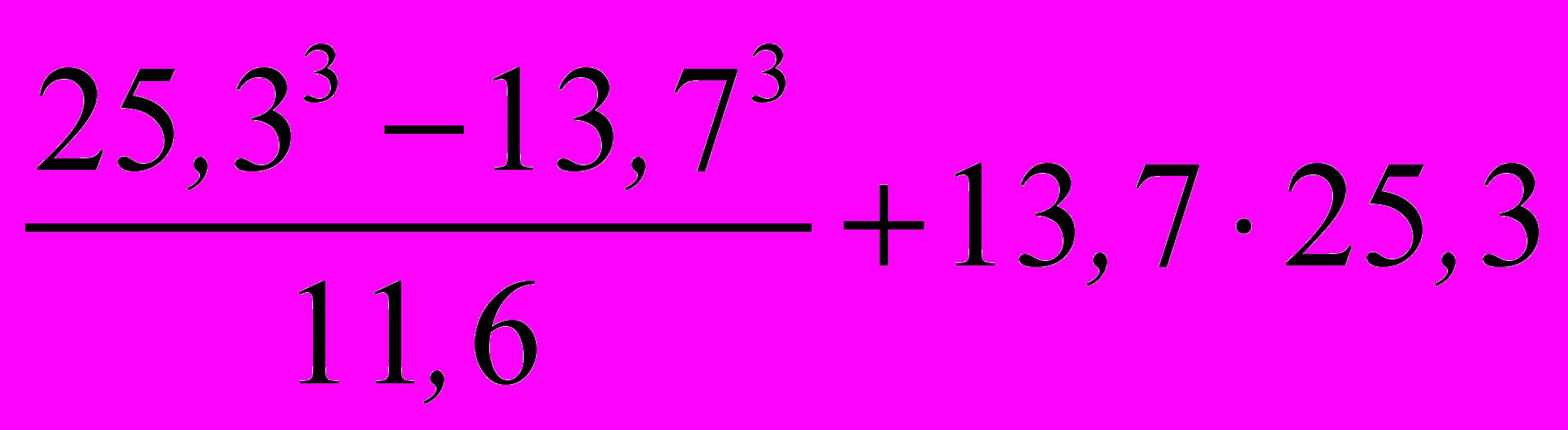 .
.Вопросы для обсуждения на занятии:
1. Этапы введения понятия тождества в курсе алгебры девятилетней школы. Методика введения понятия на каждом этапе (разработка фрагмента урока).
2. Методические особенности изучения темы «Одночлены и многочлены»:
- методика введения понятий;
- методика введения свойств степени с натуральным показателем;
- методика формирования умений и навыков по выполнению действий с одночленами (на примере умножения одночленов).
3. Фрагменты методики обучения теме «Разложение многочленов на множители».
Методика введения способов разложения многочленов на множители, включая применение тождеств сокращенного умножения. При разработке методики исследуйте целесообразность использования базовых знаний учащихся по линии числа; геометрической иллюстрации тождеств сокращенного умножения; разработки алгоритмических предписаний при формировании практических умений на первом этапе обучения.
Дидактические функции и цели проведения самостоятельных работ, требования к их организации, этапы формирования навыка самостоятельной деятельности при обучении новому материалу. Разработайте систему самостоятельных работ обучающего характера по теме.
Система самостоятельных работ по теме обучающего характера.
Система промежуточного и итогового контроля по теме.
4. Варианты разрешения методической ситуации.
Ученики при выполнении преобразований допускают ошибки такого рода: а)
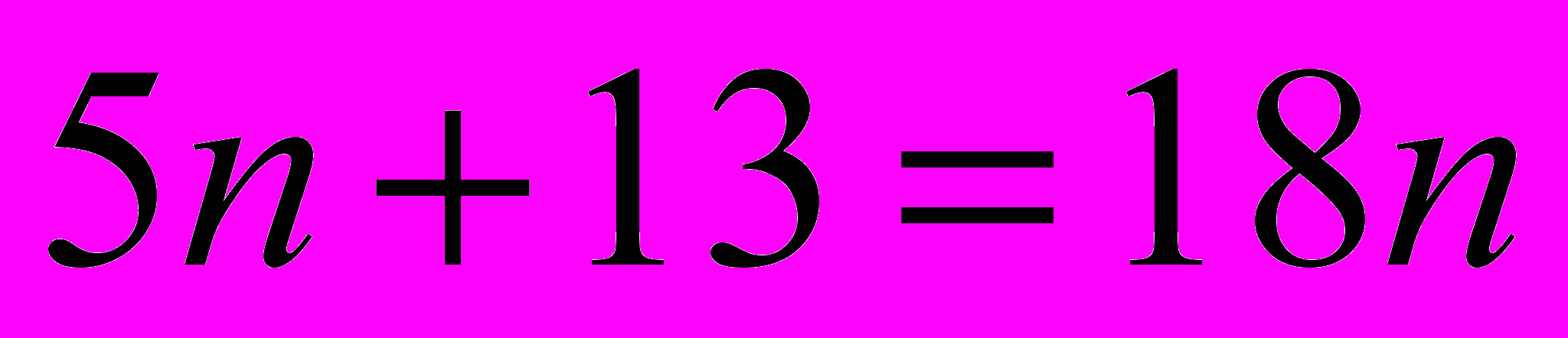 ;
; б)
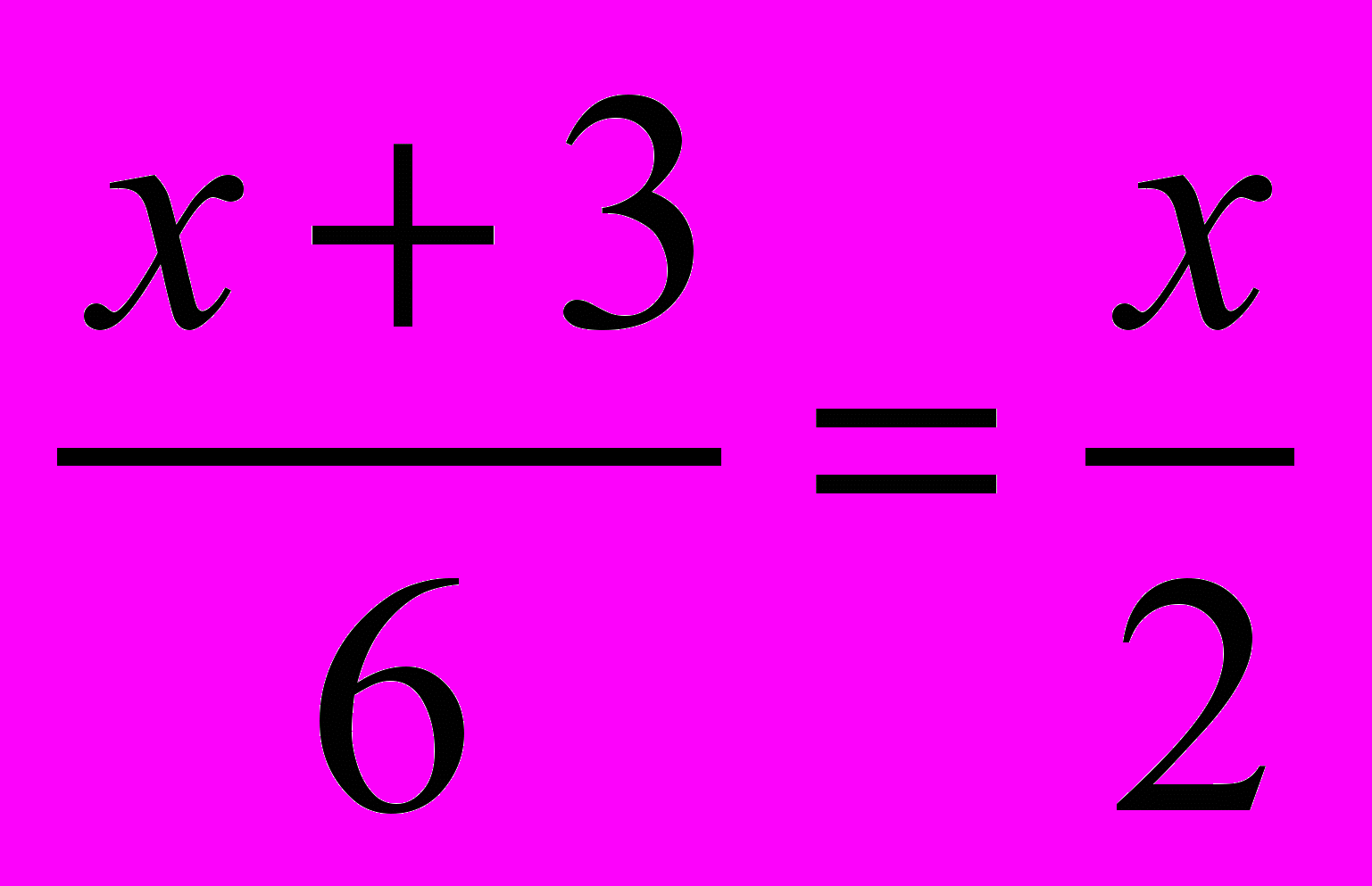 ; в)
; в) 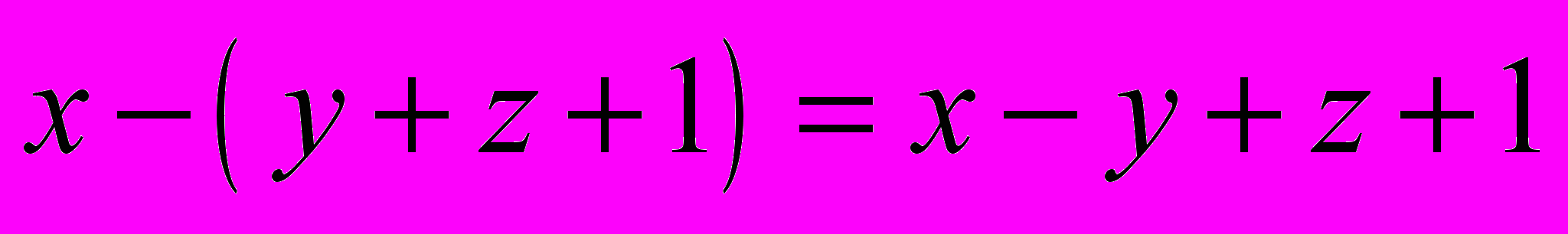 ; г)
; г) 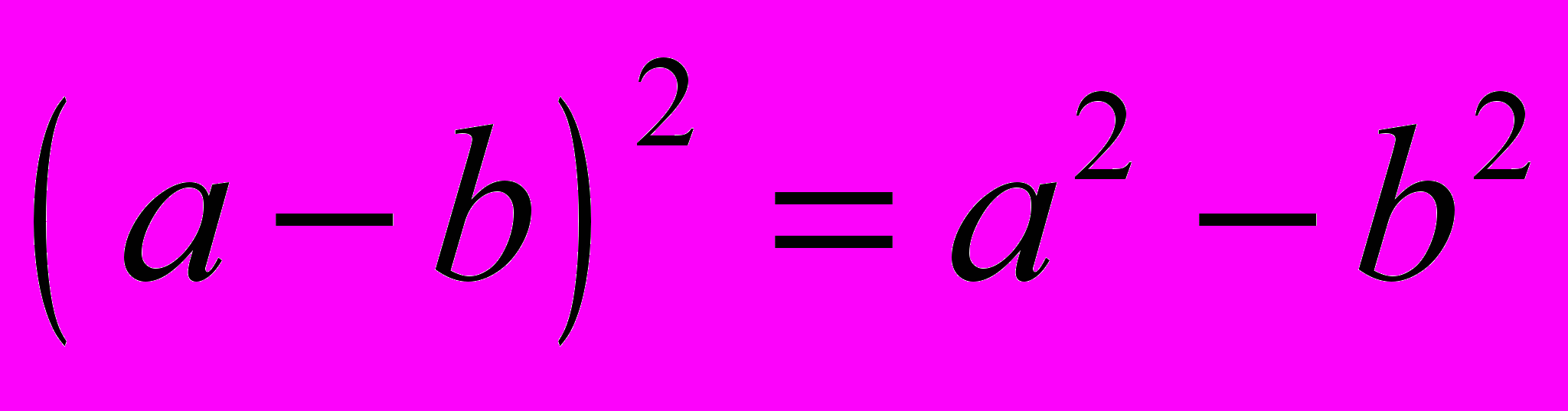 .
. Причины этих ошибок, приемы их исправления. Пути предупреждения ошибок.
Задания для подготовки к занятиям
1. Проследите линию развития учения о тождественных преобразованиях в курсе математики средней школы на основе анализа учебников алгебры и алгебры и начал анализа (в сравнительном плане рассмотрите учебники разных авторских коллективов).
2. Изучите программу по математике для девятилетней школы: содержание темы «Тождественные преобразования рациональных выражений», требования к умениям и навыкам тождественных преобразований рациональных выражений, планирование изучения темы.
3. Исследуйте вопрос о математических основах тождественных преобразований рациональных и дробно-рациональных выражений по курсу математики 7-8 классов.
Дальнейшие задания выполните на основе учебников алгебры под редакцией С.А. Теляковского.
4. Выполните логико-математический анализ теоретического содержания темы «Тождественные преобразования рациональных выражений» и методический анализ задачного материала.
5. Выделите этапы введения понятия тождества в курсе алгебры девятилетней школы. Разработайте методику введения понятия на каждом этапе (разработка фрагмента урока).
Практическое занятие №2
Тождественные преобразования тригонометрических выражений
Основные цели работы: познакомиться с содержанием темы и логикой ее изложения в школьных учебниках; продолжить формирование умения выявлять внутренние и внешние связи изучаемого материала.
Вопросы для повторения:
Блок А (вопросы для контроля и самоконтроля содержательного характера)
1. К какому виду математических выражений относятся тригонометрические выражения?
2. Углом какой четверти является угол
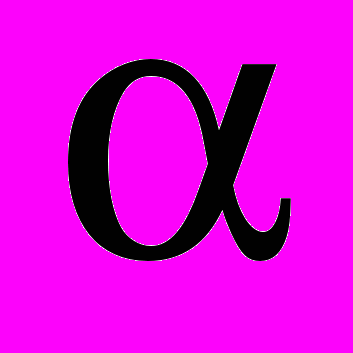 , если: а)
, если: а) 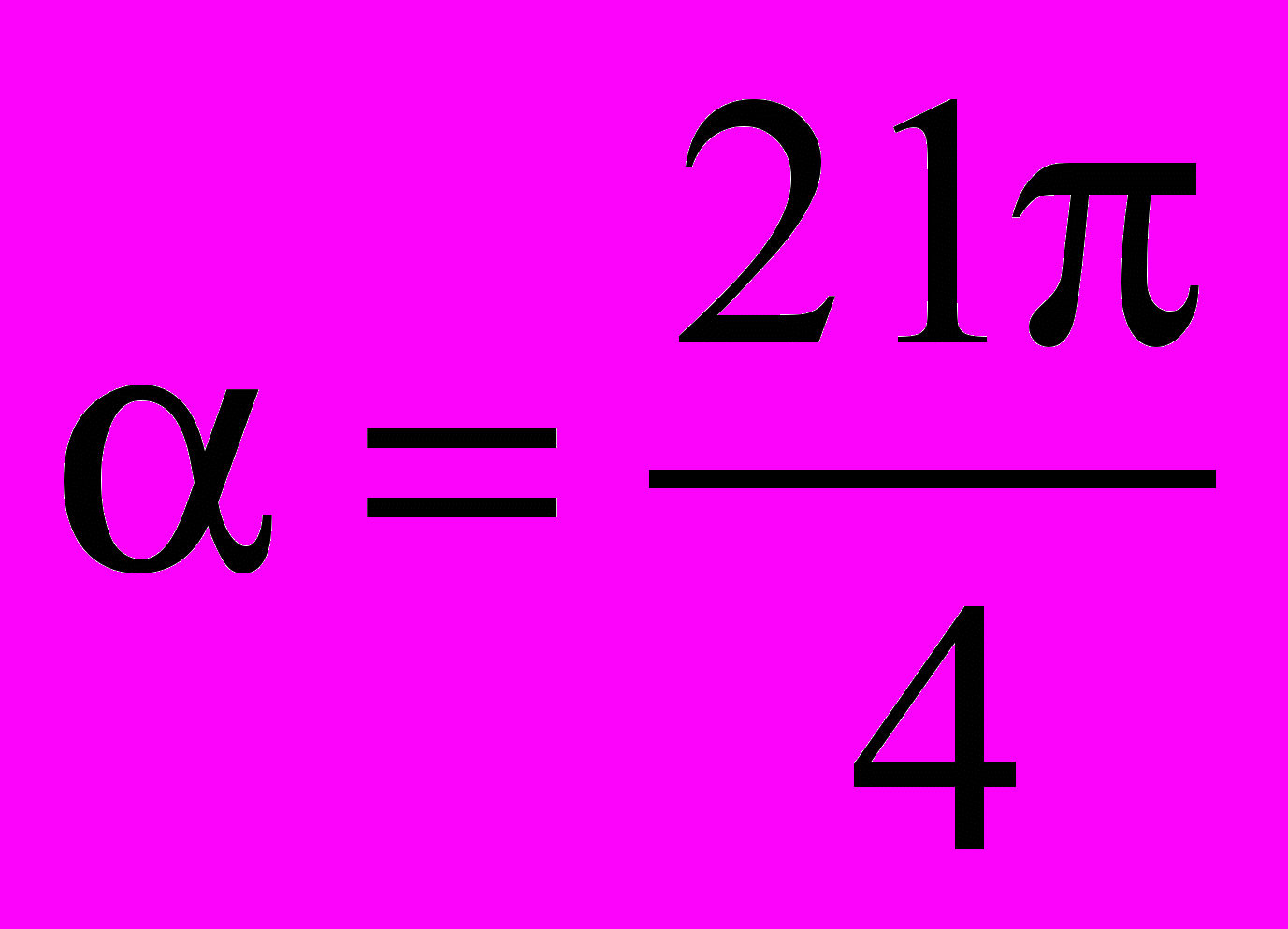 ; б)
; б) 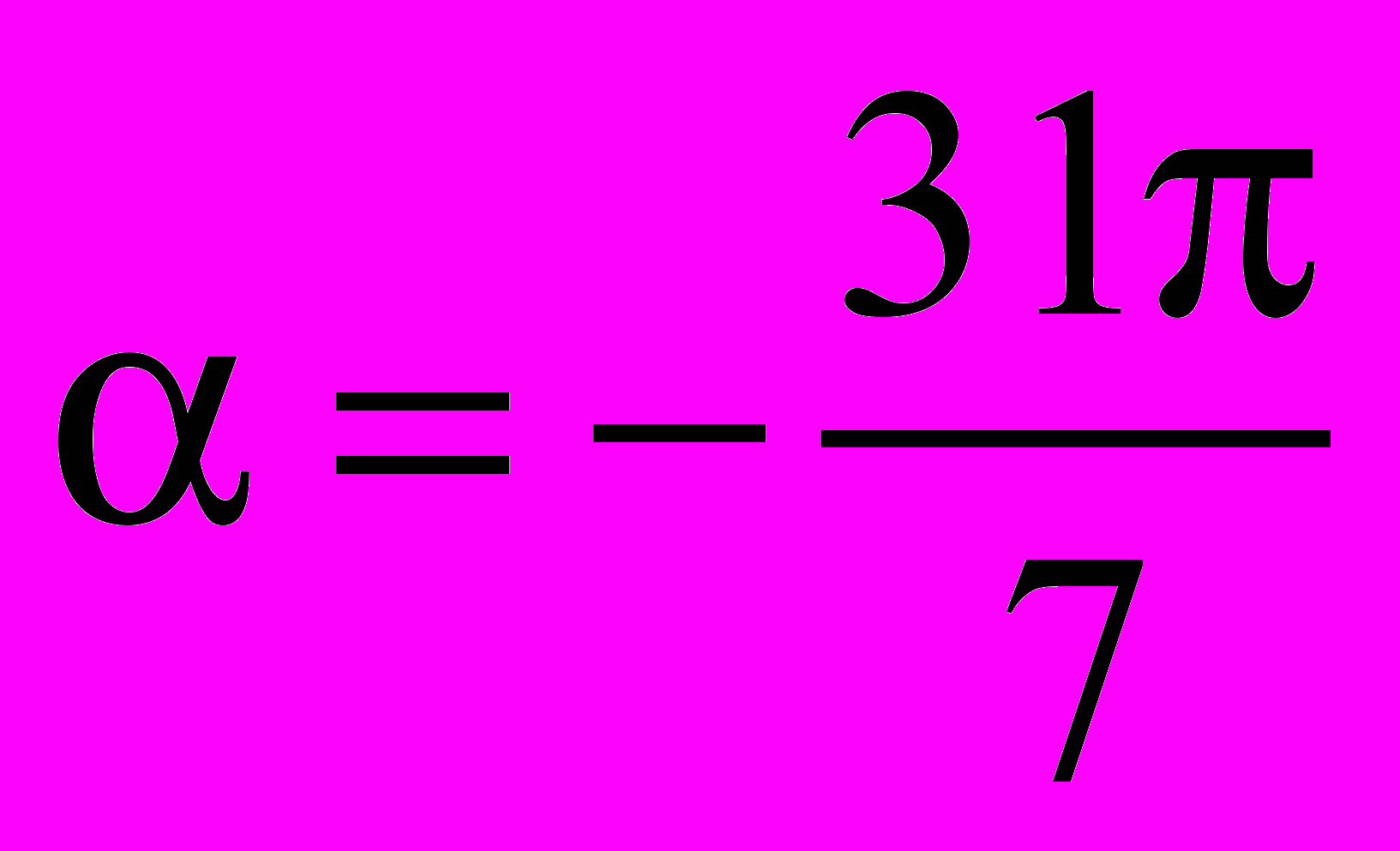 ; в)
; в) 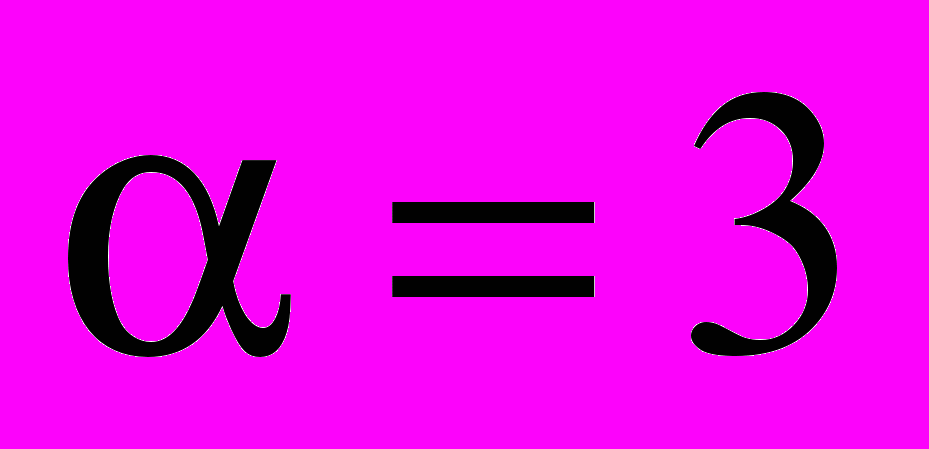 ; г)
; г) 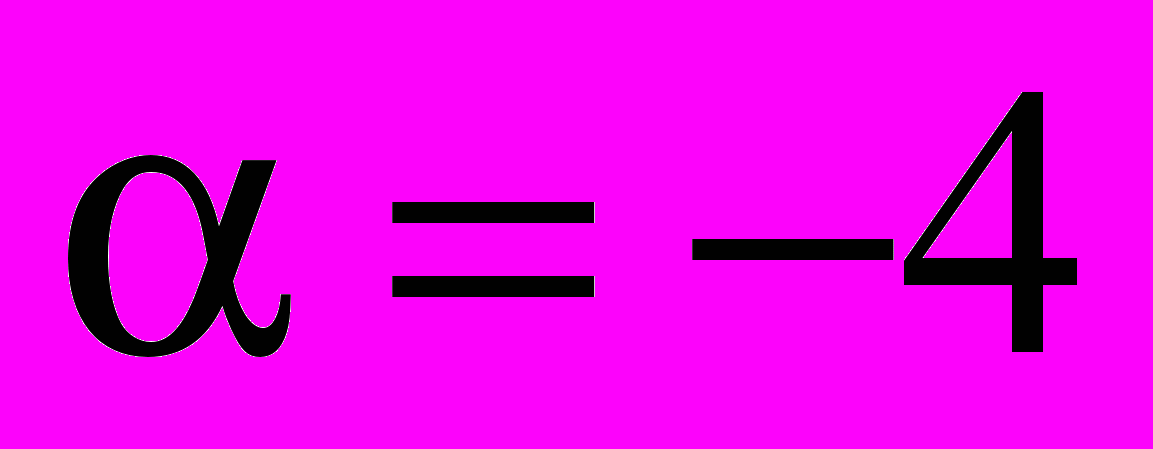 ?
? 3. Определите знак произведения tg 2· sin 3· ctg 5· cos 1.
4. Какой знак имеет произведение sin х· cos х· tg х при: а)
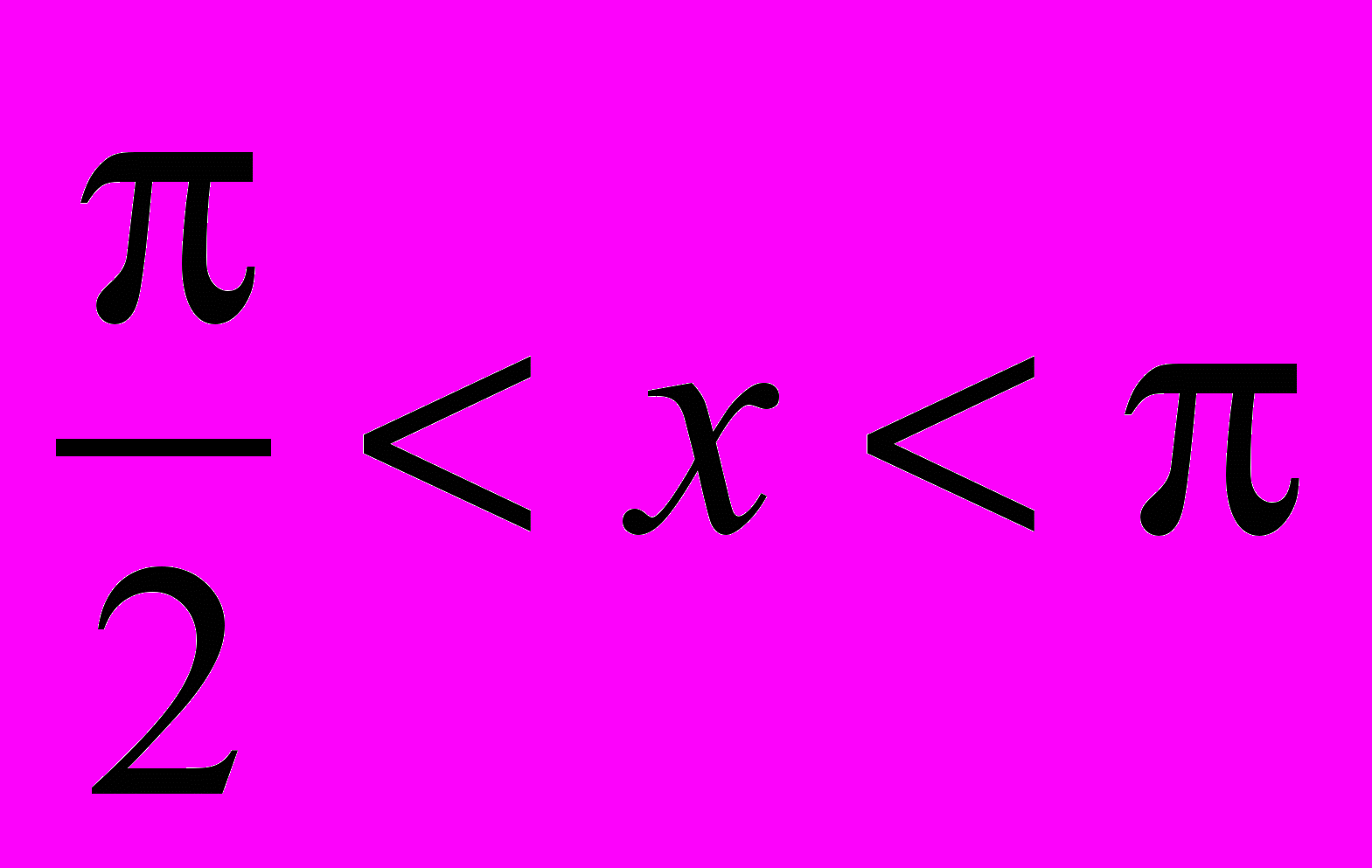 ; б)
; б) 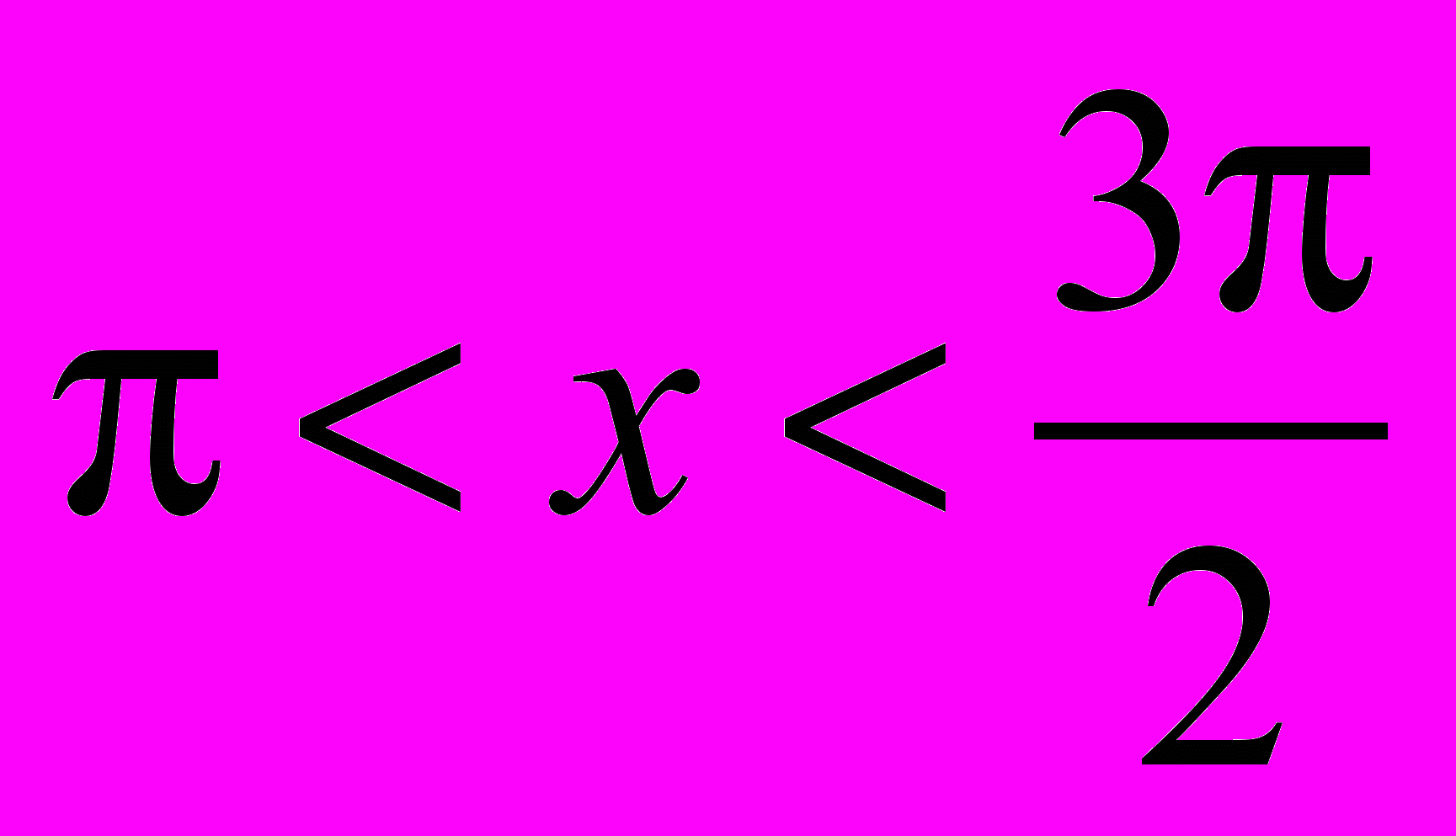 ?
? 5. Существует ли такое значение х, при котором выполняется равенство cos х sin х =
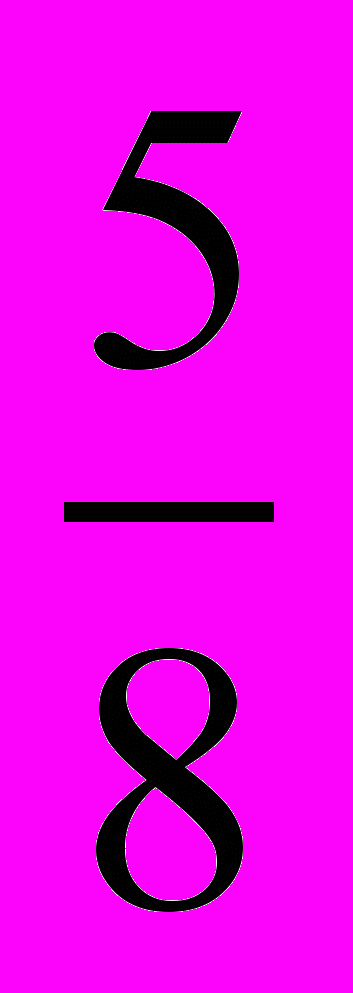 .
. 6. Упростите выражение: а)
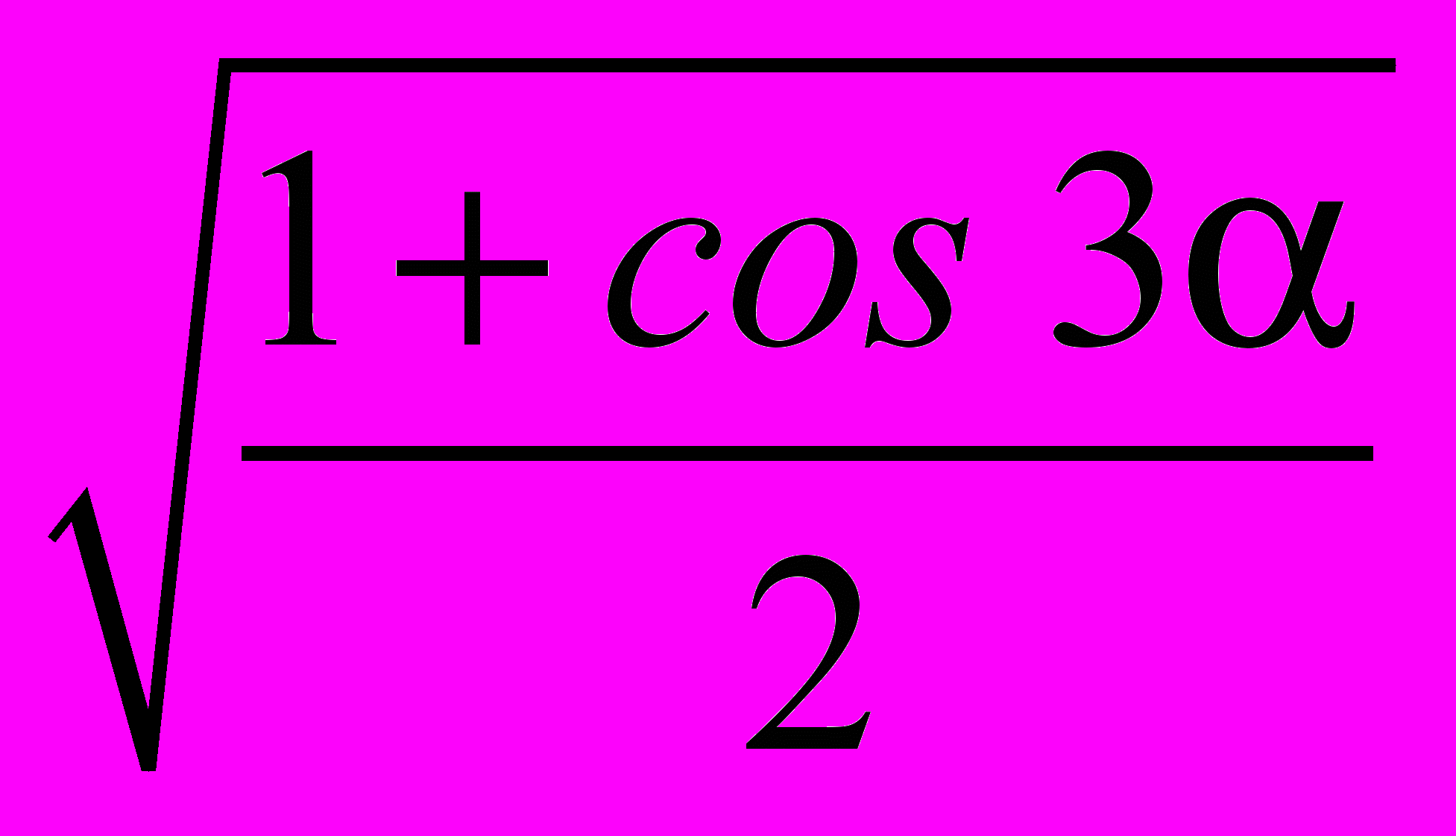 ; б)
; б) 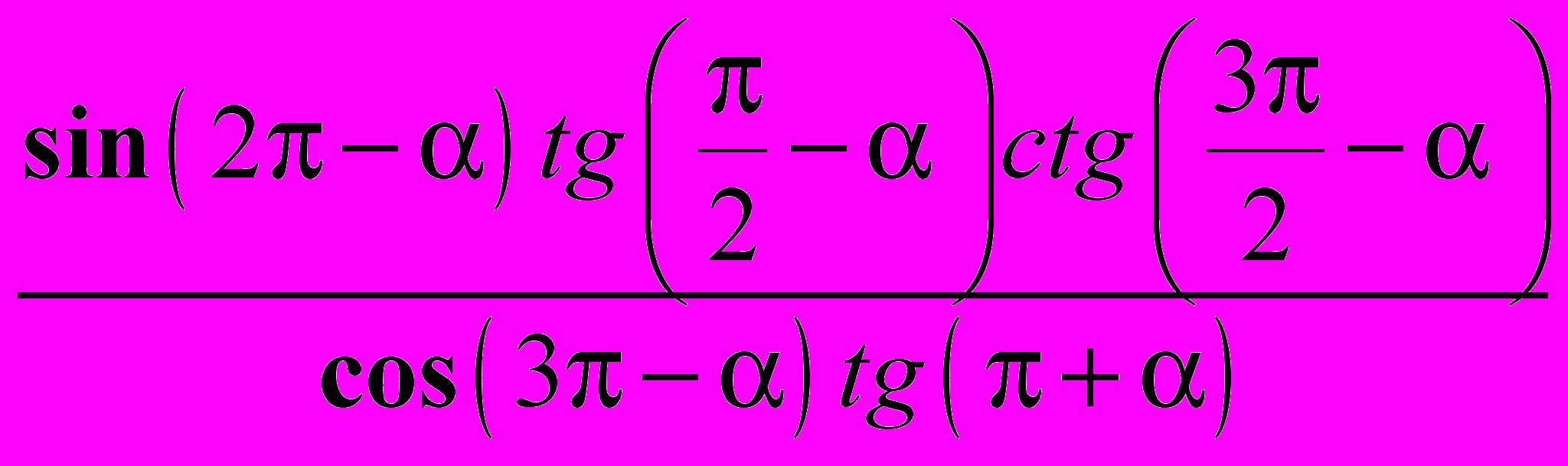
7. Вычислите: а) sin 1350 – sin 450; б) cos 750 + cos 150.
8. Вычислите tg х, если sin
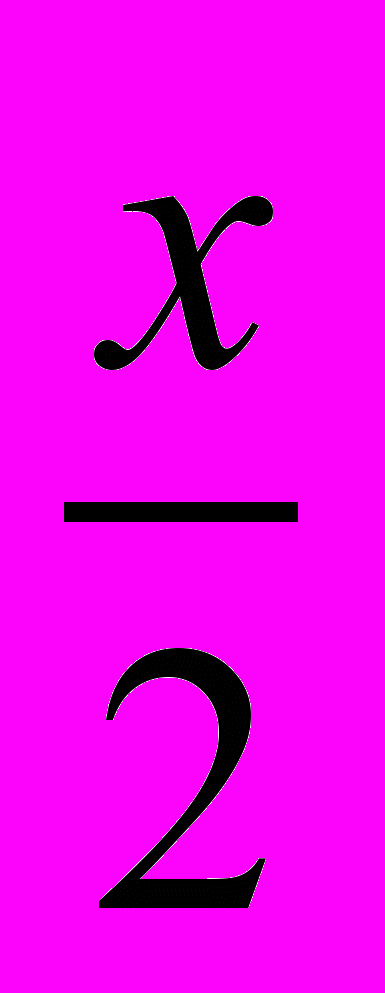 – cos
– cos 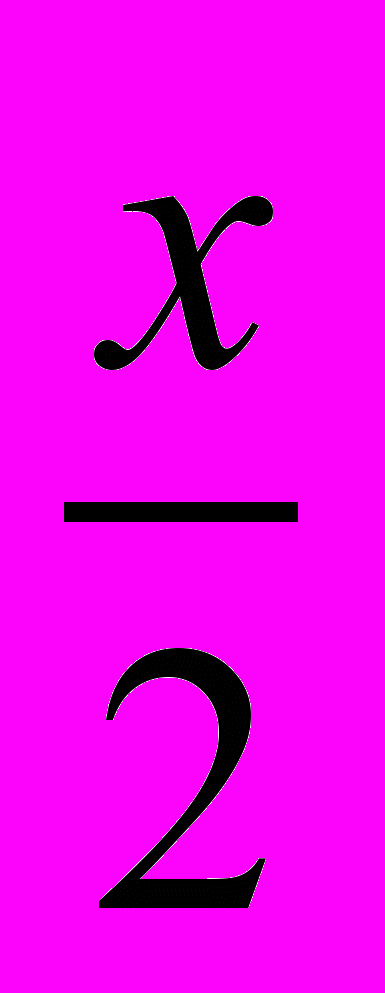 =
= 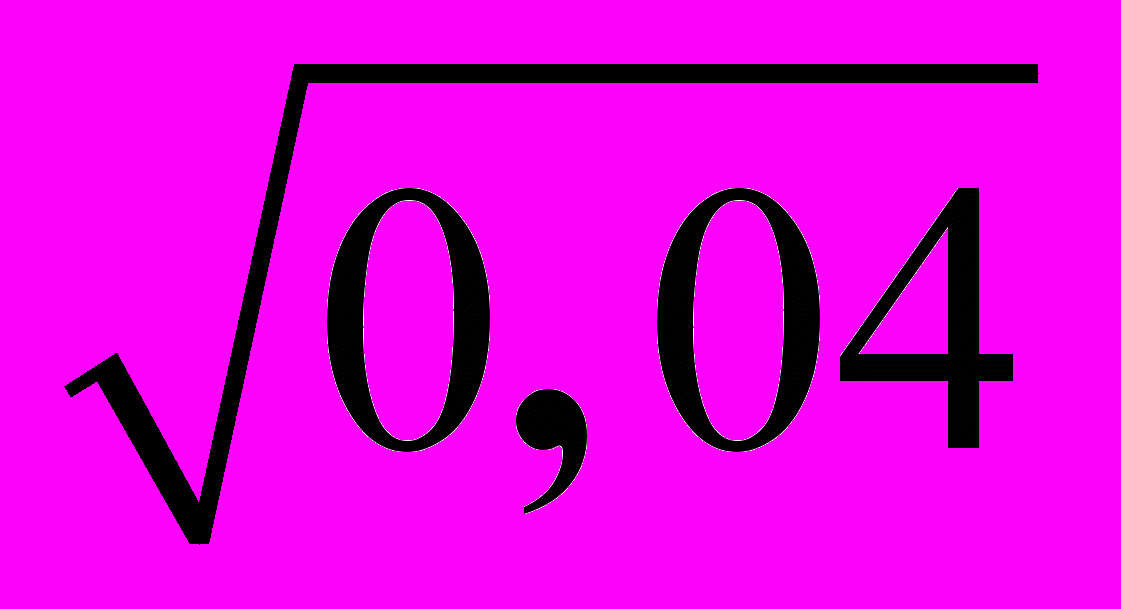 .
.9. Вычислите
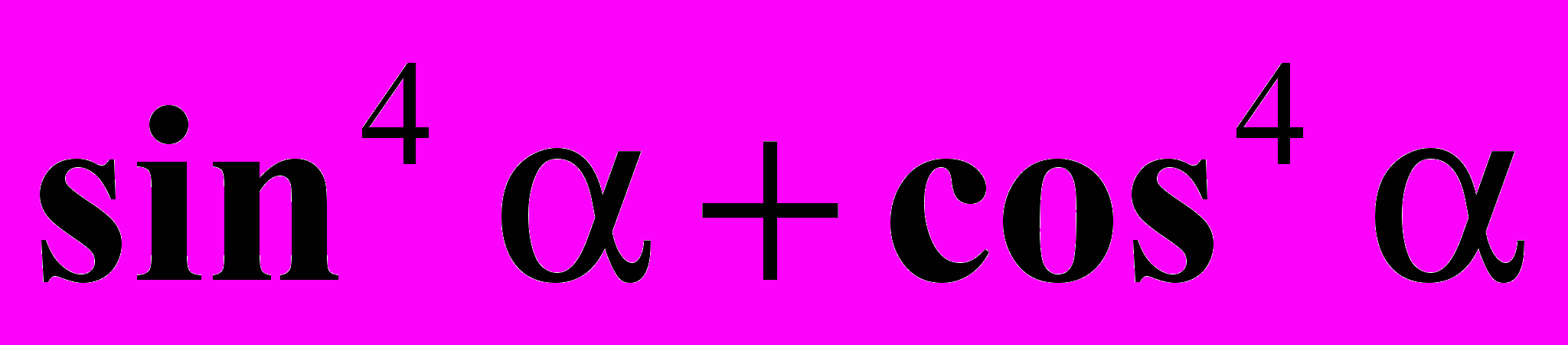 , если
, если 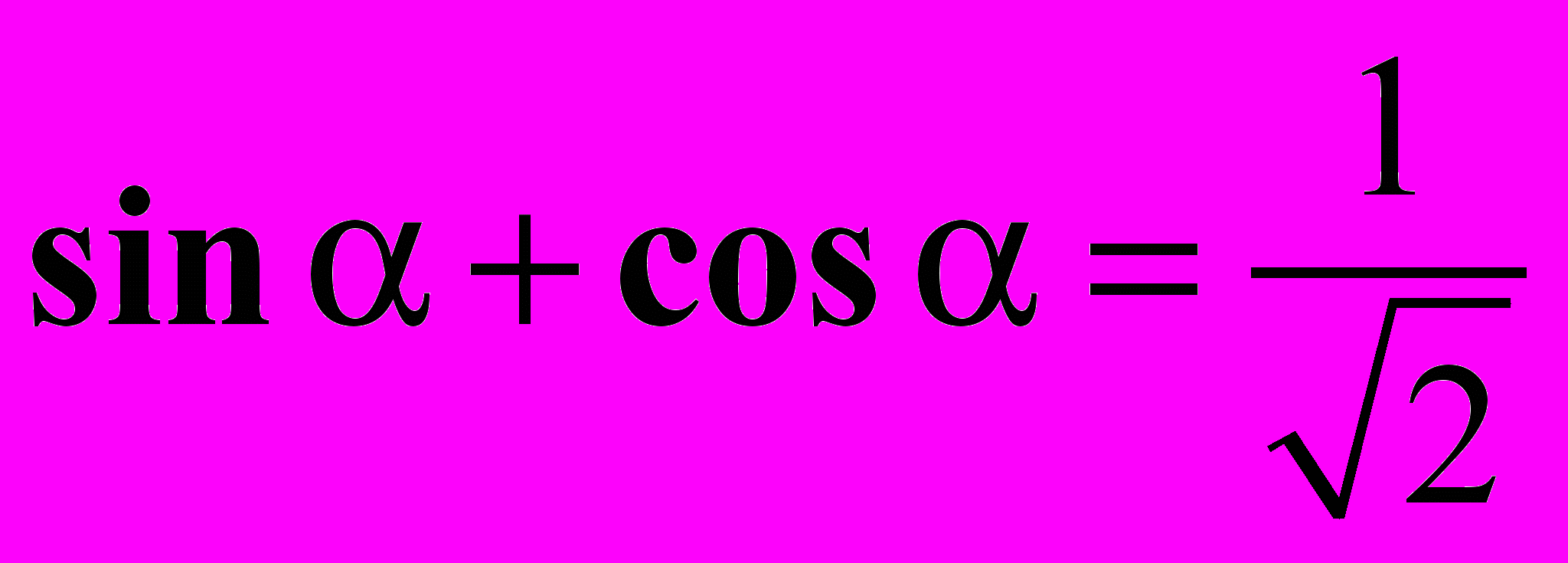 .
. 10. Вычислите
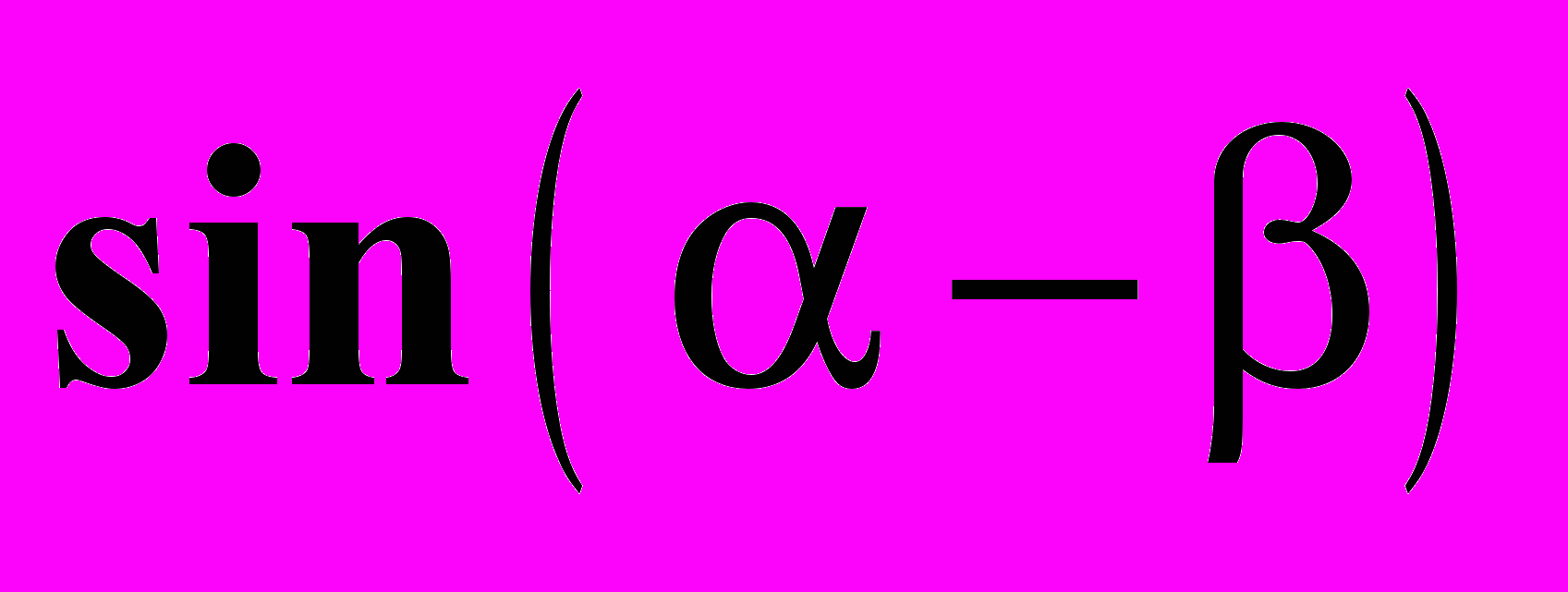 , если
, если 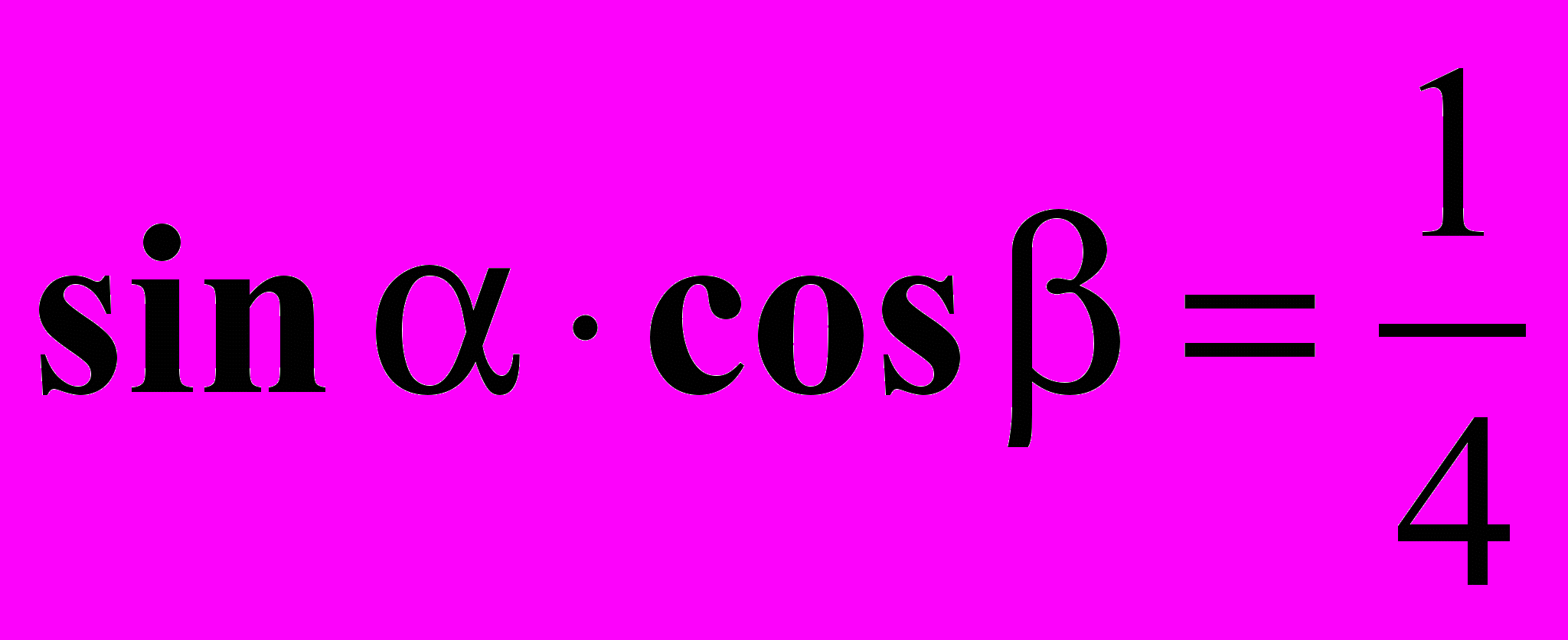 и
и 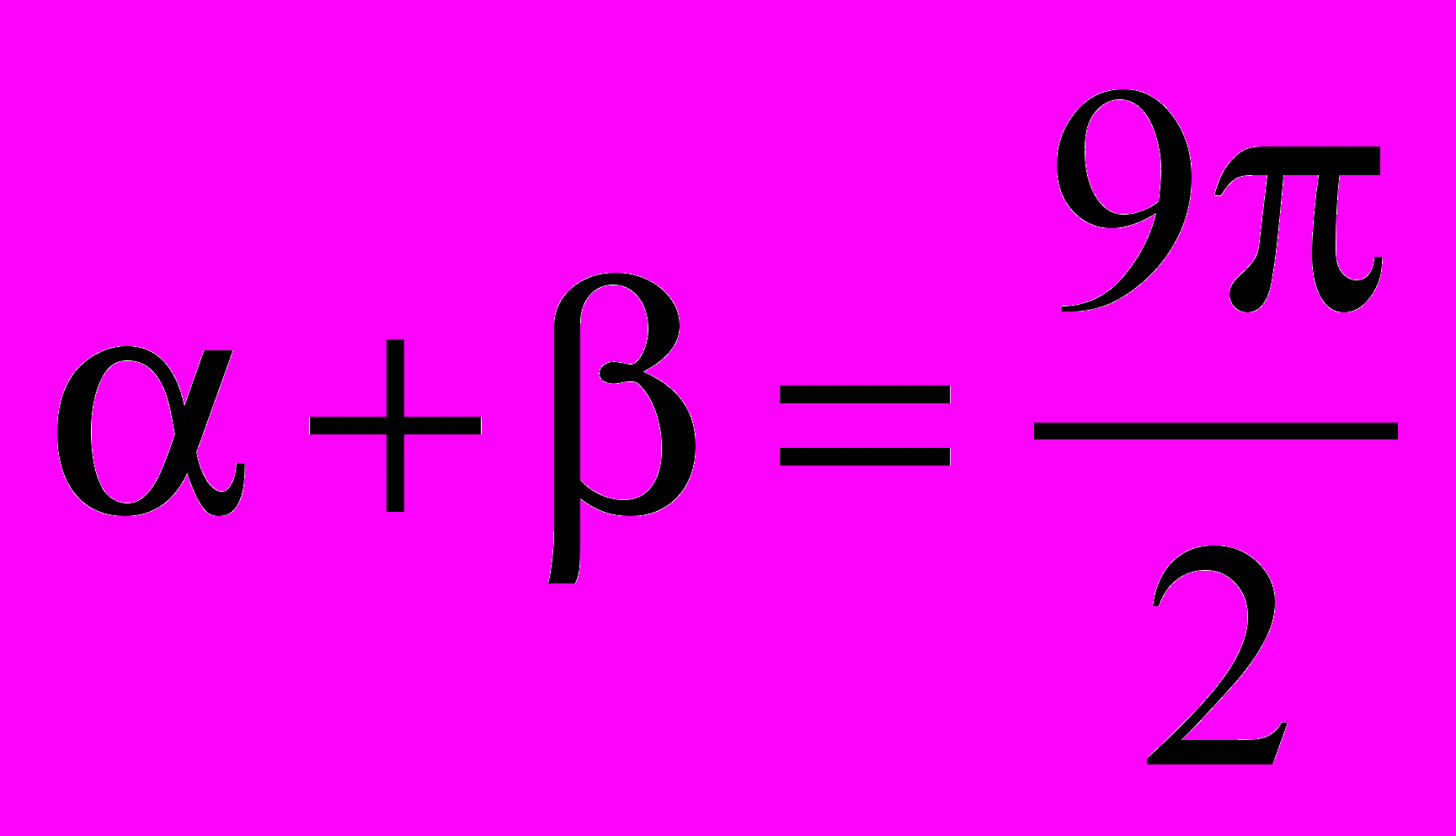 .
.Блок В (вопросы для контроля и самоконтроля методического характера)
1. Цели изучения начального этапа тригонометрии «Тригонометрические выражения и их преобразования» и требования к математической подготовке.
2. Какие ведущие линии школьного курса математики являются базовыми для обучения теме? Приведите конкретные примеры.
3. Найдите все возможные способы решения задачи. В каждом способе выделите математическую основу и умения, которыми должен владеть учащийся, чтобы задача была успешно решена.
Задача. Известно, что
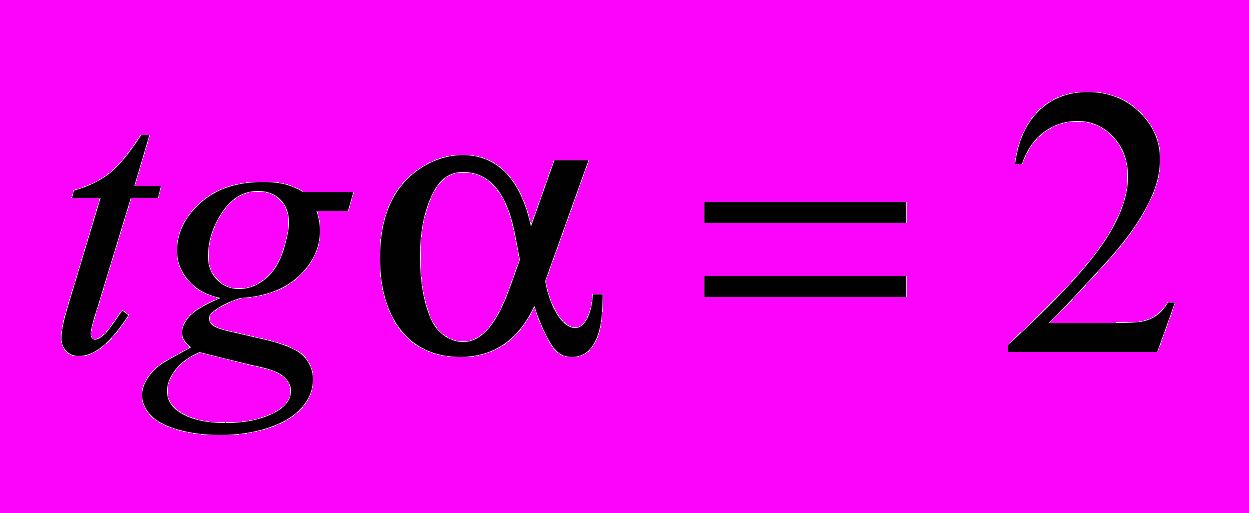 . Найдите значение выражения
. Найдите значение выражения 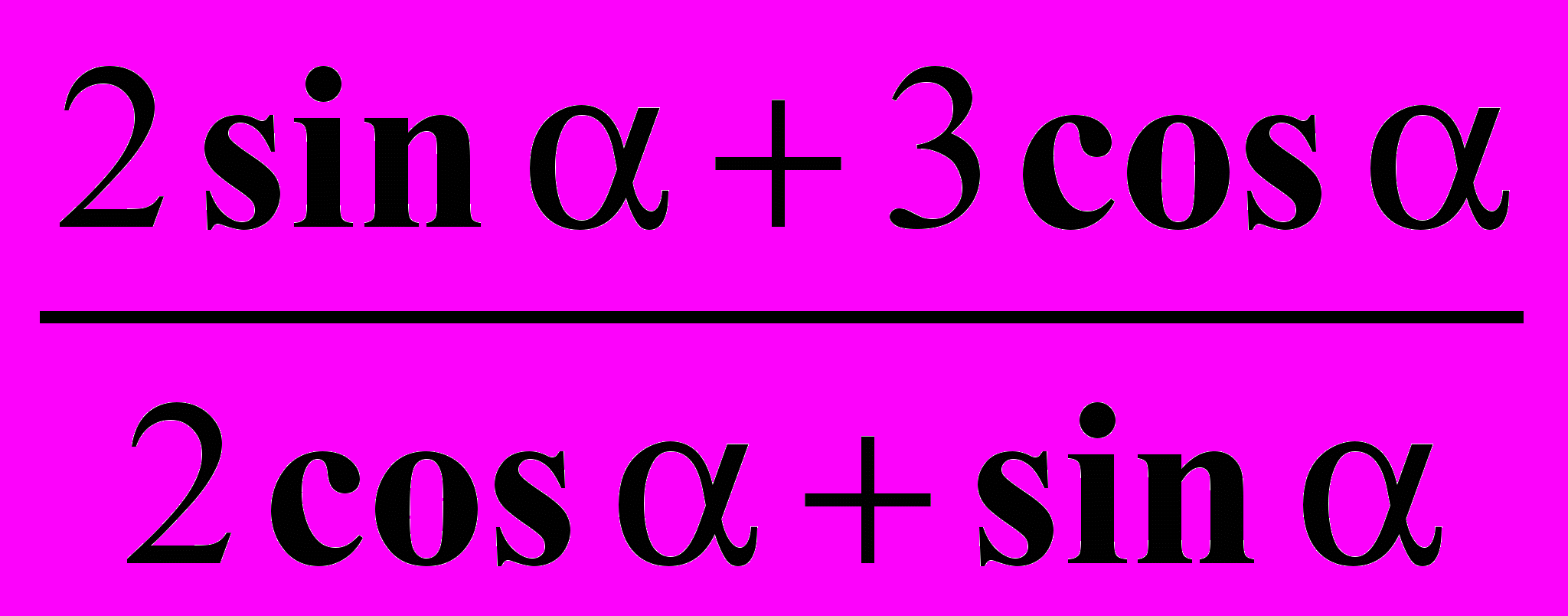 .
.Вопросы для обсуждения на занятии:
1. Содержание темы и логика его изложения в учебниках разных авторских коллективов.
2. Вводная диагностическая работа (цель, содержание, функции задач, критерии оценки).
3. Вариант методики обучения:
- формулам приведения;
- теоремам сложения.
4. Вариант построения системы теоретических знаний по теме с ориентацией на решение задач.
5. Тригонометрический круг – средство формирования пропедевтических знаний по курсу тригонометрии.
6. Система задач, выполняющих пропедевтические функции по функциональной линии и линии уравнений и неравенств.
Задания для подготовки к занятиям
1. Сформулируйте цели начального этапа изучения тригонометрии «Тригонометрические выражения и их преобразования» и требования к математической подготовке (по программе по математике для общеобразовательных учреждений).
2. Познакомьтесь с содержанием темы и логикой его изложения в учебниках разных авторских коллективов.
3. Какие ведущие линии школьного курса математики являются базовыми для обучения теме? Приведите конкретные примеры.
4. Разработайте вариант вводной диагностической работы, цель которой – актуализация базовых знании и определение степени готовности учащихся к изучению новой темы.
5. Продумайте вариант построения системы теоретических знаний по теме с ориентацией на решение задач. Установите связи между элементами этой системы.
4. Определите роль тригонометрического круга при обучении теме. Сформулируйте определение тригонометрического круга, исследуйте возможность использования тригонометрического круга в формировании пропедевтических знании по тригонометрии (линии функции, уравнений и неравенств). Разработайте систему задач, выполняющих пропедевтические функции по выделенным линиям.
