Предисловие
| Вид материала | Документы |
- Содержание предисловие 3 Введение, 2760.07kb.
- Томас Гэд предисловие Ричарда Брэнсона 4d брэндинг, 3576.37kb.
- Электронная библиотека студента Православного Гуманитарного Университета, 3857.93kb.
- Е. А. Стребелева предисловие,, 1788.12kb.
- Breach Science Publishers». Предисловие. [3] Мне доставляет удовольствие написать предисловие, 3612.65kb.
- Том Хорнер. Все о бультерьерах Предисловие, 3218.12kb.
- Предисловие предисловие petro-canada. Beyond today’s standards, 9127.08kb.
- Библейское понимание лидерства Предисловие, 2249.81kb.
- Перевод с английского А. Н. Нестеренко Предисловие и научное редактирование, 2459.72kb.
- Тесты, 4412.42kb.
Знакомство с составной задачей.
При знакомстве с составной задачей могут быть использованы различные методические приемы:
1. Рассмотрение двух простых задач с последующим объединением их
в составную.
Например:
Задача 1. Ежик нашел 2 белых гриба и 4 подосиновика. Сколько он нашел грибов?
2 + 4 = 6 (гр.)
Задача 2. Ежик нашел 6 грибов. 3 гриба он отдал белочке. Сколько грибов у него осталось?
6-3 = 3 (гр.)
Педагог рассматривает с детьми оба текста простых задач, предлагая определить, чем они похожи и чем отличаются. Затем предлагает объединить оба сюжета в одном тексте, получая таким образом составную задачу:
Задача 3. Ежик нашел 2 белых гриба и 4 подосиновика. 3 гриба он отдал белочке. Сколько грибов у него осталось?
1)2 + 4 = 6(гр.)
2)6 - 3 = 3 (гр.)
2. Рассмотрение простой задачи с последующим преобразованием ее в составную путем изменения ее вопроса.
Например:
Задача. Столяр сделал 8 книжных полок, а кухонных - на 3 меньше. Сколько кухонных полок сделал столяр?
После решения задачи учитель предлагает детям ответить на второй вопрос по тому же условию: «Сколько всего полок сделал столяр?»
Далее, сравнивая ответы на оба вопроса, устанавливают их иерархию (необходимую последовательность), приходя к выводу, что постановка второго вопроса («Сколько всего полок было сделано?») требует сначала ответить на первый вопрос («Сколько было сделано кухонных полок?»).
3. Прием рассмотрения сюжета с действием, рассредоточенным во времени.
Например:
Задача. В автобусе было 6 пассажиров. На первой остановке вошли 4 пассажира, а на второй - еще 1. Сколько пассажиров стало в автобусе?
При анализе текста педагог обращает внимание учащихся на то, что входили и выходили пассажиры не одновременно, а на разных остановках. Поэтому для ответа на вопрос задачи нужно выполнить два действия:
1) 6 + 4 = 10 (п.)
2)10 + 1 = 11 (п.)
После того как задача будет решена, полезно сравнить ее с простой задачей:
В автобусе было 6 пассажиров, на остановке вошло еще 5. Сколько пассажиров стало в автобусе?
Педагог предлагает отметить в каждом из условий те предложения, которыми отличаются тексты рассматриваемых задач. После ее решения можно обсудить вопрос: почему в той и в другой задаче получены одинаковые ответы.
4. Прием рассмотрения задач с недостающими или лишними данными.
Например:
Задача. У кормушки было 6 серых и 5 белых голубей. Один белый голубь улетел. Сколько белых голубей стало у кормушки?
Анализ текста показывает, что одно из данных лишнее - 6 серых голубей. Для ответа на вопрос оно не нужно. После решения задачи учитель предлагает внести в текст задачи такие изменения, чтобы это данное понадобилось, что приводит к составной задаче:
У кормушки было 6 серых и 5 белых голубей. Один голубь улетел. Сколько голубей осталось у кормушки?
Эти изменения условия повлекут за собой необходимость выполнять два действия: (6 + 5) - 1 или (6 - 1) + 5 или (5 - 1) + 6
Таким образом, простая задача «достраивается» до составной.
Обучение решению некоторых видов составных задач.
Умение решать текстовые задачи закладывается в начальной школе. У учащихся необходимо формировать умение осуществлять общий подход к решению любой задачи, предлагая при этом для решения задачи различных видов.
Вместе с тем овладение школьниками умением решать задачи во многом зависит от тщательной подготовки учителя, подбора подготовительных упражнений и задач в строгой методической последовательности. Учителю самому необходимо осознавать, какой новый вид задач он предлагает детям для решения, какую подготовительную работу целесообразно провести перед ознакомлением с этим видом задач, какие методические приемы лучше использовать.
В методической литературе достаточно подробно описана методика обучения решению некоторых видов составных задач. Среди них можно выделить задачи, связанные с пропорциональными величинами (на нахождение четвертого пропорционального, на пропорциональное деление, на нахождение неизвестных по двум разностям), и задачи, связанные с движением.
В последние годы помимо учебников М.И. Моро с соавторами появились учебники по математике для начальных классов других авторов, предусматривающие повышение уровня сложности текстовых задач. Так, например, в учебниках И.И. Аргинской и Л.Г. Петерсон встречаются задачи на нахождение неизвестных по их сумме и разности, на нахождение неизвестных по их сумме и отношению, на исключение неизвестных при помощи вычитания и другие виды задач. Между тем методика обучения их решению не рассматривается. Однако, как показывает практика, решение некоторых задач указанных видов вызывает затруднения не только у детей, но и у самих учителей.
В данной статье остановимся на некоторых возможных путях обучения решению таких видов задач.
1. Задачи на нахождение чисел по их сумме и отношению.
Задача 1. В столовую привезли карпов и судаков, всего 48 кг. Карпов было в 3 раза больше, чем судаков. Сколько привезли в столовую карпов и сколько судаков?
К решению задач такого вида можно приступать после того, как дети овладеют умением решать задачи на пропорциональное деление.
Прежде чем приступить к решению таких задач, целесообразно предложить детям задачи, которые помогут им осознать понятие «части».
Задачи «на части» удобно связать с задачами на пропорциональное деление.
Задача 2. Карандаши разложили в две коробки. В первую коробку положили 1 часть карандашей, во вторую–2части. Сколько карандашей в двух коробках, если в первой коробке 12 карандашей?
Задача 3. Оля и Света купили тетради. Они разделили их между собой так, что Оля получила 1 часть, а Света - 3 части. Сколько тетрадей получила Света, если Оля получила 3 тетради?
Задача 4. Саша и Миша купили 15 марок. Они разделили их между собой так, что Саша взял 2 части, а Миша -1 часть. Сколько марок взял Миша?
Благодаря тому, что в этих задачах указано количество частей, которое приходится на искомые числа, решение их не представляет особых трудностей.
После решения каждой такой задачи анализируем решение. Выясняем:
- Сколько карандашей в первой коробке?
- Сколько во второй?
- В какой коробке больше карандашей и во сколько раз? и т. д.
При решении подобных задач важно помочь детям уяснить, что одно искомое больше другого во столько раз, во сколько раз было больше частей. После этого можно перейти к решению задач, в которых отношение между искомыми выражено отвлеченным числом.
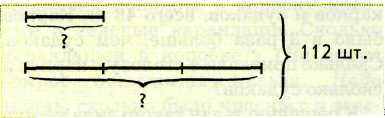 Задача 5. На двух клумбах 112 цветов. На одной из них цветов в 3 раза больше, чем на другой. Сколько цветов на каждой клумбе?
Задача 5. На двух клумбах 112 цветов. На одной из них цветов в 3 раза больше, чем на другой. Сколько цветов на каждой клумбе?При решении таких задач целесообразно использовать прием переформулирования задачи:
- Количество цветов на одной клумбе примем за 1 часть.
- Зная, что цветов на другой клумбе в 3 раза больше, как мы можем сказать это по-другому? (На другой клумбе цветов 3 части.)
- Получаем задачу: «На двух клумбах 112 цветов. На одной из них цветов 3 части, на другой - 1 часть. Сколько цветов на каждой клумбе?»
- Зная, сколько частей составляют цветы на первой и второй клумбах, что можно узнать? (Сколько всего частей составляют цветы на двух клумбах вместе.)
- Зная, сколько всего цветов на двух клумбах и сколько они составляют частей, что можно узнать? (Сколько цветов составляют 1 часть, т.е. сколько цветов на первой клумбе.)
- Зная, сколько всего цветов на двух клумбах и сколько цветов на первой клумбе, что можно узнать? (Сколько цветов на второй клумбе.)
Решение.
Примем количество цветов на первой клумбе за 1 часть, тогда цветы на второй клумбе составят 3 части.
1) 1 +3 = 4 (ч.) - составляют цветы на двух клумбах;
2) 112 : 4 = 28 (шт.) - цветов на первой клумбе;
3) 112 - 28 = 84 (шт.) - цветов на второй клумбе.
Эту задачу можно проверить, решив ее другим способом. Первые три действия остаются теми же;
4) 28 • 3 = 84 (шт.)
Ответ: на первой клумбе 28 цветов, на второй клумбе 84 цветка.
2. Задачи на нахождение чисел по их разности и отношению.
Задача 6. На запасных путях стояли два железнодорожных состава. В первом составе было на 12 вагонов больше, чем во втором. Сколько вагонов было в каждом составе, если в первом составе их было в 4 раза больше, чем во втором?
Подготовкой к решению задач этого вида могут служить задачи вида 2~4, а также задачи на нахождение неизвестных по двум разностям.
Задача 7. Яблоки разложили в две корзины так, что в первой корзине оказалась 1 часть яблок, а во второй -3 части. Сколько яблок в каждой корзине, если во второй корзине на 6 яблок больше, чем во второй?
После решения задачи необходимо обсудить с детьми:
- Сколько яблок в первой корзине?
- Сколько яблок во второй корзине?
- Во сколько раз больше яблок во второй корзине, чем в первой?
Такая беседа так же, как и при решении задач 1-3, направлена на усвоение детьми того, что одно искомое больше другого во столько раз, во сколько раз было больше частей.
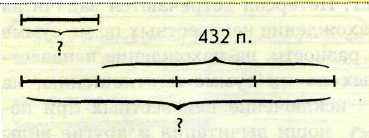 Задача 8. В плацкартных вагонах скорого поезда на 432 пассажира больше, чем в купейных. Сколько пассажиров в плацкартных и купейных вагонах отдельно, если в купейных вагонах пассажиров в 4 раза меньше, чем в плацкартных?
Задача 8. В плацкартных вагонах скорого поезда на 432 пассажира больше, чем в купейных. Сколько пассажиров в плацкартных и купейных вагонах отдельно, если в купейных вагонах пассажиров в 4 раза меньше, чем в плацкартных?При разборе содержания подобных задач также целесообразно переформулировать условие задачи:
- В каких вагонах пассажиров меньше? (В купейных.)
- Примем число пассажиров в купейных вагонах за 1 часть. Сколько частей составляют пассажиры плацкартных вагонов? (4 части.)
Получаем задачу: «В плацкартных вагонах скорого поезда на 432 пассажира больше, чем в купейных. Сколько пассажиров в плацкартных и купейных вагонах отдельно, если в купейных вагонах пассажиров 1 часть, а в плацкартных - 4 части?»
Решение.
Примем число пассажиров в купейных вагонах за 1 часть, тогда число пассажиров в плацкартных вагонах составит 4 части.
1)4-1 = 3 (ч.) - составляют 432 пассажира;
- 432 : 3 = 144 (п.) - в купейных вагонах;
- 144 • 4 = 576 (п.) - в плацкартных вагонах.
Эту задачу можно проверить, решив ее другим способом. Первые три действия остаются теми же;
4)144 + 432 = 576 (п.)
Ответ: в купейных вагонах 144 пассажира, в плацкартных — 576 пассажиров.
3. Задачи на нахождение неизвестных по их сумме и разности.
Задача 9. В двух классах 56 учащихся. Сколько учащихся в каждом классе, если в одном из них на 4 учащихся больше, чем в другом?
Эти задачи являются достаточно сложными. Усвоение их решения дается детям с большим трудом.
При обучении решению таких задач очень важен разбор содержания задачи и построение ее вспомогательной модели.
Первыми целесообразно предлагать задачи с более простой формулировкой.
Задача 10. Альбом и книга стоят 54 рубля. Книга стоит столько же, сколько альбом, и еще 26 рублей. Сколько стоит альбом и сколько стоит книга?
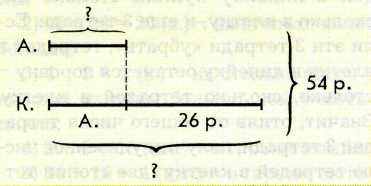 В ходе разбора содержания задачи обращаем внимание на то, что книга стоит столько же, сколько альбом, и еще 26 рублей. Строим вспомогательную модель задачи:
В ходе разбора содержания задачи обращаем внимание на то, что книга стоит столько же, сколько альбом, и еще 26 рублей. Строим вспомогательную модель задачи:Рассуждаем вместе с детьми: книга стоит столько же, сколько альбом, и еще 26 рублей. Если эти 26 рублей «убрать», книга и альбом будут стоить поровну - столько, сколько альбом. Значит, отняв от общей стоимости 26 рублей, получим стоимость двух альбомов.
Решение.
- 54 — 26 = 28 (р.) - стоят два альбома;
- 28 : 2 = 14 (р.) - стоит один альбом;
- 14 + 26 = 40 (р.) - стоит книга.
Эту задачу можно проверить, решив ее другим способом. Первые два действия остаются теми же;
3)54- 14 = 40 (р.)
Проверка. 14 + 40 = 54 (р.) - стоят альбом и книга вместе.
Ответ: книга стоит 40 рублей, альбом стоит 14 рублей.
После этого переходим к решению задач на нахождение неизвестных по их сумме и разности в обычной формулировке.
Задача 11. Купили несколько тетрадей в клетку. Тетрадей в линейку купили на 3 больше, чем тетрадей в клетку. Сколько купили тетрадей в клетку и сколько в линейку, если всего купили 13 тетрадей?
В ходе разбора содержания задачи обращаем внимание детей на то, что тетрадей в линейку купили столько же, сколько тетрадей в клетку, и еще 3 тетради. Строим вспомогательную модель задачи:
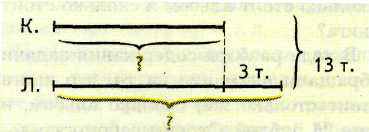
Рассуждаем вместе с детьми: тетрадей в линейку купили столько же, сколько в клетку, и еще 3 тетради. Если эти 3 тетради «убрать», тетрадей в клетку и линейку останется поровну - столько, сколько тетрадей в клетку. Значит, отняв от общего числа тетрадей 3 тетради, получим удвоенное число тетрадей в клетку (две стопки тетрадей в клетку).
Решение.
1)13 — 3 = 10 (т.) - в двух стопках тетрадей в клетку;
- 10 : 2 = 5 (т.) - тетрадей в клетку;
- 5 + 3 = 8 (т.) - тетрадей в линейку.
Эту задачу можно проверить, решив ее другим способом. Первые два действия остаются теми же;
3) 13 - 5 = 8 (т.)
Проверка. 5 + 8 = 13 (т.) - купили всего.
Ответ: купили 5 тетрадей в клетку, 8 тетрадей в линейку.
Задача 12. На двух полках 79 книг, на одной полке на 11 книг больше, чем на другой. Сколько книг на каждой полке?
 При решении подобных задач также целесообразно применять прием переформулировки. Получаем задачу: «На полках 79 книг, на одной полке несколько книг, на другой - столько же и еще 11 книг. Сколько книг на каждой полке?»
При решении подобных задач также целесообразно применять прием переформулировки. Получаем задачу: «На полках 79 книг, на одной полке несколько книг, на другой - столько же и еще 11 книг. Сколько книг на каждой полке?»Решение.
1) 79 - 11 = 68 (кн.) - удвоенное количество книг на первой полке;
2) 68 : 2 = 34 (кн.) - на первой полке;
3) 34 + 11 = 45 (кн.) - на второй полке. Эту задачу можно проверить, решив ее другим способом:
- 79 + 11 = 90 (кн.) - удвоенное количество книг на второй полке;
- 90:2 = 45 (кн.) - на второй полке;
- 45 — 11 = 34 (кн.) - на первой полке.
Ответ: на первой полке 34 книги, на второй - 45 книг.
4. Задачи на исключение одного из неизвестных.
Задача 13. В ателье на 24 пальто и 45 костюмов израсходовали 204 м ткани, а на 24 пальто и 30 костюмов - 162 м. Сколько ткани расходуется на одно пальто и сколько - на один костюм?
Такие задачи как бы являются усложнением задач на нахождение неизвестных по двум разностям. Целесообразно начинать их решение со сравнения.
1-я задача: «Таня купила 3 конверта, а Катя - 5 таких же конвертов и заплатила на 8 рублей больше Тани. Сколько стоит один конверт?»
2-я задача: «Таня купила 3 конверта и 2 ручки, заплатив за всю покупку 22 рубля. Катя купила 5 таких же конвертов и 2 таких же ручки, заплатив за всю покупку 30 рублей. Сколько стоит конверт и сколько стоит ручка?»
Учитель обращается к детям:
- Сравните две задачи. Почему Катя заплатила за свою покупку больше, чем Таня?
Для таких задач нецелесообразно выполнять краткую запись в виде таблицы, выделяя три величины — цену, количество, стоимость, поскольку такая запись в данном случае является чересчур громоздкой и не способствует поиску пути решения задачи.
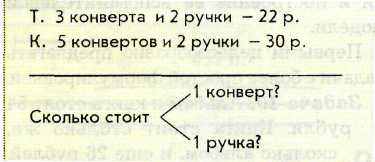 Краткую запись приведенной задачи удобнее выполнить в таком виде:
Краткую запись приведенной задачи удобнее выполнить в таком виде:Решение.
- 5 - 3 = 2 (кон.) — на столько конвертов Катя купила больше, чем Таня;
- 30 - 22 = 8 (р.) - на столько рублей Катя заплатила больше, чем Таня
(стоят два конверта);
- 8 : 2 = 4 (р.) — стоит 1 конверт;
- 4 • 5 = 20 (р.) - стоят 5 конвертов;
- 30 - 20 = 10 (р.) - стоят 2 ручки;
- 10 : 2 = 5 (р.) - стоит 1 ручка.
Эту задачу можно проверить, решив ее другим способом. Первые три действия остаются теми же;
- 4 • 3 = 12 (р.) - стоят 3 конверта;
- 22 - 12 = 10 (р.) - стоят 2 ручки;
5) 10 : 2 = 5 (р.) — стоит 1 ручка.
Ответ: конверт стоит 4 рубля, ручка стоит 5 рублей.
5. Исключение неизвестного заменой одного неизвестного другим (подстановка).
Эти задачи еще называют задачами «на предположение».
Задача 14. В гараже стояли машины и мотоциклы. У них вместе 48 колес. Сколько было мотоциклов и сколько машин, если машин и мотоциклов вместе 14.
Решение таких задач целесообразно проводить с объяснением.
Мотоциклов и машин вместе 14. У машины 4 колеса, а у мотоцикла - 2. Предположим, что в гараже были только мотоциклы. Тогда у них у всех должно быть 28 (2 ∙ 14) колес. Но по условию колес 48, т.е. на 20 (48 - 28) колес больше. Эти 20 колес оказались потому, что в гараже стояли не только мотоциклы, но и машины. Каждой машине надо «добавить» по 2 колеса, следовательно, машин столько, сколько раз по 2 содержится в 20. Разделив 20 на 2, получим 10. Значит, в гараже 10 машин. Вычтем 10 из 14, получим 4. Значит, в гараже 4 мотоцикла.
Можно предположить, что в гараже были только машины. В таком случае у них у всех было бы 56 колес. По условию колес 48, т.е. на 8 колес меньше. Эти 8 колес получились потому, что кроме машин в гараже были и мотоциклы. У каждой машины надо «забрать» 2 колеса. Значит, мотоциклов столько, сколько раз по 2 содержится в 8. Разделив 8 на 2, получим 4. Значит, в гараже 4 мотоцикла. Вычтя 4 из 14, получим 10, т.е. число машин.
Решение.
1) 2·14 = 28 (к.) - было бы колес, если бы в гараже были только мотоциклы;
- 48 - 28 = 20 (к.) - на столько колес больше;
- 4 - 2 = 2 (к.) — на столько колес у каждой машины больше, чем у мотоцикла;
- 20 : 2 = 10 (шт.) - в гараже машин;
- 14 - 10 = 4 (шт.) - в гараже мотоциклов.
Эту задачу можно проверить, решив ее другим способом:
- 4 • 14 = 56 (к.) - было бы колес, если бы в гараже были только машины;
- 56 - 48 = 8 (к.) - на столько колес меньше;
- 4 - 2 = 2 (к.) - на столько колес у каждой машины больше, чем у мотоцикла;
- 8 : 2 = 4 (шт.) - в гараже мотоциклов;
5) 14 - 4 = 10 (шт.) - в гараже машин.
Ответ: в гараже 10 машин и 4 мотоцикла.
Список литературы:
Как проектировать универсальные учебные действия в начальной школе: от действия к мысли: пособие для учителя / [А.Г. Асмолов, Г.В. Бурменская, И.А. Володарская и др.]. – М.: Просвещение, 2008.
- Белокурова Е. Е. Обучение решению комбинаторных задач с помощью таблиц и графов// Начальная школа. – 1995, № 1. – с.21.
- Белошистая А. В. Прием графического моделирования при обучении решению задач// Начальная школа.-1991, № 4.- с.18.
- Бородулько М. А., Стойлова Л. П. Обучение решению задач и моделирование// Начальная школа.-1996, № 8.- с.26.
- Григорян Н. В. Математика в начальной школе. 1-4 класс. - М.: Олма-Пресс, 2001.- с.25.
- Ивашова О. А., Полникова М. Ю. Математика. Литературные задачи. – Санкт-Петербург: СМИО Пресс, 1999.
- Левитас Г. Нестандартные задачи на уроках математики в 1-м классе (во 2-м, в 3-ем, в 4-ом)// Газета «Начальная школа». - 2001, № 41; 2002, № 12, 22, 39, 44.
- Матвеева Н. А. Комбинированная вспомогательная модель задачи// Начальная школа: плюс-минус.-2001, № 1.- с. 68.
- Пахомова Т. Л. Математика для начальных классов. Задачи, решения, примеры. - М.: Лист-Нью, 1997.- с.3.
- Подосенова И. П., Соколова Л. В. Задачи по математике на экологическую тему// Начальная школа. – 1995, № 4. – с. 24.
- Царева С. Е. Обучение решению задач// Начальная школа.-1997, №11.-с.93.
1 Классификация и примеры задач взяты из учебного пособия: Бантова М. А., Бельтюкова Г. В. Методика преподавания математики в начальных классах. – М., Просвещение, 1984.
2 Бантова М. А., Бельтюкова Г. В. Методика преподавания математики в начальных классах. – М., Просвещение, 1984.
3 Фридман Л. М., Турецкий Е. И. Как научиться решать задачи. – М., Просвещение, 1989.
4 Белошистая А. В. Методический семинар: вопросы обучения решению задач // Начальная школа: плюс До и После. – 2003, № 4.
