Тигр 2011 10-11 класс 1
| Вид материала | Конкурс |
- «Амурский тигр», 160.65kb.
- Ведущая Школы «Белый Тигр», 52.55kb.
- Тема: Амурский тигр, 25.41kb.
- Название конкурса: «бизнес класс 2011», 138.14kb.
- Офей времен Крымской войны-пушка с фрегата «Тигр», Приморский бульвар и дворцовая архитектура, 153.78kb.
- 2011 г. Рабочая программа учебного предмета математика курс 8 класс, 1008.35kb.
- Тематическое планирование на 2010/2011 учебный год География 6 класс, 148.34kb.
- Тематическое планирование на 2011/2012 учебный год География 7 класс, 162.4kb.
- Поурочно тематическое планирование 2011-2012 учебный год Предмет: музыка Класс: 2 Учитель, 35.69kb.
- Реферат на тему, 64.69kb.
Краткие решения заданий конкурса-игры «ТИГР - 2011»
10-11 класс
1. По вертикали луноход проехал: 10*(20+10-26)=40 метра, по горизонтали: 10*(30-27)=30 метра. Расстояние от исходной точки составляет:
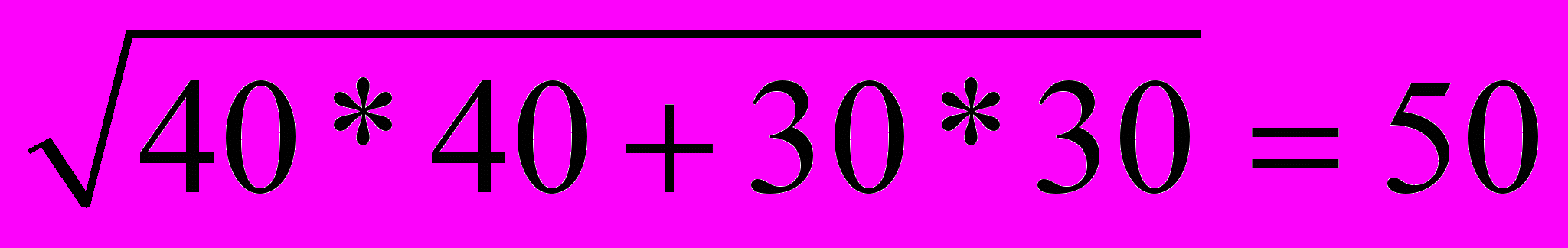
Ответ: Д.
2. Промоделируем процесс: 28, 14, 7, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1 (18 раз).
Ответ: В.
3. Поле после покраски:
Ответ: Б.
4. В итоге получится наиболее общий делитель чисел 128 и 296. НОД(128, 296)=8.
Ответ: Б.
5. Выполнив преобразования наоборот получим первоначальный текст: ОРТССТРОСОРТ.
Ответ: Б.
6. За 10 лет число карпов увеличится в 410 раз, т.е. после десяти лет будет 10*410=10485760.
Ответ: Г.
7. Так как единиц меньше всего, то лучше выяснить позицию единиц(ы) в требуемом фрагменте. Все позиции единиц определяются формулой
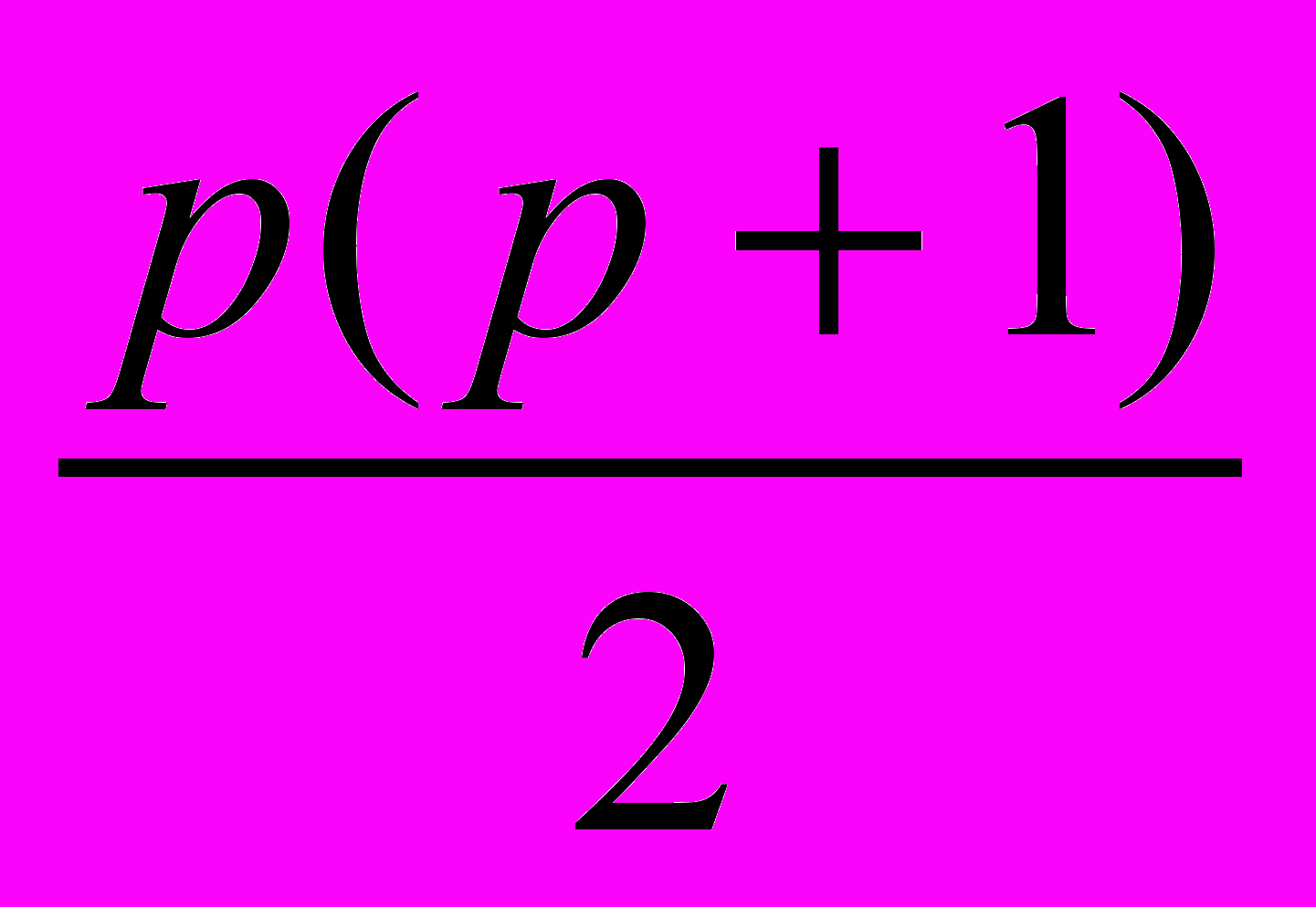(сумма от 1 до 
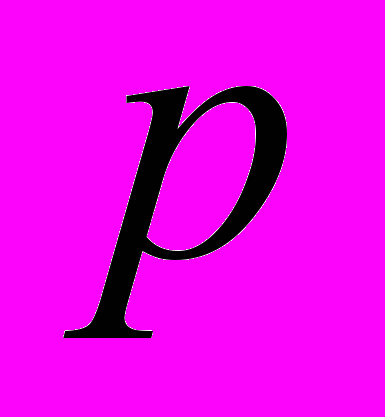), где 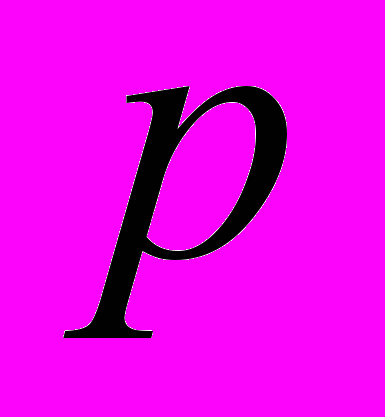- порядковый номер единицы. 19 и 20 единицы расположены на 190 и 210 местах соответственно, а между ними все 0.Ответ: А.
8. Чтобы не запутаться в старшинстве, можно нарисовать стрелки от тех, кто старше, к тем, кто младше. Тогда самыми старшими могут быть те, к кому нет стрелки, т.е. это Сережа или Гриша.
Ответ: В.
9. Вначале имеем 24 и 33 рыб в ведрах (первое число будет обозначать число рыб в синем ведре, второе – в синем). Затем 24 и 57 (57=24+33). Далее 33 (57-24=33) и 57. И, наконец, 33 и 24 (57-33=24).
Ответ: Б.
10. При четвертом вопросе число x будет равно 43. Чисел больших 43 два, поэтому однозначно угадать большее число после четвертого вопроса нельзя. Если бы это было число меньшее 43-11=32, то Антон угадал бы его еще раньше. Остается число 38.
Ответ: В.
11. После второго изменения первая по пятую страницы будут набраны 14 шрифтом. Третья страница станет второй после удаления, ее шрифт 14.
Ответ: Д.
12. Чтобы поменять местами первое и последнее число в отсортированном ряду из N элементов нужно N-1 обменов, после которых оставшиеся числа также будут образовывать отсортированную последовательность чисел, но уже из N-1 элементов. Для 2 элементов требуется всего 1 обмен. Таким образом, придется совершить 1+2+…+10+11=66 обменов.
Ответ: В.
13. Промоделируем действие Вити: 27, 54, 45, 90, … (3 операции).
Ответ: В.
14. 1024=210, т.е. через 10 мс останется 1 микрограмм вещества.
Ответ: В.
15. Если бы пираты брали монеты от 1 до 15, то всего получилось бы 1+2+…+14+15=(15*16)/2=120 монет, оставшиеся 60 монет пираты получат, если будут брать монеты, начиная с 5 (по 4 монеты каждому дополнительно). В этом случае капитан возьмет 15+4=19 монет.
Ответ: Д.
16. Динамика колонии роботов по годам: 5, 10, 20, 40, 80, 59, 38, 76, 55, 34, 68, 47, 26 (12 лет).
Ответ: В.
17. Июньск – Декабрьск – Февральск – Апрельск – Январск. Итого 4 пересадок.
Ответ: В.
18. При записи новых сведений о родителях число людей в предыдущем поколении увеличивается на 2. С учетом того, что Леонид дошел до прапрапрапрародителей, общее число всех предков составит 2+4+8+16+32=62.
Ответ: В.
19. Заметим, что как бы не ходила Катя, при удвоении Витей взятых палочек, она не сможет взять последние палочки. Витя в свою очередь будет забирать оставшиеся палочки уже своим вторым ходом.
Ответ: В.
20. Функция f(x) увеличивает текущее число в 2 раза, значит 2 в итоге перейдет в 2*221=222=4194304.
Ответ: Г.
21. Если самая маленькая страница размера 1 мегабайт, то их должно быть не меньше двух, но тогда самая большая страница не больше 8 мегабайт, далее 4 и 2 мегабайт, в сумме меньше 18. Три страницы размера 2 и еще две по 4 и 8 мегабайт соответственно дают в сумме 18.
Ответ: Б.
22. Программа содержит ошибку, т.к. включает точки всей окружности. Тогда неправильными будут те примеры, которые содержат точки в верхней половине окружности: (0; 0,5), (0,5; 0,5). Оставшиеся 3 примера будут приводить к правильному ответу.
Ответ: Г.
23. Буквы А и Р явно лишние. Их удаление сразу приведет к итоговому слову. Итого 2 операции.
Ответ: А.
24. Если вначале марсоход будет двигаться только право, а потом только вверх, то никак препятствий на своем пути он не встретит. По каждой из координат нужно 5 перемещений, в итоге 10.
Ответ: Б.
25. В условии опечатка в количестве залов (4 вместо 3)
Пример демонстрации фильмов (зеленым цветом обозначен первый фильм, коричневым – второй, синим – третий, красным – четвертый, черным - перерыв; всего 20 показов):
Ответ: А.
Если бы опечатки не было (4 зала), то правильный ответ 25
Пример:
26. Заметим, что Шехерезада может гарантировать победу только тогда, когда в конце перед ходом соперника на столе будет 4 палочки. Чтобы получить перед последними ходами 4 палочки, Шехерезаде в свою очередь необходимо, чтобы до этого перед ходом падишаха было 8 палочек. Рассуждая подобным образом, приходим к тому, что перед ходом падишаха должно быть 1000 палочек, т.е. Шехерезада вначале должна взять 1 палочки, но тогда перед последним ходом робот возьмет из кучки 3 палочки и на столе останется 4-3=1 палочка, которую и должна будет взять Шехерезада, чтобы выиграть.
Поскольку в ответе Д допущена опечатка (3 палочки и 1 палочка вместо 3 палочки в обоих случаях) подходят два варианта ответа.
Ответ: Б и Д.
27. На каждой следующей диагонали таблицы будет число на единицу больше. Правый нижний угол соответствует 199 диагонали, а значит, там будет записано число 199.
Ответ: Г.
28. Каждый новый ответ на вопрос уменьшает неопределенность в 2 раза. Если бы вопросов было 10, то мы бы смогли угадать любое число среди 210=1024 чисел. Наш диапазон содержит 900 чисел, следовательно, некоторые числа мы будем угадывать с 9 раз. В нашем случае имеем следующие поисковые границы перед каждым вопросом: [100, 999], [100, 549], (324, 549], (436, 549], (492, 549], (520, 549], (520, 534], (527, 534], (527, 530], (527, 528]. Итого 9 вопросов.
Ответ: Г.
29. Заметим, что через каждые 6 лет число монет остается прежним ((10000+5*2000)/2=10000). Через 996 лет будет 10000 монет, тогда на 1000 год их станет 10000+4*2000=18000.
Ответ: Д.
30. Чтобы перейти от буквы с порядковым номером i к букве с порядковым номером j, требуется либо max(i, j)-min(i, j) вращений в одну сторону, либо min(i, j)+N-max(i, j) вращений в другую, где N – число букв на барабане. В нашем случае буквы имеют следующие порядковые номера соответственно: 2(Б), 1(А), 18(Р), 15(Н).
АБ (1 или 32), АР (17 или 16), АН (14 или 19)
Итого получаем: 1+1+16+16+1+1+14=50 вращений.
Ответ: Б.