Учитывать рекомендации психологов по организации усвоения и пр. Необходимо добиться успешного овладения учащимися тех результатов, которые формируются в основной школе
| Вид материала | Методические рекомендации |
- Учитывать рекомендации психологов по организации усвоения и пр. Необходимо добиться, 109.67kb.
- Давыдовой Ирины Викторовны 2009 г., Пермь Введение. Добиться усвоения знаний учащимися,, 307.67kb.
- Образовательная, 144.76kb.
- Методические рекомендации по организации самостоятельной работы студентов, 256.55kb.
- Методические рекомендации по психолого педагогическому сопровождению предпрофильной, 105.97kb.
- Данное пособие можно использовать в качестве методических рекомендаций и материалов, 1039.77kb.
- Французский язык в париже для взрослых школа oise (Оксфордская Школа Интенсивного Обучения), 52.2kb.
- Рекомендации по организации внутреннего контроля в банках (небанковских кредитно-финансовых, 260.55kb.
- Рекомендации по организации профилактики наркомании в школах. Особенности организации, 70.32kb.
- Учебное пособие предназначено для студентов вузов, учащихся техникумов, для педагогов, 10828.6kb.
Управление образования и науки Белгородской области
Белгородский региональный институт повышения квалификации и профессиональной переподготовки специалистов
Методические рекомендации по планированию итогового повторения курса полной (средней) школы по математике с учетом уровневой дифференциации (с использованием банка заданий КИМ Федерального института педагогических измерений).
В условиях обязательной для всех выпускников сдачи экзамена по математике постепенное и поэтапное введение ЕГЭ дало возможность учителям по-новому подходить к подготовке и проведению уроков, учитывая необходимость обеспечить овладение всеми школьниками учебного материала на базовом уровне, а также возможность мотивированным учащимся, заинтересованным в получении высоких баллов для поступления в вуз, динамичного продвижения в овладении материалом на повышенном и высоком уровне. При проведении уроков учителям математике необходимо:
- Активнее включать в учебный процесс идеи дифференцированного обучения (дифференциация требований в процессе обучения, разноуровневый контроль);
- Использовать практические разработки по индивидуализации обучения (создание индивидуальных модулей обучения)
- Учитывать рекомендации психологов по организации усвоения и пр.
- Необходимо добиться успешного овладения учащимися тех результатов, которые формируются в основной школе.
Повторение играет важную роль на всех этапах обучения – овладение новыми знаниями и навыками не может осуществляться без опоры на прежний опыт, но особую роль учителя математики должны отводить вопросам итогового повторения.
Целесообразно организовать индивидуальное повторение, учитывающее пробелы в знаниях и умениях конкретного ученика, и с помощью диагностических работ систематически фиксировать продвижение старшеклассника по пути достижения уровня запланированных требований.
Построение итогового повторения курса математики, подготовка к единому государственному экзамену.
- Итоговое повторение учебного материала необходимо проводить, используя блочно-модульное структурирование учебного материала, укрупнение учебных единиц.
- На первом уроке повторения темы необходимо провести контрольный срез в тестовой форме по выявлению пробелов в знаниях учащихся для дальнейшей их ликвидации. На этапе подготовки тематический тест должен быть выстроен в виде логически взаимосвязанной системы, где из одного вытекает другое.
- Выстраивать повторение, соблюдая «правило спирали» - от простых заданий до заданий со звездочками, от комплексных типовых заданий до заданий раздела С.
- Тренировочные тесты необходимо проводить с жестким ограничением во времени. Темп проведения теста учитель должен задавать сразу и держать его на протяжении всего времени.
- Необходимо учить школьников использовать наличный запас, применяя различные «хитрости» и «правдоподобные рассуждения» для получения ответа наиболее простым и быстрым способом.
- Чтобы решать простейшие уравнения и уравнения повышенной сложности – использовать на уроках раздаточный материал с проверкой основных приемов и специальных методов решения простейших уравнений.
- На каждом уроке математики систематически повторять изученное ранее параллельно с изучением нового материала. Подготовка к ЕГЭ не должна подменять систематическое изучение математики. Любая традиционная подготовка к экзаменам, в том числе к ЕГЭ должна быть обеспечена планомерным повторением, обобщением и систематизацией знаний из различных разделов курса математики, варьированием стандартных условий задачи, рассмотрением новых типов заданий.
- Домашние задания должны быть подобраны для учащихся различного уровня сложности. Записи домашних заданий в журнале должны быть различными для каждой группы учащихся (слабых, средних и сильных).
Отдавая должное вводному и систематическому текущему повторению, нельзя переоценить важность и значение итогового повторения, в ходе которого осуществляется систематизация знаний по мере изучения всего курса.
Для повторения на уроках, при индивидуальной работе с учащимися необходимо использовать следующий материал по темам:
| Тема | Задания для повторения и самостоятельной работы уровня А, В, С |
| Тригонометрические выражения. Тригонометрические функции. Тригонометрические уравнения | Единый государственный экзамен: математика: методика подгот.: кн. для учителя/ Л.О.Денищева, Ю.А.Глазков, К.А.Краснянская: - М.: Просвещение, 2005 Журнал «Математика в школе», № 6- 2005 стр.2 |
| Корни степени п. Функция 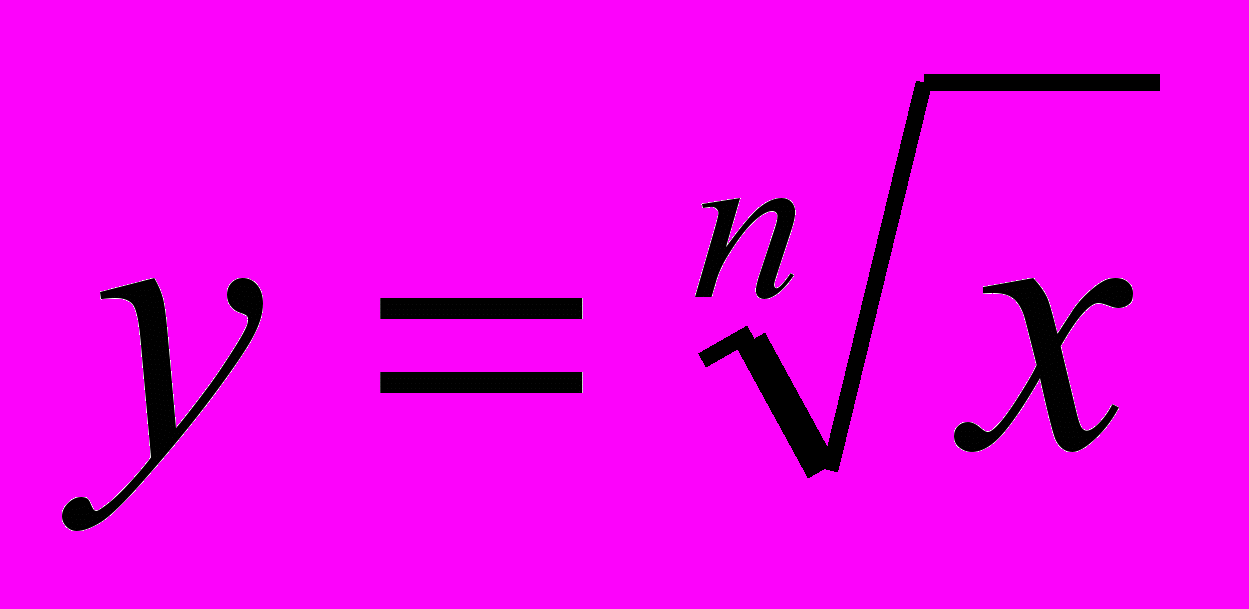 . Иррациональные уравнения. . Иррациональные уравнения. | Единый государственный экзамен: математика: методика подгот.: кн. для учителя/ Л.О.Денищева, Ю.А.Глазков, К.А.Краснянская: - М.:Просвещение, 2005 Журнал «Математика в школе», № 9- 2005 стр.2 |
| Степени. Показательная функция. Показательные уравнения и неравенства. | Единый государственный экзамен: математика: методика подгот.: кн. для учителя/ Л.О.Денищева, Ю.А.Глазков, К.А.Краснянская: - М.: Просвещение, 2005 Журнал «Математика в школе», № 9- 2005 стр.2 |
| Логарифмы. Логарифмическая функция. Логарифмические уравнения и неравенства. | Единый государственный экзамен: математика: методика подгот.: кн. для учителя/ Л.О.Денищева, Ю.А.Глазков, К.А.Краснянская: - М.:Просвещение, 2005 Журнал «Математика в школе», № 10-2005 стр.2 |
| Функция, производная и первообразная | Единый государственный экзамен: математика: методика подгот.: кн. для учителя/ Л.О.Денищева, Ю.А.Глазков, К.А.Краснянская: - М.: Просвещение, 2005 Журнал «Математика в школе», № 8 - 2005 стр.2 |
| Геометрия. Планиметрия. | Единый государственный экзамен: математика: методика подгот.: кн. для учителя/ Л.О.Денищева, Ю.А.Глазков, К.А.Краснянская: - М.: Просвещение, 2005 Журнал «Математика в школе», № 3 - 2004 стр.8, № 2-2007г. с.6 №9-2006г. с.2 |
| Геометрия. Стереометрия. | Единый государственный экзамен: математика: методика подгот.: кн. для учителя/ Л.О.Денищева, Ю.А.Глазков, К.А.Краснянская: - М.: Просвещение, 2005 Журнал «Математика в школе», № 4 - 2006 стр.2 №5-2006г., стр.2 |
Перечень учебных изданий для использования при итоговом повторении:
- Единый государственный экзамен: математика: методика подготовки: книга для учителя/ Л.О.Денищева, Ю.А.Глазков, К.А.Краснянская: - М.: Просвещение, 2005
- Единый государственный экзамен: математика: контрольно-измерительные материалы:2005-2006/ под общ. редакцией Л.О.Денищевой; Министерство образования и науки Российской Федерации, Федеральная служба в сфере образовании и науки, Федеральный институт педагогических измерений. – М.Просвещение, 2005г
- Единый государственный экзаме2007. Математика. Учебно-тренировочные материалы для подготовки учащихся/ ФИПИ авторы-составители: Л.О.Денищева, Ю.А.Глазков, К.А.Краснянская, А.Р.Рязановский, П.В.Семенов – М.Интеллект-Центр, 2007
- «ЕГЭ. Математика. Типовые тестовые задания» / Т.А. Корешкова, Ю.А.Глазков, В.В. Мирошин, Н.В. Шевелева.-М.: Издательство «Экзамен», 2006 (Серия «ЕГЭ. Типовые тестовые задания»)
- «Алгебра и начала анализа: учеб. пособие» /П.В.Семенов.- М.Мнемозина, 2007. (ЕГЭ шаг за шагом)
- Единый государственный экзамен: Математика: Контрольно-измерительные материалы: Репетиционная сессия 1. / Л.О.Денищева, А.Р.Рязановский, Е.М.Бойченко, П.М.Камаев – М.Вентана-граф, 2006
- Единый государственный экзамен: Математика: Контрольно-измерительные материалы: Репетиционная сессия 2. / Л.О.Денищева, А.Р.Рязановский, Е.М.Бойченко, П.М.Камаев – М.Вентана-граф, 2006
- Единый государственный экзамен. Математика. Сборник заданий./ Денищева Л. О. – М. М.Просвещение, 2005г (пособие для учащихся)
- Единый государственный экзамен. Математика. Книга для учителя. Денищева Л. О. – М. М.Просвещение, 2005г (пособие для учителей и методистов)
- Лысенко Ф.Ф., Калашников В.Ю., Неймарк А.Б., Давыдов Б.Е. Математика. Подготовка к ЕГЭ, подготовка к вступительным экзаменам.- Ростов-на-дону: Сфинск. 2004г, 2005г
- Журнал «Математика для школьников» (подписной индекс 80866)
- Тематические тесты. Математика. ЕГЭ -2007г. / под ред. Ф.Ф.Лысенко – изд. Легион, Ростов-на-Дону, 2007г., 256с (пособие для самостоятельной подготовки)
- Денищева Л.О., и др. Тематический контроль. Алгебра и начало анализа. 10-11 кл.- изд. Интеллект-Центр, 2007
- Денищева Л.О., Михеева Т.Ф., Карюхина Н.В. Учимся решать уравнения и неравенства. 10-11 кл.- изд. Интеллект-Центр, 2007
- Рязановский А.Р., Мирошин В.В. Готовимся к ЕГЭ. Математика. Решение задач повышенной сложности. - изд. Интеллект-Центр, 2007
- Учебно-тренировочные материалы для подготовки учащихся. ЕГЭ-2007. Математика. изд. Интеллект-Центр, 2007
Рекомендуемые электронные учебники
- Современный учебно-методический комплекс. Алгебра 7-9. Версия для школьника. Просвещение-МЕДИА. (все задачи школьной математики).
- Современный учебно-методический комплекс. Алгебра 10-11. Версия для школьника. Просвещение-МЕДИА. (все задачи школьной математики).
- Современный учебно-методический комплекс. Алгебра и начала анализа. Итоговая аттестация выпускников 11.. Просвещение-МЕДИА. (все задачи школьной математики).
Данные программы имеют до 600 различных задач разного уровня сложности. Их можно использовать как тренировочные работы для подготовки к единому государственному экзамену (А-выбор ответа, В – краткий ответ, С – полное решение задачи), предлагается решение.
- Сдаем Единый экзамен 2004. Серия «1С: Репетитор». Центр тестирования. (Варианты КИМ 2002-2004 годов, 13 учебных предметов, перечень ВУЗов – участников ЕГЭ)
- Готовимся к ЕГЭ. МАТЕМАТИКА. Решение экзаменационных задач в интерактивном режиме. Просвещение – МЕДИА.
Перечень сайтов, полезных учителю математики
и учащимся
http://www.prosv.ru - сайт издательства «Просвещение» (рубрика «Математика»)
ссылка скрытаwww.drofa.ru - сайт издательства Дрофа (рубрика «Математика»)
ссылка скрыта - методические рекомендации учителю-предметнику (представлены все школьные предметы). Материалы для самостоятельной разработки профильных проб и активизации процесса обучения в старшей школе.
ссылка скрыта - Центральный образовательный портал, содержит нормативные документы Министерства, стандарты, информацию о проведение эксперимента, сервер информационной поддержки Единого государственного экзамена.
ссылка скрыта - сайт Интернет – школы издательства Просвещение. Учебный план разработан на основе федерального базисного учебного плана для общеобразовательных учреждений РФ и представляет область знаний «Математика». На сайте представлены Интернет-уроки по алгебре и началам анализа и геометрии, включают подготовку сдачи ЕГЭ.
Методист кабинета
естественно-математических
дисциплин БелРИПКППС О.В.Вертелецкая
