Міністерство освіти та науки України
| Вид материала | Документы |
- Міністерство освіти І науки України Департамент міжнародного співробітництва та європейської, 39kb.
- Міністерство освіти І науки україни міністерство економіки україни міністерство фінансів, 18.39kb.
- Міністерство освіти І науки україни донецький обласний центр туризму та краєзнавства, 189.44kb.
- Міністерство освіти І науки україни, 335.34kb.
- Міністерство освіти І науки україни, 283.15kb.
- Міністерство освіти І науки, молоді та спорту україни, 59.16kb.
- Міністерство освіти І науки україни, 32.42kb.
- Міністерство освіти І науки, молоді та спорту України, 61.58kb.
- Міністерство освіти І науки україни положенн я про організацію фізичного виховання, 306.47kb.
- Міністерство освіти І науки україни інститут інноваційних технологій І змісту освіти, 43.77kb.
Міністерство освіти та науки України
Міжнародний економіко-гуманітарний університет
імені академіка Степана Дем’янчука
Факультет кібернетики
Кафедра математичного моделювання
С.Ю. Вурста
Побудова фрактальних поверхонь в комп’ютерній графіці
 Науковий керівник:
Науковий керівник:Р.М. Літнарович,к. т. н., доцент
Рівне – 2010
УДК 681.3
Вурста С.Ю., Літнарович Р.М. Побудова фрактальних поверхонь в комп’ютерній графіці. МЕГУ, Рівне, 2010,-250 с.
В даному проекті розроблений програмний додаток "Фрактальні ландшафти" для генерування 3D ландшафтів за допомогою алгоритму «Фрактального шуму», та з метою демонстрації можливостей цього алгоритму, бібліотеки OpenGL і візуальної бібліотеки GLScene(із завдатком ігрового ядра) по побудові ландшафту.
Для студентів, магістрантів і аспірантів факультету
Кібернетики МЕГУ.
Vursta S.Yu., Litnarovich R.M. Construction of fractal surfaces in computer graphics. IEGU, Rivne, 2010-250 p.
In this project programmatic addition is developed the "Fractal landscapes" for generuting of 3d landscapes by the algorithm of «Fractal noise», and with the purpose of demonstration of possibilities of this algorithm, library of OPENGL and visual library of Glscene(with the advance of playing kernel), on the construction of landscape.
For students, magistrations and graduate students of faculty
Cybernetics IEGU.
Рецензенти:
В.О.Боровий,доктор технічних наук,професор
В.Г.Бурачек, доктор технічних наук,професор
Є.С.Парняков, доктор технічних наук,професор
Відповідальний за випуск:
Й.В.Джунь, доктор фізико-математичних наук, професор
© Вурста С.Ю.,Літнарович Р.М.,2010
Зміст
Вступ………………………………..………………………5
1. Історія появи фракталів та їх використання………..……7
2. Довжина берегової лінії. Фрактальна розмірність. Поняття фрактала...................................................................................18
2.1. Приклади побудови фрактальних множин.Класифікація фракталів………………..…………..25
2.2. Алгоритм фрактального шуму або шум перліна..35
2.3. Реалізація алгоритму…..………………………..43
3. Історія розвитку комп’ютерної графіки та ігор ……….49
3.1 Основні поняття ЗD-графіки ….………..………65
3.2 Основні прийоми для роботи з світлом в 3D..… 72
3.3 Алгоритми рельєфного текстурування………... 74
3.3.1 Рельєфне текстурування (bump mappіng)…….74
3.3.2 Normal mapping……………… ………… 76
3.3.3 Parallax mapping…..…………………………….80
3.3.4 Relief mapping…….……… ……………. 82
3.3.5 Простий Relief Mapping……… ……… 83
3.3.6 Багатошаровий Relief Mapping… ………84
3.4 Основні прийоми для роботи з текстурами в 3D.86
3.5 Основні поняття про шейдер та види шейдерів. 91
3.6. Генерація тривимірних ландшафтів……………93
4. Опис програмного середовища Delphі…....…………… 120
4.1.Високопродуктивний компілятор в машинний код………………………………..………………... 126
4.2. Могутня об'єктно-орієнтована мова……………128
4.3. Об'єктно-орієнтована модель програмних компонент…………………………………………….132
4.4 Бібліотека візуальних компонент…………..135
4.5. Робота з компонентами.………………………146
5. Опис графічних бібліотек для написання 3D – програм та ігор……………….……………………………………151
5.1 Опис графічної бібліотеки OpenGL ..………..153
5.2 Графічна бібліотека DirectX……………………158
5.3 Візуальні бібліотеки компонентів для OpenGL та DirectX…………………………….…………….…159
5.4 Опис закладок GLScene….……..………………167
6. Проектування системи .....………………………………171
6.1 Вибір середовища реалізації…..…..……….173
6.2 Опис використаних компонент GLScene для реалізації системи……………………………175
6.3 Опис інтерфейсу розробленої системи..…..189
6.3.1 Панель інструментів ………………….190
6.3.2 Опис робочої області ….………...........196
6.3.3 Опис панелі налаштування 3D-сцени.197
Висновки……………….…………………………………….205
Список літератури…………………………………………..207
Додаток ……………………………..……………………….210
Ключові слова: фрактальні ландшафти, фрактальний шум, текстури, шейдери
Ключевые слова: фрактальные ландшафты,фрактальный шум, текстура, шейдеры
Key words: fractal landscapes , fraktal noise, textures, sheyders
Вступ
Геометрію часто називають "холодною" і "сухою". Одна з причин цього полягає в її нездатності описати форму хмари, гори, берегової лінії або дерева. Хмари - не сфери, гори - не конуси, берегові лінії - не кола, деревна кора не гладка, блискавка поширюється не по прямій. Багато природні об'єкти настільки іррегулярні і фрагментовані, що в порівнянні зі стандартною геометрією Евкліда природа має не просто більшу складність, а складність зовсім іншого рівня .
Фрактали - це геометричні об'єкти з незвичайними властивостями: будь-яка частина фрактала містить його зменшене зображення. Тобто, скільки фрактал не збільшувати, з будь-якої його частини на вас буде дивитися його маленька копія.
Роль фракталів в машинній графіці сьогодні досить велика. Вони приходять на допомогу, наприклад, коли потрібно, за допомогою декількох коефіцієнтів, задати лінії і поверхні дуже складної форми. З точки зору машинної графіки, фрактальна геометрія незамінна при створення штучних хмар, гір, поверхні моря. Фактично знайдений спосіб легкого подання складних неевклідових об'єктів, образи яких дуже схожі на природні.
Комп'ютери стають дедалі потужнішими, і все більш вражаючі ефекти вони дозволяють нам спостерігати на екрані дисплея. Нас чекає ще багато цікавих і незвичайних знахідок.
Мета даної наукової роботи полягає у пошуку способу легкого подання складних неевклідових об'єктів, образи яких дуже схожі на природні.
В даному проекті розроблений програмний додаток "Фрактальні ландшафти" для генерування 3D ландшафтів за допомогою алгоритму «Фрактального шуму», та з метою демонстрації можливостей цього алгоритму, бібліотеки OpenGL і візуальної бібліотеки GLScene(із завдатком ігрового ядра) по побудові ландшафту.
1. Історія появи фракталів та їх використання
Саме слово "фрактал" є похідним[12, 15] від латинського fractus - "зламаний, розбитий". Вперше дане визначення було застосоване в 1975 році французьким математиком Бенуа Мандельбротом, який випустив книгу "Фрактальна геометрія природи". Власне, він і понині вважається провідним дослідником в області фрактальної геометрії. Його вживають, коли дана фігура володіє якими-небудь з наступних властивостей:
1. Володіє нетривіальною структурою на всіх шкалах, так що збільшення масштабу не приводить до її спрощення, як це зазвичай відбувається з регулярними фігурами (де фрагмент, що розглядається в дуже крупному масштабі, нагадуватиме фрагмент прямої).
2. Проявляє ознаки самоподібність - повного або наближеного.
3. Володіє дробовою метричною розмірністю або метричною розмірністю, що перевершує топологічну.
4. Може бути побудована за допомогою рекурсивної процедури (рекурсія - часткове визначення об'єкту через себе, визначення об'єкту з використанням раніше визначених. Рекурсія використовується, коли можна виділити самоподібність завдання).
Хмари, крони дерев, гірські хребти, кровоносна система людини і тварин, капіляри рослин - все це так само цілком "легітимні" приклади фракталів...
Тому поява програм візуалізації для фотореалістичного відображення природних ландшафтів - річ більш ніж закономірна.
В 80-році, коли співробітник корпорації Boeing Лорен Карпентер представив на виставці SIGGRAPH двохвилинний CG-ролик під назвою Vol Libre, складний, що зображає, і надзвичайно реалістично виглядаючий ландшафт, сформований на основі фрактальних геометричних алгоритмів, самим Карпентером розроблений. Побачивши таку велич, фірма Джорджа Лукаса Industrial Light and Magic поспішила переманити Карпентера до себе - і в 1982 році чесно народ знову ахнув, побачивши у фільмі Star Trek II: The Wrath of Khan сцену "швидкого терраморфінга" цілої планети (Genesis Effect).
У фіналі трейлера видимо впізнаємо "фрактальні" ландшафти - але це зараз вони впізнанні майже для всіх, хто так чи інакше мав справу з комп'ютерною графікою. На той момент подібний спецефект приголомшував уяву кіноманів, які ще не звиклі до подібних ефектів.
У тому ж 1982 року виходить в світ нова редакція книги Бенуа Мандельброта "Фрактальна геометрія природи". Художник Річард Восс підготував ("нагенерував") для неї безліч ілюстрацій - зокрема, ландшафтів, що нагадували природні. Нові можливості для художників були в наявності... Але створенням інструментарію спочатку займалися все-таки математики і програмісти.
Згодом почали з’являтись візуальні програми для генерування реалістичних ландшафтів Bryce і MojoWorld для яких алгоритм розробив Доктор Кенет Масгрейв - учень Мандельброта - в 1993 році опублікував дисертацію під назвою "Методи реалістичної візуалізації ландшафтів" (Methods for Realistic Landscape Imaging), в якій описував відповідні тематиці алгоритми. Ці алгоритми згодом лягли в основу пакету під назвою Bryce, перша версія якого була написана в 1994 році для Macintosh. Стабільна версія для РС з'явилася тільки в 1997 році. У 2000 році компанія Corel викупила права на пакет, випустила в 2001 році версію 5.0 і прибрала Bryce в довгий ящик, відмахнувшись від поклонників програми, що нили, що їм потрібні нові можливості. Фактично Bryce якраз було списувати в abandonware, проте ж в 2004 році компанія DAZ раптово викупила Bryce і зайнялася його подальшим розвитком. Актуальна версія (випущена в березні 2007 року) носить індекс 6.1.
Пакет володіє широкою функціональністю в плані генерації і редагування натурально виглядаючого ландшафту, підтримує сторонні матеріали і текстури, додатково - починаючи з п'ятої версії - в Bryce наявний т.з. Tree Lab, комплекс алгоритмів, що дозволяють генерувати на отриманій поверхні достатньо реалістично виглядаючу рослинність. І крім того, Bryce інтегрований з пакетом тривимірного моделювання і анімації DAZ Studio, так що за бажання в сцену, що створюється в Bryce, можна імпортувати з Studio моделі, зокрема анімовані, із збереженням всіх їх параметрів.
Системні вимоги у пакету, за теперішніх часів, дуже, скажімо так, демократичні.
Версія для Mac зажадає 700-мегагерцевого процесора (рекомендується, втім, 1 Ггц), причому підтримуються і Mac Intel, і Power Macintosh; 512 мегабайт оперативної пам'яті мінімум, рекомендується 1 Гбайт, також знадобляться 10.
0 мегабайт дискового простору як мінімум (краще - 500). Що стосується відеокарти, то обов'язковою умовою буде наявність 128 мегабайт власного ОЗУ і підтримка OPENGL. Операційна система - Mac OS X 10.3.9. або вище.
Для РС системні вимоги аналогічні, причому Bryce як і раніше підтримує Windows NT 4 (Sp6), Windows 2000 (Sp2) і Windows XP. Про Windows Vista нічого не сказано. Windows 2003 Server же не підтримується зовсім.
Що стосується Масгрейва, то з 2000 року він зайнявся розробкою нового пакету аналогічної спрямованості - Mojoworld.
Це також генератор сцен і ландшафтів на фрактальній основі - але зі своїми хитрощами. Одній з головних, мабуть, можна назвати помітну строкатість отримуваних в Mojoworld зображень: сцени виходять не фотореалістичними, а, швидше, сюрреалістичними, яскравіше і фантастичніше просто нікуди.
У Mojoworld разом генерується ціла планета - на льоту. Природно, на призначеному для користувача екрані вона показана в дуже сильно пониженому дозволі, з украй низькополігональним ландшафтом і умовними позначеннями конкретних об'єктів (таких, як супутники наших віртуальних планет, наприклад). Самі розробники називають Mojoworld своєю "пісочницею", і для всіх охочих на сервері компанії Pandromeda, належною Масгрейву, викладена програма Mojoworld 3 Viewer, що дозволяє тільки "досліджувати", - не редагувати - віртуальні світи, створені користувачами Mojoworld, і рендерить з них "красиві картинки" скільки душі завгодно.
Для тих, хто хоче вникнути в суть питання серйозніше, пропонується, крім основної програми, ще неабияка кількість розширень, націлених на створення фотореалістичної рослинності, наприклад, або анімації об'єктів на сцені, і так далі.
Останні новини на сайті Pandromeda, на жаль, датовані 2006 роком. А Кен 'Doctor Mojo' Масгрейв нині прозивається Його честю Р. Кентоном Масгрейвом, і засідає в Зовнішньоторговельному суді США. Возитися йому з Mojoworld, швидше за все, ніколи. Також є ще таких програм такі як Terragen 2, E-on Vue, World Machine, VistaPro.
Якщо переглянуть, то виявиться, що вже для всіх 3D-редакторів, є свої топографічні генератори, причому в чималих кількостях. Є всі підстави вважати, що з часом їх ставатиме тільки більше. З одного боку ми спостерігаємо могутній крен у напрямі все більшій наочності (досить пригадати Sculpt-режим в Blender, редактор zbrush і так далі), яка сама по собі стала можливою лише завдяки стрибку продуктивності персональних комп'ютерів в останні півтора десятиліття, з іншої - збільшення складності завдань по візуалізації, особливо, якщо говорити про комп'ютерні ігри. Тому є серйозний попит на «економію зусиль» - якщо якийсь процес можливо автоматизувати, то це стає насущною необхідністю, так що якщо є програми, які справляються з складним завданням по візуалізації при мінімальних трудовитратах з боку людини, на них буде попит, і не тільки в професійному середовищі.
Також фрак тали[17] використовуються таких галузях як:
Економіка
Аналіз ринків - останнім часом фрактали стали популярним інструментом у трейдерів для аналізу стану біржових ринків.
Природні науки
У фізиці фрактали природним чином виникають при моделюванні нелінійних процесів, таких, як турбулентний перебіг рідини, складні процеси дифузії-адсорбції, полум'я, хмари і тому подібне Фрактали використовуються при моделюванні пористих матеріалів, наприклад, в нафтохімії. У біології вони застосовуються для моделювання популяцій і для опису систем внутрішніх органів (система кровоносних судин).
Радіотехніка
Фрактальні антени - використання фрактальної геометрії при проектуванні антенних пристроїв було вперше застосоване американським інженером Натаном Коеном, який тоді жив в центрі Бостона, де була заборонена установка зовнішніх антен на будівлі. Натан вирізував з алюмінієвої фольги фігуру у формі кривого Коха і наклеїв її на лист паперу, потім приєднав до приймача. Коену заснував власну компанію і налагодив їх серійний випуск.
Інформатика
Стиснення зображень - Існують алгоритми стиснення зображення за допомогою фракталів. Вони засновані на ідеї про те, що замість самого зображення можна зберігати стискаюче відображення, для якого це зображення (або деяке близьке до нього) є нерухомою крапкою. Один з варіантів даного алгоритму був використаний фірмою Microsoft при виданні своєї енциклопедії, але великого поширення ці алгоритми не набули.
Децентралізовані мережі
Система призначення IP-адресов в мережі Netsukuku використовує принцип фрактального стиснення інформації для компактного збереження інформації про вузли мережі. Кожен вузол мережі Netsukuku зберігає всього 4 Кб інформації про стан сусідніх вузлів, при цьому будь-який новий вузол підключається до загальної мережі без необхідності в центральному регулюванні роздачі IP-адресів, що, наприклад, характерний для мережі Інтернет. Таким чином, принцип фрактального стиснення інформації гарантує повністю децентралізованную, а отже, максимально стійку роботу всієї мережі.
2. Довжина берегової лінії. Фрактальна розмірність. Поняття фрактала.
При вивченні географії [17, 19]кожна з країн має свою площу території і довжину межі, зокрема, якщо країна омивається яким-небудь морем або океаном, то вона має морську межу певної довжини. Чи замислювалися ви коли-небудь, як цю довжину межі визначають? У 1977 р. американський математик Бенуа Мандельброт поставив перед собою наступне питання: чому рівна довжина берегової лінії Великобританії? Виявилось, що коректно відповісти на це "дитяче питання" не вдається. У 1988 р. норвезький учений Енс Федер вирішив з'ясувати, чому рівна довжина берегової лінії Норвегії. Звернете увагу на те, що побережжя Норвегії сильно порізане фіордами. Інші учені ставили собі аналогічні питання про довжини берегових ліній побережжя Австралії, Південної Африки, Німеччини, Португалії і інших країн.
Ми можемо зміряти довжину берегової лінії тільки приблизно. У міру того як ми зменшуємо масштаб, нам доводиться вимірювати все більше маленьких мисів і бухт - довжина берегової лінії збільшується, і об'єктивної межі зменшенню масштабу (і, тим самим, збільшенню довжини берегової лінії) просто не існує; ми вимушені визнати, що ця лінія має нескінченну довжину. Ми знаємо, що розмірність прямої лінії рівна одному, розмірність квадрата - двом, а розмірність куба - трьом. Мандельброт запропонував використовувати для вимірювання "жахливих" кривих дроби розмірності - розмірності Хаусдорфа - Безіковіча. Нескінченно зламані криві, подібні до берегової лінії, - не цілком лінії. Вони як би "замітають" частину площини, подібно до поверхні. Але вони і не поверхні. Значить, резонно припустити, що їх розмірність більше одного, але і менше двох, тобто це розмірні для дробу об'єкти.
Норвезький учений Е. Федер, запропонували інший спосіб вимірювання довжини берегової лінії. Карту покрили квадратною сіткою, осередки якої мають розміри е ? е. Видно, що число N(e) таких осередків, які покривають берегову лінію на карті, приблизно рівне числу кроків, за яке можна обійти по карті берегову лінію циркулем з розчином e. Якщо е зменшувати, то число N(e) зростатиме. Якби довжина берегової лінії Великобританії мала певну довжину L, те число кроків циркуля з розчином (або число квадратних осередків N(e), що покривають берегову лінію на карті) було б обернено пропорціонально, а величина Ln(e)=N(e) ? e при зменшенні до прагнула б до постійної L. На жаль, розрахунки, проведені багатьма ученими, показали, що це не зовсім так. При зменшенні кроку зміряна довжина зростає. Виявилось, що взаємозв'язок зміряної довжини L(e) і кроку e може бути описана наближеним співвідношенням
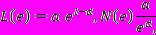
Коефіцієнт D називається фрактальною розмірністю. Слово фрактал походить від латинського слова fractal - дріб, нецілий. Множина називається фрактальною, якщо воно має нецілу розмірність. Для Норвегії D=1,52, а для Великобританії D=1,3. Таким чином, берегова лінія Норвегії і Великобританії - фрактал з фрактальною розмірністю D. Розрахунки були також проведені і для кола, і фрактальна розмірність кола D=1, що і слід було чекати. Таким чином, фрактальна розмірність - узагальнення звичайної розмірності.
Як це розуміти і що б це могло означати? Математики почали згадувати, чи було що-небудь подібне раніше в математиці чи ні? І пригадали! Розглянемо частину деякої лінії АВ на площині (Рис. 3). Візьмемо квадрат з ребром e і запитаємо себе: скільки потрібно квадратиків N(е) з ребром довжиною е, щоб покрити лінію АВ такими квадратиками? Видно, що N(e) пропорційно

Аналогічно, якщо замкнуту обмежену область на площині (Рис. 4) покрити квадратною сіткою із стороною e, то мінімальне число квадратиків із стороною е, що покривають область, буде рівне

Якщо ми розглянемо замкнуту обмежену область в тривимірному просторі і візьмемо кубик з ребром e, то кількість кубиків, що заповнюють цю область
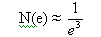
Визначимо фрактальну розмірність виходячи з вище за викладене в загальному випадку таким чином:
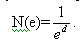
Візьмемо логарифм від лівої і правої частин

Переходячи до межі при e, прагнучому до нуля (N, прагнучому до нескінченності), отримаємо
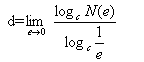
Ця рівність є визначенням розмірності яка позначається d.
Повернемося до наший початковому завданню. Розглянемо довжину берегової лінії L(е)= аoe1-d і зробимо наступні перетворення:
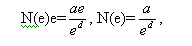
тобто N(e) пропорційно

і переходячи до межі, маємо
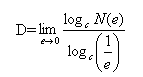
Таким чином, d - розмірність.
Розрахунки показують, що

Таким чином, берегові лінії Великобританії і Норвегії є фракталами і мають фрактальну розмірність 1,3 і 1,52, відповідно.
