Міністерство освіти та науки України
| Вид материала | Документы |
- Міністерство освіти І науки України Департамент міжнародного співробітництва та європейської, 39kb.
- Міністерство освіти І науки україни міністерство економіки україни міністерство фінансів, 18.39kb.
- Міністерство освіти І науки україни донецький обласний центр туризму та краєзнавства, 189.44kb.
- Міністерство освіти І науки україни, 335.34kb.
- Міністерство освіти І науки україни, 283.15kb.
- Міністерство освіти І науки, молоді та спорту україни, 59.16kb.
- Міністерство освіти І науки україни, 32.42kb.
- Міністерство освіти І науки, молоді та спорту України, 61.58kb.
- Міністерство освіти І науки україни положенн я про організацію фізичного виховання, 306.47kb.
- Міністерство освіти І науки україни інститут інноваційних технологій І змісту освіти, 43.77kb.
2.1. Приклади побудови фрактальних множин. Класифікація фракталів.
Проте чи існують в математиці множини[19], які мають фрактальну розмірність? Так, такі множини були відкриті в XIX і XX століттях. У 1883 р. німецький математик Георг Кантор (1845-1918) побудував множину, ім'я, що носить його (безліч Кантора). Побудова безлічі Кантора здійснюється таким чином: Одиничний відрізок розбивається на 3 рівних частини. Середня частина викидається. Що залишилися 2 частини знову розбиваються, кожна на 3 рівних частини, і середні їх частини викидаються. Відрізки, що вийшли, знову розбиваються, кожен на 3 рівних частини, і середні частини викидаються і так далі В межі виходить безліч Кантора.
Питається, чому рівна фрактальна розмірність безлічі Кантора? Застосуємо для її обчислення формулу (*). Щоб підрахувати по формулі (*), потрібно визначити e і N(e). На першому етапі побудови безлічі Кантора відрізок одиничної довжини можна покрити одним відрізком завдовжки в, тобто e = 1 і N(e)= 1.
У 1904 р. німецький математик Хельга фон Кох побудувала криву, яка в даний час носить її ім'я (крива Кох) Рис.. 1. Побудова починається з одиничного відрізання прямої. Одиничний відрізок прямої ділиться на 3 рівних частини. Середня частина віддаляється, а на місці середньої частини будується рівносторонній трикутник. У результаті виходить ламана лінія, що складається з 4 відрізань, кожен з яких рівний 1/3 .
Рис.1 «крива Коха»
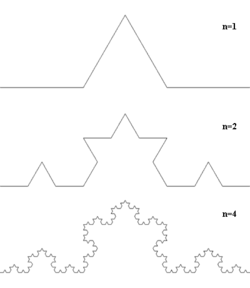
Далі, кожне з 4 відрізань знову ділиться на 3 рівних частини, на відрізках, розташованих в середині, будуються рівносторонні трикутники, і середні частини відрізань віддаляються. Ця процедура повторюється ще і ще раз. У результаті лінія стає дуже порізаною. Якщо цей процес повторювати нескінченно довго (тобто перейти до межі), то отримуємо безперервну криву, що ніде не диференціюється, і ця безперервна крива має ненульову "площу". Щоб в цьому переконатися, підрахуємо фрактальну розмірність кривий Кох. На першому етапі ми маємо один відрізок завдовжки 1, який можна покрити одним відрізком завдовжки, рівною 1, тобто e. = 1 і N(e)= 1. На другому етапі ми маємо 4 відрізання, кожен завдовжки, рівною 1/3 тому для покриття цих відрізань потрібно 4 відрізання завдовжки 1/3 тобто e=1/3 і N(e)=4.
Таким чином, ми вперше стикаємося з фрактальним множиною. Звична (або топологічна) розмірність канторової пилу рівна 0, а ось фрактальна, виявляється, нулю не рівна - вона строго більше; це і є, за визначенням Мандельброта, властивість фрактала.
Як і все в науці, фрактали прийнято ділити на класи або види. Кожен вид має своє особливе походження. Візьмемо, наприклад, геометричні фрактали. Один з найвідоміших прикладів цього вигляду - це килимок Серпінського який зображений Рис..2. Побудова його полягає в наступній: ви берете рівносторонній трикутник і в середині вирізуєте в нім дірку у вигляді такого ж трикутника, тільки перевернутого і в чотири рази меншого. Тепер в кожному з кутів у нас з'явилося по маленькому трикутнику. Повторюємо з ними те ж саме: в середині кожного вирізуємо маленький трикутник. І так далі, поки не втомитеся, або поки трикутники, що зменшуються, не зможете відрізнити від крапки.

Рис.2 Побудова килимка Серпінського
Приблизно також виходить решта всіх геометричних фракталів: ви берете якусь фігуру і починаєте застосовувати до неї, а потім до її частин, певна геометрична побудова достатня багато раз. Строго кажучи, цю процедуру треба повторювати нескінченна кількість разів. Але оскільки можливості нашого зору обмежені, та і життя не нескінченне, то можна зупинитися на побудові найдрібніших видимих деталей.
Фрактали наступного вигляду називаються алгеброю. Один з методів побудови фракталів алгебри полягає в наступному. Ви берете формулу, підставляєте в неї число і отримуєте результат. Потім підставляєте в цю ж формулу результат і отримуєте наступне число. Повторюємо цю процедуру багато раз. У математиці це називається ітераційний процес. В результаті виходить набір чисел, які є точками фрактала. Дивовижне те, що іноді ці формули до смішного прості - ви їх можете знайти в будь-якому шкільному підручнику алгебри 6-го класу. А ось фігури виходять вражаючої складності і краси. Таким чином малюють, наприклад, фрактал папороть зображений на Рис. 3.

Рис. 3 Фрактал "папороть".
Ще одним поширеним виглядом є стохастичні фрактали. Їх отримують, міняючи в ітераційному процесі деякі параметри випадковим чином. Цим способом можна намалювати такі природні об'єкти, як порізані берегові лінії, рельєф місцевості, хмари, хвилі на воді багато що інше. Тому фрактальні моделі сьогодні широко застосовують в комп'ютерних іграх, створюючи в них обстановку, яку вже важко відрізнити від реальності.
Мандельброт досліджував перетворення комплексної площини. Втім, перетворення, досліджене Мандельбротом, можна представити просто як перетворення площини. Мандельброт розглядав траєкторії крапок, які виходять при цьому перетворенні, і вивчав залежність картини, що виходить, від параметра С. Казалось би, нічого цікавого чекати не доводилося: настільки простим здавалося перетворення. Фіксуючи параметр З, Мандельброт спробував встановити ті області на площині, виходячи з яких, крапки не "тікають" на нескінченність, а утворена при ітераційному процесі послідовність залишається в обмеженій околиці. Виявилось, що значення таких параметрів З утворюють зв'язну множину з дивно химерною межею, і форма основної частини множини повторюється і повторюється в різних масштабах. Це множина і було названо безліччю Мандельброта яка зобажена на Рис. 4.

Рис. 4 Множина Мандельброта
Мандельброт опублікував дослідження знайденої ним множини в кінці 1980 року. Математики Р. Брукс і Дж. Мателськи випустили свою роботу з повідомленням про цю множину в 1978 році. Спочатку Брукс і Мателськи не надавали особливого значення своїй знахідці, проте згодом заявили, що є, щонайменше, співавторами відкриття. Дж. Хаббард повідомив, що спостерігав безліч Мандельброта на дисплеї свого комп'ютера в 1976 році. Крім того, Хаббард, Мателськи і Брукс запропонували вважати дійсним відкривачем безлічі французького математика Пьера Фату, що описав його ще в 1906 році. Проте у всіх цих випадках доводиться говорити навіть не про коріння фрактальної геометрії, а лише про її зерна - причому ще не пророслих; бо "автори" не змогли оцінити і зрозуміти сенс того, що вони знайшли. Що стикалися з безліччю Мандельброта учені вважали свої знахідки окремим випадком, майже випадковістю, і не побачили абсолютно нової області знань і досліджень. Не було осяяння, не було виходу за конкретну проблему. Тому першовідкривачем множини Мандельброта ми, без сумніву, можемо рахувати самого Б. Мандельброта. Тут варто звернути увагу на цікавий факт: Хаббард саме спостерігав безліч Мандельброта; не обчислив, не побудував - а бачив його. Точно так, як і побачив його і Мандельброт. Бачили вони одне і те ж. Це настільки схоже на відкриття в природних науках, що можна затверджувати: фрактали були відкриті експериментально. На відміну від своїх колег, Мандельброт майже знав, що він шукає, - але абсолютно не знав, що саме він знайде. Коли в своїх спогадах Мандельброт говорить про новенький комп'ютер Vax, з яким йому пощастило працювати, про погані дисплеї і принтер із слабким дозволом, що не дозволив йому відразу бачити свою множину, він говорить про них так само, як фізик про експериментальну установку, створення і застосування якої привело до відкриття.
2.2. Алгоритм фрактального шуму або шум перліна
Фрактальний шум або Шум Перліна[16,17] широко використовується в двомірній і тривимірній комп'ютерній графіці для створення таких візуальних ефектів, як дим, хмари, туман, вогонь і так далі… Він також дуже часто використовується як проста текстура, що покриває геометричну модель. На відміну від растрових текстур, шум Перліна є процедурною текстурою, і тому він не займає пам'ять, але разом з тим виконання алгоритму вимагає якихось обчислювальних ресурсів. Використання шуму перліна дуже поширене в демосценах, учасники якої використовують його в демках. Також на такому алгоритму працюють, такі програми для генерації ландшафтів, як Terragen, а також практично всі ігрові застосування, в яких робляться спроби хоч як те відобразити небо і згенерувати ландшафт.
Шум Перліна був створений Кеном Перліном (англ.) в 1983 році і згодом був названий на честь свого творця. Перлін створив свій алгоритм, працюючи в Mathematical Applications Group, Inc. У 1997 році Кен Перлін отримав нагороду Academy Award for Technical Achievement від Американської Академії кінематографічних мистецтв і наук за його внесок в створення фільму «Трон» випуску 1982 року.
Використання Perlin Noise для моделювання ландшафту і хмар є найбільш поширеним способом із-за його можливості масштабувати одно- двух- і тривимірного вигляду. Більш того, в алгоритм можна ввести четверте часове вимірювання, дозволяючи алгоритму динамічно змінювати текстури в часі і достатнього ступеня реалістичності для ряду додатків.
Взагалі кажучи, хмарна і ландшафтна поверхня володіє нерівномірною структурою, але і хаотичною. Звідси, для формування хмар і ландшафту необхідна якась хаотична функція, ядро якої підкоряється деякому певному закону. Цим умовам цілком задовольняють функції Perlin Noise, які є суть комбінація шумової функції і інтерполяційної функції. Аргументами для шумової функції виступають цілі числа (integer).
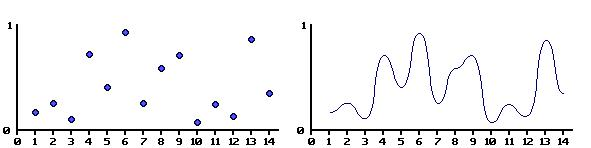
Комбінація шумової та інтерполяційної функції
Шумова функція
В результаті послідовного застосування цих двох функцій виходить, як показано на малюнках, функція, що володіє гладкістю і в теж час що володіє достатнім ступенем хаотичністю.
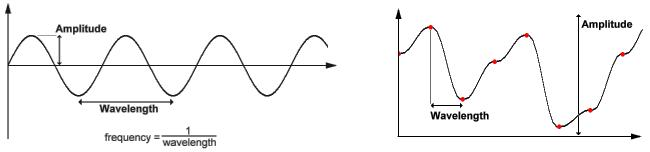
Синусна хвиля
Шумова хвиля
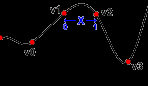
Основними величинами тут є амплітуда (amplitude) і частота (frequency). Амплітуда відповідає за висоту хвилю, частота рівна зворотному від довжини хвилі, довжина хвилі - це, по відношенню до шумової функції, відстань від однієї червоної крапки до іншої.
Але якщо фіксувати амплітуду і частоту, то отримувана функція все ще володіє достатнім ступенем рівномірністю. Рішення наступне: ми будуємо декілька функцій з різними амплітудами і частотами, а потім складаємо їх. Отримувана в результаті функція якраз задовольняє всім необхідним умовам
| початкові функції | |
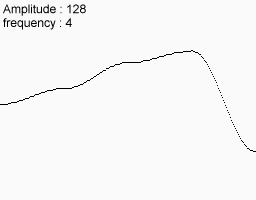 | 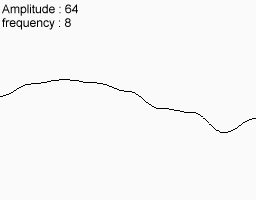 |
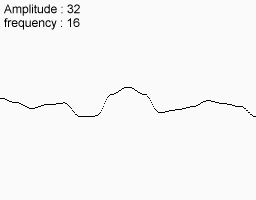 |  |
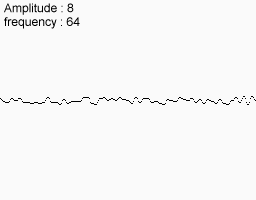 | 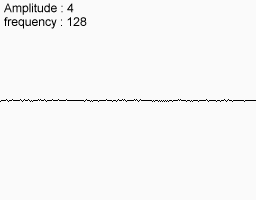 |
| Сумарна функція | |
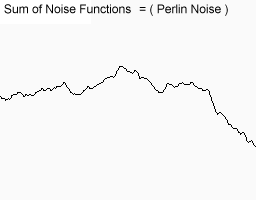 |
Амплітуду і частоту на кожному кроці змінюють по наступному закону:
frequency = 2i amplitude = persistence
де i - номер функції, що генерується. Величина persistence спеціально введена для забезпечення залежності амплітуди від частоти.
| зображення з фіксованою амплітудою і частотою | ||
 |  |  |
 |  |  |
| сумарне зображення | ||
 |
Октавою (octave) називається кожна функція, що згенерувала і додана в сумарний потік. Кількість октав, також, є основною величиною в даному процесі і впливає на якість зображення.
2.3. Реалізація алгоритму
Ядром тут служить шумова функція. Її можна визначити, наприклад, таким чином:
function IntNoise(32-bit integer: x)
x = (x<<13) x;
return ( 1.0 - ( (x * (x * x * 15731 + 789221) + 1376312589) & 7fffffff) / 1073741824.0);
end IntNoise function
Тут на вхід подається ціле число, а на виході виходить дробове число між -1.0 і 1.0.
Далі використовується інтерполяція. Тут, також, можливі деякі варіанти:
Лінійна інтерполяція:
function Linear_interpolate(а, b, x)
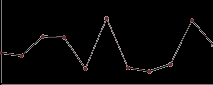
return a*(1-х)+ b*x
end of function
Це найпростіший спосіб інтерполяції: найшвидший, зате володіє поганою точністю.
Косинусна інтерполяція:
function Cosine_interpolate(а, b, x)
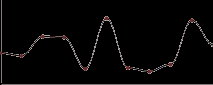
ft = x * 3.1415927
f = (1 - cos(ft)) * .5
return a*(1-f)+ b*f
end of function
Точніший метод, ніж лінійна інтерполяція (виходить гладка крива), зате повільніший за рахунок обчислення косинуса. Обчислення можна прискорити, якщо використовувати табличне завдання косинуса.
Кубічна інтерполяція:
function Cubic_interpolate(v0, v1, v2, v3,x)
P = (v3 - v2) - (v0 - v1)
Q = (v0 - v1) - P
R = v2 - v0
S = v1
return Px3 + Qx2 + Rx + S
end of function
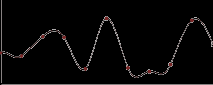
Це більш точний метод, ніж косинусна інтерполяція, але повільніший, за рахунок використання великої кількості множень. Як правило, досить використовувати лінійну або косинусную інтерполяцію.


На етапі інтерполяції відбувається згладжування кривої, але необхідно також згладжувати отримувану картинку, використовуючи двовимірні фільтри.
function Noise(x, y)
.
.
end function
function SmoothNoise_2D(x>, y)
corners = ( Noise(x-1, y-1)+Noise(x+1, y-1)+Noise(x-1, y+1)+Noise(x+1, y+1) ) / 16
sides = ( Noise(x-1, y) +Noise(x+1, y) +Noise(x, y-1) +Noise(x, y+1) ) / 8
center = Noise(x, y) / 4
return corners + sides + center
end function
Виходячи зі всіх умов і перетворень в результаті отримаємо наступний алгоритм отримання двовимірної картинки з використанням функцій Perlin Noise:
function Noise(integer x, integer y)
n = x + y * 57;
n = (n << 13) n;
return (1.0 - ((n * (n * n * 15731 + 789221) + 1376312589) & 7fffffff) / 1073741824.0);
end function
function SmoothNoise(float x, float y)
corners = (Noise(x-1, y-1) + Noise(x+1, y-1) + Noise(x-1, y+1) + Noise(x+1, y+1)) / 16
sides = (Noise(x-1, y) + Noise(x+1, y) + Noise(x, y-1) + Noise(x, y+1)) / 8
center = Noise(x, y) / 4
return corners + sides + center
end function
function InterpolatedNoise(float x, float y)
integer_X = int(x)
fractional_X = x - integer_X
integer_Y = int(y)
fractional_Y = y - integer_Y
v1 = SmoothedNoise(integer_X, integer_Y)
v2 = SmoothedNoise(integer_X + 1, integer_Y)
v3 = SmoothedNoise(integer_X, integer_Y + 1)
v4 = SmoothedNoise(integer_X + 1, integer_Y + 1)
i1 = Interpolate(v1 , v2 , fractional_X)
i2 = Interpolate(v3 , v4 , fractional_X)
return Interpolate(i1 , i2 , fractional_Y)
end function
function PerlinNoise_2D(float x, float y)
total = 0
p = persistence
n = Number_Of_Octaves - 1
loop i from 0 to n
frequency = 2i
amplitude = pi
total = total + InterpolatedNoise(x * frequency, y * frequency) * amplitude
end of i loop
return total
end function
Замість функції Interpolate зазвичай вибирається функція або лінійною, або косинусной інтерполяції.
Інтерактивна зміна наприклад хмарності істотно підвищує ступінь застосовності застосування. Зміна хмарності в реальному часі дозволяє точніше визначити можливості програми, а також відобразити ефект впливу хмар на підвищення реалістичності сцени як цілого.

Рис..5 «Зміна хмарності»
Якщо для моделювання хмар використовується Perlin noise, то для зміни хмарності досить відняти попіксельно деяку константу (оскільки отримуєм у результаті роботи алгоритму Perlin Noise карту інтенсивностей) і зробити значення менші нуля рівними нулю як це показано на Рис.5.
3. Історія розвитку комп’ютерної графіки та ігор
Найперші ігри для персональних комп'ютерів умовно можна було розділити на два типи - плоскі і векторні[2]. До першого відносилися незабутні "Arcanoid", "Тетріс". Всі вони надавали гравцеві поле для дії, розмір якої зазвичай відповідав розміру графічного екрану, і все відбувалося в двох вимірюваннях.
Інші ж ігри, наприклад авіасимулятор "F-19" гордо називалися "тривимірними", і в них віртуальність була конструкцією з ліній і багатокутників, координати якої обраховувалися із зміною ігровій ситуації, і потім вся вона проектувалася на площину, що співпадала з площиною екрану.
Трохи випередила розвиток комп'ютерів фірма Id Software, яка випустила спочатку "Catacomb Abyss", а потім і "Wolfenstein 3d". Ігри ці йшли ще на 2S6 процесорах, і є яскравим прикладом нового способу зображення віртуальності - текстурування.
По-перше, при цьому способі, стіни коридору, по яких бігає головний герой, - це не просто одноколірні прямокутники, а прямокутні растрові картинки (тобто, що складаються з точок), наприклад, рельєф цегляної стіни, або чий-небудь портрет. По-друге, зображення ворогів, яких гравець бачив "очима" персонажа, також були растровими. Ефект присутності в грі створювало масштабування - при наближенні до стіни її зображення збільшувалося, і відповідним чином масштабувався малюнок її текстури.
Перші тривимірні ігри - мова саме про полігональні движки, а не про псевдотривимірну піксельну графіку - катастрофічно не вистачало продуктивності CPU/GPU. Силоньок кремнієвих коней минулого рвали узду, закушували вудила, але ніяк не могли нормально справитися з прорахунком тривимірних сцен в режимі реального часу. Чи варто говорити, що віртуальні світи, хоч і були повністю тривимірними, не відрізнялися деталізацією.
Розробники, може, і ради були б зготувати з полігонів тривимірні гайки, картини на стіни, люстри і факели. Ось тільки куди до таких надмірностей, коли процесор і з опрацьовуванням основної геометрії не справляється? Адже глибина простору, його об'єм багато в чому залежить саме від дрібниць. Поступали просто: всі «дрібні» елементи - тіні, відблиски, шорсткості, знос і пошкодження - малювали пензликом на текстурах. Виходило, звичайно, плоско, але хоч якось. Як мовиться, не до жиру, бути б хоч трохи об'ємним.
Але «залізна» індустрія розвивалася, потужності процесорів росли, комп'ютерні ігри на місці теж не стояли. Як тільки заповітні мегагерци виросли до прийнятних величин, а в системних блоках більшості геймерів поселилися тривимірні прискорювачі, розробники почали замислюватися: з чого це раптом особливості поверхні намертво зашиті в текстуру? Адже метал, камінь, пластик та і будь-яка інша поверхня залежно від освітлення виглядає по-різному. Грязь, наприклад, погано відображає падаюче світло, потертості, навпаки, краще. Адже є ще і тіні, які прораховуються найпримітивнішим чином.
І були придумані шейдери - процедури, що визначають візуалізацію поверхні об'єкту залежно від різних вхідних даних. Світло, маски прозорості (задаючи області застосування шейдерів), карти віддзеркалення і карти рельєфу - під все були створені свої шейдери. Особливу увагу розробники стали приділяти саме картам рельєфу. Адже раніше тінь на текстурі... правильно, малювали пензликом. А що це за тінь, яка не міняє свого положення залежно від джерела світла?! Карта рельєфу ж відразу дозволила розраховувати тіні в реальному часі. Та і деталізація об'єктів помітно зросла: начебто, полігонів стільки ж, а «об'ємність» простору виросла на порядок.
За останній десяток років графічні карти [1], пізніше названі ЗD-акселераторами, пройшли чималий шлях розвитку - від перших SVGA- прискорювачів, про 3D узагалі нічого не знали, і до найсучасніших ігрових "монстрів", що беруть на собі усі функції, зв'язані з підготовкою і формуванням тривимірного зображення, що виробники іменують "кінематографічним". Природно, з кожним новим поколінням відеокарт творці додавали їм не тільки додаткові мегагерци і мегабайти відеопам'яті, Але і безліч самих різних функцій і ефектів. Давайте ж подивимося, чому, а головне і, навіщо навчилися акселератори останніх років, і що це дає нам, аматорам тривимірних ігор.
Але спочатку незайвим буде з'ясувати, які дії робить програма (чи гра) для того, щоб одержати в підсумку тривимірну картинку на екрані монітора. Набір таких дій прийнято називати 3D-конвеєром - кожен етап у конвеєрі працює з результатами попереднього. На першому, підготовчому, етапі програма визначає, які об'єкти (3D-моделі, частини тривимірного світу, спрайти та інше), з якими текстурами й ефектами, у яких місцях і в якій фазі анімації потрібно відобразити на екрані. Також вибираються положення й орієнтація віртуальної камери, через яку глядач дивуватися на світ. Весь цей вихідний матеріал, що підлягає подальшій обробці, називається ЗD-сценою.
Д

Рис.6.«Нефотореалістичний рендеринг»: використовування рейдерів для відтворення «плоскої» картини. Намальовану вручну.
алі настає черга власне 3D-конвейера. Першим кроком у ньому є теселяція - процес розподілу складних поверхонь на трикутники. Наступні обов'язкові етапи - взаємозалежні процеси трансформації чи координат крапок вершин, з яких складаються об'єкти,
їхнього висвітлення, а також відсікання
невидимих ділянок сцени.
Розглянемо трансформацію координат. У нас є тривимірний світ, у якому розташовані різні тривимірні ж об'єкти, а в підсумку потрібно одержати двовимірне плоске зображення цього світу на моніторі. Тому всі об'єкти проходять кілька стадій перетворення в різні системи координат, називаних ще просторами (sрасеs). Спочатку локальні, чи модельні, координати кожного об'єкта перетворюються в глобальні, чи світові, координати. Тобто , використовуючи інформацію про розташування, орієнтацію, масштаб і потоковому кадрі анімації кожного об'єкта, програма одержує вже набір трикутників у єдиній системі координат. Потім слідує перетворення в систему координат камери (саmеrа sрасе), за допомогою якої мі дивимося на модельований світ. Після чого відлік буде починатися з фокуса цієї камери - по суті як би "з очей" спостерігача. Тепер легше усього виключити з подальшої обробки цілком невидимі (відбраковування, чи cullіng) і "обрізати" частково видимі (відсікання, чи clіppіng) для спостерігача фрагменти сцени.
Паралельно виробляється висвітлення (lіghtіng). За інформацією про розташування, колір, тип і силі всіх розміщених у сцені джерел світла розраховується ступінь освітленості і колір кожної вершини трикутника. Ці дані будуть використані пізніше при растерізації. У самому кінці, після корекції перспективи, координати трансформуються ще раз, тепер вже в екранний простір (screen space).
На цьому закінчується тривимірна векторна обробка зображення і настає черга двовимірної, тобто текстурування і растерізації. Сцена тепер являє собою псевдо тривимірні трикутники, що лежати в площині екрана, Але ще з інформацією про глибину щодо площини екрана кожної з вершин. Растерізатор обчислює колір усіх пік селів, що складають трикутник, і заносити його в кадровий буфер. Для цього на трикутники накладаються текстури, часто в кілька шарів (основна текстура, текстура висвітлення, детальна текстура і т.д. ) і з різними режимами модуляції. Також виробляється остаточний розрахунок висвітлення з використанням якої-небудь моделі затінення, тепер уже для шкірного пікселя зображення. На цьому ж етапі виконується остаточне видалення невидимих ділянок сцени. Адже трикутники можуть розташовуватися на різній відстані від спостерігача, перекривати один одного чи цілком частково, а ті і перетинатися. Зараз повсюдно застосовується алгоритм із використанням Z-буфера. Результуючі пікселі заносяться в Z-буфер, і як тільки всі зображення буде готовий, його можна відображати на екрані і починати будувати наступне.
Тепер, коли нам зрозумілий пристрій ЗD-конвеєра в загальному виді, давайте глянемо на архітектурні розходження різних поколінь ЗD-прискорювачів. Кожна стадія ЗD-конвеєра дуже ресурсоємна, вимагає мільйонів і мільярдів операцій для одержання одному кадру зображення, причому двовимірні етапи текстурування і растерізації набагато прожерливе" геометричної обробки на ранніх, векторних, стадіях конвеєра. Так що перенос як можна більшої кількості стадій у "відео залізо" благотворно впливає на швидкість обробки ЗD-графіки і значно розвантажує CPU. Перше покоління прискорювачів брало на свої плечі тільки останній етап - текстуруваня і растерізацію, усі попередні кроки програма повинна була прорахувати сама за допомогою CPU. Рендерінг відбувався куди швидше, ніж при повній відсутності ЗD-акселерації, адже відео карта уже виконувала найбільш важку частину роботи. Але все-таки зі збільшенням складності сцен у ЗD-іграх програмна трансформації і висвітлення ставали вузькою шийкою, що перешкоджає збільшенню швидкості. Тому в ЗD-акселератори починаючи з перших моделей NVіdіa GeForce і АTі Radeon був доданий блок, іменований T&L-блоком. Як видно з назви, він відповідає за трансформацію і висвітлення, тобто тепер і за початкові стадії ЗD-конвейера. Його навіть вірніше називати Т&L-блоком (Transformatіon-Clіppіng-Lіghtіng), оскільки відсікання - теж його задача. Таким чином, гра, що використовує апаратний Т&L, практично цілком звільняє центральний процесор від роботи над графікою, а виходить, появляється можливість "навантажити" його іншими розрахунками, чи то чи фізика або штучний інтелект. Здавалося б, усі добрі і чого ще бажати? Але не варто забувати, що будь-який перенос функцій " у залізо " означає відмовлення від гнучкості, властивим програмним рішенням. І з появою апаратного T&L у програмістів і дизайнерів, що бажають реалізувати якийсь незвичайний ефект, залишилося лише три варіанти дій: вони могли або повністю відмовитися від T&L і повернутися до повільних, Але гнучким програмним алгоритмам, або намагатися втручатися в цей процес, виконуючи пост обробку зображення (що не завжди можливо і вуж точно дуже повільно)... або чекати реалізації потрібної функції в наступному поколінні відео карт. Виробників апаратури такий розклад теж не влаштовував - адже кожне додаткове T&L-розширення приводити до ускладнення графічного чипа і "роздуванню" драйверів відео карт.
Як ми бачимо, не вистачало способу гнучко, на "мікрорівні", керувати відеокартою. І така можливість була підказана професійними пакетами для створення ЗD-графіки. Називається вона шейдер (shader). По суті, шейдер - це невелика програма, що складається з набору елементарних операцій, що часто застосовуються в 3D-гpaфіці. Програма, що завантажується в акселератор і безпосередньо керуючою роботою самого графічного процесора. Якщо раніше програміст був обмежений набором заздалегідь визначених способів обробки й ефектів, те тепер він може складати з простих інструкцій будь-які програми, що дозволяють реалізовувати самі різні ефекти.
За своїми функціями шейдери поділяються на двох груп: вершинні (vertex shaders) і піксельні (pіxel shaders). Перші заміняють собою усю функціональність Т&L-блоку відеокарти і, як видно з назви, працюють з вершинами трикутників. В останніх моделях акселераторів цей блок фактично прибраний - його емулює відеодрайвер за допомогою вершного шейдера. Піксельні ж шейдери надають гнучкі можливості для програмування блоку мультитекстурування і працюють уже з окремими пікселями екрана.
Шейдери також характеризуються номером версії - кожна наступна додає до попередніх усі нові і нові можливості. Найбільш свіжою специфікацією піксельних і вершинних шейдерів на сьогоднішній день являється версія 3.0, підтримувана Dіrect 9, - на неї і будуть орієнтуватися як виробники акселераторів, так і розроблювачі нових ігор. На їхню підтримку апаратурою варто звертати увагу і користувачів, що бажає придбати сучасну ігрову відео карту. Проте експансія ігор, побудованих на шейдерних технологіях, тільки починається, так що і більш старі верхові шейдери (1.1), і піксельні (1.3 і 1.4) будуть використовуватися ще як мінімум рік, хоча б для створення порівняно простих ефектів - поки Dіrect 9-сумісні акселератори не одержати більшого розповсюдження.
Перші шейдери складалися усього з декількох команд, і їх неважко було написати на низькорівневому мові ассемблера. Але з ростом складності шейдерних ефектів, що нараховують іноді десятки і сотні команд, виникла необхідність у більш зручному, високорівневому мові написання шейдерів. Їх з'явилося відразу два: NVіdіa Cg (С for graphіcs) і Mіcrosoft HLSL (Hіgh Level Shadіng Language) - останній є частиною стандарту Dіrect 9. Тепер подивимося що необхідно для того, що б одержати всі ті можливості, що дає настільки остання технологія, як шейдери останнього покоління. А ну: Але наступне:
- сама свіжа версія Dіrect на даний момент це Dіrect 9.0с;
- відеокарта з підтримці Dіrect 9;
- самі свіжі драйвер відеокарти (у більш старі деякі функції можуть бути відсутні);
- гра, що використовує всі його можливості.
Відразу хотілося б розвіяти ймовірні омани. Деякі трактують популярний нині термін "Dіrect 9-сумісна відеокарта" у такий спосіб: "така відеокарта буде працювати і розкриваючи усі свої можливості тільки під APІ Dіrect 9", чи "Dіrect 9 варто встановлювати на комп'ютер тільки з такою відеокартою". Це не зовсім вірно. Подібне визначення скоріше означає: "дана відеокарта має можливості, необхідними від її специфікацією Dіrect 9".
