Нейроинформатика 2

Вид материала

Документы

Содержание Глава1. Нейроинформатика 1.1 Нейронные сети 1.1.1 Параллели из биологии 1.1.2 Базовая искусственная модель 1.1.3 Как работает нейросеть 1.1.4 Как построить сеть 1.1.5 Обучение нейросети 1.2 Применение нейросети 1.2.2 Кластеризация и поиск зависимостей Глава2. Применение нейросетевых методов обработки изображений 2.1 Дефектоскопия при производстве печатных плат - как объект применения нейросетевых методов 2.2 Виды нейросетей, применяемых для распознавания образов. 2.2.1 Сеть Хопфилда (HOPFIELD NET). 2.2.2 Сеть Хемминга (HAMMING NET) 2.2.3 Сеть Кохонена (KOHONEN'S NEURAL NETWORK) 2.2.4 Сеть поиска максимума (MAXNET) 2.2.5 Входная звезда (INSTAR) 2.3 Пример построения аппаратно-программного комплекса распознавания образов

Подобный материал:

• Труды V всероссийской научно-технической конференции "нейроинформатика-2003",, 33.45kb.
• Об интеграции системы: мозг-компьютер, 63.66kb.
• Уважаемые коллеги, студенты, аспиранты, 74.58kb.
• Уважаемые коллеги, студенты, аспиранты, 41.27kb.
• Уважаемые коллеги, студенты, аспиранты, 92.01kb.
• Уважаемые коллеги, студенты, аспиранты, 69.38kb.
• Рабочая программа дисциплины «нейроинформатика» Рекомендуется для направления подготовки, 160.94kb.
• Isbn 978-5-7262-1226 нейроинформатика 2010, 142.85kb.
• Isbn 978-5-7262-1377 нейроинформатика 2011, 107.92kb.
• Isbn 978-5-7262-1375 нейроинформатика 2011, 25.66kb.

Глава1. Нейроинформатика

В предшествующее десятилетие развитие средств вычислительной техники во всем мире испытало сильное влияние со стороны инициированной Японией программы "Пятое поколение компьютеров". Основным лозунгом этой программы было развитие систем искусственного интеллекта на основе алгоритмических языков. В 1992 г. программа "Пятое поколение" была завершена и ей на смену пришла программа "Вычисления в Реальном мире".

В ней речь идет, прежде всего о том, чтобы дать вычислительным и управляющим системам возможность самостоятельно, без помощи "переводчика" - человека воспринимать воздействия внешнего мира и действовать в нем. Авторы программы огромную роль - до 30-40% ее содержания отводят исследованию естественных и созданию искусственных нейросетевых систем.

Искусственные нейронные сети, они же коннекционистские или связевые системы представляют собой устройства, использующие огромное число элементарных условных рефлексов, называемых по имени недавно умершего канадского физиолога синапсами Хебба. Такой синапс, как основу возможных механизмов памяти и поведения, Д.Хебб описал теоретически в 1949 году, т.е. в первые годы после рождения кибернетики. Уже сейчас искусственные нейронные сети применяются для решения очень многих задач обработки изображений, управления роботами и непрерывными производствами, для понимания и синтеза речи, для диагностики заболеваний людей и технических неполадок в машинах и приборах, для предсказания курсов валют и результатов скачек. Та часть работ, которая связана с разработкой устройств переработки информации на основе принципов работы естественных нейронных систем относится к области нейроинформатики или нейровычислений (нейрокомпьютинга). Термины эти появились недавно - в середине 80-х годов.

Суть всех подходов нейроинформатики: разработка методов создания (синтеза) нейронных схем, решающих те или иные задачи. Нейрон при этом выглядит как устройство очень простое: нечто вроде усилителя с большим числом входов и одним выходом. Различие между подходами и методами - в деталях представлений о работе нейрона, и, конечно, в представлениях о работе связей. Собственно, как уже отмечалось выше, устройства нейроинформатики представляют собой связевые системы. В отличие от цифровых микропроцессорных систем, представляющих собой сложные комбинации процессорных и запоминающих блоков, нейропроцессоры содержат память, распределенную в связях между очень простыми процессорами. Тем самым основная нагрузка на выполнение конкретных функций процессорами ложится на архитектуру системы, детали которой в свою очередь определяются межнейронными связями.

1.1 Нейронные сети

В последние несколько лет мы наблюдаем взрыв интереса к нейронным сетям, которые успешно применяются в самых различных областях - бизнесе, медицине, технике, геологии, физике. Нейронные сети вошли в практику везде, где нужно решать задачи прогнозирования, классификации или управления. Такой впечатляющий успех определяется несколькими причинами:

• Богатые возможности. Нейронные сети - исключительно мощный метод моделирования, позволяющий воспроизводить чрезвычайно сложные зависимости. В частности, нейронные сети нелинейны по свой природе. На протяжении многих лет линейное моделирование было основным методом моделирования в большинстве областей, поскольку для него хорошо разработаны процедуры оптимизации. В задачах, где линейная аппроксимация неудовлетворительна (а таких достаточно много), линейные модели работают плохо. Кроме того, нейронные сети справляются с "проклятием размерности", которое не позволяет моделировать линейные зависимости в случае большого числа переменных.
  
• Простота в использовании. Нейронные сети учатся на примерах. Пользователь нейронной сети подбирает представительные данные, а затем запускает алгоритм обучения, который автоматически воспринимает структуру данных. При этом от пользователя, конечно, требуется какой-то набор эвристических знаний о том, как следует отбирать и подготавливать данные, выбирать нужную архитектуру сети и интерпретировать результаты, однако уровень знаний, необходимый для успешного применения нейронных сетей, гораздо скромнее, чем, например, при использовании традиционных методов статистики.
  

Нейронные сети привлекательны с интуитивной точки зрения, ибо они основаны на примитивной биологической модели нервных систем. В будущем развитие таких нейробиологических моделей может привести к созданию действительно мыслящих компьютеров.

1.1.1 Параллели из биологии

Нейронные сети возникли из исследований в области искусственного интеллекта, а именно, из попыток воспроизвести способность биологических нервных систем обучаться и исправлять ошибки, моделируя низкоуровневую структуру мозга (Patterson, 1996). Основной областью исследований по искусственному интеллекту в 60-е - 80-е годы были экспертные системы. Такие системы основывались на высокоуровневом моделировании процесса мышления (в частности, на представлении, что процесс нашего мышления построен на манипуляциях с символами). Скоро стало ясно, что подобные системы, хотя и могут принести пользу в некоторых областях, не ухватывают некоторые ключевые аспекты человеческого интеллекта. Согласно одной из точек зрения, причина этого состоит в том, что они не в состоянии воспроизвести структуру мозга. Чтобы создать искусственный интеллект, необходимо построить систему с похожей архитектурой.

Мозг состоит из очень большого числа (приблизительно 10,000,000,000) нейронов, соединенных многочисленными связями (в среднем несколько тысяч связей на один нейрон, однако это число может сильно колебаться). Нейроны - это специальные клетки, способные распространять электрохимические сигналы. Нейрон имеет разветвленную структуру ввода информации (дендриты), ядро и разветвляющийся выход (аксон). Аксоны клетки соединяются с дендритами других клеток с помощью синапсов. При активации нейрон посылает электрохимический сигнал по своему аксону. Через синапсы этот сигнал достигает других нейронов, которые могут в свою очередь активироваться. Нейрон активируется тогда, когда суммарный уровень сигналов, пришедших в его ядро из дендритов, превысит определенный уровень (порог активации).






Нетрудно построить математическую модель описанного процесса. На следующем рисунке изображена модель нейрона с тремя входами (дендритами), причем синапсы этих дендритов имеют веса w1, w2, w3. Пусть к синапсам поступают импульсы силы x1, x2, x3 соответственно, тогда после прохождения синапсов и дендритов к нейрону поступают импульсы w1x1, w2x2, w3x3. Нейрон преобразует полученный суммарный импульс x=w1x1+ w2x2+ w3x3 в соответствии с некоторой передаточной функцией f(x). Сила выходного импульса равна y=f(x)=f(w1x1+ w2x2+ w3x3).





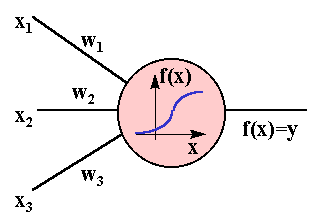
Таким образом, нейрон полностью описывается своими весами wk и передаточной функцией f(x). Получив набор чисел (вектор) xk в качестве входов, нейрон выдает некоторое число y на выходе.

Интенсивность сигнала, получаемого нейроном (а следовательно и возможность его активации), сильно зависит от активности синапсов. Каждый синапс имеет протяженность, и специальные химические вещества передают сигнал вдоль него. Один из самых авторитетных исследователей нейросистем, Дональд Хебб, высказал постулат, что обучение заключается в первую очередь в изменениях "силы" синаптических связей. Например, в классическом опыте Павлова, каждый раз непосредственно перед кормлением собаки звонил колокольчик, и собака быстро научилась связывать звонок колокольчика с пищей. Синаптические связи между участками коры головного мозга, ответственными за слух, и слюнными железами усилились, и при возбуждении коры звуком колокольчика у собаки начиналось слюноотделение.


Таким образом, будучи построен из очень большого числа совсем простых элементов (каждый из которых берет взвешенную сумму входных сигналов и в случае, если суммарный вход превышает определенный уровень, передает дальше двоичный сигнал), мозг способен решать чрезвычайно сложные задачи. Разумеется, мы не затронули здесь многих сложных аспектов устройства мозга, однако интересно то, что искусственные нейронные сети способны достичь замечательных результатов, используя модель, которая ненамного сложнее, чем описанная выше.

1.1.2 Базовая искусственная модель

Чтобы отразить суть биологических нейронных систем, определение искусственного нейрона дается следующим образом:

• Он получает входные сигналы (исходные данные либо выходные сигналы других нейронов нейронной сети) через несколько входных каналов. Каждый входной сигнал проходит через соединение, имеющее определенную интенсивность (или вес); этот вес соответствует синаптической активности биологического нейрона. С каждым нейроном связано определенное пороговое значение. Вычисляется взвешенная сумма входов, из нее вычитается пороговое значение и в результате получается величина активации нейрона (она также называется постсинаптическим потенциалом нейрона - PSP).
  
• Сигнал активации преобразуется с помощью функции активации (или передаточной функции) и в результате получается выходной сигнал нейрона.
  

Если при этом использовать ступенчатую функцию активации (т.е., выход нейрона равен нулю, если вход отрицательный, и единице, если вход нулевой или положительный), то такой нейрон будет работать точно так же, как описанный выше естественный нейрон (вычесть пороговое значение из взвешенной суммы и сравнить результат с нулем - это то же самое, что сравнить взвешенную сумму с пороговым значением). В действительности, как мы скоро увидим, пороговые функции редко используются в искусственных нейронных сетях. Учтите, что веса могут быть отрицательными, - это значит, что синапс оказывает на нейрон не возбуждающее, а тормозящее воздействие (в мозге присутствуют тормозящие нейроны).


Это было описание отдельного нейрона. Теперь возникает вопрос: как соединять нейроны друг с другом? Если сеть предполагается для чего-то использовать, то у нее должны быть входы (принимающие значения интересующих нас переменных из внешнего мира) и выходы (прогнозы или управляющие сигналы). Входы и выходы соответствуют сенсорным и двигательным нервам - например, соответственно, идущим от глаз и в руки. Кроме этого, однако, в сети может быть еще много промежуточных (скрытых) нейронов, выполняющих внутренние функции. Входные, скрытые и выходные нейроны должны быть связаны между собой.


Ключевой вопрос здесь - обратная связь (Haykin, 1994). Простейшая сеть имеет структуру прямой передачи сигнала: Сигналы проходят от входов через скрытые элементы и в конце концов приходят на выходные элементы. Такая структура имеет устойчивое поведение. Если же сеть рекуррентная (т.е. содержит связи, ведущие назад от более дальних к более ближним нейронам), то она может быть неустойчива и иметь очень сложную динамику поведения. Рекуррентные сети представляют большой интерес для исследователей в области нейронных сетей, однако при решении практических задач, по крайней мере до сих пор, наиболее полезными оказались структуры прямой передачи.

1.1.3 Как работает нейросеть

Искусственная нейронная сеть (ИНС, нейросеть) - это набор нейронов, соединенных между собой. Как правило, передаточные функции всех нейронов в сети фиксированы, а веса являются параметрами сети и могут изменяться. Некоторые входы нейронов помечены как внешние входы сети, а некоторые выходы - как внешние выходы сети. Подавая любые числа на входы сети, мы получаем какой-то набор чисел на выходах сети. Таким образом, работа нейросети состоит в преобразовании входного вектора в выходной вектор, причем это преобразование задается весами сети.

Практически любую задачу можно свести к задаче, решаемой нейросетью. В этой таблице показано, каким образом следует сформулировать в терминах нейросети задачу распознавания рукописных букв.

Задача распознавания рукописных букв
Дано: растровое черно-белое изображение буквы размером 30x30 пикселов	Надо: определить, какая это буква (в алфавите 33 буквы)
Формулировка для нейросети
Дано: входной вектор из 900 двоичных символов (900=30x30)	Надо: построить нейросеть с 900 входами и 33 выходами, которые помечены буквами. Если на входе сети - изображение буквы "А", то максимальное значение выходного сигнала достигается на выходе "А". Аналогично сеть работает для всех 33 букв.

Поясним, зачем требуется выбирать выход с максимальным уровнем сигнала. Дело в том, что уровень выходного сигнала, как правило, может принимать любые значения из какого-то отрезка. Однако, в данной задаче нас интересует не аналоговый ответ, а всего лишь номер категории (номер буквы в алфавите). Поэтому используется следующий подход - каждой категории сопоставляется свой выход, а ответом сети считается та категория, на чьем выходе уровень сигнала максимален. В определенном смысле уровень сигнала на выходе "А" - это достоверность того, что на вход была подана рукописная буква "A". Задачи, в которых нужно отнести входные данные к одной из известных категорий, называются задачами классификации. Изложенный подход - стандартный способ классификации с помощью нейронных сетей.

1.1.4 Как построить сеть

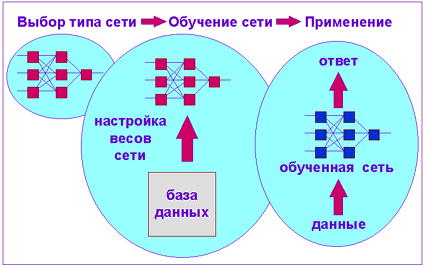
Теперь, когда стало ясно, что именно мы хотим построить, мы можем переходить к вопросу "как строить такую сеть". Этот вопрос решается в два этапа:

1. Выбор типа (архитектуры) сети.
   
2. Подбор весов (обучение) сети.
   

На первом этапе следует выбрать следующее:

• какие нейроны мы хотим использовать (число входов, передаточные функции);
  
• каким образом следует соединить их между собой;
  
• что взять в качестве входов и выходов сети.
  

Эта задача на первый взгляд кажется необозримой, но, к счастью, нам необязательно придумывать нейросеть "с нуля" - существует несколько десятков различных нейросетевых архитектур, причем эффективность многих из них доказана математически. Наиболее популярные и изученные архитектуры - это многослойный перцептрон, нейросеть с общей регрессией, сети Кохонена и другие.

На втором этапе нам следует "обучить" выбранную сеть, то есть подобрать такие значения ее весов, чтобы сеть работала нужным образом. Необученная сеть подобна ребенку - ее можно научить чему угодно. В используемых на практике нейросетях количество весов может составлять несколько десятков тысяч, поэтому обучение - действительно сложный процесс. Для многих архитектур разработаны специальные алгоритмы обучения, которые позволяют настроить веса сети определенным образом. Наиболее популярный из этих алгоритмов - метод обратного распространения ошибки (Error Back Propagation), используемый, например, для обучения перцептрона.

1.1.5 Обучение нейросети

Обучить нейросеть - значит, сообщить ей, чего мы от нее добиваемся. Этот процесс очень похож на обучение ребенка алфавиту. Показав ребенку изображение буквы "А", мы спрашиваем его: "Какая это буква?" Если ответ неверен, мы сообщаем ребенку тот ответ, который мы хотели бы от него получить: "Это буква А". Ребенок запоминает этот пример вместе с верным ответом, то есть в его памяти происходят некоторые изменения в нужном направлении. Мы будем повторять процесс предъявления букв снова и снова до тех пор, когда все 33 буквы будут твердо запомнены. Такой процесс называют "обучение с учителем".

При обучении сети мы действуем совершенно аналогично. У нас имеется некоторая база данных, содержащая примеры (набор рукописных изображений букв). Предъявляя изображение буквы "А" на вход сети, мы получаем от нее некоторый ответ, не обязательно верный. Нам известен и верный (желаемый) ответ - в данном случае нам хотелось бы, чтобы на выходе с меткой "А" уровень сигнала был максимален. Обычно в качестве желаемого выхода в задаче классификации берут набор (1, 0, 0, ...), где 1 стоит на выходе с меткой "А", а 0 - на всех остальных выходах. Вычисляя разность между желаемым ответом и реальным ответом сети, мы получаем 33 числа - вектор ошибки. Алгоритм обратного распространения ошибки - это набор формул, который позволяет по вектору ошибки вычислить требуемые поправки для весов сети. Одну и ту же букву (а также различные изображения одной и той же буквы) мы можем предъявлять сети много раз. В этом смысле обучение скорее напоминает повторение упражнений в спорте - тренировку.






Оказывается, что после многократного предъявления примеров веса сети стабилизируются, причем сеть дает правильные ответы на все (или почти все) примеры из базы данных. В таком случае говорят, что "сеть выучила все примеры", " сеть обучена", или "сеть натренирована". В программных реализациях можно видеть, что в процессе обучения величина ошибки (сумма квадратов ошибок по всем выходам) постепенно уменьшается. Когда величина ошибки достигает нуля или приемлемого малого уровня, тренировку останавливают, а полученную сеть считают натренированной и готовой к применению на новых данных.

Важно отметить, что вся информация, которую сеть имеет о задаче, содержится в наборе примеров. Поэтому качество обучения сети напрямую зависит от количества примеров в обучающей выборке, а также от того, насколько полно эти примеры описывают данную задачу. Так, например, бессмысленно использовать сеть для предсказания финансового кризиса, если в обучающей выборке кризисов не представлено. Считается, что для полноценной тренировки требуется хотя бы несколько десятков (а лучше сотен) примеров.

Повторим еще раз, что обучение сети - сложный и наукоемкий процесс. Алгоритмы обучения имеют различные параметры и настройки, для управления которыми требуется понимание их влияния.

1.2 Применение нейросети

После того, как сеть обучена, мы можем применять ее для решения полезных задач. Важнейшая особенность человеческого мозга состоит в том, что, однажды обучившись определенному процессу, он может верно действовать и в тех ситуациях, в которых он не бывал в процессе обучения. Например, мы можем читать почти любой почерк, даже если видим его первый раз в жизни. Так же и нейросеть, грамотным образом обученная, может с большой вероятностью правильно реагировать на новые, не предъявленные ей ранее данные. Например, мы можем нарисовать букву "А" другим почерком, а затем предложить нашей сети классифицировать новое изображение. Веса обученной сети хранят достаточно много информации о сходстве и различиях букв, поэтому можно рассчитывать на правильный ответ и для нового варианта изображения.

1.2.1 Классификация

Отметим, что задачи классификации (типа распознавания букв) очень плохо алгоритмизуются. Если в случае распознавания букв верный ответ очевиден для нас заранее, то в более сложных практических задачах обученная нейросеть выступает как эксперт, обладающий большим опытом и способный дать ответ на трудный вопрос.

Примером такой задачи служит медицинская диагностика, где сеть может учитывать большое количество числовых параметров (энцефалограмма, давление, вес и т.д.). Конечно, "мнение" сети в этом случае нельзя считать окончательным.





Классификация предприятий по степени их перспективности - это уже привычный способ использования нейросетей в практике западных компаний. При этом сеть также использует множество экономических показателей, сложным образом связанных между собой.





Нейросетевой подход особенно эффективен в задачах экспертной оценки по той причине, что он сочетает в себе способность компьютера к обработке чисел и способность мозга к обобщению и распознаванию. Говорят, что у хорошего врача способность к распознаванию в своей области столь велика, что он может провести приблизительную диагностику уже по внешнему виду пациента. Можно согласиться также, что опытный трейдер чувствует направление движения рынка по виду графика. Однако в первом случае все факторы наглядны, то есть характеристики пациента мгновенно воспринимаются мозгом как "бледное лицо", "блеск в глазах" и т.д. Во втором же случае учитывается только один фактор, показанный на графике - курс за определенный период времени. Нейросеть позволяет обрабатывать огромное количество факторов (до нескольких тысяч), независимо от их наглядности - это универсальный "хороший врач", который может поставить свой диагноз в любой области.

1.2.2 Кластеризация и поиск зависимостей

Помимо задач классификации, нейросети широко используются для поиска зависимостей в данных и кластеризации.

Например, нейросеть на основе методики МГУА (метод группового учета аргументов) позволяет на основе обучающей выборки построить зависимость одного параметра от других в виде полинома. Такая сеть может не только мгновенно выучить таблицу умножения, но и найти сложные скрытые зависимости в данных (например, финансовых), которые не обнаруживаются стандартными статистическими методами.


Кластеризация - это разбиение набора примеров на несколько компактных областей (кластеров), причем число кластеров заранее неизвестно. Кластеризация позволяет представить неоднородные данные в более наглядном виде и использовать далее для исследования каждого кластера различные методы. Например, таким образом можно быстро выявить фальсифицированные страховые случаи или недобросовестные предприятия.

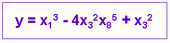
1.2.3 Прогнозирование

Задачи прогнозирования особенно важны для практики, в частности, для финансовых приложений, поэтому поясним способы применения нейросетей в этой области более подробно.

Рассмотрим практическую задачу, ответ в которой неочевиден - задачу прогнозирования курса акций на 1 день вперед.

Пусть у нас имеется база данных, содержащая значения курса за последние 300 дней. Простейший вариант в данном случае - попытаться построить прогноз завтрашней цены на основе курсов за последние несколько дней. Понятно, что прогнозирующая сеть должна иметь всего один выход и столько входов, сколько предыдущих значений мы хотим использовать для прогноза - например, 4 последних значения. Составить обучающий пример очень просто - входными значениями будут курсы за 4 последовательных дня, а желаемым выходом - известный нам курс в следующий день за этими четырьмя.

Если нейросеть совместима с какой-либо системой обработки электронных таблиц (например, Excel), то подготовка обучающей выборки состоит из следующих операций:

1. Скопировать столбец данных значений котировок в 4 соседних столбца.
   
2. Сдвинуть второй столбец на 1 ячейку вверх, третий столбец - на 2 ячейки вверх и т.д.
   

Смысл этой подготовки легко увидеть на рисунке - теперь каждая строка таблицы представляет собой обучающий пример, где первые 4 числа - входные значения сети, а пятое число - желаемое значение выхода. Исключение составляют последние 4 строки, где данных недостаточно - эти строки не учитываются при тренировке. Заметим, что в четвертой снизу строке заданы все 4 входных значения, но неизвестно значение выхода. Именно к этой строке мы применим обученную сеть и получим прогноз на следующий день.





Как видно из этого примера, объем обучающей выборки зависит от выбранного нами количества входов. Если сделать 299 входов, то такая сеть потенциально могла бы строить лучший прогноз, чем сеть с 4 входами, однако в этом случае мы имеем всего 1 обучающий пример, и обучение бессмысленно. При выборе числа входов следует учитывать это, выбирая разумный компромисс между глубиной предсказания (число входов) и качеством обучения (объем тренировочного набора).

Глава2. Применение нейросетевых методов обработки изображений

Все вышеперечисленные и аналогичные задачи тесным образом связаны с понятием образ и распознавание образа. Образ, класс — классификационная группировка в системе классификации, объединяющая (выделяющая) определенную группу объектов по некоторому признаку. Образное восприятие мира — одно из загадочных свойств живого мозга, позволяющее разобраться в бесконечном потоке воспринимаемой информации и сохранять ориентацию в океане разрозненных данных о внешнем мире. Воспринимая внешний мир, мы всегда производим классификацию воспринимаемых ощущений, т. е. разбиваем их на группы похожих, но не тождественных явлений.


Образы обладают характерным свойством, проявляющимся в том, что ознакомление с конечным числом явлений из одного и того же множества дает возможность узнавать сколь угодно большое число его представителей. В качестве образа можно рассматривать и некоторую совокупность состояний объекта управления, причем вся эта совокупность состояний характеризуется тем, что для достижения заданной цели требуется одинаковое воздействие на объект. Образы обладают характерными объективными свойствами в том смысле, что разные люди, обучающиеся на различном материале наблюдений, большей частью одинаково и независимо друг от друга классифицируют одни и те же объекты. Именно эта объективность образов позволяет людям всего мира понимать друг друга.


Способность восприятия внешнего мира в форме образов позволяет с определенной достоверностью узнавать бесконечное число объектов на основании ознакомления с конечным их числом, а объективный характер основного свойства образов позволяет моделировать процесс их распознавания. Будучи отражением объективной реальности, понятие образа столь же объективно, как и сама реальность, а поэтому это понятие может быть само по себе объектом специального исследования.


В целом проблема распознавания образов состоит из двух частей: обучения и распознавания. Обучение осуществляется путем показа отдельных объектов с указанием их принадлежности тому или другому образу. В результате обучения распознающая система должна приобрести способность реагировать одинаковыми реакциями на все объекты одного образа и различными — на все объекты различных образов. Очень важно, что процесс обучения должен завершиться только путем показов конечного числа объектов без каких-либо других подсказок. В качестве объектов обучения могут быть либо картинки, либо другие визуальные изображения (буквы), либо различные явления внешнего мира, например звуки, состояния организма при медицинском диагнозе, состояние технического объекта в системах управления и др. Важно, что в процессе обучения указываются только сами объекты и их принадлежность образу. За обучением следует процесс распознавания новых объектов, который характеризует действия уже обученной системы. Автоматизация этих процедур и составляет проблему обучения распознаванию образов. В том случае, когда человек сам разгадывает или придумывает, а затем навязывает машине правило классификации, проблема распознавания решается частично, так как основную и главную часть проблемы (обучение) человек берет на себя.

2.1 Дефектоскопия при производстве печатных плат - как объект применения нейросетевых методов

Традиционно контроль качества металлизированных отверстий печатных плат (ПП) осуществляется непосредственно на микрошлифах путем визуальной оценки геометрии и качества слоя металлизации. Структуру гальванической меди сравнивают с эталоном. Реально на производстве эту работу выполнят рабочий, в лучшем случае, высокой квалификации, но никак не технолог. Поскольку процесс выполняется визуальным методом, то время данной технологической операции велико, вероятность ошибок высока, кроме того, рабочий не может делать никакого анализа, кроме как “брак” или “не брак”.


Автоматизация данного контроля дает ряд преимуществ:

1. Уменьшение время на данную операцию.
   
2. Уменьшение вероятности ошибки, кроме того, в ответственном производстве технолог будет иметь возможность (по необходимости) контролировать правильность работы со своего рабочего места (при сетевой реализации программного комплекса) в режиме реального времени.
   
3. Если программный комплекс будет включать экспертную систему (она должна будет “знать” о структуре техпроцесса, его параметрах и режимах), то программный комплекс сможет оценить возможную причину брака и выработать рекомендации по методам его устранения (снижения). Экспертная система будет иметь возможность оценить процент брака при выборочных методах контроля.
   
4. Технологический отдел будет иметь возможность собирать различную статистическую информацию и, учитывая рекомендации программного комплекса, принимать решения о целесообразности использования тех или иных ТП.
   
5. При автоматизированном контроле качества металлизированных отверстий ПП необходимо распознавать образы микрошлифов на наличие различных видов дефектов.
   

Примеры характерных дефектов металлизированных отверстий ПП:






а) Разрыв металлизации






б) “Слезы”





в) Бочкообразная форма

Из примеров наглядно видно, что проблема анализа качества микрошлифов является непростой задачей даже для человека, т.к. человек, выполняющий данную работу, не является опытным технологом, а изготовить образцы микрошлифов на все разнообразие плат является не эффективным способом решения проблемы. Следовательно, система распознавания должна уметь не только грамотно классифицировать образы, но должна также быть обучена и проверена группой технологов.

2.2 Виды нейросетей, применяемых для распознавания образов.

Наибольшее использование для решения задач распознавания образов находят следующие нейросетевые методы: нейросетевой гауссов классификатор (Neural Gaussian Classifier), Сеть Хопфилда (HOPFIELD NET), Сеть Хемминга (HAMMING NET), Сеть Кохонена (KOHONEN'S NEURAL NETWORK), Сеть поиска максимума, Классификатор Карпентера/Гроссберга, Сеть встречного распространения (COUNTERPROPAGATION NETWORK), Сеть поиска максимума с прямыми связями(Feed-forward MAXNET ), Входная звезда (INSTAR).


Теоретически число слоев и число нейронов в каждом слое может быть произвольным, однако фактически оно ограничено ресурсами компьютера или специализированной микросхемы, на которых обычно реализуется НС. Чем сложнее НС, тем масштабнее задачи, подвластные ей.


Обучение НС может вестись с учителем или без него. В первом случае сети предъявляются значения как входных, так и желательных выходных сигналов, и она по некоторому внутреннему алгоритму подстраивает веса своих синаптических связей. Во втором случае выходы НС формируются самостоятельно, а веса изменяются по алгоритму, учитывающему только входные и производные от них сигналы.


Существует великое множество различных алгоритмов обучения, которые, однако, делятся на два больших класса: детерминистские и стохастические. В первом из них подстройка весов представляет собой жесткую последовательность действий, во втором – она производится на основе действий, подчиняющихся некоторому случайному процессу.


Еще одна классификация делит НС на синхронные и асинхронные. В первом случае в каждый момент времени свое состояние меняет лишь один нейрон. Во втором – состояние меняется сразу у целой группы нейронов, как правило, у всего слоя. Алгоритмически ход времени в НС задается итерационным выполнением однотипных действий над нейронами.

2.2.1 Сеть Хопфилда (HOPFIELD NET).

В основном сеть Хопфилда используется как ассоциативная память. Исходными данными для расчета значений синаптических весов сети являются векторы - образцы классов. Сеть функционирует циклически. Выход каждого из нейронов подается на входы всех остальных нейронов. Нейроны сети имеют жесткие пороговые функции.






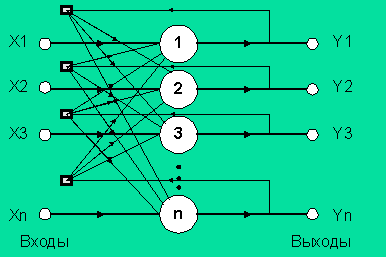
Итерации сети завершаются после того, как выходные сигналы нейронов перестают меняться. Размерности входных и выходных сигналов совпадают. Сеть, содержащая N нейронов может запомнить не более M=0.15*N образов. При этом запоминаемые образы не должны быть сильно коррелированы.


Недостатки :

• Сеть обладает небольшой емкостью.
  
• Наряду с запомненными образами в сети храняться и их негативы.
  
• Размерность и тип входных сигналов в точностью совпадают с размерностью и типом выходных сигналов. Это существенно ограничивает применение сети в задаче распознавания образов.
  
• При использовании коррелированных векторов-образцов возможно зацикливание сети в процессе функционирования.
  
• Квадратичный рост числа синапсов при увеличении размерности входного сигнала также можно считать недостатком сети.
  

2.2.2 Сеть Хемминга (HAMMING NET)

Использование вычисления расстояния Хемминга в задаче передачи двоичных сигналов фиксированной длины исследовалось в теории информации.


Р
асстояние Хемминга между двумя бинарными векторами одинаковой длины - это число несовпадающих бит в этих векторах. Нейронная сеть, которая реализует параллельное вычисление расстояний Хемминга от входного вектора до нескольких векторов- образцов, носит название сети Хемминга.


Размерности входных и выходных сигналов могут не совпадать. Число синапсов в сети: (n*m).


Недостатки :

• Сеть способна правильно распознавать (классифицировать) только слабо зашумленные входные сигналы.
  
• Возможность использования только бинарных входных сигналов существенно ограничивает область применения.
  

Преимущества:

• Сеть работает предельно просто и быстро.
  
• Выходной сигнал (решение задачи) формируется в результате прохода через всего лишь один слой нейронов. Для сравнения: в многослойных сетях сигнал проходит через несколько слоев. В сетях циклического функционирования сигнал многократно проходит через нейроны сети, причем число итераций, необходимое для получения решения, бывает заранее не известно.
  
• В модели использован один из самых простых алгоритмов формирования синаптических весов и смещений сети.
  
• В отличие от сети Хопфилда, емкость сети Хемминга не зависит от размерности входного сигнала, она в точности равна количеству нейронов (M). Сеть Хопфилда с входным сигналом размерностью 100 может запомнить 10 образцов, при этом у нее будет 10000 синапсов. У сети Хемминга с такой же емкостью будет всего лишь 1000 синапсов.
  

2.2.3 Сеть Кохонена (KOHONEN'S NEURAL NETWORK)

В мозге нейроны располагаются в определенном порядке так, что некоторые внешние физические воздействия вызывают ответную реакцию нейронов из определенной области мозга. Например, в той части мозга, которая отвечает за восприятие звуковых сигналов, нейроны группируются в соответствии с частотами входного сигнала, на которых они резонируют. Хотя строение мозга в значительной степени предопределяется генетически, отдельные структуры мозга формируются в процессе самоорганизации. Алгоритм Кохонена в некоторой степени напоминает процессы, происходящие в мозге. Алгоритм Кохонена дает возможность строить нейронную сеть для разделения векторов входных сигналов на подгруппы. Сеть состоит из M нейронов, образующих прямоугольную решетку на плоскости. Элементы входных сигналов подаются на входы всех нейронов сети. В процессе работы алгоритма настраиваются синаптические веса нейронов.






Входные сигналы - вектора действительных чисел - последовательно предъявляются сети. Желаемые выходные сигналы не определяются. После того, как было предъявлено достаточное число входных векторов, синаптические веса сети определяют кластеры. Кроме того, веса организуются так, что топологически близкие узлы чувствительны к похожим внешним воздействиям (входным сигналам).

Для реализации алгоритма необходимо определить меру соседства нейронов (меру близости).


Недостатки:

Сеть может быть использована для кластерного анализа только в том случае, если заранее известно число кластеров.


Преимущества:

В отличие от сети ART Гроссберга, сеть Кохонена способна функционировать в условиях помех, так как число классов фиксировано, веса модифицируются медленно, настройка весов заканчивается после обучения

2.2.4 Сеть поиска максимума (MAXNET)

Сеть циклического функционирования. На каждой итерации большие сигналы на выходах нейронов подавляют слабые сигналы на выходах других нейронов. Если в начале функционирования сети сигнал на выходе одного из нейронов имел максимальное значение, то в конце функционирования все выходы нейронов, кроме максимального, имеют значения, близкие к нулю. Таким образом, нейрон с наибольшим выходным сигналом побеждает. Это достигается за счет использования латеральных связей.





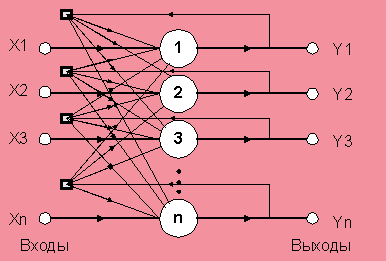
Итерации сети завершаются после того, как выходные сигналы нейронов перестают меняться.


Недостатки:

• Число итераций функционирования сети заранее не определено.
  
• Сеть определяет, какой из входных сигналов имеет максимальное значение, но в процессе функционирования теряет само значение максимального сигнала.
  

2.2.5 Входная звезда (INSTAR)

Входная звезда состоит из нейрона, на который подается группа входов через синаптические веса. Входные и выходные звезды могут быть взаимно соединены в сети любой сложности. Гроссберг рассматривал входные звезды как модели отдельных участков биологического мозга.





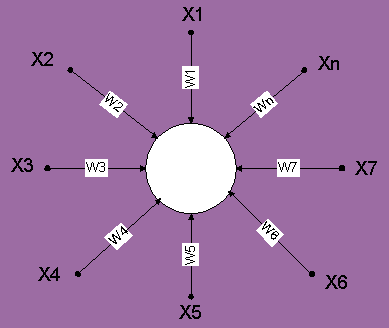
Входная звезда обучается реагировать на определенный входной вектор X и ни на какой другой. Это обучение реализуется путем настройки весов таким образом, чтобы они соответствовали входному вектору. Выход звезды определяется как взвешенная сумма ее входов. С другой точки зрения, выход можно рассматривать как свертку входного вектора с весовым вектором. Следовательно, нейрон должен реагировать наиболее сильно на входной образ, которому был обучен.


Недостатки:

Каждая звезда в отдельности реализует слишком простую функцию. Из таких звезд невозможно построить нейронную сеть, которая реализовала бы любое заданное отображение. Это ограничивает практическое применение входных звезд.


Преимущества:

Входная звезда хорошо моделирует некоторые функции компонент живых (биологических) нейронных сетей. Сеть, включающая в себя входные звезды, может быть достаточно хорошей моделью отдельных участков мозга.

2.3 Пример построения аппаратно-программного комплекса распознавания образов

Аппаратно-программный комплекс дефектоскопии печатных плат состояит из микроскопа, видеокамеры, средств ввода видеосигнала в ПК и специализированного прикладного программного обеспечения (ППО). Ядром ППО является подсистема распознавания образов, которая состоит из 6 модулей: модуль организации обмена с базами данных, модуль обработки обучающих пар, модуль обработки входной информации, нейроэмулятор, модуль алгоритмов обучения, модуль обработки выходных данных. На рисунке представлена функциональная схема системы и связи ее модулей в двух режимах работы системы: режиме обучения и режиме реальной работы





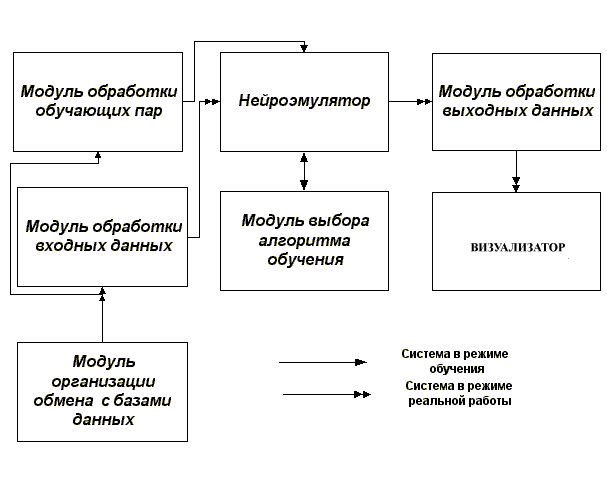
Интерфейс системы представляет собой стандартный оконный интерфейс Windows-приложения.





Выводы.


Совершенно ясно, что будущее методов неразрушающего контроля и дефектоскопии, связанных с обработкой видеообразов именно за использованием нейросетевых парадигм. Пока еще современные системы дефектоскопии и идентификации отнюдь не идеальны, осталось еще много нерешенных проблем. Например, система распознавания отпечатков пальцев плохо справляется с жирными пальцами или заляпанным стеклом у сканера и здесь на помощь разработчику могут прийти нейросетевых парадигмы.