Методические указания по определению устойчивости энергосистем
| Вид материала | Методические указания |
- Методические указания по определению величины накладных расходов в строительстве, 1125.86kb.
- Методические указания по определению величины накладных расходов в строительстве, (мдс, 1587.24kb.
- Методические указания по определению погрешностей при измерениях в лабораторном практикуме, 296.5kb.
- Методические указания по нормированию топливно-энергетических ресурсов при производстве, 3182.98kb.
- Методические рекомендации по определению норм потребления энергоресурсов бюджетными, 448.93kb.
- Методические указания, контрольные задания и указания на курсовой проект по дисциплине, 410.04kb.
- Методические указания по нормированию топливно-энергетических ресурсов при производстве, 1982.9kb.
- Т. В. Фёдоров методические указания по технологической практике студентов IV курса, 107.4kb.
- Методические указания по проведению диагностирования технического состояния и определению, 1416.48kb.
- Методические указания Методические указания по выполнению, оформлению и защите дипломного, 337.96kb.
2.2. Учет коэффициентов трансформации трансформаторов
и автотрансформаторов при составлении расчетных схем.
Приведение схемы к базисным условиям
2.2.1. Расчеты режимов и переходных процессов могут выполняться как в именованных, так и в относительных единицах. В последнем случае все параметры схемы и режима выражаются в долях соответствующих величин, принятых за базисные.
2.2.2. При перспективных расчетах на 5, 10, 15 лет вперед допустимо использовать средние номинальные коэффициенты трансформации. При этом среднее расчетное напряжение
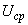составляет для каждой ступени трансформации одно из следующих значений: 1150; 750; 500; 330; 230; 154; 115; 37; 20; 15,75; 13,8; 10,5; 6,3; 3,15; 0,525 кВ.В случае конкретных расчетов, когда известны номинальное коэффициенты трансформации трансформаторов, но отсутствуют данные по установленным ответвлениям трансформаторов, рекомендуется осуществлять приведение параметров схемы по номинальным коэффициентам трансформации трансформаторов.
2.2.3. Если произведение коэффициентов трансформации, входящих в замкнутый контур, отлично от единицы, в расчетную схему должен быть введен дополнительный элемент - идеальный трансформатор. Такой трансформатор характеризуется только коэффициентом трансформации
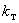при 
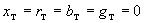.Идеальный трансформатор включается в замкнутый контур, причем все сопротивления электрической системы приводят к одному напряжению через выбранный расчетный коэффициент трансформации (как правило, за расчетный коэффициент трансформации принимают коэффициент трансформации одного из трансформаторов). Например, если электрические сети 220 и 110 кВ связаны трансформаторами, которые имеют коэффициенты трансформации 242/121 и 209/115, и если считать основным трансформатор с коэффициентом трансформации 242/121, то в точке включения другого трансформатора следует поместить идеальный трансформатор с коэффициентом трансформации 242/121·115/209=1,1, работающий на повышение напряжения в направлении шин 110 кВ.
2.2.4. При расчетах в системе относительных единиц за базисные величины при определении сопротивлений и параметров режима электрической системы произвольно могут быть выбраны из следующих четырех: кажущаяся мощность, ток, напряжение и полное сопротивление. Обычно в качестве базисных величин удобно принимать мощность
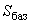и напряжение 
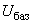на одной из ступеней трансформации. Тогда на этой ступени трансформации базисные сопротивление и ток определяются по формулам
; 
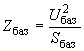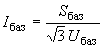. (2.55)На других ступенях трансформации базисные сопротивление и ток вычисляются по аналогичным формулам с тем лишь различием, что в них подставляется базисное напряжение
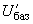, предварительно пересчитанное через коэффициенты трансформации к рассматриваемой ступени
; 
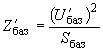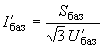. (2.56)Параметры схемы и ее режима (отн.ед.) на каждой из ступеней трансформации определяются по абсолютным значениям с помощью формул
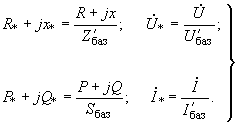(2.57)2.2.5. При определении в относительных единицах постоянных времени
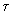и параметров, характеризующих механическое движение элементов электрической системы, за базисные величины принимаются синхронная частота 
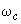и время поворотa ротора 
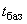на угол в один радиан при синхронной частоте вращения, т.е.
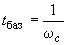. (2.58)Поэтому в относительных единицах
; 
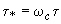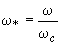. (2.59)Постоянные инерции агрегатов системы должны приводиться к базисной мощности:
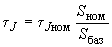. (2.60)2.3. Преобразование (эквивалентирование) сложных электрических систем
2.3.1. Решение многих практических задач может быть существенно упрощено, если выполнить упрощающие преобразования схемы энергосистемы так, чтобы в расчетной схеме уменьшить количество генераторных станций и узлов нагрузки [Л.32-38].
Преобразованная электрическая система может рассматриваться как эквивалентная исходной системе, но не во всех своих свойствах. С этой особенностью следует считаться при выполнении упрощающих преобразований, осуществляя их при возможно полном сохранении тех свойств системы, которые являются целью исследования.
2.3.2. Оценку возможных упрощений cлeдует делать при составлении схемы замещения электрической системы. При этом надо решить, необходимо ли воспроизводить всю схему системы или достаточно воспроизвести подробно только ее часть, а другую часть упростить. Упрощения могут быть сделаны как весьма грубые, так и более точные. Так, например, при оценке устойчивости протяженной электропередачи, связывающей станцию с мощной энергетической системой, в последней можно произвести грубые упрощения. К числу таких упрощений относится отбрасывание мелких станций и нагрузок, замена небольших станций и нагрузок одной эквивалентной станцией или нагрузкой, перенос нагрузок или станций в точку присоединения другой станции или нагрузки, разрыв слабых связей, объединение общими шинами пунктов, связанных короткими линиями и т.п. В том же случае, когда в задачу входит исследование устойчивости протяженной электропередачи при коротких замыканиях в приемной энергосистеме, часть системы, где предполагают делать короткие замыкания, следует воспроизвести в расчетной схеме с минимальными упрощениями.
2.3.3. Первым этапом упрощения расчетной схемы является исключение второстепенных элементов схемы: мелких нагрузок, параллельных линий, некоторых замкнутых контуров и т.д. При этом осуществляется перенос мелких нагрузок в узловые точки схемы, преобразование пассивных элементов путем осуществления эквивалентных ее преобразований. Следующим этапом расчета может явиться упрощение схем замещения станции, при котором генераторы приводятся к одному эквивалентному.
2.3.4. Значение
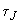эквивалентного генератора определяется по формуле
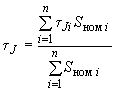, (2.61)где
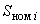- номинальная кажущаяся мощность 
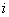-го из объединяемых агрегатов.Значение постоянной времени
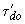эквивалентного генератора
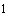определяется по формуле 
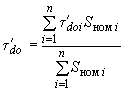, (2.62)_________________
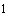Определение терминов см. в приложении 1.2.3.5. На заключительном этапе выполняются эквивалентные преобразования предварительно упрощенной схемы. При этом рекомендуется применять изложенную ниже методику, предусматривающую замену группы станций одной эквивалентной.
2.3.6. При анализе устойчивости энергосистемы объединение генераторных станций в одну, которую условно можно назвать эквивалентной, должно осуществляться таким образом, чтобы изменения ее угла
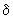наилучшим образом отразили движение группы объединяемых станций относительно остальных станций системы. Эта задача может быть решена, если в эквивалентную объединяются станции, относительные углы сдвига роторов которых остаются неизменными в течение всего расчетного интервала переходного процесса.Погрешность эквивалентирования тем меньше, чем ближе реальное движение объединяемых станций к идеально синфазному и, следовательно, находится в прямой связи с тем, насколько удачно выбрана группа станций для объединения. Для такого выбора рекомендуется пользоваться либо опытом эксплуатации, либо результатами ранее выполненных расчетов переходных процессов, либо, наконец, выполнить специальные расчеты режима объединяемых станций в условиях, которые позволят в той или иной мере оценить расхождение относительных углов. В простейшем случае предусматривается объединение станций с близкими значениями постоянных инерции и примерно равными значениями собственных проводимостей и взаимных проводимостей между ветвями объединяемых станций, а также между этими ветвями и ветвью, в которой предполагается расчетное короткое замыкание.
2.3.7. Объединению не подлежат станции, система автоматического регулирования которых может вызвать самораскачивание генераторов в исследуемых режимах системы. Опыт показывает, что самораскачивание в системах практически возможно при применении тех или иных систем сильного регулирования, поэтому станции, снабженные такими регуляторами, должны учитываться в схеме замещения системы как самостоятельные элементы, не входящие и преобразуемые участки схемы.
2.3.8. В схеме энергосистемы (рис.2.9) выделяются узловые точки, к которым подключены генераторные станции системы. Участки сети на рис.2.9 условно показаны в виде прямоугольников; связь между участками системы осуществляется ветвями 1, 2, ...,
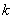, которые в дальнейшем называются ветвями примыкания преобразуемого участка системы к остальной системе. Для пояснения этого понятия на рис.2.10 показан участок электрической сети, связывающей преобразуемые и непреобразуемые участки системы, в которой выделена ветвь примыкания.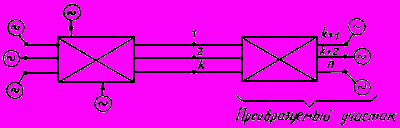
Рис.2.9. Условная схема сложной энергосистемы
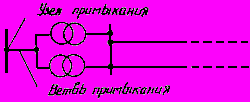
Рис.2.10. Узел и ветвь примыкания
Преобразуемый участок энергосистемы после эквивалентирования в общем случае будет представлен
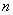-угольником, вершинами которого являются:- узлы примыкания к неэквивалентируемой части системы (рис.2.10);
- узел эквивалентного генератора;
- узел нулевого потенциала ("земля").
Большинство применяемых методов требует:
- приведения эквивалентируемого участка к одной ступени напряжения;
- объединения шин генераторов станций преобразуемого участка в один узел эквивалентного генератора.
В случае если узлы примыкания представляются в дальнейших расчетах узлами на разных ступенях напряжения, соответствующие ветви полученного эквивалентного
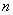-угольника становятся трансформаторами.2.3.9. Для практического использования рекомендуются методы эквивалентирования, основанные на:
1) расчете собственных и взаимных сопротивлений между узлами примыкания, узлом эквивалентного генератора и узлом нулевого потенциала;
2) разнесении нагрузок по правилу моментов в сети, представленной только реактивными сопротивлениями;
3) расчете собственных и взаимных сопротивлений с учетом режима сети и сохранением режима в узлах и ветвях примыкания (см. рис.2.9).
2.3.10. Основные положения первого метода заключаются в следующем:
а) эквивалентируемый участок системы представляется как активными, так и реактивными сопротивлениями;
б) эквивалентируемый участок системы приводится к одной ступени напряжения;
в) генераторы эквивалентируемого участка объединяются в один эквивалентный генератор на их шинах. Активные и реактивные сопротивления, характеризующие эквивалентный генератор, определяются параллельным сложением соответствующих сопротивлений, объединяемых генераторов. Постоянная инерции определяется по формуле (2.61), а постоянные времени - по формуле (2.62);
г) нагрузки эквивалентируемого участка системы представляются постоянными сопротивлениями, определяемыми по номинальному напряжению сети;
д) эквивалентный
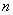-угольник определяется расчетом собственных и взаимных сопротивлений (проводимостей) по любому из известных методов и программ;е) баланс мощности для эквивалентного генератора и эквивалентного
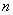-угольника для последующей установки режима определяется ориентировочно вручную.Этот метод применяется для эквивалентирования удаленных частей энергосистем. К недостаткам метода следует отнести: возможность появления отрицательных активных сопротивлений в эквивалентном
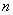-угольнике, затрудняющих моделирование сети, а также трудности баланса и установки режима в узлах и ветвях примыкания.2.3.11. Основные положения второго метода по пп.б, в, е совпадают с первым методом, а отличающиеся пп.а, г, д выполняются следующим образом:
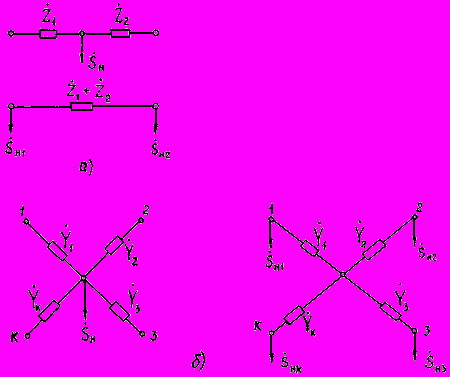
Рис.2.11. Перенос нагрузок из промежуточной точки:
а - в два соседних узла; б - в несколько соседних узлов
- эквивалентируемый участок системы представляется только реактивными сопротивлениями;
- нагрузки эквивалентируемого участка системы представляются мощностями и разносятся по правилу моментов на шины генераторного напряжения и в узлы примыкания. При этом перенос нагрузки из промежуточной точки в два соседних узла (рис.2.11) выполняется по формуле
; 
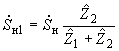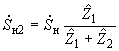. (2.63)Перенос нагрузки из промежуточной точки в несколько соседних узлов (см. рис.2.11, б) осуществляется по формуле
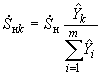; (2.64)- эквивалентный
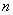-угольник определяется или расчетом собственных и взаимных сопротивлений (проводимостей) по любому из известных методов и программ или с помощью широко известных преобразований "треугольник в звезду", "звезда в треугольник", "многолучевая звезда в многоугольник" и т.п. Поскольку этот метод применяется при ручном эквивалентировании, часто разнесение нагрузок и преобразование сети выполняют последовательно друг за другом - сначала разносят нагрузки, затем преобразуют свободный от нагрузок участок сети, затем снова разносят нагрузки и преобразуют сеть до тех пор, пока все нагрузки не оказываются приложенными в узлах примыкания и в узле эквивалентного генератора, а сеть не превратится в эквивалентны 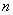-угольник. Поскольку при таком методе эквивалентирования при преобразовании сети не учитывается емкостная проводимость линий, следует, подсчитав суммарную генерацию реактивной мощности этими линиями, уменьшить на это значение реактивную мощность нагрузок в окончательной эквивалентной схеме.Этот метод применяется при эквивалентировании энергосистем, сравнительно удаленных от места возмущения, при эквивалентировании вручную сравнительно небольших участков систем, при представлении электростанций одним эквивалентным генератором и т.д. К недостаткам метода следует отнести трудности расчета режима в эквивалентной схеме.
2.3.12. Третий метод - эквивалентирование с учетом режима сети и сохранением режима в узлах и ветвях примыкания - является наиболее точным и перспективным методом. Связанный с обязательным использованием цифровых вычислительных машин метод позволяет определить режимные параметры эквивалентного генератора и сохранить заранее известный режим в ветвях и узлах примыкания.
Если считать, что станции
, 
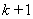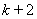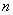, ..., на рис.2.9, выделенные для объединения, работают синфазно, то условиями эквивалентности режима исходной и преобразованной систем являются [Л.10]: равенство мощностей в ветвях примыкания в обоих схемах; равенство мощности эквивалентной станции сумме мощностей объединяемых станций; определение постоянной инерции эквивалентной станции по (2.61). Предполагается, что синхронные машины замещаются постоянными ЭДС и постоянными сопротивлениями.2.3.13. При определении параметров схемы замещения преобразованного участка системы следует различать два случая:
- режим преобразуемого участка предварительно рассчитан, причем найдены напряжения во всех узловых точках сети, а также определены ЭДС объединяемых генераторных станций по значению и фазе;
- известна схема электрических соединений преобразуемого участка системы, мощности нагрузок этого участка, мощности, протекающие в ветвях примыкания, и напряжения в соответствующих им узлах (см. рис.2.10), тогда как для определения режима, работы каждой из объединяемых станций нет достаточно достоверных данных.
Первый случай обычно имеет место при анализе переходных процессов уже существующей системы, для которой хорошо известны и параметры оборудования, и условия экономически целесообразного распределения мощности между ее электрическими станциями. Второй случай имеет место при исследовании перспективных режимов существующих систем или при проектных расчетах. В этих условиях строгий расчет нормального режима может быть затруднен и не всегда оправдан из-за отсутствия полных сведений о ряде параметров системы и ее режима.
2.3.14. В первом из указанных случаев сформулированные выше условия эквивалентности режима исходной и преобразованной систем удовлетворяются тогда, когда схема замещения преобразованной части системы имеет структуру, показанную на рис.2.12. Эта схема представляет собой многоугольник с диагоналями и нагрузочными ветвями в узлах примыкания и узле эквивалентной станции. Отличительная особенность схемы заключается в том, что значения входящих в нее сопротивлений должны приниматься различными в зависимости от того, определяется ли режим ветвей примыкания (см. рис.2.12, а) или эквивалентной генераторной станции (см. рис.2.12, б).
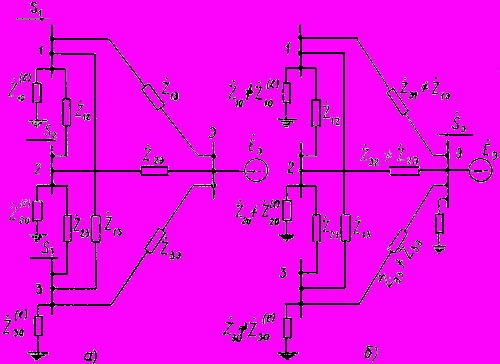
Рис.2.12. Схема замещения преобразованной части энергосистемы для частного случая трех ветвей примыкания:
а - для расчета режима ветвей примыкания; б - для расчета режима эквивалентной станции
2.3.15. При определении параметров схемы замещения, предназначенной для нахождения мощностей, токов или напряжений в ветвях и узлах примыкания, а также в непреобразуемой части схемы (см. рис.2.12, а), ЭДС эквивалентной станции должна выбираться произвольно как по модулю, так и по фазе. Целесообразно эти значения устанавливать такого же порядка, который характерен для ЭДС объединяемых станций. При выбранной ЭДС
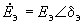взаимные проводимости между ветвями примыкания и ветвью эквивалентной станции 
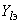вычисляются по
, 
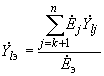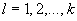. (2.65)Числитель этой формулы представляет сумму произведений, каждое из которых в качестве сомножителей содержит ЭДС одной из объединяемых станций
(
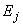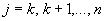) и взаимною проводимость 
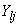между ветвью этой 
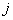-й станции и той ветвью примыкания 
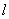, для которой вычисляется искомая проводимость эквивалентной схемы.Взаимные проводимости между ветвями примыкания
(
; ; 
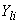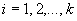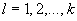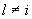) в эквивалентной схеме, также как и собственные проводимости этих ветвей 
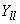, имеют те же значения, что и в исходной непреобразованной схеме. При известных собственных и взаимных проводимостях проводимости нагрузочных ветвей в схеме замещения определяются выражениями
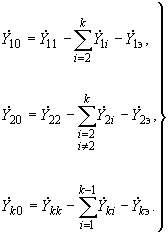(2.66)Для частного случая трех ветвей примыкания (см. рис.2.12)
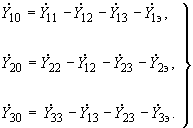(2.67)Проводимость нагрузочной ветви эквивалентной станции в рассматриваемой схеме принимается равной нулю.
2.3.16. Параметры схемы замещения, предназначенной для определения мощностей и токов эквивалентной станции (см. рис.2.12, б), вычисляются в аналогичной последовательности. При принятой ЭДС эквивалентной станции определяются взаимные проводимости между ветвями примыкания и ветвью эквивалентной станции
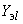, но по иной, нежели в первом случае, формуле: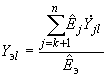
(2.68)
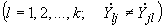.2.3.17. Взаимные проводимости между ветвями примыкания и собственные проводимости этих ветвей принимаются равными соответствующим значениям в первой схеме, проводимости нагрузочных ветвей вычисляются по формулам
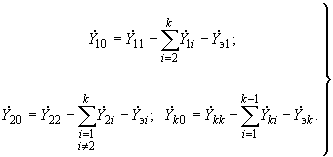(2.69)
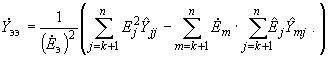(2.70)2.3.18. Все приведенные выше формулы справедливы при любом числе ветвей примыкания и объединяемых станций. Для частного случая одной ветви примыкания в схеме возможен также и другой подход к определению параметров схемы замещения преобразуемого участка системы. В этом случае условия эквивалентности режима исходной и преобразованной систем могут быть удовлетворены при одних и тех же сопротивлениях схемы как при определении характеристик режима ветви примыкания и непреобразованной части системы, так и при вычислении мощностей и токов в ветви эквивалентной станции. Однако ЭДС эквивалентной станции при этом должна быть принята разной в зависимости от того, режим какой из ветвей примыкания рассчитывается.
В этом случае при вычислении параметров схемы (рис.2.13) следует произвольно задаться модулем взаимной проводимости между ветвью примыкания и ветвью эквивалентной станции. Удобно при этом принимать
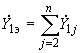. (2.71)Тогда модуль ЭДС эквивалентной станции
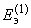, которая должна учитываться в схеме при расчете характеристик ветви примыкания, определяется по формуле
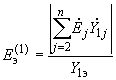, (2.72)а при расчете режима эквивалентной станции -
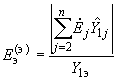. (2.73)Собственная проводимость в ветви привыкания в преобразованной схеме имеет то же значение, что и в исходной схеме, т.е.
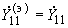, (2.74)собственная же проводимость ветви эквивалентной станции определяется выражением
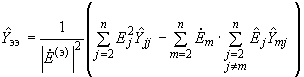. (2.75)Фазные углы (
;
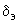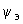) комплексных ЭДС эквивалентной станции и взаимной проводимости 
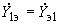должны вычисляться по формулам
; 
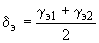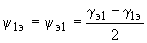, (2.76)где
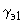и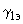 
- аргументы комплексных выражений.
; 
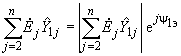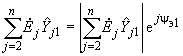. (2.77)Результаты всех выполненных расчетов позволяют получить все параметры П-образной схемы замещения, показанной на рис.2.13, причем
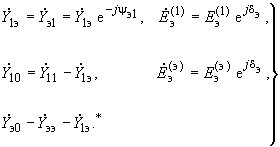(2.78)_______________
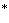Формула соответствует оригиналу. - Примечание "КОДЕКС".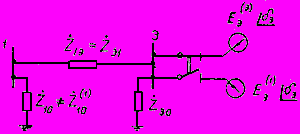
Рис.2.13. Схема замещения при наличии одной ветви примыкания
Обе ЭДС эквивалентной станции характеризуются одним и тем же фазным углом
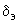.2.3.19. При выполнении преобразований в условиях, когда отсутствуют достоверные данные о режиме работы каждой из объединяемых станций, т.е. при приближенном эквивалентировании, преобразуемый участок системы также представляется схемой замещения, имеющей вид многоугольника с диагоналями и нагрузочными сопротивлениями. Причем в этом случае все параметры схемы, а также ЭДС эквивалентной станции не меняются в зависимости от того, режим какой из ветвей предполагается определять на основании такой схемы.
Для их определения составляется полная схема замещения преобразуемого участка системы, в которую нагрузки вводятся постоянными сопротивлениями, вычисляемыми по их заданным мощностям и номинальному напряжению сети. В эту схему входят сопротивления всех элементов системы, ограниченной узлами примыкания и шинами генераторного напряжения объединяемых станций. Применительно к этой схеме вычисляются собственные проводимости ветвей примыкания и взаимные проводимости между этими ветвями (в соответствии с расчетной схемой, приведенной на рис.2.14). Определяется также собственная проводимость эквивалентной станции, для чего шины генераторного напряжения объединяемых станций считаются соединенными с общим источником напряжения
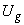, а ветви примыкания - замкнутыми накоротко. Расчетная схема для определения собственной проводимости эквивалентной станции показана на рис.2.15, из которого следует, что
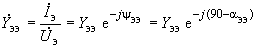. (2.79)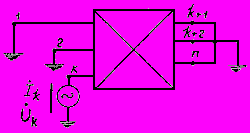
Рис.2.14. Расчетная схема преобразуемого участка системы
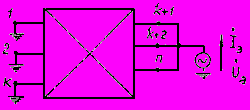
Рис.2.15. Расчетная схема для определения собственной проводимости эквивалентной станции
2.3.20. Все эти данные служат для определения напряжения на шинах эквивалентной станции по величине и фазе, взаимных проводимостей между ветвью этой станции и ветвями примыкания, а также нагрузочных сопротивлений эквивалентной схемы замещения. Исходными данными при этом служат также суммарные активная
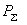и реактивная 
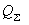мощности объединяемых станций, которые устанавливаются приближенно, причем
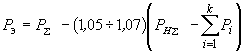; (2.80)
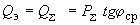, (2.81)где
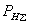- сумма активных мощностей преобразуемого участка системы;
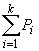- сумма активных мощностей в ветвях примыкания, которые считаются положительными при направлении к преобразуемому участку;
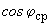- средний коэффициент мощности объединяемых станций, устанавливаемый либо по данным эксплуатации, либо в зависимости от числа трансформаций основного напряжения сети и среднего коэффициента мощности нагрузки.2.3.21. На основании всех этих величин фазный угол напряжения на шинах
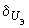эквивалентной станции определяется из следующего трансцендентного уравнения [Л.10], которое может быть решено графоаналитическим методом
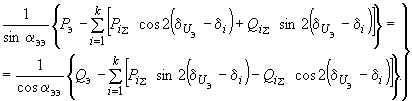(2.82)В этой формуле
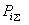и 
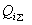- соответственно активная и реактивная мощности, состоящие из нескольких слагающих мощностей, протекающие в 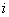-й ветви примыкания, причем
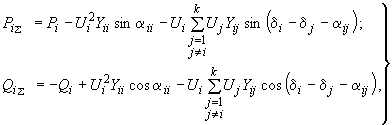(2.83)где
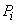и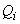 
- активная и реактивная мощности, заданные в 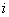-й ветви примыкания;
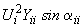и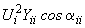 
- собственные активная и реактивная мощности в 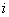-й ветви привыкания.Последние члены в формулах (2.83) характеризуют взаимные мощности в ветвях примыкания, определяемые взаимными сопротивлениями и напряжениями в узлах примыкания. В частном случае при равенстве напряжений в узлах примыкания по фазе (
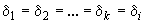) уравнение приводится к квадратному и, следовательно, решается в общем виде. При этом
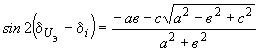, (2.84)где
;
;
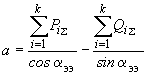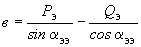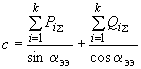.2.3.22. Модуль напряжения на шинах эквивалентной станции определяется по формуле
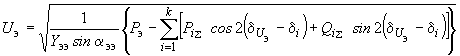. (2.85)Взаимные проводимости
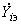между ветвью эквивалентной станции и ветвями примыкания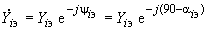
определяются расчетом из выражения
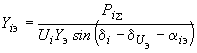, (2.86)причем
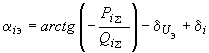. (2.87)В частном случае при одной ветви примыкания
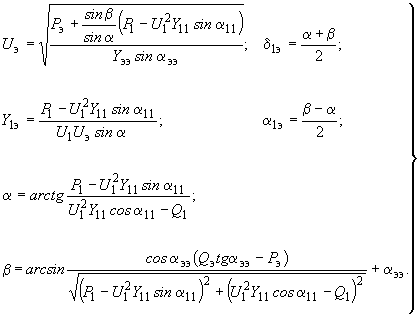(2.88)2.3.23. Вне зависимости от принятого метода эквивалентирования правильность его результатов должна быть обязательно проверена. Для этого следует по найденным эквивалентным параметрам преобразованной схемы определить полную мощность ветвей примыкания и полную мощность эквивалентной станции. Совпадение значений этих мощностей с заданными мощностями в ветвях примыкания и с суммой мощностей объединяемых станций свидетельствует об отсутствии ошибок в расчетах эквивалентных параметров.
2.4. Определение собственных и взаимных проводимостей схемы замещения электрической системы
2.4.1. Первый метод заключается в приведении схемы замещения системы путем последовательно выполняемых преобразований к виду многоугольника с диагоналями и нагрузочными сопротивлениями в узлах. При этом применяются в последовательности, зависящей от конфигурации схемы, следующие преобразования: замена треугольника эквивалентной звездой и обратно, замена многолучевой звезды эквивалентным многоугольником, последовательное и параллельное сложение сопротивлений отдельных ветвей.
2.4.2. В многоугольнике, являющемся конечным результатом преобразований, сопротивления сторон и диагоналей представляют собой значения, обратные взаимным проводимостям, с индексами, отвечающими нумерации узлов, между которыми включены указанные сопротивления. Собственные проводимости ветвей схемы
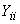определяются по формуле
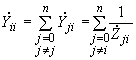. (2.89)Недостатком рассматриваемого метода является отсутствие общего алгоритма расчета, последовательность которого варьируется в зависимости от структуры системы. Этот метод преобразований рекомендуется для определения собственных и взаимных проводимостей только сравнительно простых схем.
2.4.3. Второй метод состоит в том, что все ветви в схеме замещения, для которых определяются собственные и взаимные проводимости, кроме одной (
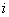-й), замкнуты на обратный провод, а в одну из ветвей включен источник напряжения 
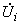. По результатам этого расчета определяются проводимости
, 
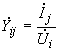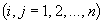, (2.90)где
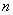- число ветвей, для которых определяются искомые проводимости.Расчеты повторяются при включении источника напряжения последовательно во все ветви, для которых определяются собственные и взаимные проводимости.
2.4.4. При использовании ЦВМ для определения проводимостей по данному методу в ветвь каждой из генераторных станций (последовательно) включается источник напряжения, тогда как ЭДС других генераторных станций считаются равными нулю. Результаты такого расчета позволяют определить собственные и взаимные проводимости по формуле (2.90).
2.4.5. Третий метод рекомендуется для схем с двумя генераторными станциями, соединенными схемой электропередачи. Собственные
, 
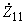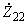и взаимные 
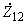сопротивления определяются через комплексные константы 
, 
, 
, 
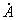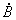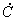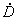соответствующего четырехполюсника по формулам
; 
; 
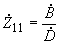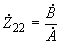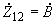. (2.91)2.4.6. Для определения констант
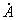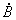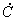, , и 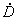анализируемая схема должна быть разбита на участки, для каждого из которых (рассматриваемого в свою очередь в качестве четырехполюсника) известны значения констант. Схема электропередачи с установкой продольной компенсации и шунтирующими реакторами (рис.2.16) содержит пять последовательно включенных четырехполюсников: два из них соответствуют участкам линии, один - батарее конденсаторов и два - шунтирующим реакторам. Константы четырехполюсников определяются следующим образом:- для участка линии длиной
;
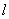
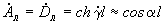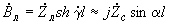; (2.92)
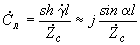,где
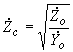- волновое сопротивление линии;
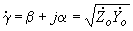- коэффициент распространения волны на единицу длины линии;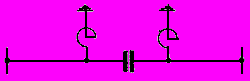
Рис.2.16. Схема замещения электропередачи
- для установки продольной компенсации
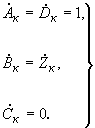(2.93)где
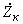- сопротивление батареи конденсаторов;- для шунтирующих реакторов с сопротивлением, равным
,
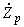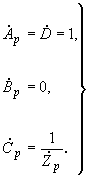(2.94)2.4.7. Константы всей совокупности взаимно связанных четырехполюсников вычисляются по правилам сложения четырехполюсников. При последовательном сложении двух четырехполюсников (рис.2.17) эквивалентные параметры находятся путем перемножения квадратных матриц, составленных из констант первого и второго четырехполюсников:
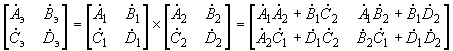. (2.95)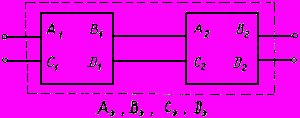
Рис.2.17. Схема сложения двух четырехполюсников
Таким образом,
;
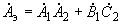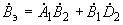;(2.96)
;
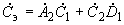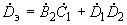.Для
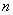последовательно включенных четырехполюсников эквивалентные константы определяют произведения матриц
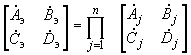. (2.97)2.4.8. При расчете собственных и взаимных проводимостей очень сложных и разветвленных электрических систем могут встретиться случаи, когда одним расчетом не удается определить все искомые величины из-за ограниченного объема памяти ЦВМ. В этих случаях cxему замещения следует разбить на отдельные подсхемы, для каждой из которых вычислить собственно проводимости ветвей примыкания подсхем друг к другу и взаимные проводимости между этими ветвями. В результате такого расчета каждая из выделенных подсхем будет представлена схемой замещения, имеющей вид многоугольника с диагоналями и нагрузочными сопротивлениями в узлах примыкания. Если расчет собственных и взаимных проводимостей выполнен методом преобразований, то в результате непосредственно определяются параметры такой схемы замещения. Если расчет ведется иным образом и результатом его являются значения собственных и взаимных проводимостей для каждой из ветвей примыкания, то для получения значений нагрузочных сопротивлений используется формула
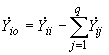, (2.98)где
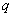- число сторон и диагоналей многоугольника, связанных с 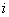-м узлом.Возможно также представление части выделенных из общей схемы участков в виде многоугольника с диагоналями и нагрузочными сопротивлениями при сохранении исходной схемы замещения, составленной из сопротивлений элементов системы для других участков. Такая схема может быть также получена не только при определении собственных и взаимных проводимостей какого-либо выделенного участка системы, но и при упрощающих преобразованиях этого участка с целью уменьшения числа генераторных станций в его расчетной схеме. В каждом из этих случаев полученная схема может служить для вычисления собственных и взаимных проводимостей исходной системы. При выполнении соответствующих расчетов могут быть применены все указанные выше методы.
2.4.9. Если нужно определять собственные и взаимные проводимости для схем, отличающихся друг от друга лишь сопротивлением ограниченного числа элементов, то соответствующие расчеты могут быть существенно упрощены, если за исходные данные принять собственные и взаимные проводимости участка системы, не претерпевающего изменений при переходе от одной расчетной схемы к другой. Тогда изменение схемы может рассматриваться как включение дополнительных сопротивлений в те или иные ее ветви. При включении такого сопротивления
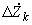в ветвь 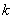схемы, имеющей 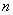ветвей, для которых вычисляются собственные и взаимные проводимости, новые значения искомых проводимостей определяются по формулам
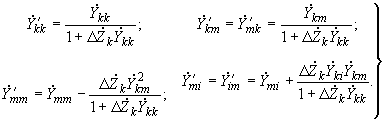(2.99)При включении дополнительных сопротивлений в две ветви и более приведенные формулы следует применять последовательно для постепенно усложняющихся схем. Каждая последующая из них должна отличаться от предыдущей включением дополнительного сопротивления лишь в одну из ветвей первоначальной схемы.
2.4.10. Для частного случая двухмашинной схемы замещения системы собственные и взаимные проводимости при включении дополнительных сопротивлений в цепи обеих генераторных станций могут быть найдены по формулам
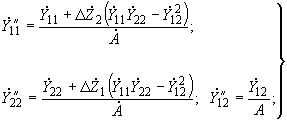(2.100)где
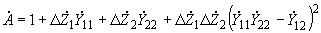.2.4.11. При определении собственных и взаимных проводимостей для ветвей сложной системы при изменениях параметров некоторых элементов и схемы замещения можно также воспользоваться приемом разделения схемы замещения на две части (подсхемы), связанные друг с другом одной ветвью примыкания. Одна из подсхем (I) при этом должна включать ветви, сопротивлениям которых при расчете переходных процессов предполагается придавать несколько значений. Другая подсхема (II) состоит из элементов с неизменяющимися сопротивлениями. При таком подходе подсхема I характеризуется рядом значений собственных и взаимных проводимостей, тогда как каждая из проводимостей ветвей подсхемы II имеет одно единственное значение.
Собственные и взаимные проводимости для схемы замещения всей системы в целом определяются по приведенным ниже формулам, в которые входят собственные и взаимные проводимости, предварительно вычисленные для подсхем I и II. При этом [Л.10] собственная проводимость
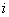-й станции, расположенной в подсхеме I, определяется по формуле
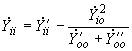; (2.101)для взаимной проводимости между ветвью
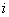и ветвью 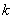, расположенной в подсхеме II, справедлива формула
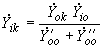. (2.102)Взаимная проводимость между ветвям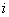и
и 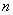, расположенными в одной и той же подсхеме I, определяется по формуле
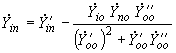, (2.103)где
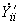- собственная проводимость ветви 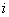подсхемы I;
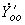- собственная проводимость ветви примыкания в подсхеме I;
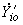- взаимная проводимость между ветвью 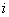и ветвью примыкания в подсхеме I;
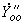- собственная проводимость ветви примыкания в подсхеме II;
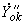- взаимная проводимость между ветвью 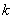и ветвью примыкания в подсхеме II;
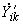- взаимная проводимость между ветвям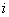и и 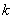в подсхеме I*._________________
* По этим алгоритмам в проблемной лаборатории электрических систем МЭИ составлена программа на языке АЛГОЛ-60.
2.4.12. Некоторые частные случаи расчета параметров установившегося режима приведены в приложении 2.