Geum.ru

Рич Р. К. Политология. Методы исследования: Пер с англ. / Предисл. А. К. Соколова

Вид материалаАнализ

Содержание


15. Статистика ii: изучение взаимосвязей между двумя переменными
Измерение связи и статистической значимости
Подобный материал:
1   ...   23   24   25   26   27   28   29   30   ...   35
[c.402]

Возьмем группу из 11 человек, 10 из которых зарабатывают 10.000 долларов в год, а один – 1 млн. Значение среднего геометрического дохода для этой группы – 100.000 долларов.



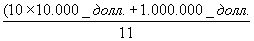
Но 10 из 11 членов группы зарабатывают, по сути дела, десятую часть этого количества. Таким образом, среднее геометрическое, хотя и точно подсчитанное, тем не менее не так репрезентативно, как, скажем, медиана, которая в другом случае равна 10.000 долларов. Вообще говоря, статистические процедуры с меньшими возможностями (предназначенные для более низких уровней измерения) всегда можно использовать в анализе данных, и, хотя они теряют некоторую информацию (например, расстояние до предельного значения, как здесь), иногда с их помощью можно получить более значимые результаты. Поспешим отметить, однако, что обратное неверно; статистические процедуры с высоким уровнем возможностей не имеют ни малейшей ценности для шкал низких уровней.

Наиболее часто употребляемый способ измерения дисперсии для интервальных данных, стандартное отклонение, из всех видов статистических процедур, которые мы используем, вероятно, один из интереснейших. На первый взгляд может показаться, что если мы хотим определить, насколько по отношению к распределению в целом типично среднее геометрическое, то все, что нужно сделать, – это измерить расстояние от его точки до каждого случая, сложить их и разделить на количество случаев N. Иными словами, мы подсчитаем среднее геометрическое расстояний вокруг среднего геометрического распределения по формуле:



Чем больше дисперсия для данного распределения, тем менее типично среднее геометрическое, и, чем меньше дисперсия, тем более типично среднее геометрическое. [c.403]

Но если мы попробуем сделать все это на примере, скажем, рис. 14.2в, возникнут некоторые проблемы. Применив формулу к этому случаю, мы получим:



Даже в случае распределения с таким сильным отклонением, как в примере с доходами, мы получим:



И в любом случае среднего геометрического для любого распределения результат будет тот же. Причина проста. Мы, по сути дела, определили среднее геометрическое как такую точку, где все веса и интервалы уравновешены, точку или значение, относительно которых все остальное сбалансировано. Следовательно, при подсчете среднего геометрического вряд ли стоит удивляться, что мы получим [c.404] как раз то, что предполагалось. Тем не менее искушение измерить дисперсию путем измерения близости признаков к или удаления их от среднего геометрического сохраняет свою притягательность. Введем понятие стандартного отклонения.

Стандартное отклонение (s) является тем математическим инструментом, который может помочь выполнить вашу задачу. По сути дела, это процедура, которая сводит на нет свойства разнонаправленных интервалов уравновешивать друг друга путем простого возведения в квадрат утих интервалов (и избавляясь таким образом от отрицательных значений), измерения разброса квадратов интервалов вокруг среднего геометрического и затем извлечения из результата квадратного корня, с тем чтобы вернуться к начальным единицам интервалов. Формула, по которой все это вычисляется, напоминает прежнюю, акромe возведения в квадрат и извлечения квадратного корня. Формула эта такова:



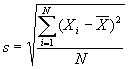
где Xi – значение каждого отдельного случая;
– среднее геометрическое;
N – количество случаев;
– знак суммы всех отдельных случаев от 1 до N.

Таким образом, для примера на рис. 14.2в



Она выражена в тех же единицах, что и исходные данные. Если переменные измеряются в одних и тех же или единицах, то стандартное отклонение может основой для выяснения репрезентативности средних геометрических; чем больше стандартное отклонение, ее репрезентативно среднее геометрическое. Но если единицы принципиально отличны или если анализируется одна переменная, интерпретация стандартного отклонения уже не столь проста.

Существует одно исключение из этого: переменные, чье [c.405] распределение близко к нормальному, т.е. такие, у которых существует единственная мода в самом центре распределения, а частоты симметрично убывают по направлениям к предельным значениям (графическое изображение нормального распределения, с которым вы, наверно, хорошо знакомы, – это просто колоколообразная кривая). Известно (из рассуждений, которые не входят в рамки нашего разговора), что в таких случаях 68,3% всех случаев лежат в пределах одного стандартного отклонения, от среднего геометрического (± s), 95,5% – в пределах двух стандартных отклонений от среднего геометрического (± 2s) и 99,7% – в пределах трех стандартных отклонений от среднего геометрического ( ± 3s). Фактически в случае таких распределений мы для любой точки можем определить, на сколько стандартных отклонений ниже или выше среднего геометрического она находится, и затем использовать эту информацию для выяснения относительного положения двух признаков в одной переменной или, наоборот, относительного значения двух переменных для одного и того же признака. Позволяет это сделать нам стандартная оценка, (z), которая вычисляется по следующей формуле: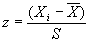



Представьте, что мы располагаем данными, например, по затратам на образование на душу населения в каждом штате, количеству работающих преподавателей на 1000 студентов в каждом штате и количеству награжденных выпускников средней школы на 100.000 населения в каждом штате в определенном году и что значения этих переменных по штатам распределяются по кривой, близкой к нормальной. Представьте затем, что мы хотим использовать эти данные для изучения политики в области образования в Аризоне и Виргинии. Мы сначала подсчитаем среднее геометрическое () и стандартное отклонение (s) для каждой переменной по всем 50 штатам, затем определим соответствующие стандартные оценки (z) для каждой переменной по двум нужным нам штатам. Результатом будут два набора значений в стандартных единицах (уже не в долларах, количестве учителей и документов, а в количестве стандартных отклонений от среднего [c.406] геометрического), которые могут быть использованы для определения индексов политики в области образования, для выяснения относительной позиции Аризоны и Виргинии среди других штатов или для стандартизации при необходимости cравнения принципиально отличных измерений. Таким образом, при использовании стандартного подсчета стандартное отклонение может оказаться очень полезным. [c.407]

ЗАКЛЮЧЕНИЕ

В этой главе мы остановились на статистических процедурах, которые описывают распределения в рамках одной переменной. Поскольку эта статистика характеризует отдельные переменные, ее часто называют одномерной. Мы видели, что различные одномерные статистические процедуры подходят для переменных различного уровня измерений – номинального, порядкового и интервального. В ссылка скрыта мы рассмотрим двумерную статистику, т.е. такую, которая включает взаимосвязи двух переменных. [c.407]

Дополнительная литература

Если вы захотите глубже изучить статистику, см. литературу к гл. 16. Сейчас же будет полезнее начать с книг, которые облегчат применение диагностики и помогут овладеть некоторыми основными ее принципами. Мы предлагаем классическую и, вместе с тем, веселую кн.: Darrel H. How to Lie with Statistics. – N.Y.: Norton, 1954. Даррел определяет статистику как “статистикуляцию”. Гораздо более полное и легко читающееся издание по статистике: Schutte J.G. Everything You Always Wanted to Know About Elementary Statistics (but were afraid to Englewood Cliffs (NJ.): Prentice-Hall, 1977. [c.407]

15. СТАТИСТИКА II: ИЗУЧЕНИЕ ВЗАИМОСВЯЗЕЙ МЕЖДУ ДВУМЯ ПЕРЕМЕННЫМИ

Чаще всего в политологических исследованиях мы заинтересованы в изучении распределений по одной переменной меньше, чем в определении того, взаимосвязаны ли две или более переменных и если да, то каким образом и насколько тесно. Именно эти двумерные (относящиеся к двум переменным) и многомерные (относящиеся к более чем двум переменным) взаимосвязи обычно проливают свет на самые интересные исследовательские вопросы.

Обычно при изучении взаимосвязей между двумя переменными встает три важнейших вопроса; вы, должно быть, помните о них из ссылка скрыта. Первый заключается в том, влияют ли и до какой степени изменения значений одной переменной – обычно независимой переменной – на изменения значений другой – зависимой – переменной. Второй вопрос касается формы и направления любой связи, которая может существовать. Третий рассматривает возможность того, что любая взаимосвязь, существующая между признаками, которые представляют выборку из более крупной совокупности, действительно является характеристикой этой совокупности, а не просто артефактом меньшей и потенциально нерепрезентативной выборки. В этой главе мы познакомимся со статистическими приемами, которые чаще всего используются при ответах на эти вопросы, и объясним, когда правомерно их использование. [c.408]

ИЗМЕРЕНИЕ СВЯЗИ И СТАТИСТИЧЕСКОЙ ЗНАЧИМОСТИ

В том случае, если знание значений одной переменной по определенному случаю позволяет сделать некоторые предположения относительно соответствующих значений другой переменной, между этими переменными существует связь 1. Если, например, мы исследуем взаимосвязь между численностью населения какой-либо страны и долей взрослых, получивших высшее образование (принимая во внимание, что мы располагаем такими данными), то возможны три вывода: (1) более крупные страны [c.408] обычно имеют большую долю взрослых, получивших высшее образование, чем менее крупные; (2) малые страны обычно имеют большую долю взрослых, получивших высшее образование, чем более крупные, и (3) систематических различий нет; некоторые страны из обеих групп имеют относительно высокую долю таких людей, а другие – тоже из обеих групп – относительно низкую. Если исследование покажет, что верен случай 1 или случай 2, то мы можем использовать знание значений независимой переменной – количество населения, – для того чтобы примерно представить или предсказать значения зависимой переменной – доля взрослых, получивших высшее образование – для любой из взятых стран. В первом случае для густонаселенных стран можно предсказать и относительно высокую долю взрослых с высшим образованием, а для малонаселенных стран – более низкую их долю. Во втором случае наши предположения будут прямо противоположны. В обоих случаях, хотя мы можем и не угадать каждый случай точно, мы будем чаще всего правы, поскольку между этими переменными существует связь. И конечно, чем теснее связь между двумя переменными, тем более вероятно, что наши догадки в каждом отдельном случае будут верны. Если существует полная зависимость значений одной переменной от значений другой, т. е. высокие значения одной переменной вызывают высокие значения другой или, наоборот, высокие значения одной вызывают низкие значения другой, мы можем вывести одну из другой с довольно большой степенью точности. Все это в корне отличается от третьего случая, который не позволяет с достаточной долей точности предугадать значения переменной образование, основываясь на знании количества населения. Если признаки по двум переменным распределяются, по сути дела, произвольно, то считается, что эти переменные не имеют связи.

Чтобы понять, как же выглядит эта самая “сильная связь”, рассмотрим две схематические карты, изображенные на рис. 15.5. (ссылка скрыта), которые представляют уровень убийств в Вашингтоне в 1988 г. На схеме 15.5а указаны известные рынки, производящие торговлю наркотиками в столице. На схеме 15.5б показаны места, где происходили убийства. Обе схемы отражают данные, полученные в городской полиции. Легко заметить, что [c.409] сосредоточение точек, обозначающих места продажи наркотиков и убийств, практически одинаково, и таким образом выявляется связь между двумя этими феноменами.

Понятно, что между переменными может существовать более или менее сильная связь. Естественно, возникает вопрос, насколько сильна эта связь. На помощь приходит статистика. Из статистики возьмем показатель, который называется коэффициентом связи. Коэффициент связи – это показатель, который обозначает степень возможности определения значений одной переменной для любого случая, базируясь на значении другой. В нашем примере этот коэффициент может показать, насколько знание количества населения страны поможет в определении доли взрослых, получивших высшее образование. Чем больше коэффициент, тем сильнее связь и, следовательно, выше наши возможности прогноза. Вообще коэффициент колеблется в переделах от 0 до 1 или от –1 до 1, где значения, близкие к единице, обозначают относительно сильную связь, а значения, близкие к 0, – относительно слабую. Как было в случае с одномерной статистикой – и по тем же причинам, – каждый уровень измерения требует своего типа исчислений, и поэтому каждый из них требует своего способа измерения связи.

В дополнение к величине связи полезно также знать направление или форму взаимоотношений между двумя переменными. Еще раз обратите внимание на вышеприведенный пример, особенно на варианты 1 и 2. Мы уже предположили, что, чем теснее связаны признаки, тем больше будет коэффициент связи и тем выше шансы угадать долю взрослых с высшим образованием на основании знаний о количестве населения в данной стране. Очевидно, однако, что наши прогнозы относительно каждого случая будут совершенно противоположны. В первом случае большие значения одной переменной вероятнее всего связаны с большими значениями другой, тогда как во втором случае большие значения одной переменной вероятнее всего связаны с меньшими значениями другой. Такие связи называются связями, имеющими разное направление. А такой тип связей, как в первом случае, когда обе переменные возрастают и убывают одновременно, называется прямой, или положительной, связью. Тип связей второго случая, когда значения постоянно изменяются в [c.410] разных направлениях, называется обратной, или отрицательной, связью. Эта добавочная информация – о знаке (плюс или минус) перед коэффициентом связи – способна сделать наши предположения более эффективными. Таким образом, коэффициент, равный –0,87 (отрицательный и близкий к единице), может описывать относительно сильную взаимосвязь, в которой значения двух данных переменных обратно связаны (изменяются в разных направлениях), коэффициент же, равный 0,10 (положительный – знак “плюс” обычно опускают – и близкий скорее к 0), может описывать слабую прямую связь.

Для всех случаев понятие направления или формы имеет разный смысл для разных уровней измерения. На номинальном уровне, где цифры играют роль просто обозначений, концепция направления вообще не имеет смысла и, соответственно, номинальные коэффициенты связи не изменяют знака. Все они положительны и просто показывают силу связи. На интервальном же уровне, наоборот, знаки могут не только изменяться, но и иметь достаточно сложную геометрическую интерпретацию. Проверка на связь на этом уровне измерений обладает очень высокими прогностическими способностями, причем знак коэффициента является в этом случае ключевым элементом.

Наконец, несколько слов о проверке статистической значимости, хотя обсуждение этого сюжета будет сознательно ограничено2. Если мы делаем предположительно репрезентативную выборку некоторого определенного размера и используем эту выборку для формулирования каких-то выводов о той генеральной совокупности, из которой она была сделана, мы несколько рискуем получить неверные выводы. Это так, потому что существует вероятность, что выборка, по сути дела, нерепрезентативна и что в действительности ошибка измерений превышает уровень, допустимый для выборки данного размера (см. табл. ссылка скрыта и ссылка скрыта в приложении А). Вероятность подобных неверных обобщений в принципе известна, однако в каждом отдельном случае мы не всегда можем сказать, имеются они или нет. Для доверительного уровня 0,95 вероятность этого составит 0,05 или 1 – 0,95, для доверительного уровня 0,99 – 0,01. Эти величины 0,05 и 0,01 или 5% и 1% свидетельствуют о том, что любое обобщение, [c.411] сделанное по выборке и относящееся к генеральной совокупности, даже подпадающее под подсчитанный уровень ошибки выборки, просто-напросто неверно.

Проверки на статистическую значимость играют ту же роль для оценки измерений связи. Они определяют, насколько вероятна связь, зафиксированная между двумя признаками в выборке. Давайте попробуем пояснить этот пункт.

Продолжая наш пример, представьте, что у нас есть совокупность из 200 стран, для которых доподлинно известно, что коэффициент связи между количеством населения и долей взрослых, получивших высшее образование, равен 0, т. е. в реальности такой связи нет. Представьте далее, что в силу тех или иных причин мы считаем необходимым взять выборку только в 30 стран и подсчитать для них связь между этими двумя переменными. Он также может оказаться равным 0, но в действительности это маловероятно, поскольку сила связи теперь зависит не от всех 200 стран, а только от 30 и, возможно, будет отражать их характерные особенности. Другими словами, величина коэффициента предопределена тем, какие именно 30 стран мы выберем. Если случайно мы выберем те 30 стран, которые действительно репрезентативны относительно всех 200, связь не обнаружится. Но тот же случай может привести нас к тому, что мы выберем такие 30 стран, для которых связь между количеством населения и уровнем образования необычайно высока, скажем 0,60. В этом случае наш подсчитанный со всей тщательностью коэффициент будет характеризовать данную выборку, но, если мы распространим эту характеристику на генеральную совокупность, наши выводы будут неверны. Зная это, конечно, необходимо отвергнуть измерение связи на основании именно этой выборки.

Проблема заключается в том, что в действительности мы не знаем глубинные параметры совокупности, например истинную степень связи признаков в ней. Безусловно, причина, по которой мы вынуждены прибегать к выборкам, прежде всего в том, что мы просто не в состоянии изучать совокупности в целом. А отсюда в свою очередь следует, что чаще всего мы будем иметь в распоряжении только те проверки связей, которые основаны на выборках. Более того, эти подсчеты будут основаны только на одной выборке. Тогда встает вопрос, насколько можно [c.412] быть уверенным в том, что проверка связей, основанная на единственной подгруппе генеральной совокупности, точно отражает глубинные характеристики этой совокупности. Задача проверки на статистическую значимость и заключается в том, чтобы дать цифровое выражение этой уверенности, измерить возможность или вероятность того, что мы делаем верные, или, наоборот, неверные обобщения.

Для того чтобы увидеть, как все это работает, давайте продолжим наш пример. Представьте, что мы сделали не одну выборку в 30 стран из всей совокупности в 200 стран, а 100 или даже 1000 отдельных и независимых выборок равного размера и что для каждой подсчитан коэффициент связи. Поскольку верный для всей совокупности коэффициент, по сути, равен 0, большинство коэффициентов в наших 100 или 1000 выборках тоже будут равны 0 или близки к этому. Они ведь, кроме всего прочего, основаны на измерении характеристик одних и тех же стран в конце концов. Некоторые комбинации из 30 стран могут показать относительно высокие значения (это если нам случайно удастся выбрать те страны, где эти переменные связаны по типу высоких или низких связей), но большинство будет близким к параметрам всей совокупности. Безусловно, чем ближе к истинному значению коэффициента, тем большее количество выборок будет его иметь. Эти распределения, по сути дела, будут всегда располагаться по нормальной кривой, которую мы упомянули ранее. Это показано на рис. 15.1, где высота кривой в любой точке представляет количество выборок, для которых коэффициент связи имеет значение, отмеченное на оси ординат.



Рис. 15.1. Кривая нормального распределения для коэффициента для выборки из 30 случаев.

Какова же тогда вероятность того, что любое значение коэффициента – это просто случайное отклонение от истинного нулевого параметра? Или, другими словами, если мы возьмем выборку из какой-нибудь совокупности и выявим в этой выборке устойчивую связь, но при. этом нам не будут с определенностью известны соответствующие характеристики всей совокупности, каковы шансы того, что мы ошибемся, перенося такую сильную связь с выборки на всю совокупность? Нормальная кривая имеет некоторые особенности, которые мы не будем здесь обсуждать, не позволяющие нам ответить на этот вопрос с достаточной точностью.