Независимые и доминирующие множества вершин и родственные задачи
| Вид материала | Задача |
- Алгоритмы на графах. Обходы графов. Кратчайшие пути. Остовные деревья, 114.51kb.
- Задание бинарных отношений графами. Теорема Эйлера о необходимых и достаточных условиях, 22.76kb.
- Лекция №19, 121.08kb.
- Α Множество всех подмножеств данного множества называется булеаном данного множества., 83.26kb.
- Вопросы к экзамену «дискретная математика» (пм-91), 26.54kb.
- Введение в математическую логику, 29.8kb.
- Ия, в котором искомые переменные имели бы целочисленные значения, а иногда и значения, 104.18kb.
- Третє тисячоліття це вік наукового й технічного прогресу, коли без знань, науки, 119.55kb.
- Методические рекомендации по проведению 20-ти звездных дней «Двадцать вершин Независимости», 147.53kb.
- Для кафедр пм и к вопросы по курсу «Дискретная математика». 19. 05. 2010г, 52.29kb.
Раздел 1.Независимые и доминирующие множества вершин и родственные задачи
1.1.Независимые множества
Во многих прикладных задачах требуется найти в конечном множестве объектов максимальную систему объектов, попарно не связанных друг с другом, или же выбрать минимальную систему объектов, связанных со всеми другими. Формулировки подобных задач на языке теории графов приводят к понятиям независимости и покрытия.
Множество вершин U графа G = (V,X) называется независимым (внутренне устойчивым), если никакие две вершины из этого множества не смежны. Другими словами, если U V и U независимо в графе G, то порожденный подграф G(U) является пустым. Очевидно, что если при этом U* U, то U* - также независимое множество.
Внутренне устойчивое множество называется максимальным, если оно не является собственным подмножеством некоторого другого независимого множества.
Наибольшее по мощности независимое множество называется наибольшим.
Ясно, что наибольшее независимое множество является максимальным. Обратное, вообще говоря, неверно.
Число вершин в наибольшем независимом множестве графа G называется числом независимости (или числом внутренней устойчивости) этого графа и обозначается (G).
2

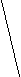

1
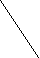
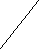



 3 7
3 7
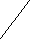





5
 4 6
4 68
Рис. 1.
Например, для графа G, изображенного на рис.1., (G)=4, множества вершин {1,2,3,7}, {1,2,3,8}, {2,3,5,7}, {2,3,5,8} являются наибольшими независимыми, а {4,7} – максимальное независимое множество, не являющееся наибольшим.
Понятие внутренней устойчивости естественным образом переносятся и на случай ориентированного графа.
1.1.1Алгоритм с возвратом
Очевидный алгоритм, который можно применить для нахождения независимых множеств вершин, это «полный перебор всех возможностей»: генерируем все возможные подмножества вершин заданного графа или орграфа и проверяем, является ли оно независимым. Среди всех независимых множеств выбираем максимальные. Опишем теперь общий метод, позволяющий значительно сократить число шагов в алгоритмах полного перебора всех возможностей. Чтобы применить этот метод, представим искомое решение в виде последовательности
-
Построить наибольшее независимое множество вершин в орграфе, используя алгоритм с возвратом.
Построить все максимальные независимые множества вершин в орграфе, используя алгоритм с возвратом.
1.1.2Метод Магу для нахождения максимальных внутренне устойчивых подмножеств орграфа
Пусть U - максимальное внутренне устойчивое множество вершин в орграфе D=(V,X), A(D)={aij}- матрица смежности орграфа D. Каждой вершине vi орграфа поставим в соответствие булеву переменную yi по следующему правилу: если vi U , то yi = 0 (или
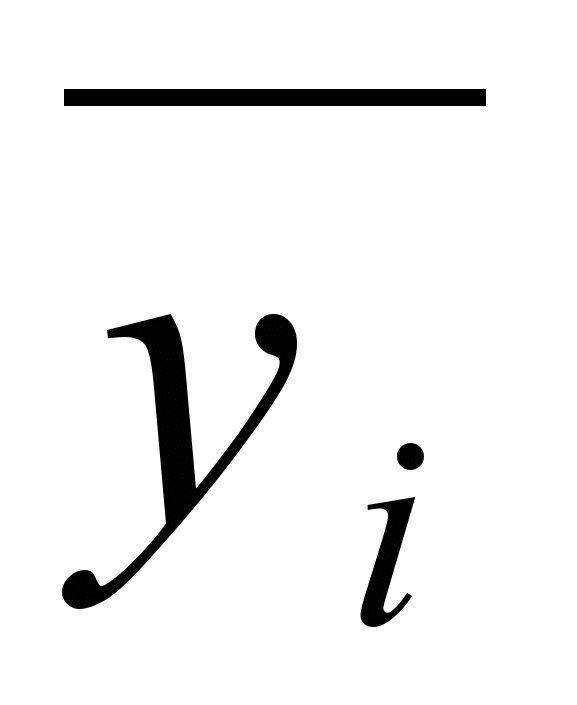 =1).
=1). Тогда для любых двух вершин vi, vj (ij) выполняется: если вершина vi U, а vj Гvi (ij), то вершина vj U . Запишем это выражение с помощью логических связок, учитывая при этом, что, если vj Гvi, то aij = 1, а если vj Гvi , то aij = 0. В результате получим (yi &aij)
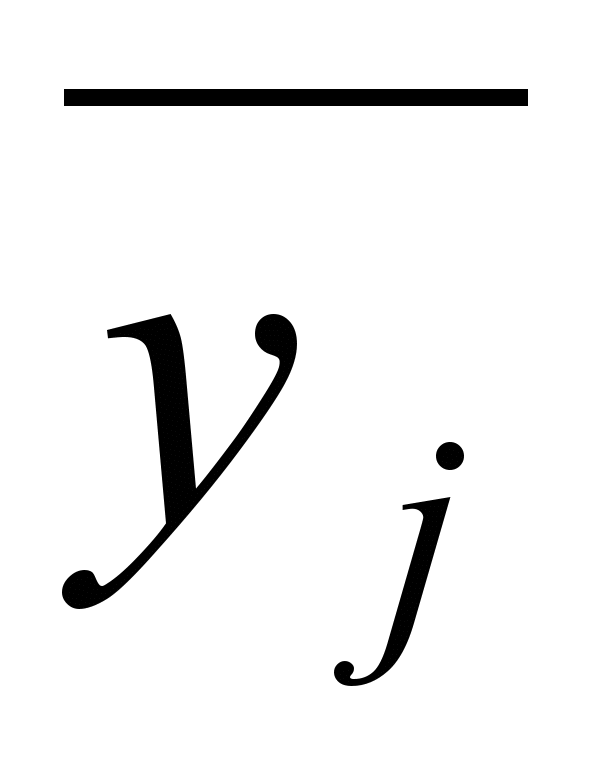 1. Преобразуем это выражение:
1. Преобразуем это выражение: 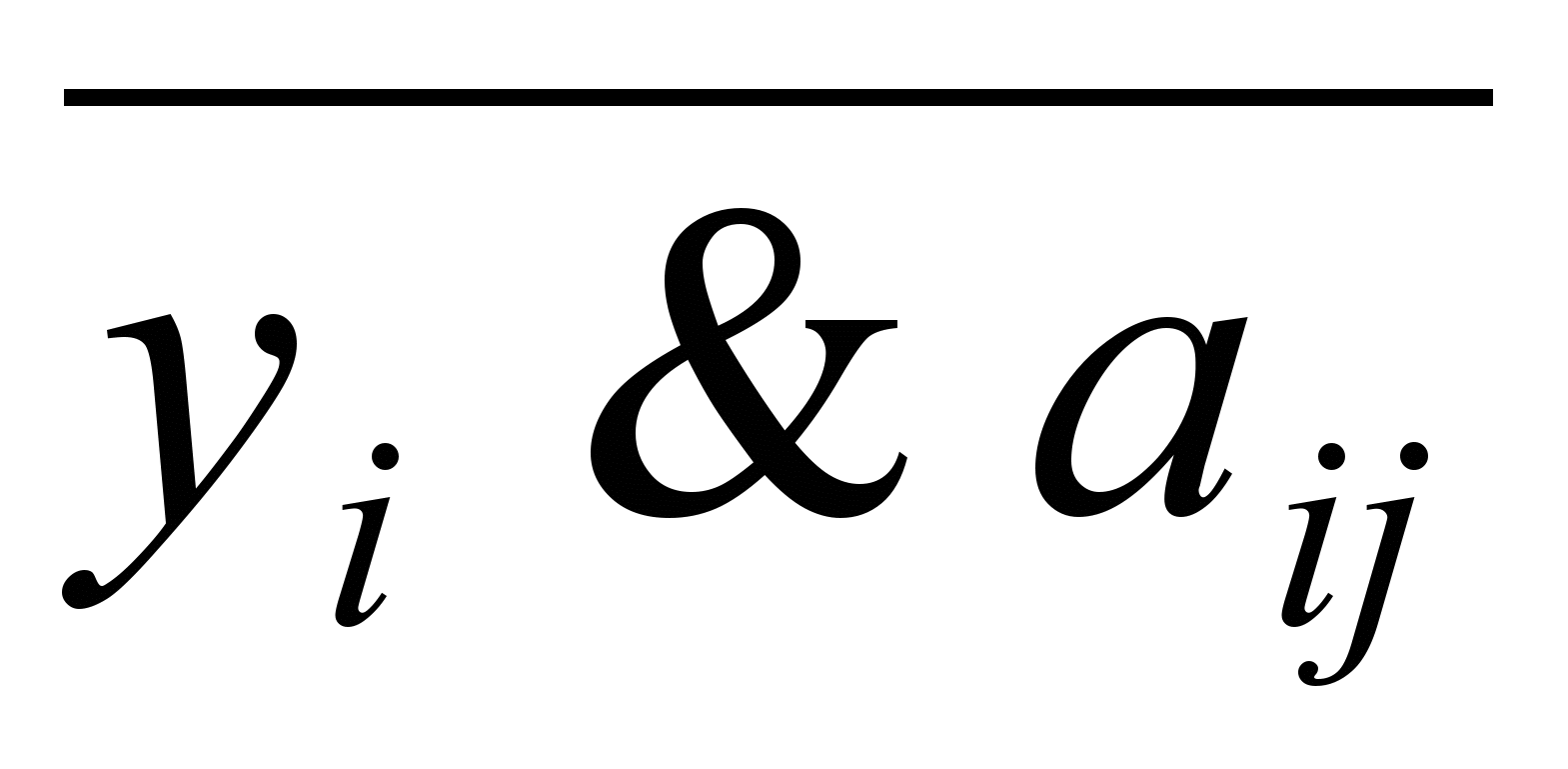
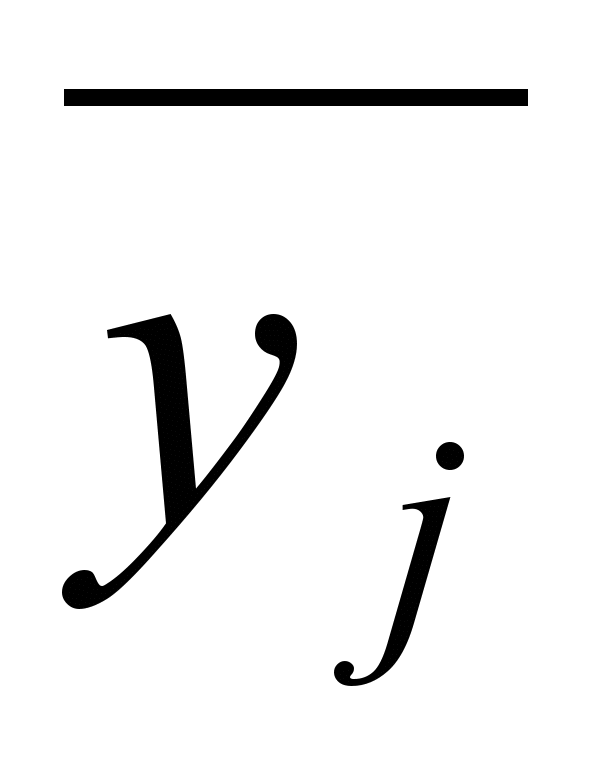 1 или
1 или 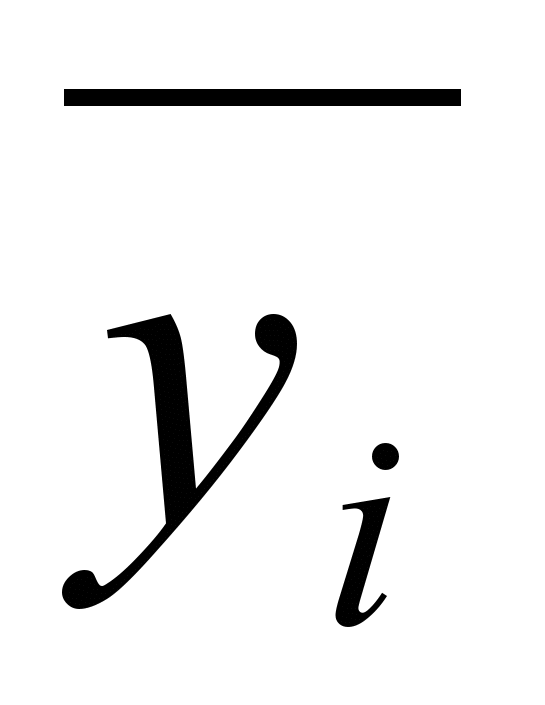

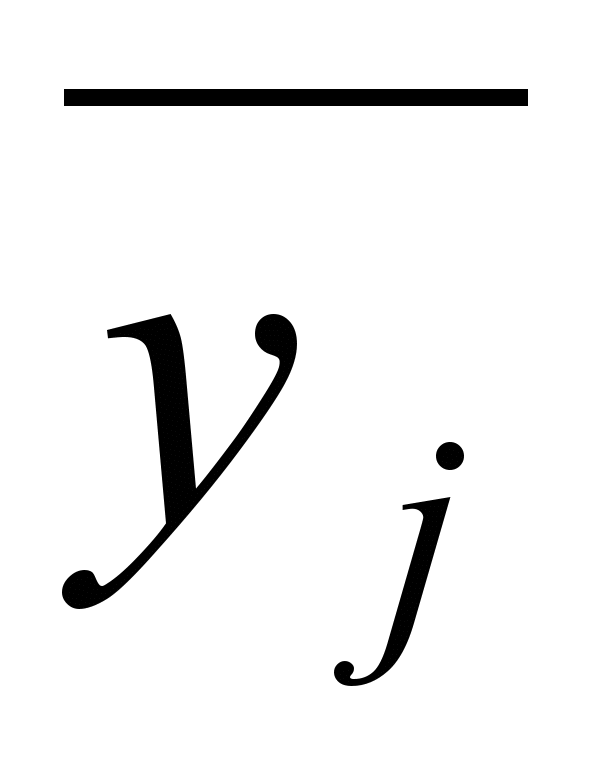 1.
1. Рассмотрим конъюнкцию по всем вершинам
=
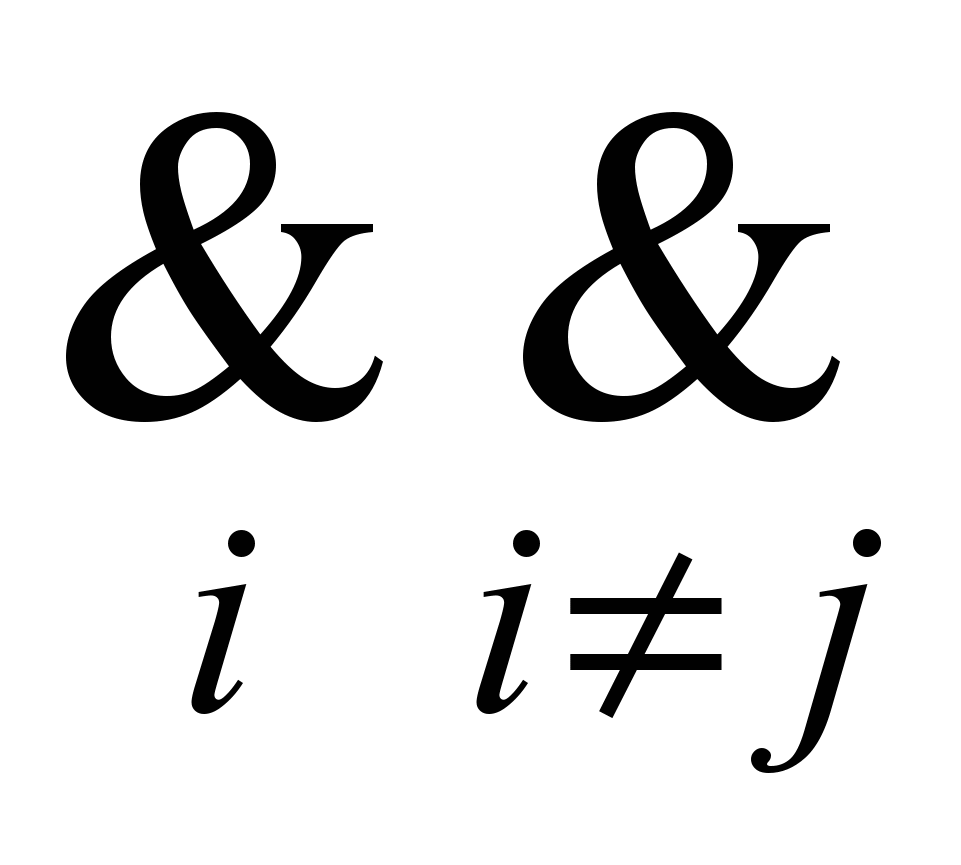 (
(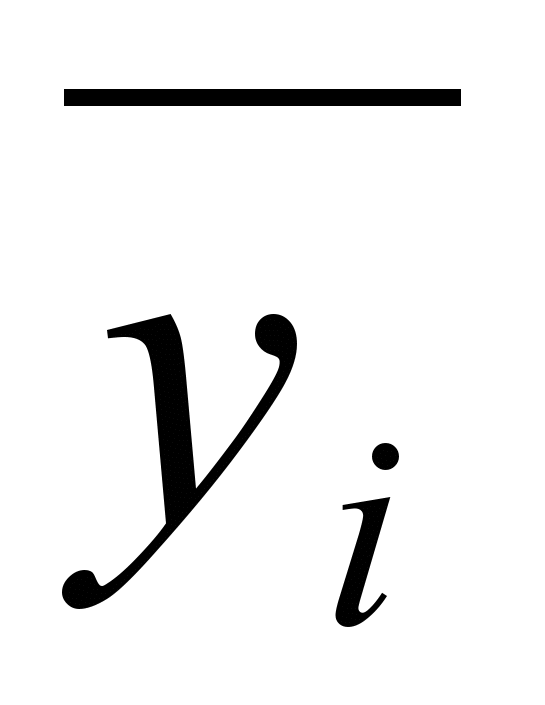

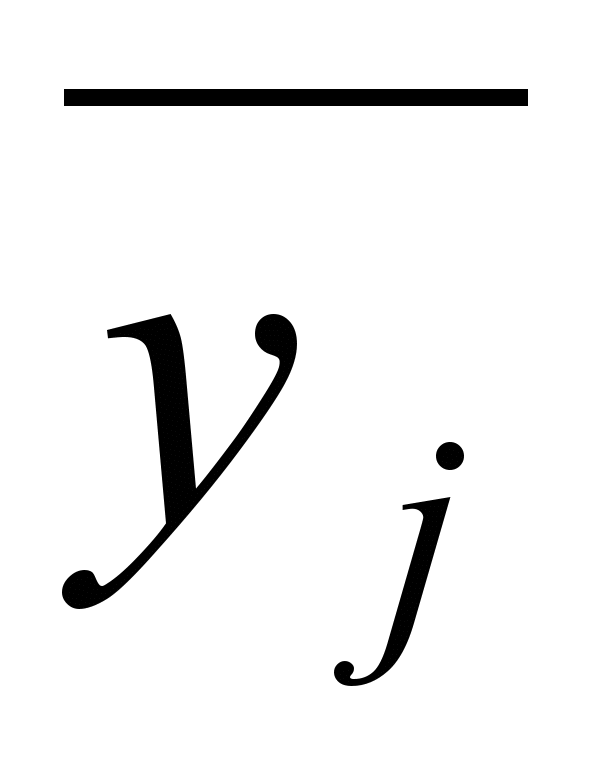 ) 1.
) 1.Если aij=0, то
 =1,
=1, 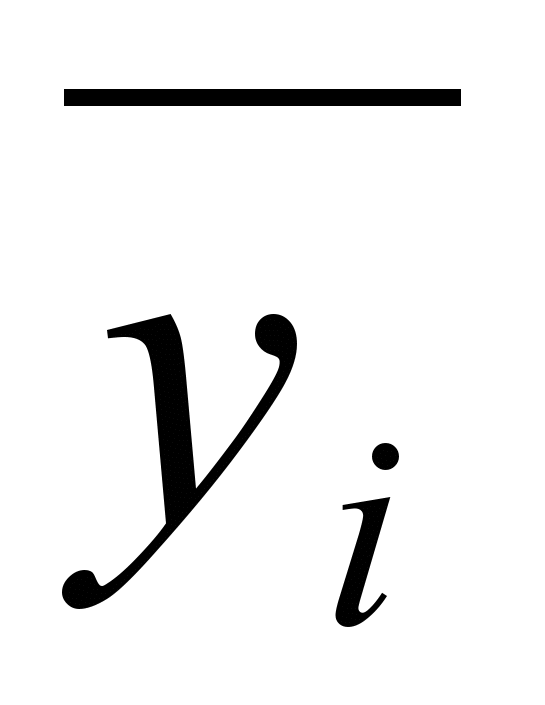 1
1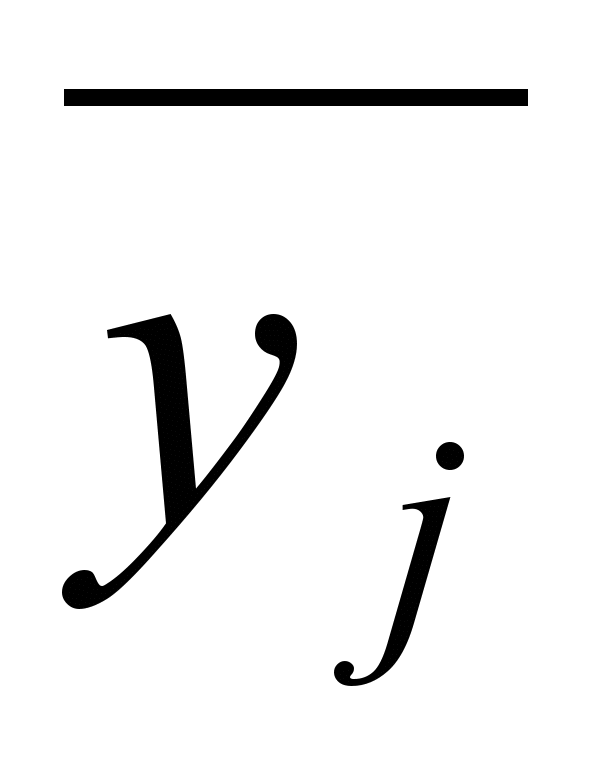 =1 и эту дизъюнкцию можно опустить. Если aij=1, то
=1 и эту дизъюнкцию можно опустить. Если aij=1, то  =0 и
=0 и 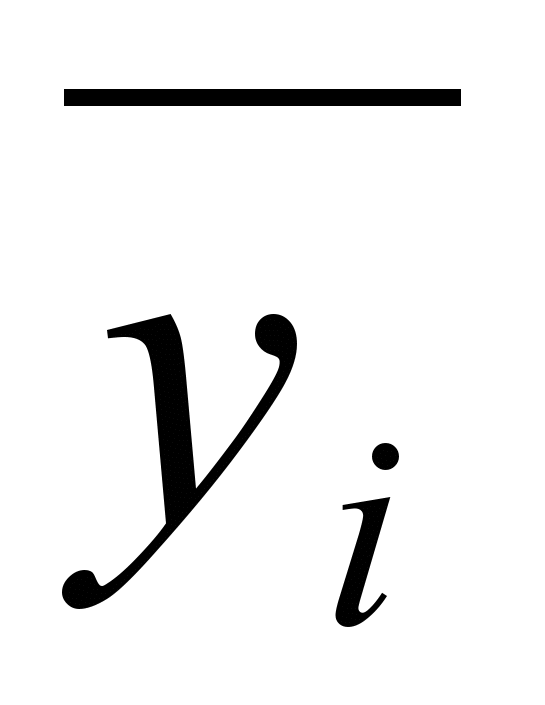 0
0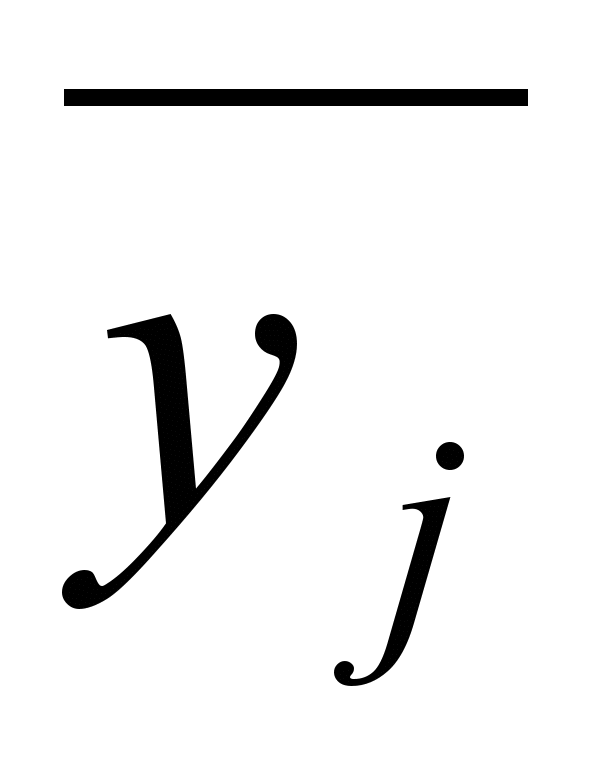 =
= 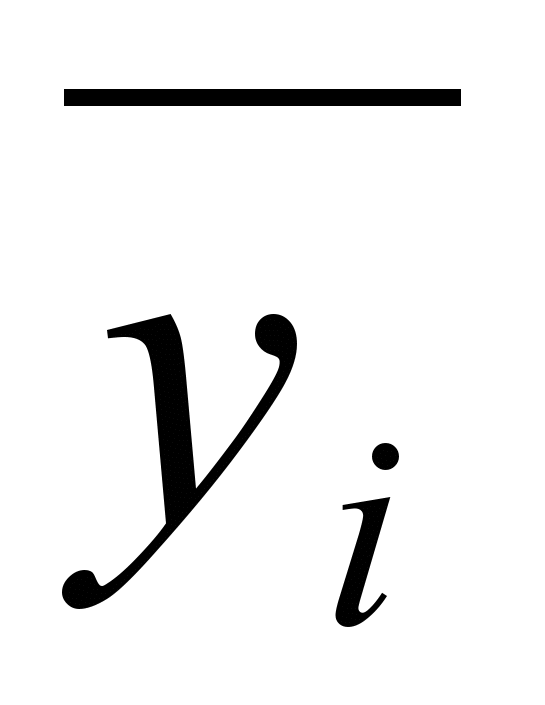
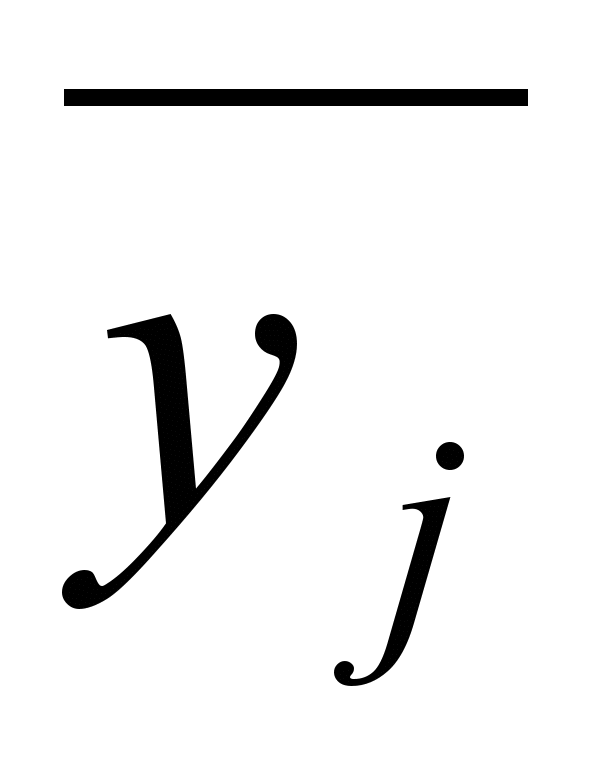 . Тогда
. Тогда =
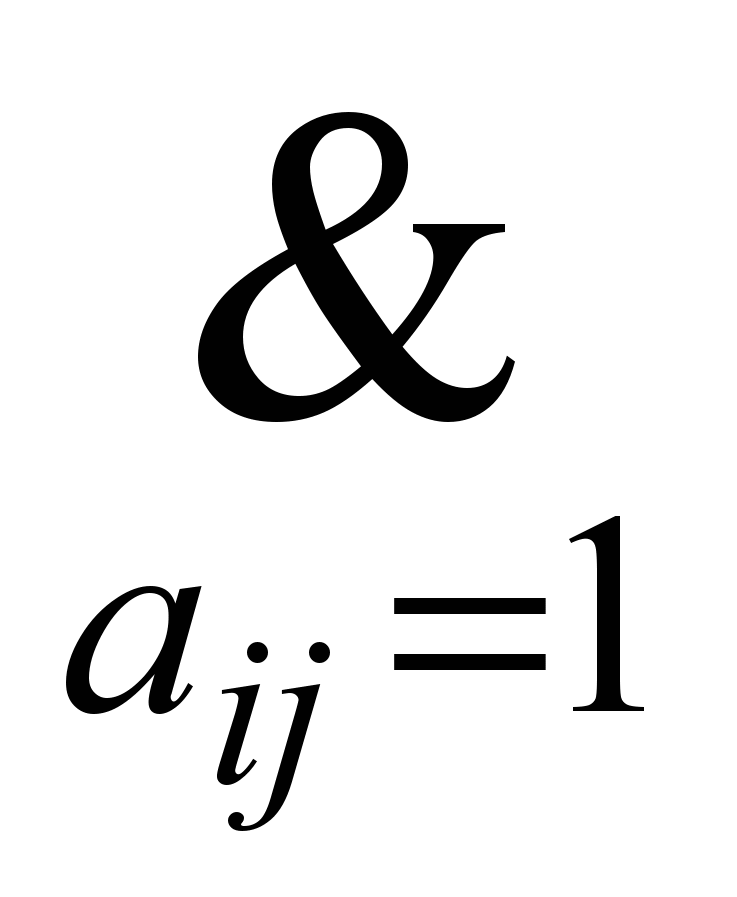 (
(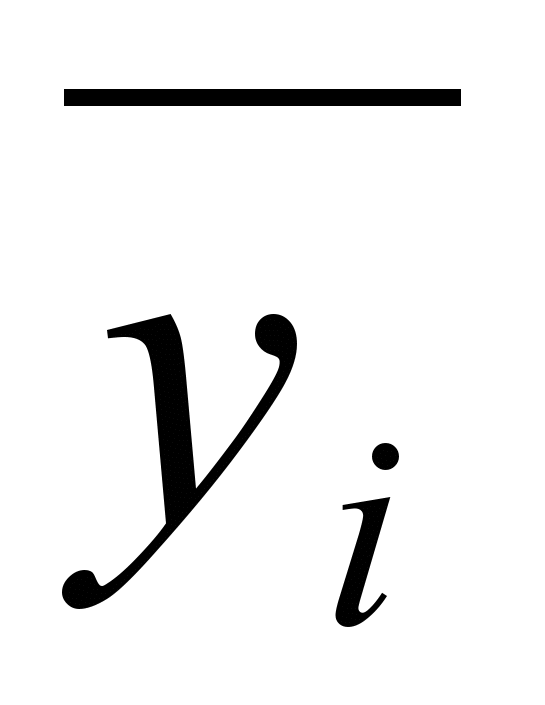
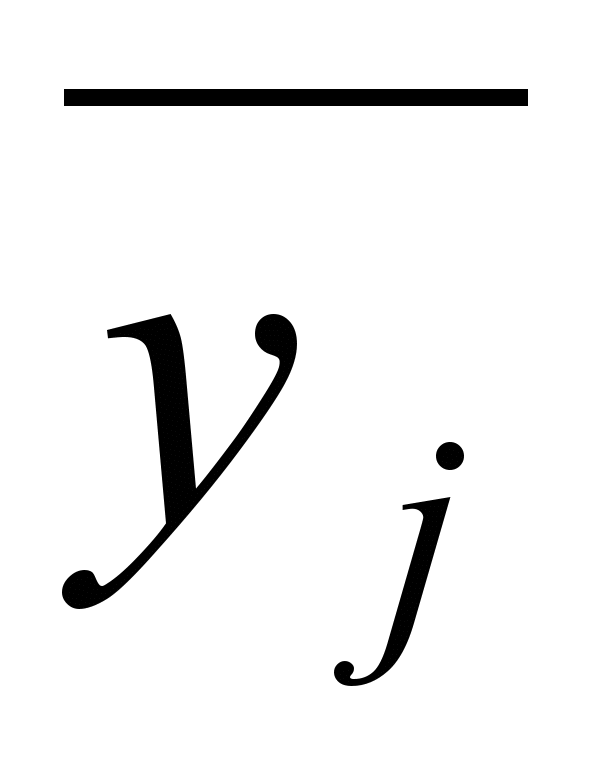 ) 1.
) 1.Раскрывая в данном выражении скобки и пользуясь законом поглощения А (А&В) А, приведем данную формулу к ДНФ. Тогда каждый дизъюнктивный член
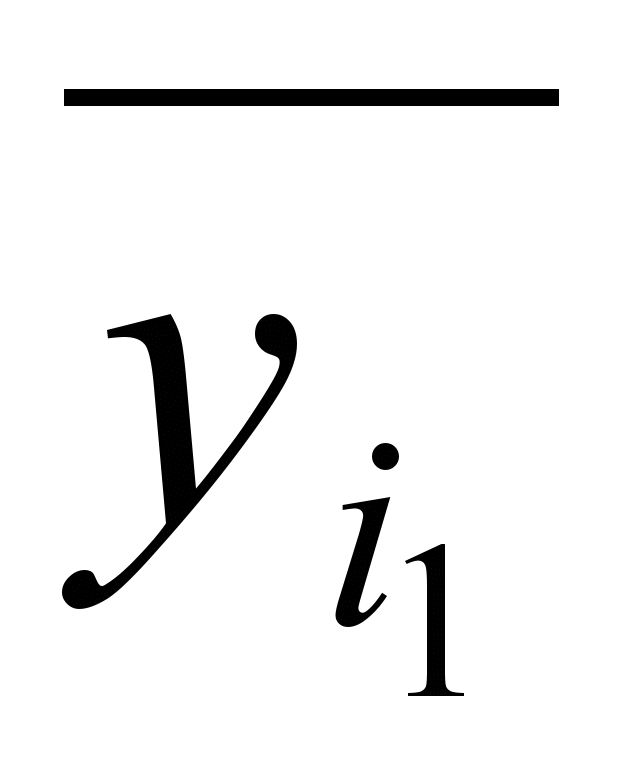
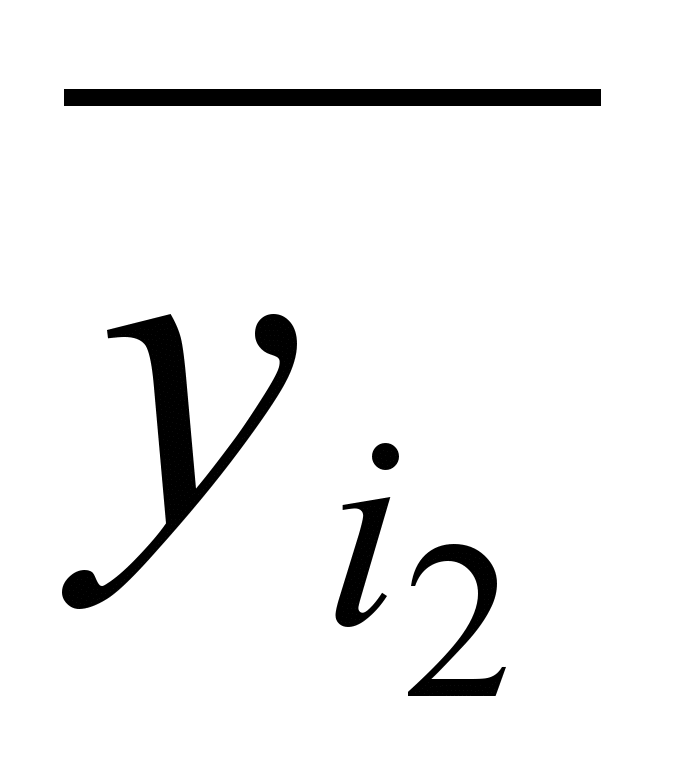 …
…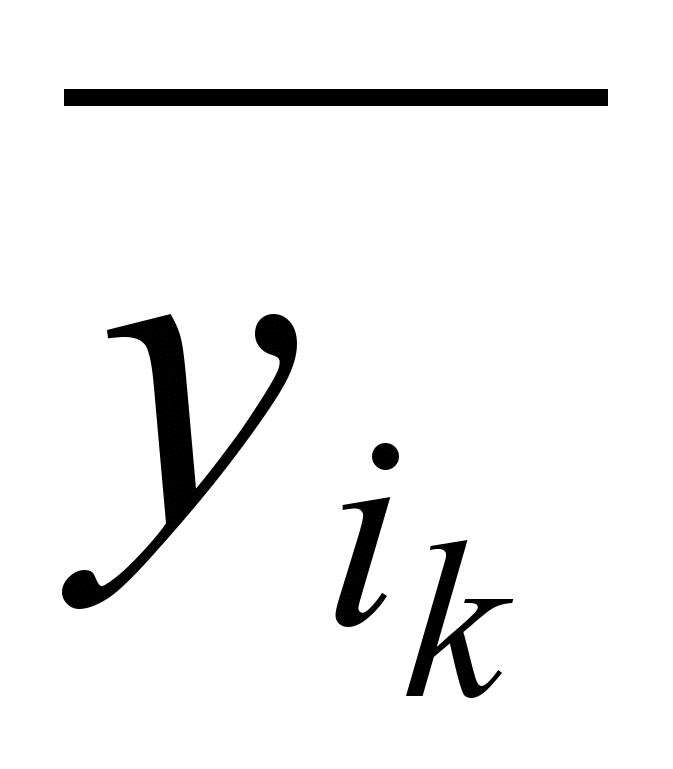 даст внутренне устойчивое множество, причем это множество образуют те вершины, которые не входят в данный член. Т.к. каждый дизъюнктивный член содержит только переменные с отрицанием, то к множеству U нельзя добавить ни одной переменной yi, содержащейся в элементарной конъюнкции, а значит, каждое множество U является максимальным внутренне устойчивым множеством.
даст внутренне устойчивое множество, причем это множество образуют те вершины, которые не входят в данный член. Т.к. каждый дизъюнктивный член содержит только переменные с отрицанием, то к множеству U нельзя добавить ни одной переменной yi, содержащейся в элементарной конъюнкции, а значит, каждое множество U является максимальным внутренне устойчивым множеством. Пример.
Найти максимальные внутренне устойчивые множества вершин для орграфа D, заданного матрицей смежности
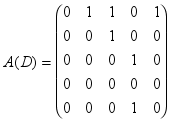 .
.Решение.
Запишем формулу Ф для данного орграфа
Ф=
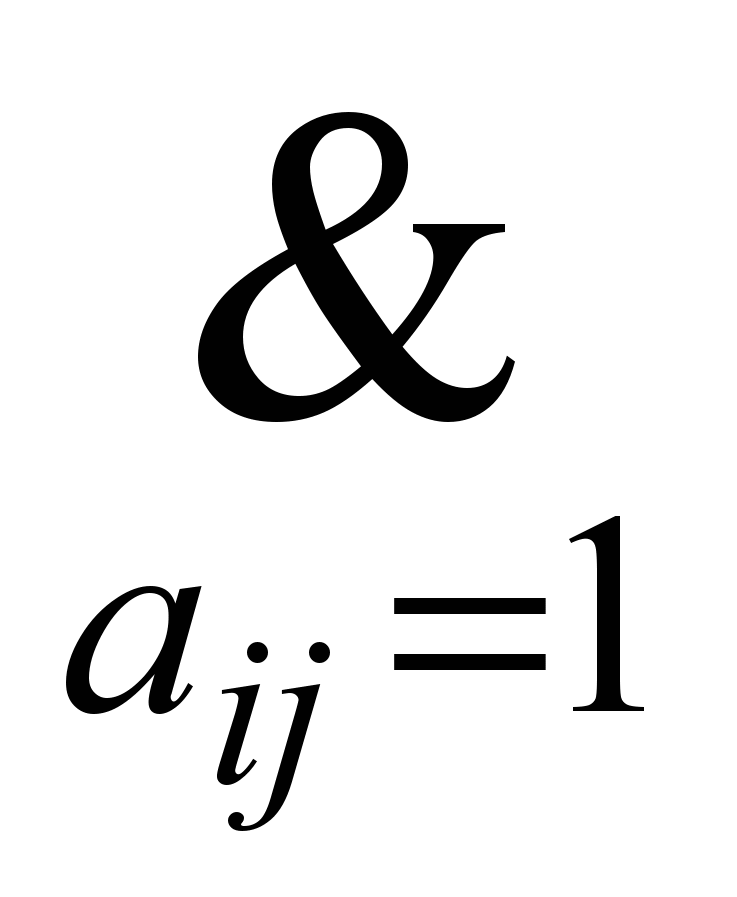 (
(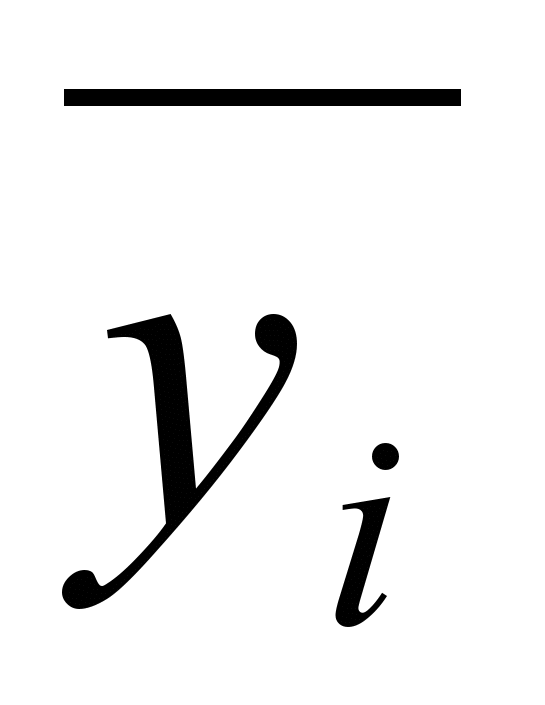
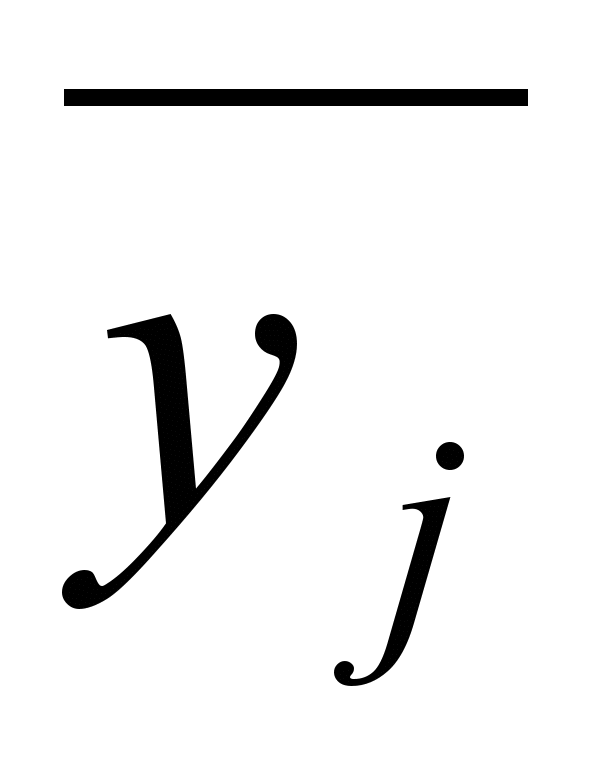 )=(
)=(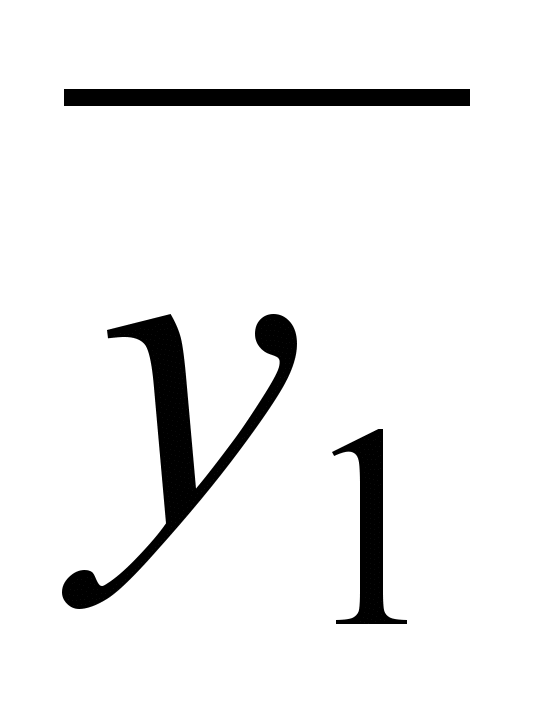
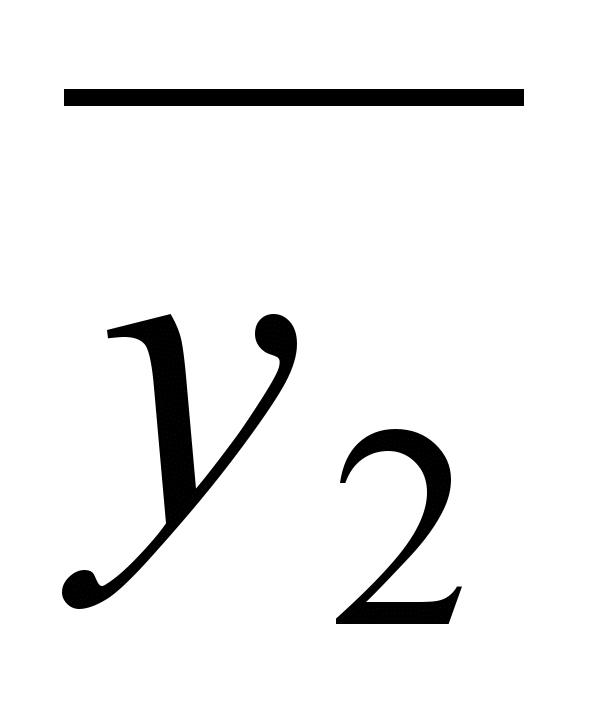 )(
)(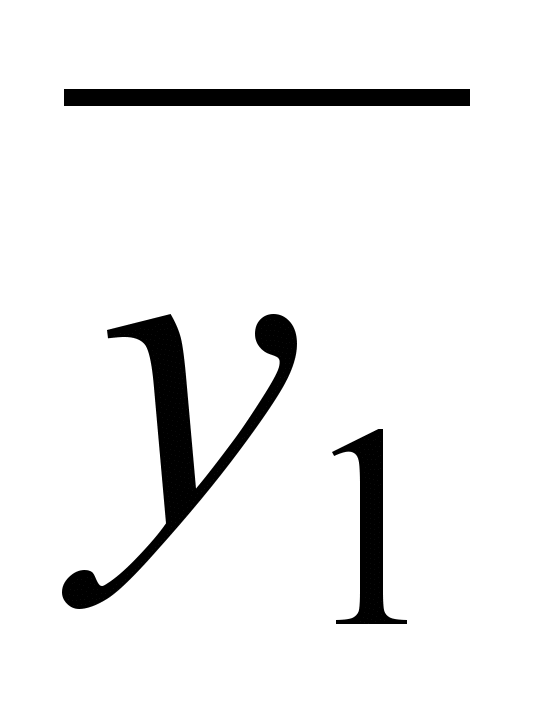
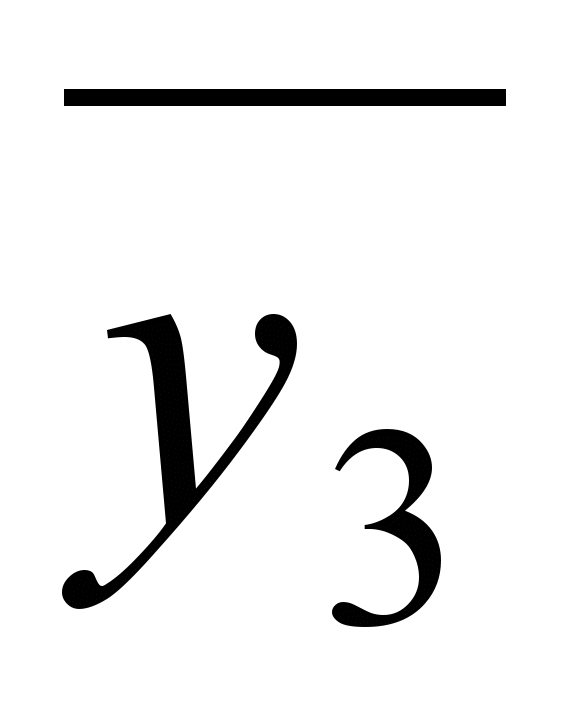 )(
)(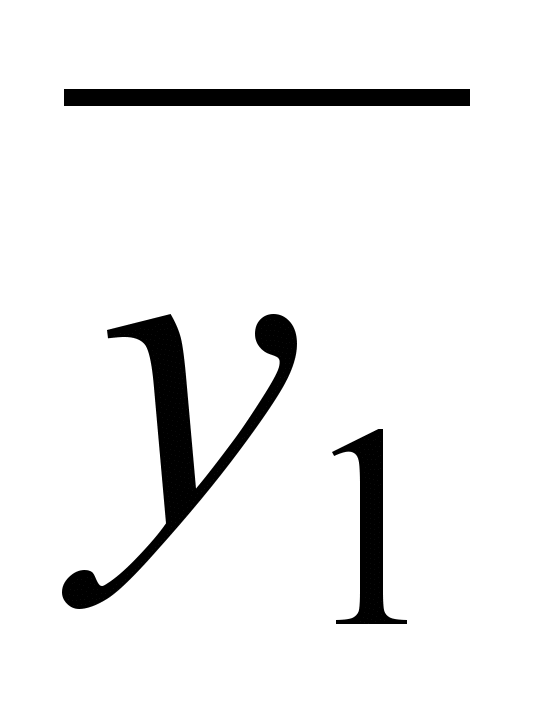
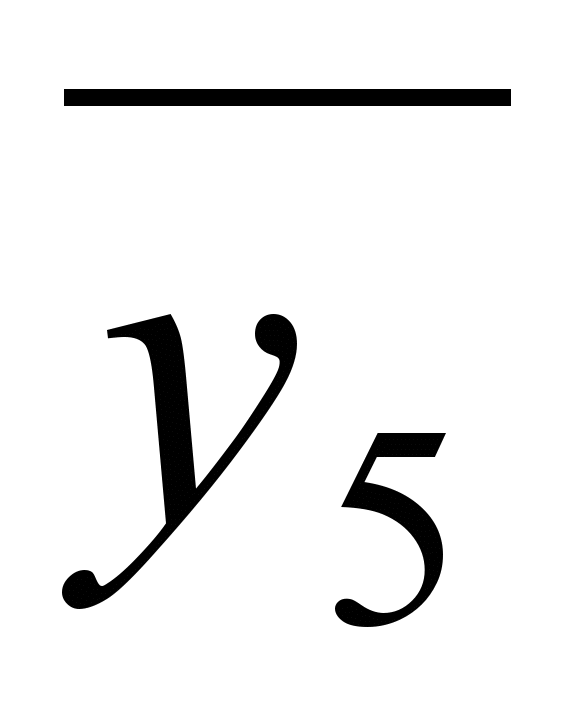 )(
)(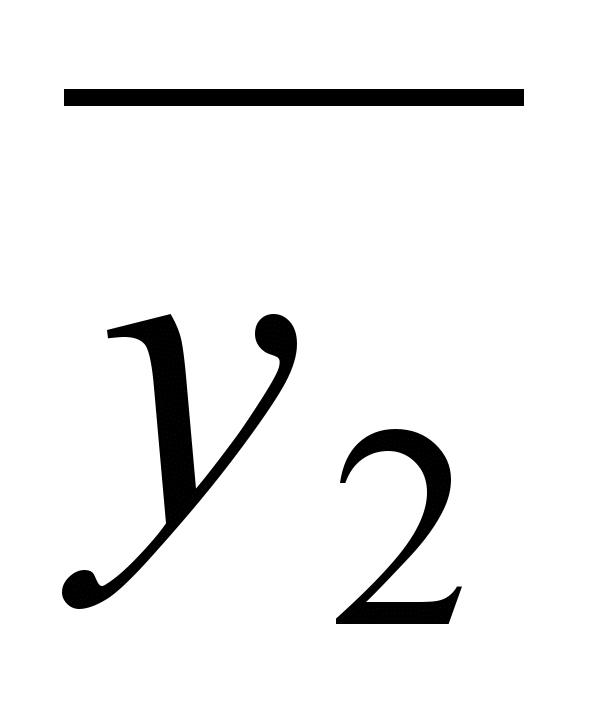
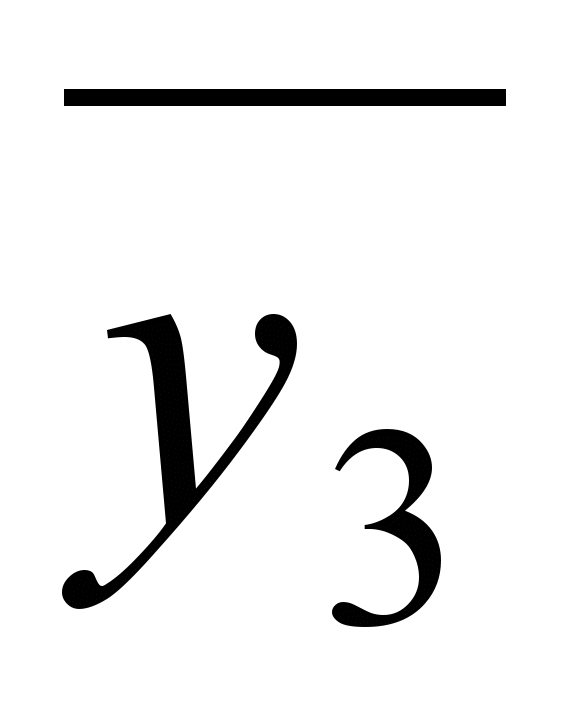 )(
)(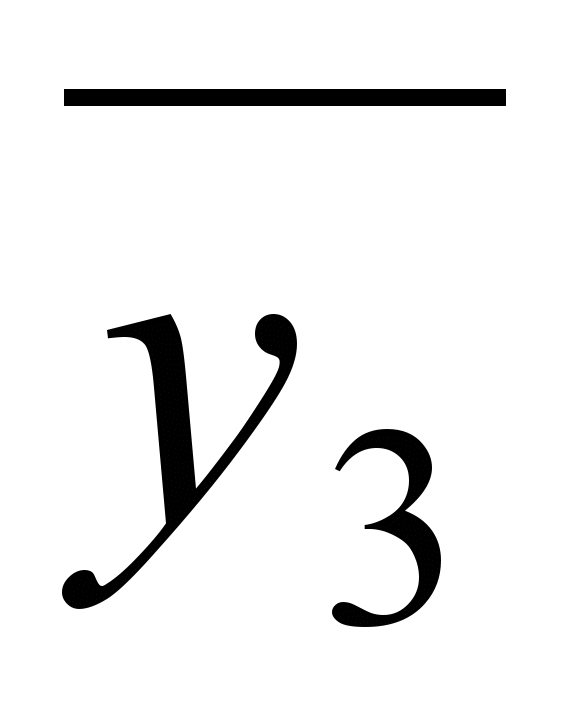
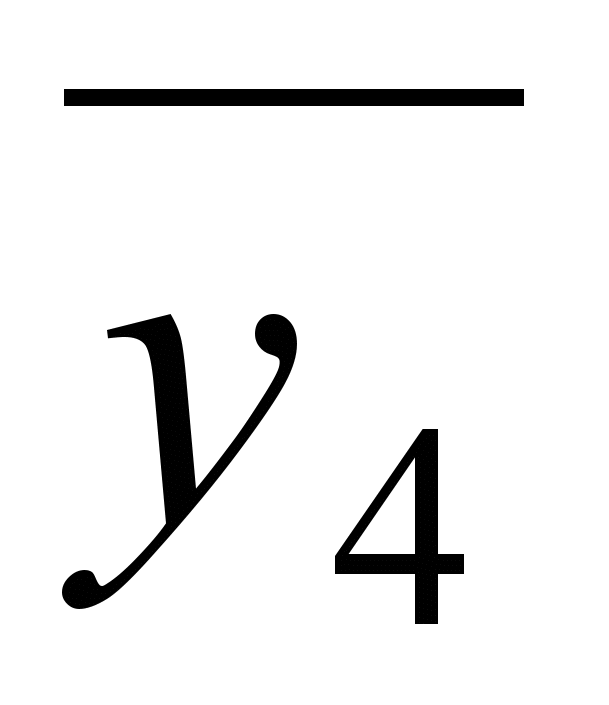 )(
)(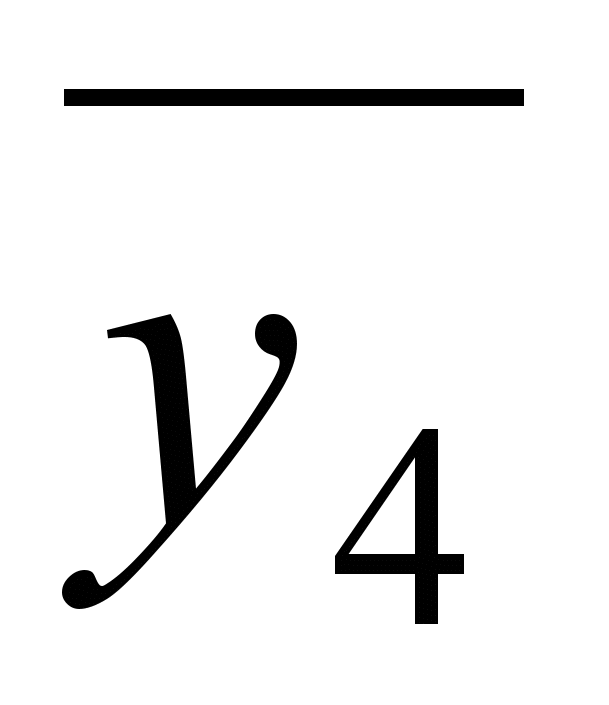
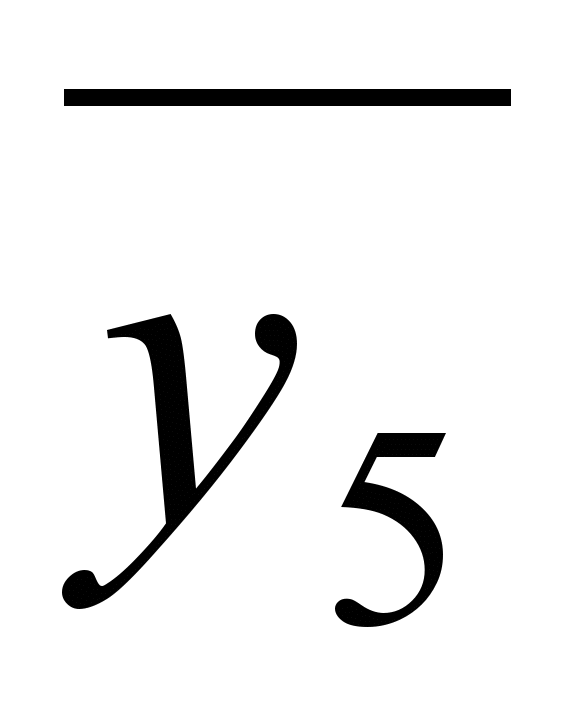 )1.
)1.Упростим эту формулу, пользуясь законами А&А=А, А(В&А)=А, А(В&С)=(АВ)&(АС)
Ф=(
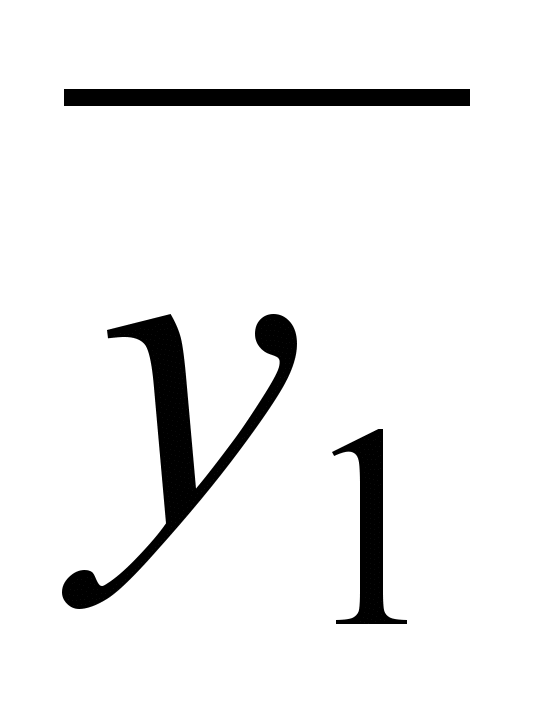
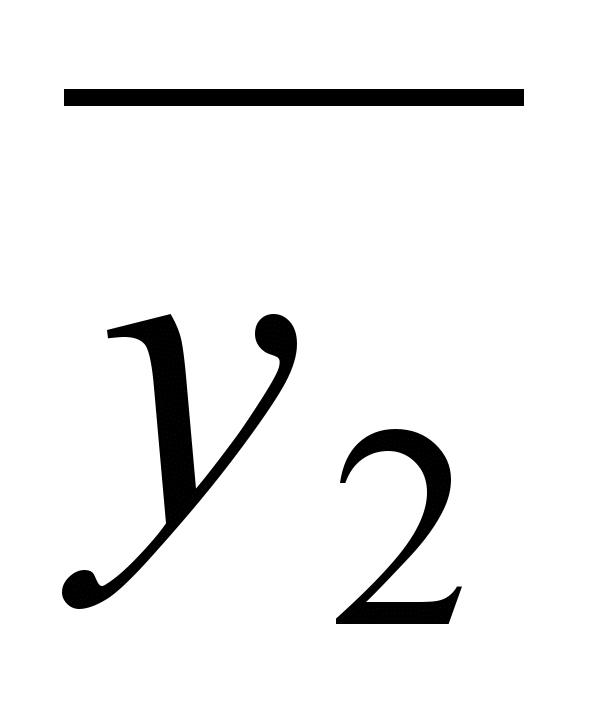
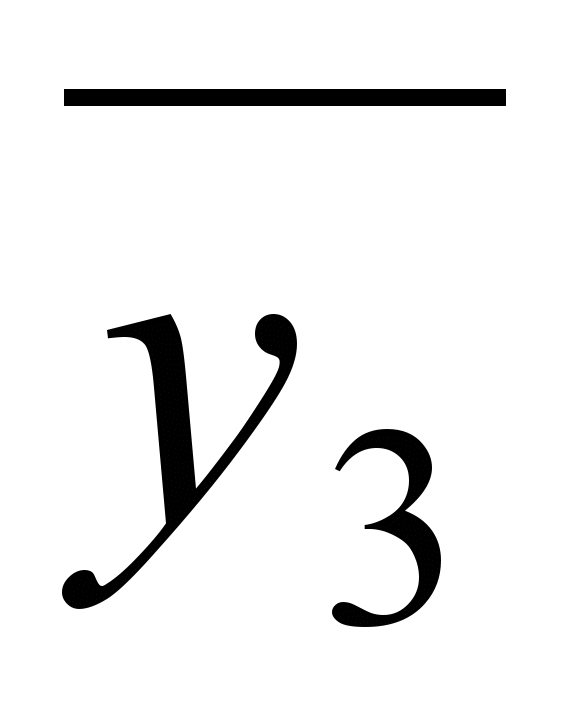
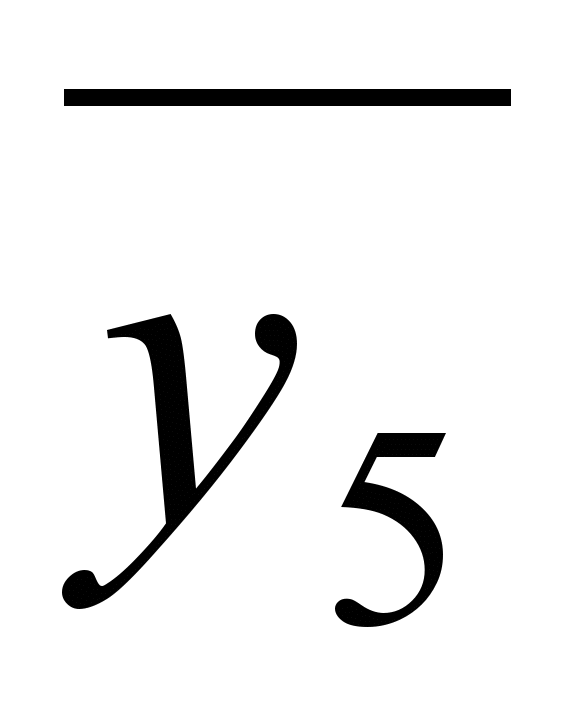 )(
)(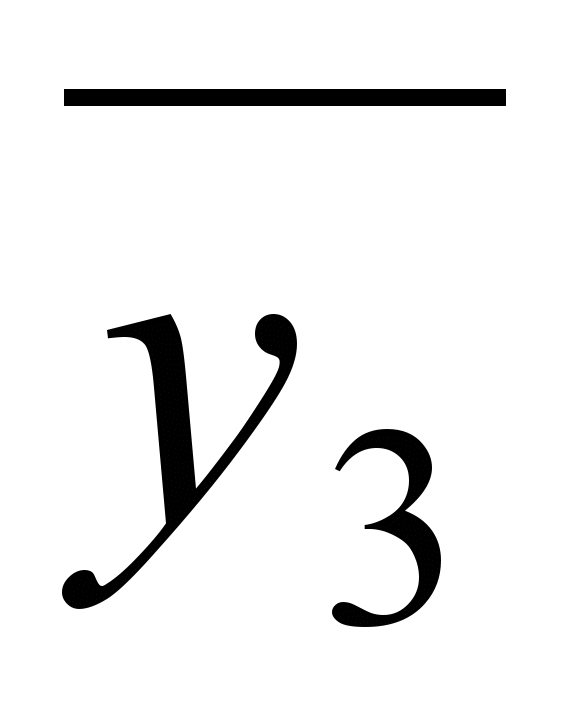
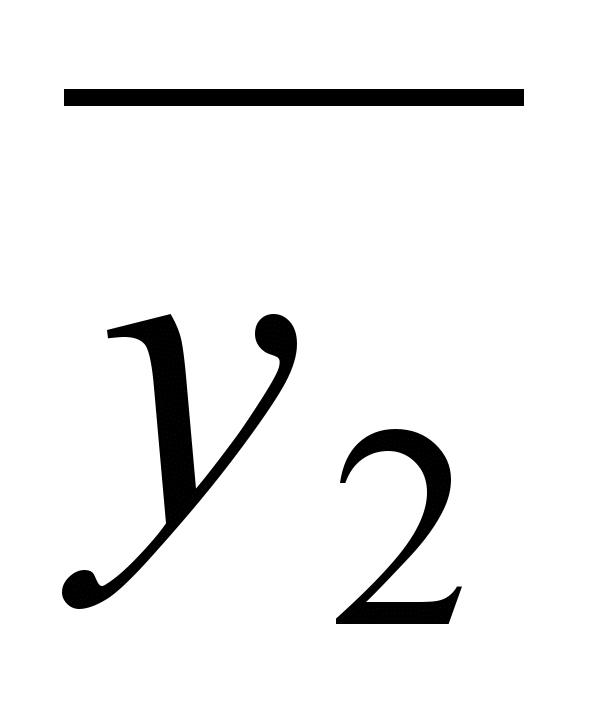
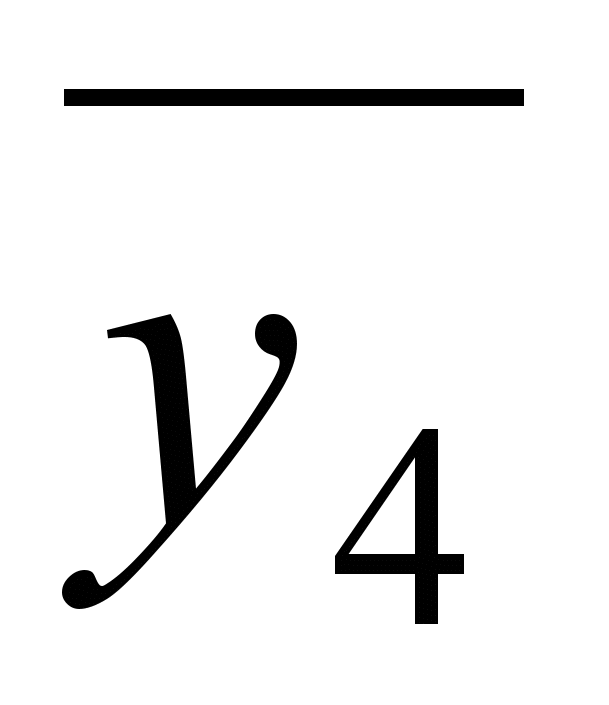 )(
)(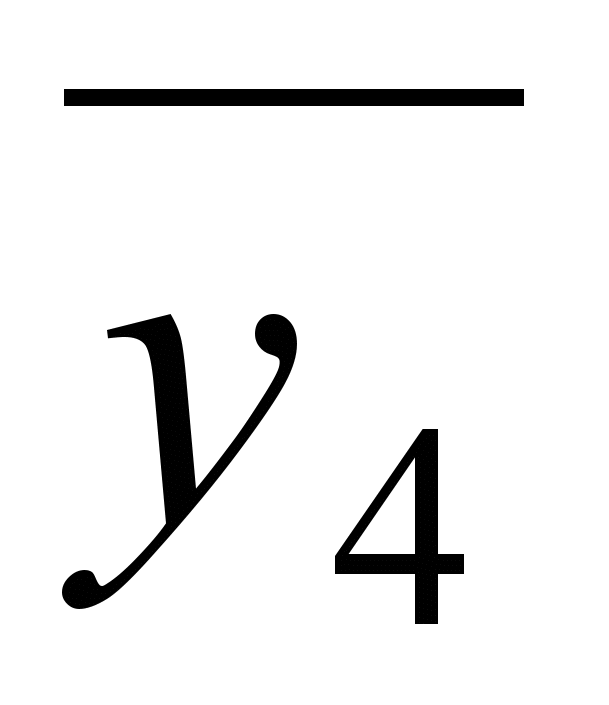
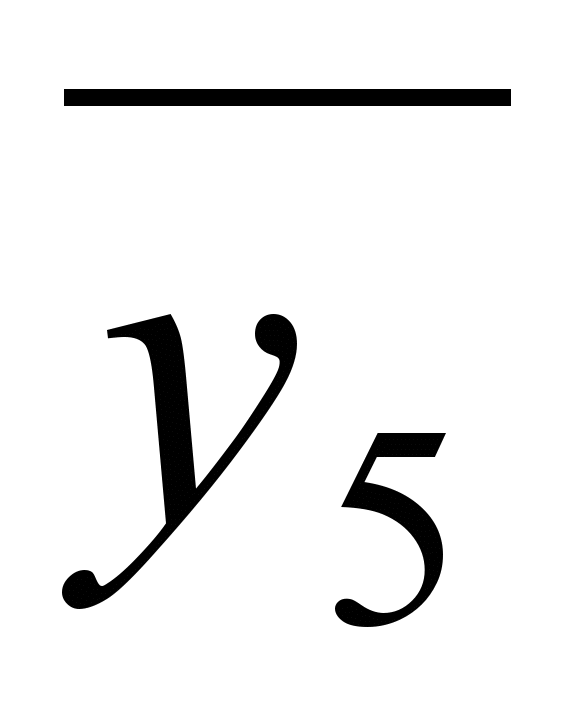 )
)(
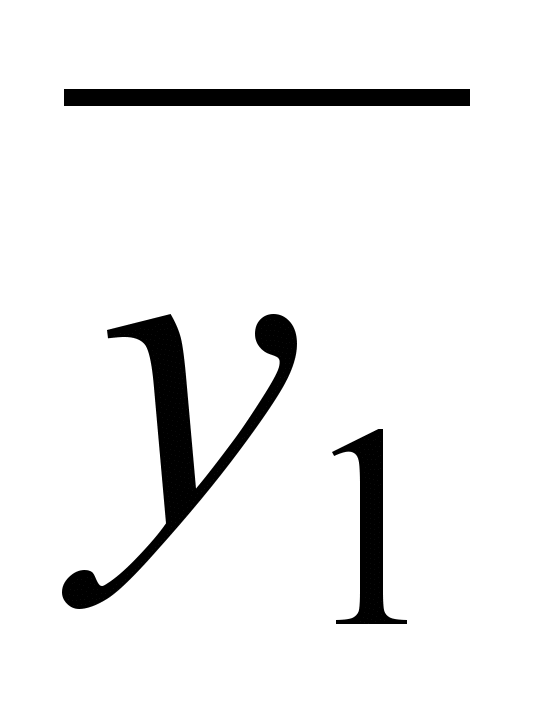
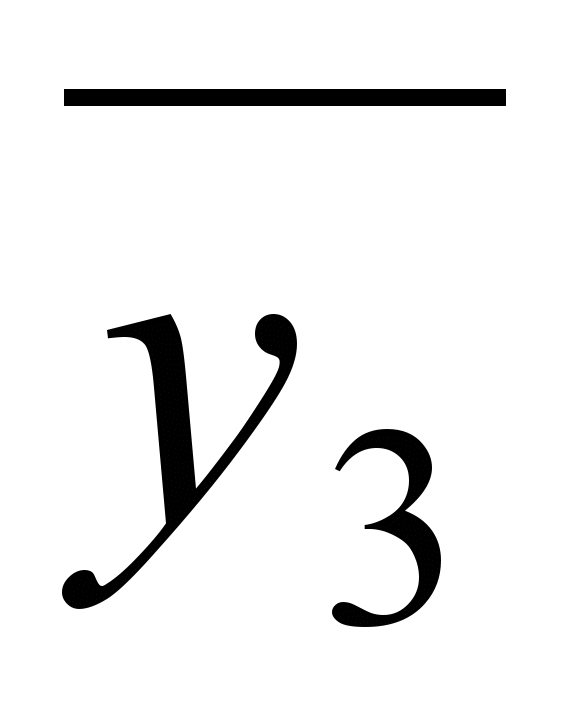
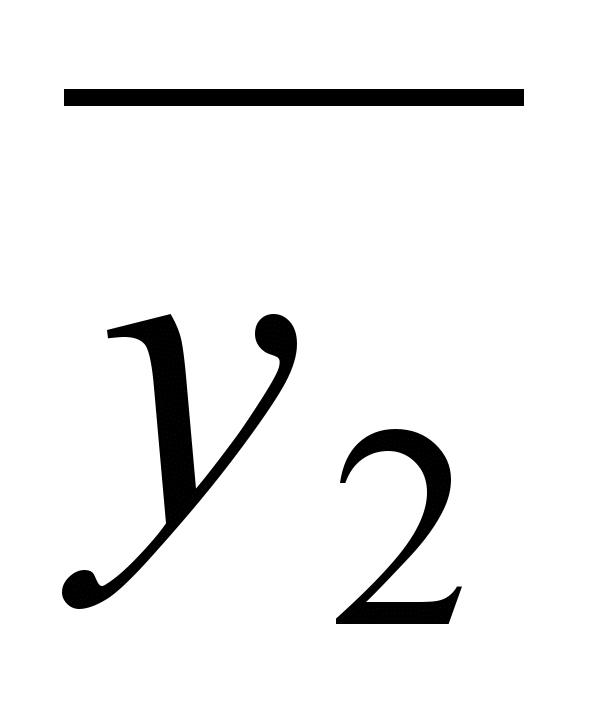
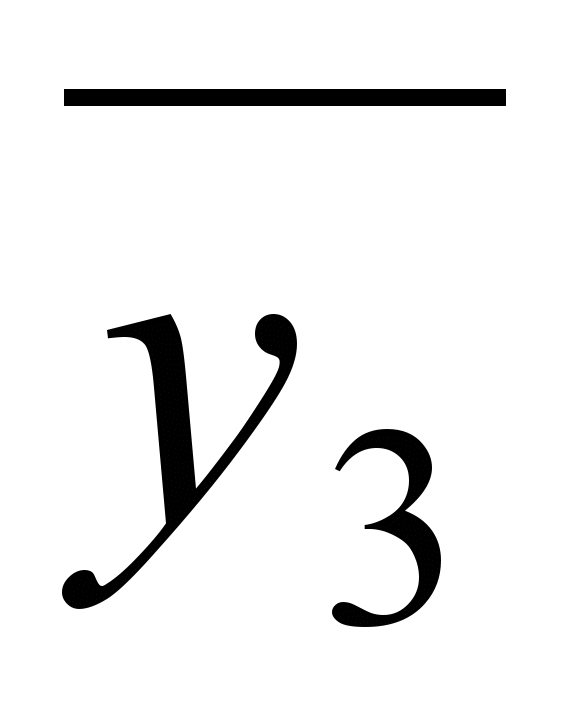
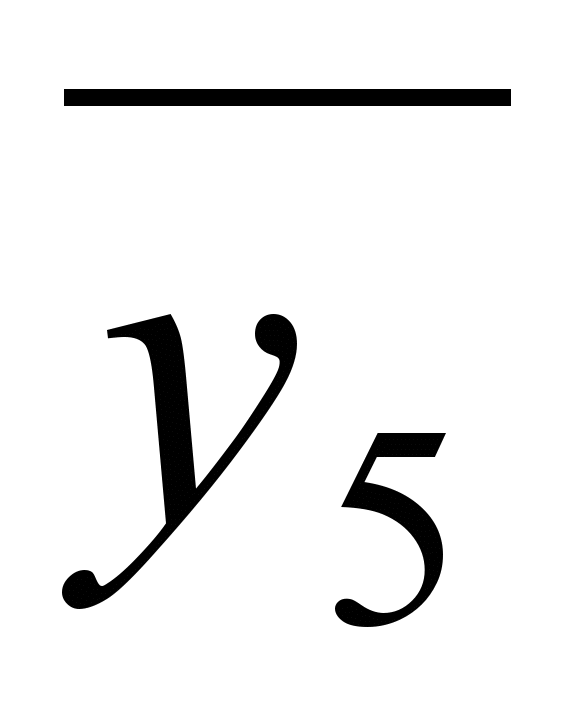
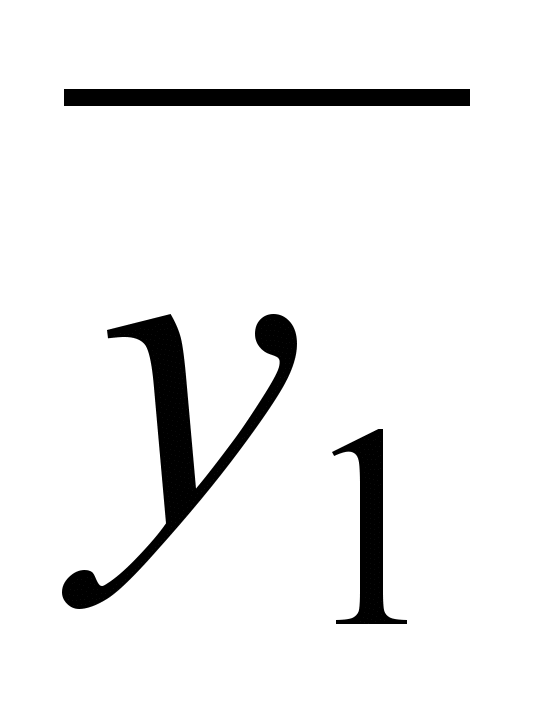
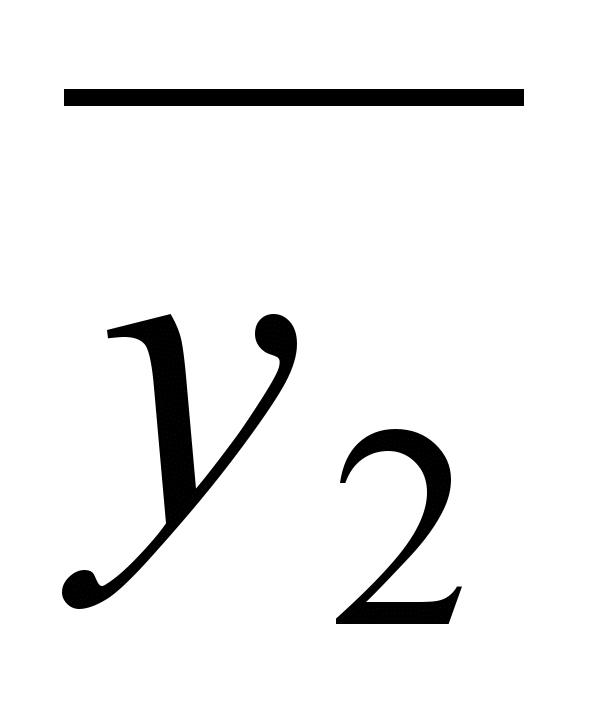
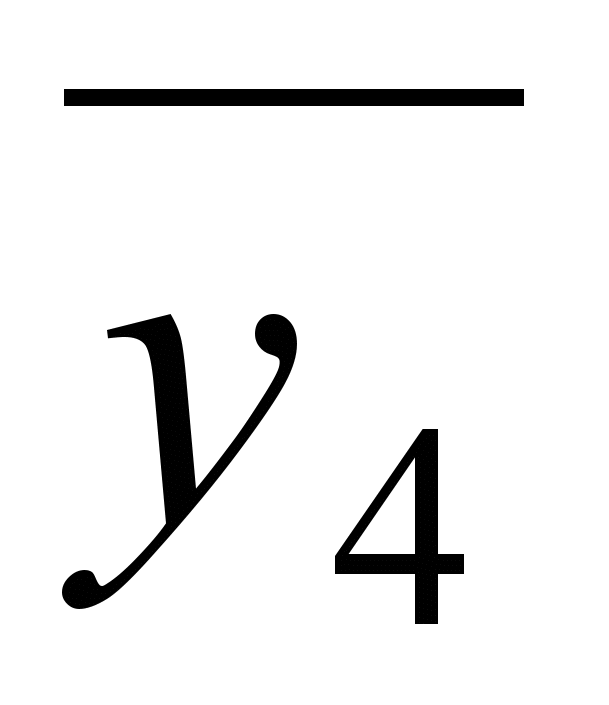
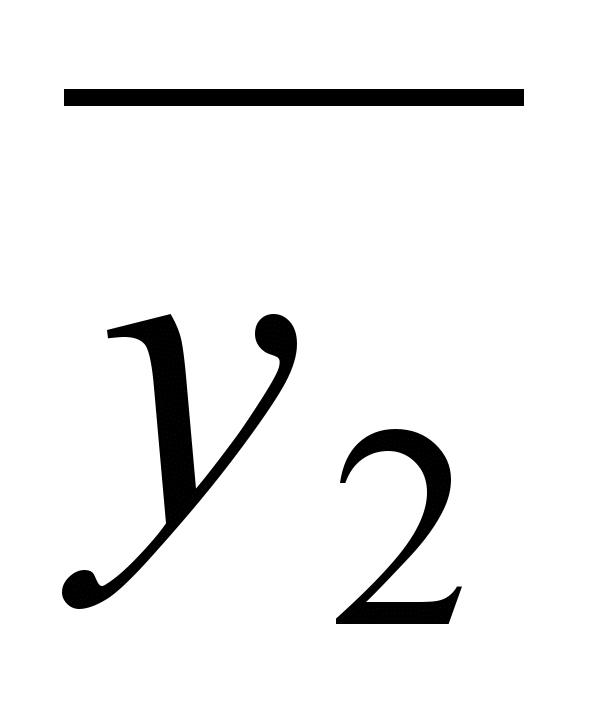
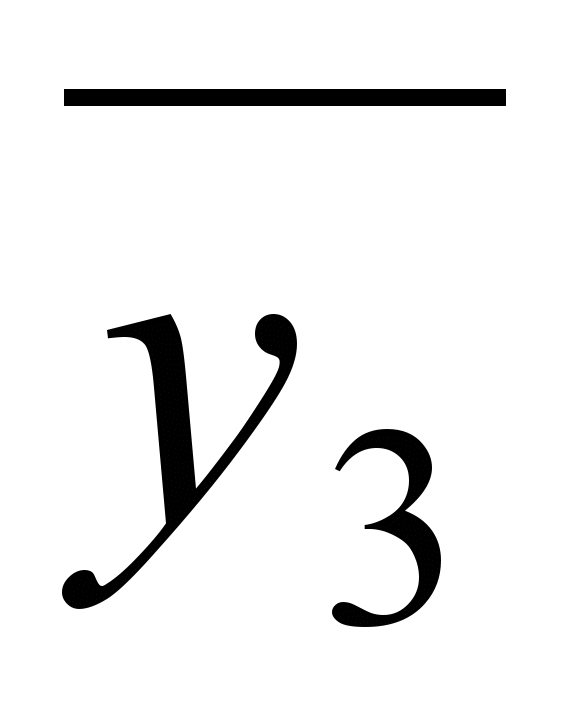
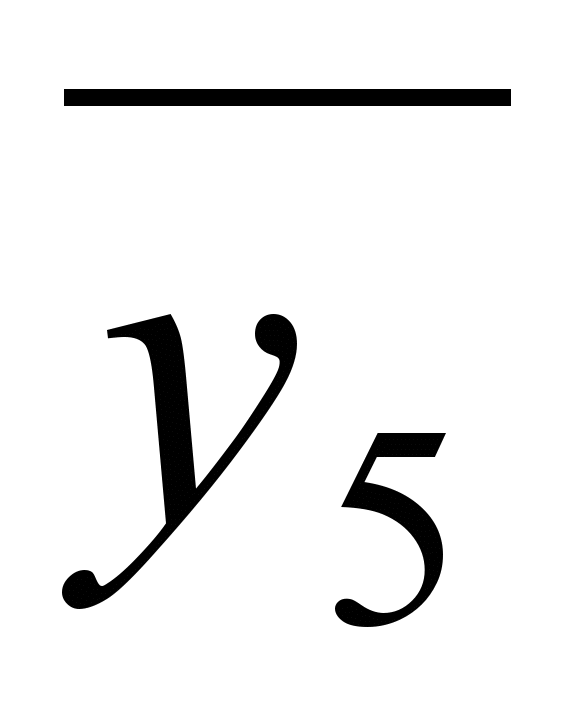
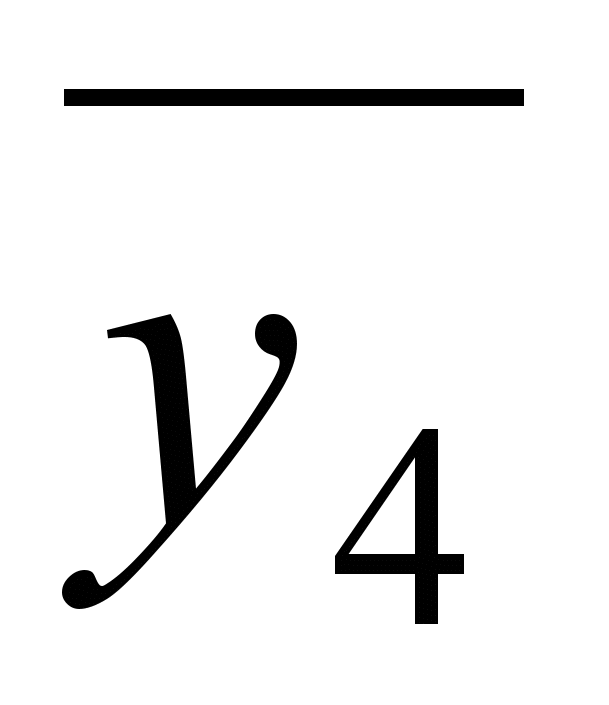 )(
)(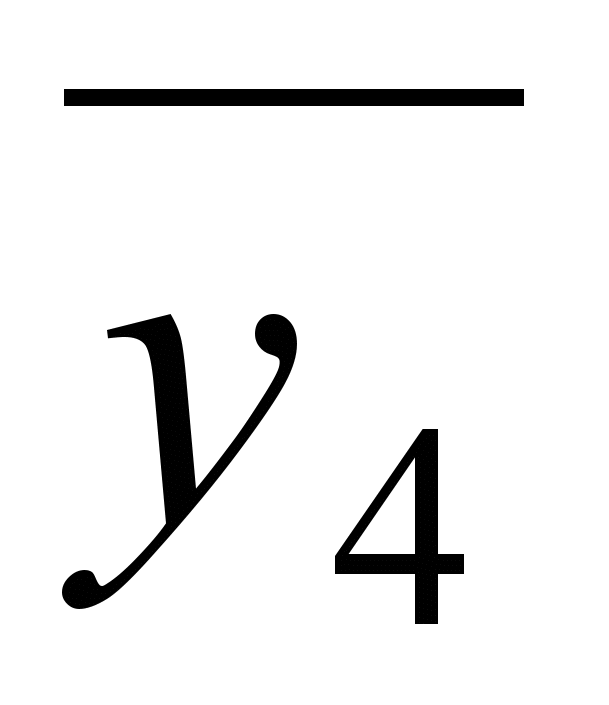
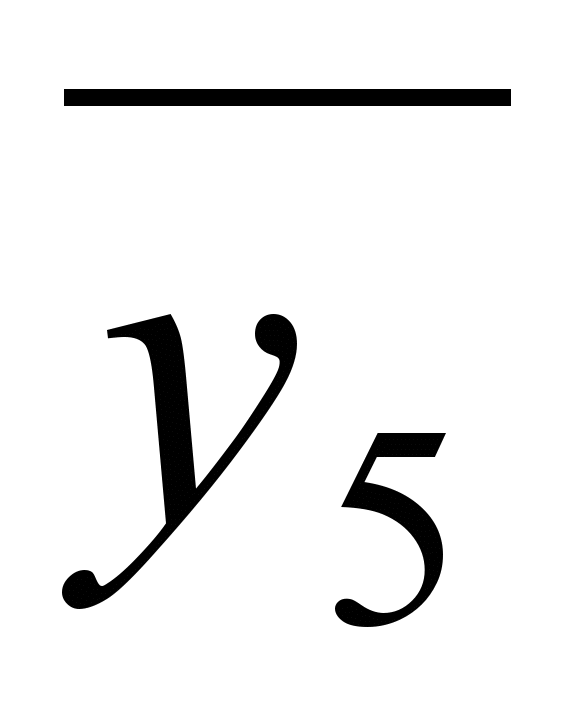 )
)
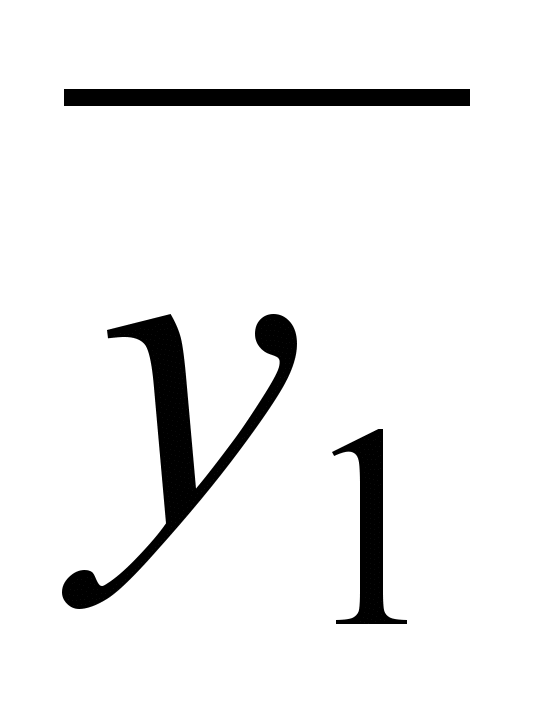
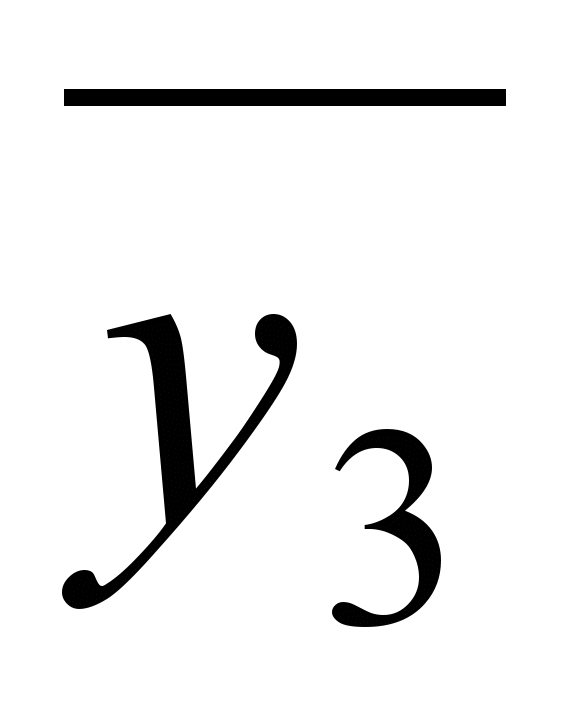
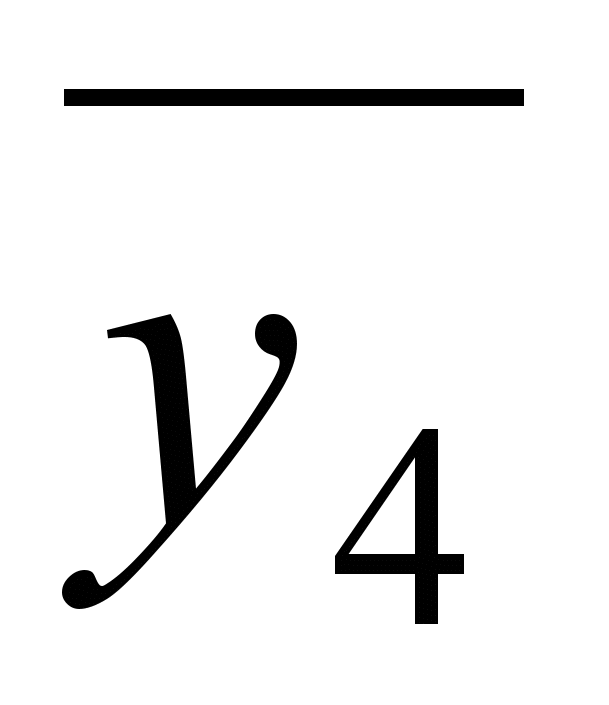
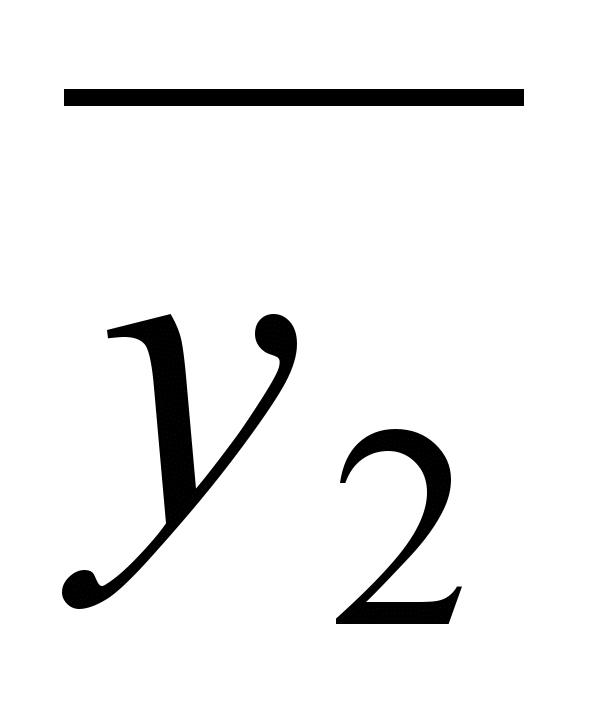
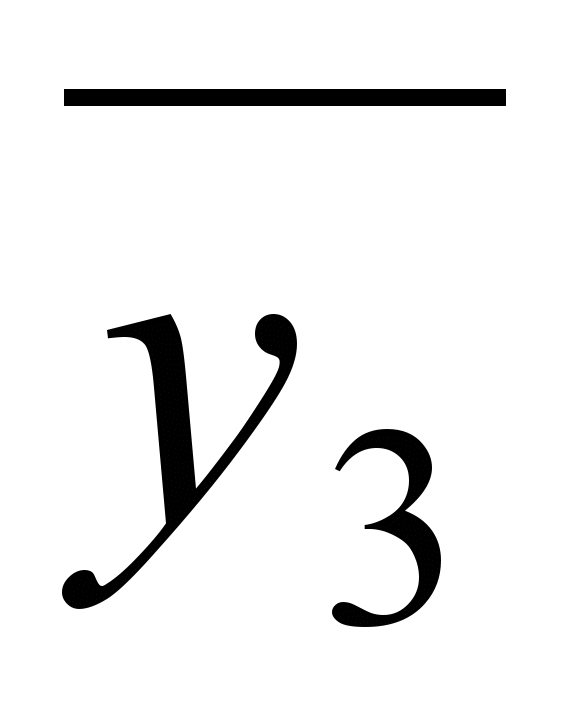
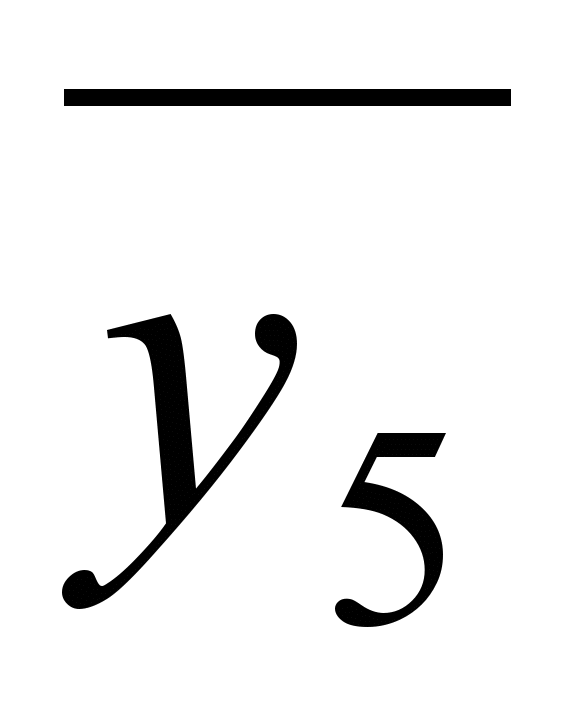
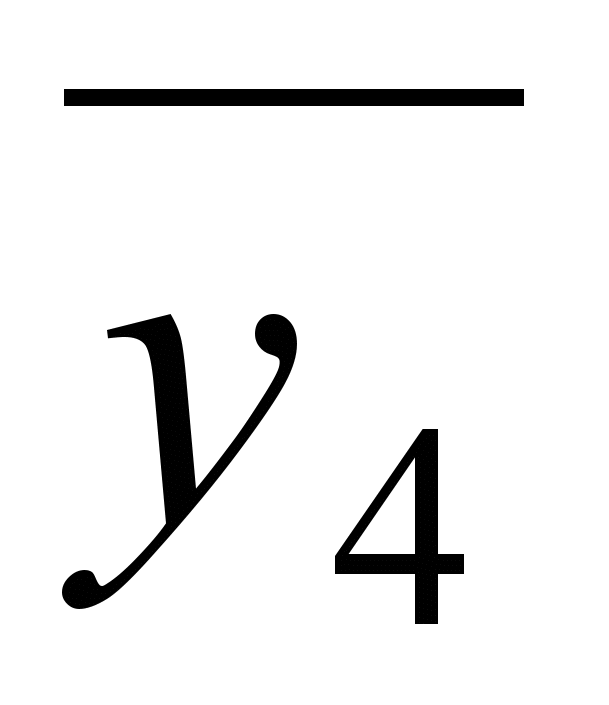
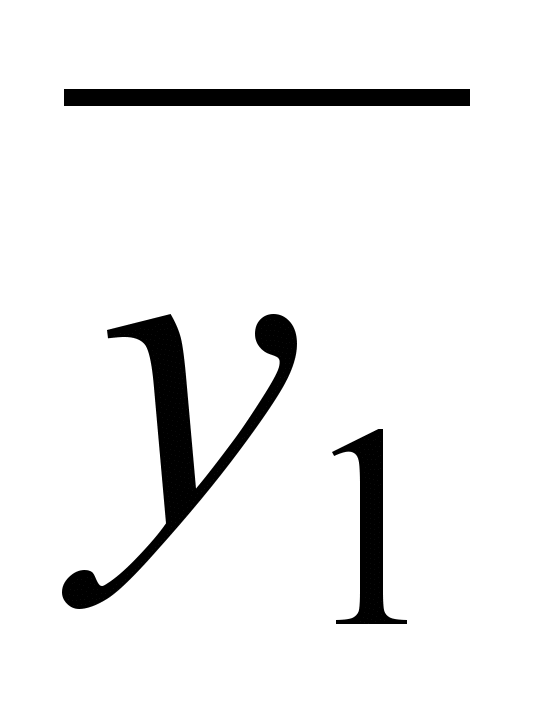
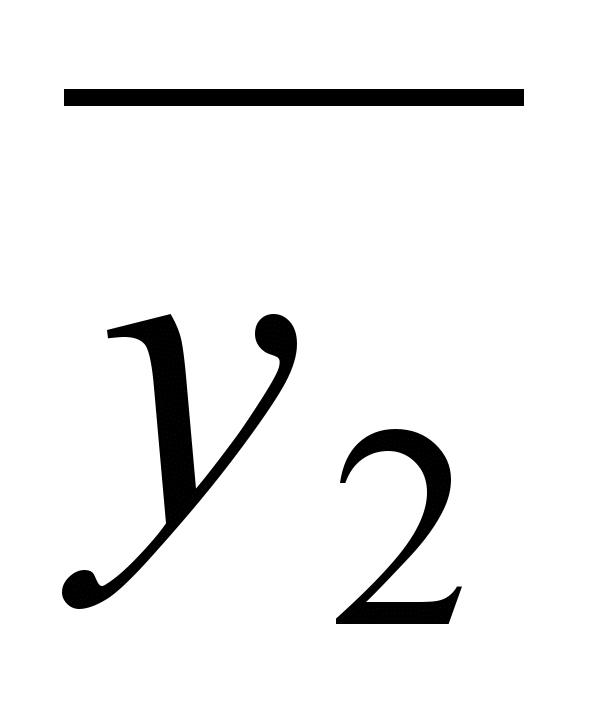
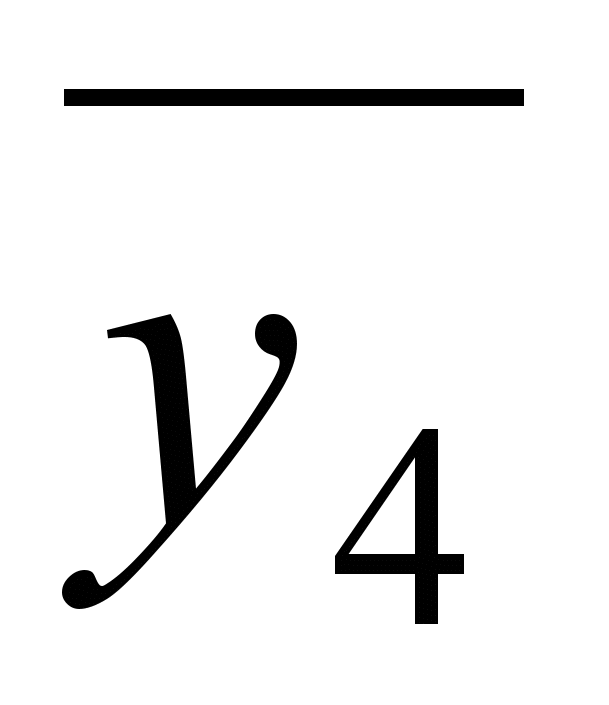
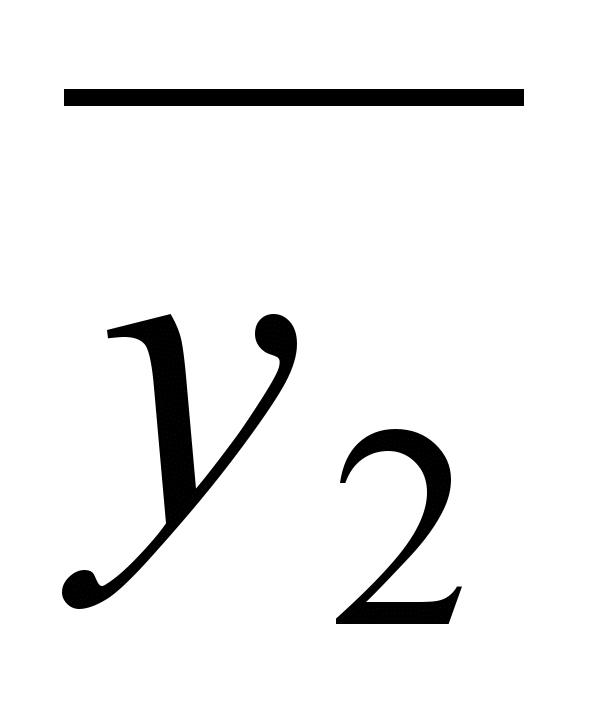
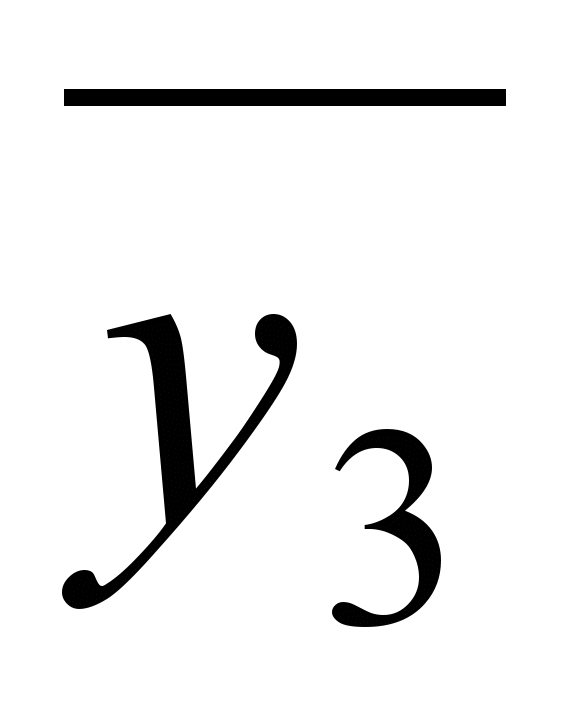
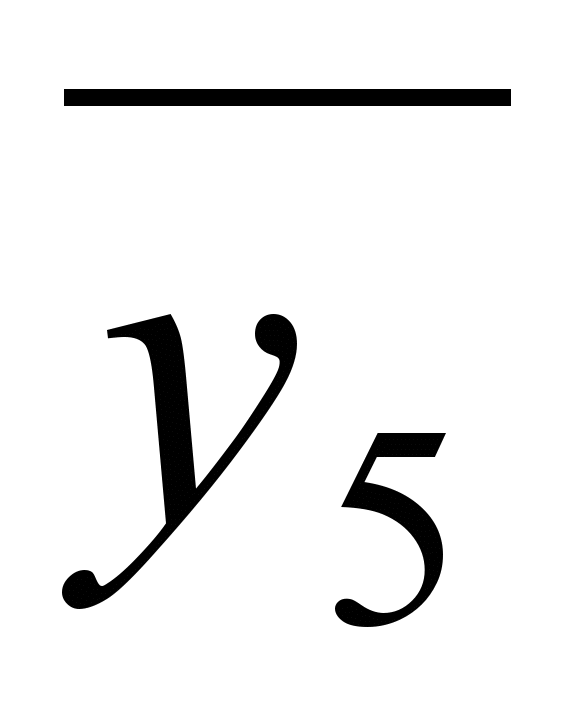
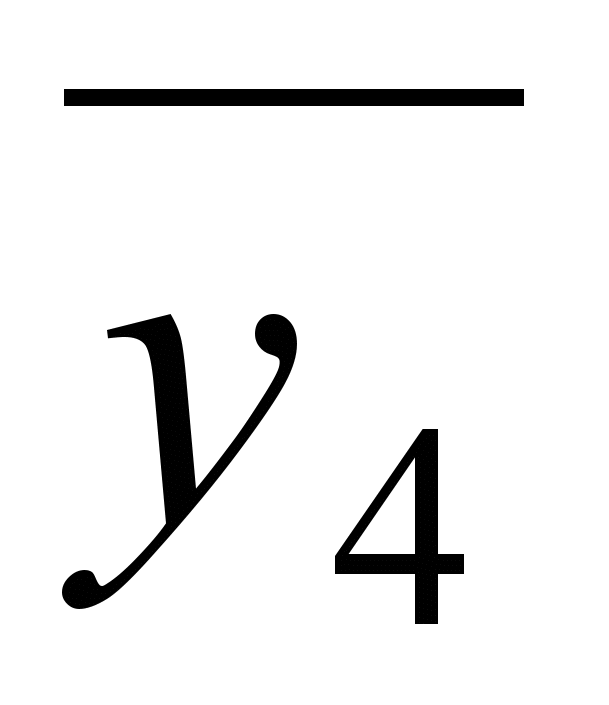
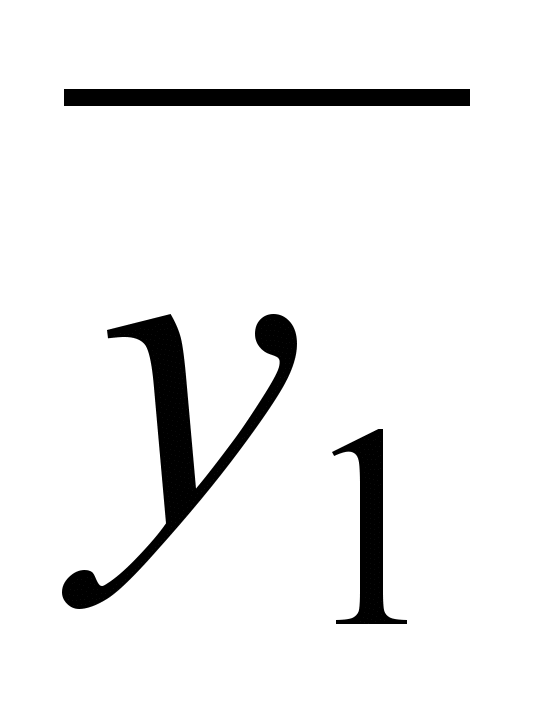
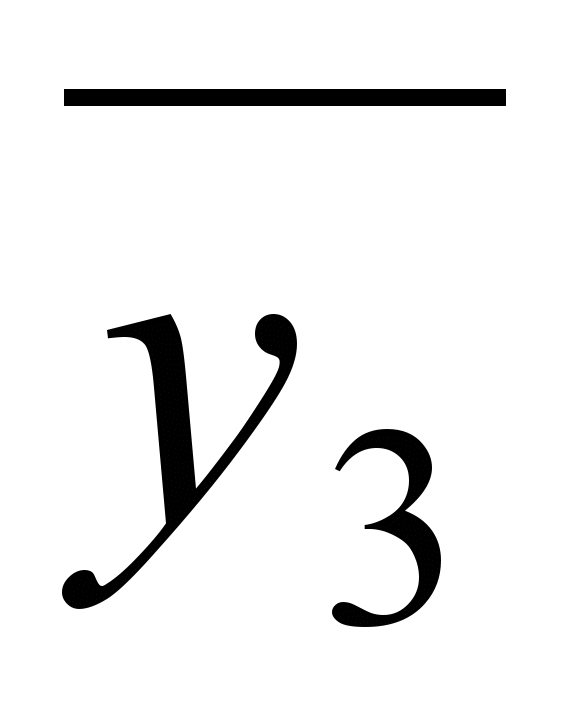
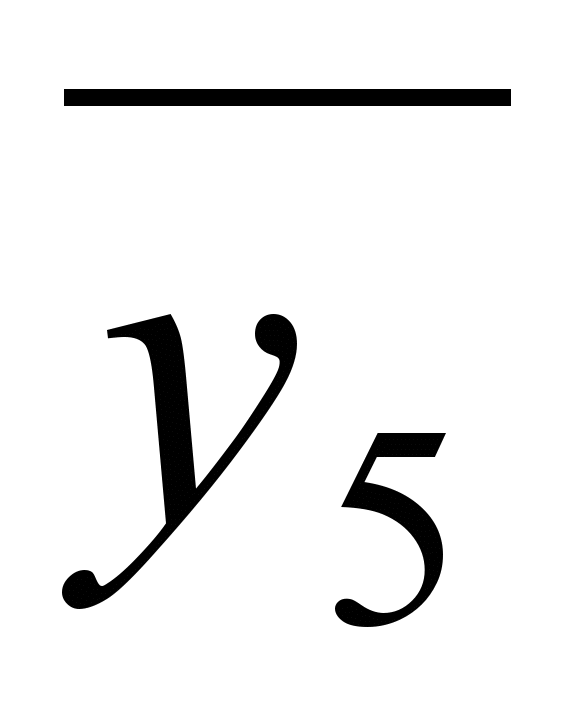
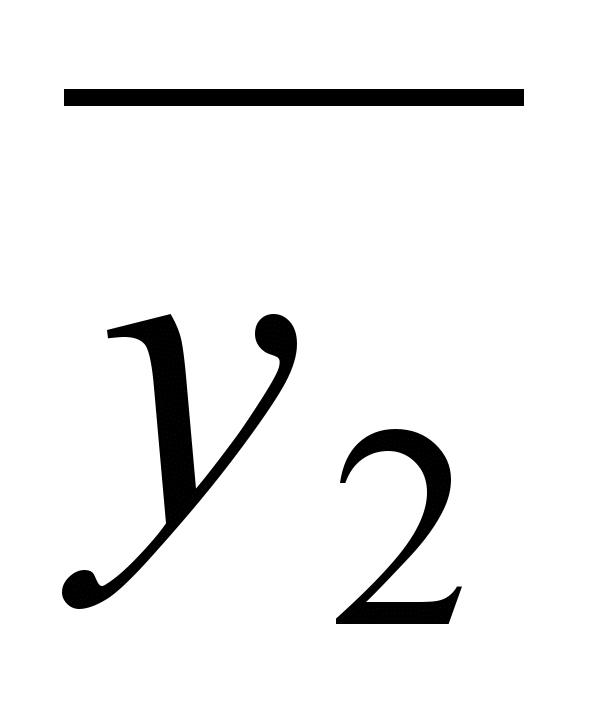
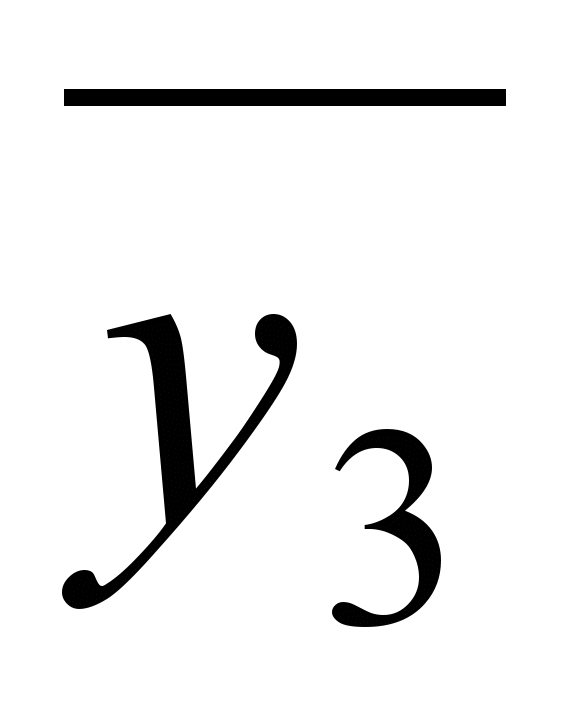
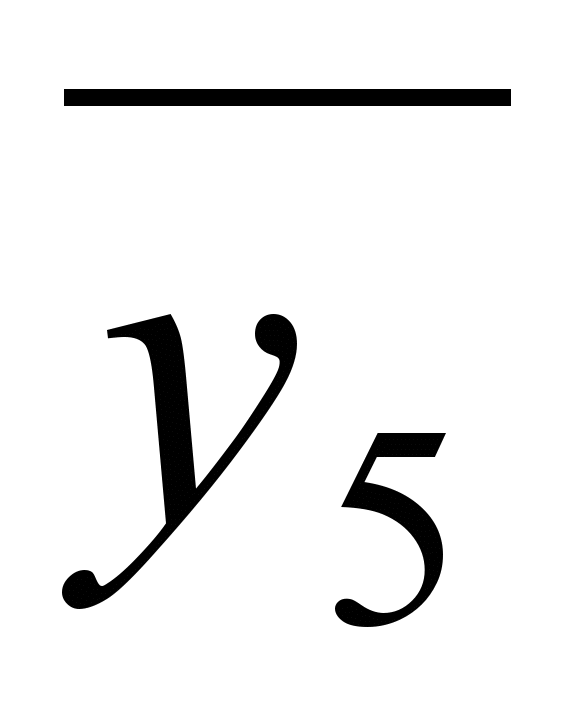
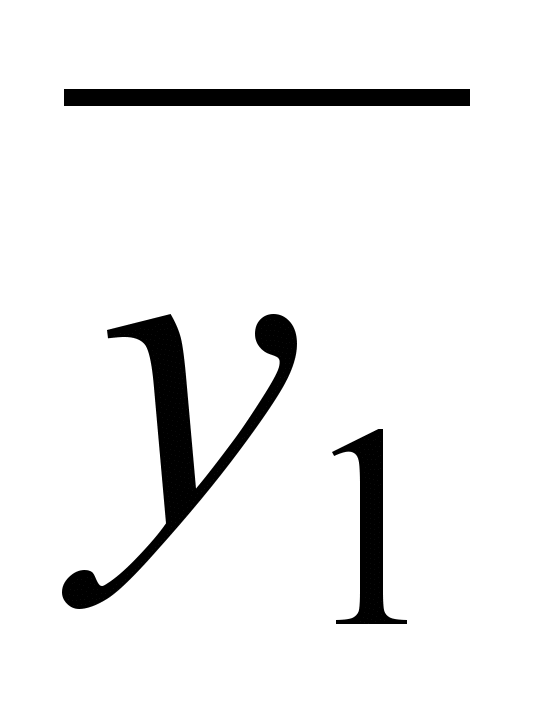
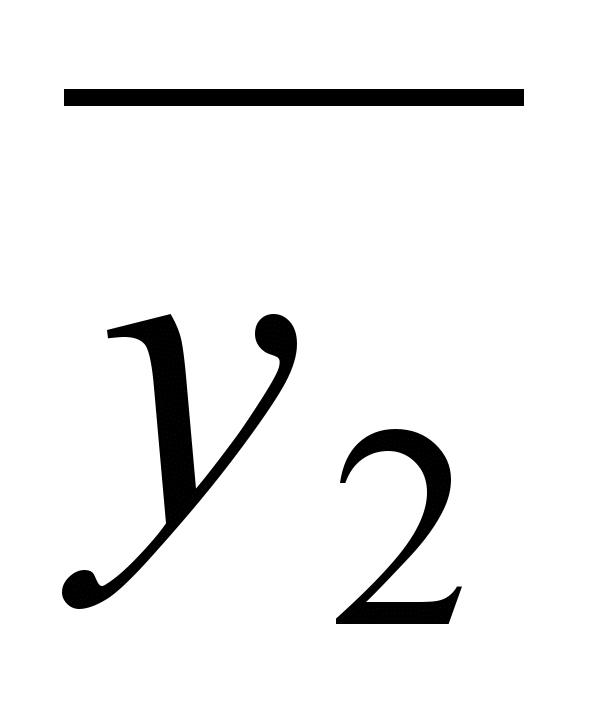
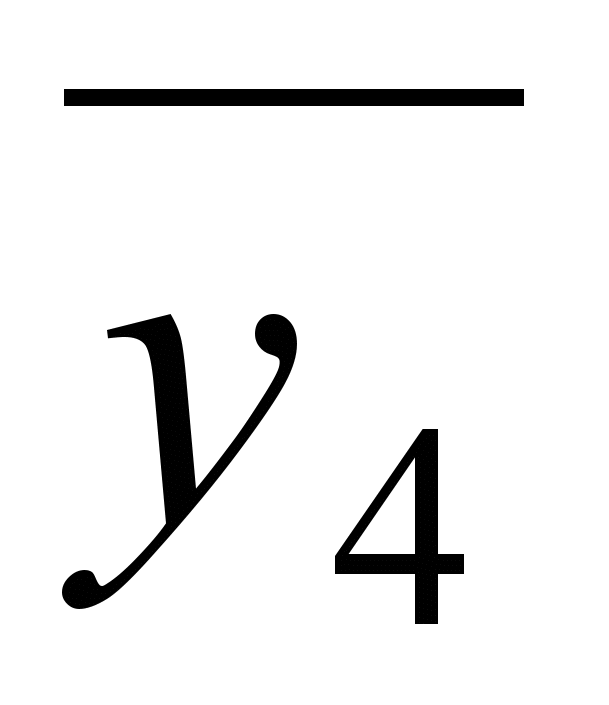
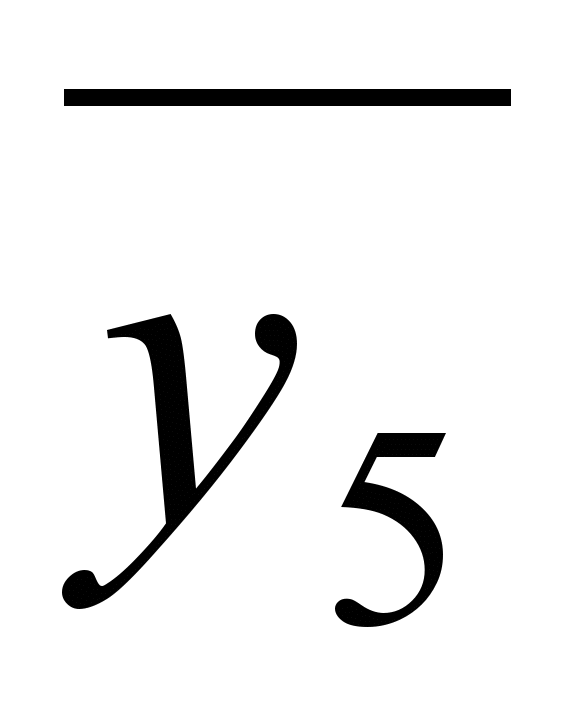
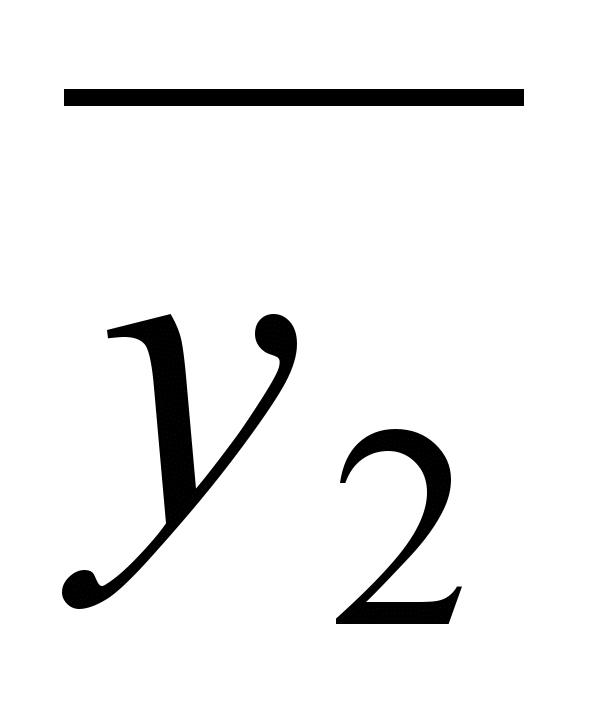
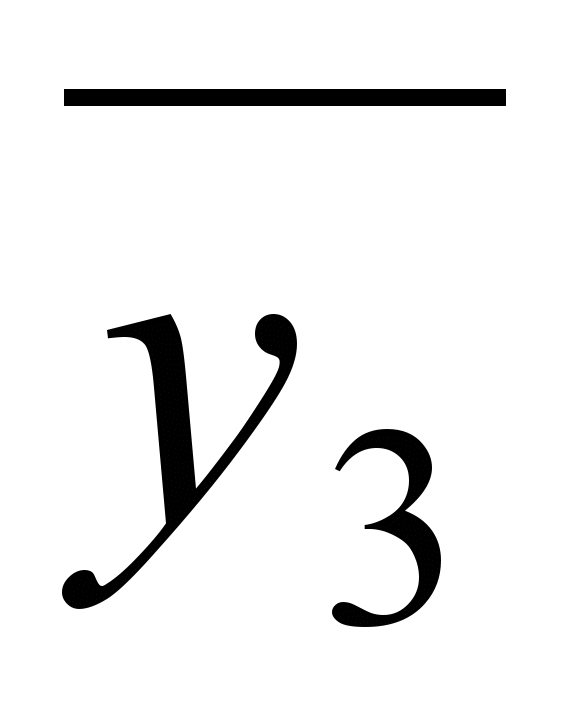
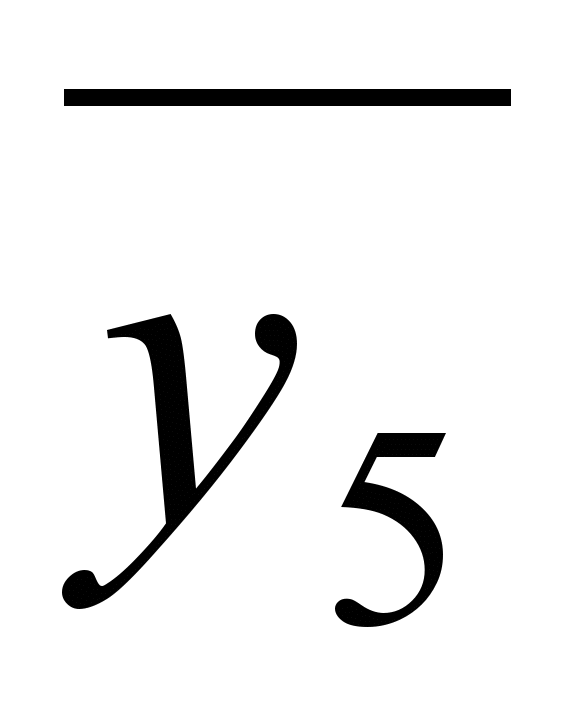
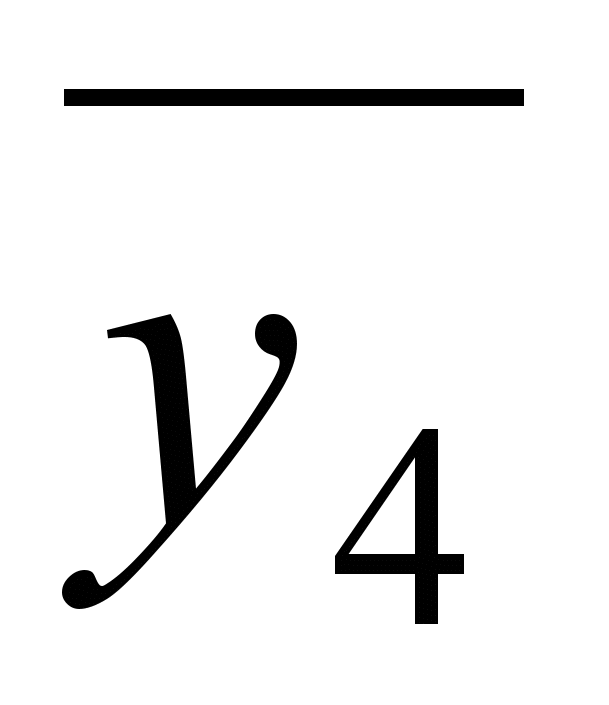 )
)
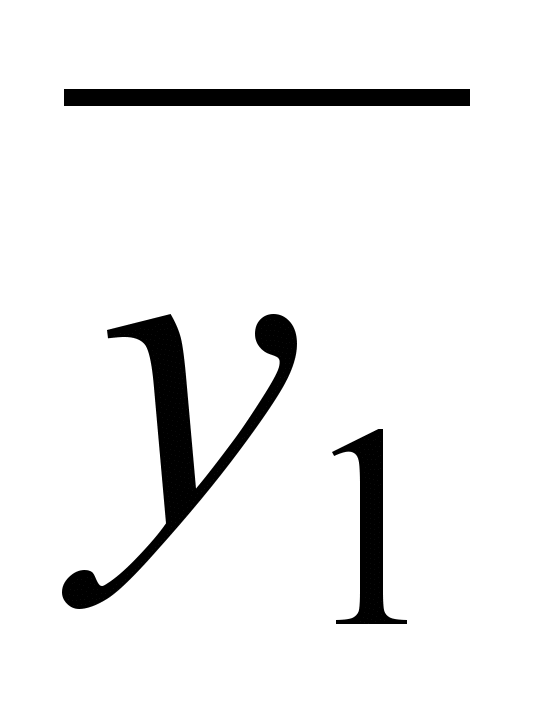
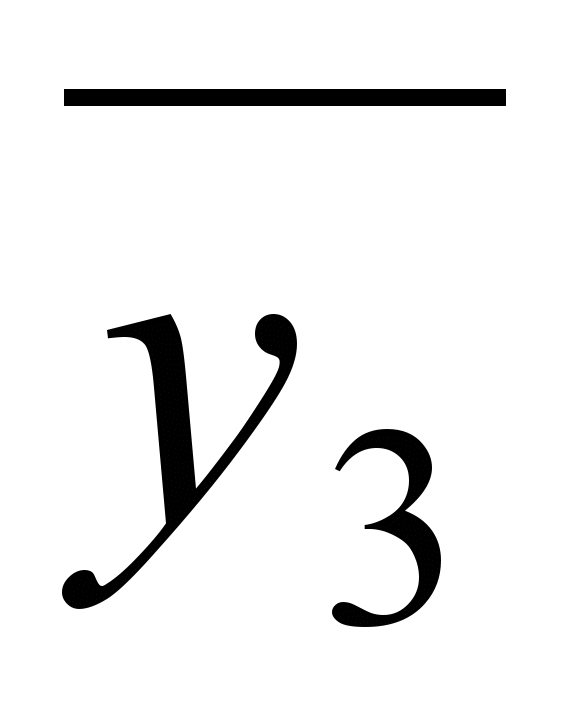
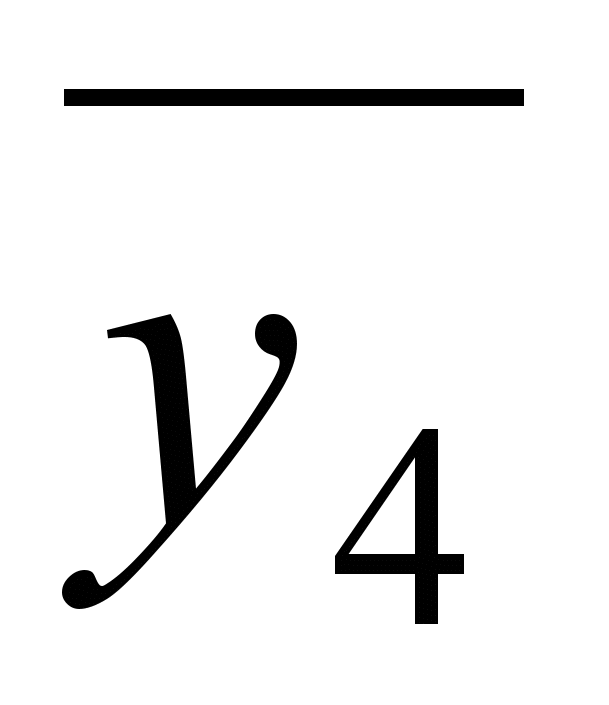
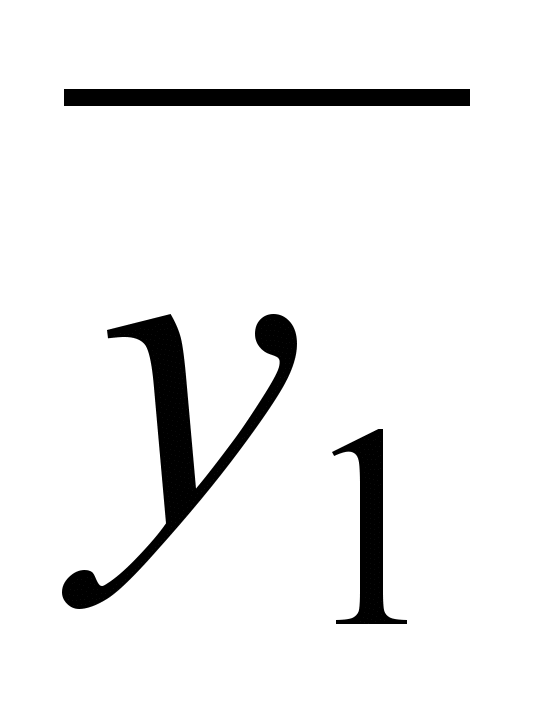
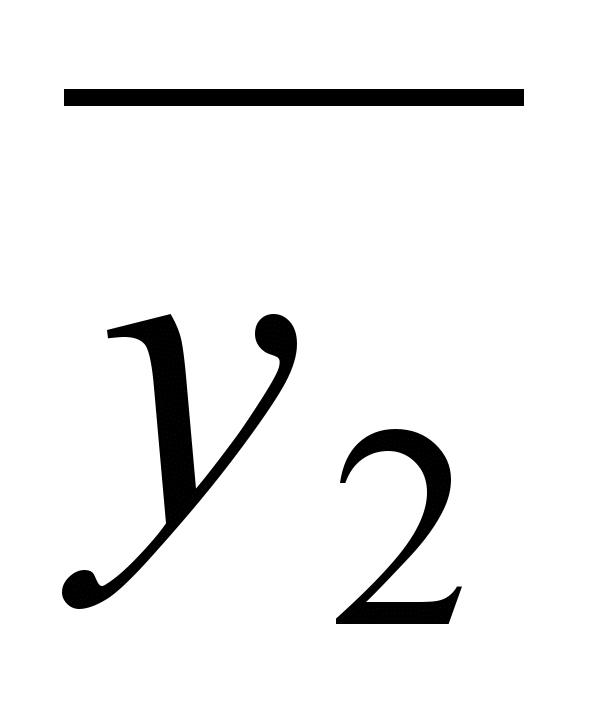
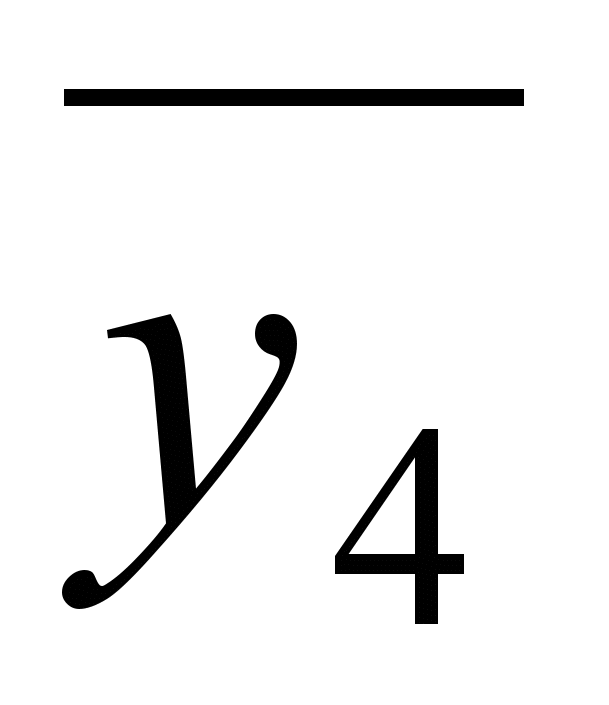
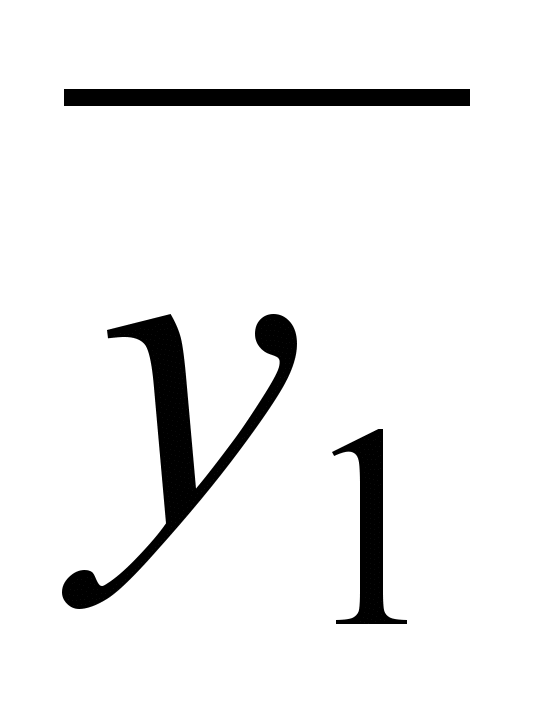
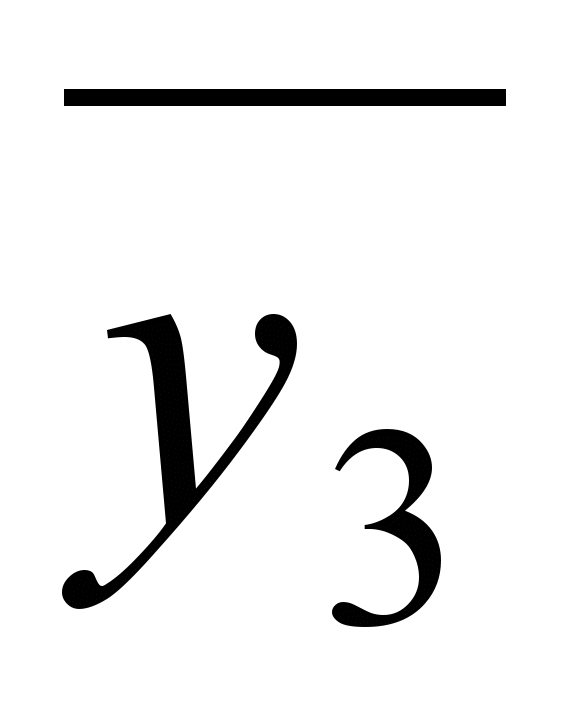
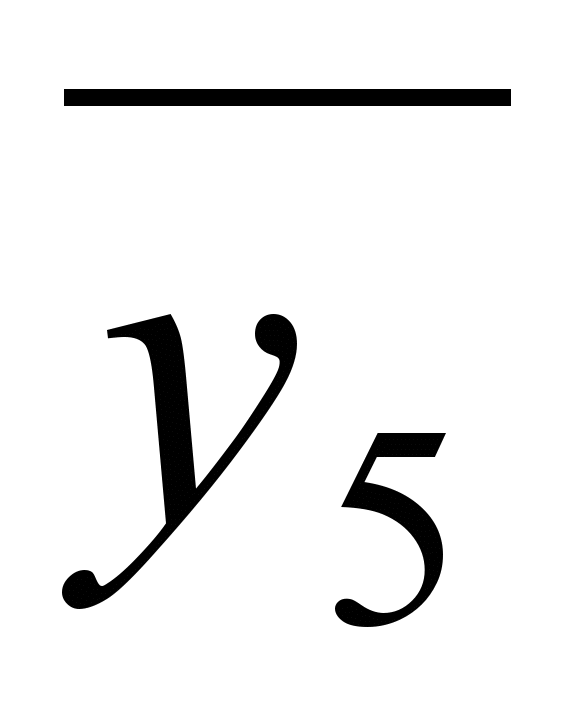
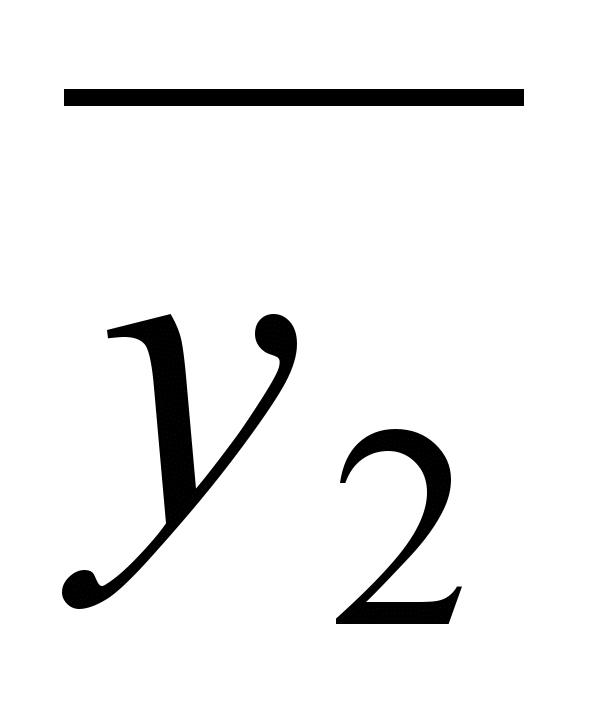
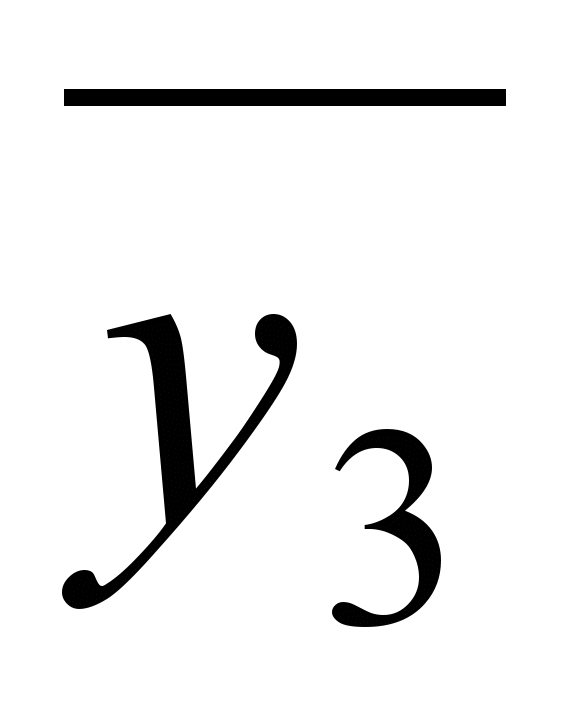
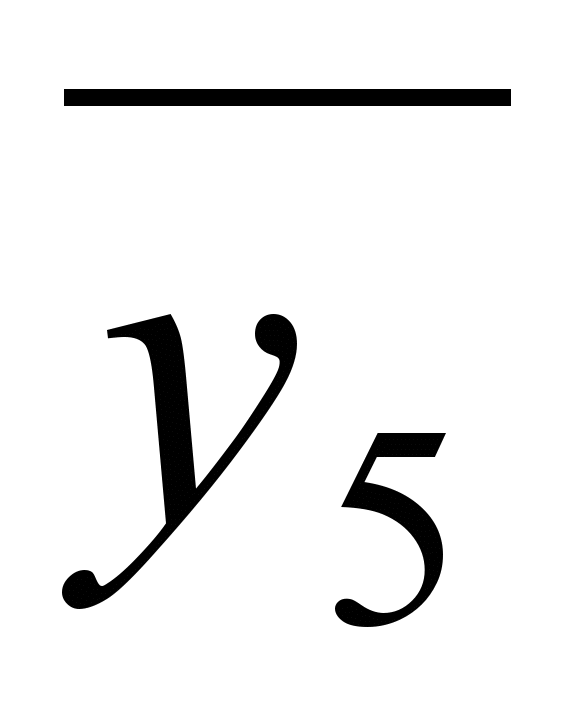 1.
1.В результате имеем четыре внутренне устойчивых множества: {v2,v4}, {v1,v4}, {v2,v5 }, {v3,v5}.
-
Построить наибольшее независимое множество вершин в орграфе, используя алгоритм Магу.
Построить все максимальные независимые множества вершин в орграфе, используя алгоритм Магу
1.2.Внешняя устойчивость
С понятием независимости в графе связано понятие доминирования или внешней устойчивости.
Подмножество вершин U графа G = (V,X) называется доминирующим или внешне устойчивым, если каждая вершина из V\U смежна с некоторой вершиной из U. Иначе говоря, каждая вершина графа находится на расстоянии не более 1 от доминирующего множества.
Внешне устойчивое множество U называется минимальным, если при удалении из него вершины получается множество, не являющееся внешне устойчивым.
Доминирующее множество, состоящее из наименьшего числа вершин, называется наименьшим.
Так для графа, изображенного на рис. 1, минимальным внешне устойчивым множеством является множество 4,6.
Подмножество вершин графа, являющееся как внутренне устойчивым, так и внешне устойчивым, называется ядром.
Очевидно, что ядра графа – это максимальные независимые и минимальные доминирующие множества.
Понятия независимого, доминирующего множеств, а также ядра естественным образом переносится на ориентированные графы.
1.2.1Метод Магу для нахождения семейства минимальных внешне устойчивых подмножеств орграфа
Каждой вершине орграфа D=(V,X) поставим в соответствие некоторую булеву переменную yi следующим образом: если вершина vi U, то yi положим равным 1. Определение внешне устойчивого множества можно записать так: для любой вершины vi из множества V выполняется одно из условий:
вершина vi U;
- вершина vi U , тогда существует вершина vj (j=1n), что vjU и vjГvi.
Запишем это условие в виде формулы алгебры логики, т.е.
yi
 (yj&aij) 1.
(yj&aij) 1.Рассмотрим конъюнкцию по всем вершинам:
F=
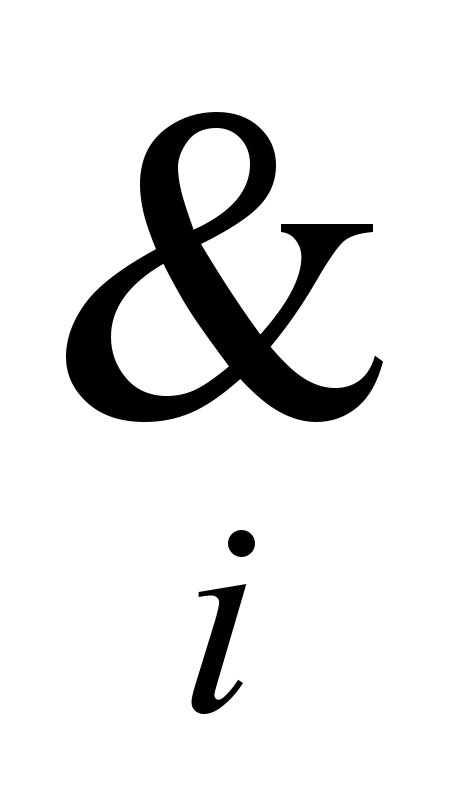 ( yi
( yi (yj&aij)) 1 или
(yj&aij)) 1 илиF=
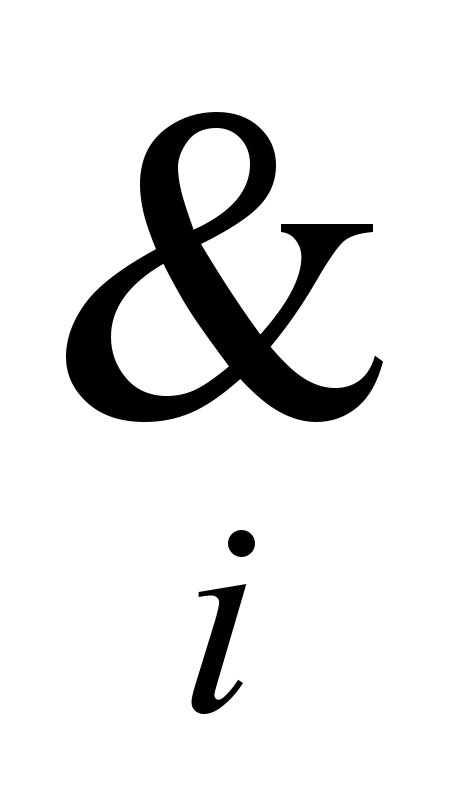 ( yi
( yi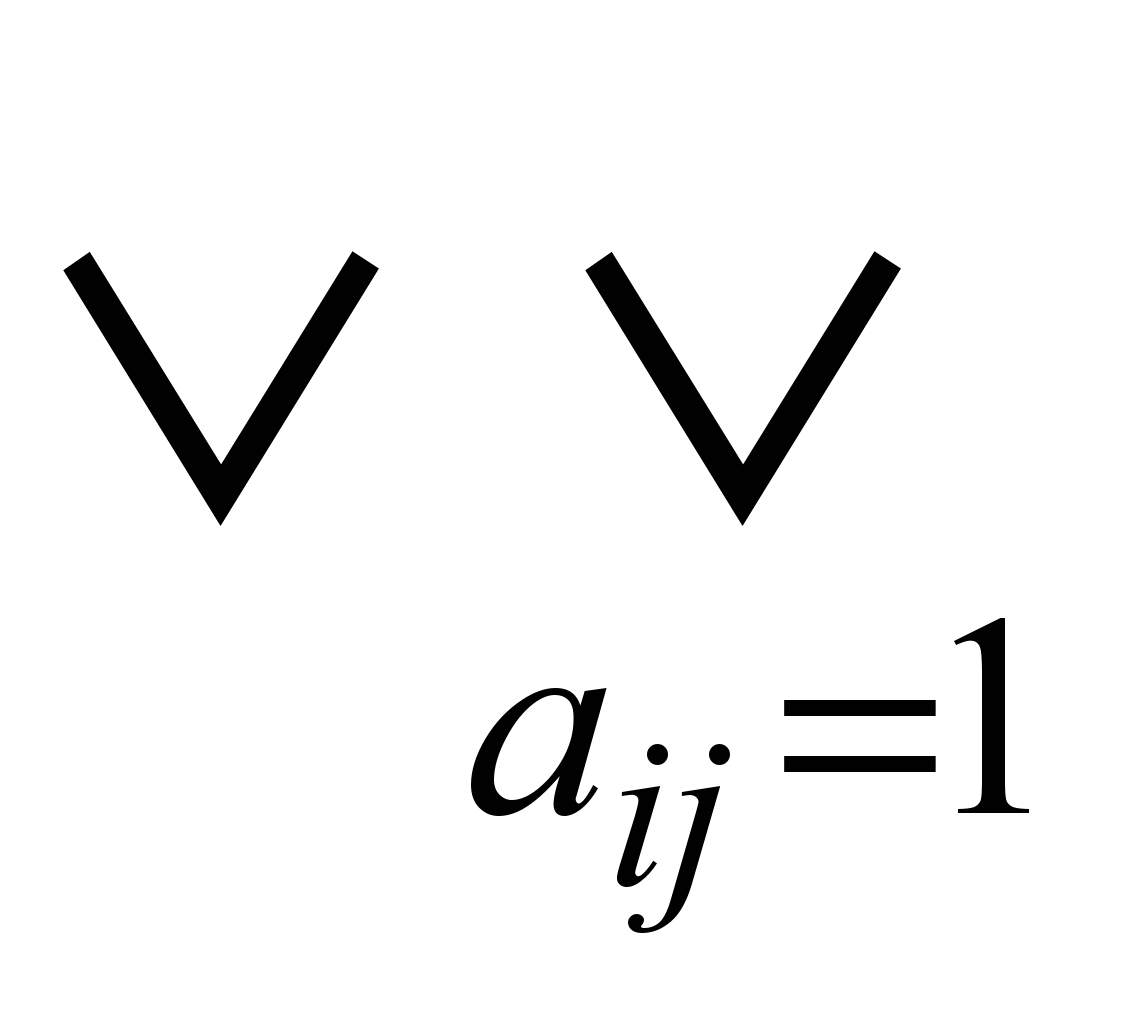 yj) 1.
yj) 1.Учитывая, что ААВ А и А(АВ) А, приведем формулу F к ДНФ. Тогда каждый дизъюнктивный член даст минимальное внешне устойчивое подмножество. Действительно, такой член не содержит переменных с отрицанием и поэтому из множества вершин Vi, соответствующих переменным yi, встречающихся в этом члене, нельзя удалить ни одну.
Пример.
Найти минимальные внешне устойчивые множества вершин для орграфа D, заданного в предыдущем примере.
Решение.
Запишем формулу F. Имеем
F = (y1 y2 y3 y5 )( y2 y3)( y3 y4) y4 (y5 y4) 1.
Упростим формулу, пользуясь формулами поглощения
F = ( y2 y3) y4 1 или F = y2 y4 y3y4 1.
Итак, имеем два минимальных внешне устойчивых множества: {v2,v4 }, {v3,v4}.
-
Найти все максимальные внутренне устойчивые множества заданного орграфа, используя алгоритм Магу.
Найти все минимальные внешне устойчивые множества заданного орграфа, используя алгоритм Магу.
-
Найти все наибольшие внутренне устойчивые множества заданного орграфа, используя алгоритм Магу.
Найти все наименьшие внешне устойчивые множества заданного орграфа, используя алгоритм Магу.
1.3.Покрытия
Введем еще одно понятие, связанное с понятием внутренне устойчивого множества.
Будем говорить, что вершина v и ребро x графа покрывают друг друга, если они инцидентны. Таким образом, ребро x={v,w} покрывает вершины v и w, а каждая из этих вершин покрывает ребро x.
Подмножество вершин UV называется покрытием (вершинным покрытием, опорой) графа G, если каждое ребро из X инцидентно хотя бы одной вершине из U.
Покрытие графа называется минимальным, если оно не содержит покрытия с меньшим числом вершин, и наименьшим, если число вершин в нем наименьшее среди всех покрытий графа G.
Число вершин в наименьшем покрытии графа G называется числом покрытия ( или числом вершинного покрытия) графа G и обозначается через 0(G).
Например, для графа, изображенного на рис.1, каждое из множеств U1={4,5,6,8}, U2={4,5,6,7}, U3={1,2,3,5,6,8} является покрытием, причем U1 и U2 – наименьшие покрытия, а U3 – минимальное покрытие.
Между покрытиями и независимыми множествами в графе существует тесная связь, а именно, множество вершин U графа G является (наименьшим, минимальным) покрытием тогда и только тогда, когда U*= V \U – (наибольшее, максимальное) независимое множество.
-
Найти все минимальные опоры в заданном орграфе, используя алгоритм с возвратом для нахождения независимых множеств U*.
Найти наименьшую опору в заданном орграфе, используя алгоритм с возвратом для нахождения независимых множеств U*.
1.4.Клика
Антиподом понятия независимого множества является понятие клики.
Подмножество U вершин графа G называется кликой, если любые две входящие в него вершины смежны, т.е. если порожденный подграф G(U) является полным.
Клика называется максимальной, если она не содержится в клике с большим числом вершин, и наибольшей, если число вершин в ней наибольшее среди всех клик.
Число вершин в наибольшей клике графа G называется его плотностью (или кликовым числом) и обозначается через (G). Как и в случае независимых множеств, максимальная клика графа может оказаться не наибольшей.
Понятие клики, в частности максимальной клики, используется в различных социологических теориях ( вопросы, связанные с голосованием, альянсами и т.п.), а также в теории игр.
Очевидно следующее утверждение: подмножество вершин графа G является кликой тогда и только тогда, когда оно является независимым множеством в дополнительном графе G*.
-
Найти все максимальные клики в заданном орграфе, используя алгоритм нахождения независимых множеств в дополнительном графе.
-
Найти наибольшую клику в заданном орграфе, используя алгоритм нахождения независимых множеств в дополнительном графе.
1.5.Раскраска графа
Задачи раскраски вершин или ребер графа занимают важное место в теории графов. К построению раскрасок сводится целый ряд практических задач. Характерной особенностью этих задач является существование объектов, которые по каким-либо причинам не могут быть объединены в одну группу.
Пусть G – некоторый граф, k – натуральное число. Произвольная функция вида f: V → {1,2,…,k} называется вершинной k-раскраской или просто k-раскраской графа G.
Раскраска называется правильной, если f(v)≠f(u) для любых смежных вершин v и u. Граф, для которого существует правильная k-раскраска, называется k-раскрашиваемым.
Минимальное число k, при котором граф G является k-раскрашиваемым, называется хроматическим числом этого графа и обозначается χ (G). Если χ (G)=k, то граф называется k-хроматическим. Правильная k-раскраска графа при k =χ (G) называется минимальной.
Алгоритм раскрашивания графов
- Выберем в графе G некоторое максимальное независимое множество вершин U (лучше наибольшее). Покрасим все вершины данного множества в один цвет.
- Выберем максимальное независимое множество вершин U1 в графе G1, который получается из графа G удалением множества вершин U и всех инцидентных им ребер. Покрасим вершины множества U1 в очередной цвет.
- Шаг 2 повторять до тех пор, пока в графе G не будут раскрашены все вершины.
Реберной k-раскраской графа G называется функция φ, ставящая в соответствие каждому его ребру x число φ(x) из множества {1,2,…,k}. Реберная окраска называется правильной, если смежные ребра имеют разные цвета. Граф, допускающий правильную реберную k-раскраску, называется реберно k-раскрашиваемым. Минимальное число k, при котором граф G является реберно k-раскрашиваемым, называется хроматическим классом (хроматическим индексом или реберным хроматическим числом) графа G и обозначается через χ ‘(G). Если χ ‘(G)=k, то граф называется реберно k-хроматическим.
Независимые множества ребер графа G находятся во взаимно однозначном соответствии с независимыми множествами вершин реберного графа L(G)=(V1,X1), который для графа G=(V,X) определяется следующими двумя условиями:
- V1 = X,
- вершины х1 и х2 смежны в L(G) тогда и только тогда, когда ребра х1 и х2 смежны в G.
На рис. 2 изображены два графа – G и L(G). Вершины графа G – темные кружки, вершины графа L(G) – светлые кружки. Ребра графа G – тонкие линии, ребра графа L(G) – жирные линии.















Рис. 2
Поскольку ребра любого графа G смежны тогда, когда смежны соответствующие вершины реберного графа L(G) (правило построения реберного графа смотри ниже), то χ ‘(G) можно определить как хроматическое число графа L(G), т.е. χ ‘(G)=χ (L(G)).
Найти хроматическое число заданного графа, используя алгоритм с возвратом для нахождения независимых множеств вершин, указать, какие вершины в какой цвет окрашиваются.
Найти хроматический класс заданного графа, используя алгоритм с возвратом для нахождения независимых множеств вершин реберного графа, указать, какие ребра в какой цвет окрашиваются.
1.6.Паросочетания
Не менее важным, чем понятие вершинной независимости, является понятие реберной независимости.
Произвольное подмножество попарно несмежных ребер графа называется паросочетанием ( или независимым множеством ребер).
В качестве иллюстрации рассмотрим граф, изображенный на рис.2. В нем паросочетаниями являются, например, х1,х3,х5,х7, х1, х2, х2,х6.









х1 х2 х3 х4 х5 х6 х7



Рис. 3.
Паросочетание графа G называется максимальным, если оно не содержится в паросочетании с большим числом ребер, и наибольшим, если число ребер в нем наибольшее среди всех паросочетаний графа G.
Число ребер в наибольшем паросочетании графа G называется числом паросочетания и обозначается 1(G).
Независимые множества ребер графа G находятся во взаимно однозначном соответствии с независимыми множествами вершин реберного графа L(G)=(V1,X1), который для графа G=(V,X) определяется следующими двумя условиями:
- V1 = X,
- вершины х1 и х2 смежны в L(G) тогда и только тогда, когда ребра х1 и х2 смежны в G.















Рис. 4
На рис. 4 изображены два графа – G и L(G). Вершины графа G – темные кружки, вершины графа L(G) – светлые кружки. Ребра графа G – тонкие линии, ребра графа L(G) – жирные линии.
-
Найти все максимальные паросочетания в заданном графе, используя алгоритм с возвратом для нахождения независимых множеств вершин реберного графа.
Найти наибольшее паросочетание в заданном графе, используя алгоритм с возвратом для нахождения независимых множеств вершин реберного графа.
