Программа, методические указания и контрольные задания по курсу «основы программирования на языке паскаль» Для студентов бакалавриата направления 230400с заочной формы обучения

Вид материала

Программа

Содержание Методические указания к выполнению задания 5 Пример выполнения задачи 5 Задание 6. Программирование с использованием подпрограмм Задания к задаче 5

Подобный материал:

• Рабочая программа методические указания контрольные задания для студентов специальности, 833.92kb.
• Низкотемпературных и пищевых технологий, 526.64kb.
• Методические указания и контрольные задания для студентов заочной формы обучения Составитель:, 672.87kb.
• Методические указания к практическим занятиям для студентов экономических специальностей, 560.21kb.
• Финанс ы методические указания и контрольные задания для студентов заочной формы обучения, 825.1kb.
• Программа, методические указания и контрольные задания по дисциплине концепции современного, 717.75kb.
• Программа, методические указания и контрольные задания по учебной дисциплине «риторика», 1732.52kb.
• Программа, методические указания и контрольные задания для студентов специальности, 1197.59kb.
• Методические указания и контрольные задания для студентов заочной формы обучения, специальность, 838.97kb.
• Общая химическая технология, 419.5kb.

Методические указания к выполнению задания 5

Перед выполнением задачи необходимо изучить раздел 3.10 программы, затем разработать алгоритм задачи, после чего составить программу.

Пример выполнения задачи 5

Дана матрица А(55), содержащая положительные и отрицательные целые числа. Сформировать матрицу С по принципу: если а_{i j}< 0 (i = 1,2,…, 5, j = 1,2,…, 5), элементу c_{i j} присвоить значение, равное –1, в противном случае – равное +1. Перебор элементов исходной матрицы вести по строкам. Использо­вать операторы For и Repeat.

Алгоритм

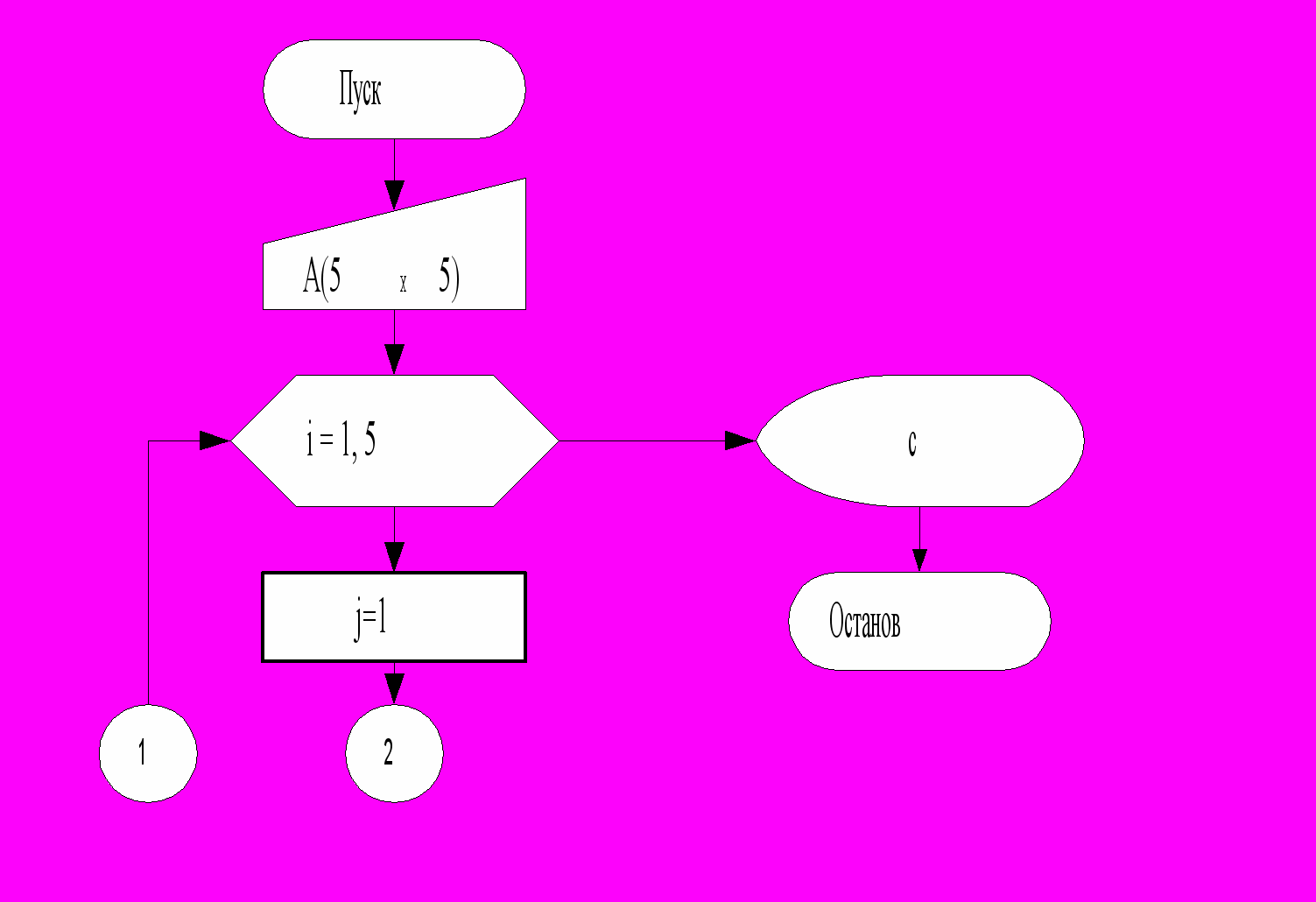
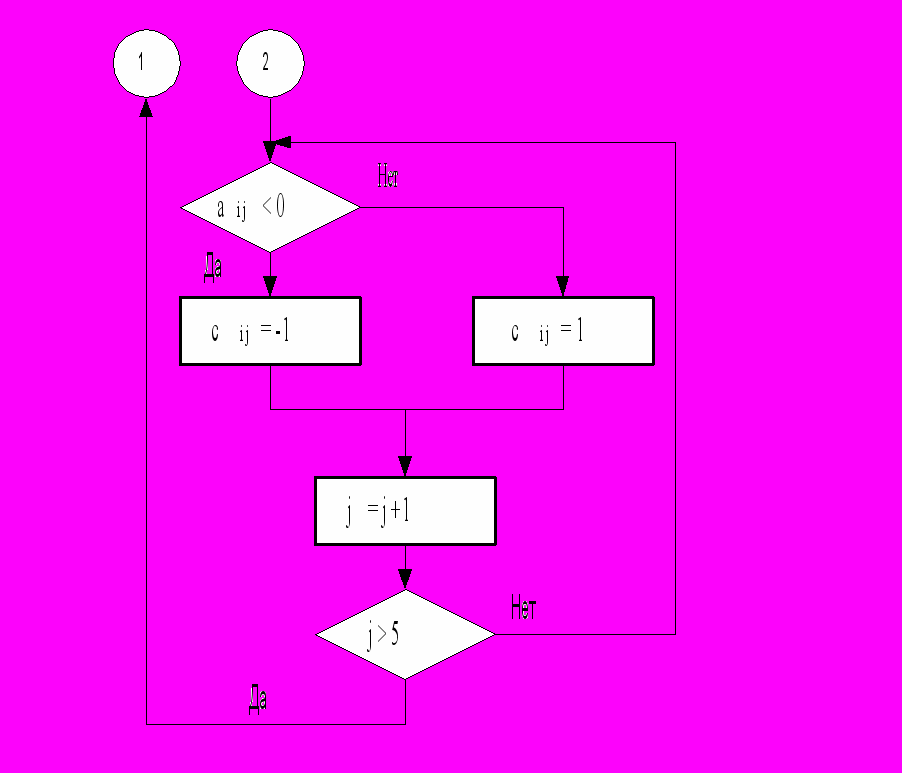
Программа

Program z4;

Var a, c: Array [1..5, 1..5] of Real;

i, j: integer;

Begin

Writeln (’ Введите матрицу’);

For i:=1 To 5 Do

For j:=1 To 5 Do Read (a[i, j]);

For i:=1 To 5 Do

Begin

j:=1;

Repeat

If a[i, j] < 0 Then c[i, j]:= –1 Else c[i, j]:= 1;

j:=j+1

Until j > 5

End;

For i:=1 To 5 Do

Begin

For j:=1 To 5 Do Write (c[i, j]); Writeln

End

End.

Задание 6. Программирование с использованием подпрограмм

Составить схему алгоритма главной программы и подпрограммы, главную программу и подпрограмму. Значения исходных данных выбрать самостоятельно. Варианты заданий приведены в табл. 5.

Задания к задаче 5

0. При решении задачи использовать подпрограмму-функцию. Обмен данными между главной программой и подпрограммой – через списки формальных и фактических параметров.
   
1. При решении задачи использовать подпрограмму-процедуру. Обмен данными между главной программой и подпрограммой – через списки формальных и фактических параметров.
   
2. При решении задачи использовать подпрограмму-функцию. Обмен данными между главной программой и подпрограммой при помощи глобальных переменных.
   
3. При решении задачи использовать подпрограмму-процедуру. Обмен данными между главной программой и подпрограммой при помощи глобальных переменных.
   
4. При решении задачи использовать подпрограмму-функцию. Обмен данными между главной программой и подпрограммой – через списки формальных и фактических параметров.
   
5. При решении задачи использовать подпрограмму-процедуру. Обмен данными между главной программой и подпрограммой – через списки формальных и фактических параметров.
   
6. При решении задачи использовать подпрограмму-функцию. Обмен данными между главной программой и подпрограммой при помощи глобальных переменных.
   
7. При решении задачи использовать подпрограмму-процедуру. Обмен данными между главной программой и подпрограммой при помощи глобальных переменных.
   
8. При решении задачи использовать подпрограмму-функцию. Обмен данными между главной программой и подпрограммой – через списки формальных и фактических параметров.
   
9. При решении задачи использовать подпрограмму-процедуру. Обмен данными между главной программой и подпрограммой – через списки формальных и фактических параметров.
   

Таблица 5

Номер варианта	Вариант
1	2
0	Вычислить число сочетаний из m элементов по n, используя формулу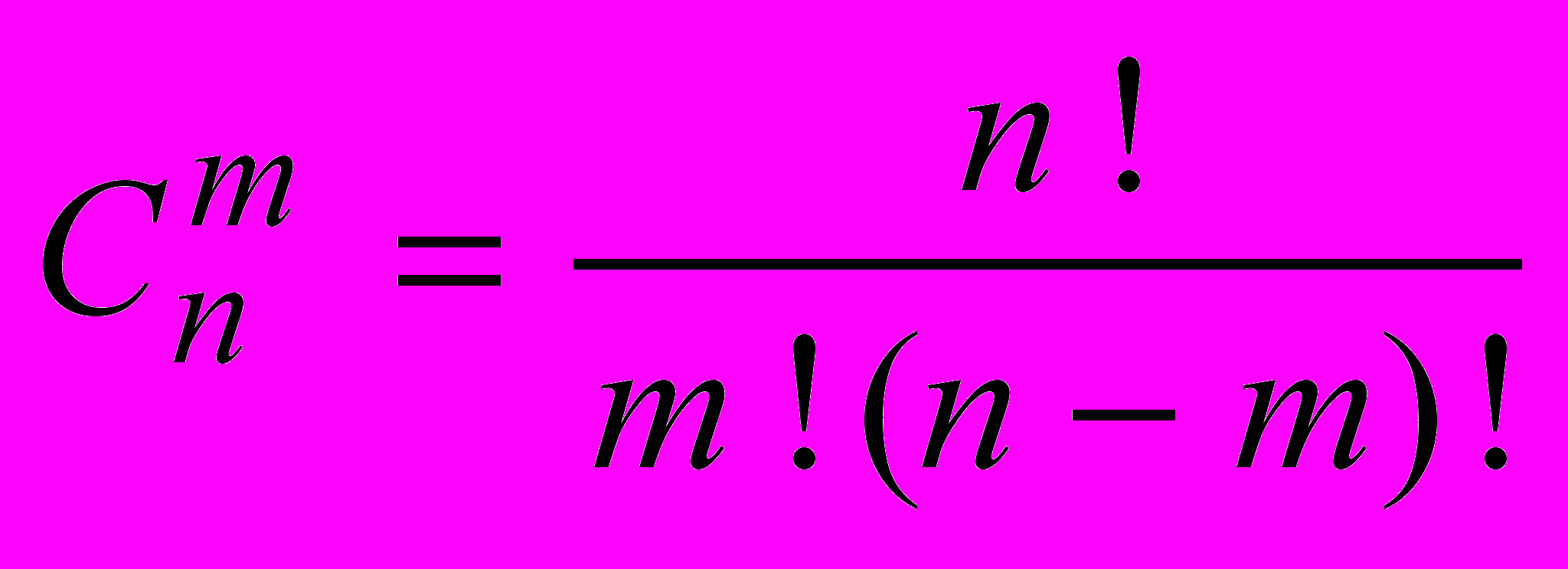
1	Даны матрицы A(mn) и B(nn). Для каждой из них найти наибольший по модулю элемент, лежащий на побочной диагонали. Вывести его индексы.
2	Определить, след какой из матриц А(33) или В(44) является наименьшим. След матрицы – сумма элементов, расположенных на главной диагонали.
3	Даны два целых числа N1 и N2. Определить, на какие из чисел натурального ряда числа N1 и N2 делятся нацело. Единицу делителем не считать. N1=1365; N2=330.
4	Пусть точки А1(х1,у1), А2(х2,у2), А3(х3,у3) – вершины треугольника, тогда его площадь 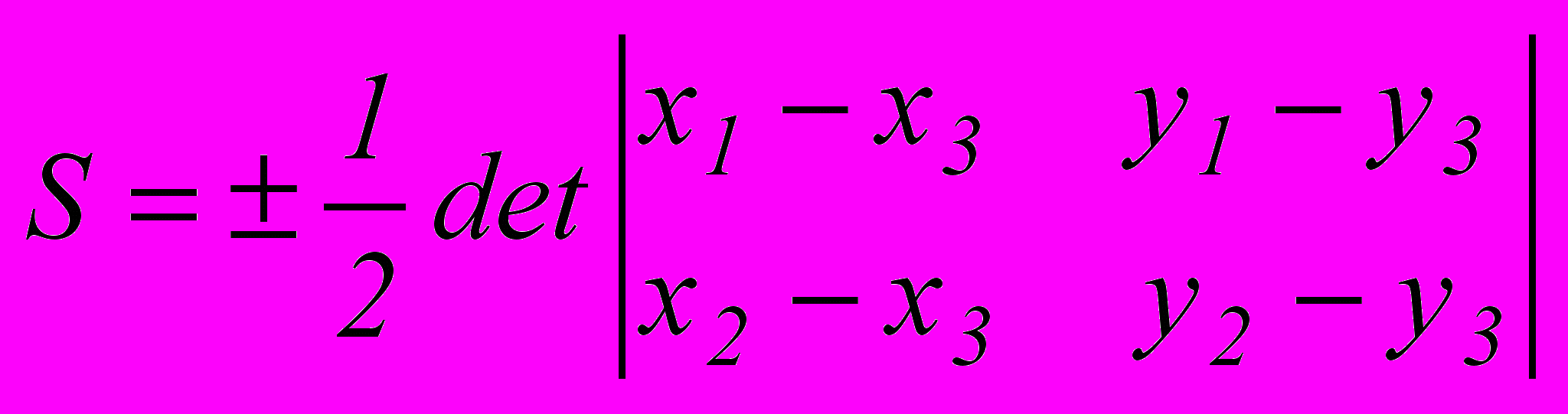. Найти площадь четырехугольника с вершинами ( 3;3), (4;3), (4;-3), (-4;4).
5	Решить систему уравнений 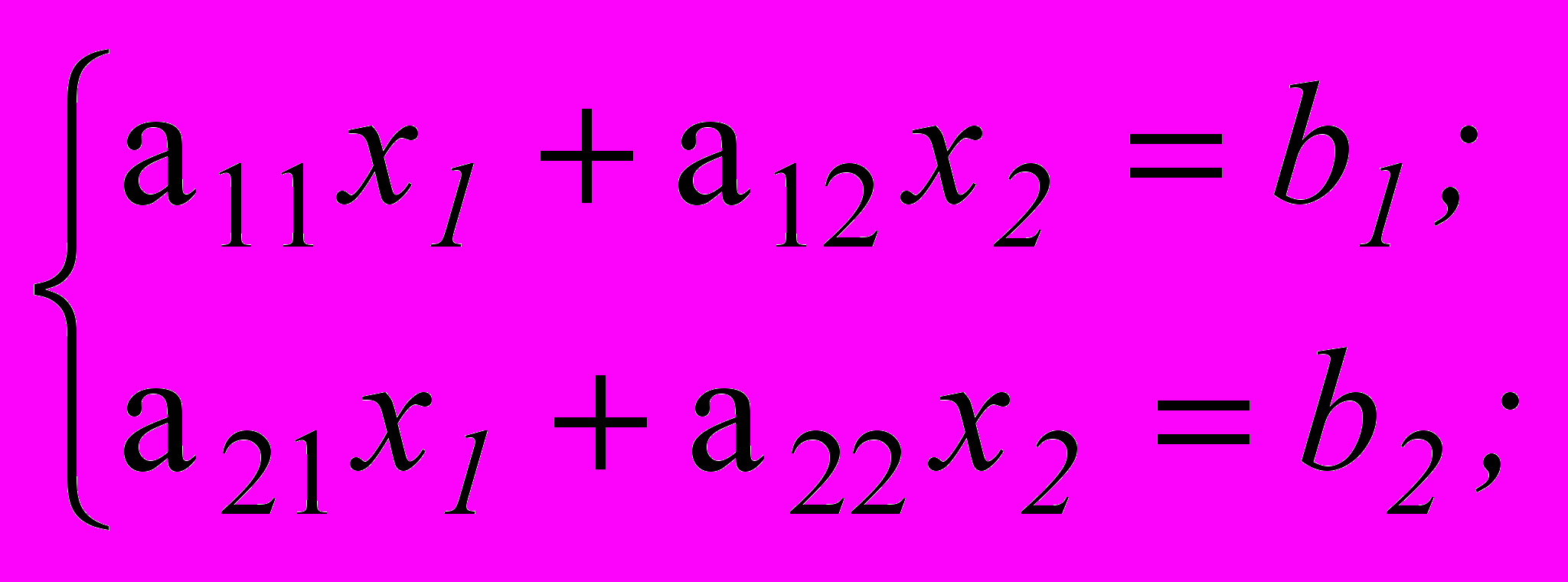используя метод Крамера.
6	Дан массив А(18). Найти сумму наибольших элементов в группах элементов массива с индексами 1 – 3, 4 ­ – 7, 8 – 12, 13 – 18.
7 1 2 3 4 5 1 2 3 4 5	Дана матрица С(55). Найти наибольший элемент в закрашенной области.

Окончание табл. 5

1	2
8	Даны четыре вектора А(1; 2; 3), В(2; 8; 6; 33), С(3,7; 1,3; 6,5; –5,3) и D(–2; 5; 3; 4). Переменной Х присвоить значение –1, если скалярное произведение векторов А и В меньше скалярного произведения векторов C и D. А противном случае переменной Х присвоить 1.
9	Даны четыре отрезка длиной a, b, c и d. Для каждой тройки отрезков, из которых можно построить треугольник, вычислить площадь этого треугольника и его периметр.