Границы области

Вид материала

Задача

Содержание Границы области F(x) = const Границы области Этап I. Поиск первого опорного плана Этап II. Улучшение опорного плана Этап I. Поиск первого опорного плана Этап II. Улучшение опорного плана Шаг №1. 1. Проводим редукцию матрицы по строкам 2. Методом проб и ошибок 4. Методом проб и ошибок определяем матрицу назначения Х Этап I. Поиск первого опорного плана Этап II. Улучшение опорного плана Границы области F(x) = const

Подобный материал:

• Финляндия. Общие сведения. Официальное название, 38.29kb.
• Административные правонарушения в области защиты государственной границы Российской, 34.87kb.
• Венецианские сказания, 229.17kb.
• Атомистические механизмы зернограничного проскальзывания. Моделирование поведения границы, 83.28kb.
• Формирование китайско-бирманской границы, 284.31kb.
• Весе нние детские каникулы, 488.21kb.
• 9 + 1 б/пл, 109.75kb.
• Описание территорий и границ судебных участков мировых судей ростовской области, 568.37kb.
• Россия сам больш страна мира площ-ю 17 млн кв км. Она находится в сев полушарии,, 534.18kb.
• Экскурсионная программа: 1 дн Отправление из Бреста. Пересечение границы. Транзит, 23.43kb.

Задача№1

Необходимо найти максимальное значение целевой функции F = 4X₁+5X₂ → max, при системе ограничений:

10x1+5x2≤310	(1)
5x1+4x2≤120	(2)
3x1+13x2≤250	(3)
x1≥0	(4)
x2≥0	(5)

Начало формы

Построим область допустимых решений, т.е. решим графически систему неравенств. Для этого построим каждую прямую и определим полуплоскости, заданные неравенствами (полуплоскости обозначены штрихом).

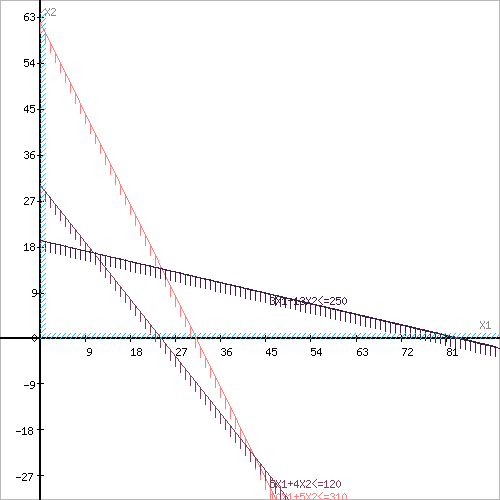
Границы области

Обозначим границы области многоугольника решений.

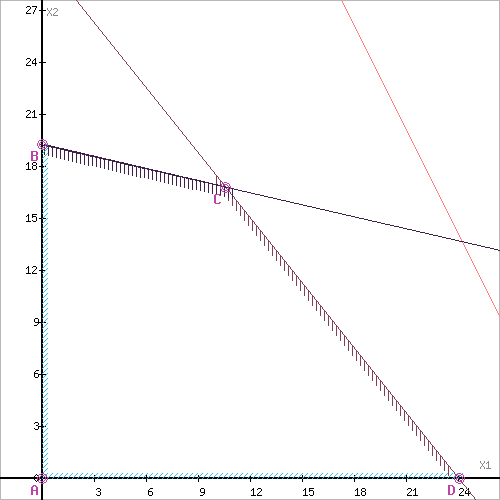
Целевая функция F(x) → max

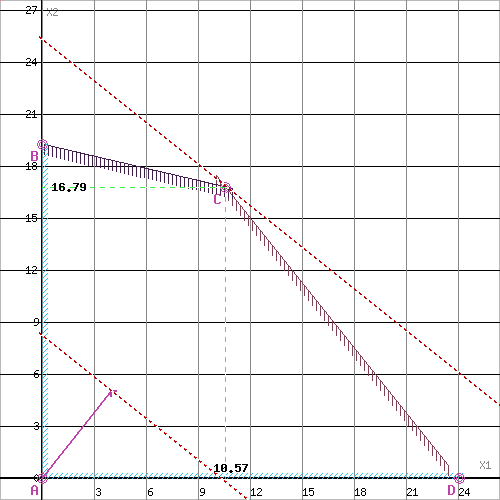
Рассмотрим целевую функцию задачи F = 4X₁+5X₂ → max.
Построим прямую, отвечающую значению функции F = 0: F = 4X₁+5X₂ = 0. Будем двигать эту прямую параллельным образом. Поскольку нас интересует максимальное решение, поэтому двигаем прямую до последнего касания обозначенной области. На графике эта прямая обозначена пунктирной линией.



Равный масштаб



Конец формы


Пересечением полуплоскостей будет являться область, которая представляет собой многоугольник, координаты точек которого удовлетворяют условию неравенствам системы ограничений задачи.

Прямая F(x) = const пересекает область в точке C. Так как точка C получена в результате пересечения прямых (2) и (3), то ее координаты удовлетворяют уравнениям этих прямых:
5x₁+4x₂≤120
3x₁+13x₂≤250
Решив систему уравнений, получим: x₁ = 10.566, x₂ = 16.7925
Откуда найдем максимальное значение целевой функции:
F(X) = 4*10.566 + 5*16.7925 = 126.23


Задача№2

Необходимо найти минимальное значение целевой функции F = 59X₁+11X₂ → min, при системе ограничений:

x1+3x2≥9	(1)
5x1+2x2≥9	(2)
2x1+8x2≥8	(3)
3x1+4x2≥49	(4)
x1≥0	(5)
x2≥0	(6)

Начало формы

Построим область допустимых решений, т.е. решим графически систему неравенств. Для этого построим каждую прямую и определим полуплоскости, заданные неравенствами (полуплоскости обозначены штрихом).

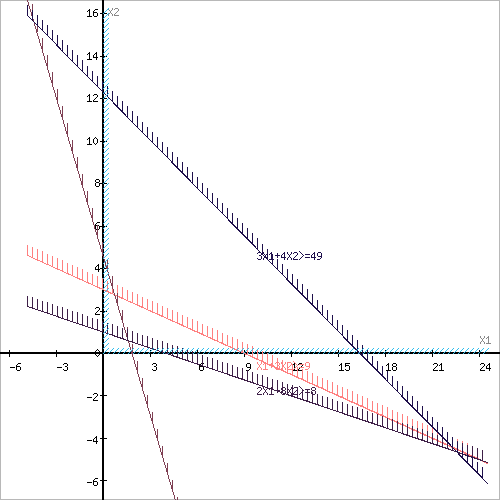
Границы области

Обозначим границы области многоугольника решений.

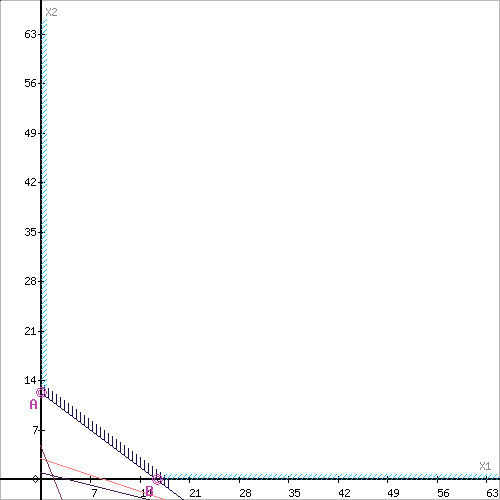
Целевая функция F(x) → min

Рассмотрим целевую функцию задачи F = 59X₁+11X₂ → min.
Построим прямую, отвечающую значению функции F = 0: F = 59X₁+11X₂ = 0. Будем двигать эту прямую параллельным образом. Поскольку нас интересует минимальное решение, поэтому двигаем прямую до первого касания обозначенной области. На графике эта прямая обозначена пунктирной линией.



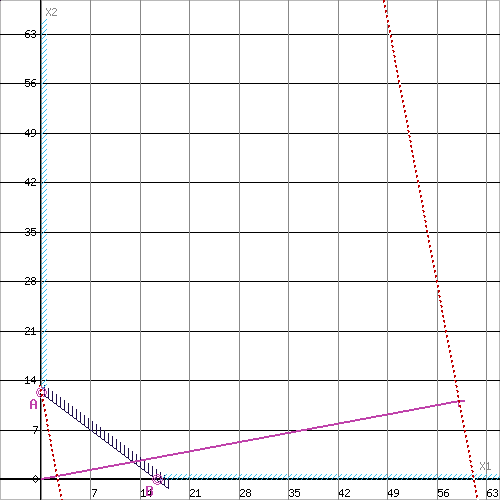
Равный масштаб



Конец формы


Область допустимых значений неограниченна.
3x₁+4x₂≥49
=
Решив систему уравнений, получим: x₁ = 0, x₂ = 12.25
Откуда найдем значение целевой функции:
F(X) = 59*0 + 11*12.25 = 134.75


Задача№3

Стоимость доставки единицы груза из каждого пункта отправления в соответствующие пункты назначения задана матрицей тарифов

	1	2	3	4	Запасы
1	2	5	8	5	226
2	8	2	4	2	240
3	2	4	3	6	84
4	2	4	3	5	70
Потребности	292	170	111	40

Проверим необходимое и достаточное условие разрешимости задачи.

∑a = 226 + 240 + 84 + 70 = 620

∑b = 292 + 170 + 111 + 40 = 613

Занесем исходные данные в распределительную таблицу.

	1	2	3	4	5	Запасы
1	2	5	8	5	0	226
2	8	2	4	2	0	240
3	2	4	3	6	0	84
4	2	4	3	5	0	70
Потребности	292	170	111	40	7

Этап I. Поиск первого опорного плана.

1. Используя метод наименьшей стоимости, построим первый опорный план транспортной задачи.

	1	2	3	4	5	Запасы
1	2[226]	5	8	5	0	226
2	8	2[170]	4[23]	2[40]	0[7]	240
3	2[66]	4	3[18]	6	0	84
4	2	4	3[70]	5	0	70
Потребности	292	170	111	40	7

В результате получен первый опорный план, который является допустимым, так как все грузы из баз вывезены, потребность магазинов удовлетворена, а план соответствует системе ограничений транспортной задачи.

2. Подсчитаем число занятых клеток таблицы, их 8, а должно быть m + n - 1 = 8. Следовательно, опорный план является невырожденным.

Значение целевой функции для этого опорного плана равно:

F(x) = 2*226 + 2*170 + 4*23 + 2*40 + 0*7 + 2*66 + 3*18 + 3*70 = 1360

Этап II. Улучшение опорного плана.

Проверим оптимальность опорного плана. Найдем предварительные потенциалы u_i, v_i. по занятым клеткам таблицы, в которых u_i + v_i = c_ij, полагая, что u₁ = 0.

	v1=2	v2=1	v3=3	v4=1	v5=-1
u1=0	2[226]	5	8	5	0
u2=1	8	2[170]	4[23]	2[40]	0[7]
u3=0	2[66]	4	3[18]	6	0
u4=0	2	4	3[70]	5	0

Опорный план является оптимальным, так все оценки свободных клеток удовлетворяют условию u_i + v_i <= c_ij.

Минимальные затраты составят:

F(x) = 2*226 + 2*170 + 4*23 + 2*40 + 0*7 + 2*66 + 3*18 + 3*70 = 1360

Задача№4

Стоимость доставки единицы груза из каждого пункта отправления в соответствующие пункты назначения задана матрицей тарифов

	1	2	3	4	Запасы
1	30	42	53	31	17
2	42	25	61	20	18
3	31	40	52	40	16
Потребности	8	4	8	8

Проверим необходимое и достаточное условие разрешимости задачи.

∑a = 17 + 18 + 16 = 51

∑b = 8 + 4 + 8 + 8 = 28

Занесем исходные данные в распределительную таблицу.

	1	2	3	4	5	Запасы
1	30	42	53	31	0	17
2	42	25	61	20	0	18
3	31	40	52	40	0	16
Потребности	8	4	8	8	23

Этап I. Поиск первого опорного плана.

1. Используя метод наименьшей стоимости, построим первый опорный план транспортной задачи.

	1	2	3	4	5	Запасы
1	30[8]	42	53	31	0[9]	17
2	42	25[4]	61	20[8]	0[6]	18
3	31	40	52[8]	40	0[8]	16
Потребности	8	4	8	8	23

В результате получен первый опорный план, который является допустимым, так как все грузы из баз вывезены, потребность магазинов удовлетворена, а план соответствует системе ограничений транспортной задачи.

2. Подсчитаем число занятых клеток таблицы, их 7, а должно быть m + n - 1 = 7. Следовательно, опорный план является невырожденным.

Значение целевой функции для этого опорного плана равно:

F(x) = 30*8 + 0*9 + 25*4 + 20*8 + 0*6 + 52*8 + 0*8 = 916

Этап II. Улучшение опорного плана.

Проверим оптимальность опорного плана. Найдем предварительные потенциалы u_i, v_i. по занятым клеткам таблицы, в которых u_i + v_i = c_ij, полагая, что u₁ = 0.

	v1=30	v2=25	v3=52	v4=20	v5=0
u1=0	30[8]	42	53	31	0[9]
u2=0	42	25[4]	61	20[8]	0[6]
u3=0	31	40	52[8]	40	0[8]

Опорный план является оптимальным, так все оценки свободных клеток удовлетворяют условию u_i + v_i <= c_ij.

Минимальные затраты составят:

F(x) = 30*8 + 0*9 + 25*4 + 20*8 + 0*6 + 52*8 + 0*8 = 916


Задача №5

Исходная матрица имеет вид:

13	13	15	8	9
12	11	6	14	6
13	7	9	5	6
10	10	7	8	7
12	11	6	9	9

Шаг №1.

1. Проводим редукцию матрицы по строкам. В связи с этим во вновь полученной матрице в каждой строке будет как минимум один ноль.

5	5	7	0	1	8
6	5	0	8	0	6
8	2	4	0	1	5
3	3	0	1	0	7
6	5	0	3	3	6

Затем такую же операцию редукции проводим по столбцам, для чего в каждом столбце находим минимальный элемент:

2	3	7	0	1
3	3	0	8	0
5	0	4	0	1
0	1	0	1	0
3	3	0	3	3
3	2	0	0	0

После вычитания минимальных элементов получаем полностью редуцированную матрицу.

2. Методом проб и ошибок проводим поиск допустимого решения, для которого все назначения имеют нулевую стоимость.

В итоге получаем следующую матрицу:

2	3	7	[0]	1
3	3	[-0-]	8	[0]
5	[0]	4	[-0-]	1
[0]	1	[-0-]	1	[-0-]
3	3	[0]	3	3

Количество найденных нулей равно k = 5. В результате получаем эквивалентную матрицу Сэ:

2	3	7	0	1
3	3	0	8	0
5	0	4	0	1
0	1	0	1	0
3	3	0	3	3

4. Методом проб и ошибок определяем матрицу назначения Х, которая позволяет по аналогично расположенным элементам исходной матрицы (в квадратах) вычислить минимальную стоимость назначения.

2	3	7	[0]	1
3	3	[-0-]	8	[0]
5	[0]	4	[-0-]	1
[0]	1	[-0-]	1	[-0-]
3	3	[0]	3	3

Cmin = 6 + 8 + 7 + 10 + 6 = 37


Задача№7

Стоимость доставки единицы груза из каждого пункта отправления в соответствующие пункты назначения задана матрицей тарифов

	1	2	3	4	Запасы
1	15	7	8	10	100
2	11	18	16	29	201
3	9	15	3	15	300
4	5	8	14	4	201
5	10	16	10	15	700
Потребности	501	501	300	200

Проверим необходимое и достаточное условие разрешимости задачи.

∑a = 100 + 201 + 300 + 201 + 700 = 1502

∑b = 501 + 501 + 300 + 200 = 1502

Занесем исходные данные в распределительную таблицу.

	1	2	3	4	Запасы
1	15	7	8	10	100
2	11	18	16	29	201
3	9	15	3	15	300
4	5	8	14	4	201
5	10	16	10	15	700
Потребности	501	501	300	200

Этап I. Поиск первого опорного плана.

1. Используя метод наименьшей стоимости, построим первый опорный план транспортной задачи.

	1	2	3	4	Запасы
1	15	7[100]	8	10	100
2	11	18[201]	16	29	201
3	9	15	3[300]	15	300
4	5[1]	8	14	4[200]	201
5	10[500]	16[200]	10	15	700
Потребности	501	501	300	200

2. Подсчитаем число занятых клеток таблицы, их 7, а должно быть m + n - 1 = 8. Следовательно, опорный план является вырожденным.

Строим новый план.

Значение целевой функции для этого опорного плана равно:

F(x) = 7*100 + 18*201 + 3*300 + 5*1 + 4*200 + 10*500 + 16*200 = 14223

	1	2	3	4	Запасы
1	15	7[100]	8	10	100
2	11	18[201]	16	29	201
3	9	15	3[300]	15	300
4	5[1]	8	14	4[200]	201
5	10[500]	16[200]	10	15	700
Потребности	501	501	300	200

2. Подсчитаем число занятых клеток таблицы, их 7, а должно быть m + n - 1 = 8. Следовательно, опорный план является вырожденным.

Строим новый план.

Значение целевой функции для этого опорного плана равно:

F(x) = 7*100 + 18*201 + 3*300 + 5*1 + 4*200 + 10*500 + 16*200 = 14223

	1	2	3	4	Запасы
1	15	7[100]	8	10	100
2	11	18[201]	16	29	201
3	9	15	3[300]	15	300
4	5[201]	8	14	4	201
5	10[300]	16[200]	10	15[200]	700
Потребности	501	501	300	200

2. Подсчитаем число занятых клеток таблицы, их 7, а должно быть m + n - 1 = 8. Следовательно, опорный план является вырожденным.

Строим новый план.

Значение целевой функции для этого опорного плана равно:

F(x) = 7*100 + 18*201 + 3*300 + 5*201 + 10*300 + 16*200 + 15*200 = 15423

	1	2	3	4	Запасы
1	15	7[100]	8	10	100
2	11	18[201]	16	29	201
3	9	15	3[300]	15	300
4	5[1]	8	14	4[200]	201
5	10[500]	16[200]	10	15	700
Потребности	501	501	300	200

2. Подсчитаем число занятых клеток таблицы, их 7, а должно быть m + n - 1 = 8. Следовательно, опорный план является вырожденным.

Строим новый план.

Значение целевой функции для этого опорного плана равно:

F(x) = 7*100 + 18*201 + 3*300 + 5*1 + 4*200 + 10*500 + 16*200 = 14223

	1	2	3	4	Запасы
1	15	7	8[100]	10	100
2	11	18[201]	16	29	201
3	9[100]	15	3[200]	15	300
4	5[1]	8	14	4[200]	201
5	10[400]	16[300]	10	15	700
Потребности	501	501	300	200

В результате получен первый опорный план, который является допустимым, так как все грузы из баз вывезены, потребность магазинов удовлетворена, а план соответствует системе ограничений транспортной задачи.

2. Подсчитаем число занятых клеток таблицы, их 8, а должно быть m + n - 1 = 8. Следовательно, опорный план является невырожденным.

Значение целевой функции для этого опорного плана равно:

F(x) = 8*100 + 18*201 + 9*100 + 3*200 + 5*1 + 4*200 + 10*400 + 16*300 = 15523

Этап II. Улучшение опорного плана.

Проверим оптимальность опорного плана. Найдем предварительные потенциалы u_i, v_i. по занятым клеткам таблицы, в которых u_i + v_i = c_ij, полагая, что u₁ = 0.

	v1=14	v2=20	v3=8	v4=13
u1=0	15	7	8[100]	10
u2=-2	11	18[201]	16	29
u3=-5	9[100]	15	3[200]	15
u4=-9	5[1]	8	14	4[200]
u5=-4	10[400]	16[300]	10	15

Опорный план не является оптимальным, так как существуют оценки свободных клеток, для которых u_i + v_i > c_ij

Выбираем максимальную оценку свободной клетки (1;2): 7

Для этого в перспективную клетку (1;2) поставим знак «+», а в остальных вершинах многоугольника чередующиеся знаки «-», «+», «-».

	1	2	3	4	Запасы
1	15	7[+]	8[100][-]	10	100
2	11	18[201]	16	29	201
3	9[100][-]	15	3[200][+]	15	300
4	5[1]	8	14	4[200]	201
5	10[400][+]	16[300][-]	10	15	700
Потребности	501	501	300	200

Цикл приведен в таблице (1,2; 1,3; 3,3; 3,1; 5,1; 5,2; ).

Из грузов х_ij стоящих в минусовых клетках, выбираем наименьшее, т.е. у = min (1, 3) = 100. Прибавляем 100 к объемам грузов, стоящих в плюсовых клетках и вычитаем 100 из Х_ij, стоящих в минусовых клетках. В результате получим новый опорный план.

	1	2	3	4	Запасы
1	15	7[100]	8	10	100
2	11	18[201]	16	29	201
3	9[0]	15	3[300]	15	300
4	5[1]	8	14	4[200]	201
5	10[500]	16[200]	10	15	700
Потребности	501	501	300	200

Проверим оптимальность опорного плана. Найдем предварительные потенциалы u_i, v_i. по занятым клеткам таблицы, в которых u_i + v_i = c_ij, полагая, что u₁ = 0.

	v1=1	v2=7	v3=-5	v4=0
u1=0	15	7[100]	8	10
u2=11	11	18[201]	16	29
u3=8	9[0]	15	3[300]	15
u4=4	5[1]	8	14	4[200]
u5=9	10[500]	16[200]	10	15

Опорный план не является оптимальным, так как существуют оценки свободных клеток, для которых u_i + v_i > c_ij

Выбираем максимальную оценку свободной клетки (4;2): 8

Для этого в перспективную клетку (4;2) поставим знак «+», а в остальных вершинах многоугольника чередующиеся знаки «-», «+», «-».

	1	2	3	4	Запасы
1	15	7[100]	8	10	100
2	11	18[201]	16	29	201
3	9[0]	15	3[300]	15	300
4	5[1][-]	8[+]	14	4[200]	201
5	10[500][+]	16[200][-]	10	15	700
Потребности	501	501	300	200

Цикл приведен в таблице (4,2; 4,1; 5,1; 5,2; ).

Из грузов х_ij стоящих в минусовых клетках, выбираем наименьшее, т.е. у = min (4, 1) = 1. Прибавляем 1 к объемам грузов, стоящих в плюсовых клетках и вычитаем 1 из Х_ij, стоящих в минусовых клетках. В результате получим новый опорный план.

	1	2	3	4	Запасы
1	15	7[100]	8	10	100
2	11	18[201]	16	29	201
3	9[0]	15	3[300]	15	300
4	5	8[1]	14	4[200]	201
5	10[501]	16[199]	10	15	700
Потребности	501	501	300	200

Проверим оптимальность опорного плана. Найдем предварительные потенциалы u_i, v_i. по занятым клеткам таблицы, в которых u_i + v_i = c_ij, полагая, что u₁ = 0.

	v1=1	v2=7	v3=-5	v4=3
u1=0	15	7[100]	8	10
u2=11	11	18[201]	16	29
u3=8	9[0]	15	3[300]	15
u4=1	5	8[1]	14	4[200]
u5=9	10[501]	16[199]	10	15

Опорный план не является оптимальным, так как существуют оценки свободных клеток, для которых u_i + v_i > c_ij

Выбираем максимальную оценку свободной клетки (2;1): 11

Для этого в перспективную клетку (2;1) поставим знак «+», а в остальных вершинах многоугольника чередующиеся знаки «-», «+», «-».

	1	2	3	4	Запасы
1	15	7[100]	8	10	100
2	11[+]	18[201][-]	16	29	201
3	9[0]	15	3[300]	15	300
4	5	8[1]	14	4[200]	201
5	10[501][-]	16[199][+]	10	15	700
Потребности	501	501	300	200

Цикл приведен в таблице (2,1; 2,2; 5,2; 5,1; ).

Из грузов х_ij стоящих в минусовых клетках, выбираем наименьшее, т.е. у = min (2, 2) = 201. Прибавляем 201 к объемам грузов, стоящих в плюсовых клетках и вычитаем 201 из Х_ij, стоящих в минусовых клетках. В результате получим новый опорный план.

	1	2	3	4	Запасы
1	15	7[100]	8	10	100
2	11[201]	18	16	29	201
3	9[0]	15	3[300]	15	300
4	5	8[1]	14	4[200]	201
5	10[300]	16[400]	10	15	700
Потребности	501	501	300	200

Проверим оптимальность опорного плана. Найдем предварительные потенциалы u_i, v_i. по занятым клеткам таблицы, в которых u_i + v_i = c_ij, полагая, что u₁ = 0.

	v1=1	v2=7	v3=-5	v4=3
u1=0	15	7[100]	8	10
u2=10	11[201]	18	16	29
u3=8	9[0]	15	3[300]	15
u4=1	5	8[1]	14	4[200]
u5=9	10[300]	16[400]	10	15

Опорный план является оптимальным, так все оценки свободных клеток удовлетворяют условию u_i + v_i <= c_ij.

Минимальные затраты составят:

F(x) = 7*100 + 11*201 + 3*300 + 8*1 + 4*200 + 10*300 + 16*400 = 14019


Задача№9

Необходимо найти максимальное значение целевой функции F = 5X₁+6X₂ → max, при системе ограничений:

3x1+2x2≥6	(1)
10x1+6x2≤60	(2)
x1≤11	(3)
x1≥0	(4)
x2≥0	(5)

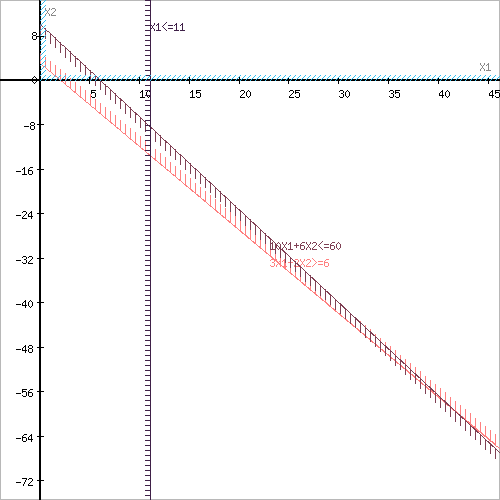
Начало формы

Построим область допустимых решений, т.е. решим графически систему неравенств. Для этого построим каждую прямую и определим полуплоскости, заданные неравенствами (полуплоскости обозначены штрихом).