Границы области

Вид материала

Задача

Содержание Границы области F(x) = const

Подобный материал:

• Финляндия. Общие сведения. Официальное название, 38.29kb.
• Административные правонарушения в области защиты государственной границы Российской, 34.87kb.
• Венецианские сказания, 229.17kb.
• Атомистические механизмы зернограничного проскальзывания. Моделирование поведения границы, 83.28kb.
• Формирование китайско-бирманской границы, 284.31kb.
• Весе нние детские каникулы, 488.21kb.
• 9 + 1 б/пл, 109.75kb.
• Описание территорий и границ судебных участков мировых судей ростовской области, 568.37kb.
• Россия сам больш страна мира площ-ю 17 млн кв км. Она находится в сев полушарии,, 534.18kb.
• Экскурсионная программа: 1 дн Отправление из Бреста. Пересечение границы. Транзит, 23.43kb.

Границы области

Обозначим границы области многоугольника решений.

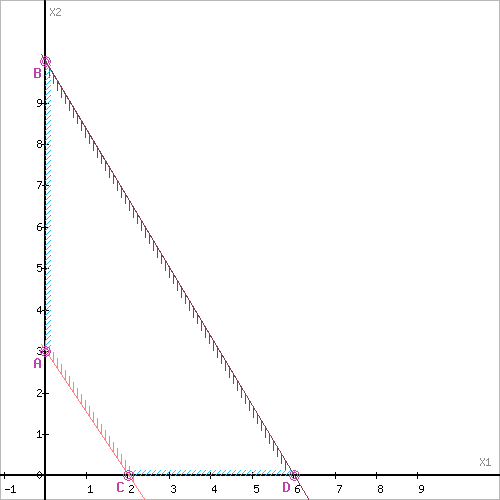
Целевая функция F(x) → max

Рассмотрим целевую функцию задачи F = 5X₁+6X₂ → max.
Построим прямую, отвечающую значению функции F = 0: F = 5X₁+6X₂ = 0. Будем двигать эту прямую параллельным образом. Поскольку нас интересует максимальное решение, поэтому двигаем прямую до последнего касания обозначенной области. На графике эта прямая обозначена пунктирной линией.



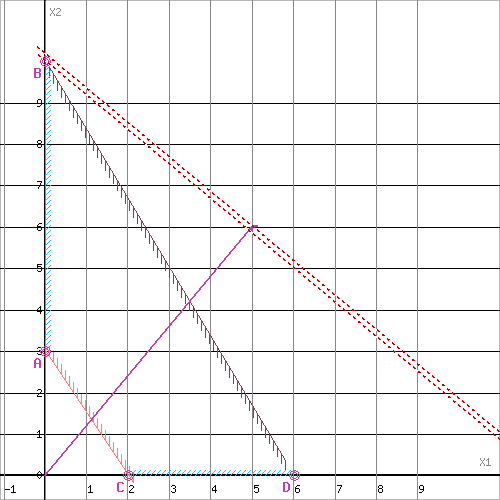
Равный масштаб



Конец формы


Пересечением полуплоскостей будет являться область, которая представляет собой многоугольник, координаты точек которого удовлетворяют условию неравенствам системы ограничений задачи.

Прямая F(x) = const пересекает область в точке B. Так как точка B получена в результате пересечения прямых (2) и (5), то ее координаты удовлетворяют уравнениям этих прямых:
10x₁+6x₂≤60
x₁=0
Решив систему уравнений, получим: x₁ = 0, x₂ = 10
Откуда найдем максимальное значение целевой функции:
F(X) = 5*0 + 6*10 = 60

Решим прямую задачу линейного программирования симплексным методом, с использованием симплексной таблицы.

Определим максимальное значение целевой функции F(X) = 5x₁ + 6x₂ при следующих условиях-ограничений.

3x₁ + 2x₂≥6

10x₁ + 6x₂≤60

11x₁≤11

Для построения первого опорного плана систему неравенств приведем к системе уравнений путем введения дополнительных переменных (переход к канонической форме).

В 1-м неравенстве смысла (≥) вводим базисную переменную x₃ со знаком минус. В 2-м неравенстве смысла (≤) вводим базисную переменную x₄. В 3-м неравенстве смысла (≤) вводим базисную переменную x₅.

3x₁ + 2x₂-1x₃ + 0x₄ + 0x₅ = 6

10x₁ + 6x₂ + 0x₃ + 1x₄ + 0x₅ = 60

11x₁ + 0x₂ + 0x₃ + 0x₄ + 1x₅ = 11

Введем искусственные переменные x: в 1-м равенстве вводим переменную x₆;

3x₁ + 2x₂-1x₃ + 0x₄ + 0x₅ + 1x₆ = 6

10x₁ + 6x₂ + 0x₃ + 1x₄ + 0x₅ + 0x₆ = 60

11x₁ + 0x₂ + 0x₃ + 0x₄ + 1x₅ + 0x₆ = 11

Для постановки задачи на максимум целевую функцию запишем так:

F(X) = 5x₁+6x₂ - Mx₆ => max

Из уравнений выражаем искусственные переменные:

x₆ = 6-3x₁-2x₂+x₃

которые подставим в целевую функцию:

F(X) = (5+3M)x₁+(6+2M)x₂+(-1M)x₃+(-6M) => max

Матрица коэффициентов A = a(ij) этой системы уравнений имеет вид:


Решим систему уравнений относительно базисных переменных:

x₆, x₄, x₅,

Полагая, что свободные переменные равны 0, получим первый опорный план:

X1 = (0,0,0,60,11,6)

Базис	B	x1	x2	x3	x4	x5	x6
x6	6	3	2	-1	0	0	1
x4	60	10	6	0	1	0	0
x5	11	11	0	0	0	1	0
F(X0)	-6M	-5-3M	-6-2M	1M	0	0	0

Переходим к основному алгоритму симплекс-метода.

Итерация №0.

Текущий опорный план неоптимален, так как в индексной строке находятся отрицательные коэффициенты.

В качестве ведущего выберем столбец, соответствующий переменной x₁, так как это наибольший коэффициент по модулю.

Вычислим значения D_i по строкам как частное от деления: b_i / a_i1

и из них выберем наименьшее:

min (6 : 3 , 60 : 10 , 11 : 11 ) = 1

Следовательно, 3-ая строка является ведущей.

Разрешающий элемент равен (11) и находится на пересечении ведущего столбца и ведущей строки.

Базис	B	x1	x2	x3	x4	x5	x6	min
x6	6	3	2	-1	0	0	1	2
x4	60	10	6	0	1	0	0	6
x5	11	11	0	0	0	1	0	1
F(X1)	-6M	-5-3M	-6-2M	1M	0	0	0	0

Получаем новую симплекс-таблицу:

Базис	B	x1	x2	x3	x4	x5	x6
x6	3	0	2	-1	0	-3/11	1
x4	50	0	6	0	1	-10/11	0
x1	1	1	0	0	0	1/11	0
F(X1)	5-3M	0	-6-2M	1M	0	5/11+3/11M	0

Итерация №1.

Текущий опорный план неоптимален, так как в индексной строке находятся отрицательные коэффициенты.

В качестве ведущего выберем столбец, соответствующий переменной x₂, так как это наибольший коэффициент по модулю.

Вычислим значения D_i по строкам как частное от деления: b_i / a_i2

и из них выберем наименьшее:

min (3 : 2 , 50 : 6 , - ) = 1¹/₂

Следовательно, 1-ая строка является ведущей.

Разрешающий элемент равен (2) и находится на пересечении ведущего столбца и ведущей строки.

Базис	B	x1	x2	x3	x4	x5	x6	min
x6	3	0	2	-1	0	-3/11	1	11/2
x4	50	0	6	0	1	-10/11	0	81/3
x1	1	1	0	0	0	1/11	0	-
F(X2)	5-3M	0	-6-2M	1M	0	5/11+3/11M	0	0

Получаем новую симплекс-таблицу:

Базис	B	x1	x2	x3	x4	x5	x6
x2	11/2	0	1	-1/2	0	-3/22	1/2
x4	41	0	0	3	1	-1/11	-3
x1	1	1	0	0	0	1/11	0
F(X2)	14	0	0	-3	0	-4/11	3+1M

Итерация №2.

Текущий опорный план неоптимален, так как в индексной строке находятся отрицательные коэффициенты.

В качестве ведущего выберем столбец, соответствующий переменной x₃, так как это наибольший коэффициент по модулю.

Вычислим значения D_i по строкам как частное от деления: b_i / a_i3

и из них выберем наименьшее:

min (- , 41 : 3 , - ) = 13²/₃

Следовательно, 2-ая строка является ведущей.

Разрешающий элемент равен (3) и находится на пересечении ведущего столбца и ведущей строки.

Базис	B	x1	x2	x3	x4	x5	x6	min
x2	11/2	0	1	-1/2	0	-3/22	1/2	-
x4	41	0	0	3	1	-1/11	-3	132/3
x1	1	1	0	0	0	1/11	0	-
F(X3)	14	0	0	-3	0	-4/11	3+1M	0

Получаем новую симплекс-таблицу:

Базис	B	x1	x2	x3	x4	x5	x6
x2	81/3	0	1	0	1/6	-5/33	0
x3	132/3	0	0	1	1/3	-1/33	-1
x1	1	1	0	0	0	1/11	0
F(X3)	55	0	0	0	1	-5/11	1M