И. Н. Горькавый вмик мгу ilya gor@rambler ru Вдоклад

Вид материала

Содержание

Тип участка и его размер
Первое отражение
4. Интерфейс и визуализация
5.1. Матричный метод описания процесса обработки данных
5.2. Метод и критерии выделения связных множеств матричных элементов
5.3. Метод МВП для удаления неструктурированных объектов поверхности
5.4. Накопление ошибок

Подобный материал:

Программные средства и математические методы обработки и классификации трехмерных данных

И. Н. Горькавый

ВМиК МГУ

ilya_gor@rambler.ru

В докладе рассмотрены итоги диссертационной работы, в которой разработан комплексный подход к автоматизации обработки трехмерных данных лазерного и радарного авиасканирования. В работе развиты необходимые математические методы и программные средства, написаны автоматизированные программные комплексы АКС-ЛИДАР для получения инфракрасных изображений и АКС-ЛИДАР-3D для создания высокоточных цифровых моделей рельефа. Программные комплексы были успешно применены для обработки больших объемов 3D данных LIDAR и IFSAR.

1. Введение

Последнее десятилетие можно назвать революционным для развития методов сбора трехмерных данных. Получили широкое распространение интерферометрические радары с синтезированной апертурой (IFSAR), лазерные сканеры (LIDAR) и фотоаппараты объёмного изображения. Для сбора 3D данных используются самые разнообразные платформы: переносные треноги и двигающиеся автомобили; суда и локомотивы; вертолеты и самолеты; спутники Земли и межпланетные станции; мобильные роботы и дирижабли [1-5].

Лидары, размещенные на небольших самолетах, популярны для создания трехмерной модели рельефа с точностью 1-2 метра по горизонтали и 10-18 см по вертикали. Такие модели используются для целого ряда задач – от проектирования магистральных нефтепроводов до расчета возможных наводнений. Обработка трехмерных данных, получаемых традиционным способом стереофотографии, требовала постоянного участия оператора. Развитие технологии получения высококачественных трехмерных изображений как зданий, так и обширных районов земной поверхности, привели к резкому росту объема 3D данных, и потребовали развития соответствующих математических методов обработки и максимальной автоматизации программных средств [1-8].

Таблица 1 показывает примеры лидарной статистики из трех проектов (каждая из первых трёх строк таблицы соответствует разным проектам). Размер участков в первых трёх строчках показывает площадь типичных прямоугольных областей, на которые разбивался первоначальный массив данных. Проекты отличаются по типу лидара: в первых двух проектах используется один и тот же лидар, а последние строчки таблицы относятся к третьему проекту, реализованному с помощью лидара другого производителя - фирмы Optech. Таблица показывает актуальность проблемы классификации лидарных данных: для получения модели «голой земли» из исходных файлов нужно удалить от 20% до 80% отражений, соответствующих деревьям и зданиям.

Тип участка и его размер (км²)	Общее кол-во точек	Плот-ность точек (1/м²)	Первое отражение	Последнее отражение	Единственное отражение	Точек отражения от рельефа	Точек отражения от наземных объектов и леса
Гористая местность, 4.9	4,246,006	0.87	0.6%	0.6%	98.8%	79.5%	20.5%
Лесистая равнина, 0.34	1,218,185	3.58	24.5%	24.6%	50.9%	34.2%	65.8%
Лес, русло реки, 2.2	1,738,686	0.79	50%	50%	_	24%	76%
Большая область, 1313	730 млн	0.56	50%	50%	_	80.1%	19.9%

Таблица 1. Статистика лидарных отражений для различных областей и проектов

Создание программных средств и математических методов для обработки данных LIDAR – бурно развивающейся технологии получения трехмерных изображений – актуальная задача. Получение высокоточной 3D модели рельефа тоже имеет большое практическое значение.

Принципиальной особенностью трехмерных лидарных данных, отличающая их от классических 2D изображений, является неполнота 3D данных и сильная вариабельность их качества. Существует четыре вида неполноты трехмерных данных, связанных с геометрией сканирования и потерей части отражений:

Неполнота представления затененных частей объекта: у дома, сканируемого сверху, большинство отражений приходится на крышу.
В случае падения на поверхность воды или стекла, лазерный луч может зеркально отразиться в сторону, и приемник не зарегистрирует обратного отражения. Водоемы становятся участками, на которых измерения полностью или частично отсутствуют.
Механическое движение сканирующего устройства и самолета приводит к зигзагообразному движению лазерного луча. Такое движение оставляет неравномерные щели между траекториями движения луча.
Процесс авиасканирования состоит в челночном движении самолета над зоной проекта с перекрытием сканируемых полос. Между полосами сканирования могут остаться значительные непокрытые участки.

Эти особенности лидарных данных – далеко не единственные – демонстрируют специфичность проблем, возникающих при обработке трёхмерных облаков точек.

В данной работе обсуждаются программные средства и математические методы обработки 3D данных, и два автоматизированных комплекса для обработки больших объемов лидарных и радарных данных. Комплексы были созданы автором в 2003-2008 годах в ходе работы с данными авиасканирования.

В [4] были сформулированы общие принципы создания автоматизированных программных средств для обработки современных трехмерных данных лазерного сканирования.

На основе этих общих принципов автором были разработаны и реализованы два новых высокоэффективных комплекса программных средств для автоматизации процесса обработки данных LIDAR:

Автоматизированный комплекс (программных) средств АКС-ЛИДАР для получения инфракрасных изображений высокого разрешения [3].
Комплекс АКС-ЛИДАР-3D для генерации цифровой модели рельефа [1,2,4].

Для комплекса АКС-ЛИДАР-3D разработан новый математический метод классификации лидарных данных [1].

Оба комплекса прошли серьезную апробацию: с их помощью для 20 тысяч кв. километров земной поверхности, сканированной самолетным лидаром, получены инфракрасные изображения с разрешением 1 метр, а также трехмерные модели рельефа с разрешением 2 метра и точностью высот ~15 сантиметров. Еще для 22 тысяч квадратных километров была получена модель земной поверхности с 5-м разрешением (по данным IFSAR).

2. Автоматизированный комплекс программных средств АКС-ЛИДАР

Главной задачей АКС-ЛИДАР является компенсация неполноты лидарных данных и получение ИК-изображений высокого разрешения [3].

Лидарные системы определяют как координаты точки, так и интенсивность отражения луча в ней. Лазерное освещение в ближнем инфракрасном диапазоне 0.8 - 1.5 мкм позволяет получить черно-белое изображение, близкое к бестеневой фотографии видимого света. Величина лазерного отражения или, другими словами, инфракрасное альбедо земной поверхности используется для картирования водоёмов, создания векторных данных для дорог и контуров берегов, а также характеристик растительности и строений.

Архитектура автоматизированного комплекса АКС-ЛИДАР включает в себя модули: калибровки интенсивности лазерных отражений; сегментирования и преобразования координат; растеризации изображений и обработки артефактов; интерполяции и нормализации.

АКС-ЛИДАР позволяет ускорить и полностью автоматизировать процесс получения ИК изображений: комплекс начинает работу с «сырыми» данными и создает на выходе набор, например, GeoTIFF изображений, готовых к интеграции в ГИС. Функциональность комплекса легко расширяется за счет добавочных модулей; он использует минимум ресурсов обрабатывающей системы.

Работа над описанным программным комплексом АКС-ЛИДАР начата в 2003 году, он постоянно дорабатывается с учётом новых требований. За 2003-2006 годы с его помощью из лидарных данных было получено около 20 тыс. кв.км ИК изображений с 1-м разрешением (пример - на рис. 1). В частности, комплекс АКС-ЛИДАР применялся в ходе проекта номер три из таблицы 1. Плотность данных в 0.56 точек на кв.м означает что, при растеризации таких данных на 1-м сетку, большинство пикселов окажется пустым, причём пустые пикселы будут группироваться в длинные щели. Поэтому лидарные данные такой плотности используют для получения моделей поверхности с 2-м разрешением: процент пустых пикселов в таком случае не превосходит нескольких процентов. Но комплекс АКС-ЛИДАР так успешно компенсирует неполноту данных, что с его помощью из таких лидарных данных можно получать ИК-изображения 1-м разрешения.

Комплекс АКС-ЛИДАР оказался эффективным и при получении 12 кв.км ИК изображений с 30-см разрешением из данных вертолетного лидара.

Рис. 1. Лидарное ИК изображение размером 900х494 м, пиксел 1 м (обработка АКС-ЛИДАР). Возле аэропорта видны самолеты класса «Цессна», размещённые на стоянке.

3. Автоматизированный комплекс программных средств АКС-ЛИДАР-3D

Данный комплекс служит для обработки и классификации трехмерных данных LIDAR, с целью моделирования трехмерных поверхностей [1, 2, 4].

Лидарные данные содержат отражения луча не только от рельефа, но и от зданий, растительности, линий электропередач и других объектов. Лидарные компании доставляют 3D данные в виде файлов, содержащих список координат точек отражений (и некоторых атрибутов, таких как интенсивность отражения). Общий объём одного такого файла зависит от длины пролёта при самолетном сканировании и может достигать десятков гигабайт. Для получения цифровой модели рельефа (ЦМР) данные необходимо отсортировать, интерполировать, классифицировать и визуализировать. Существующие программные средства не предусматривают эффективной автоматизации обработки 3D данных, обеспечивая решение лишь отдельных типичных задач.

Комплекс АКС-ЛИДАР-3D предоставляет оператору возможность:

оптимизации параметров обработки;
нахождения и исправления проблем в данных;
сортировки данных по прямоугольным участкам заданного размера и растеризацию;
интерполяции данных для заполнения пустот любого размера;
работы с данными в распространенных системах географических координат;
классификации данных на «голую землю» и на растительность и здания;
визуализации 3D поверхности для проверки качества обработки;
интерактивного исправления локальных недостатков полученной ЦМР.

Реализация каждой из этих функций комплекса требует значительных усилий. Например, пункт 5 – проблема перевода данных из одних географических координат в другие. Первоначально была сделана попытка использовать для этой цели сторонний продукт Corpscon 5.11, но его производительность и устаревший код ввода-вывода не позволяли выполнить задачу за приемлемое время. Поэтому в 2003 был разработан собственный модуль CONVERT для перевода координат из универсальной равноугольной поперечно-цилиндрической проекции Меркатора в локальную систему. Он основан на коде Corpscon, который был переработан для более высокой производительности: ~1 млн. преобразований координат в секунду, что в несколько раз быстрее оригинального кода. Кроме того, разработанный модуль может без проблем работать с большими файлами в сотни мегабайт.

Для создания высокоточной ЦМР, данные лидара должны быть классифицированы как минимум на два класса – отразившиеся от рельефа и все остальные отражения. Существует несколько методов такой классификации, но у каждого метода есть свой набор недостатков и идеального пока никто не предложил. Разработанный автором метод виртуальной поверхности (МВП) для классификации на растре рассмотрен в [1] (см. также разделы 5.1, 5.3). МВП тоже имеет свои недостатки, но применяется в комплексе с хорошо дополняющим его методом выделения связных структур (МВСС) (см. раздел 5.2).

Важной особенностью описываемого комплекса является возможность автоматического подстраивания параметров фильтрации под особенности местности. Например, в густом лесу фильтрация должна быть агрессивнее.

В исходной ЦМР присутствуют пикселы разного происхождения и различной достоверности. Поэтому, при необходимости, создается матрица достоверности, которая сохраняет историю преобразований каждого пиксела (см. также раздел 5.4).

АКС-ЛИДАР-3D по мере своего развития прошел в 2003-2008 годах апробацию на большом объёме данных LIDAR. Данным комплексом было обработано свыше 40 тыс. кв. км, сканированных с разрешением 2 и 5 метров, а также небольшие объемы данных (сотни кв. км) с разрешением 1 м и 30 см. Скорость обработки с помощью АКС-ЛИДАР-3D с учетом затрат времени на вмешательство оператора и контроль качества, достигала 500 кв. км в неделю (для 2-м разрешения), и точность ЦМР соответствовала признанным стандартам (среднеквадратичная ошибка, или RMSE < 18.5 см). Типичная ошибка по высоте составляла ~15 см при размере пиксела в 2 метра на равнинной местности с пологими холмами. Для лидарных авиаданных высокого качества и плотности (размер пиксела выбран в 1.2 метра) была достигнута среднеквадратичная ошибка в 6-8 см.

Комплекс АКС-ЛИДАР-3D продемонстрировал эффективную работу на высоком уровне автоматизации – участие оператора в процессе обработки было минимальным. Комплекс эффективно интерполирует пустоты, которые на некоторых участках могли достигать 50%, и генерирует ЦМР, где участки земной поверхности с разным качеством сканирования мало чем отличаются.

4. Интерфейс и визуализация

Рассмотрим программные средства для эффективной визуализации и активной коррекции лидарных данных в ходе их обработки [4].

Даже лучшие автоматизированные программные средства могут ошибаться и для исправления их ошибок требуется вмешательство человека. В комплексе АКС-ЛИДАР-3D разработан удобный интерфейс активного вмешательства, который позволяет в течение 1-2 минут пересчитать модель данного участка с уточнёнными параметрами и избавиться от оставшихся артефактов. Но для обнаружения ошибки нужно визуализировать и сравнивать трехмерные поверхности до и после обработки.

Качество и скорость полученной визуализации (рис.2) вполне сравнимы с популярными коммерческими продуктами ГИС, такими как ESRI ArcGIS Desktop и APL Quick Terrain Modeler. Производительности графического движка вполне хватает для работы с рельефом, состоящем из 4 миллионов и более точек, в то же время популярные коммерческие продукты от Golden Software и ESRI испытывают проблемы при обработке более чем нескольких сотен тысяч точек. Основным преимуществом визуализационного модуля АКС-ЛИДАР-3D перед ESRI ArcGIS и Quick Terrain Modeler является возможность оперативно исправлять рельеф и на месте оценивать результаты работы алгоритмов классификации.

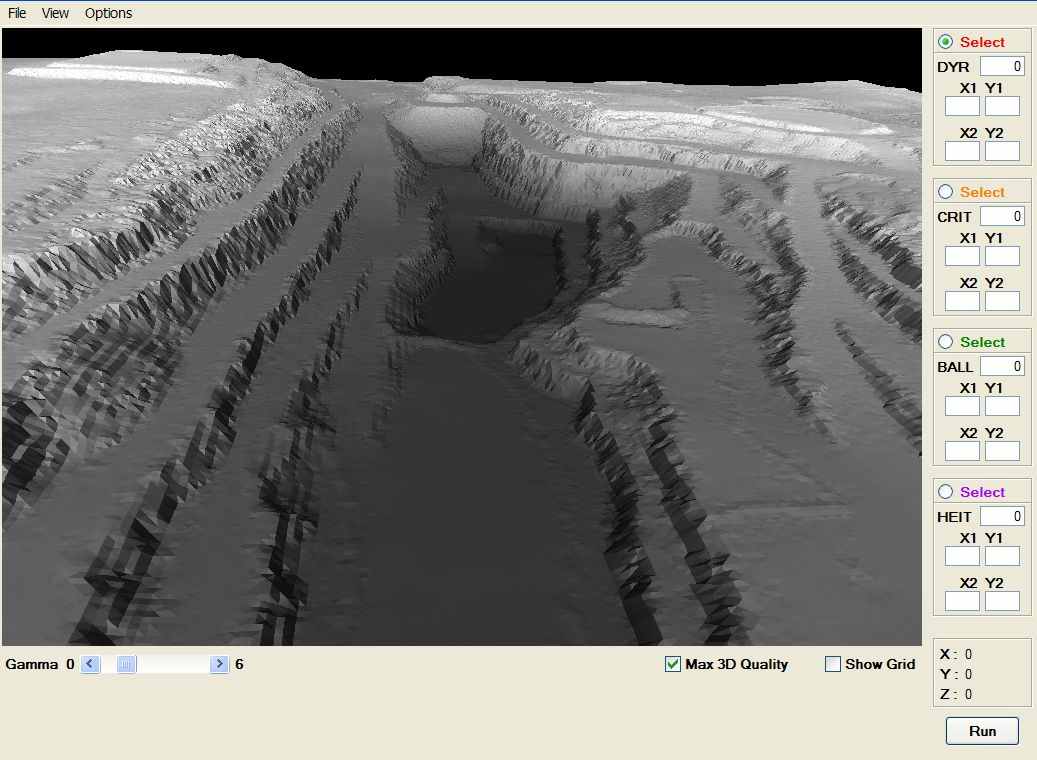
Рис. 2. Трехмерное изображение вытянутого карьера километровой длины, визуализировано комплексом АКС-ЛИДАР-3D.

Комплекс с встроенным модулем «GUI» включает следующие методы активной коррекции получаемых трехмерных моделей (каждый из них может применятся, как глобально – ко всему участку, так и к локальной прямоугольной области, выделенной оператором):

Изменение радиуса фильтрующего элемента в МВП
Агрессивная фильтрация артефактов
Удаление объектов с заданной высотой
Локальное отключение классификации

АКС-ЛИДАР-3D позволяет также совмещать трехмерный рельеф с двумерными изображениями высокого разрешения.

Для лучшей визуализации и распознавания рельефа часто требуется использовать текстурные карты местности. Реализованный в АКС-ЛИДАР-3D модуль 3D рендеринга рельефа, за счет многочисленных оптимизирующих алгоритмов, позволяет работать с большими объемами 3D данных. Например, для российского программного комплекса CREDO оптимальный объем загружаемой ЦМР составляет 50 тысяч точек для компьютера с GeForce3, P4 1.7GHz. Комплекс АКС-ЛИДАР-3D позволяет работать с ЦМР в 4 миллиона точек с текстурной картой 6420x6420, на машине с Radeon 7000 32Mb, P4 2.8GHz со скоростью ~ 10 fps; объем используемой памяти < 400MB. На современных машинах с мощными видеокартами скорость составляет ~ 500 fps.

5. Математические методы классификации трехмерных данных и генерации моделей земного рельефа

Для успешной классификации и оценки ошибок обработки трехмерных данных, необходимо использовать соответствующий математический аппарат. Автором были проанализированы большинство работ в этом направлениии и проблемы, с которыми столкнулись разработчики различных методов классификации, что позволило создать и реализовать относительно эффективный алгоритм обработки с высокой степенью автоматизации.

5.1. Матричный метод описания процесса обработки данных

Одним из важнейших методов представления полученных лидарных данных является их растеризация – перенесение на прямоугольную сетку с пикселом определенного размера. После чего, все процессы обработки этих данных будут протекать в пределах полученной таблицы или матрицы и выражаться в изменении числового значения каждого элемента матрицы.

Первичное множество N точек лазерных отражений, каждая из которых представляет точку в четырёхмерном пространстве координат X,Y,Z и интенсивности I, обычно рассортировывают в три двумерные матрицы:

Z_min _i_,_k – матрицу минимального значения высот отражений;

Z_max _i_,_k – матрицу максимального значения высот отражений;

I_av _i_,_k – матрицу среднего значения интенсивности отражения.

Для формализованного представления процесса обработки, автор разработал метод матричного описания обработки данных (метод МООД).

Опишем растеризованное представление данных матрицей Z_ik , где, например, i = 1, ..., 600; k = 1, ..., 900.

Каждой процедуре обработки данных сопоставим оператор Â_j . Тогда процедура, например, интерполяции пустот в оригинальных данных (или нулевых элементов в матрице данных), которая идет первой среди других процедур, запишется в виде уравнения

Z₁_ik = Â₁ Z_ik (1)

где матрица Z_ik является исходной матрицей, а Z₁ _ik - результирующей матрицей после первой процедуры обработки. Вторая процедура обработки применяется последовательно:

Z₂_ik = Â₂ Z₁_ik = Â₂ Â₁ Z_ik (2)

Всю последовательность обработки лидарных или любых других данных, представленных в матричном виде, можно описать следующим уравнением:

Z_jik = Â_j … Â₁ Z_ik (3)

Развитый матричный метод описания обработки данных положен в основу обсуждаемых автоматизированных комплексов программных средств обработки лидарных данных.

5.2. Метод и критерии выделения связных множеств матричных элементов

Фундаментальной задачей обработки матриц лазерных данных является извлечение и распознавание всех объектов или структур, содержащихся в данных. Типичная структура, которая отличается от фона своей яркостью или выделяется по высоте, хорошо описывается понятием связного множества.

Тем самым, задача извлечения и распознавания структур сводится к выделению (и определению их характеристик) всех непересекающихся связных подмножеств из максимального конечного множества матричных элементов.

Критериями выделения подмножеств являются следующие:

«Критерий величины». Сравнение величины матричного элемента (например, яркости) с некоторой величиной. Эта величина может быть заранее заданной, или определяться из анализа заданного набора элементов, вплоть до анализа всех элементов множества. Таким способом можно выделять, к примеру, самые яркие объекты.
«Критерий гладкости». Сравнение величины матричного элемента (например, высоты) с соседними элементами. Тем самым, можно выделить подмножество элементов, образующих достаточно гладкую (монотонную) структуру.
Комбинация вышеперечисленных критериев. Это позволит выделять одновременно яркие и гладкие структуры.

Процедура выделения искомых связных множеств в случае критерия первого типа:

- построчно анализируются элементы матрицы a_i_,_k, начиная с первого. Определяется соответствие величины данного элемента искомому критерию, например, a_i_,_k> a_crit , и принадлежность этого элемента к уже найденным подмножествам A_j;

- если для элемента a_i_,_k не выполняется критерий a_i_,_k> a_crit , то переходим к анализу следующего элемента, например, a_i_+1,_k. Если критерий выполняется, но элемент принадлежит к одному из уже найденных подмножеств A_j_, то снова переходим к анализу следующего элемента;

- если критерий выполняется, и элемент не принадлежит к ранее найденным подмножествам A_i_, то он образует первый элемент нового подмножества A_i₊₁. Построчное сканирование сменяется анализом всех соседних (по горизонтали или вертикали) матричных элементов – для выяснения, принадлежат ли они новому подмножеству. Этот анализ заканчивается только тогда, когда новое связное подмножество окажется окруженным со всех сторон элементами, которые не могут быть в него включены.

Процедура выделения подмножеств по второму критерию отличается тем, что вопрос о включении элемента в множество решается лишь после сравнения его с соседним элементом. Если значения обоих элементов удовлетворяют поставленному условию, то в подмножество включаются сразу оба матричных элемента. Если для выделения подмножества используется смешанный критерий третьего типа, то после удовлетворения критерия гладкости проводится дополнительная проверка на соответствие обоих элементов критерию величины.

Вышеперечисленные процедуры позволяют составить списки элементов каждого подмножества и получить его интегральные параметры:

- суммарную площадь элементов;

- длину периметра (пропорциональную количеству граничных элементов, не принадлежащих подмножеству);

- средние параметры значения элементов подмножества и разброс от среднего.

Вычисление этих параметров позволяет эффективно распознать в подмножествах объекты определённого типа (здание, дерево, водоём, дорога), которые значительно различаются по площади, яркостным и высотным характеристикам.

Сумма выделенных подмножеств или структур может быть как меньше максимального множества, например, в случае использования «критерия величины», так и равна ему

A₁ + A₂ + ... +A_j= A (4)

Сумма непересекающихся связных подмножеств равна максимальному подмножеству в случае применения «критерия гладкости», который группирует пикселы в гладкие структуры или кластеры элементов. Если элемент значительно отличается от всех соседей, то он формирует собственное подмножество из одного элемента.

Если «критерий гладкости» применяется к Z_min _i_,_k, матрице минимального значения высот отражений, то получается набор гладких по высоте структур, самая большая - по площади - из них будет соответствовать поверхности земли. Здания будут выглядеть как связные кластеры с небольшой площадью, которые испытывают скачок высот или значительный их градиент на границе здания. Этот градиентный критерий исключительно полезен для эффективного выделения невысоких зданий большой площади (супермаркеты, склады), извлечение которых является проблемой для распространенных методов генерации ЦМР.

5.3. Метод МВП для удаления неструктурированных объектов поверхности

В реальности всегда можно найти небольшие поверхностные элементы (дома сложной формы, пологие кусты или кластеры деревьев), для которых не выполняются критерии структуры или связного множества. Для убирания таких неструктурированных объектов в комплексе АКС-ЛИДАР-3D разработан и применяется новый математический метод классификации лазерных отражений, соответствующих земной поверхности - метод виртуальных поверхностей [1].

Воссельман [6] разработал, а Ситхоул [7] усовершенствовал алгоритм фильтрации лазерных данных, основанный на анализе наклона поверхности (slope-based filter или SB-фильтр). Для каждой точки лидарного отражения строится фильтрующий элемент – выпуклая поверхность в виде гиперболоида или конуса с вершиной в рассматриваемой точке. Если внутри заданной поверхности нет других точек отражений, то рассматриваемая точка считается земной поверхностью.

IPF-метод [8] совмещает фильтрацию с интерполированием и строит по точкам отражений усредненную поверхность. Самые высокие точки отбрасываются, а оставшиеся используются для поверхности следующего приближения и т.д.

Эти популярные методы при практическом применении демонстрируют существенные недостатки [1]. Метод виртуальной поверхности (МВП) для фильтрации 3D данных обладает положительными качествами SB-фильтра и IPF-метода, но свободен от наиболее серьезных проблем этих алгоритмов [1].

Важным элементом МВП является фильтрующий элемент в виде поверхности шара, которые применяется не к исходному облаку точек отражений, а к уже растеризованным данным. МВП работает, учитывая первые и последние лидарные отражения в каждом пикселе и автоматически варьируя степень фильтрации - в зависимости от густоты растительности.

МВП заключается в следующем [1]:

1. В точке (X_i, Y_j) (центр каждого пиксела) по оси Z из глубины всплывает сфера с радиусом R (параметр метода) – до тех пор, пока сфера не наткнётся на центр любого пиксела поверхности. Формула для нахождения центра остановившейся сферы:

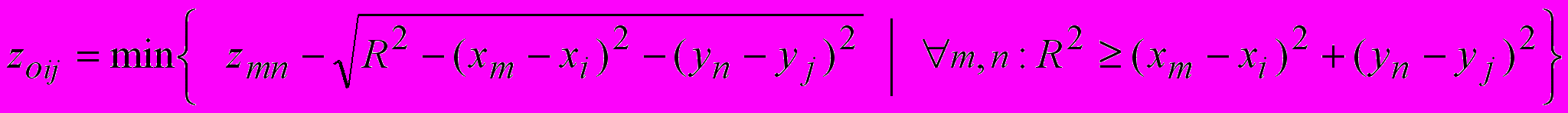(5)

2. Набор из сфер, построенных для каждого пиксела, образует многослойную поверхность. Z-координаты точек земной поверхности (или виртуальной модели этой поверхности) можно получить, выбрав для каждого пиксела максимальную высоту из всех полусфер:

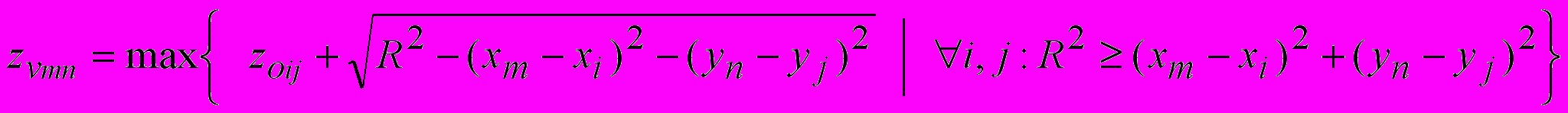(6)

На рис. 3 показан лесистый район до фильтрации и после. После применения МВП становятся заметными детали рельефа, связанные с перемещением грунта.

5.4. Накопление ошибок

Количество последовательных процедур обработки матрицы 3D данных может исчисляться десятками. Каждая процедура меняет значение элемента и, строго говоря, вносит ошибку в это значение. В конечном варианте матрицы часть элементов окажется пришедшей непосредственно из лидарных измерений, а часть – претерпевшей множественные процедуры обработки и интерполяции, и им можно доверять лишь в некоторой степени. Как отследить историю преобразования каждого пиксела и как оценить накапливающуюся ошибку обработки в любом пикселе?

Определим матрицу изменений, происходящих при каждом j-ом преобразовании данных:

D_jik = Â_j … Â₁ Z_ik - Â_j_-1 … Â₁ Z_ik (7)

Матрица самого первого изменения будет выглядеть так:

D₁_ik = Â₁ Z_ik - Z_ik (8)

Введем матрицу операций, элементы которой принимают значения «0» или «1» и определяются следующим образом:

0, если D_jik = 0

P_jik = { (9)

1, если D_jik≠ 0

a

а

б

Рис. 3. а) Участок на краю леса; б) МВП отфильтровывает растительность и выявляет два старых котлована с местами вывала грунта. Обработка и визуализация с помощью АКС-ЛИДАР-3D.

Неравенство нулю элемента матрицы P_jik означает, что над значением i,k-элемента матрицы (над пикселом) была прозведена j-операция обработки.

Хотя трехмерная матрица кажется громоздким и неудобным для работы объектом, но на практике её можно свести к достаточно удобной двумерной матрице упакованной побитно. Значение каждого элемента будет содержать в разных битах информацию об использованных процедурах обработки данного пиксела.

Введём вектор ошибки ε_j, каждая компонента которого соответствует средней ошибке, вносимой j-операцией обработки. В рамках развитого формализма мы легко можем описать процесс накопления ошибок в ходе обработки матрицы данных. Зная матрицу операций и вектор ошибки, для каждого i,k-пиксела мы можем записать уравнение суммарной ошибки:

E_ik = Σ ε_jP_jik = ε₁P₁_ik + ε₂P₂_ik + ... + ε_jP_jik (10)

Используя этот метод, можно определить – заполнен ли итоговый пиксел ЦМР высотой из оригинальных лидарных измерений, или он получил своё значение с помощью достаточно надежной интерполяции из соседнего пиксела или ненадёжной крупномасштабной интерполяции.

6. Заключение

В результате выполненной работы были разработаны:

Комплекс программных средств АКС-ЛИДАР для обработки лидарных данных, компенсирования их неполноты и получения инфракрасных изображений высокого разрешения
Комплекс программных средств АКС-ЛИДАР-3D для обработки и классификации данных лазерного и радарного сканирования, а также моделирования трехмерных поверхностей. Комплекс включает программные средства для визуализации и активной коррекции трехмерных данных в процессе их обработки
Матричный метод описания процесса обработки 3D данных, включающий математический метод виртуальной поверхности, разработанный для классификации данных LIDAR и генерации трехмерных моделей земного рельефа

Благодарности. Автор благодарит научного руководителя, д.т.н, профессора В.А. Сухомлина за помощь и поддержку при выполнении данной работы.

Литература

Горькавый И.Н. Метод виртуальной поверхности для классификации данных LIDAR и генерации трехмерной модели земного рельефа. //Труды Первой Международной научно-практической конференции «Современные информационные технологии и ИТ-образование». /Ред. Сухомлин В.А., ВМК МГУ, 2005. С.583-597.
Горькавый И.Н. Автоматизация обработки данных лазерного сканирования для получения высокоточных трехмерных моделей земного рельефа. //Труды Второй Международной научно-практической конференции «Современные информационные технологии и ИТ-образование». /Ред. Сухомлин В.А., ВМК МГУ, 2006. С.367-377.
Горькавый И.Н. Комплексный подход к автоматизации процесса обработки данных LIDAR для получения инфракрасных изображений высокого разрешения. //Известия высших учебных заведений. Геодезия и аэрофотосъемка. 2007. Вып.5. С.148-162.
Горькавый И.Н. Автоматизированные программные средства обработки трехмерных данных лазерного сканирования. //Известия высших учебных заведений. Геодезия и аэрофотосъемка. 2008. Вып.4. С.22-34.
Gorkavyi I.N. 3D Laser Scanning for Asteroids and Comets, Proc. The 10th “Asteroids, Comets, Meteors” Meeting, 14-18 July 2008, Baltimore, Maryland, USA.
Vosselman G. Slope based filtering of laser altimetry data. Int. Arch. Photogramm. Remote Sens., pt. B4, Vol.33, 2000. P.958-964.
Sithole G. Filtering of laser altimetry data using a slope adaptive filter. Int. Arch. Photogramm. Remote Sens. pt. 3/W4, 2001. P.203-210.
Kraus K., Pfeifer N. Advanced DTM generation from LIDAR data. //Int. Arch. Photogramm. Remote Sens., pt. 3-2W3, Vol.32, 1997.

Blog