Задача о колодце Лотоса рассматривалась в №4 журнала «Математика в школе» за 1997 г сразу в двух статьях. Наиболее известным источником сведений, связанных с этой задачей, является рассказ писателя-фантаста А. П. Казанцева «Колодец Лотоса»

Вид материала

Содержание

РQ высота трапеции. Из подобия треугольников АОD
Загадка из древнего египта
Первый шаг.
Второй шаг.
Четвертый шаг.
Рис. 3 рассматриваемого итерационного процесса. Рекуррентные соотношения (6) и (7) показывают, что а
Пятый шаг.

Подобный материал:

ЕЩЕ РАЗ О КОЛОДЦЕ ЛОТОСА

Задача о колодце Лотоса рассматривалась в № 4 журнала «Математика в школе» за 1997 г. сразу в двух статьях. Наиболее известным источником сведений, связанных с этой задачей, является рассказ писателя-фантаста А.П.Казанцева «Колодец Лотоса»

Завязка рассказа такова. Археолог Детрие, проводящий раскопки храма бога Ра в древнеегипетском городе Гелиополе, обнаруживает надпись, в которой излагается условие следующей задачи:

В колодец (см. рис. 1) погружены две тростинки длиной 2 и 3 меры. Вода доходит до точки их пересечения, которая находится выше дна колодца ровно на одну меру. Требуется определить диаметр колодца.

Тот, кто сможет решить эту задачу, становится жрецом бога Ра. Но если соискатель этого высокого звания потерпит неудачу, то погибнет, замурованный в камере возле колодца Лотоса.

Чтобы разобраться в сути задачи, археолог вызывает из Парижа своего друга - профессионального математика, графа де Лайе. Тому удается с помощью достаточно сложных методов аналитической геометрии и алгебры составить уравнение четвертой степени с одним неизвестным. После этого по методу итальянского ученого XVI в. Феррари можно получить точное решение.

Вывод уравнения в рассказе неоправданно сложен. На самом деле достаточно использовать теорему Пифагора и следующую теорему о трапеции.

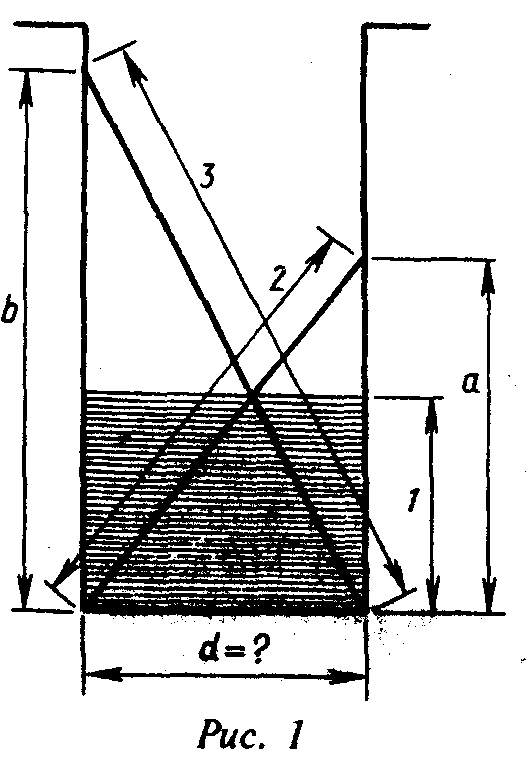
Рис.1

Теорема. Длина отрезка, концы которого лежат на боковых сторонах трапеции, а сам он параллелен ее основаниям и проходит через точку пересечения диагоналей, равна среднему гармоническому длин оснований трапеции. Кроме того, точка пересечения диагоналей делит данный отрезок пополам (см рис.2).

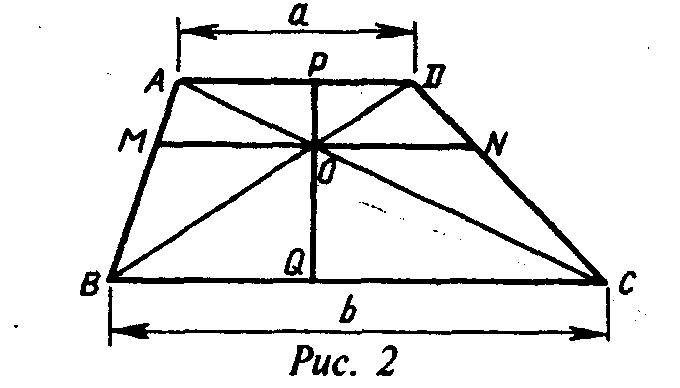
Пусть РQ высота трапеции. Из подобия треугольников АОD и СОВ следует, что РО : а = OQ : b. Или РО : а == (РQ — РО) : b. Отсюда легко получить, что РО = РQ • а : (а + b). Из подобия треугольников АВС и АМО следует пропорция РО : РQ = МО : b. А значит, МО = a • b: (а + b). То же самое вычисление действительно и для ОN.

Легко установить, что МО = ОN и МN = 2аb : (а + b). А это и есть среднее гармоническое оснований. Обратившись к исходной задаче, мы увидим, что имеем дело с прямоугольной трапецией, для которой МО = -1. Ориентируясь на обозначения величин, приведенные на рис.1, мы можем записать два уравнения:

a ∙ b

=

1 и 3² – b² = 2² – а².

a + b

И

спользуя тот факт, что а = √4 – d² и b = √9 – d² получаем уравнение, которое понадобится нам в дальнейшем:

√

4 – d² + √9 – d² = √4 – d² • √9 – d² (1)

Однако чаще идут другим путем. Исключают сначала переменную d, получая уравнение b² - а² = 5. Затем с помощью равенства аb = а + b выражают b через а и подставляют в уравнение b² — a² = 5. В результате получается уравнение четвертой степени с неизвестным a:

a⁴- 2• а³+ 5• а²-10 • а + 5 = 0. (2)

После достаточно сложных преобразований, в том числе и с комплексными числами, метод Феррари позволяет получить точное решение задачи:

√r + - r – 7 + 1 3 3

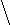√r 395 + 60√39 + 395 – 60√39 -7

a = , где r =

2 3

С чисто математической точки зрения тема закрыта, однако интерес к этой задаче не ослабевает. Вопрос стоит так: «Как решали эту задачу древние египтяне?» К сожалению, в статьях, посвященных обсуждаемой задаче, обычно выводят уравнение (2) и дают его приближенное решение, причем приближенный метод выбирается произвольно.

На самом деле нас не способно удовлетворить даже точное решение, поскольку оно заведомо не соответствует уровню знаний древних математиков. В еще большей мере это относится к приближенным решениям, получаемым методами, базирующимися на идеях математического анализа.

Задачу о колодце Лотоса интересно было бы решить в соответствии с уровнем древней математики. Кроме того, драматизм условия заставляет каждого невольно примерить задачу к своим способностям. Недаром археолог Детрие после нескольких дней безуспешных размышлений пришел к выводу, что ему так и пришлось бы остаться возле колодца навсегда. Неужели все, кто жил раньше Феррари и Ньютона, были обречены?

В этом отношении следует отдать должное А.П. Казанцеву. До начала своей писательской карьеры он был инженером и поэтому знал математику. Его рассказ интересен тем, что кроме формулировки задачи и романтической истории о царице Хатшепсут и зодчем Сененмуте в нем предложен один из вариантов решения задачи, доступный кандидатам на звание жреца. Этот метод состоит в непосредственном измерении диаметра колодца Лотоса с помощью тростинок. После довольно замысловатых манипуляций, использующих мокрые части тростинок, Сененмуту удается получить приближенное значение диаметра колодца d, равное 37/30.

Однако непосредственное измерение уже существующего колодца не объясняет, каким образом его диаметр могли бы вычислить «проектировщики». Что они стали бы измерять? Поскольку мы рассматриваем задачу с точки зрения истории математики, следует сформулировать предположения о допустимых способах ее решения.

Первое из наших предположений состоит в следующем. Наука древнего мира ориентировалась не на теоретическое решение той или иной задачи, а прежде всего на получение практического результата. Такой подход можно условно назвать инженерным. Одним из его вариантов является принятие без особых обосновании более или менее правдоподобной гипотезы, значительно облегчающей вычисления. После получения приближенного результата его можно проверить дополнительными вычислениями на этот раз без гипотетических предположений. Подобным способом можно оценить точность результата. Если он не является достаточно точным, то можно его уточнить, используя новые допущения.

Для уточнения решений мы воспользуемся преобразованиями, напоминающими выделение полного квадрата, и будем решать квадратные уравнения. Это наше второе допущение, которое мы обоснуем ссылкой на мнение известного историка математики М.Я. Выгодского, считавшего, что египетская математика имела уровень, не уступающий вавилонской математике. Вот что он пишет в своей книге «Арифметика и алгебра в древнем мире» (2-е изд. М.: Наука, 1967. С. 233).

«В самом деле, из какого источника возникли квадратные уравнения вавилонской математики? Несомненно, из геометрических задач, в свою очередь отражавших прямо или косвенно потребности практики. Какие это были потребности? Вавилонские источники отвечают на этот вопрос с полной определенностью; в них мы находим задачи на расчет фундамента здания, плотин, осадных насыпей и т.п. Мы видели, что и терминология геометрических задач свидетельствует об их происхождении (так, полоса треугольника именуется «каналом»).

Но ведь строительная техника египтян стояла не на более низком уровне, чем вавилонская; плотины египтяне должны были делать не хуже, чем вавилоняне;

устройство каналов приняло у них грандиозные размеры, архитектура же была поистине изумительна. При этих условиях отмеченное нами сходство становится вполне понятным, и естественно ожидать, что оно шло значительно дальше. Мы не имеем прямых данных о том, что египтяне решали полные квадратные уравнения. Но предположение об этом представляется нам весьма вероятным».

Каким же был уровень вавилонской математики? Снова сошлемся на М.Я. Выгодского: «Оказалось, что ученики древневавилонских школ умели решать задачи, требующие применения «теоремы Пифагора» в общем ее виде, по меньшей мере за 1000 лет до Пифагора и что решение полного квадратного уравнения не представляло для них никакой трудности» (там же, с. 82). И далее: «В частности, стало совершенно несомненным, что вавилонская математическая культура имела под собой прочную теоретическую базу и еще за 2000 лет до нашей эры вышла из периода эмпирического накопления знаний» (там же, с. 85).

Основой нашего метода станет приближенный способ извлечения квадратных корней, известный с древнейших времен. При этом использовалась формула

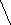
r

a

² + r ≈ a + ,

2a

r 2 r 2 r 2

о

снованная на том, что a + = а² + r + — и слагаемое

2a 2a 2a

мало.

Приступим к решению задачи и получим приближенное значение d₀ — диаметра колодца. Вспомнив, что b² — a² = 5 сделаем «инженерное» предположение: среднее гармоническое чисел а и b приближенно равно их среднему арифметическому. Мы делаем это предположение без обоснований, так сказать, на глазок. (Лучший результат дала бы замена среднего гармонического на среднее геометрическое.)

Практически мы считаем, что длина отрезка МО на рис. 2 равна половине средней линии трапеции. В результате предположения мы получаем систему двух уравнений, которая решается исключением одной из переменных без всякого труда:

a + b = 4

b² — a² = 5

В итоге: а = 11 / 8, b = 21 / 8. Легко вычислить, что диаметр d₀ в этом случае приблизительно равен 1,45, а высота воды в колодце при таком диаметре — около 0,9.

Покажем, как это решение можно уточнить с помощью уравнения (1) и приема, основанного на формуле (3). Обозначим через d₁ уточненное решение уравнения (1) и положим, что d₁ = d₀ – s. Тогда

d₀

4 – d₁² = 4 – (d₀ – s)² = 4 – d₀² + 2d₀ ∙ s – s² = a² + 2d₀ ∙ s – s² ≈ a + s

a

d₀

(опущен член, содержащий s²). Аналогично 9 – d₁² ≈ b + s.

b

(Отметим, что мы использовали формулу (3) не для арифметических, а для алгебраических преобразований. Основанием для этого служит наличие теоретической базы в вавилонской, а значит, с большой вероятностью, и в египетской математике.) Теперь уравнение (1) можно переписать в виде:

d₀d₀d₀d₀

(

a + s) + (b + s) = (a + s) + (b + s). (4)

a b a b

Это квадратное уравнение относительно s. Его положительный корень выражается формулой

a = 11 / 8, b = 21 / 8 и (5). Его положительный корень выражается формулой

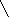(a +b) – (a² – b²) + (a² – b²)² – 2(a² – b²) (a – b) + (a + b)²

s

= (5)

2d₀

Подставив в нее значения a = 11 / 8, b = 21 / 8 и d₀ = 1,45 , а также используя равенства а + b = 4 и b² — а² = 5, получим, что s = 0,19, а d₁ = 1,26. По данному значению диаметра можно вычислить соответствующие ему значения величин a₁ и b₁ после чего формулу (5) можно использовать для второго уточнения значения диаметра d и величин a и b. Таким образом, мы пришли к итерационному процессу, идея которого понятна любому вычислителю: при вычислениях отбрасываются высокие степени небольших чисел ввиду их малости.

Для наглядности приведем таблицу первых четырех итераций, проведенных на компьютере с помощью формулы (5).

Таблица 1

Итерация	s	d₀	1/a + 1/b
1	0,190107	1,259893	1,106717
2	0,028195	1,231698	1,011093
3	0,000512	1,231186	1,000192
4	0,0000001	1,231186	1,000000

Рассмотрение задачи о колодце Лотоса будет неполным, если не коснуться особенностей эстетики Древнего Египта.

Египтян привлекали геометрические конфигурации, отличающиеся максимальной простотой и характеризующиеся отношениями небольших целых чисел. Для египтянина естественно было искать решение задач в виде дробей с малыми знаменателями.

Если рассматривать дробные числа со знаменателями не более 5, то неплохое приближение диаметра колодца дают дроби 5/4 и 6/5. Обе эти дроби хорошо соответствуют духу египетской математики, где было принято записывать произвольную дробь в виде суммы дробей с числителями, равными

5 1 6 1

1: — = 1 + —, — = 1+ — .

4 4 5 5

Каждое из этих двух значений диаметра занесем в табл. 2:

Таблица2

d диаметр	a	b	а• b : (а + b) — высота воды
5/4	1,56	2,73	0,99
6/5	1,4	2,75	1,01

Мы получили два приблизительных решения (d = 1,25 и d = 1,2), дающих хорошие практические результаты. Первое из них несколько точнее, но с точки зрения красоты числовых соотношений предпочтение следует отдать второму значению. Дело в том, что величина равная 1,2 является половиной среднего гармонического длины диагоналей трапеции. Действительно, 2 • 3 : (2 + 3) = 1,2. Такие числовые соотношения указывают на гармоничное построение колодца.

ЕСЛИ ЭТО И НЕ ПРАВДА, ТО ХОРОШО ПРИДУМАНО

Любителя истории от специалиста-историка отличает прежде всего критическое отношение к источникам информации. Обратим внимание: ни в публикациях из №4-97 Р.М.Нижегородцева [1] и А.В.Шевкина [2], ни в статье М.Е.Степанова [3] нет ссылок на труды историков математики. В статье [1] упомянуто, что раскопки велись в 1912 г. Вряд ли такой сенсационный результат — обнаружение нового математического текста — не стал бы известен М.Я.Выгодскому, книга которого вышла в середине нашего века. Но в ней, как и в изданиях других историков, задача про колодец Лотоса не встречается.

Напрашивается вывод, что задача о колодце Лотоса — просто плод фантазии писателя А.П.Казанцева. Его рассказ «Колодец Лотоса» мастерски написан, и там речь идет о реально живших людях: царице Хатшепсут — дочери великого фараона Тутмоса I (1506 — 1494 до н. э.) и ее современнике - великом зодчем Сененмуте. В рассказе описана дружба, соединявшая этих двух людей. Эта гипотеза основана на каких-то изображениях Сененмута, но не более того.

Писатель-фантаст, закрутивший сюжет, на основе выдуманных им трогательных взаимоотношениях царицы и зодчего, мог придумать и задачу, ставшую испытанием для будущего жреца-зодчего.

По этим соображениям редакция не решилась публиковать статьи [1] - [3] в разделе «История математики». Мы признаем за ними лишь дидактическую ценность, пока у нас нет сведений об исторических источниках задачи о колодце Лотоса. Рассказ учителя о трагических последствиях, которые ожидали Сененмута, если бы он не справился с задачей, может подогреть интерес к ней у многих учащихся.

Правдоподобные исторические выдумки встречаются весьма часто. Всём известны, например, слова Галилея «А все-таки она вертится», произнесенные сразу после отречения от теории Коперника. Есть даже картина, воспроизведшая сей исторический момент. Беда только в том, что такого момента никогда не было. Был молчаливый, тайный труд Галилея и его учеников по развитию теории Коперника. Таким образом, выдумка оказалась правдивее правды. Она описала внутреннее состояние ученого лучше любых исторических изысков.

Так и рассказ писателя А.П.Казанцева открывает нам такие глубинные исторические пласты, до которых мы никогда не смогли бы докопаться без помощи воображения. Наша фантазия помогает нам победить время. Но не стоит ей слишком доверяться, фантазируя, нужно отличать красивый вымысел от «голой» правды.

ЗАГАДКА ИЗ ДРЕВНЕГО ЕГИПТА

В 1912 г. во время раскопок в дельте Нила ученые обнаружили полуразрушенный храм, на стенах которого сохранились письмена. На одной стене огромной комнаты, построенной из гранитных глыб, оказался текст математической задачи, которая заключалась в следующем:

"Ты стоишь перед стеной, за ней колодец Лотоса, круглый, как Солнце. В колодец опущены два тростниковых стебля, длина одного из которых три меры, другого — две меры. Стебли перекрещиваются на уровне поверхности воды, а уровень воды в колодце равен одной мере. Кто укажет длину самой длинной прямой, которая может уместиться в основании колодца Лотоса, тот возьмет тростниковые стебли и станет жрецом бога Ра".

Легко видеть, что данная задача имеет планиметрический смысл. Два прямоугольных треугольника с общим катетом имеют гипотенузы, равные 3 и 2 и пересекающиеся на расстоянии 1 от общего катета этих треугольников, длину которого требуется найти (рис. 1). Исследуем эту задачу.

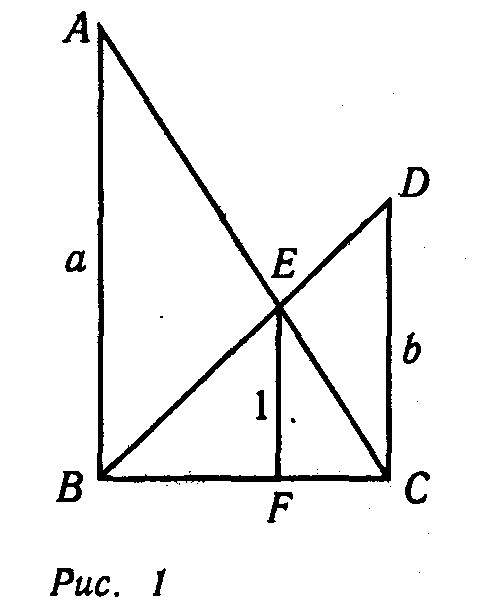
Первый шаг. Пусть AС = 3, BD=2, EF = 1, требуется определить ВС. Обозначим АВ = a, CD = b, ВС = х. Тогда из подобия треугольников АВС и EFC получим —

1 FC 1 BF

— = —, а из подобия треугольников BCD и BFE — — = — .

a x b x

Складывая эти два равенства, будем иметь

1 1

— + — = 1. (1)

a b

В то же время из прямоугольных треугольников АВС и BCD получим а² + х² = 9,

b² + x² = 4, откуда

а²- b² = 5. (2)

Равенства (1) и (2) образуют систему уравнений, которая сводится к уравнению 4-й степени

a⁴- 2a³- 5a²+ 10a - 5=0.

Однако в Древнем Египте не умели решать уравнений 4-й степени, а приближенное определение корня этого уравнения путем подбора требует исследования вопроса о существовании и единственности этого корня. "Эмпирическое" решение этой задачи путем непосредственных измерений, по-видимому, также исключается, поскольку, согласно условию задачи, колодец Лотоса был недоступен решающему.

Второй шаг. Из условия вытекает, что допустимые значения а и b лежат в пределах 1 < а < 3, 1 < b < 2. Решая уравнение (2) относительно а, а уравнение (1) относительно b, будем иметь

а = √5+b²;

a

b = —— (3)

a -1

откуда

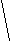a²

a = 5 + —— (4)

(a – 1)²

Возводя обе части уравнения (4) в квадрат и группируя члены, содержащие а², получим

a³ (а – 2)

= 5 (5)

(a – 1)²

Обозначим левую часть формулы (5) через f(а). Эта функция имеет корни а = 0 (кратный корень) и а = 2 и бесконечный разрыв в точке а = 1. Производная этой функции

2a² (а² – 3a + 3)

f ' (a) =

(a – 1)³

отрицательна при a < 1 и положительна при а > 1. Следовательно, при а > 1 f(a) монотонно возрастает, устремляясь в бесконечность с бесконечным ростом а. Поскольку f(2) = 0, a f(3) = 6,75, то искомый корень a₀ уравнения (5) существует, единствен и лежит в пределах 2 < a₀ < 3. График функции f(a) схематично изображен на рис. 2.

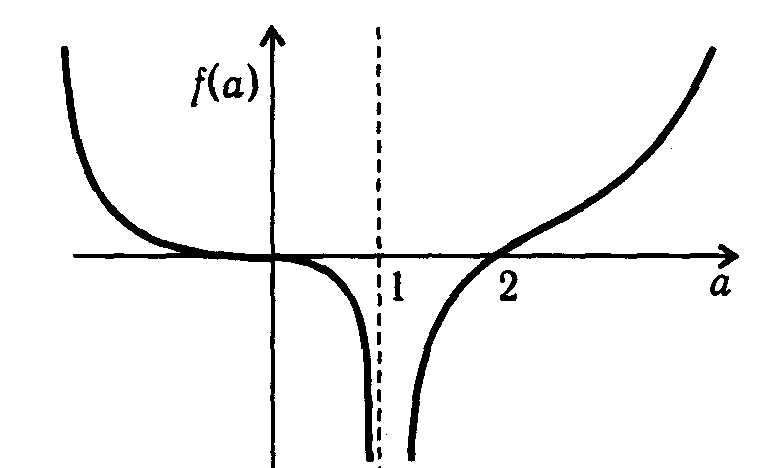
Рис. 2

Третий шаг. Используя систему (3), организуем итерационный процесс, полагая a _n₊₁ = √5 + b_n²; (6)

a_n

b_n = (7)

a_n – 1

И

терационный процесс заключается в том, что по n-му приближению a_n вычисляется соответствующее ему значение b_n, а с его помощью получается следующее приближение а_n₊₁ и т. д. Можно записать рекуррентную систему (6)—(7) в виде одного уравнения

a_n²

a_n₊₁= 5 + —— (8)

(a_n– 1)²

Переходя к пределу в (8), получим (4), поэтому предел последовательности (а_n), если он существует, равен искомому значению a₀. Остается лишь доказать сходимость данного итерационного процесса.

Заметим, что, согласно (7), все b_i > 1, поэтому из (6) вытекает, что все члены

п

оследовательности (а_n) больше, чем √6.

Теперь оценим разность |а_n²₊₁ - а₀²|. Воспользуемся тем, что а_n₊₁ удовлетворяет соотношению (8), а а₀ есть корень уравнения (4):

а_n² a₀² |а_n - а₀| (2а_n а₀- а_n- а₀)

|

а_n²₊₁ - а₀²| = - = .

(а_n - 1)² (а₀– 1)² (а_n - 1)² (а₀– 1)²

Отсюда получим |а_n - а₀| (2а_n а₀- а_n- а₀)

|

а_n+1 - а₀| < |а_n - а₀| x ,

(а_n+₁ + a₀) (а_n– 1)²(a₀ – 1)²

или

|а_n₊₁ - а₀| < k |а_n - а₀| ,

где

2а_n а₀- а_n- а₀

k =

(а_n₊₁ + a₀) (а_n– 1)²(a₀ – 1)²

Поскольку все а_i (включая, разумеется, искомое a₀) лежат между √6 и 3, то

будем иметь

18 - 2√6

k =

2(а_n₊₁ + a₀) (а_n– 1)²(a₀ – 1)²

Т

еперь, каково бы ни было а₁€ √ 6, 3), для любого п

|а_n₊₁ - а₀| < kⁿ |а₁ - а₀| (9)

(это неравенство можно строго доказать методом математической индукции). Поскольку k < 1, то правая часть (9) стремится к нулю с бесконечным ростом п, поэтому предел последовательности (а_n) существует и равен a₀.

a₀

З

аметим, что поскольку a₀ < 3, то > 1,5

a₀ – 1

оэтому из (4) следует, что a₀ > √7,25. Этот факт позволяет при необходимости существенно улучшить оценку для k. Кроме того, значение √7,25 ≈ 2,693 можно считать хорошим начальным приближением для а₀.

Сейчас уже можно было бы произвести необходимые вычисления и получить а₀, а с ним и искомое значение х. Однако исследование задачи часто бывает важнее и интереснее получения ответа, поэтому мы делаем четвертый шаг.

Четвертый шаг. Обозначим правую часть равенства (4) через g(а). Найдем производную этой функции:

1 a

g(a) = - ∙ < 0

g(a) (a – 1)³

при а > 1. Следовательно, функция g(а) монотонно убывает при а > 1. Поскольку

g

(2) = 3 > 2, g(3) = √7,25 < 3, то уравнение а = g(а), эквивалентное (4), при а > 1 имеет единственный корень, лежащий между 2 и 3.

Смысл итерационного процесса, задаваемого формулой (8), графически изображен на рис. 3. Вначале выбирается исходное приближение а₁ и вычисляется g(a₁) (стрелка 1). Затем найденное значение g(а₁) принимается за следующее приближение а₂ (стрелка 2). Затем вычисляется g(а₂) (стрелка 3) и принимается за a₃ и т.д.

Можно доказать, что при 2 < а < 3 g'(а) > -1, т.е. функция у = g(а) убывает медленнее, чем растет функция у = а. Это обстоятельство существенно для сходимости

Рис. 3

рассматриваемого итерационного процесса.

Рекуррентные соотношения (6) и (7) показывают, что а_n₊₁ есть возрастающая функция b_п, а b_п, напротив, есть убывающая функция а_n, поэтому любые два соседних члена последовательности (а_n) лежат по разные стороны от ее предела a₀. Как показывает неравенство (9), члены этой последовательности приближаются к ее пределу со скоростью не меньшей, чем скорость убывания геометрической прогрессии.

Пятый шаг. Используя рекуррентные формулы (6) и (7), можно найти значение а₀ с любой требуемой точностью. С точностью до десятитысячных долей a₀= 2,73572, соответствующее ему значение

a₀

b

₀ = = 1,57613,

a₀-1

а ответ задачи х= 1,23119 (как всегда в подобной записи, ошибка результата не превосходит половины последнего записанного разряда).

Нам не известно, каким способом решали эту задачу в Древнем Египте. Возможно, применялся итерационный процесс, аналогичный описанному. Во всяком случае, для того чтобы воспользоваться методом итераций, в то время не было необходимости доказывать сходимость итерационного процесса, ибо правомерность осуществляемых вычислений не подлежала сомнению, если в итоге получался осмысленный и приемлемый по точности результат.

Разумеется, сегодняшним школьникам легче воспринять алгоритм решения данной задачи, поскольку к их услугам аппарат математического анализа, позволяющий строго доказать законность производимых расчетов и осмыслить их результаты.

На стене древнеегипетского храма под текстом данной задачи было обнаружено пояснение, из которого следует, что эта задача служила испытанием для желающих стать жрецами бога Ра. Вошедший в комнату для решения этой задачи оказывался отрезан от внешнего мира, так что решивший ее становился жрецом, а не решивший умирал голодной смертью. Предупреждение под текстом задачи заканчивалось словами:

"Через стену колодца Лотоса прошли многие, но мало кто стал жрецом бога Ра. Думай. Цени свою жизнь. Так советуют тебе жрецы бога Ра".

«Загадка из древнего Египта»

Решение задачи в статье Р.М. Нижегородцева приводит к уравнению четвертой степени:

а⁴- 2а³- 5а²+ 10а – 5 = 0. (*)

Заметим, что если это уравнение имеет рациональный корень, то он целый и является делителем числа 5. Так как 1 не является корнем уравнения, то на отрезке [1; 3] уравнение (*) не имеет рациональных корней. Именно это обстоятельство заставляет искать нетрадиционные способы решения уравнения, один из которых приведен в статье Р.М. Нижегородцева.

Обратим внимание на возможность решения той же задачи с помощью несложной программы, принцип работы которой описан в нашей статье "Задачи о делении доходов и метод половинного деления отрезков" (Математика в школе. 1996. № 3). Чтобы воспользоваться этим вторым способом решения, к уравнению (*) можно прийти с меньшим числом обозначений.

Для решения задачи рассмотрим функцию

f(а) = а⁴ - 2а³ - 5а² + 10а - 5

на отрезке [1;3]. Эта функция непрерывна, как всякий многочлен, на концах отрезка функция принимает значения разных знаков, но она не является монотонной. Поэтому для доказательства единственности корня уравнения требуется дополнительное исследование. Уточним характер поведения функции на отрезке [1; 3].

f '(а) = 4а³ - 6а² - 10а + 10, f ' (1) = - 2 < 0;

f '' (а) = 12а²- 12а - 10.

3 + √39

На отрезке [1; 3] имеется одна точка а₁ = ≈ 1,54,

6

в которой f "(а) = 0. При а < a₁ f "(а) < 0, график имеет выпуклость вверх, при а > а₁ f "(а) > 0, график имеет выпуклость вниз (см. рис.). Следовательно, на отрезке [1; 3] существует только одна точка а, в которой f(а) = 0. Единственность корня уравнения на отрезке [1; 3] установлена. Найдем приближенное значение корня методом половинного деления отрезка.

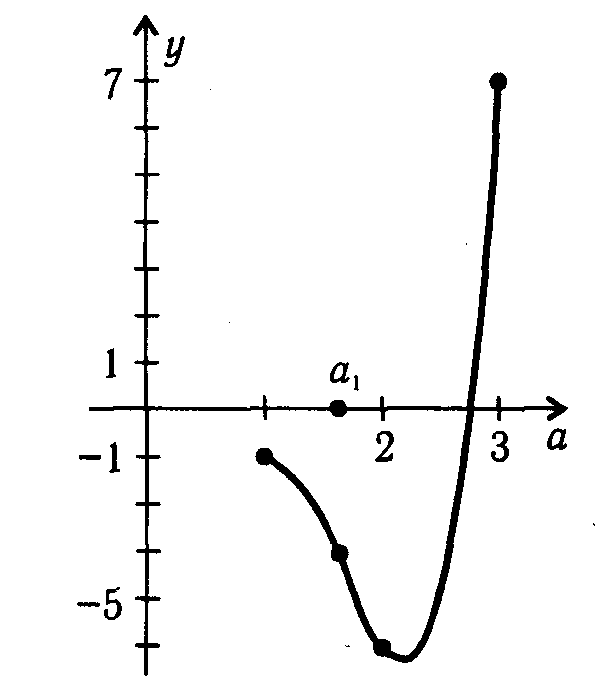
Рис.

Внесем исправления в программу 1 из упомянутой выше статьи и получим программу для поиска корня уравнения.

10 К = 1: N = 3

20 А = (К+N) / 2

30 IF N - К < .000002 ТНЕN GОТО 70

40 F = А 4 – 2 * А 3 - 5*А2 + 10*А - 5

50 IF Р < 0 ТНЕN К = А: GОТО 20

60 N = А: GОТО 20

70 Х = SQR(9 - А2)

80 РRINТ "ответ: а = " ; А

90 РRINT х = " ; Х

100 ЕND

Координаты концов первоначального отрезка обозначены здесь К и N. Проверка условия F = 0 пропущена, так как во внутренней рациональной точке отрезка это условие не выполняется (уравнение не имеет рациональных корней). В строке 70 вычисляется ответ по формуле х = √9 - а². После запуска программы получим ответ:

а = 2.735723

х = 1.231187.

Последний результат подтверждает ответ, полученный Р. М. Нижегородцевым: х = 1,231119.

Заметим, что способ, которым могли бы воспользоваться египетские жрецы при отборе достойных кандидатов в жрецы, нам не известен. Можно только предполагать, что он был все же геометрическим, так как сколько-нибудь развитой техники решения уравнений тогда еще не было. Может быть наши ученики найдут его?

Blog

Содержание