Применение метода сопряженных градиентов для решения задачи сейсмической томографии на модельных примерах
| Вид материала | Документы |
- Решение уравнения теплопроводности Постановка задачи, 83.2kb.
- Isbn 978-5-7262-1226 нейроинформатика 2010, 124.83kb.
- Задачи Способы решения Нахождение оптимального положения электродов на поверхности, 27.21kb.
- Точные решения некоторых нелинейных эволюционных уравнений, встречающихся при описании, 28.05kb.
- Некорректные задачи, 36.86kb.
- Ю. В. Новоселов Вработе описывается применение метода решения поставленной задачи, 122.75kb.
- Секция “Краевые задачи механики сплошной среды, численные и численно-аналитические, 67.85kb.
- Выносимых на итоговый государственный экзамен, 118.84kb.
- Основы кейс-метода когда возник кейс-метод и как развивался, 1526.98kb.
- 2 Выбор метода решения задачи, 55.54kb.
Применение метода сопряженных градиентов для решения задачи сейсмической томографии на модельных примерах
Shishkin A.A.
Введение. Предлагаемая работа посвящена новому и быстро развивающемуся направлению в сейсмике, получившему название сейсмическая томография. Под этим термином по аналогии с медицинской (рентгеновской) томографией подразумевается методика восстановления структуры определенных областей геологической среды, исходя из наблюдаемых значений параметров облучающего ее волнового сейсмического поля.
В силу ряда физических причин и условий эксперимента сейсмическая томография по достоверности и разрешающей способности получаемых изображений заметно уступает рентгеновской; тем не менее достигнутые с ее помощью геофизические результаты являются интересными и обнадеживающими.
1. Описание геометрии наблюдения
Чтобы сделать нашу работу более наглядной, выполним небольшие геометрические построения, иллюстрирующие геометрию наблюдений. Рассмотрим рисунок 1, на котором представлена наша модель.
Рисунок 1 – Модель однородного поля скоростей с высокоскоростной аномалией в центре.
На приведенном рисунке 1 есть некоторая исследуемая область, которую мы разбиваем на 8 ячеек по оси y и 12 ячеек по оси x, т.е. в совокупности 96 ячеек. Размеры ячеек и скорость сейсмических волн мы задаем. В нашем примере скорость во всех ячейках постоянна и равна
, и только в нескольких ячейках в центре 
.В верхней части рисунка 1 расположены 7 источников сейсмических волн, которые могут быть вызваны взрывом или вибросейсмическим источником. В нижней части рисунка 1 расположены 14 приемников. Комбинация из 7 источников и 14 приемников дает в сумме 98 лучей, по которым сейсмические волны распространяются от источников к приемникам. Для упрощения будем считать, что лучи у нас прямолинейны, т.е. мы пренебрегаем преломлением на границе ячеек, в которых скорость равна
, и ячеек, в которых скорость равна 
.Для заданной скоростной функции
и заданной геометрии наблюдений (положение источников, приемников и ячеек) были рассчитаны модельные времена пробега сейсмических волн по прямолинейным лучам, т.е. мы решили прямую задачу.2. Модель связи поля сейсмических скоростей и времен пробега сейсмических волн
Рассмотрим модель (2.1) связи между двумя векторными величинами x и y.
(2.1)В контексте (сейсмической) томографии она может быть проинтерпретирована следующим образом:
- А - матрица размерности
, каждый элемент которой 
обозначает длину сегмента k-го (сейсмического) луча в j-й клетке разбиения пространства;
- x –вектор размерности
, координата которого 
обозначает медленность (величину, обратную скорости) в ячейке j
- y –вектор размерности
, координата которого 
обозначает полное время пробега сейсмической волны по k-му лучу.
Так как в данной работе не было возможности провести реальный эксперимент и измерить экспериментальные времена пробега сейсмических волн, в нашей работе были использованы модельные времена пробега сейсмических волн. Модельные времена пробега были получены путем решения прямой задачи, используя вышеупомянутую модель.
3. Использование математического аппарата сейсмической томографии
Следующий раздел посвящен обратной задаче, в которой связь данных наблюдений (времена пробега)
и параметров среды описывается линейным интегральным уравнением. Например, скорость распространения сейсмических волн может быть связана с наблюдаемыми временами пробега волн криволинейным интегралом (3.1) по лучевой траектории 
.
(3.1)Сейсмическая томография-это обращение таких интегральных соотношений с целью получения оценок поля скоростей
внутри некоторой области пространства, пересеченной лучами. Криволинейный интеграл можно аппроксимировать суммой
(3.2)где
-расстояние, пробегаемое лучом в пределах j-й ячейки;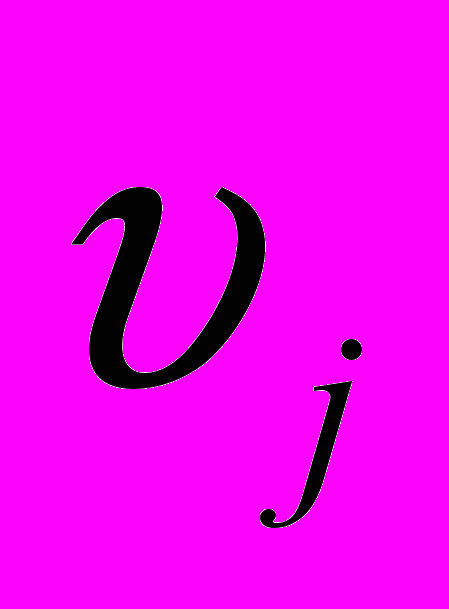 
-скорость распространения сейсмических волн в j-и ячейке. Сумма берется по всем ячейкам, которые пересекает k-я лучевая траектория. Система соответствует матричному уравнению 
, где 
-матрица размерности 
, элементами которой являются значения . Здесь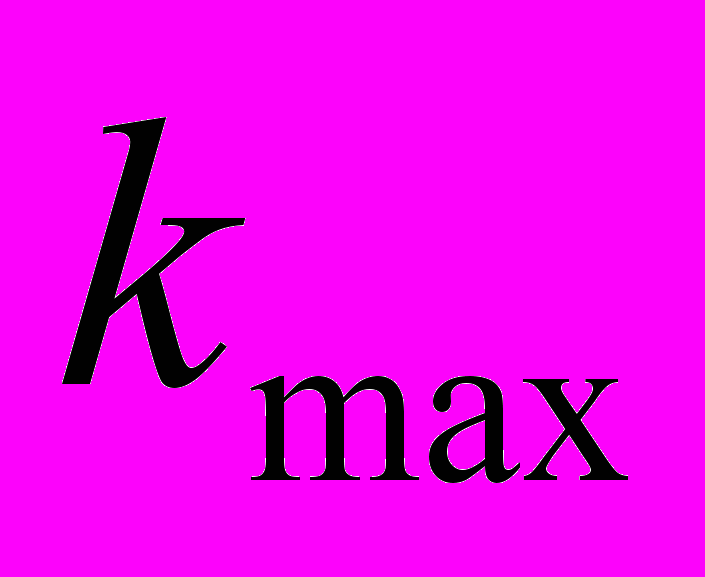 
- общее число траекторий, пересекающих исследуемую область, и 
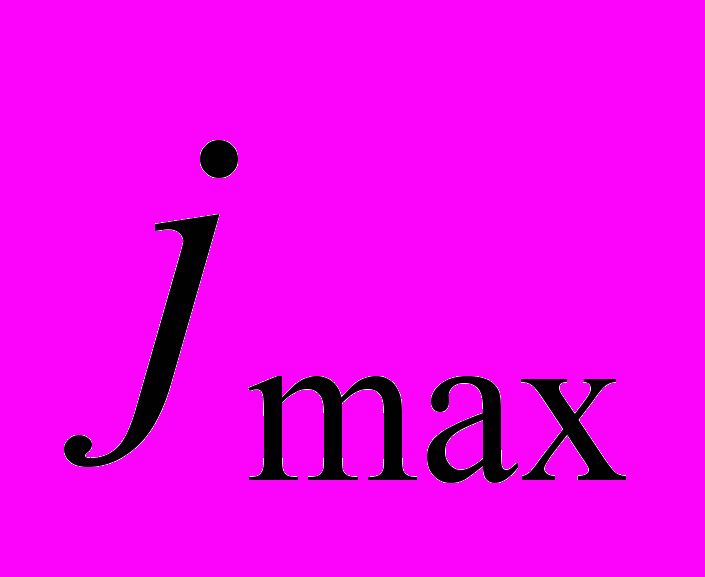- общее количество ячеек. Заметим, что - относительно разреженная матрица, поскольку каждый луч пересекает, как правило, лишь небольшую часть ячеек в пределах исследуемой области.Чтобы сформировать матрицу
, нужно знать, как идет луч от источника к приемнику. На практике можно применить следующий способ. Лучи трассируются в соответствии с заданной моделью, что позволяет сформировать . Система линейных уравнений может быть решена методом сопряженных градиентов. 4. Метод сопряженных градиентов
Приведем без вывода алгоритм метода сопряженных градиентов, позволяющий решать системы линейных алгебраических уравнений таким способом.
1. Задать
(начальный вектор) и число 
(уровень допустимых погрешностей).2. Вычислить вектор
(невязка начального приближения).3. Положить
(номер итерации).4. Вычислить скаляр
.5. Вычислить вектор
(очередное приближение).6. Вычислить
(невязка (k+1)— го приближения). Полагая 
, видим, что в силу 5,
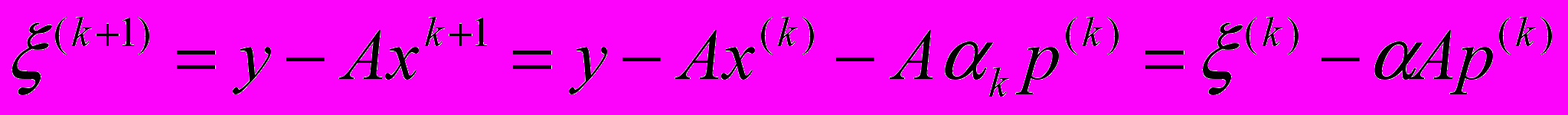.Такое выражение невязки позволяет обходиться без вычисления вектора
7. Проверить выполнение неравенства
; если «да», остановить работу алгоритма и вывести результаты.8. Вычислить скаляр
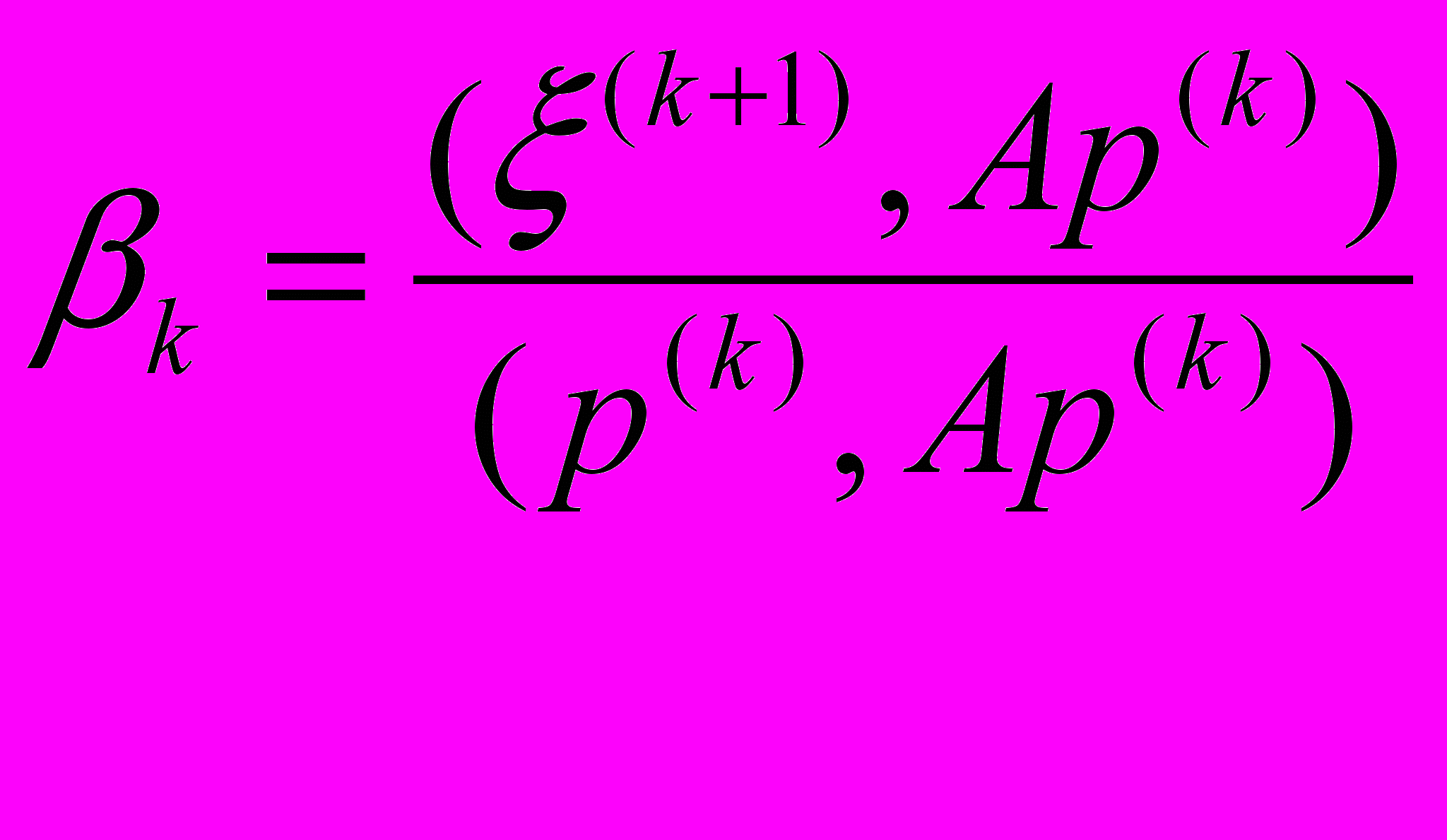.9. Вычислить вектор
(новое направление минимизации).10. Положить k := k + 1 и вернуться к шагу 4.
Рисунок 2а - изображает модельную функцию скоростей
Рисунок 2б - изображает модельную функцию скоростей
Рисунок 3а – Реконструкция поля скоростей
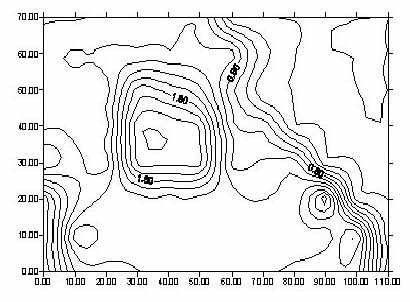
Рисунок 3б - Реконструкция поля скоростей
На рисунках 2а, 2б мы изображаем модельную функцию скоростей
, для которой, решая прямую задачу, формируем модельные времена пробега 
по прямолинейным траекториям. Затем эти модельные времена были обращены и была получена оценка поля скоростей 
рисунки 3а, 3б.И так с помощью метода сопряженных градиентов была решена система линейных уравнений относительно неизвестного вектора скоростей
. Результаты решения приводиться на рисунках 3а, 3б.Приведенный пример томографической реконструкции основан на модельных данных
. Он дает некоторое представление о возможностях метода сопряженных градиентов для картирования скоростных аномалий .Реконструкция
на рисунках 3а, 3б несовершенна по двум причинам. Первая - не была учтена кривизна лучей, и вторая - недостаточное полное покрытие области лучами, что ведет к некоторому ухудшению разрешающей способности. Тем не менее основная скоростная аномалия в центре успешна восстановлена.Работа выполнена при поддержке гранта - Президента РФ МД-1544.2009.1
Литература:
- Сейсмическая томография / Г. Нолет, К. Чепмен. – Москва: “МИР”, 1990. – 416 с.
- Обработка сейсмических данных / Л. Хаттон, М. Уэрдингтон, Дж. Мейкин. – Москва: “МИР”, 1989. – 216 с.
- Сейсмическое изображение земных недр / Д.Ф. Клаербоут. – Москва: “НЕДРА”, 1989. – 407 с.
- Математические задачи компьютерной томографии / А.Н. Тихонов, В.Я. Арсенин, А.А. Тимонов. – Москва: “НАУКА”, 1987. – 160 с.
- Начала информатики / С.А. Абрамов, Е.В. Зима. – Москва: “НАУКА”, 1989. – 256 с.
- Некорректные задачи. Численные методы и приложения / А.Б. Бакушинский, А.В. Гончарский. – Изд-во Моск. ун-та, 1989. – 199 с.