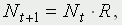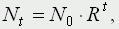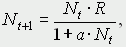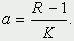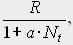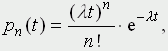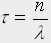Учебно-методический комплекс по дисциплине дс. В. 05 Основы компьютерного моделирования в физике ( Ч. 1 ) ( индекс по гос/наименование дисциплины
| Вид материала | Учебно-методический комплекс |
СодержаниеВычисление площадей методом Монте-Карло. Задача Бюффона. Модели случайных и хаотических блужданий 3. Имитационное моделирование. Игра "Жизнь". Динамические модели популяций. Детерминированные модели. Моделирование свободного падения тела. Модель движения тела, брошенного под углом к горизонту. Уравнения матфизики. Классификация уравнений матфизики. Моделирование процесса теплопроводности. Экология и моделирование. Модели внутривидовой конкуренции. Рис. 2. Изменение численности популяции согласно уравнению (3) при R C - численность популяции хищника и N Очередь к одному "продавцу" A записаны случайные числа - промежутки между приходами покупателей (в минутах), в колонке B Табл 1. Моделирование очереди Таким образом, при данных случайных наборах чисел в колонках A G), и продавцу - в ожидании покупателя (колонка H ... 5 6 2. ссылка скрыта Понятие случайных событий. В вероятностных моделях смена состояний моделируемой системы определяется случайными величинами. Событие называется случайным, если оно достоверно непредсказуемо. Случайность окружает наш мир и чаще всего играет отрицательную роль в нашей жизни. Однако есть обстоятельства, в которых случайность может оказаться полезной. Одним из распространенных приближенных методов решения задач вычислительной математики является случайный метод, называемый метод Монте-Карло. Сущность метода заключается в том, что для решения какой-либо математической задачи, связанной с вычислением числа I, строится некоторая случайная величина ξ, такая, что математическое ожидание этой случайной величины E(ξ) является значением искомого решения. Проведя серию вычислительных экспериментов со случайной величиной ξ, мы можем найти приближенное решение как среднее значение результатов эксперимента. Вычисление площадей методом Монте-Карло. С помощью этого метода можно найти площадь любой фигуры G, которая имеет сложный контур, который сложно описать аналитически или сложно проинтегрировать. Нужно вписать эту фигуру в фигуру известной площади, скажем в прямоугольник со сторонами a b и бросать точку на эту фигуру. Вероятность попадания точки в G будет равна отношению площадей. Задача Бюффона. Также с помощью случайного метода можно вычислить число π. Для этого необходимо решить задачу Бюффона. Французский математик Бюффон (XYIII в.) определил, что если на поле, разграфленное параллельными прямыми, расстояние между которыми L, бросается наугад игла длиной l, то вероятность того, что игла пересечет хотя бы одну прямую, определяется формулой: 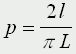 Эта задача дала способ вычисления числа π. Действительно, если L=2l, то 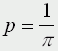 Таким образом, автором было вычислено 200 знаков после запятой числа π. Точность получаемого решения зависит от количества проведенных экспериментов. Задачу Бюффона можно легко смоделировать на компьютере Известно, что P=N1/N , где N - число бросаний, N1 - число пересечений иглы с линиями. Как определить, пересекла игла прямую или нет? Положение иглы можно однозначно определить заданием координаты центра иглы y_0 из [-l/2,l/2] и угла α, задаваемых случайным образом Тогда координаты концов иглы определяются по следующим формулам: 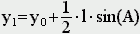 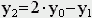 Условие пересечения прямой - y1*y2<0 Модели случайных и хаотических блужданий. На случайности основана так называемая "модель пьяницы", которая используется для моделирования всевозможных хаотических движений частиц скажем движений молекул каких-либо газов или жидкостей, с помощью этой модели моделируются многие химические и физические процессы, проходящие в дискретных средах - в газах и жидкостях - явления диффузии, всевозможные потоки частиц, ветер, водопад, взрыв и т.д. Есть точка на прямой, имеющая начальную координату x0, которая движется вправо или влево в зависимости от случайной величины r из интервала [0,1] если r>0,5, то точка делает шаг вправо x1=х0+h, в противном случае x1=x0-h. Шаг может быть как постоянный, так и переменный. Значение шага в свою очередь может быть случайное число из интервала [0,hmax]. Точка может двигаться по плоскости, может быть n точек - получается модель броуновского движения. Можно ввести различные скорости движения частиц, можно изменять условие, скажем если ri>0,8, то точка делает шаг вправо x1=х0+h, в противном случае x1=x0-h. - получим модель поступательного движения частиц вправо - стая комаров, подхваченных ветром. Если первоначально все частицы сконцентрировать в одной точке, а потом пронаблюдать их распространение - то это будет модель взрыва. Если провести вертикальную черту - перегородку, и частицы по разную строну перегородки закрасить разным цветом - получим модель диффузии - смешивания различных газов или жидкостей и т.д. В модели пьяницы не предусматривается столкновение частиц. Если случайным образом задать первоначальное положение частиц, направление их движения и скорость и определить, что далее частица будет двигаться равномерно и прямолинейно до столкновения с другой частицей, а в случае столкновения произойдет зеркальное упругое отражение, то получим модель движения частиц, называемую моделью бильярдного шара. Эта модель описывает поведение идеального газа. С помощью этой модельки можно посчитать, допустим, давление газа на стенки сосуда - ограничить частицы прямоугольником (количество частиц установить пропорциональным плотности газа), предусмотреть зеркальное отражение частиц от стенок и посчитать число ударов в стенки сосуда. Давление газа будет пропорционально числу ударов о стенки. 3. ссылка скрыта Применение. Модели подобного типа называют также имитационными моделями. Имитационное моделирование широко применяется в биологии. Рассмотрим одну из самых распространенных имитационных моделей, предложенную Джоном Канвеем - игра "Жизнь" Игра "Жизнь". Для построения алгоритма игры рассмотрим квадратное поле из n+1 столбцов и строк с обычной нумерацией от 0 до n. Крайние граничные столбцы и строки для удобства определим как "мертвую зону", они играют лишь вспомогательную роль. Для любой внутренней клетки поля с координатами (i,j) можно определить 8 соседей. Примем, что если клетка живая, то ее закрашиваем, если клетка мертвая, то она пустая. Зададим правила игры. Если клетка (i,j) живая и в окружении более трех живых клеток, то она погибает (от перенаселения). Живая клетка также погибает, если в окружении менее двух живых клеток (от одиночества). Мертвая клетка оживает, если вокруг нее имеется три живые клетки. Начальное количество живых клеток и расположение их на поле определяется либо случайным образом, либо мы можем задать нужное нам количество живых клеток и определить их расположение определенным образом и смотреть, как они будут себя вести. Есть устойчивые структуры - пропеллер - три клетки в ряд, есть стабильные структуры - квадрат с просветом внутри, есть структуры, которые повторяют себя через определенное количество циклов и т.д. Если располагать клетки случайным образом, то с помощью игры жизнь можно построить модель внутривидовой конкуренции (трава - зайцы), межвидовой конкуренции (зайцы - лисы), модель распространения инфекции и т.д. Динамические модели популяций. Мы говорили, что при моделировании биологических процессов используется метод индукции - от частного к общему, от гипотез. Именно таким образом строятся в биологии так называемые динамические модели популяций. Популяция в биологии - это совокупность особей одного вида, существующих в одно и занимающих определенную территорию. Взаимодействие особей внутри популяции определяется внутривидовой конкуренцией, взаимодействие между популяциями - межвидовой конкуренцией. Человечество как биологический вид можно также рассматривать как популяцию, причем популяцию без внутривидовой конкуренции Рассмотрим сначала простейшую модель роста населения. Ni+1=Ni+aNi-bNi Модель численности популяции с учетом внутривидовой конкуренции Ni+1=(Ni+aNi-bNi)/(1+cNi) Знаменатель отражает наличие внутривидовой конкуренции, делающей скорость роста тем меньше, чем больше численность популяции, с - параметр, характеризующий интенсивность внутривидовой конкуренции. 4. ссылка скрыта Детерминированные модели. Физика - это наука, в которой математическое моделирование является весьма важным методом исследования. Исторически так сложилось что моделирование начиналось именно с построения моделей физических процессов. Наряду с традиционным делением физики на экспериментальную и теоретическую, сейчас выделяется третий фундаментальный раздел - вычислительная физика. При максимальном проникновении в физику математических методов, порой доходящем до фактического сращивания этих наук (есть такая известная дисциплина - уравнения математической физики), реальные возможности решения математических задач традиционными аналитическими методами очень ограниченны. Во-первых, реальные физические процессы только в первом, очень грубом приближении можно описать простыми линейными уравнениями реально же, как правило, приходится иметь дело с нелинейными и дифференциальными уравнениями, во-вторых, при моделировании физических процессов необходимо учитывать совместное движение или влияние друг на друга многих тел, что приводит к необходимости решения систем уравнений высокого порядка (N=100). Такие задачи эффективнее не решаются не аналитическими методами, а численными методами, т.е. используется аппарат не чистой математики, скажем алгебры, а аппарат вычислительной математики. При построении моделей используются два принципа: дедукции (от общего к частному) и индукции (от частного к общему). В зависимости от способа построения различают дедуктивные или детерминированные и индуктивные (недетерминированные) модели. Построение детерминированных моделей основано на использовании фундаментальных законов - именно такие модели строятся при моделировании физических процессов, если же фундаментальные законы, управляющие моделируемым явлением неизвестны, как это часто бывает при моделировании в биологии, социологии, экономике - то используются гипотезы. Рассмотрим две простые детерминированные модели, модели двух простых физических явлений. Моделирование свободного падения тела. Примем, что тело массой m падает с высоты h с начальной скоростью V0. На тело действует сила тяжести F=mg, направленная вниз и сила сопротивления среды Fc= k1v+k2v2. Падение тела описывается 2 законом Ньютона: ma=mg-Fc в одномерной системе координат с осью х, направленной вниз, и с началом в точке начального падения тела. Сила сопротивления среды Fc= k1v+k2v2 зависит от скорости тела и его сечения, k1 - коэффициент Стокса, зависит от вязкости среды, большая величина; k2 - коэффициент лобового сопротивления, зависит от площади сечения тела, маленькая величина. Если скорость не очень большая, то доминирует линейная составляющая, квадратичной же составляющей можно пренебречь, при более высоких скоростях напротив, резко возрастает квадратичная составляющая, а линейной составляющей можно пренебречь. Что подразумевается под моделированием движения какого-либо тела? Это означает, что в каждый момент времени ti мы должны знать положение тела в пространстве или пройденный им путь x=x(t), его скорость v=v(t) и ускорение a=a(t), которые будут являться функциями от времени. В начальный момент времени t0=0, x0=0, v0=0, a0=g Для построения расчетной модели предположим, что в течение малого промежутка времени Δt=τ движение равноускоренно, тогда можно использовать известные законы прямолинейного равноускоренного движения. x=x0+v0τ +aτ2/2 v=v0+aτ a=const
Осталось определить задачи исследования и соответственно определить параметры модели для этих целей. Задача о безопасности парашютиста. Пусть парашютист прыгает с высоты h м. Определить необходимый радиус парашюта, другими словами, нам нужно подобрать коэффициент сопротивления k2, при котором имеем безопасное приземление. Кстати, оценить скорость безопасного приземления можно из следующих соображений. С какой высоты прыжок человека на землю безопасен? С первого этажа даже ребенку не страшно, а со второго надо постараться удачно приземлиться. Значит, можно взять среднюю высоту между первым и вторым этажом, скажем, 3 метра. Тогда при свободном падении тела за время t=v2h/g=0.8 сек величина скорости приземления Vp=g*t=10*0.8=8 (м/сек.) Другими словами, скорость безопасного приземления - 8-10 м/с. Таким образом, параметрами модели будут являться: статические параметры модели: h - высота, с которой падает тело; Vн - начальная скорость падения, в частности, Vн=0; m - масса тела; g - ускорение свободного падения; динамические параметры для моделирования: τ - шаг по времени, k - коэффициент сопротивления. Быстрее всего протекает процесс без сопротивления (нижняя оценка), и наоборот, самый медленный процесс, когда ускорение равно нулю, т.е. движение установившееся и происходит с постоянной скоростью, например Vp. В качестве теста зададим k=0, тогда расчеты должны совпадать с формулами закона равноускоренного движения при a=g. Если k=mg, то практически мгновенно движение устанавливается (а=0) и тело либо зависает (V=0), либо медленно опускается с постоянной скоростью. Подобное проверочное тестирование в случае удачи дает основания к уверенной работе с моделью. Теперь можно проводить эксперименты с моделью. Попытаемся подобрать k таким образом, чтобы скорость установления была близка к значению 10 м/с. Модель движения тела, брошенного под углом к горизонту. Тело бросают с высоты h под углом α к горизонту. Модель движения тела, брошенного под углом к горизонту строиться аналогично предыдущей модели, только вектора скорости и ускорения необходимо будет разложить по двум осям и учитывать составляющие вектора скорости v по x и по y vx vy и вектора ускорения a по x и по y ax ay. Сила сопротивления будет направлена обратно движению, сила тяжести - по-прежнему вниз. X: max=-k1vx-k2vx2 Y: may=-(mg-k1vy-k2vy2) Начальные условия в этой модели:
Расчетные формулы: x=x+vxτ+axτ2/2 y=y+vyτ+ayτ2/2 vx=vx+axτ vy=vy+ayτ ax=-(k1vx- k2vx2/m ay=(mg-k1vy- k2vy2)/m Условие окончания процесса y=0. Параметры модели: h - начальная высота бросания, в частности, h=0; v0 - начальная скорость бросания тела; α - угол бросания; m - масса тела; k1 - коэффициент сопротивления среды; k2 - коэффициент лобового сопротивления; g - ускорение свободного падения; τ - шаг по времени. Можно ставить следующие задачи: задача о подводной охоте (под каким углом следует выстрелить охотнику, если акула находится от него на расстоянии l метров?), задача о теннисном шарике (какой должна быть высота крытого корта, если угол α, под которым теннесист отправляет шарик заключен в диапазоне от α1 до α2? Если начальная скорость теннисного шарика v0 (которая зависит от силы ударов по нему) заключена в диапазоне от v01 до v02?) Тесты могут быть следующие:
Движение под углом к горизонту без сопротивления: h=0; A=45; u0>0; k=0; g=9,8 м/с Уравнения матфизики. Для более сложных физических явлений, таких как процессы колебания, волновые процессы, процессы теплопроводности не всегда удается построить такие простенькие модельки. Реально эти процессы описываются дифференциальными уравнениями 2 порядка, уравнениями в частных производных, называемых уравнениями матфизики. Напомню, что дифференциальным уравнением называется уравнение, куда входит искомая функция со своими производными F(x,y(x),y'(x),y''(x):y(n)(x))=0 Наивысший порядок производной, входящей в уравнение, называется порядком дифференциального уравнения. Решением дифура является не число, а функция, x называется независимой переменной. Если искомая функция является функцией одной переменной, то дифуравнение называется обыкновенным дифуравнением, если искомая функция является функцией нескольких переменных, то дифуравнение называется уравнением в частных производных. В случае двух независимых переменных x и y уравнения матфизики, которые являются как правило уравнениями первого и второго порядков, линейными относительно входящих в них производных можно записать в виде 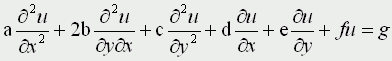 В случае двух независимых переменных x и y уравнения матфизики, которые являются как правило уравнениями первого и второго порядков, линейными относительно входящих в них производных можно записать в виде Обычно одна из переменных - это время t 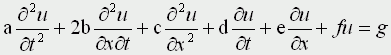 Классификация уравнений матфизики. Различают типы уравнений в зависимости от соотношения между коэффициентами. 1) При a=b=c=f=0, d не 0, e не 0 получаем уравнение первого порядка вида 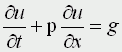 называемое уравнением переноса. Такие уравнения описывают процессы переноса частиц в различных средах, распространение возмущений и т.д. Искомая функция u=u(t,x) зависит от времени и от пространственной переменной, коэффициент p характеризует скорость переноса. 2) Если хотя бы один из коэффициентов a,b,c будет отличен от нуля, то уравнение будет иметь второй порядок и в зависимости от знака дискриминанта D=b2-4ac Будет принадлежать к одному из трех типов D>0 - гиперболическое, D=0 - параболическое, D<0 - эллиптическое. А) Гиперболическое уравнение 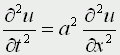 Называется волновым, оно описывает различные виды колебаний. Если в уравнение входит одна пространственная переменная, то оно описывает продольные колебания стержня, а также поперечные колебания струны. В этом случае a2=T/ρ, где T - это натяжение струны, а ρ - ее линейная плотность. Двухмерное волновое уравнение используется для описания колебаний тонкой пластины (мембраны) 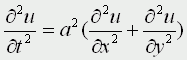 Трехмерное волновое уравнение 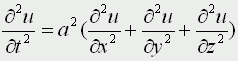 Описывает распространение волн в пространстве (например звуковые волны в различных средах, упругие волны в сплошной среде и т.д.) Б) параболическое уравнение 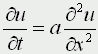 называется уравнением теплопроводности или диффузии с помощью него описываются различные процессы, связанные с передачей чего-либо: передачей тепла, передачей импульса, передачей энергии. В) Эллептическое уравнение 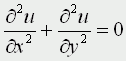 Уравнение Лапласа 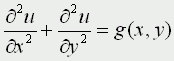 Уравнение Пуассона К уравнениям такого типа приводят стационарные, не зависящие от времени, физические задачи (исследования потенциальных течений жидкости, определение формы нагруженной мембраны и т.д.) Моделирование процесса теплопроводности. В качестве примера модели, в основе которой лежит уравнение матфизики, рассмотрим модель распространения тепла в однородном стрежне. Задача теплопроводности. Процесс теплопроводности возникает, если тело неоднородно нагрето. Простейшая для изучения теплопроводности система - линейный однородный стержень. В простой модели боковая поверхность стержня считается теплоизолированной, т.е. через нее нет обмена теплом с окружающей средой. Обозначим температуру стержня в точке с координатой х в момент времени t через u(x,t). Уравнение теплопроводности имеет вид 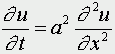 , ,где а - коэффициент температуропроводности, зависящий в первую очередь от вещества, из которого сделан стержень. Уравнение теплопроводности сопровождается начальными и краевыми условиями, делающими постановку задачи физически однозначной Напомню, что если для дифуравнения заданы начальные условия (условия в начальный момент времени), то такая задача называется задачей Коши, если же заданы краевые условия (на границах исследуемой области), то такая задача называется краевой задачей, если заданы и начальные и граничные условия, то мы имеем смешанную краевую задачу. Начальное условие задает распределение температуры в стержне в начальный момент времени (считаем его равным нулю): u(x,0) = φ(x) Краевые условия (их должно быть в данном случае два) указывают, в простейшем варианте, какая температура поддерживается на концах стержня: u(0,t)=ψ0(t), u(l,t)=ψl(t) Заметим, что начальные и граничные условия должны быть согласованы, т.е. u(0,0) = φ(0)=ψ0(0) u(l,0) = φ(l)=ψl(0) Моделирование процесса теплопроводности связано с дискретизацией как временного изменения температуры, так и пространственного. Введем равномерную прямоугольную сетку с помощью координатных линий xi=ih, i=0,1,....n, tj=jτ, j=0,1,....m, где h - это шаг по пространству, по координате х, а τ - шаг по времени. Значения функции в узлах сетки обозначим uij=u(xi,tj). Входящие в уравнение производные заменим их конечно-разностными аппроксимациями 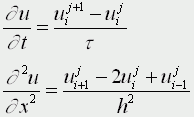 получим 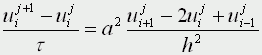 или 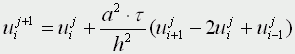 , ,где i=1,2,:.n-1, j=0,1,:.m-1. Получилась явная разностная схема, удобная в применении, но устойчивая лишь при выполнении условия 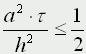 Это следует учитывать, выбирая шаги по времени и пространству. Совокупность узлов в фиксированный момент времени называется слоем. Построенная схема позволяет нам находить значение функции температур на j+1 слое через значения на j слое. Для начало счета при j=0 необходимо знать значения функции температур на нулевом слое. Они нам известны из начальных условий. Если использовать другие конечно разностные соотношения для аппроксимации производных, 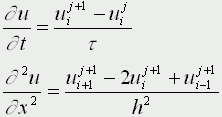 то получим существенно более устойчивую неявную схему 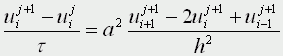 или 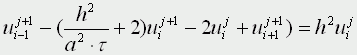 В отличие от явной схемы каждое разностное уравнение второй схемы содержит на каждом новом слое три неизвестные значения, которые невозможно определить сразу же, как мы поступали в явной схеме. При этом вторая разностная схема состоит из линейных трех точечных уравнений, т.е. каждое уравнение содержит неизвестную функцию в трех точках нового слоя. Такие системы линейных уравнений, системы с трехдиагональной матрицей, могут быть легко решены методом прогонки. Таким образом, в случае неявной схемы, чтобы посчитать значения функции температур в каждый следующий момент времени, т.е., чтобы перейти на следующий слой по времени, необходимо каждый раз решать методом прогонки линейную систему. Это - система линейных алгебраических уравнений с трехдиагональной матрицей. Для ее решения наиболее эффективен метод прогонки. Так можно моделировать физические явления применяя математический аппарат во всей его мощи. Однако это довольно сложно. При моделировании явления теплопроводности можно пойти другим путем. Пусть задана квадратная пластина, на краях которой известна температура. Требуется определить температуру во внутренних точках. Если предположить, что теплоотвода внутри нет, то можно смоделировать решение путем вычисления среднего значения T=(t1+t2+t3+t4)/4. Однако это очень грубое приближение, ведь в разных точках пластины температура различна. Разобьем квадрат на четыре части и для каждого малого квадратика применим ту же процедуру: T11 = (t1 + T12 + T21 + t4)/4 T12 = (t1 + T11 + T22 + t2)/4 T21 = (t4 + T11 + T22 + t3)/4 T22 = (t2 + T21 + T12 + t3)/4 Или в другом виде 4T11 - T12 - T21 = t1 + t4 -T11 + 4T12 - T22 = t1 + t2 -T11 + 4T21 - T22 = t3 + t4 -T12 - T21 + 4T22 = t2 + t3 который представляет систему линейных уравнений относительно неизвестных T11, T 5. ссылка скрыта Экология и моделирование. Экология - одно из слов, появившихся сравнительно недавно у всех на устах и на стра-ницах газет и журналов. Еще в 60-х годах нашего столетия почти никто, кроме узких специалистов, его не знал, да и большинство из тех, кто знал, использовал в таком смысле, который вряд ли способен заинтересовать широкую общественность. А между тем, термину более 120 лет. В 1869 г. немецкий естествоиспытатель Эрнст Геккель предложил составной термин "экология" ("эко" - дом, жилище, местопребывание и "логос" - наука, знание) как название раздела биологии, ставшего самостоятельным. Классическая экология - наука о взаимодействии организмов и окружающей среды. Сегодня, говоря об экологии, чаще всего имеют в виду не классическую, а, так называемую, социальную экологию, офор-мившуюся как научное направление и направление общественно-политической деятель-ности на 100 лет позднее, и занимающуюся проблемами охраны окружающей среды, взаимодействием с ней человеческого сообщества. В данной главе мы ограничимся некоторыми классическими моделями "старой" эко-логии, что обусловлено следующими причинами. Во-первых, они достаточно просты и изучены, постановка их вполне очевидна и в познавательном плане интересна и полезна. Во-вторых, модели распространения загрязнений окружающей среды требуют использо-вания весьма сложного математического аппарата, да и сами еще не вполне устоялись. Проблемы охраны окружающей среды чрезвычайно важны, но их обсуждение выходит за пределы нашего курса. Однако, для того, чтобы дать представление о задачах, стоящих перед современными исследователями в этой области, в следующем параграфе приведено описание одной из глобальных моделей, пытающихся выяснить пути взаимодействия экосистемы планеты с индустриальной и экономической системами современного общества. Остановимся на некоторых понятиях, которые будут встречаться в этой главе. Под особью понимается отдельный индивидуум, отдельный организм. Популяция - это совокупность особей одного вида, существующих в одно и то же время и занимающих определенную территорию. И, наконец, сообщество - это совокупность совместно сосуществующих популяций. В классической экологии рассматриваются взаимодействия нескольких типов:
Математические модели в экологии используются практически с момента возникнове-ния этой науки. И, хотя поведение организмов в живой природе гораздо труднее адекватно описать средствами математики, чем самые сложные физические процессы, модели помогают установить некоторые закономерности и общие тенденции развития отдельных популяций, а также сообществ. Кажется удивительным, что люди, занимающиеся живой природой, воссоздают ее в искусственной математической форме, но есть веские причи-ны, которые стимулируют эти занятия. Вот некоторые цели создания математических моделей в классической экологии.
При построении моделей в математической экологии используется опыт математиче-ского моделирования механических и физических систем, однако с учетом специфических особенностей биологических систем:
Привлечение компьютеров существенно раздвинуло границы моделирования экологи-ческих процессов. С одной стороны, появилась возможность всесторонней реализации сложных математических моделей, не допускающих аналитического исследования, с другой - возникли принципиально новые направления, и прежде всего - имитационное моделирование. Модели внутривидовой конкуренции. Рассмотрим простейшую из указанных моделей для вида с дискретными периодами размножения, в которой численность популяции в момент времени t равна Nt и изменяет-ся во времени пропорционально величине основной чистой скорости воспроизводства R. Такими видами являются, например, большая часть растений, некоторые виды насекомых, у которых разные поколения четко разнесены во времени. Коэффициент R характеризует количество особей, которое воспроизводится в расчете на одну существующую, а также выживание уже существующих. Данная модель может быть выражена уравнением
решение которого имеет вид
где N0 - начальная численность популяции. Эта модель, однако, описывает популяцию, в которой отсутствует конкуренция и в которой R является константой; если R>1, то числен-ность популяции будет бесконечно увеличиваться. В реальности в какой-то момент начинают работать механизмы сдерживания роста популяции. В литературе приводится немало интересных примеров быстрого роста численности популяций, если бы для их размножения существовали идеальные условия. Особенно это относится к насекомым, растениям и микроорганизмам, которые могли бы покрыть земной шар толстым слоем, если им создать благоприятные условия для размножения. Но в действительности такого роста популяций, когда их численность увеличивается в геометрической прогрессии, на сколько-нибудь длительных промежутках времени не наблюдается. Следовательно, в первую очередь необходимо изменить уравнение (1) таким образом, чтобы чистая скорость воспроизводства зависела от внутривидовой конкуренции. Конкуренцию можно определить как использование некоего ресурса (пищи, воды, света, пространства) каким-либо организмом, который тем самым уменьшает доступность этого ресурса для других организмов. Если конкурирующие организмы принадлежат к одному виду, то взаимоотношения между ними называют внутривидовой конкуренцией; если же они относятся к разным видам, то их взаимоотношения называют межвидовой конкуренцией. 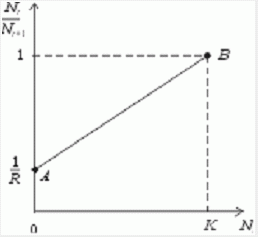 Рис. 1. К вопросу об ограничении скорости роста популяции На рис. 1 показана простейшая возможная зависимость скорости воспроизводства от численности популяции. Точка A отражает ситуацию, в которой численность популяции близка к нулю, конкуренция при этом практически отсутствует, и фактическую скорость воспроизводства вполне можно описывать параметром R в его первоначальном виде. Следовательно, при низкой плотности популяции уравнение (1) вполне справедливо. В преобразованном виде оно выглядит так: 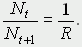 Точка B, напротив, отражает ситуацию, в которой численность популяции высока, и в значительной степени проявляется внутривидовая конкуренция. Фактическая скорость воспроизводства в результате конкуренции настолько снижена, что популяция в целом может не более чем восстанавливать в каждом поколении свою численность, потому что количество родившихся особей уравновешивается количеством погибших. Гипотезе, отраженной на рис. 1, соответствует уравнение
Это уравнение представляет собой модель роста популяции, ограниченного внутривидовой конкуренцией. Суть этой модели в том, что константа R в уравнении (1) заменена на фактическую скорость воспроизводства,
которая уменьшается по мере роста численности популяции Nt. Достоинство полученного уравнения заключается в его простоте. Такой тип конкуренции приводит к саморегуляции численности популяции, изображенной на рис. 2 (для некоторого набора параметров модели; численное решение). 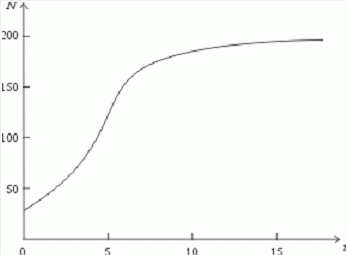 Рис. 2. Изменение численности популяции согласно уравнению (3) при R = 2, K = 200, N0 = 20 Динамика численности популяций хищника и жертвы. Рассматривая динамику численности популяций хищника и жертвы, экологи прежде всего стремятся понять ее закономерности и разъяснить различия между типами динамик. В простейших моделях хищник и жертва рассматриваются безотносительно влияния на них других видов. Одна из самых первых и простых моделей была предложена, как и модель межвидовой конкуренции, Лоткой и Вольтеррой, и носит их имя. Модель состоит из двух компонентов: C - численность популяции хищника и N - численность популяции жертвы. Предполагается, что в отсутствие хищника популяция жертвы растет экспоненциально. Чем больше численность той и другой популяции, тем чаще происходят встречи. Число встреченных и съеденных жертв будет зависеть от эффективности, с которой хищник находит и ловит жертву. Если обозначить через a′ "эффективность поиска", то скорость поедания жертвы будет равна a′·C·N, и окончательно для численности жертвы получаем 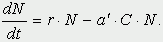 В отсутствие пищи отдельные особи хищника голодают и гибнут. Предположим вновь, что численность хищника в отсутствие пищи будет уменьшаться экспоненциально: 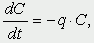 (q - смертность). Скорость рождения новых особей в данной модели полагается зависящей от двух обстоятельств: скорости потребления пищи a′·C·N, и эффективности f, с которой эта пища переходит в потомство хищника. Итак, для численности хищника окончательно получаем  Так как процессы надо рассматривать вместе, объединим уравнения в систему: 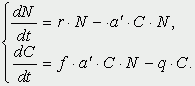 Как и в предыдущем пункте, свойства этой модели можно исследовать, построив изо-клины. Для жертвы имеем 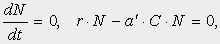 или, выражая C, получаем 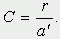 Соответствующее уравнение изоклины для популяции хищника 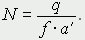 Если поместить обе изоклины на одном рисунке, получим картину взаимодействия популяций (рис. 3). 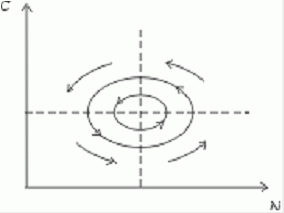 Рис. 3. Динамика численности популяции хищника и жертвы. Численность обеих популяций совершает периодические колебания Как видно на рис. 4, численности популяций хищника и жертвы совершают периодические колебания: при увеличении численности хищников уменьшается численность популяции жертвы и наоборот. Такие колебания численности будут продолжаться в соответствии с моделью до тех пор, пока какое-либо внешнее воздействие не изменит численность популяций, после чего произойдет переход в новое устойчивое состояние (такая ситуация называется "нейтральные устойчивые циклы"). 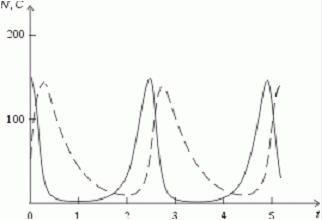 Рис. 3. Динамика численности популяции хищника и жертвы при r = 5, a′ = 0,1, q = 2, f = 0,6, N0 = 150, C0 = 50. Сплошная линия - численность жертвы, штриховая - хищника Моделирование в системах массового обслуживания. Кому не случалось стоять в очереди и с нетерпением прикидывать, успеет ли он сделать покупку (или заплатить за квартиру, покататься на карусели и т.д.) за некоторое имеющееся в его распоряжении время? Или, пытаясь позвонить по телефону в справочную и натыкаясь несколько раз на короткие гудки, нервничать и оценивать - дозвонюсь или нет? Из таких "простых" проблем в начале XX века родилась весьма непростая наука - теория массового обслуживания, использующая аппарат теории вероятностей и математической статистики, дифференциальных уравнений и численных методов. Основоположником ее стал датский ученый А.К.Эрланг, исследовавший проблемы функционирования телефонных станций. Впоследствии выяснилось, что новая наука имеет многочисленные выходы в экономику, военное дело, организацию производства, биологию и экологию; по ней написаны десятки книг, тысячи журнальных статей. Компьютерное моделирование при решении задач массового обслуживания, реализуемое в виде метода статистических испытаний (метода Монте-Карло), хоть и не является в теории массового обслуживания основным, но играет в ней важную роль. Основная линия в ней - получение результатов аналитических, т.е. представленных формулами. Однако, возможности аналитических методов весьма ограничены, в то время как метод статистических испытаний универсален и весьма прост для понимания (по крайней мере кажется таковым). Очередь к одному "продавцу" Рассмотрим одну из простейших задач данного класса. Имеется магазин с одним продавцом, в который случайным образом входят покупатели. Если продавец свободен, он начинает обслуживать покупателя сразу, если покупателей несколько, выстраивается очередь. Вот аналогичные задачи:
Будем для определенности говорить о магазине, покупателях и продавце. Рассмотрим возникающие здесь проблемы, которые заслуживают математического исследования и, как выясняется, весьма серьезного. Итак, на входе этой задачи случайный процесс прихода покупателей в магазин. Он является "марковским", т.е. промежутки между приходами любой последовательной пары покупателей - независимые случайные события, распределенные по некоторому закону. Реальный характер этого закона может быть установлен лишь путем многочисленных наблюдений; в качестве простейшей модельной функции плотности вероятности можно взять равновероятное распределение в диапазоне времени от 0 до некоторого T - максимально возможного промежутка между приходами двух последовательных покупателей. При этом распределении вероятность того, что между приходами двух покупателей пройдет 1 минута, 3 минуты или 8 минут одинакова (если T > 8). Такое распределение, конечно, малореалистично; реально оно имеет при некотором значении t = τ максимум и быстро спадает при больших t, т.е. имеет вид, изображенный на рис. 1. Можно, конечно, подобрать немало элементарных функций, графики которых похожи на тот, что изображен на рис. 1. Например, семейство функций Пуассона, широко используемых в теории массового обслуживания:
где λ - некоторая константа, n - произвольное целое.
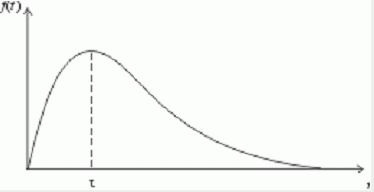 Рис. 1. Типичная плотность вероятности распределения времени между приходами покупателей Второй случайный процесс в этой задаче, никак не связанный с первым, сводится к последовательности случайных событий - длительностей обслуживания каждого из покупателей. Распределение вероятностей длительности обслуживания качественно имеет тот же вид, что и в предыдущем случае; при отработке первичных навыков моделирования методом статистических испытаний вполне уместно принять модель равновероятного распределения. В таблице 1 в колонке A записаны случайные числа - промежутки между приходами покупателей (в минутах), в колонке B - случайные числа - длительности обслуживания (в минутах). Для определенности взято amax = 10 и bmax = 5. Из этой короткой таблицы, разумеется, невозможно установить, каковы законы распределения приняты для величин A и B; в данном обсуждении это не играет никакой роли. Остальные колонки предусмотрены для удобства анализа; входящие в них числа находятся путем элементарного расчета. В колонке C представлено условное время прихода покупателя, в колонке D - момент начала обслуживания, E - момент конца обслуживания, F - длительность времени, проведенного покупателем в магазине в целом, G - в очереди в ожидании обслуживания, H - время, проведенное продавцом в ожидании покупателя (магазин пуст). Таблицу удобно заполнять по горизонтали, переходя от строчки к строчке. Приведем для удобства соответствующие формулы (в них i = 1, 2, 3, ...): 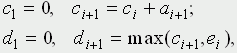 - так как начало обслуживания очередного покупателя определяется либо временем его прихода, если магазин пуст, либо временем ухода предыдущего покупателя; 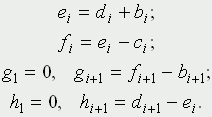
Табл 1. Моделирование очереди Таким образом, при данных случайных наборах чисел в колонках A и B и покупателям приходилось стоять в очереди (колонка G), и продавцу - в ожидании покупателя (колонка H). При моделировании систем такого вида возникают следующие вопросы. Какое среднее время приходится стоять в очереди к прилавку? Чтобы ответить на него, следует найти 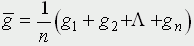 в некоторой серии испытаний. Аналогично можно найти среднее значение величины h. Конечно, эти выборочные средние сами по себе - случайные величины; в другой выборке того же объема они будут иметь другие значения (при больших объемах выборки, не слишком отличающиеся друг от друга). Доверительные интервалы, в которых находятся точные средние значения (т.е. математические ожидания соответствующих случайных величин) при заданных доверительных вероятностях находятся методами математической статистики. Сложнее ответить на вопрос, каково распределение случайных величин G и H при заданных распределениях случайных величин A и B. Допустим, в простейшем моделировании мы примем гипотезу о равновероятных распределениях величин A и B - скажем, для A в диапазоне от 0 до 10 минут и B - от 0 до 5 минут. Для построения методом статистических испытаний распределений величин G и H поступим так: найдем в достаточно длинной серии испытаний (реально - в десятках тысяч, что на компьютере делается достаточно быстро) значения gmax (для H все делается аналогично) и разделим промежуток [0, gmax] на m равных частей - скажем, вначале на 10 - так, чтобы в каждую часть попало много значений gi. Разделив число попаданий nk в каждую из частей на общее число испытаний n, получим набор чисел 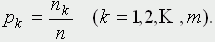 Построенные по ним гистограммы дают представление о функциях плотностей вероятности соответствующих распределений. По гистограмме можно составить представление о функции плотности распределения соответствующей случайной величины. Для проверки же гипотезы о принадлежности такого эмпирически найденного распределения тому или иному конкретному виду служат известные статистические критерии. Располагая функцией распределения (пусть даже эмпирической, но достаточно надежной), можно ответить на любой вопрос о характере процесса ожидания в очереди. Например: какова вероятность прождать дольше m минут? Ответ будет получен, если найти отношение площади криволинейной трапеции, ограниченной графиком плотности распределения, прямой x = m и y = 0, к площади всей фигуры. Программа ссылка скрыта позволяет моделировать описанный выше процесс. На выходе она дает средние значения и дисперсии случайных величин g и h, полученные по выборке, максимальный объем которой порядка 10000 (ограничение связано с малой допустимой длиной массива в PASCALе; чтобы его смягчить, использовано динамическое описание массивов g и h). Кроме того, программа строит гистограммы распределений величин g и h. 4.4 Основные понятия и категории В технологии компьютерного моделирования можно выделить следующие основные понятия. Модель - искусственно созданный объект, который воспроизводит в определенном виде реальный объект - оригинал. Компьютерная модель - представление информации о моделируемой системе средствами компьютера. Система - совокупность взаимосвязанных элементов, обладающих свойствами, отличными от свойств отдельных элементов. Элемент - это объект, обладающий свойствами, важными для целей моделирования. В компьютерной модели свойства элемента представляются величинами - характеристиками элемента. Связь между элементами описывается с помощью величин и алгоритмов, в частности вычислительных формул. Состояние системы представляется в компьютерной модели набором характеристик элементов и связей между элементами. Структура данных, описывающих состояние, не зависит от конкретного состояния и не меняется при смене состояний, меняется только значение характеристик. Если состояния системы функционально зависят от некоторого параметра, то процессом называют набор состояний, соответствующий упорядоченному изменению параметра. Параметры в системе могут меняться как непрерывно, так и дискретно. В компьютерной модели изменение параметра всегда дискретно. Непрерывные процессы можно моделировать на компьютере, выбирая дискретную серию значений параметра так, чтобы последовательные состояния мало чем отличались друг от друга, или, другими словами, минимизируя шаг по времени. В свете введенных определений можно дать более строгие определения некоторым классам моделей. Статистические модели - модели, в которых предоставлена информация об одном состоянии системы. Динамические модели - модели, в которых предоставлена информация о состояниях системы и процессах смены состояний. Оптимизационные, имитационные и вероятностные модели являются динамическими моделями. В оптимизационных и имитационных моделях последовательность смены состояний соответствует изменению моделируемой системы во времени. В вероятностных моделях смена состояний определяется случайными величинами.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||