Geum.ru

Вопросы и задания к экзамену по предмету

Вид материалаРешение
Подобный материал:
Вопросы и задания к экзамену по предмету

«Численные методы».

Теоретические вопросы:
  1. Точные и приближённые числа. Источники погрешностей.
  2. Точные и приближённые числа. Классификация погрешностей.
  3. Абсолютная и относительная погрешность. Правила округления чисел.
  4. Значащая цифра числа. Верная значащая цифра. Правила округления чисел.
  5. Погрешности суммы (слагаемые имеют одинаковые знаки).
  6. Погрешности суммы (слагаемые имеют разные знаки).
  7. Погрешности произведения.
  8. Число верных знаков произведения.
  9. Погрешности частного.
  10. Число верных знаков частного.
  11. Погрешности степени и корня.
  12. Алгебраические и трансцендентные уравнения. Общие методы решения нелинейных уравнений.
  13. Графические методы решения нелинейных уравнений.
  14. Отделение корней. Графический метод отделения корней.
  15. Отделение корней. Аналитический метод отделения корней.
  16. Уточнение корней методом проб.
  17. Нахождение корней уравнений методом последовательных приближений (итераций).
  18. Геометрическая интерпретация метода итераций.
  19. Приближённое решение систем уравнений. Метод Ньютона для решения системы двух уравнений.
  20. Общие свойства алгебраических уравнений. Определение числа действительных корней алгебраического уравнения.
  21. Вычисление значений многочлена. Теорема Безу.
  22. Схема Горнера для вычисления значений многочлена.
  23. Формулы Крамера для решения систем линейных уравнений.
  24. Метод последовательного исключения переменных для приближённого решения систем линейных уравнений.
  25. Решение систем линейных уравнений методом последовательных приближений (итераций). Оценка погрешностей.
  26. Условия сходимости и оценка погрешности итерационного процесса.
  27. Решение систем линейных уравнений методом Зейделя.
  28. Условия сходимости и оценка погрешности процесса Зейделя.
  29. Способы задания функций. Математические таблицы.
  30. Математическая постановка задачи интерполирования.
  31. Интерполяционный многочлен Лагранжа для решения нелинейных уравнений.
  32. Оценка погрешности интерполяционного многочлена Лагранжа.
  33. Первая интерполяционная формула Ньютона.
  34. Вторая интерполяционная формула Ньютона.
  35. Оценка погрешности первой интерполяционной формулы Ньютона.
  36. Оценка погрешности второй интерполяционной формулы Ньютона.
  37. Понятие линейного интерполирования.
  38. Линейное интерполирование по Эйткину.
  39. Разделённые разности.
  40. Интерполяционные формулы Гаусса.
  41. Обратное интерполирование. Случай неравноотстоящих узлов интерполирования.
  42. Обратное интерполирование. Случай равноотстоящих узлов интерполирования.
  43. Численное интегрирование. Простейшие квадратурные формулы.
  44. Квадратурная формула правых прямоугольников для вычисления интегралов.
  45. Квадратурная формула левых прямоугольников для вычисления интегралов.
  46. Квадратурные формулы трапеций для вычисления интегралов.
  47. Квадратурные формулы Симпсона для вычисления интегралов.
  48. Квадратурные формулы Ньютона-Котеса для вычисления интегралов.
  49. Частные случаи формулы Ньютона-Котеса.
  50. Квадратурные формулы Чебышева для вычисления интегралов.
  51. Квадратурные формулы Гаусса для вычисления интегралов.
  52. Численное дифференцирование. Формулы приближённого дифференцирования, основанные на интерполяционных формулах Ньютона.
  53. Формула приближённого дифференцирования, основанная на интерполяционной формуле Лагранжа.
  54. Графическое дифференцирование функций.
  55. Понятие о дифференциальном уравнении первого и второго порядка.
  56. Интегрирование дифференциальных уравнений с помощью степенных рядов.
  57. Метод Эйлера для решения дифференциальных уравнений (вывод основных формул).
  58. Этапы метода Эйлера. Оценка погрешности.
  59. Численное интегрирование систем дифференциальных уравнений. Метод Эйлера (вывод основных формул).
  60. Усовершенствованный метод Эйлера для решения дифференциальных уравнений.
  61. Метод Рунге-Кутта (вывод основных формул).
  62. Этапы метода Рунге-Кутта. Оценка погрешности.
  63. Экстраполяционный метод Адамса.
  64. Понятие последовательности и ряда.
  65. Ряд Фурье. Теорема Дирихле.
  66. Определение коэффициентов ряда Фурье с помощью численных методов.
  67. Разложение функции в ряд Фурье по чётным и нечётным степеням.



Практические задания:


  1. Построить интерполяционный многочлен Лагранжа для функции, заданной таблично:

    x
    -2
    -1
    2
    3

    y
    -12
    -8
    3
    5
  2. Отделить корни уравнения аналитическим методом.
  3. Методом последовательных приближений решить систему:


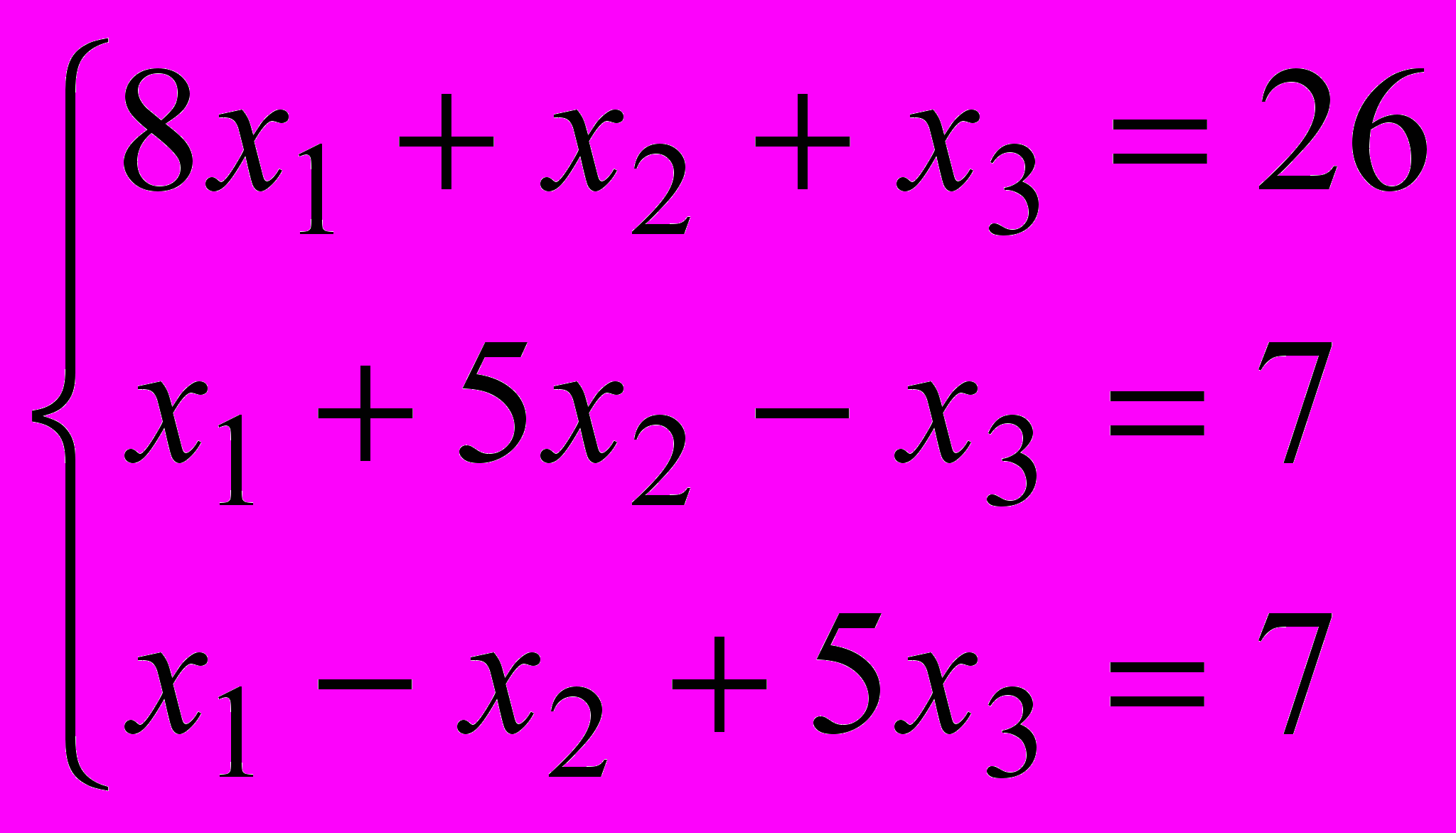
  1. Определить коэффициенты Фурье используя численные методы


  1. Методом Зейделя решить систему:


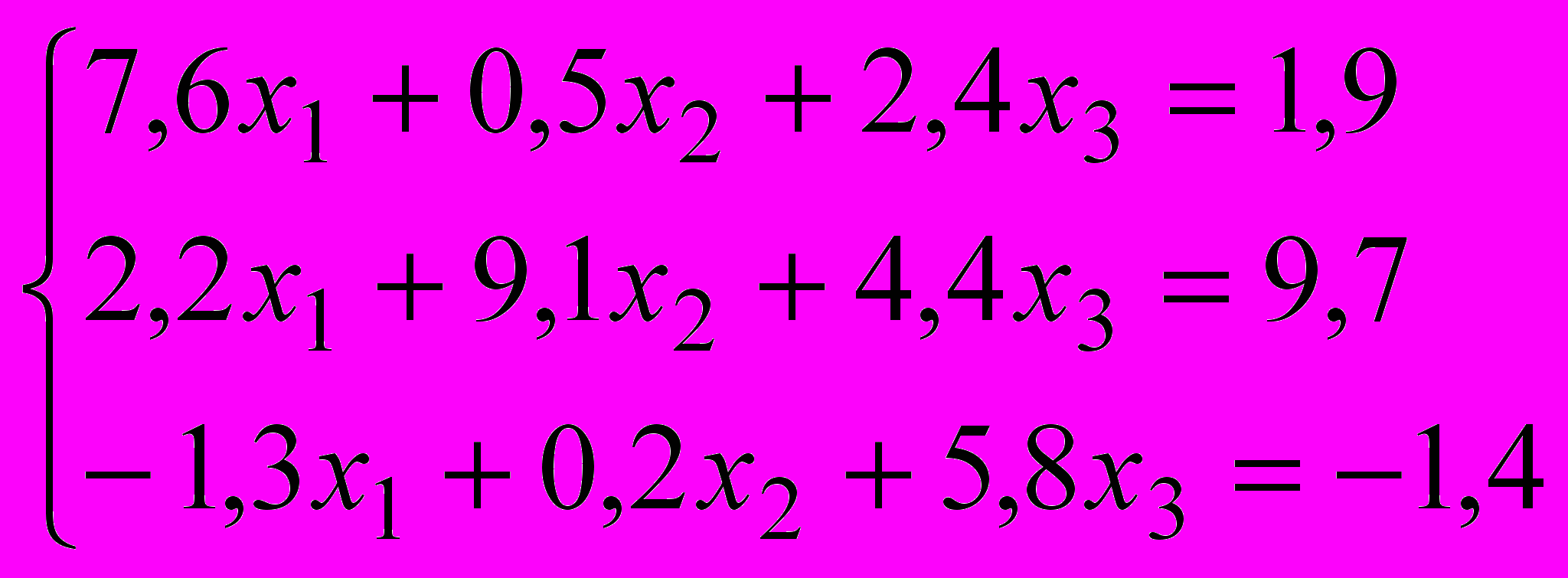
  1. Построить интерполяционный многочлен Лагранжа для функции, заданной

    x
    1
    2
    3
    5

    y
    1
    5
    14
    81
  2. Отделить корни уравнения 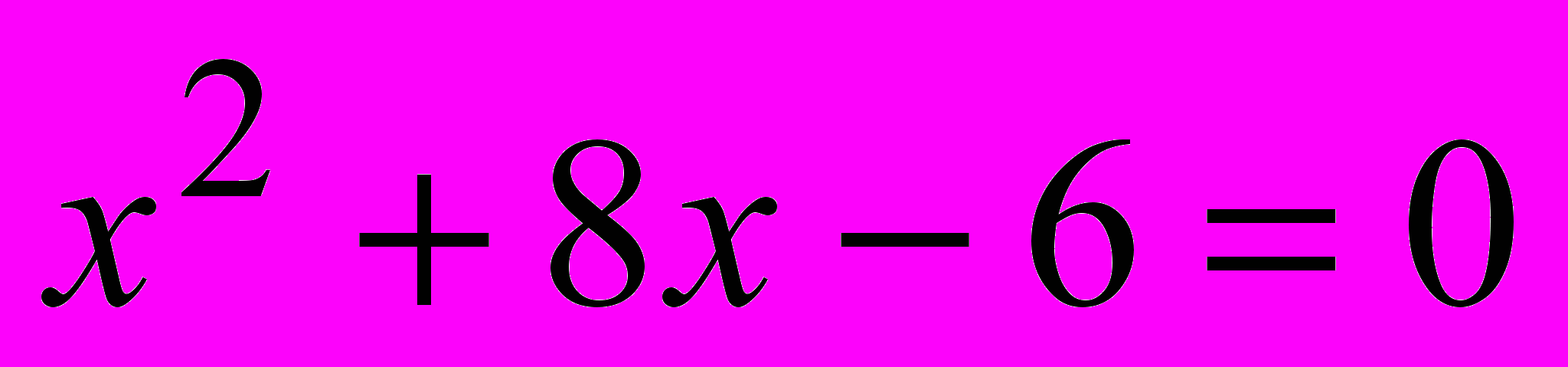аналитическим методом.
  3. Определить, какое равенство точнее:

или
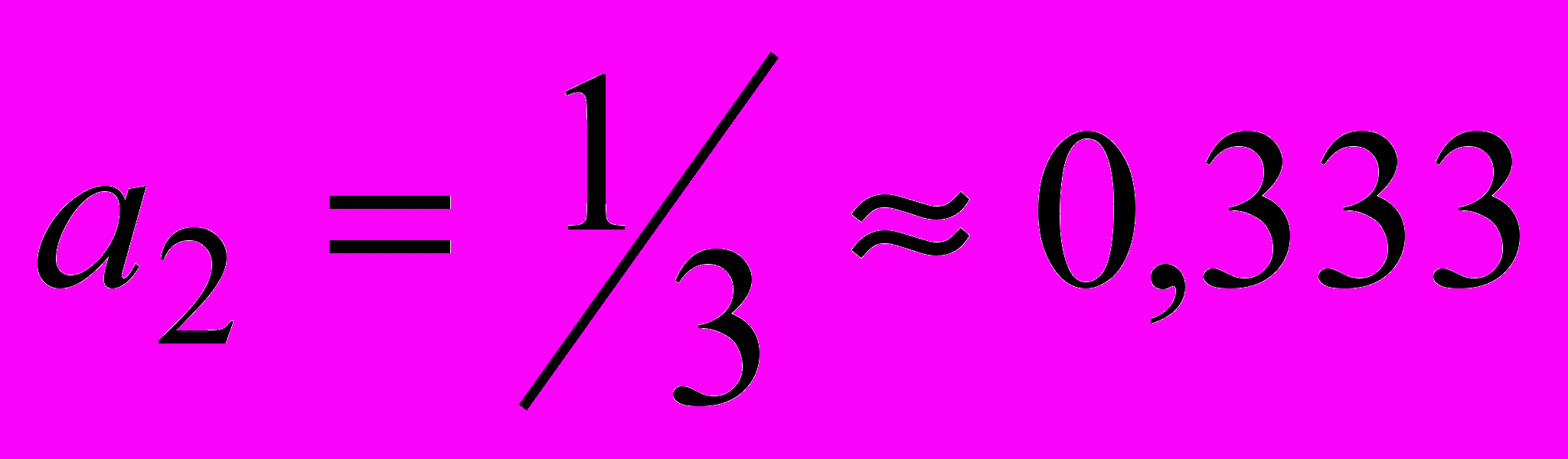
  1. Найти разность 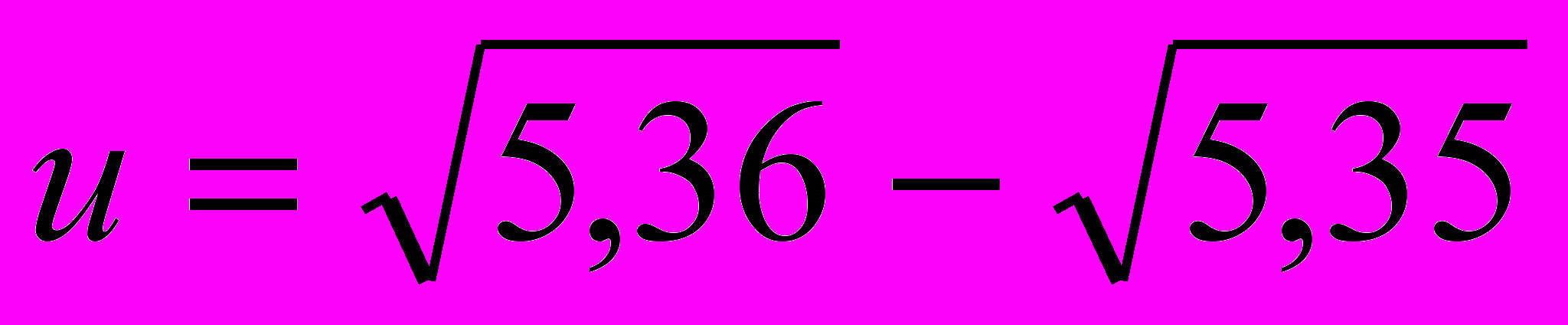с тремя верными знаками.
  2. Определить произведение 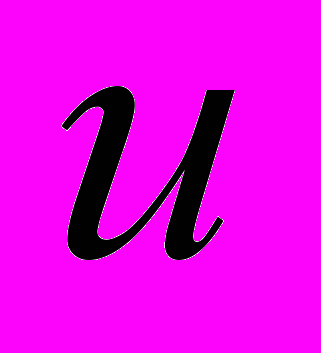приближённых чисел 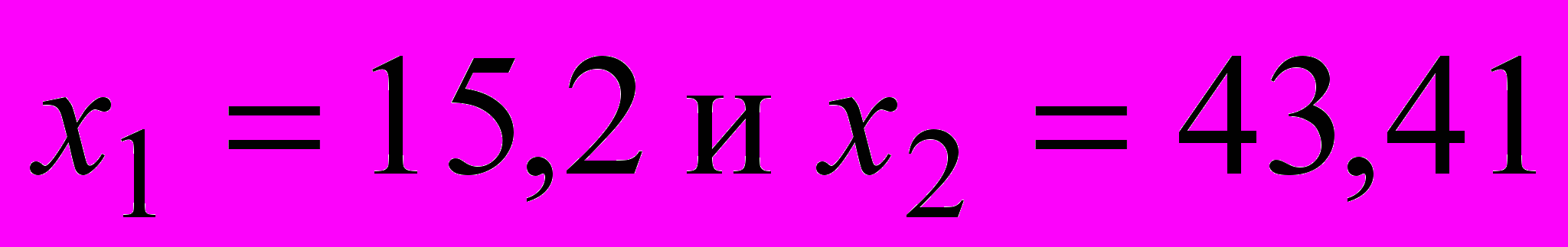и число верных знаков в нём, если все написанные цифры сомножителей верны (в узком смысле).
  3. Функция 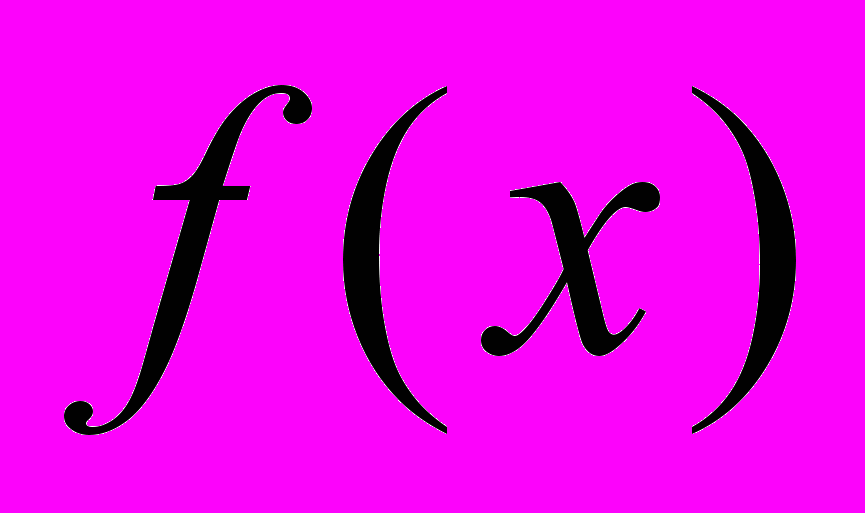задана таблично:

x
0
1
2
6

y
-1
-3
3
1187

Пользуясь интерполяционным многочленом Лагранжа, найти её значения в точке .
  1. Функция задана таблично:

x
1,522
1,523
1,524

y
20,477
20,906
21,354

Определить её значение в точке 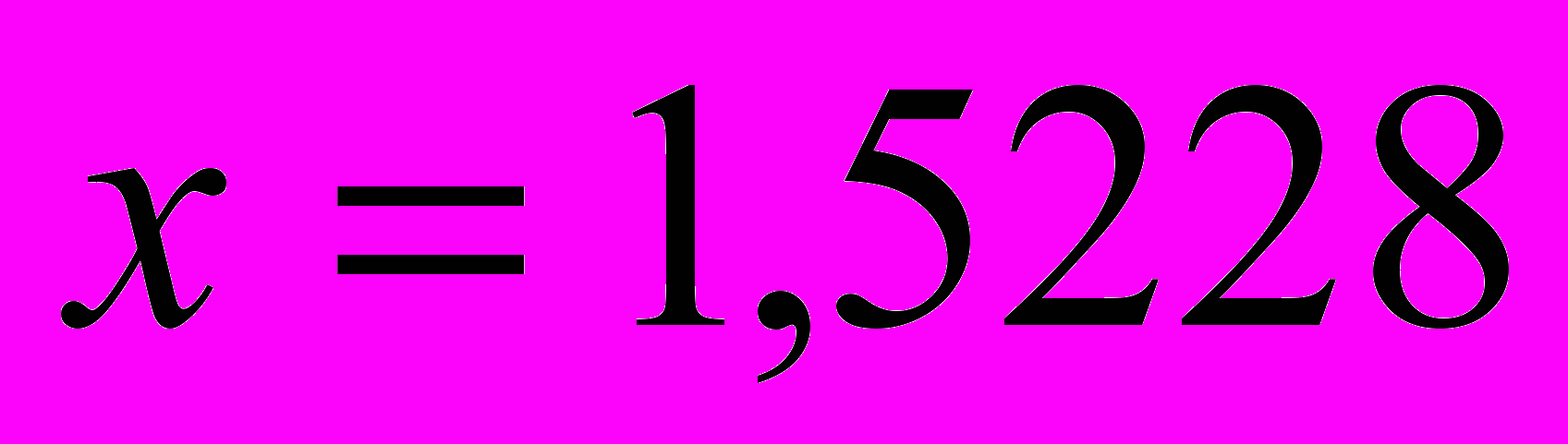с помощью первой интерполяционной формулы Ньютона.
  1. Функция задана таблично:

x
1,529
1,530
1,531

y
23,911
24,498
25,115

Определить её значения в точке x=1,5303, пользуясь второй интерполяционной формулой Ньютона.
  1. Пользуясь схемой Эйткина, вычислить значения 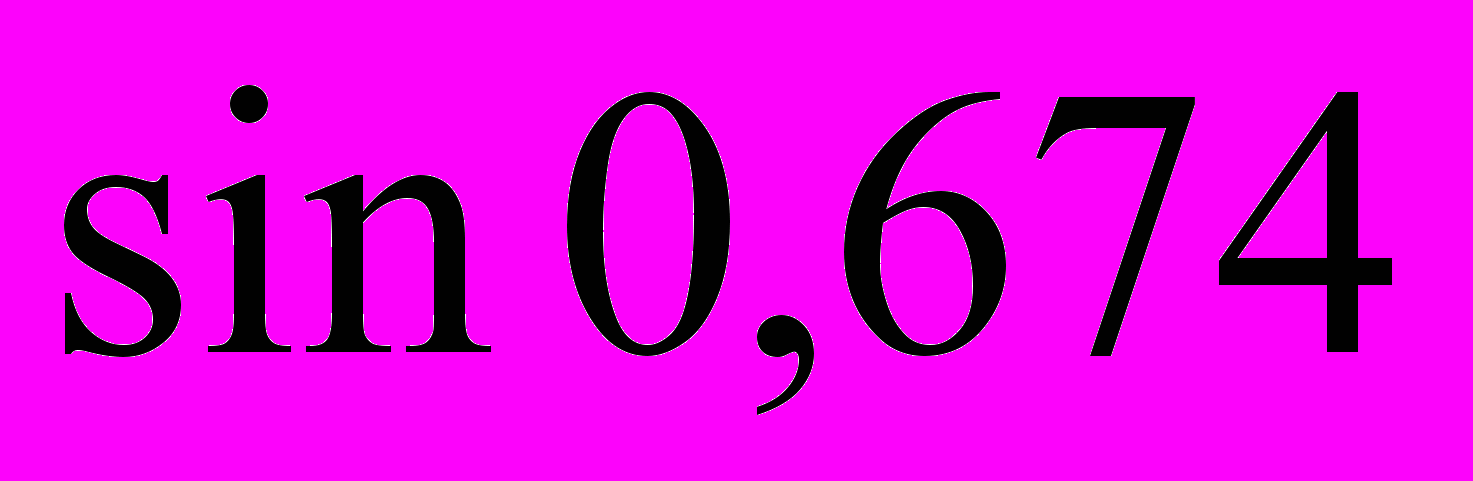для функции

    xi
    x0=0,66
    x1=0,67
    x2=0,68

    yi=sin xi
    y0=0,61312
    y1=0,62099
    y2=0,62879
  2. Составить таблицу разделённых разностей для функции, заданной таблично:

    x
    -2
    -1
    0
    1
    2
    3

    y
    10
    5
    1
    -15
    -50
    -100
  3. Вычислить значение функции в точке х=1,34627, пользуясь формулой Гаусса, если функция задана таблично:

    x
    1,335
    1,340
    1,345
    1,350
    1,355
    1,360

    y
    4,16206
    4,25562
    4,35325
    4,45522
    4,56184
    4,67344
  4. Для функции , заданной таблично:

x
1,03
1,08
1,016
1,23
1,26
1,33
1,39

y
2,80107
2,94468
3,18993
3,42123
3,52542
3,78104
4,01485

вычислить значение в точке х=1,21555, пользуясь формулой Эйткина.
  1. Составить таблицу разделённых разностей для функции, заданной таблично:

    x
    -3
    1
    0
    2
    3

    y
    -15
    -7
    1
    25
    47
  2. Для функции, заданной таблично:

x
1,435
1,440
1,445

y
0,892687
0,893698
0,894700

определить значение аргумента, соответствующее значению функции 0,892914.
  1. Функция задана таблично:

x
10
15
17
20

y
3
7
11
17

Найти значение аргумента х, для которого y=10.
  1. Вычислить определённый интеграл

, пользуясь формулой левых прямоугольников при n=6.
  1. Дано дифференциальное уравнение с начальным условием y(0)=1,5. Вычислить с точностью до 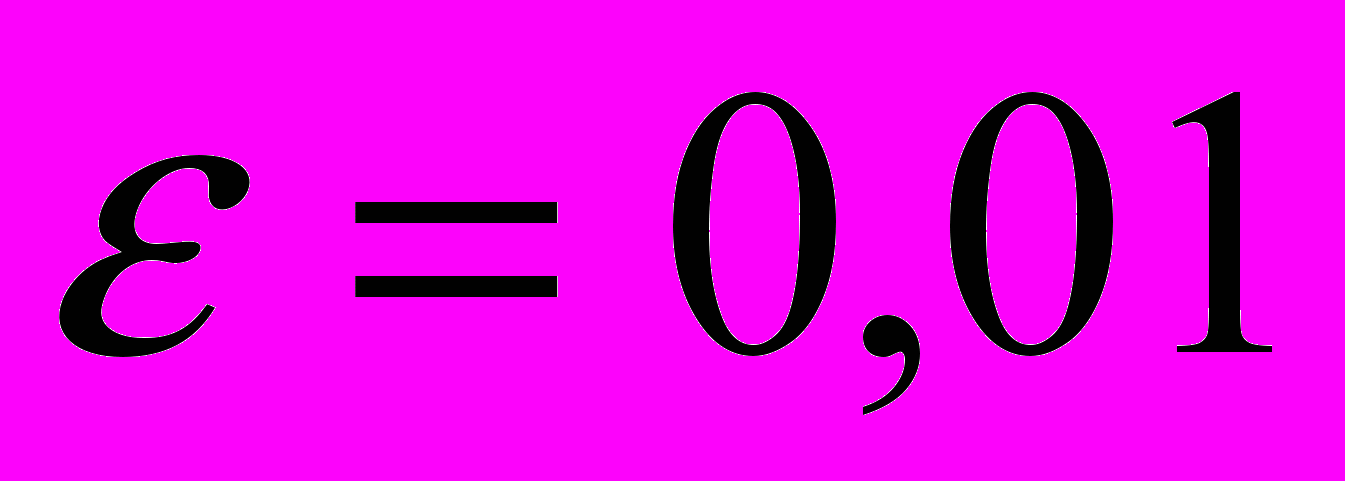решение этого уравнения при х=0,5. Вычисления провести по Методу Рунге-Кутта с двумя запасными знаками.
  2. Проинтегрировать методом Эйлера дифференциальное уравнение с начальным условием x0=0, y0=1,5 на отрезке [0;1,5], приняв h=0,25. Вычисления вести с четырьмя знаками после запятой.
  3. Найти решение уравнения 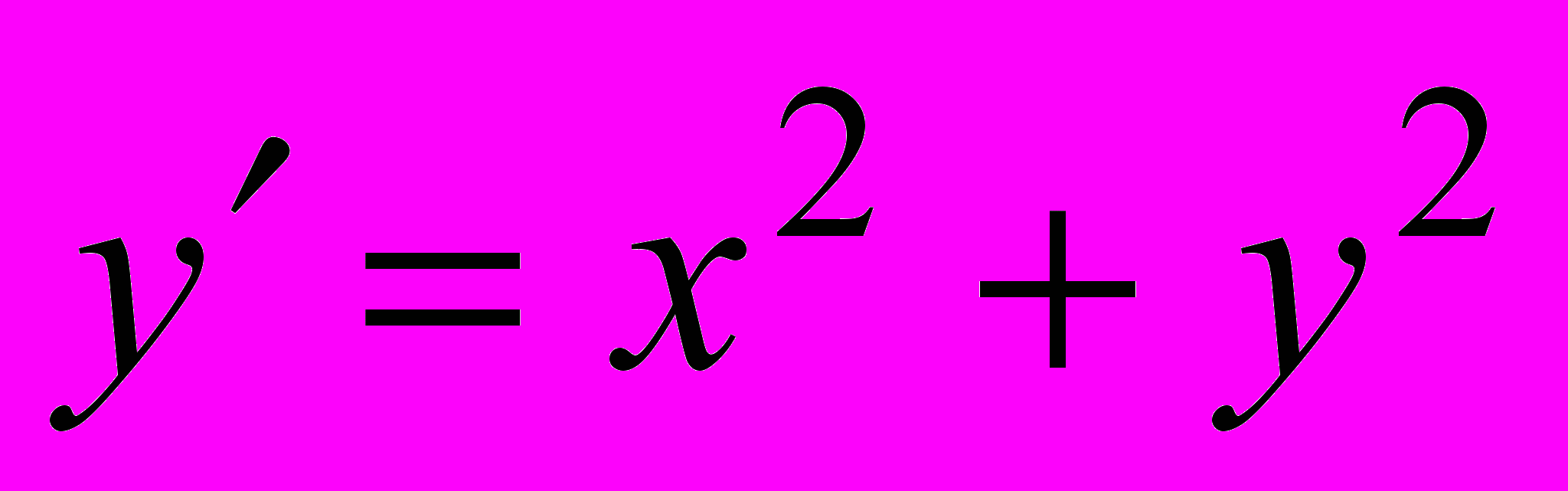, удовлетворяющее условию x0=0, y0=0.
  4. Найти решение дифференциального уравнения 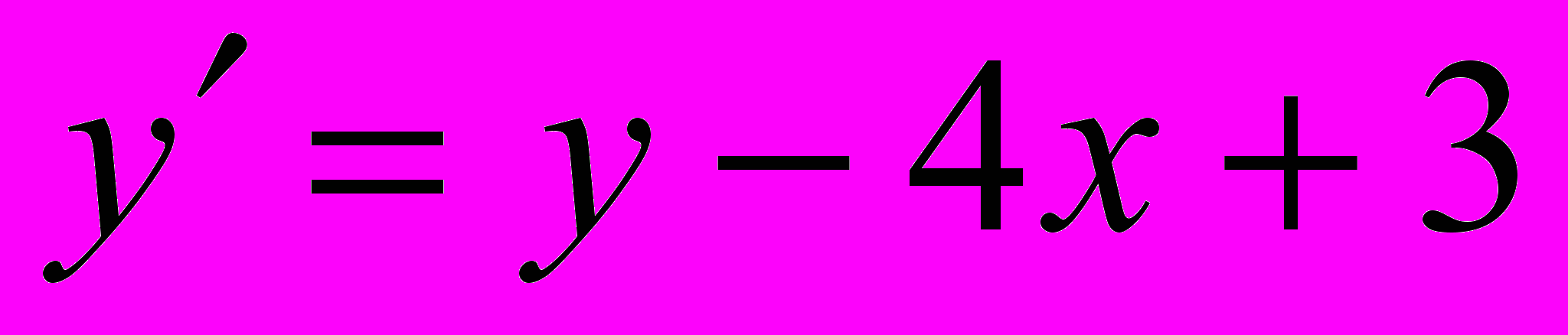с начальным условием х0=0, y0=3.
  5. Определить, является ли 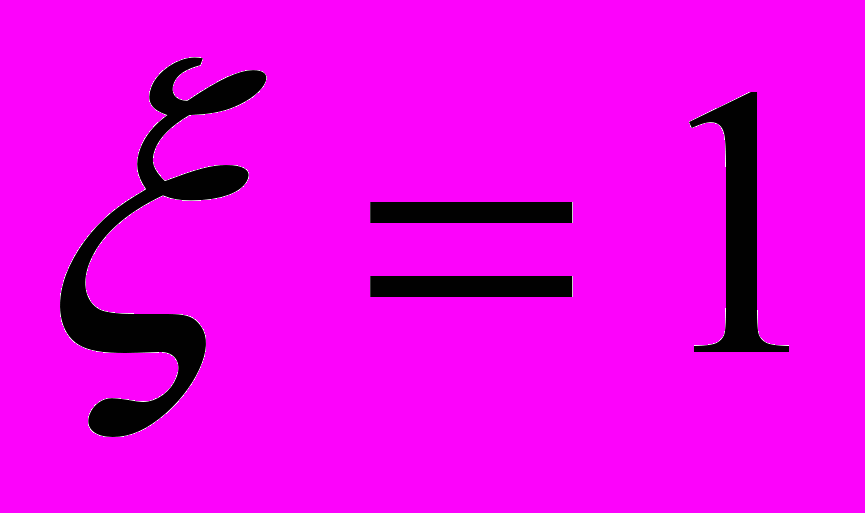корнем уравнения .
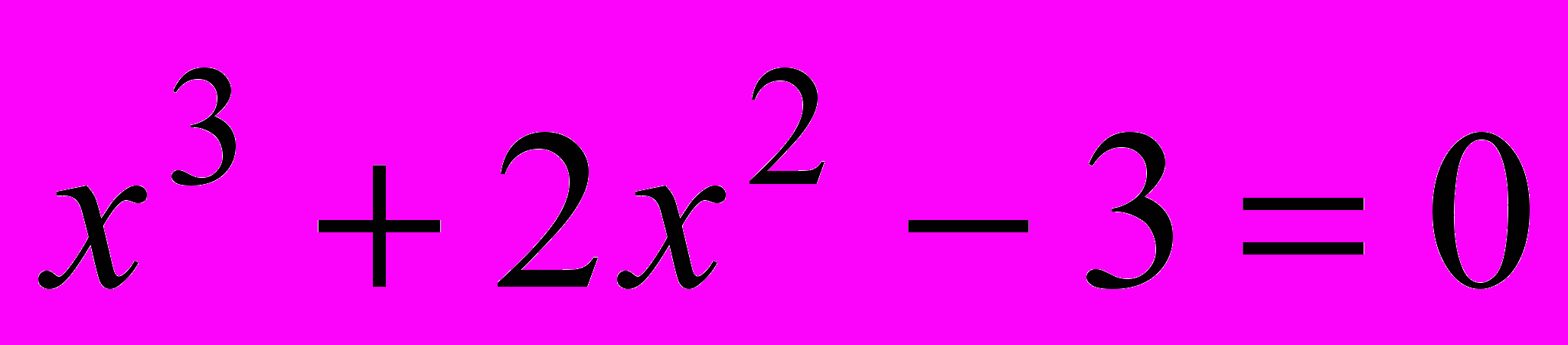  6. Пользуясь формулой правых прямоугольников при n=8, вычислить

.
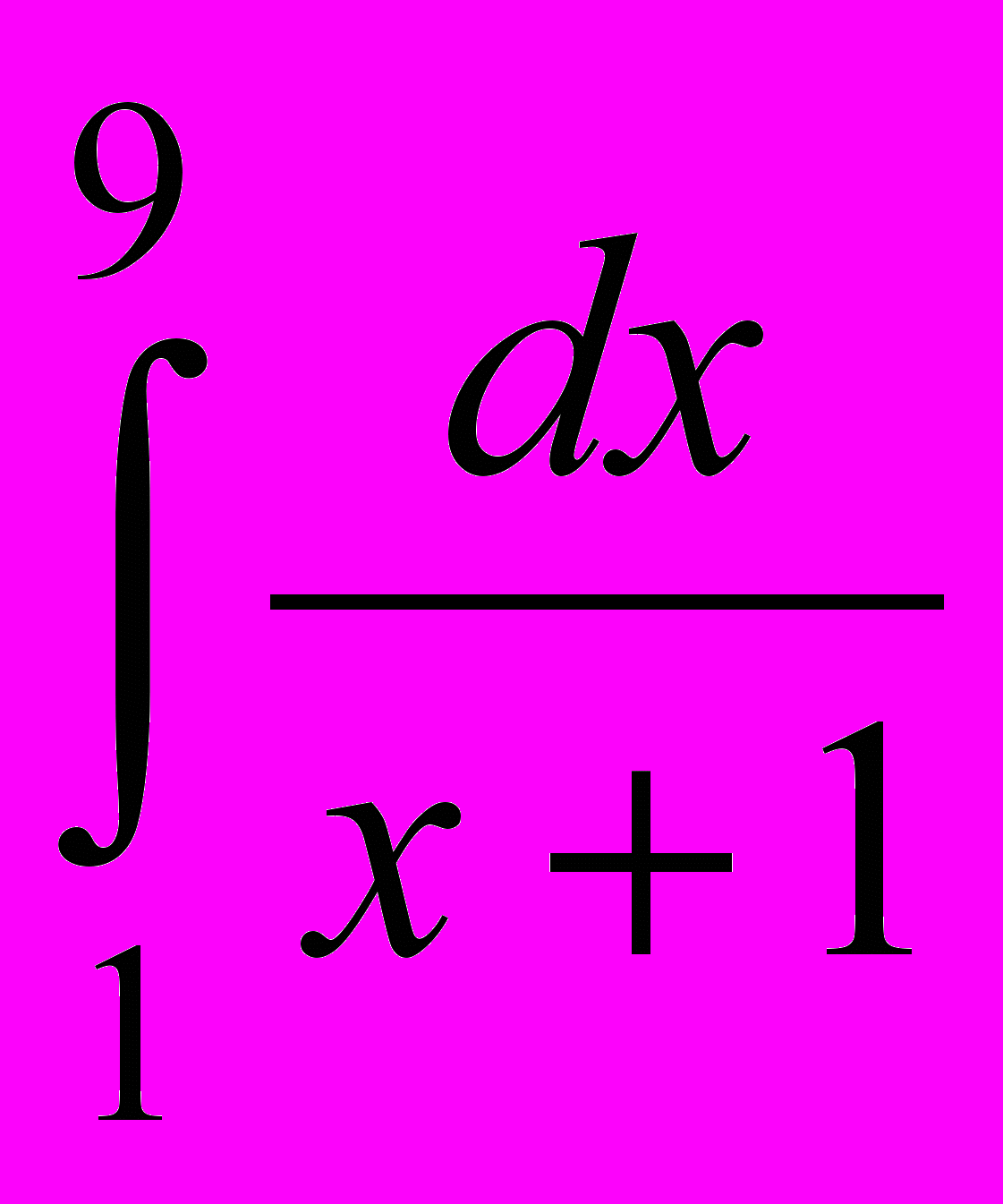  1. Пользуясь формулой трапеций при n=8, вычислить .
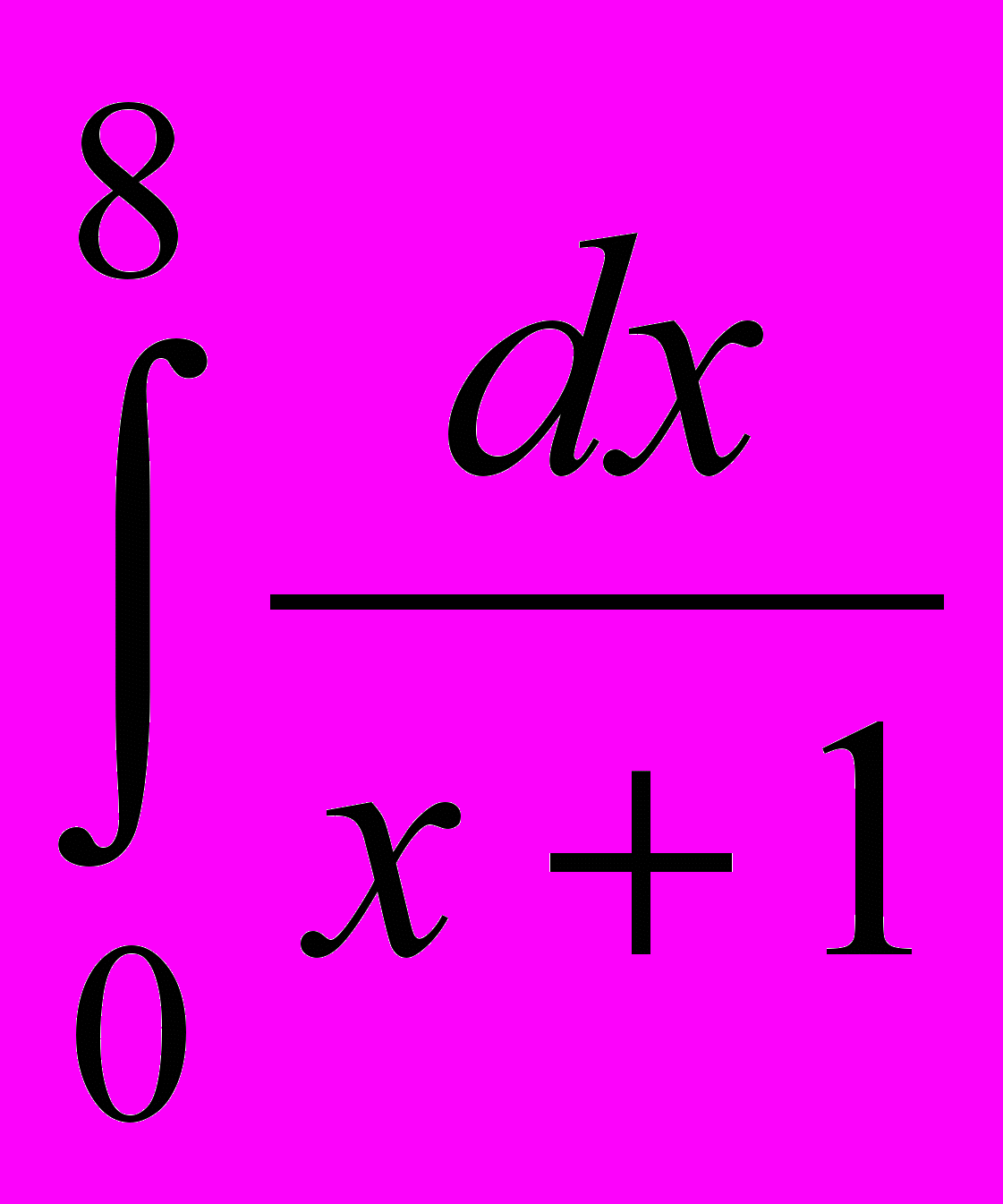  2. Пользуясь схемой Горнера, произвести деление многочлена

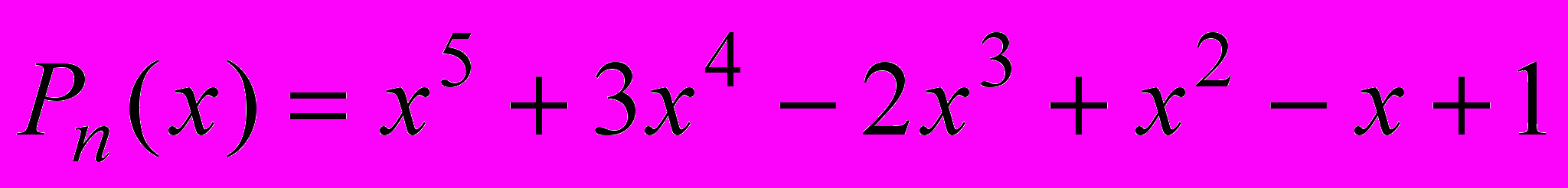на двучлен х-3.
  1. Найти производную первого порядка в точке х=50 для функции, заданной таблично:

    x
    50
    55
    60
    65

    y
    1,6990
    1,7404
    1,7782
    1,8129
  2. Функция задана таблично

x
0,525
0,526
0,527
0,528

y
0,50121
0,50208
0,50294
0,50381

Методом численного дифференцирования найти первую производную в точке х=0,525.
  1. По формуле трапеций вычислить полагая n=5.
  2. По формуле Симпсона вычислить 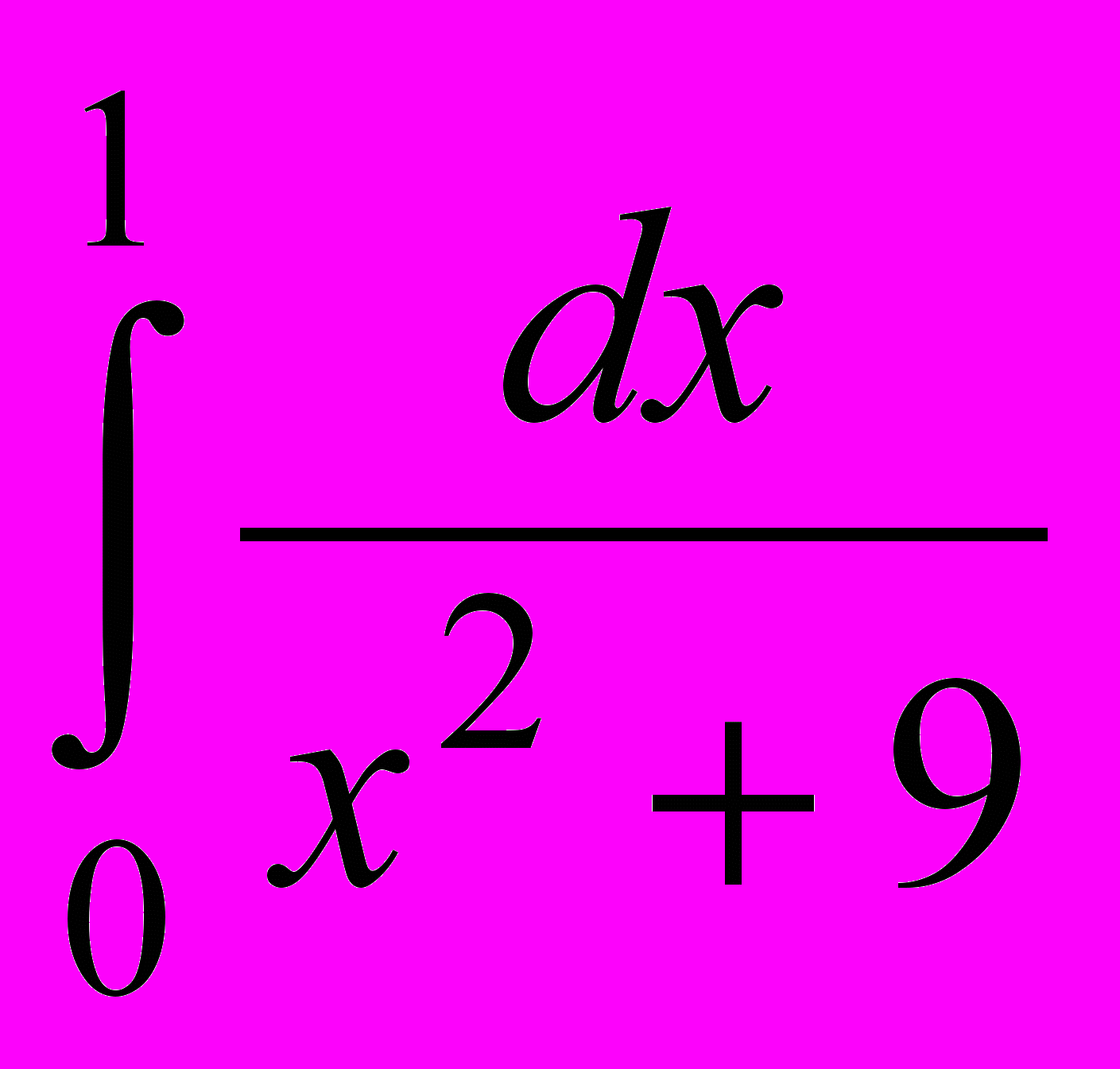полагая 2n=10.
  3. Вычислить интеграл пользуясь формулой Гаусса при n=5

(-х1=х5=0,906180; -х2=х4=0,538470; х3=0; с1=с5=0,236927; с2=с4=0,478629; с3=0,568889).
  1. . Вычислить интеграл пользуясь формулой Чебышева при n=6

(-х1=х6=0,866247; -х2=х5=0,422519; -х3=х4=0,266635).