Интерполяция и приближение данных в matlab
| Вид материала | Обзор |
- 1. Интерполяция и приближение функций, 31.83kb.
- 1. Интерполяция и приближение функций, 31.15kb.
- Обзор средств matlab и ToolBox'ов для приближения данных, 622.57kb.
- Структура программы пакета MatLab Простые переменные и основные типы данных в MatLab, 615.94kb.
- Правила округления и представления экспериментальных данных. Методы устного счета., 23.96kb.
- Лабораторна робота №1 операцiї з матрицями. Графічні засоби matlab, 206.02kb.
- «Математические методы в химии» Общая трудоёмкость дисциплины составляет, 22.21kb.
- Использование matlab в преподавании курса «моделировании электромеханических систем», 25.86kb.
- «Применение matlab для моделирования физических процессов», 123.4kb.
- П. П. Порешин московский инженерно-физический институт (государственный университет), 23.75kb.
| Интерполяция и приближение данных в MATLAB - среда для изучения сплайнов и работы ними. Функции пакета, в сочетании с языком MATLAB и подробным руководством пользователя, облегчают понимание сплайнов и их применение к решению разнообразных задач. В пакет включены программы для работы с двумя наиболее употребительными формами представления сплайнов: B-формой и кусочными полиномами. Пакет включает функции для создания, отображения, интерполяции, аппроксимации и обработки сплайнов в В-форме и в виде кусочных полиномов. Представлен обзор средств MATLAB, Spline Toolbox и Curve Fitting Toolbox для решения задач аппроксимации данных. Рассматриваются: приближение различными типами сплайнов, задачи о подборе параметров, линейно и нелинейно входящих в модель, работа с разбросанными данными и другие задачи, связанные с аппроксимацией и интерполированием. Демонстрируется как использование приложений с графическим интерфейсом, так и функций MATLAB и Toolbox'ов. Материалы раздела Интерполяция и приближение данных в MATLAB: Обзор средств MATLAB и ToolBox'ов для приближения данных. Средства MATLAB. Приложение Basic Fitting Запуск приложения Basic Fitting и его основные компоненты. Приближение данных полиномами по методу наименьших квадратов и сплайнами в приложении Basic Fitting. Сохранение приближений и их значений в рабочей среде MATLAB и некоторые операции с ними. Работа с несколькими наборами данных. Какие функции MATLAB и методы используются в приложении Basic Fitting. Приближение полиномами в смысле наименьших квадратов. Задача о приближении данных полиномом в смысле наименьших квадратов. Метод наименьших квадратов. Когда функция polyfit выдает предупреждения, плохая обусловленность, центрирование и масштабирование данных. Операции с полиномиальными приближениями. Интерполяция. Интерполяция одномерных данных сплайнами. Интерполяция кубическими сплайнами. Интерполяция сплайнами, сохраняющими форму (кубическими полиномами Эрмита). Интерполяция одномерных данных при помощи быстрого дискретного преобразования Фурье. Интерполяция двумерных и многомерных данных сплайнами. Построение параметрических моделей для приближения данных. Регрессия. Работа с разбросанными данными. Нахождение выпуклой оболочки множества точек и ее визуализация Триангуляция Делоне Построение диаграммы Вороного Как связаны выпуклая оболочка, триангуляция Делоне и диаграмма Вороного Нахождение площади многоугольника и пересечения четырехугольников Нахождение ближайшей точки и симплекса, содержащего точку Приближение разбросанных данных Основы работы в Curve Fitting Toolbox. Обзор возможностей и средств Spline Toolbox 3.2. Функции для аппроксимации и интерполирования. Функции для конструирования сплайнов. Функции для выполнения операций над сплайнами и визуализации сплайнов. Функции для работы с узлами, точками разрыва и полюсами интерполяции. Функции для метода коллокаций и работы с почти блочно-диагональными матрицами. Приложения для изучения сплайнов, интерполяции и аппроксимации. Интерполяция кубическими сплайнами, функция csape Задание граничных условий в функции csape Функция csapi для интерполяции с условиями отсутствия узла (not-a-knot) Другие типы интерполяции в MATLAB Интерполяция кусочными полиномами Эрмита Построение интерполяционных сплайнов в B-форме Интерполирование при помощи функции spapi B-форма, базисные сплайны Выбор узлов B-сплайнов Интерполирование B-сплайнами с заданными значениями производных Обзор средств MATLAB и ToolBox'ов для приближения данныхMATLAB и ряд ToolBox'ов предоставляют широкие возможности для приближения и интерполяции одномерных и многомерных данных. Причем эти возможности реализованы на различных уровнях: от достаточно простых средств графического окна для приближения уже визуализированных данных, до специальных функций MATLAB и ToolBox'ов, включая среды с графическим интерфейсом пользователя, которые позволяют импортировать данные, производить их предварительную обработку и сглаживание, приближать и интерполировать данные различными методами. В состав MATLAB входят функции для решения некоторых задач вычислительной геометрии. Функции MATLAB и ряда ToolBox'ов позволяют решать следующие задачи:
Перед приближением данных параметрической или непараметрической моделью возможна их предварительная обработка: исключение данных вручную или по некоторому критерию, задание различных весов. Имеются средства для сглаживания данных при помощи фильтрации или локальной регрессии. Построив интерполянт или параметрическую модель, легко производить с ними различные действия: при помощи функций MATLAB и ToolBox'ов:
Мы рассмотрим применение базовых средств и встроенных функций MATLAB, а также Spline ToolBox и Curve Fitting ToolBox для решения задач о приближении данных. Часть функций и средств MATLAB и перечисленных ToolBox'ов дублируют друг друга. Например, некоторые задачи, в которых требуется интерполяция сплайнами, могут быть решены как при помощи встроенных функций MATLAB, так и в Curve Fitting ToolBox и Spline ToolBox. В справочной системе по MATLAB и ToolBox'ам сведения об интерполяции и приближении данных размещены в следующих разделах (вкладка Contents):
Также полезно посмотреть демонстрации (вкладка Demos в окне справочной системы):
Средства MATLAB В набор базовых функций MATLAB включены функции и средства для решения следующих задач: приближения данных полиномами в смысле наименьших квадратов, интерполирования одномерных и многомерных данных сплайнами, интерполяция разбросанных данных и решение некоторых задач вычислительной геометрии. Используя функции минимизации MATLAB, довольно просто самостоятельно реализовать подбор параметров в нелинейной модели. Сначала рассмотрим решение задачи о приближении одномерных данных при помощи самого простого, но вполне функционального средства - Basic Fitting, доступного из меню графического окна. Приложение Basic Fitting Это приложение предоставляет простой графический интерфейс к некоторым функциям MATLAB, предназначенным для приближения данных и позволяет интерполировать одномерные данные кубическими сплайнами, сплайнами, сохраняющими форму и монотонность данных (кубическими полиномами Эрмита) и приближать данные полиномами в смысле наименьших квадратов. График полученного приближения выводится на оси графического окна. Кроме того, возможно вычислить норму ошибки и построить график распределения ошибки, а так же вычислить значение приближающей функции в заданных точках. Одновременная работа может вестись с несколькими наборами одномерных данных. Разумеется, для оформления графиков доступны все стандартные средства графического окна. Средства приложения Basic Fitting позволяют экспортировать информацию о построенном сплайне или полиноме в рабочую среду MATLAB в виде структуры со значениями коэффициентов полинома или информацией о сплайне. Вычисленные значения сплайна или полинома могут быть также экспортированы в рабочую среду. Эти данные могут быть использованы в рабочей среде для последующих действий с построенным приближением функциями MATLAB и ToolBox'ов. Запуск приложения Basic Fitting и его основные компоненты Запуск приложения Basic Fitting выполняется из меню Tools графического окна в пункте Basic Fitting. Поэтому для запуска приложения сначала желательно визуализировать данные. Пусть, например, наши данные заданы двумя массивами x и y следующим образом: x = 0:0.25:2; y = sin(exp(x)); Построим их график круглыми маркерами, используя функцию plot: plot(x, y, 'o') и запустим приложение Basic Fitting из меню Tools графического окна:  Рядом с графическим окном появляется окно приложения Basic Fitting с панелью Plot Fits, набор данных получает имя data1 и в графическом окне появляется легенда. Основные элементы окна приложения Basic Fitting приведены на рисунке: 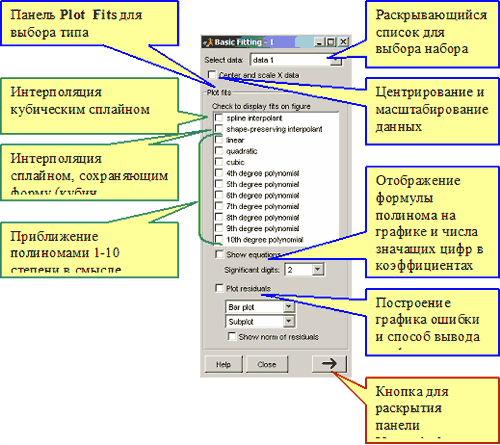 Раскрывающийся список Select Data содержит только одну строку, поскольку в графическом окне на осях построен один набор данных, которому автоматически присвоено имя data1 (его можно изменить, см. Работа с несколькими наборами данных). Установка флага Center and Scale X Data позволяет при вычислениях использовать отмасштабированные данные с нулевым средним и дисперсией равной 1 для уменьшения вычислительной ошибки. На панели Plot Fits расположены флаги для выбора типа приближения см. Какие функции MATLAB и методы используются в приложении Basic Fitting:
Установка флага Show equation приводит к отображению в графическом окне формулы полинома с числом значащих цифр в коэффициентах, указанном в списке Significant digits (это работает только для полиномов при приближении по методу наименьших квадратов, а при интерполяции сплайнами выводится только тип сплайна). Для вывода графика ошибки следует установить флаг Plot residuals и определить способ в первом под этим флагом раскрывающемся списке:
Разумеется, для сплайнов, норма ошибки приближения должна быть нулевой (или очень малой, что связано с погрешностью вычислений), поскольку как кубический сплайн так и сплайн, сохраняющий форму, являются интерполяционными сплайнами и их значения совпадают в полюсах интерполяции с значениями данных. График ошибки приближения выводится в том же самом графическом окне на дополнительные нижние оси, т.к. в нижнем раскрывающемся списке по умолчанию стоит Subplot. Если требуется получить распределение ошибки приближения в отдельном окне, то следует выбрать в нем Separate figure. Для отображения численного значения ошибки в евклидовой норме (корень из суммы квадратов разностей значений данных и приближающего их полинома) на осях с графиком ошибки, следует установить флаг Show norm of residuals. В правом нижнем углу окна находится кнопка  для отображения панели Numerical results, при ее нажатии данная панель оказывается справа от Plot Fits: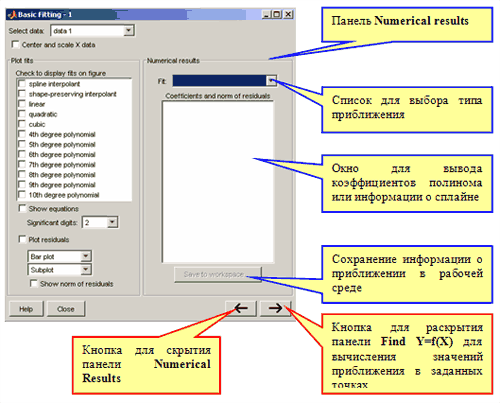 Панель Numerical Results позволяет выбрать тип приближения в раскрывающемся списке Fit и посмотреть на коэффициенты полинома и ошибку приближения в евклидовой норме в окне Coefficients and norm of residuals. Полученные результаты можно сохранить в виде переменных в рабочей среде MATLAB при помощи кнопки Save to workspace (она сейчас недоступна, поскольку пока мы не построили ни одного приближения). Кнопка  служит для скрытия панели Numerical Results, а кнопка предназначена для раскрытия последней панели Find Y=f(X) приложения Basic Fitting, служащей для вычисления значений построенного сплайна или полинома и сохранения результатов в переменных рабочей среды MATLAB. При нажатии на эту кнопку справа появляется панели Find Y=f(X) и окно приложения Basic Fitting приобретает вид: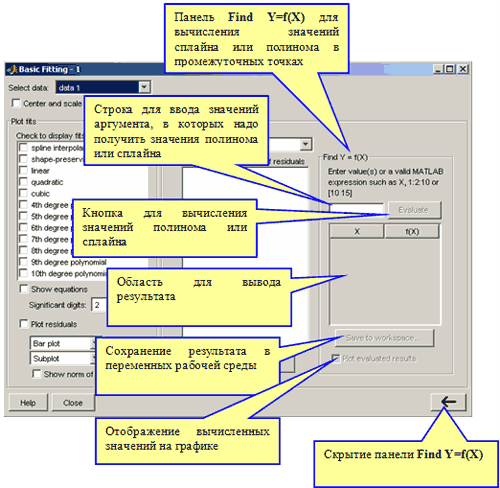 Для вычисления значений построенного полинома или сплайна в промежуточных точках следует задать их в строке ввода в виде, понятном MATLAB, и нажать кнопку Evaluate. Значения независимой переменной могут быть заданы:
Полученные результаты выводятся в таблице и их можно экспортировать в переменные рабочей среды, воспользовавшись кнопкой Save to workspace. Для отображения полученных значений маркерами на осях с данными и приближением следует установить флаг Plot evaluated results. Панель Find Y=f(X) скрывается при помощи кнопки , расположенной в ее правом нижнем углу.Приближение данных полиномами по методу наименьших квадратов и сплайнами в приложении Basic Fitting Поставим задачу приблизить данные, введенные в предыдущем разделе Запуск приложения Basic Fitting и его основные компоненты, полиномом 5-ой степени в смысле наименьших квадратов и кубическими сплайнами, вывести график распределения ошибки и ее норму и вычислить значения полученного полинома в точках с координатами 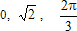 . Для этого раскроем все три панели приложения Basic Fitting и на панели Plot Fits установим флаги spline interpolant и 5th degree polynomial. При этом в графическом окне сразу же строятся графики сплайна и полинома. Для вывода на график выражения для полинома достаточно установить флаг Show equation и выбрать число значащих цифр в списке Significant digits (можно оставить две, как по умолчанию). Следует иметь ввиду, что вне зависимости от выбранного числа значащих цифр для отображения результата, MATLAB производит все вычисления с двойной точностью). Построим графики распределения ошибки и выведем ее значение в среднеквадратичной норме в отдельном графическом окне, для чего на панели Plot Fits выберем в самом нижнем списке Separate figure и установим флаг Show norm of residual. В результате получаем такие графики с данными, сплайном, полиномом и ошибками приближений: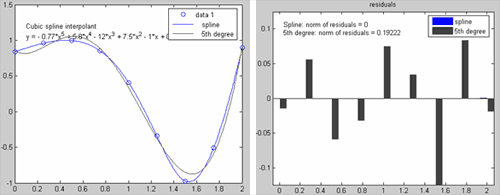 Очевидно, что поскольку кубический сплайн является интерполяционным, то ошибка приближения сплайном равна нулю. Для полинома пятой степени, приближающего данные в смысле наименьших квадратов, ее значение в среднеквадратичной норме составляет 0.19222, т.е. учетом округления в пятом знаке после десятичной точки: 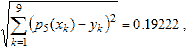 где - построенный полином пятой степени, а 9 - число данных (длина векторов x и y). Для получения нулевой ошибки при приближении полиномом следовало бы построить полином 8-ой степени, поскольку через девять точек, заданных нашими векторами x и y, проходит единственный полином восьмой степени, который является интерполяционным (его девять коэффициентов однозначно определяются девятью условиями прохождения через заданные точки). Приблизим наши данные полиномом восьмой степени, установив флаг 8th degree polynomial на панели Plot Fits. График полинома выводится на тех же осях, что и предыдущие приближения, распределение ошибки и ее значение в среднеквадратичной норме добавляется на второй график. Однако, поскольку приближение производится по методу наименьших квадратов), то для нахождения коэффициентов полинома решается система линейных алгебраических уравнений. Из-за ошибок округления она решается неточно, чем и обусловлена ненулевая норма ошибки приближения полиномом восьмой степени (порядка 10-13). Полиномы степени большей восьми в нашем примере будут неединственными (в них коэффициентов больше, чем условий прохождения графика полинома через точки данных). Выбор девятой или десятой степеней приведет к появлению окна с соответствующим предупреждением "Polynomial is not unique; degree >= number of points". Продолжим работу со сплайном и полиномом пятой степени, оставив только флаги spline interpolant и 5th degree polynomial на панели Plot Fits. При сбрасывании флага, график соответствующего приближения автоматически удаляется с осей. Вычислим значение полинома в точках 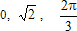и отобразим их маркерами на графике. Для этого:
На панели Find Y=f(X) появилась таблица значений полинома и они размечены на графике маркерами. Как было замечено в пункте Запуск приложения Basic Fitting и его основные компоненты, можно было воспользоваться и глобальной переменной рабочей среды, т.е., если бы мы создали вектор X, например, в командной строке: >> X = [0 sqrt(2) 2*pi/3]; то на шаге 2) в строке ввода можно было указать имя переменной X. Обратите внимание, что последняя точка с абсциссой 2П/3 лежит вне наших данных. В данном случае мы проделали экстраполяцию. Аналогичным образом можно вычислить значения сплайна в заданных точках, выбрав на шаге 1) spline interpolant в раскрывающемся списке Fit на панели Numerical results. Рассмотрим теперь, как передавать в рабочую среду информацию о приближениях, построенных в приложении Basic Fitting, и дальнейшие возможные действия с ней. Сохранение приближений и их значений в рабочей среде MATLAB и некоторые операции с ними Приложение Basic Fitting позволяет сохранить информацию о построенном приближении полиномами или сплайнами в рабочей среде MATLAB, а также их значения в заданных точках, вычисленные при помощи панели Find Y=f(X). Построение полинома пятой степени, приближающего данные x = 0:0.25:2; y = sin(exp(x)); в смысле наименьших квадратов, а так же интерполяционного кубического сплайна описано в разделе Приближение данных полиномами по методу наименьших квадратов и сплайнами в приложении Basic Fitting. Будем считать, что окно приложения Basic Fitting открыто и эти приближения построены. Полиномы и сплайны сохраняются в различных форматах. Начнем с полиномов. Для сохранения нужного приближения в рабочей среде следует выбрать его в раскрывающемся списке Fit на панели Numerical results, выберем в нем 5th degree polynomial и нажмем кнопку Save to workspace (сохранить в рабочей среде). Появляется диалоговое окно сохранения Save Fit to Workspace, приведенное ниже 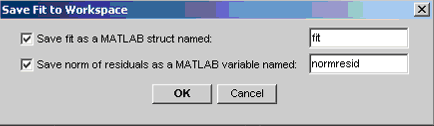 В нем при помощи флагов следует выбрать, что именно нужно сохранить:
По умолчанию при первом сохранении предлагается записать информацию о приближении в структуру с именем fit, а значение среднеквадратической нормы ошибки в переменной normresid, что можно изменить в соответствующих строках ввода. Изменим fit на poly5, а normresid на norm5. Примечание. В MATLAB следует давать имя переменной, предварительно убедившись, что оно не занято под функцию самого пакета. Для того, чтобы проверить, безопасно ли в этом смысле желаемое имя, можно обратиться к функции exist (это нужно делать до открытия окна Save Fit to Workspace), например: >> exist('poly5') ans = 0 Если ответ 0, то имя не занято и его можно использовать. Более подробная информация по возвращаемым функцией exist значениям есть в справочной системе (>> doc exist), где приведено, что обозначает тот или иной возвращаемый результат. Имена poly5 и norm5 не зарезервированы в MATLAB (в отличие, например от poly и norm), поэтому мы будем ими пользоваться. После изменения имен следует нажать кнопку OK и перейти к окну MATLAB. В командное окно вывелось сообщение "Variables have been created in the current workspace" о создании новых переменных. Соответствующие переменные появились в рабочей среде, в чем несложно убедиться посмотрев в окно Workspace. (Если окно Workspace) отсутствует на экране, то следует в меню Desktop окна MATLAB выбрать пункт Workspace). С переменной norm5 все ясно, она содержит среднеквадратичную норму ошибки. Переменная poly5 является структурой с полями type и coeff, для ее просмотра достаточно сделать двойной щелчок мышью в окне Workspace по ее имени для отображения содержимого переменной в появляющемся окне Array Editor редактора массивов. Второй способ - набрать ее имя в командной строке и нажать Enter. >> poly5 poly5 = type: 'polynomial degree 5' coeff: [-0.7681 5.8165 -12.0474 7.4945 -1.0141 0.8553] Для тех, кто не знаком с работой со структурами в MATLAB, достаточно заметить, что для доступа к коэффициентам полинома следует использовать конструкцию, в которой имя структуры poly5 отделено от названия поля точкой, т.е. оператор >> c5 = poly5.coeff c5 = -0.7681 5.8165 -12.0474 7.4945 -1.0141 0.8553 перепишет значение коэффициентов нашего полинома пятой степени в вектор-строку, которую можно использовать в дальнейшей работе. В MATLAB предполагается, что полиномы представлены вектором их коэффициентов, начиная с коэффициента при старшей степени с учетом нулевых коэффициентов, т.е. например полином записывается вектором [4 0 2 7]. Работа с полиномами описана в следующих разделах справочной системы:
Разумеется, доступны средства Symbolic Math ToolBox для произведения символьных вычислений с полиномами. С построенными средствами приложения Basic Fitting полиномами можно производить, например, следующие действия:
Приведем несколько примеров для нашего экспортированного в рабочую среду из приложения Basic Fitting полинома. Пример 1. Интегрирование полинома, приближающего данные. Напомним, что исходные табличные данные содержались в массивах x = 0:0.25:2; y = sin(exp(x)); рабочей среды. Требуется проинтегрировать полином пятого порядка, приближающий их в смысле наименьших квадратов, коэффициенты которого хранятся в векторе c5. Для этого сначала воспользуемся функцией polyint для получения вектора с коэффициентами полинома, являющегося его первообразной В качестве входного аргумента функции polyint задается вектор коэффициентов интегрируемого полинома, а возвращает она вектор коэффициентов его первообразной, длина которого на единицу больше (т.к. степень первообразной на единицу выше степени исходного полинома), причем коэффициент первообразной при нулевой степени равен нулю. >> Ic5 = polyint(c5) Ic5 = -0.1280 1.1633 -3.0118 2.4982 -0.5071 0.8553 0 Теперь для вычисления определенного интеграла от полинома, приближающего данные в смысле наименьших квадратов, осталось найти разность значений первообразной в правой и левой точках интервала, на котором заданы данные. Для этого применим функцию polyval, вызвав ее с двумя входными аргументами - вектором с коэффициентами первообразной Ic5 и значением аргумента, при котором ее надо вычислить, т.е. x(end) и x(1). >> I = polyval(Ic5, x(end)) - polyval(Ic5, x(1)) I = 0.5113 Задача решена. Пример 2. Поиск корней полинома, приближающего табличные данные. Найдем корни полинома пятой степени, приближающего наши табличные данные x = 0:0.25:2; y = sin(exp(x)); в смысле наименьших квадратов, который мы построили средствами приложения Basic Fitting, и отобразим вещественные корни на графике с данными и приближением. Для этого воспользуемся функцией root, которая возвращает вектор, содержащий все корни полинома, включая комплексные. Ее входным аргументом является вектор коэффициентов полинома: >> r=roots(c5) r = 4.6289 1.8786 1.1178 -0.0262 + 0.3375i -0.0262 - 0.3375i Нам подходят только второй и третий корни, поскольку только они принадлежат отрезку [0, 2] на котором определены данные. Осталось нанести их на график с данными и приближением, например красными маркерами-звездочками. Следует только предварительно выполнить hold on для того, чтобы графики данных и полиномиального приближения сохранились на осях: >> hold on >> plot([r(2) r(3)], 0, '*r') 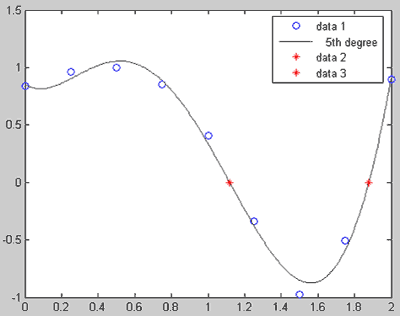 В легенде появились строки data 2 и data 3, поскольку приложение Basic Fitting считает, что мы добавили новые данные. Эти строки легко изменить, перейдя в режим редактирования легенды двойным щелчком мыши. Для отделения вещественных корней полинома, попадающих в отрезок [0, 2] можно было воспользоваться логическим индексированием, сформировав подходящее условие. Это удобно, когда корней много или требуется автоматизировать процесс выбора нужных корней. В нашем случае условие отбора корней является составным - требуется проверить, что корень является вещественным, больше или равен нуля и меньше или равен двум: >> R = r(imag(r)==0 & r>=0 & r<=2) R = 1.8786 1.1178 Более подробные сведения о логическом индексировании, операциях сравнения и условных операторов содержатся в справочной системе MATLAB в разделах:
Описанные выше примеры были посвящены экспорту полиномиальных приближений из приложения Basic Fitting в рабочую среду MATLAB в виде структуры. Информация о сплайнах так же передается в рабочую среду в структуре, которая содержит больше полей, чем в случае с полиномом. Экспортируем кубический сплайн, интерполирующий наши данные x = 0:0.25:2; y = sin(exp(x)); выбрав spline interpolant в раскрывающемся списке Fit на панели Numerical results (если сплайна нет, то его предварительно следует построить, см. Приближение данных полиномами по методу наименьших квадратов и сплайнами в приложении Basic Fitting). После нажатия на кнопку Save to workspace появляется диалоговое окно сохранения Save Fit to Workspace, в нем можно ввести имя для структуры, в которую будет записана информация о сплайне и имя переменной для значения среднеквадратичной нормы ошибки. Норма ошибки в данном случае равна нулю, поскольку сплайн интерполяционный, и соответствующий флаг окно сохранения Save Fit to Workspace можно сбросить. Введем имя для структуры sp3 и нажмем кнопку ОК. В рабочей среде создалась структура (о чем вывелось сообщение в командное окно "Variables have been created in the current workspace"), выведем ее >> sp3 sp3 = type: 'spline' coeff: [1x1 struct] Структура sp3 содержит два поля: поле type с информацией о том, что это сплайн, и поле coeff, которое также является структурой. Запишем его содержимое в новую структуру s3 >> s3 = sp3.coeff s3 = form: 'pp' breaks: [0 0.2500 0.5000 0.7500 1 1.2500 1.5000 1.7500 2] coefs: [8x4 double] pieces: 8 order: 4 dim: 1 Это формат представления сплайна принятый в MATLAB и Spline Toolbox. Ряд функций, предназначенных для работы со сплайнами (поиск корней, интегрирование и т. д.), требуют задания сплайна именно в этом формате. Смысл полей структуры следующий:
Проделаем с кубическим сплайном, записанным в структуру s3, те же самые действия, что описаны выше для полинома пятой степени, приближающего данные по методу наименьших квадратов: найдем его корни и проинтегрируем на том отрезке, на котором определены данные. Пример 3. Интегрирование интерполяционного кубического сплайна, приближающего табличные данные. Для вычисления определенного интеграла от сплайна по отрезку [0, 2], на котором определены данные воспользуемся функциями fnint и fnval, входящими в Spline ToolBox. Функция fnint вычисляет первообразную для сплайна, принимающую нулевое значение на левой границе интервала. Её входным аргументом является приведенная выше структура с информацией об интегрируемом сплайне, а возвращает результат она в том же самом формате - в виде структуры с полями, имеющими те же названия. Разумеется, значение поля order для первообразной будет на единицу большей. >> Is3 = fnint(s3) Is3 = form: 'pp' breaks: [0 0.2500 0.5000 0.7500 1 1.2500 1.5000 1.7500 2] coefs: [8x5 double] pieces: 8 order: 5 dim: 1 Функция fnval предназначена для нахождения значений сплайна в заданных точках, ее входными аргументами являются: структура со сплайном и значение аргумента (или вектор значений). >> I=fnval(Is3,2)-fnval(Is3,0) I = 0.5348 Полученный результат немного отличается от того, что был получен при интегрировании полинома, поскольку эти приближения не совпадают. Пример 4. Поиск корней сплайна, приближающего табличные данные. Для решения этой задачи воспользуемся функцией fnzeros, входящей в состав Spline ToolBox. Если в качестве ее входного аргумента указать структуру со сплайном, то она вернет матрицу, состоящую из двух строк, которая строка которой содержит информацию о корнях сплайна. Вычисление корней производится на всем промежутке задания сплайна. Смысл элементов возвращаемой матрицы в данном случае простой:
Для нашего сплайна, информация о котором записана в структуре s3, результат будет следующим: >> r = fnzeros(s3) r = 1.1453 1.8551 1.1453 1.8551 Т.е. корни сплайна имеют значения 1.1453 и 1.8551. Работа с несколькими наборами данных Приложение Basic Fitting позволяет работать с несколькими наборами данных. Их можно или сразу отобразить в графическом окне, либо добавлять данные при запущенном приложении Basiс Fitting (выполнив предварительно hold on для того, чтобы предыдущие данные не удалились с осей графического окна). Каждый набор данных автоматически получает имя: data1, data2 и т. д. Для перехода к требуемому набору следует использовать раскрывающийся список Select data приложения Basic Fitting. Для смены имени существует два способа:
Если графики данных построены в нескольких графических окнах, то для каждого из окон следует запустить свою копию приложения Basic Fitting, которая позволит работать с данными именно этого графического окна. Если графики данных построены на разных осях в пределах одного графического окна, к примеру: figure x = 0:0.25:2; sublot(2,1,1) plot(x, sin(x), 'o') sublot(2,1,2) plot(x, cos(x), 'o') то запуск приложения Basic Fitting позволит приближать данные, построенные на всех осях. Какие функции MATLAB и методы используются в приложении Basic Fitting Приложение Basic Fitting служит графической оболочкой для следующих функций MATLAB: spline - для построения кубических сплайнов с граничным условием отсутствия узла (not-a-knot condition). Смысл этих условий пояснен в разделе Интерполяция одномерных данных сплайнами. pchip - для построения сплайнов, сохраняющих форму данных, т.е. кубических полиномов Эрмита. Кубические полиномы Эрмита описаны в разделе Интерполяция сплайнами, сохраняющими форму (кубическими полиномами Эрмита). polyfit - для приближения данных полиномами в смысле наименьших квадратов. Применение метода наименьших квадратов для приближения данных описано в разделе Приближение полиномами в смысле наименьших квадратов. norm - для вычисления среднеквадратичной нормы ошибки. | |