Geum.ru

Программа по математике Обязательная литература

Вид материалаПрограмма

Содержание


Домашние задания
Полезные ссылки
Обязательная литература
Полезные ссылки
Балльно - рейтинговая система
Экзаменационные вопросы по математике
Подобный материал:
Российский Университет Дружбы Народов

Институт иностранных языков

Кафедра математики, физики и информатики


В.Ф.Тюрин, С.А.Зельдинова


МАТЕРИАЛЫ ПО МАТЕМАТИКЕ

ссылка скрыта

ссылка скрыта

ссылка скрыта

ссылка скрыта

ссылка скрыта

ссылка скрыта

ссылка скрыта

Экзаменационные вопросы

Программа по математике

Обязательная литература

Балльно-рейтинговая система

Календарный план

Полезные ссылки


Лекции по математике

находятся в разделе ссылка скрытассылка скрытассылка скрыта


Российский Университет Дружбы Народов

Институт иностранных языков

Кафедра математики, физики и информатики


ПРОГРАММА по МАТЕМАТИКЕ


для студентов специальности математика – индекс НМ, шифр 511200

автор: д.т.н., профессор Тюрин В.Ф.


Настоящая программа курса «Математика» составлена на основе федерального компонента государственного стандарта среднего (полного) общего образования на базовом уровне. Предназначена для вновь принятых студентов специальности НМ, которые в течение одного академического года изучают иностранный язык в ИИЯ РУДН и параллельно с этим углубляют свои познания в области естественнонаучных дисциплин.

Положения программы опираются, с одной стороны, на программу средней школы по математике, рассматривая ее как отправной пункт. С другой стороны настоящая программа нацелена на подготовку студентов к более качественному овладению знаниями по программе изучения курса ЕН.Ф.01 на первом и последующих курсах основного этапа обучения в РУДН.

Полная учебная нагрузка составляет 228 часов, из которых 76 часа отводятся на лекционные и 152 часа на практические занятия.

Математика является не только мощным средством решения прикладных задач и универсальным языком науки, но также и элементом общей культуры. Поэтому математическое образование следует рассматривать как важнейшую составляющую фундаментальной подготовки специалиста физико-математических и естественных наук.


Цель курса
  • привить студенту элементы математического мышления, дать начальные сведения о высшей математике, формировать умения, способы и приемы решения математических задач;
  • расширить философски-мировоззренческие представления студента об окружающем мире, привитие навыков использования математических методов в практической деятельности.

Идейное содержание курса

Программа курса и система обучения построена таким образом, чтобы в рамках поставленных целей и задач обучения достичь должного уровня в общеобразовательной подготовке студента как будущего специалиста.

Фундаментальность математической подготовки включает в себя достаточную общность математических понятий и конструкций, обеспечивающую широкий спектр их применимости, разумную точность формулировок математических свойств изучаемых объектов, логическую строгость изложения математики, опирающуюся на адекватный современный математический язык.

Освоивший программу студент должен иметь представление о наиболее существенных математических понятиях и способах их использования, что должно облегчить ему возможность усвоения материала при дальнейшем обучении.


Организационно-методическое построение курса


Курс состоит из лекций и практических занятий.

Лекции представляют собой краткое, но систематическое изложение содержания курса математики. Содержанием такого общего курса является последовательное изложение основных положений математики, ее языка и теорий, а также обсуждение основных математических задач, их сущности и методов решения.

Практические занятия направлены на усвоение, повторение и закрепление лекционного материала через активное обсуждение и объяснения важных теоретических положений и методов в процессе анализа, поиска и решения системы математических задач с последующей повторной их отработкой в рамках самостоятельной аудиторной и домашней работы.

В начале каждого занятия в форме диалога излагается основной материал с уточнением всех тех трудностей, с которыми пришлось встретиться студентам учебной группы при работе над очередным домашним заданием. Далее силами преподавателя и студентов (в общем опросе или у доски) проговариваются в форме беседы основные положения по теме занятия, пишутся основные формулы, проговариваются определения в рамках темы занятия и только затем ведется последовательный аналитический разбор задач, предлагаемых педагогом. В процессе решения каждой задачи со стороны преподавателя ставятся такие вопросы: «с чего следует начинать решение задачи», «каковы условия и требования задачи», «нужна ли для задачи схематическая запись, т. е. нужно ли перефразировать условия задачи», «стоит ли разукрупнить задачу, т.е. представить в виде нескольких задач», «требуется ли графическая интерпретация условий задачи» и т. п. Только после активного обсуждения поставленных вопросов по решению предложенной задачи студентам учебной группы ставится со стороны преподавателя уже главный вопрос – «Какова вся структура процесса решения обсуждаемой задачи! », в надежде на то, что каждый студент сможет уже сам грамотно освоить основные этапы решения задачи и самостоятельно их реализовать на практике.

Таким образом, решая в определенной последовательности набор задач по каждой теме курса «Высшая математика» и многократно от задачи, к задаче проговаривая необходимые правила и подходы их решения, студент постепенно осваивает технику решения математических задач, причем, как стандартных, так и нестандартных задач по всем темам курса. Более того, усваивая методологические и предметные знания по математике, проявив должное при этом упорство и желание, сам может под наблюдением педагога последовательно формировать те необходимые умения и способности, которые очень важны и как для самостоятельного решения математических задач, так и для решения большого класса уже прикладных задач, включенных в данный курс и почерпнутые из других научных областей знания.

В заключении, с целью отработки каждой темы курса на практических занятиях студентам предлагаются задачи уже для самостоятельной работы как на занятии, так и дома для усвоения и закрепления учебного материала.

Особое значение в процессе обучения для студентов выступают такие виды учебной деятельности как выполнение контрольных работ или курсовых работ. Предусмотрены в рамках курса три контрольные работы в каждом семестре.

Согласно Учебному плану 1-ый семестр заканчивается зачетом, а 2-ой семестр – зачетом и экзаменом, где аттестация каждого студента на всех этапах его обучения определяется в рамках бальной рейтинговой системы по результатам набранных им по рейтингу баллов за каждый семестр.


Содержание курса

В курсе содержатся главы из следующих разделов высшей математики: элементы теории множеств, линейной алгебры, элементы общей алгебры и аналитической геометрии, введение в математический анализ, исчисление функций одной переменной, исследование функций с помощью производной, элементы комбинаторики, метод математической индукции.

Тема 1

Предмет и методы элементарной и высшей математики. Реальная действительность и математическая абстракция, роль математики в научной и практической деятельности. Алгебра и геометрия – старейшие ветви математики, диалектическая связь между ними. Числовые множества, действительная числовая ось, координата точки. Модуль числа, его геометрический смысл. Уравнения и неравенства с одним неизвестным (с геометрической интерпретацией решений).

Тема 2

Системы неравенств первой степени с одним неизвестным. Решение уравнений и неравенств, содержащих неизвестное под знаком модуля.

Тема 3

Элементы теории множеств. Множество. Подмножество. Операции над множествами. Основные свойства множеств. Декартово произведение. Бинарные отношения. Рефлексивность. Симметричность. Транзитивность. Отношение эквивалентности. Отображения. Обратное отображение. Композиция отображений.

Тема 4

Числа. Натуральные числа. Целые числа. Простые и составные числа. Наибольший общий делитель. Наименьшее общее кратное чисел. Рациональные числа. Иррациональные числа. Действительные числа.

Тема 5

Комплексные числа. Поле комплексных чисел. Понятие комплексного числа. Алгебраическая форма комплексного числа. Тригонометрическая форма комплексного числа. Возведение в степень и извлечение корня из комплексного числа. Формула Муавра.

Тема 6

Элементы векторной алгебры. Вектор. Проекции вектора на плоскости. Проекции вектора в пространстве. Линейные операции над векторами. Координаты точки. Скалярное произведение. Векторное и смешанное произведения в прямоугольных координатах. Декартовая система координат. Полярная система координат. Преобразование координат. Графики.

Тема 7

Элементы аналитической геометрии на плоскости. Ось и отрезок оси. Координаты на прямой. Декартовы прямоугольные координаты на плоскости. Отрезок, его проекции, длина, полярный угол. Расстояние между двумя точками. Деление отрезка в данном отношении. Площадь треугольника. Преобразование координат.

Тема 8

Уравнение линии. Функции двух переменных. Задание линии при помощи уравнения. Вывод уравнения заранее данных линий. Параметрические уравнения линии. Линии первого порядка. Общее уравнение прямой. Уравнение прямой с угловым коэффициентом. Угол между двумя прямыми. Уравнение прямой в отрезках. Нормальное уравнение прямой. Расстояние от точки до прямой. Уравнение пучка прямых. Полярное уравнение прямой.


Тема 9

Алгебраические линии второго порядка на плоскости. Парабола. Эллипс. Гипербола. Каноническое уравнение линий второго порядка. Компактная запись общего уравнения. Геометрические свойства линий второго порядка. Центр линии второго порядка. Диаметры линий второго порядка. Полярные уравнения линий второго порядка. Уравнения некоторых кривых, встречающихся в математике и ее приложениях.

Тема 10

Кольцо многочленов. Многочлены над полем вещественных чисел. Деление многочленов. Корни многочленов. Разложение многочлена на множители.

Тема 11

Элементы теории матриц. Виды матриц. Операции над матрицами. Линейные операции. Умножение матриц. Транспонирование матрицы. Элементарные преобразования матрицы. Ранг матрицы.

Тема 12

Определитель. Перестановки. Свойства определителя. Построение определителя n-го порядка. Вычисление определителя. Минор и алгебраическое дополнение. Разложение определителя по строке (столбцу). Обратная матрица. Условие обратимости матрицы.

Тема 13

Системы линейных алгебраических уравнений. Основные определения и понятия. Компактная запись системы. Системы с квадратной невырожденной матрицей. Решение систем уравнений методом Гаусса. Теорема Крамера. Совместимость системы. Общее решение системы. Однородные системы. Общее решение неоднородной системы.

Тема 14

Алгебраические структуры. Группа. Кольцо. Тело. Поле. Векторное пространство. Алгебраические законы.

Тема 15

Алгебраическое решение уравнений третьей и четвертой степеней.

Тема 16

Комбинаторика. Элементы комбинаторики. Арифметическая и геометрическая прогрессии. Метод математической индукции. Бином Ньютона. Общая формула разложения бинома в многочлен n-ой степени при произвольном n. Арифметическая и геометрическая прогрессии.

Тема 17

Последовательности. Числовые последовательности. Ограниченность. Сходимость. Теоремы о числовых последовательностях. Последовательности точек. Предел числовой последовательности. Нахождение числовой последовательности по общему члену. Вычисление пределов числовых последовательностей.

Особо ценится активная работа студента на занятиях, полное выполнение всех домашних заданий, успешное выполнение письменных контрольных в течение семестра. Математика изучается в группе, т.е. коллективно, с обсуждением всех возникающих вопросов. А написание контрольной (зачётной) работы – дело сугубо индивидуальное. Недопустимо пользоваться чужими выполненными домашними заданиями; во время контрольной работы, на зачёте или на экзамене недопустимо пользоваться недозволенными источниками, обращаться с вопросами к соседям и, тем более, списывать, т.е. присваивать чужую интеллектуальную собственность.


ОБЯЗАТЕЛЬНАЯ ЛИТЕРАТУРА



Учебники и учебные пособия

  1. Зайцев В.В., Рыжков В.В., Сканави М.И. Элементарная математика. М.: УДН. 1984.
  2. Ефимов А.В Краткий курс аналитической геометрии. – М.: Издательство Физматлит, 2006. – 240с.
  3. Фадеев Д.К., Сочинский И.С. Алгебра. – М.: Издательство физико-математической литературы, 1966. –528с.
  4. Михеев В. И., Павлюченко Ю. В. Высшая математика // Учебное пособие - М.: Изд-во РУДН, 2005.- 182с. (ВМП)
  5. Письменный Д. Т. Конспект лекций по высшей математике. Часть 1, 2. М., Айрис-Пресс, 2005.
  6. Привалов И.И., Гальперин С.А. Основы анализа бесконечно малых. – М.: Физматгиз, 1966. – 266с.
  7. Фор Р., Кофман А., Дени-Папен М. Современная математика. – М.: Мир, 1966. –272с.
  8. Курош А.Г. Лекции по общей алгебре. – Издательство «Лань», 2005. – 416с.


Задачники
  1. Ефимов А.В., Каракулин А.Ф. и другие. Сборник задач по математике. – М.: Издательство физико-математической литературы. В 4-х частях. Часть 2. –2003.-432с.
  2. Клетеник Д. В. Сборник задач по аналитической геометрии: Учебное пособие для втузов. Издательство Профессия. Серия «Специалист», 2007. – 199с.
  3. Цубербиллер О. Н. Задачи и упражнения по аналитической геометрии. Издательство «Лань», 2005. – 336с.
  4. Демидович Б.П. Сборник задач и упражнений по математическому анализу. М.: ООО Издательство «Астрель», 2003. –558с.
  5. Кузнецов Л.А. Сборник задач по высшей математике. Типовые расчеты. СПб.: Лань, 2005.- 240с.

Дополнительная литература

Учебники и учебные пособия
  1. Михеев В.И., Павлюченко Ю.В. Методическое пособие по курсу «Высшая математика» для ИГБ-1 и ИРБ-1. - Москва: Издательство РУДН, 2006.
  2. Фихтенгольц Г.М. Основы математического анализа. В 2-х ч. Ч: 1. Издательство «Лань», 2006. – 448с.
  3. Боревич З.И. Определители и матрицы. – Издательство «Лань», 2004..- 184с.


Задачники


17. Минорский В.П. Сборник задач по высшей математике. Учебное пособие для втузов- М.: Издательство физико-математической литературы. 2001. – 336с.
  1. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах: В 2 т. Ч.1,2. – М.: ОНИКС 21 век, Мир и образование, 2003.
  2. Фадеев Д.К., Соминский И.С. Сборник задач по высшей алгебре. – М.: Издательство физико-математической литературы, 1972. –304с.
  3. Лунгу К.Н., Письменный Д.Т. Сборник задач по высшей математике: с контрольными работами. Айрис-Пресс, 2007.- 576с.
  4. Рябушко А.П., Бархатов В.В. Сборник индивидуальных заданий по высшей математике. Минск: Издательство «Высшая школа», 1990. Ч.1.- 270с.




ПОЛЕЗНЫЕ ССЫЛКИ





учебный портал РУДН

Федеральный портал "Российское образование"

Образовательный математический сайт

На сайте представлены этюды, выполненные с использованием современной

компьютерной 3D-графики, увлекательно и интересно рассказывающие о математике и

ее приложениях.




Монографии по истории математики (на англ. языке)  

Электронный ресурс издательства Springer. Кроме всего прочего содержит ссылка скрыта, переведенных на английский язык (полнотекстовые варианты).  

Поиск электронных книг

Электронная библиотека книг по математике
    • u/

Высшая математика (лекции, примеры решения задач)

Математика, физика (лекции, задачи, учебники).


БАЛЛЬНО - РЕЙТИНГОВАЯ СИСТЕМА



В семестре проводится 4 контрольных работы (максимально 18 баллов за каждую);

За отсутствие на занятиях минус 2 балла;

За работу у доски (положительно) плюс 1 балл (засчитывается не более одного раза за занятие);

За невыполнение домашнего задания минуc 1 балл;

Индивидуальные домашние задания. Все студенты в обязательном порядке выполняют индивидуальные домашние задания.

Формула подсчета числа баллов, набранных студентом за семестр:

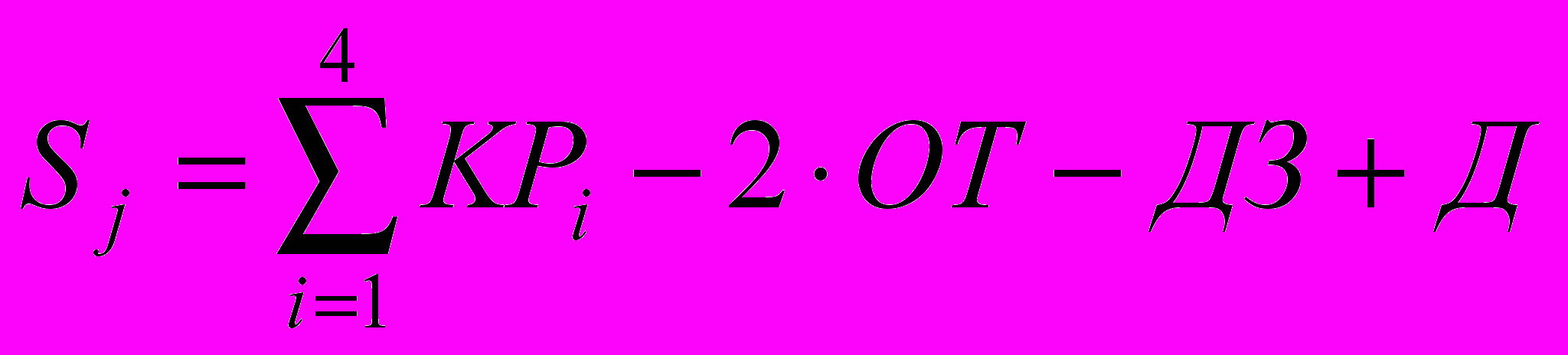, где

Sj – суммарное число баллов за семестр j (j = 1, 2);

КРi – число баллов за i контрольную работу;

ОТ – число пропущенных занятий;

ДЗ – число невыполненных домашних заданий;

Д – число положительных выходов к доске.

ЗАЧЕТ

Максимальное число баллов за семестр: S = 100 баллов.

Студент получает зачет при числе баллов S ≥ 70 при условии выполнения индивидуального домашнего задания.

ЭКЗАМЕН

Число баллов для балльно-рейтинговой аттестации подсчитывается по формуле:

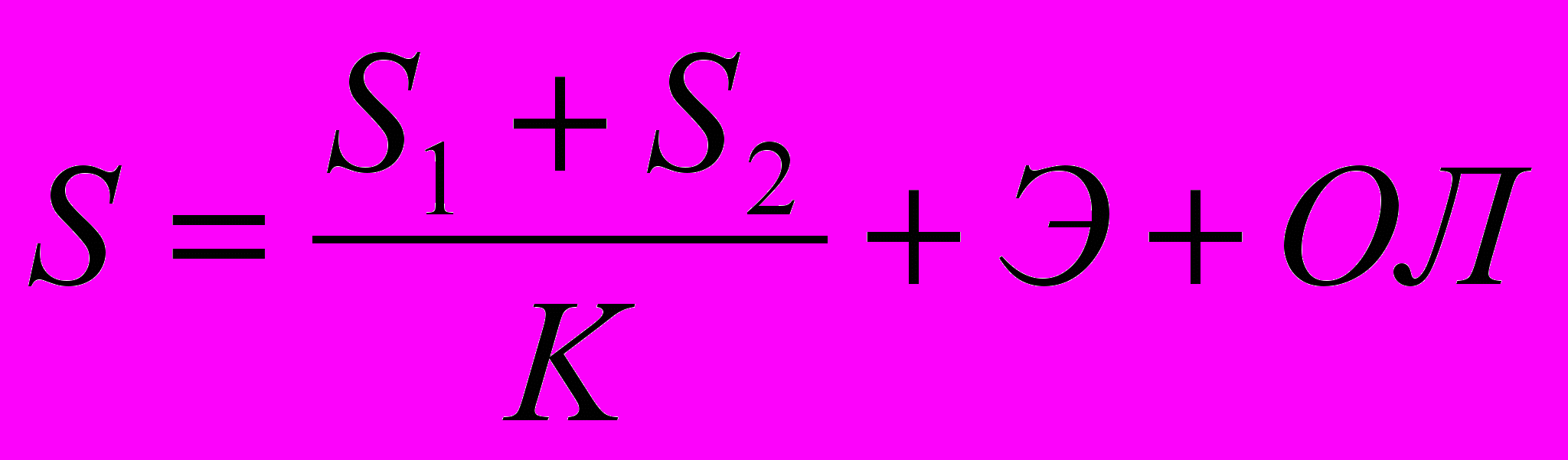, где

К – коэффициент для учета работы студента в течение года (К = 20);

Э – число баллов, полученных студентом за экзамен. За письменную экзаменационную работу максимальное число баллов 60;

ОЛ – число баллов, заработанных студентом на олимпиаде.

По результатам балльно-рейтинговой аттестации выставляются следующие оценки:


Баллы
Оценка

56 - 70
отлично*

41 - 55
хорошо

23 - 40
удовлетворительно


Примечание. *Для получения отличной оценки необходимым условием является выполнение 75% практических задач экзаменационной работы.


ЭКЗАМЕНАЦИОННЫЕ ВОПРОСЫ ПО МАТЕМАТИКЕ

для групп НМ, НП, НК (1-10)

  1. 1. Эллипс. Определение. Вывод уравнения эллипса в канонической системе координат.

2. Гипербола. Определение. Вывод уравнения гиперболы в канонической системе

координат.
  1. 3. Парабола. Определение. Вывод уравнения параболы в канонической системе координат.
  2. 4. Кривые второго порядка. Определение.
  3. 5. Приведение кривой второго порядка к каноническому виду.
  4. 6. Признак распадения линий второго порядка. Доказательство.
  5. 7. Классификация кривых 2 порядка.
  6. 8. Квадратичная форма. Представление линии второго порядка в матричном виде.
  7. 9. Скалярное произведение. Выражение скалярного произведения векторов в прямоугольной системе координат.
  8. 10. Собственные значения и собственные векторы вещественной симметричной квадратной матрицы. Теорема об ортогональности собственных векторов, отвечающих различным собственным числам вещественной симметричной матрицы.
  9. 11. Теорема о приведении к каноническому виду квадратичной формы ортогональным преобразованием.
  10. 12. Теорема о коэффициентах квадратичной формы, приведенной к каноническому виду ортогональным преобразованием (они являются собственными числами).
  11. 13. Линейно независимые системы векторов и их свойства.
  12. 14. Определение собственных чисел и собственных векторов. Теорема о характеристических многочленах.
  13. 15. Приведение матрицы к верхнему треугольному виду элементарными преобразованиями.
  14. 16. Матрицы. Операции над ними.
  15. 17. Определитель матрицы. Свойства определителей.
  16. 18. Алгебраическое дополнение. Теорема о разложении определителя по любой строке.
  17. 19. Теорема об определителе произведения квадратных матриц.
  18. 20. Теорема о существовании обратной матрицы. Вычисление обратной матрицы.
  19. 21. Теорема о необходимом и достаточном условиях линейной зависимости строк (столбцов) матрицы.
  20. 22. Ранг матрицы. Теорема о базисном миноре.
  21. 23. Системы линейных уравнений. Теорема о существовании нетривиального решения однородной системы.
  22. 24. Системы линейных уравнений. Условия их совместности, определенности, равносильности.
  23. 25. Теорема Кронекера-Капелли о совместности системы линейных уравнений.
  24. 26. Теорема Крамера для системы линейных уравнений.
  25. 27. Собственные векторы и собственные значения линейного преобразования. О приведении матрицы линейного преобразования к диагональному виду.
  26. 28. Метод Гаусса.
  27. 29. Матричный метод решения систем линейных алгебраических уравнений.
  28. 30. Условия коллинеарности и компланарности векторов. Направляющиеся косинусы.
  29. 31. Определение базиса векторов и координат вектора.
  30. 32. Прямоугольная система координат. Координаты точки и вектора в прямоугольной системе координат.
  31. 33. Проекция вектора на ось. Свойства проекций.
  32. 34. Векторное произведение векторов. Определение, свойства, координатное представление.
  33. 35. Смешанное произведение векторов. Определение, свойства, координатное представление.
  34. 36. Расстояние от точки до прямой, пересечение прямых. Вывод формул.
  35. 37. Преобразование координат на плоскости.
  36. 38. Полярная система координат.
  37. 39. Комплексные числа. Сопряженное комплексное число. Модуль комплексного числа. Геометрическая интерпретация. Алгебраическая и тригонометрическая формы комплексного числа. Операции над комплексными числами.
  38. 40. Метод математической индукции.
  39. 41. Комбинаторика. Правило произведения. Правило суммы.
  40. 42. Перестановки.
  41. 43. Размещения.
  42. 44. Сочетания.
  43. 45. Бином Ньютона.
  44. 46. Способы задания функции, явная форма функции, обратная, четная, нечетная, периодическая функции.
  45. 47. Определение основных элементарных функций.
  46. 48. Определение числовой последовательности, ее предела.
  47. 49. Определение бесконечно малой величины, предельного процесса, предела функции.
  48. 50. Доказательства лемм о бесконечно малых. Сравнение бесконечно малых.
  49. 51. Доказательства теорем о пределах.
  50. 52. Непрерывность функции в точке. Свойства непрерывных функций.
  51. 53. Теорема Вейерштрасса. Всякая монотонная ограниченная последовательность имеет предел.
  52. 54. Бесконечно малые функции. Определения и основные теоремы.
  53. 55. Признаки существования пределов.
  54. 56. Эквивалентные бесконечно малые функции.
  55. 57. Вывод первого замечательного предела .
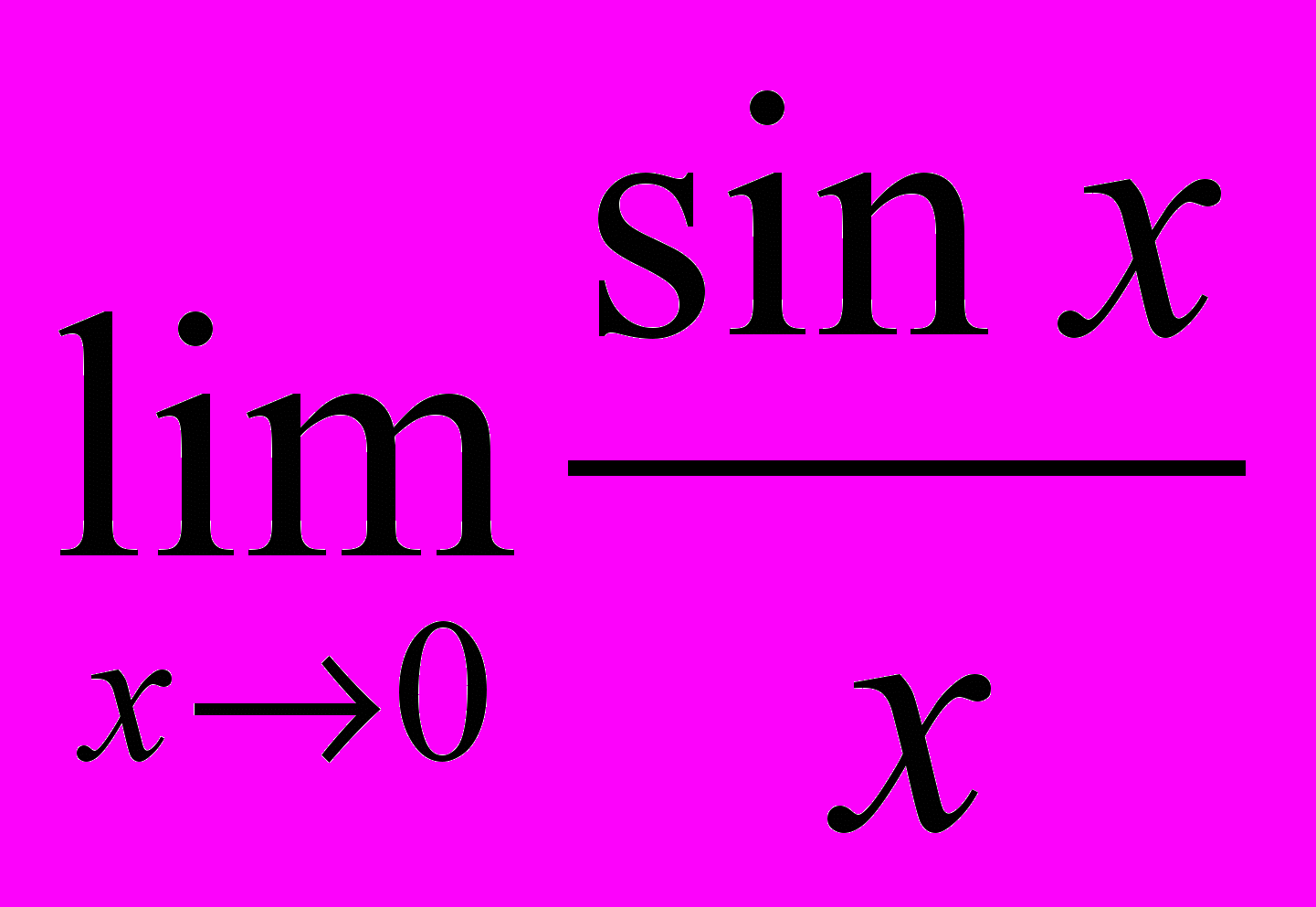  56. 58. Число е. Вывод второго замечательного предела .
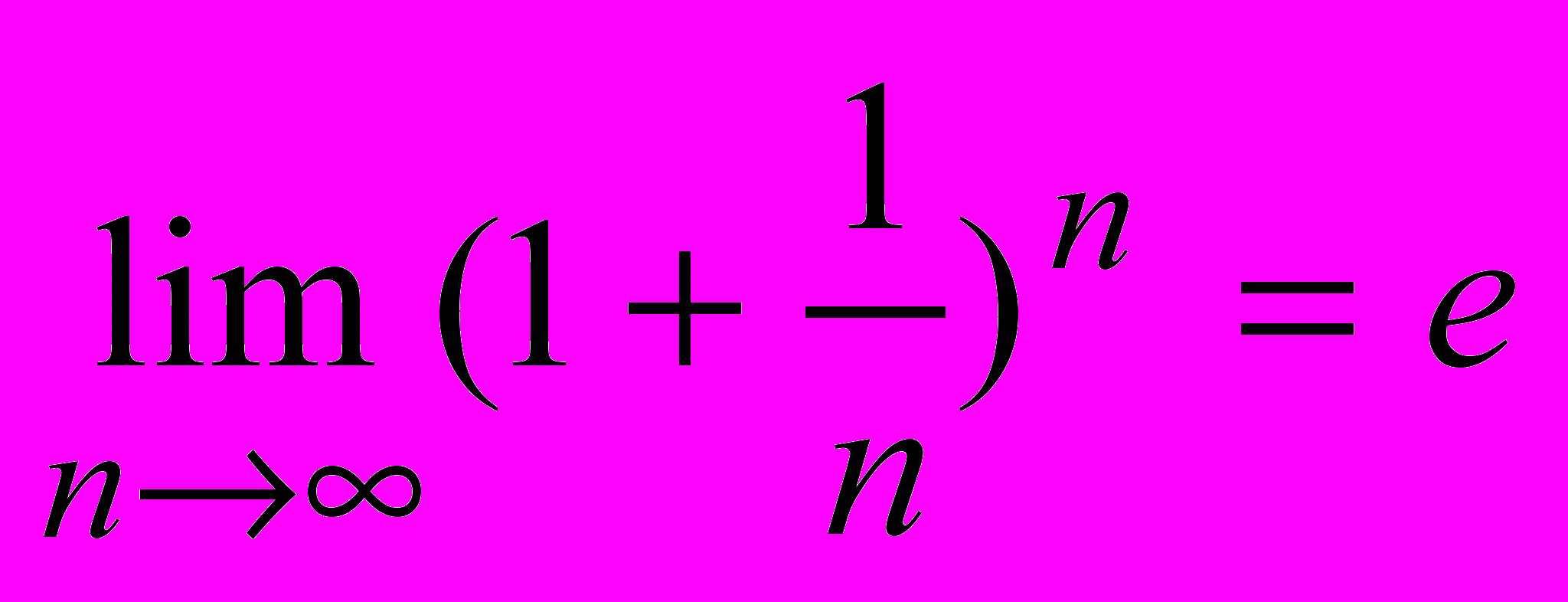  57. 59. Вывод предела .
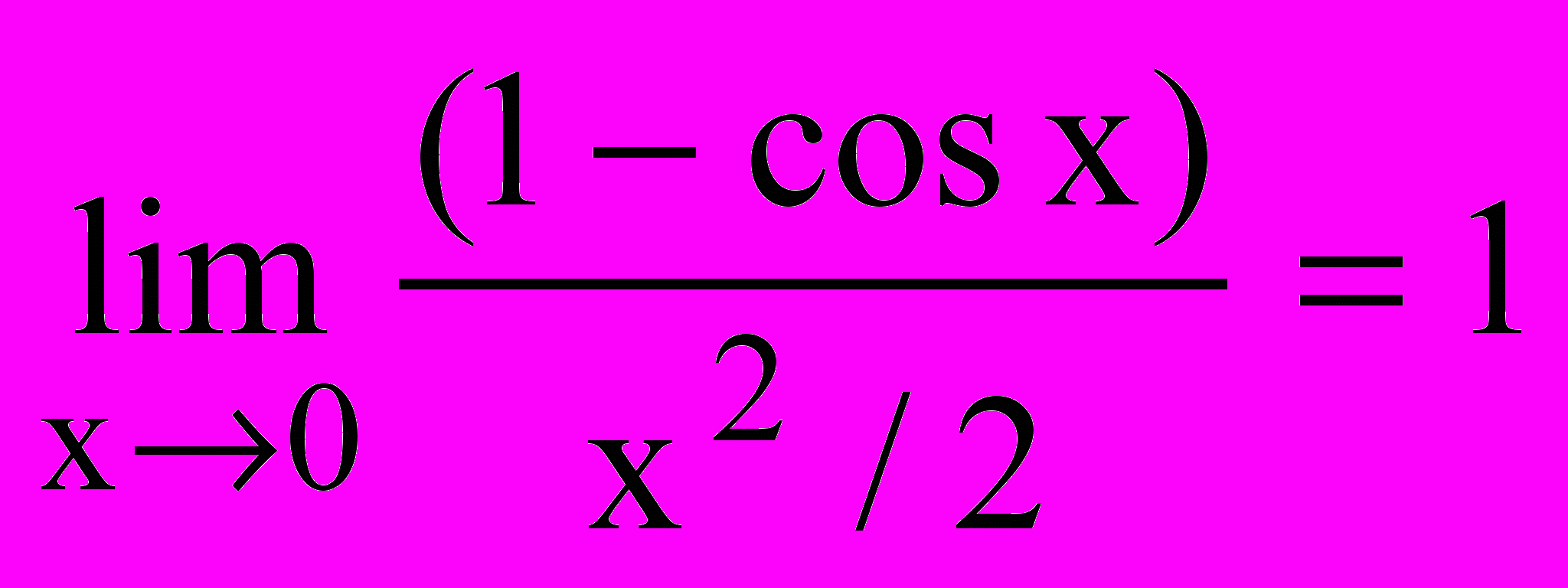  58. 60. Общие правила раскрытия неопределенностей.
  59. 61. Критерий Коши сходимости числовой последовательности.