Г. А. Нестационарные задачи термоупругости слоистых композитых конструкций

Вид материала

Документы

Содержание Материалы и методика исследований. H, G – матрицы теплопроводности,  t – K – матрица жесткости, u

Подобный материал:

• Разработка технологии соединения элементов титановых слоистых конструкций давлением, 260.62kb.
• Указания по монтажу металлических и деревянных конструкций монтаж металлических конструкций, 297.4kb.
• Определение функций параметрической чувствительности механических характеристик конструкций, 51.79kb.
• Пособие по проектированию каменных и армокаменных конструкций (к #M12291 9056429СНип, 13145.52kb.
• Iii международный симпозиум актуальные проблемы компьютерного моделирования конструкций, 77.34kb.
• 2 Современные тенденции развития российской индустрии строительных металлических конструкций, 43.67kb.
• Название доклада, 129.66kb.
• Программа дисциплины дпп. Дс. 03 Конструктивное моделирование цели и задачи дисциплины:, 244.75kb.
• Роко используется при изготовлении строительных металлических конструкций в заводских, 1408.09kb.
• Задачи дисциплины, 94.25kb.

УДК539.5

к.т.н., ст. преп. Козуб Г.А.

НЕСТАЦИОНАРНЫЕ ЗАДАЧИ ТЕРМОУПРУГОСТИ СЛОИСТЫХ КОМПОЗИТЫХ КОНСТРУКЦИЙ

В статье предложена математическая модель поведения слоистого материала для решения нестационарных задач термоупругости на основе метода конечных элементов. Алгоритм решения нестационарных задач основан на применении неявной схемы дискретизации по времени.

У статті запропоновано математичну модель поводження шаруватого матеріалу для розв’язання нестаціонарних задач термопружності на основі методу скінчених елементів. Алгоритм розв’язання нестаціонарних задач оснований на використанні неявної схеми дискретизації за часом.

The mathematical model of behavior of layer material for solution of non-stationary problem of thermoelasticity based on finite element method is presented in this article. The algorithm for solution of non-stationary problem is based on application of non-explicit scheme of time sampling.


Введение. В современной технике все более широкое применение находят слоистые композитные материалы. Анизотропные свойства таких материалов позволяют создавать рациональные конструкции и конструктивные элементы. Достижения в области расчета и проектирования таких конструкций достаточно широко обсуждаются в литературе. Но в то же время остается неисследованным вопрос о решении нестационарных задач термоупругости для конструкций, изготовленных их анизотропных материалов, в частности, из слоистых композитов. Применение аналитических методов для таких задач связано с определенными затруднениями, обусловлены различными причинами, например, достаточно сложной геометрической формой конструктивного элемента или сложным характером нагружения. Основной целью настоящей работы является разработка методики численного решения задач термоупругости на основе применения метода конечных элементов (МКЭ) в трехмерной постановке.

Материалы и методика исследований. На первом этапе решения задачи термоупругости необходимо определить температурное поле в теле. Для этого следует решить задачу теплопроводности. Применению МКЭ к задачам теплопроводности посвящено достаточно много опубликованных работ. Это связано, прежде всего, с большим количеством новых внедряемых в промышленность материалов и разнообразием конструкций из таких материалов. Кроме того, в большинстве работ применение МКЭ осуществляется на основе каких либо упрощающих гипотез. Рассмотрим методику решения задачи нестационарной теплопроводности для конструкций из слоистых материалов.

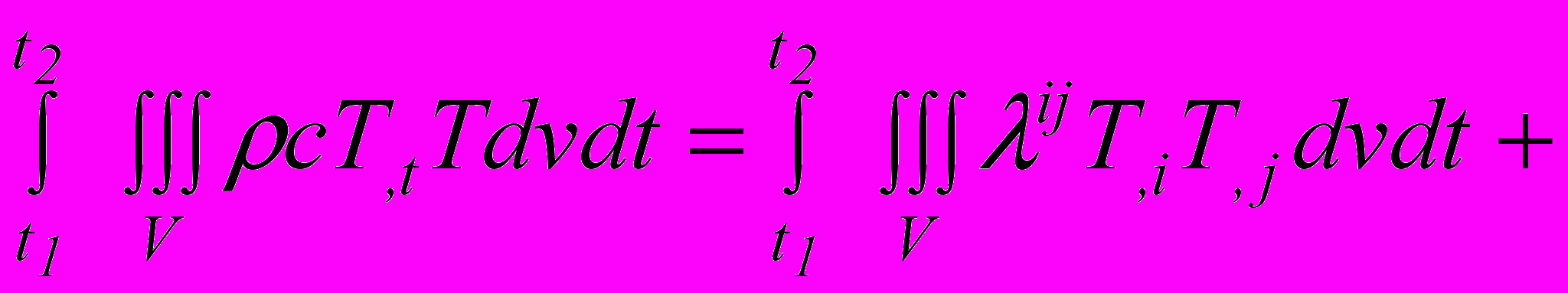
Уравнение нестационарной теплопроводности для анизотропного тела можно представить в виде 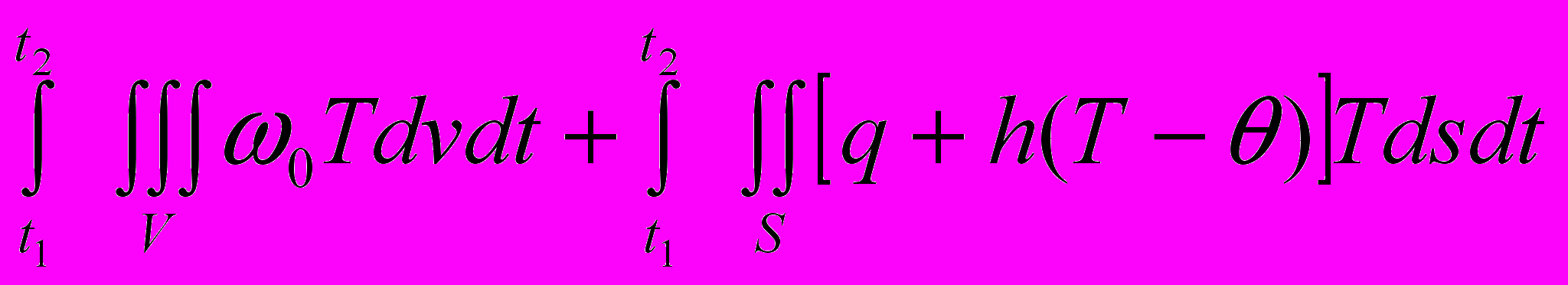[1]

, (1)

где -– плотность, с – теплоемкость, ^ij – тензор теплопроводности, ₀ – мощность внутренних источников тепла, q – интенсивность тепловых потоков, h – коэффициент теплопередачи,  – температура окружающей среды.

Применяя конечно-элементную дискретизацию по координатам и времени уравнение (1) можно привести к системе алгебраических уравнений. Функцию температуры можно представить в виде

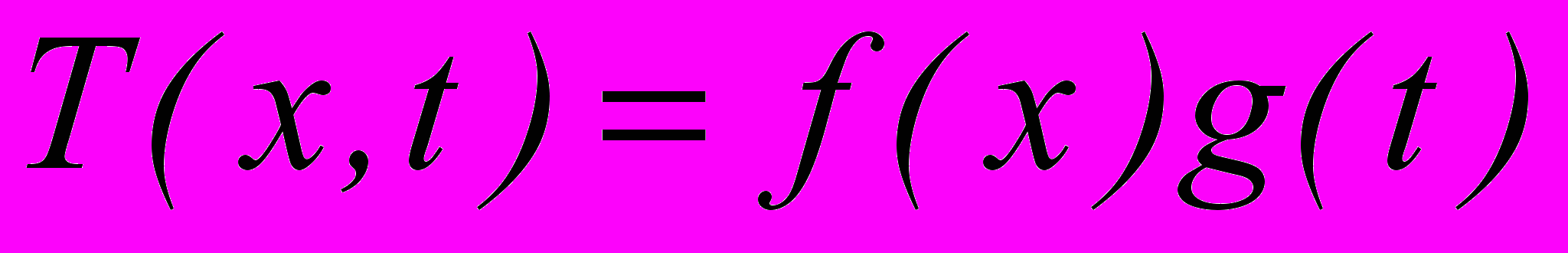(2)

Для конечного элемента, моделирующего поведение слоистого элемента конструкции, функция координат может быть представлена в виде

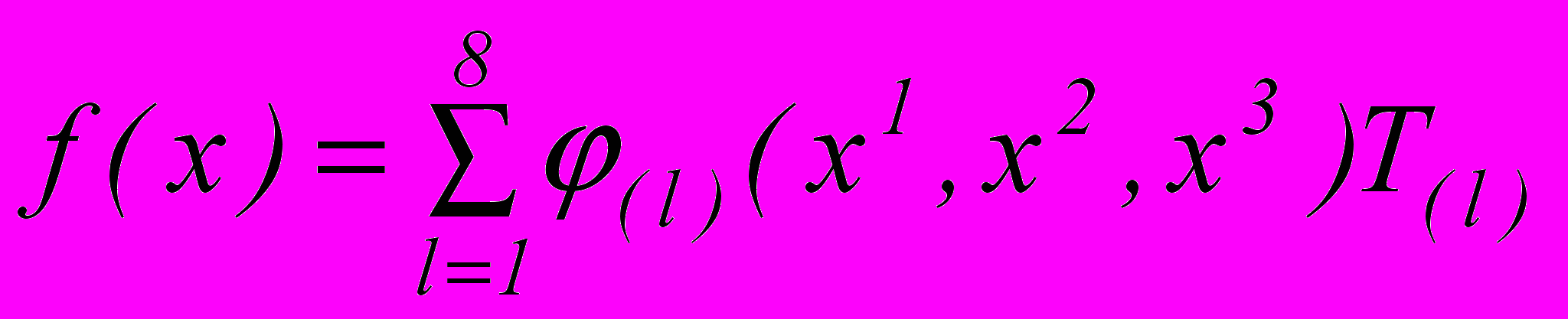(3)

где _(l) – функции формы слоистого конечного элемента.

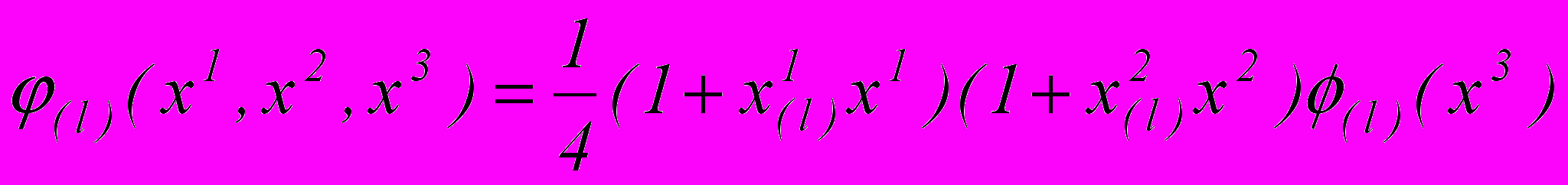. (4)

Функция _(l) определяется из условия линейности распределения температуры в слоях в трансверсальном направлении

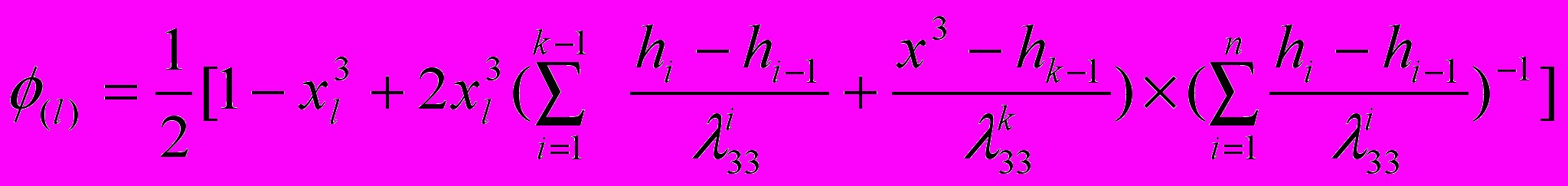(5)

где h_i – толщина і – го слоя.

Функция времени 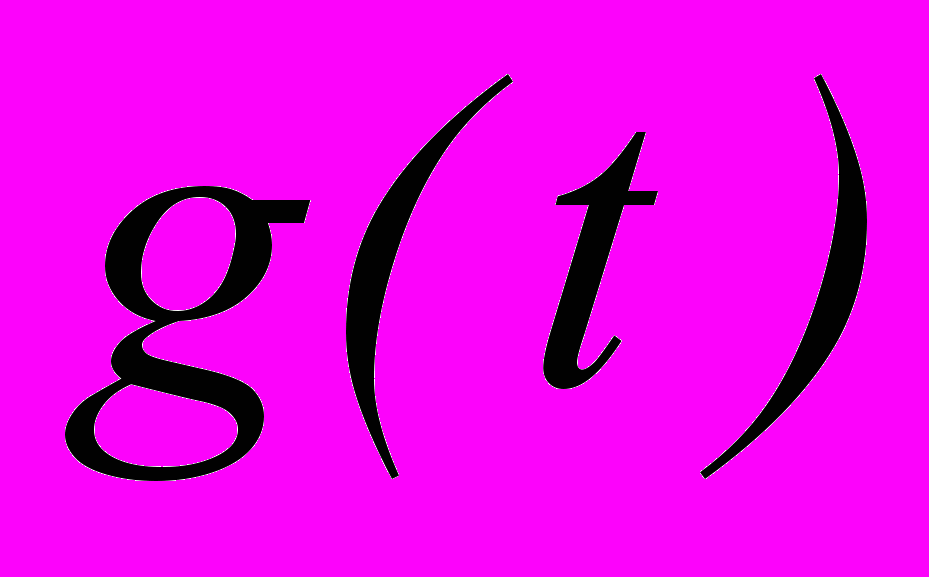принимается линейной.

Применяя конечноразностную аппроксимацию частной производной по времении с применением схемы Кранка – Николсона [2] получаем матричное уравнение

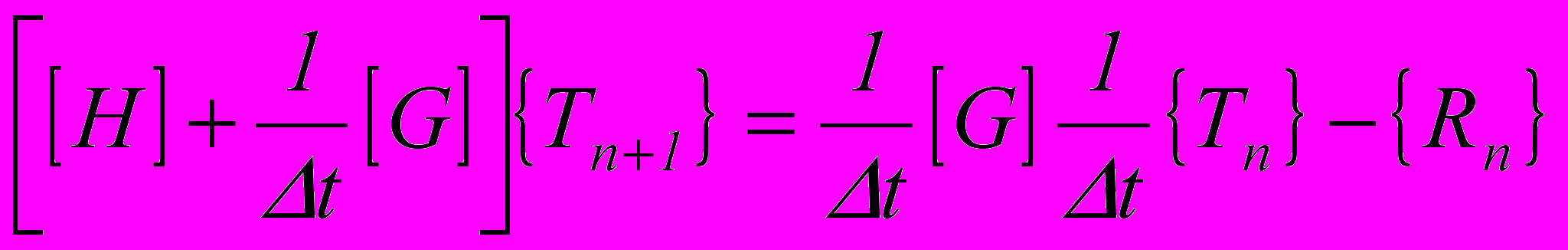, (6)

где H, G – матрицы теплопроводности,  t – шаг по времени, T, R – векторы узловых температур и тепловой нагрузки.

Для решения задач термоупругости используется МКЭ с применением субпараметрических конечных элементов [3], моделирующих свойства слоистого материала из предположения неразрывности поля перемещений точек слоев.

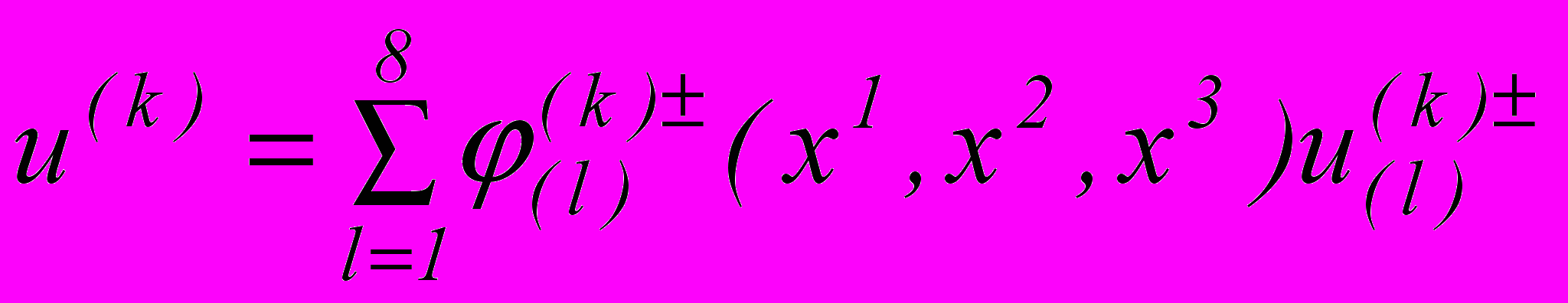, (7)

где 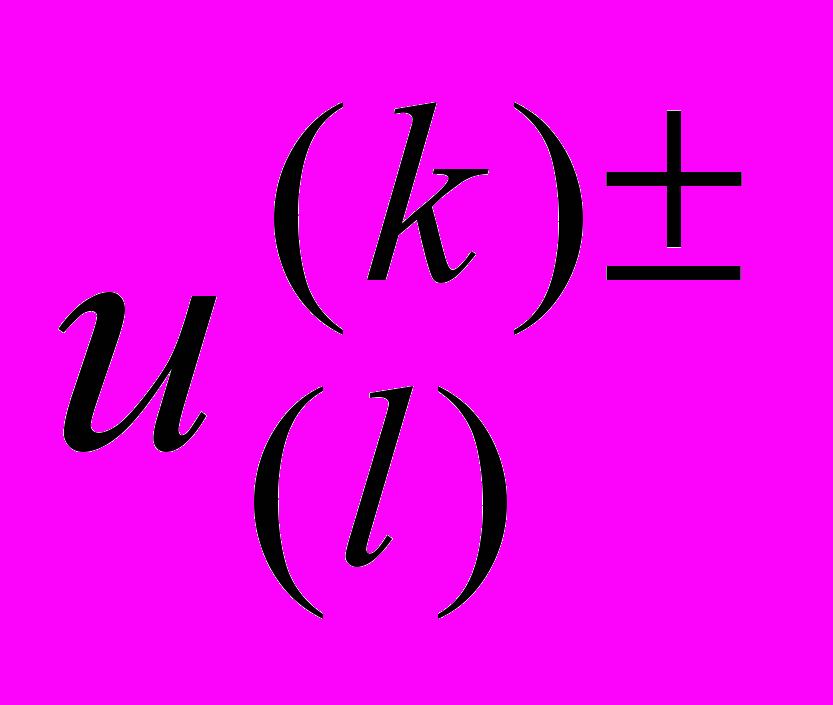– вектор перемещений узловых точек k-го слоя КЭ, 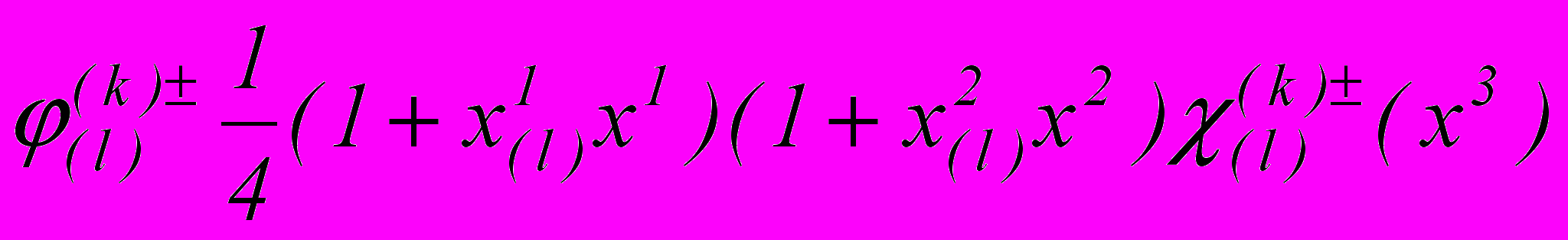. (8)

Причем для k-го слоя аппроксимация перемещений осуществляется с помощью функции

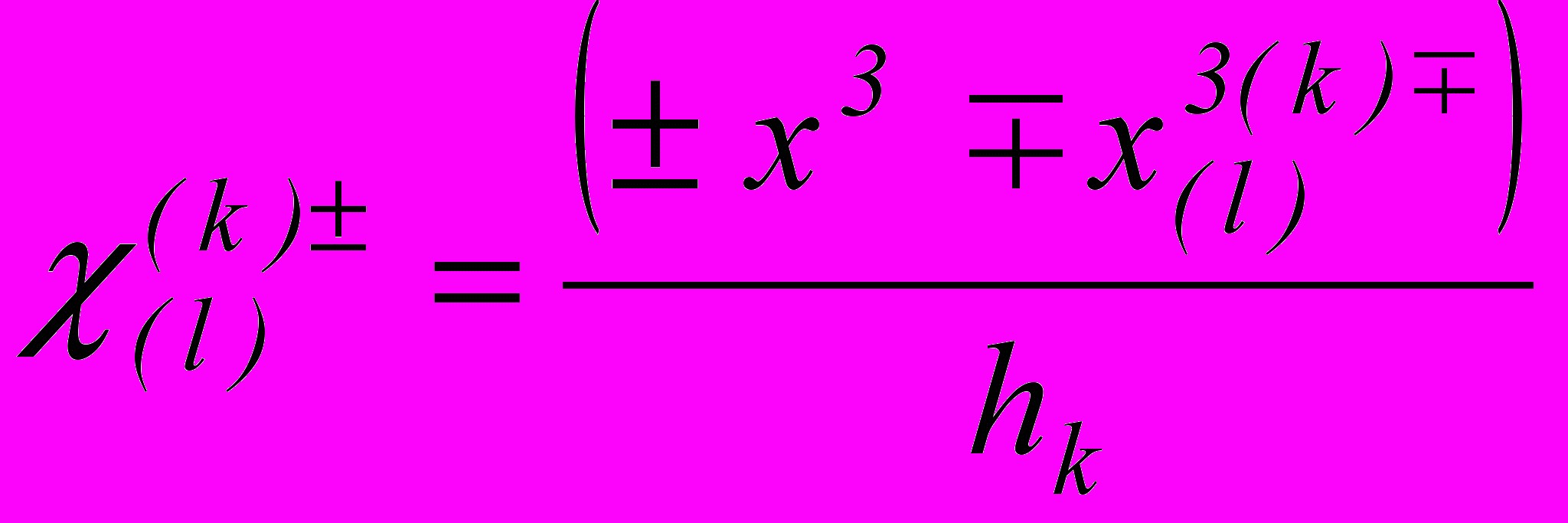, (9)

Исходя из закона сохранения энергии, вариационное уравнение термоупругости Био как обобщение вариационного принципа Лагранжа имеет вид 1,2

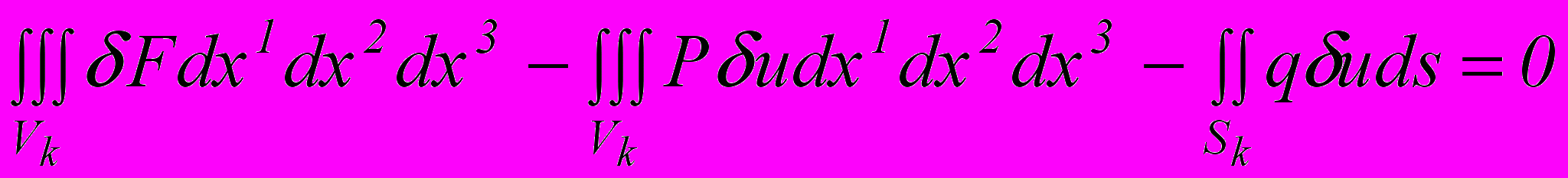. (10)

Вариация свободной энергии вычисляется по формуле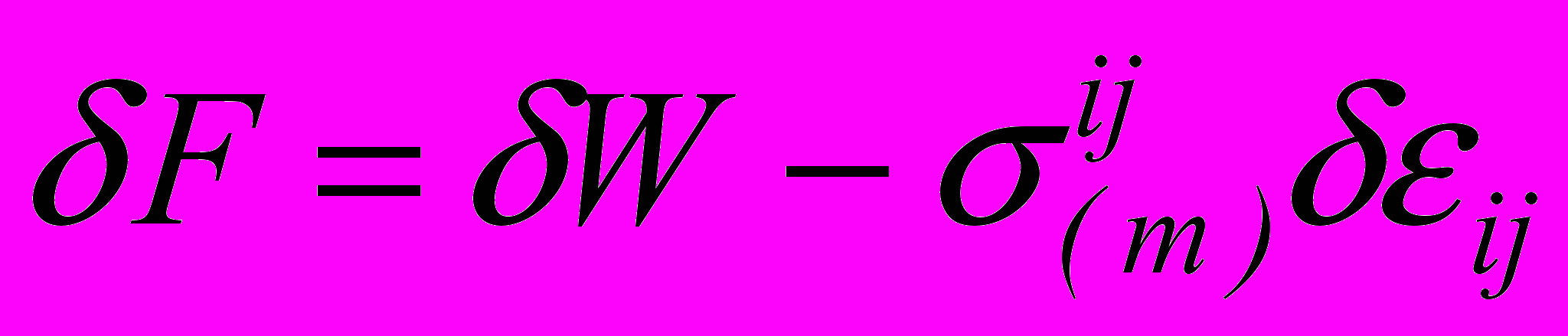

, (11)

здесь 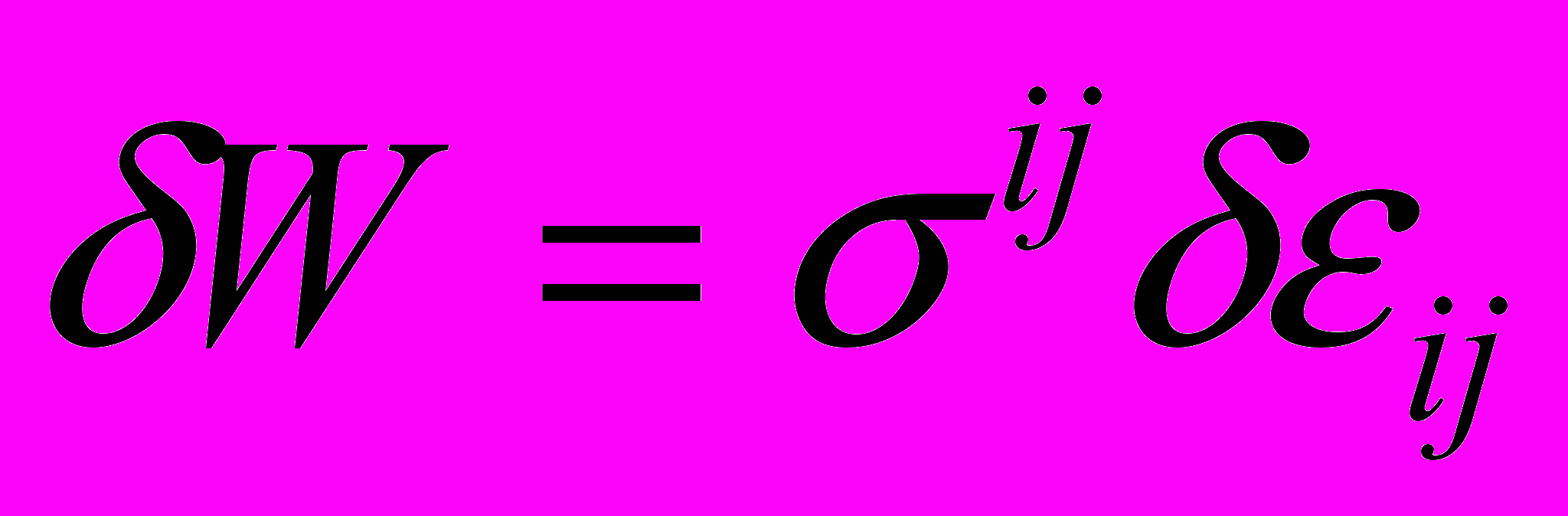- вариация упругой энергии деформации

Использование конечноэлементной аппроксимации позволяет получить матричное уравнение на каждом временном шаге в виде

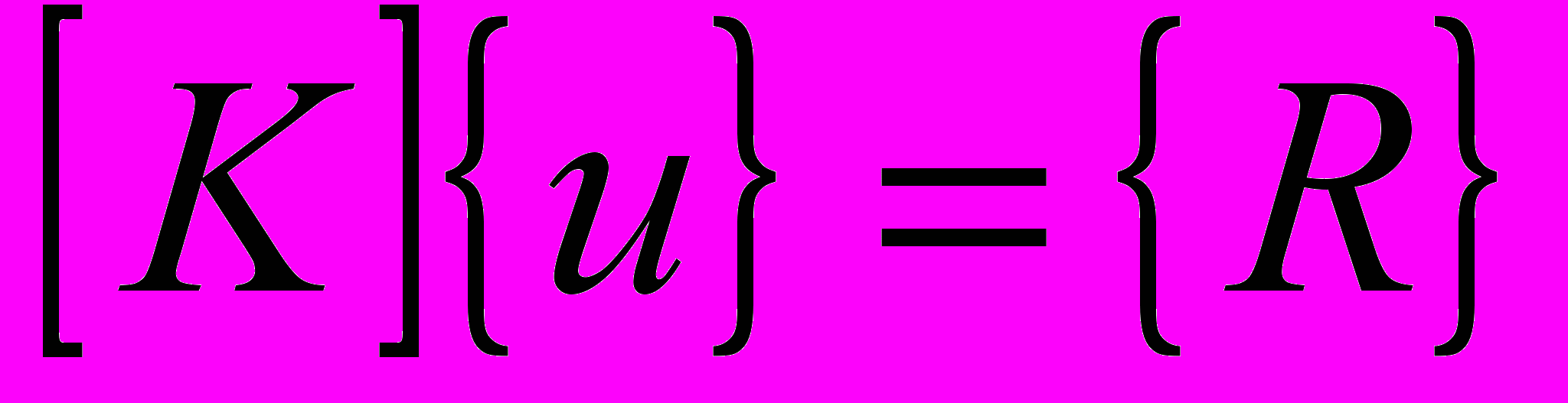, (12)

где K – матрица жесткости, u – вектор узловых перемещений, R – вектор узловых нагрузок, обусловленных действием механических и тепловых нагрузок.

В рамках рассмотренного подхода решен ряд задач.

Задача 1. Нестационарная одномерная задача теплопроводности для составной области. Данный пример рассмотрен в 4. Толщины слоев 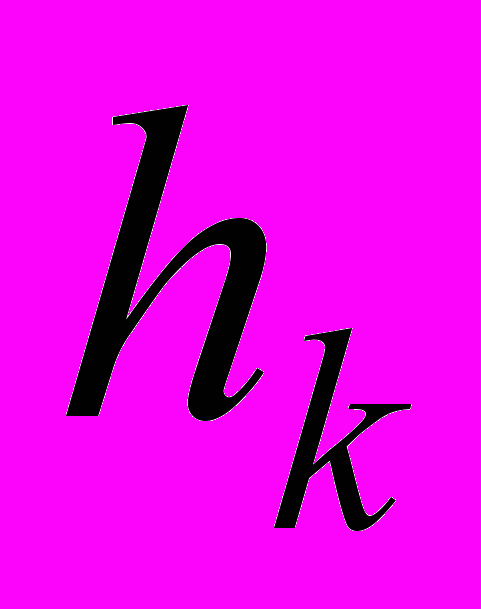=(1/3; 1/3; 1/3)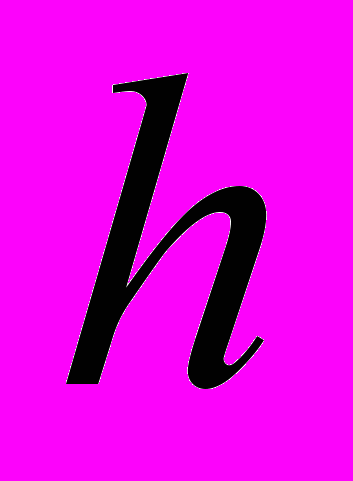, где 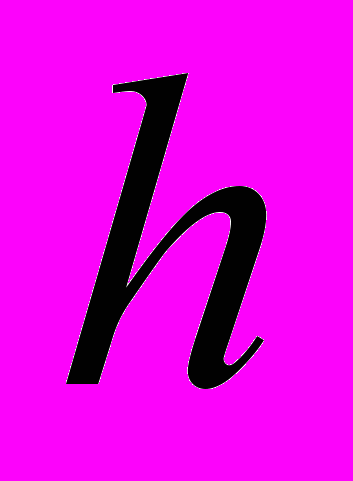=6 см – общая толщина пакета. Теплофизические характеристики: ^(k) = (34,5; 202; 65,6)Вт/(мК); ^(k)= (11340; 2700, 7400)кг/м³; c_p^(k) = (129.9; 758.4; 226.3)Дж/(кгК) (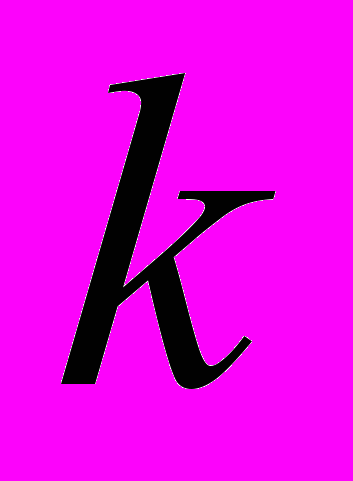=1, 2, 3). Начальная температура пакета 0^оС. В момент времени 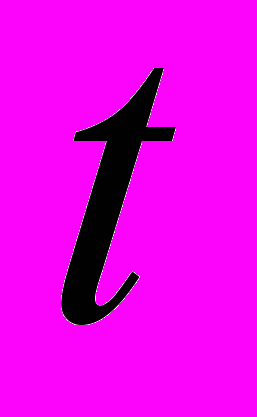=0 температура нижней поверхности (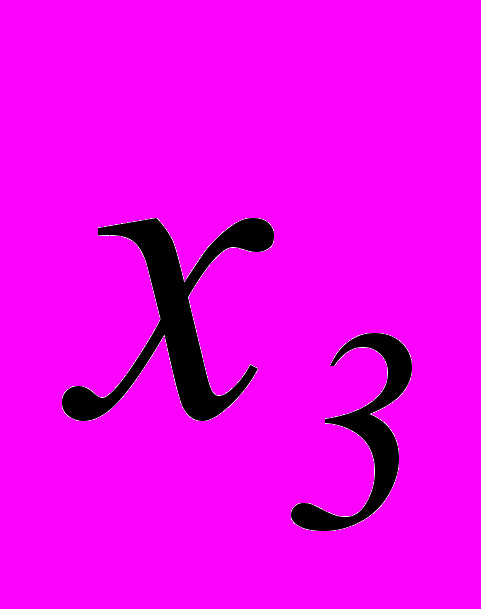=0) повышается от 0 до 400 ^оС и поддерживается такой на протяжении всего процесса. На рис. 1. дано распределение температуры по толщине пакета в момент времени 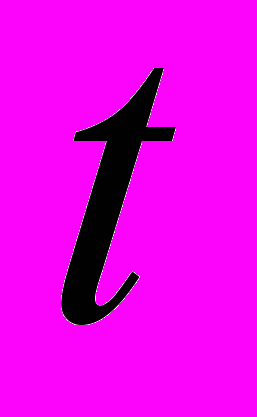. Конечно-элементное решение, полученное на основе трехмерных КЭ, практически совпадает с аналитическим, приведенным в 4. Погрешность не превышает 1,5%, поэтому результаты представлены одной кривой. Кривые 1, 2, 3 соответствуют распределению температуры при t= 810^-4 , 5010^-4 , 1 (c).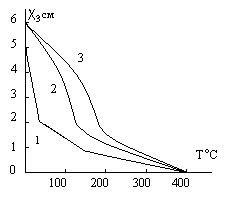



Рис. 1.

Задача 2. Нестационарная задача теплопроводности для двухслойного цилиндра при сложном температурном нагружении. Необходимо отметить, что в научной литературе практически отсутствуют точные решения нестационарных задач теплопроводности для слоистых композитных систем.

Рассмотрим двухслойный цилиндр с толщиной слоев 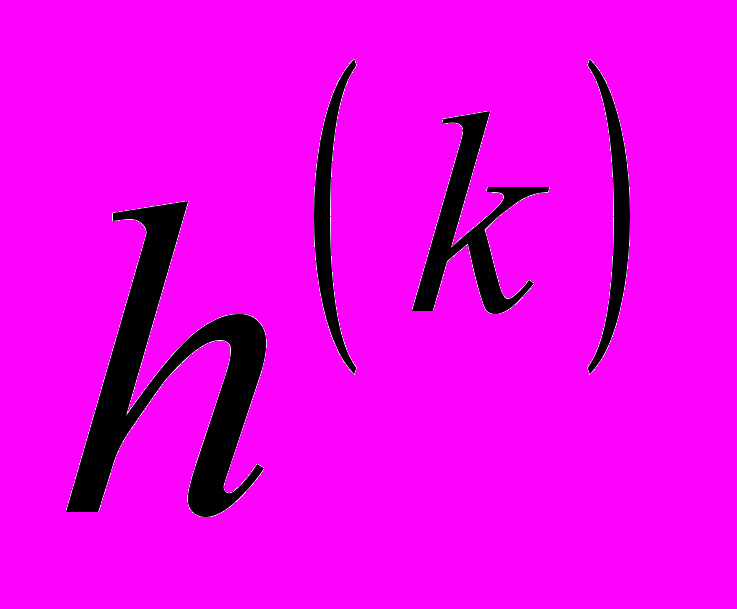=(2/3, 1/3)h, где h=0,3 см – общая толщина пакета. Начальная температура —20 ^оС. Теплофизические характеристики следующие: ^(k) =(2, 23,3)Вт/(мК); c_p^(k) = (2,0, 4,413)10⁶ Дж/(м³ К). Со стороны наружной поверхности температура окружающей среды меняется по закону Т=500(1+0,1cos)^оС. Внутренняя поверхность цилиндра и торец x₂ =10 см теплоизолированы, а на торце x₂ =0 задан конвективный теплообмен с окружающей средой =300^оС. Коэффициенты теплоотдачи на наружной и торцевой (x₂ =0) поверхностях приняты одинаковыми и равными 1000Вт/(м²К). Применена неявная схема дискретизации по времени с шагом t=0,2с. Распределение температуры по внутренней и внешней поверхности цилиндра вдоль образующей для сечения =180^о при t =10с приведено на рис.2. Результаты, полученные на основе предлагаемого подхода (сплошная кривая), хорошо согласуются с решением 5, полученным с помощью полуаналитического метода конечных элементов.

Задача 3. Задача термоупругости для цилиндра (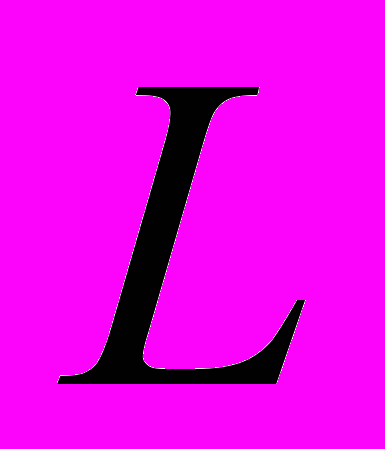=2 м; =4 м; 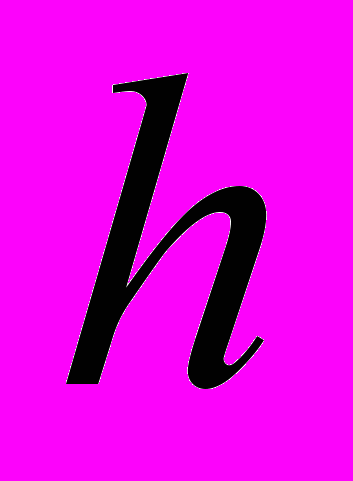=0,4 м) трехслойной структуры из термочувствительных материалов. Торцы оболочки жестко защемлены. Зависимость характеристик материала слоев от температуры аппроксимируется линейными функциями

,

, ,

,

, ,

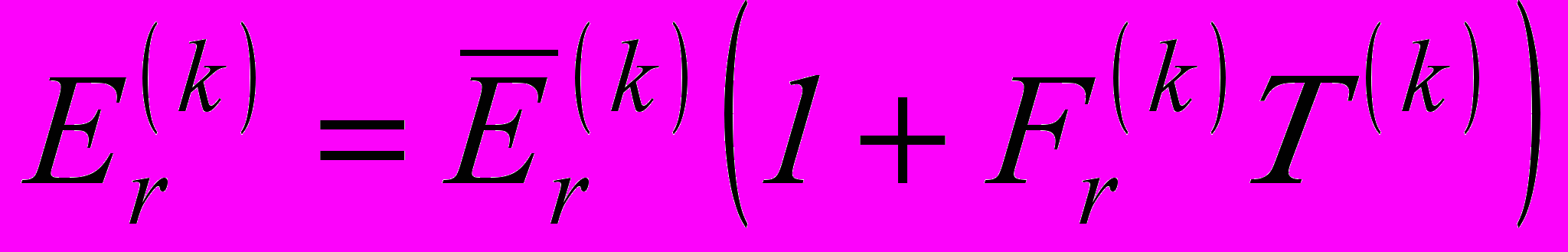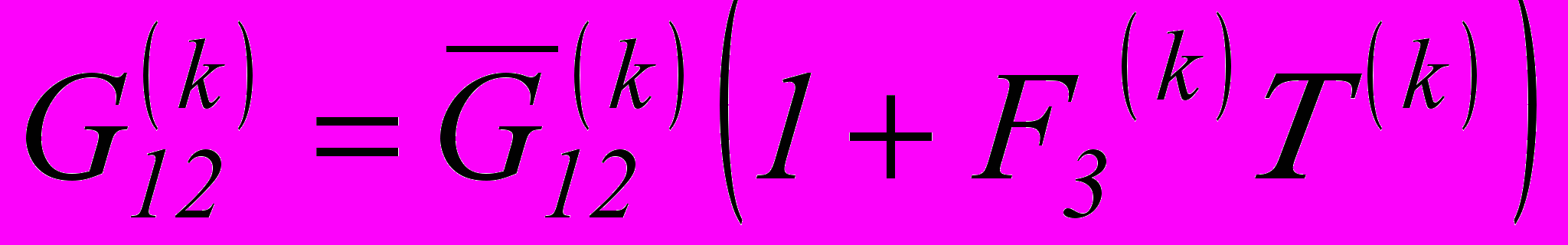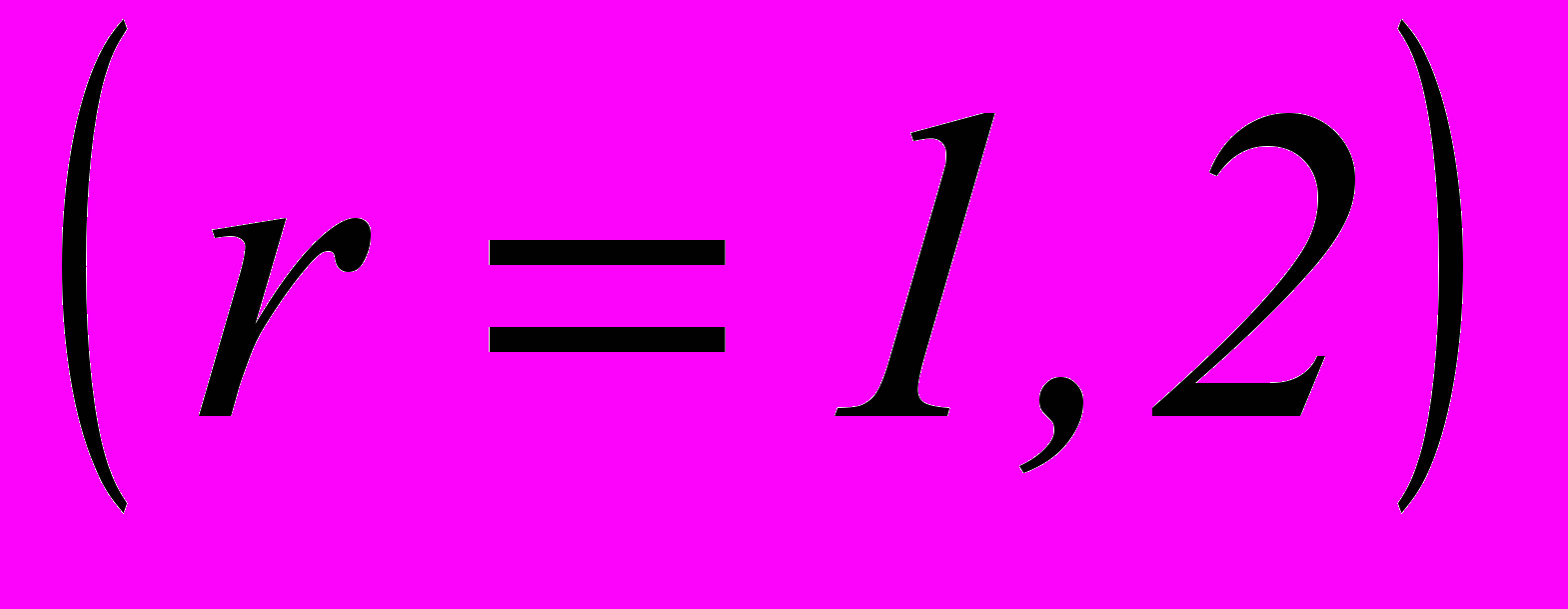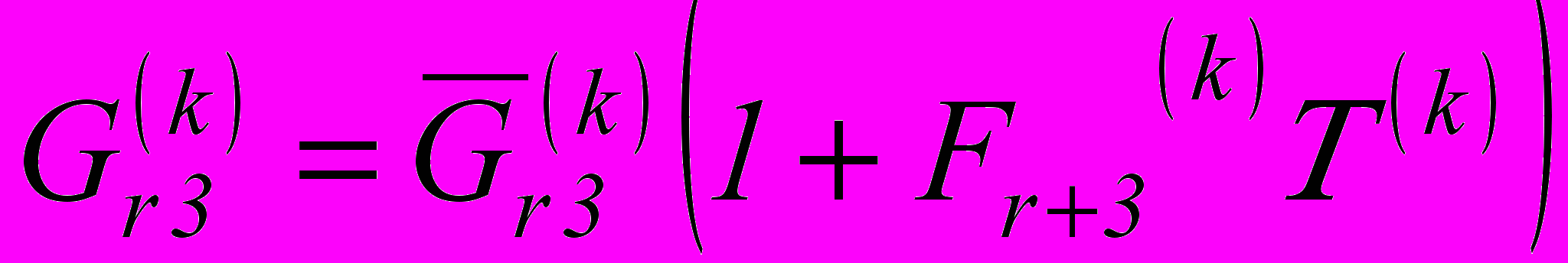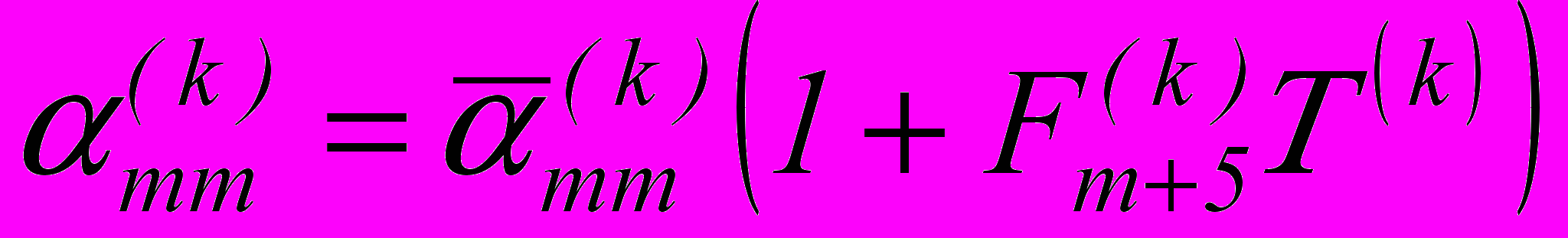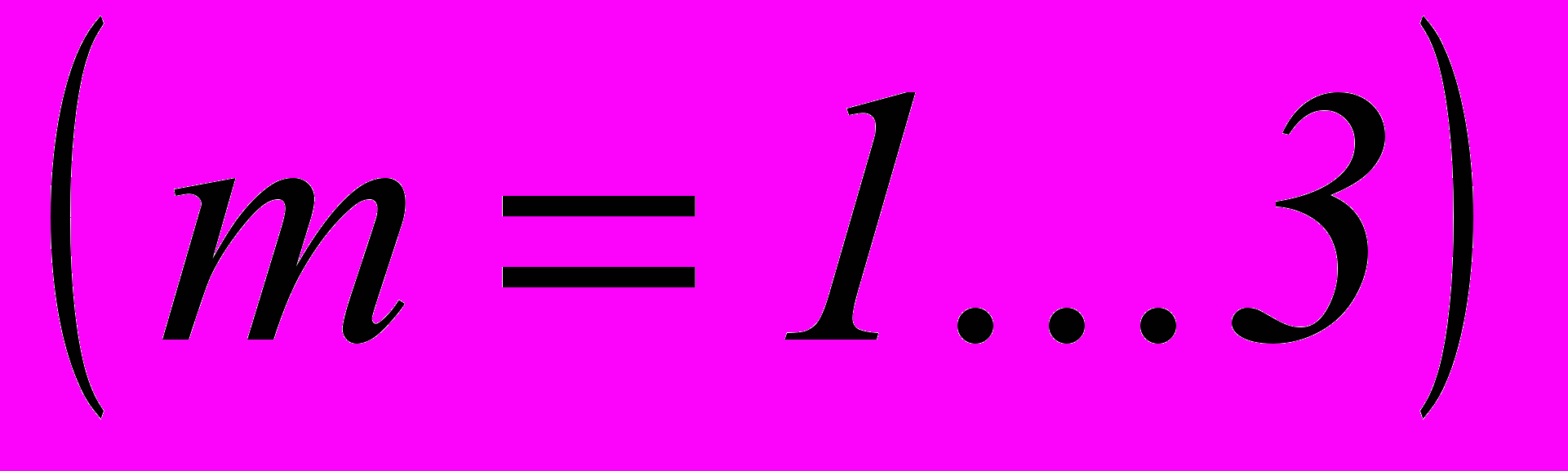где 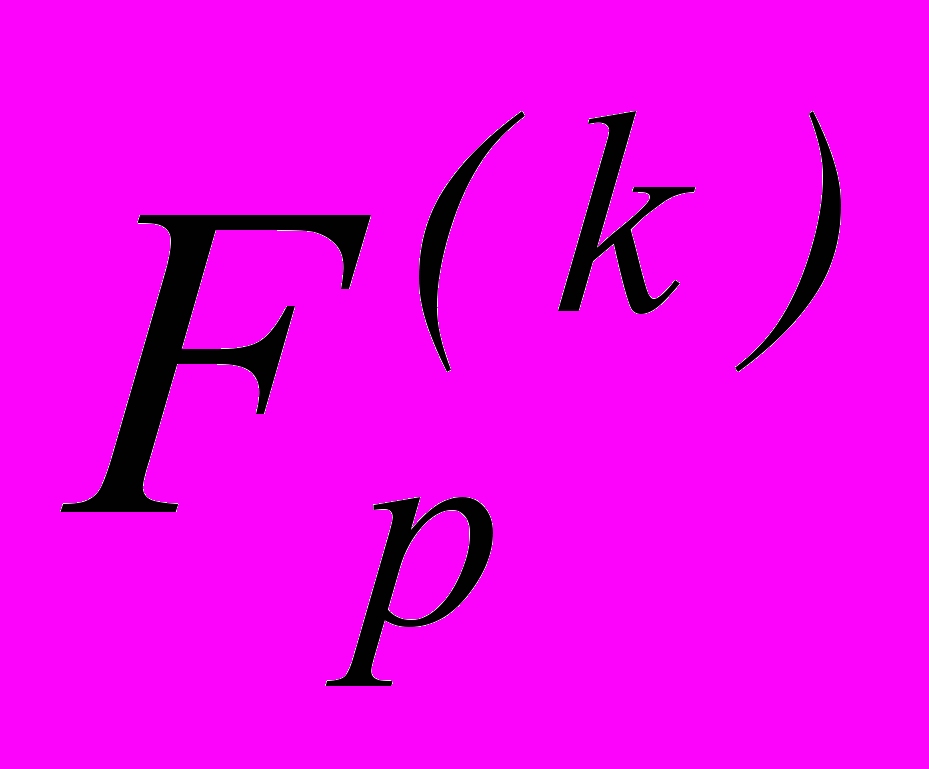– постоянные, определяемые экспериментально.

Толщины слоев 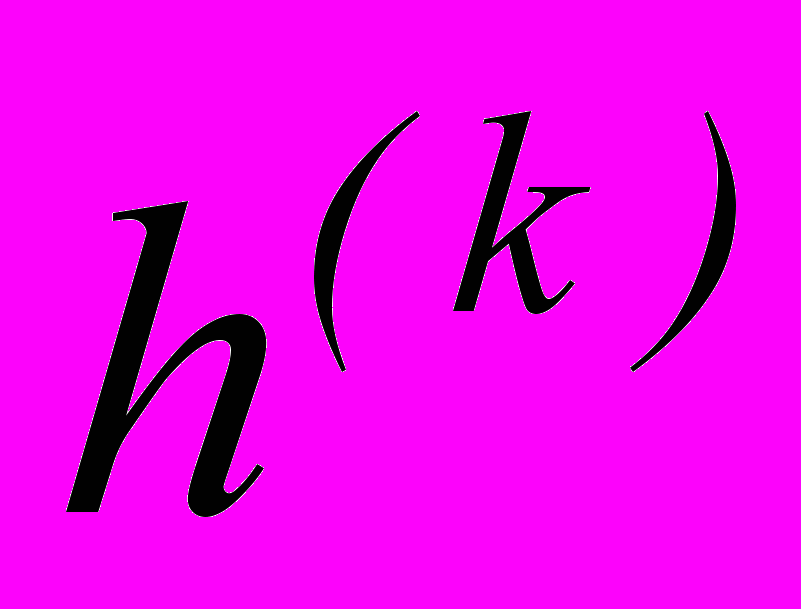=(0,025, 0,35 0,025)м. Характеристики внешних слоев (k=1,3) не зависят от температуры (E⁽¹⁾=E⁽³⁾=710⁴MПа; ⁽¹⁾=⁽³⁾=0,3; ⁽¹⁾=⁽³⁾=22,410^-6 K^-1). Характеристики внутреннего термочувствительного слоя (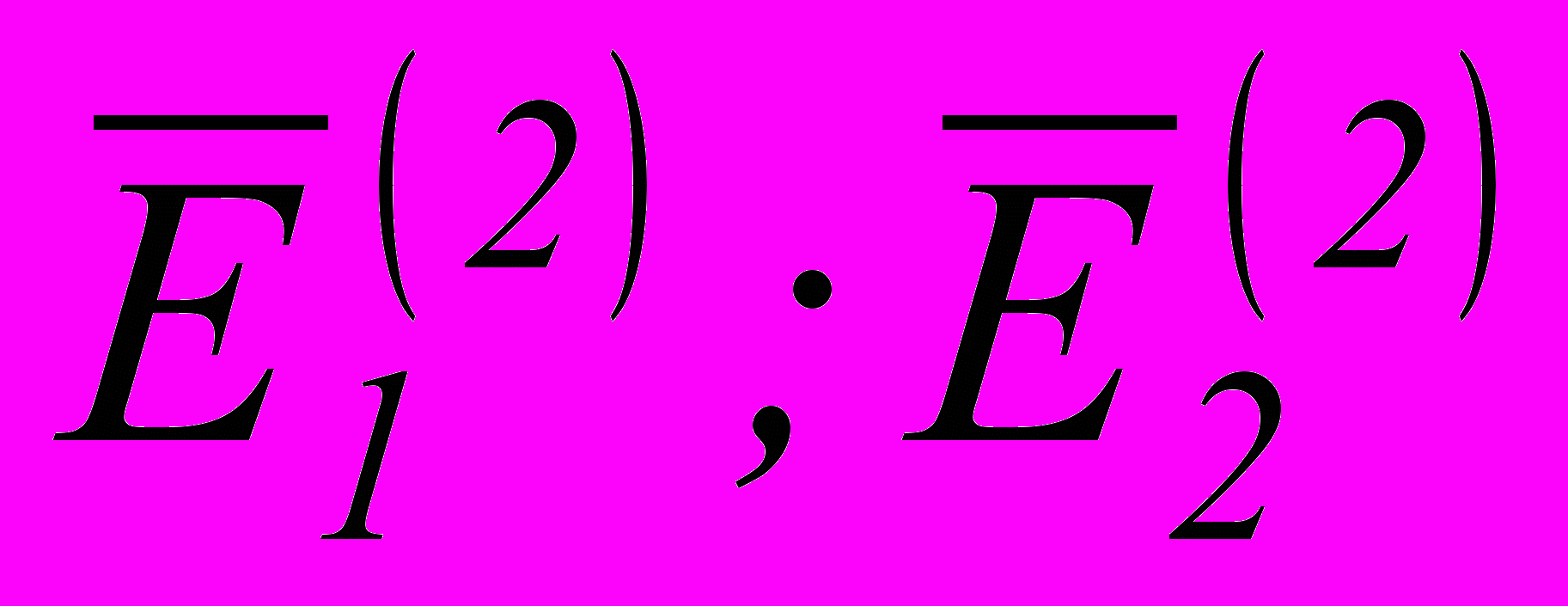)=(1,704;2,808)10⁴MПа; ₂₁=0,106; =0; (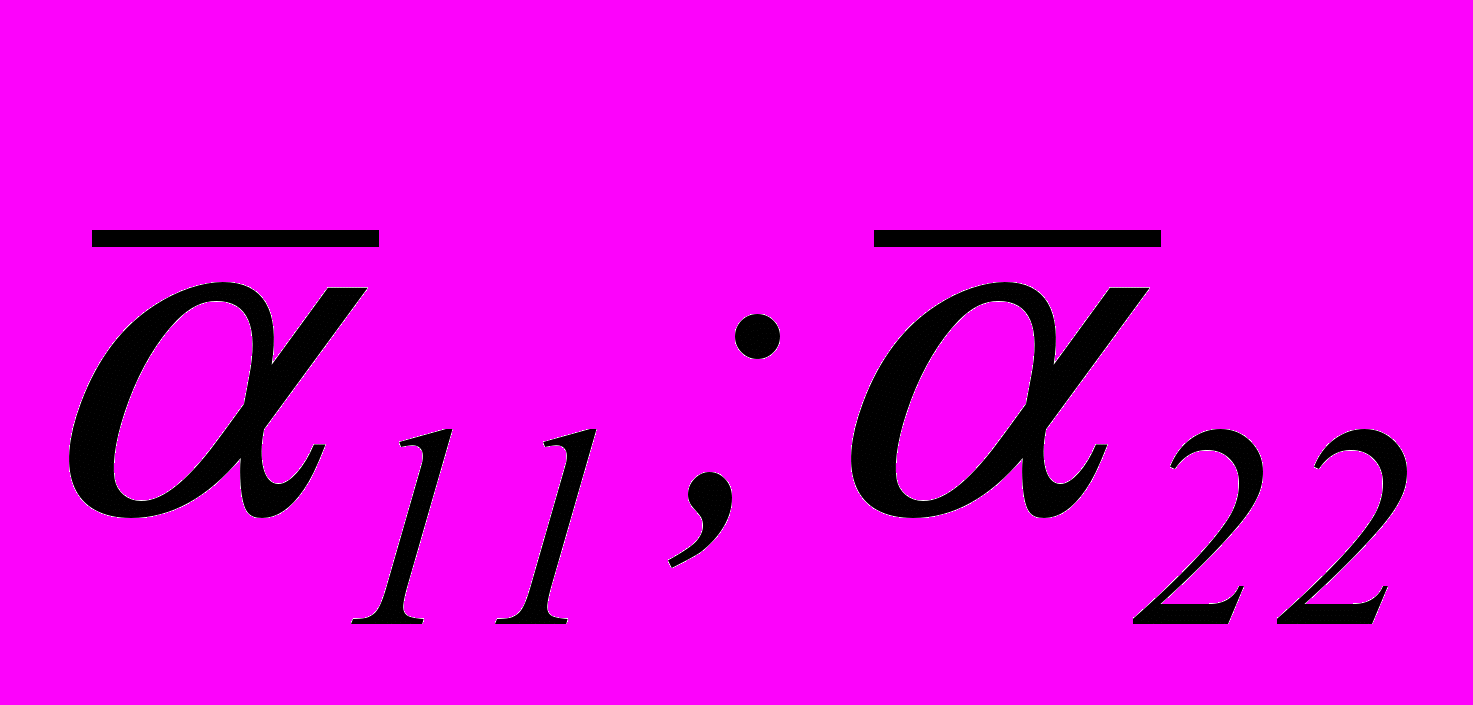)=(1,134;1,418)10^-5 K^-1; ₂₁=0,106; F_p=-2,510^-3 K^-1 (p=1-5); F₆=-2,41310^-8 K^-1; F₇=F₈=-2,44510^-8 K^-1. Температурное поле изменяется по закону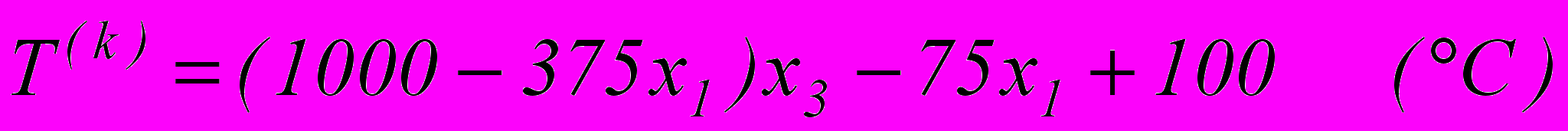



Нормальные перемещения на уровне срединной поверхности, полученные на основе описанного подхода, представлены в табл.1. Для сравнения в таблице приведены данные работы [6].



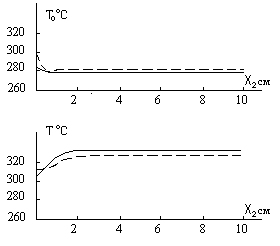
Рис.2.

Табл. 1.Нормальные перемещения на уровне срединной поверхности

x1 , м	Решение	103 u3, м
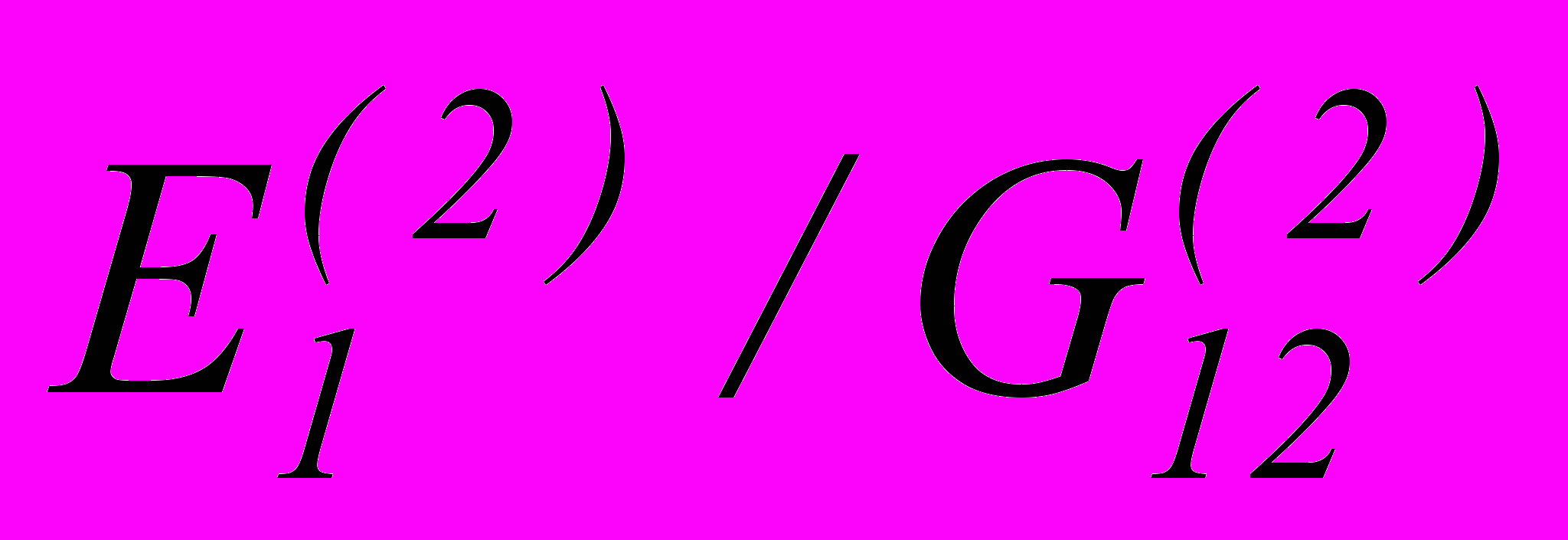		10	100	300
0,3	МКЭ	0,984	1,485	1,531
	[6]	0,968	1,409	1,470
0,6	МКЭ	1,443	2,551	2,834
	[6]	1,439	2,508	2,741
1,0	МКЭ	1,011	1,756	2,023
	[6]	1,021	1,772	1,890
1,5	МКЭ	0,59	-0,139	-0,263
	[6]	0,071	-0,169	0,316

Выводы. Разработанная методика, основанная на использовании тремерных конечных элементов, позволяет проводить расчет реальних слоистых конструкций на тепловые нагрузки, в том числе с учетом термочувствительности материала слоев. При этом удается избежать применения упрощающих гипотез, сводящих трехмерную задачу к плоской постановке.


Литература

1. Киричевский В.В., Сахаров А.С. Нелинейные задачи термомеханики конструкций из слабосжимаемых эластомеров. – К.: Будівельник, 1992. – 216с.
   
2. Метод конечных элементов в вычислительном комплексе «МІРЕЛА+» // Под общ.ред. Киричевского В.В. –К.: Наук.думка, 2005. – 403с.
   
3. Киричевский В.В., Козуб Г.А., Дохняк Б.М. Построение матрицы жесткости конструкций из анизотропных материалов для задач термоупругости // «Весник ВУНУ»- Луганск: ВУНУ им.Даля, №3(97),2006г. – стр.59-66.
   
4. Mikhailov M. D., Oziscr M. N., Vulchanov N. L. Diffusion in composite layers with automatic solution of the eigenvalue problem // J. of Hear and Mass Transfer — 1983. — Vol. 11, N 8. —P.1131–1141.
   
5. Савченко В.Г. Исследование нестационарных температурных полей в телах вращения при неосесимметричном нагреве // Пробл. проч. — 1982. — №1. — С.33-36.
   
6. Рассказов А.О., Соколовская И.И., Шульга Н.А. Теория и расчет слоистых ортотропных пластин и оболочек. – К.: КАДИ, 1986. – 191с.