Задача 3

Вид материала

Задача

Подобный материал:

• Программа курса лекций «Математические методы и модели исследования операций», 27.98kb.
• Т. М. Боровська кандидат технічних наук, доцент І. С. Колесник, 118.17kb.
• Разновозрастная итоговая проектная задача 1-4 классы, 87.27kb.
• Программа дисциплины Алгоритмы на графах Семестр, 13.21kb.
• Гиперкомплексных Динамических Систем (гдс) задача, 214.67kb.
• Домашнее задание по Теории информационных процессов и систем, 267.24kb.
• Задача линейного программирования Задача о «расшивке узких мест», 5.51kb.
• Программа учебной дисциплины вариационные методы в физике (спецкурс, дисциплины, 147.31kb.
• Варианты контрольных работ контрольная работа №1 (3 семестр), 237.84kb.
• Ручаевского Дмитрия Александровича. Карасик Л. В 1997-98 уч год. Основная часть Античная, 202.33kb.

Сложив шесть полученных произведений (три - со знаком "+" и три - со знаком "-") a₁₁a₂₂a₃₃ - a₁₁a₂₃a₃₂ - a₁₂a₂₁a₃₃ + a₁₁a₂₃a₃₂ +a₁₃a₂₁a₃₂ - a₁₃a₂₂a_31, получим искомый определитель det A".

Кстати, изложенный выше способ вычисления определителя 3-го порядка называется "разложение по первой строке".


Задача 4.3. Вычислить определитель 3-го порядка:




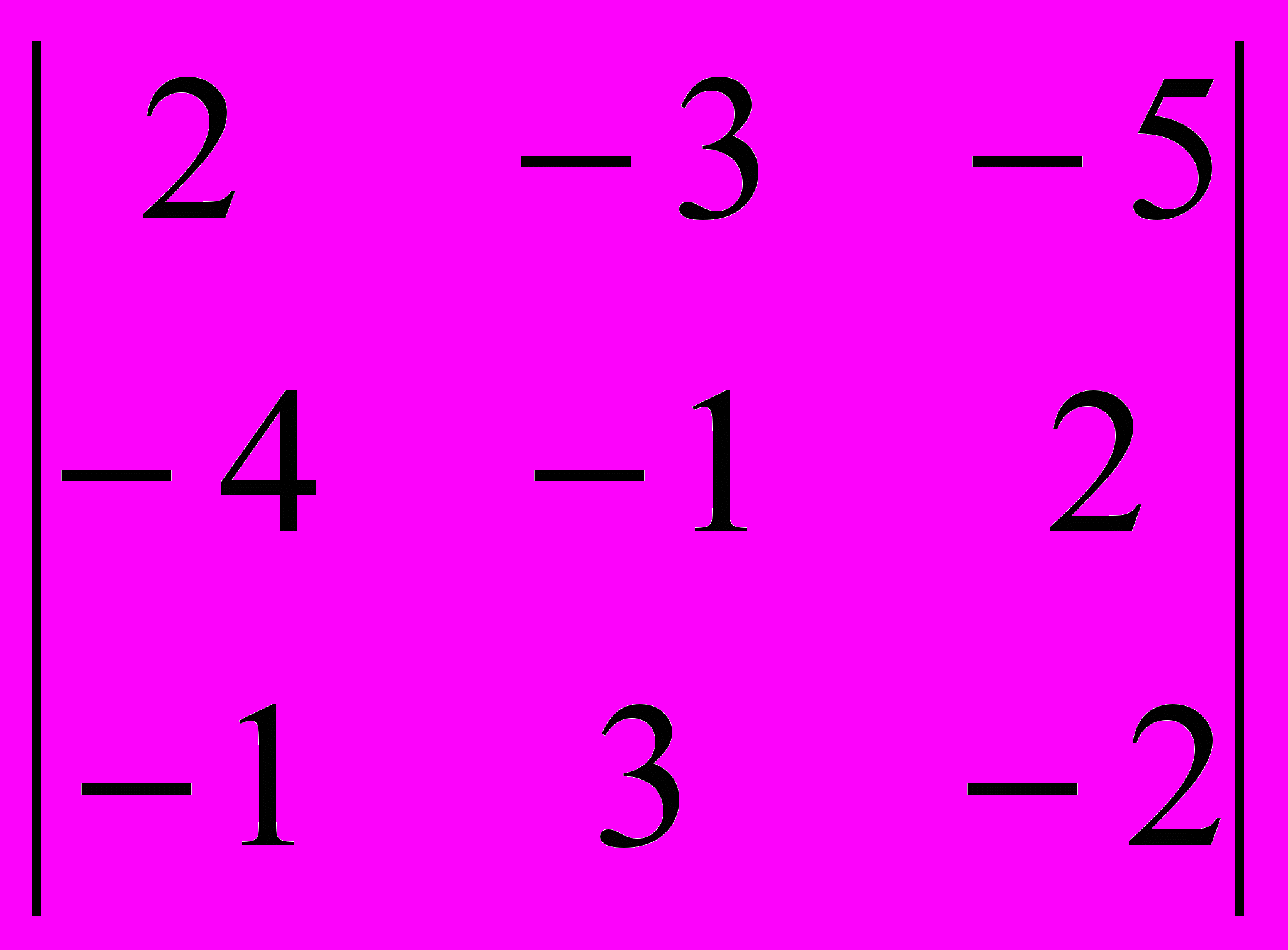
Решение:

Вычисляем определитель, применяя разложение по первой строке:











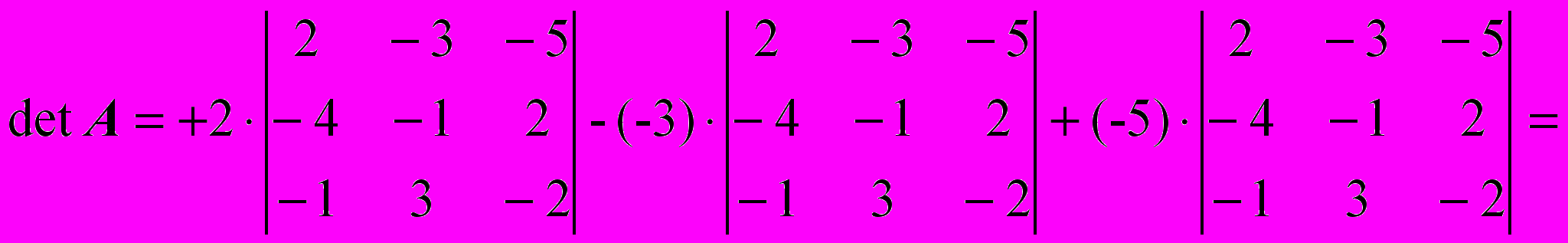
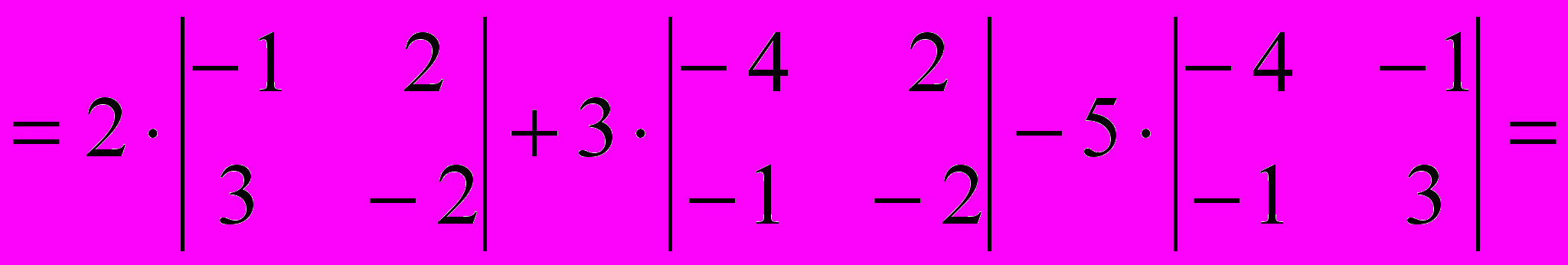
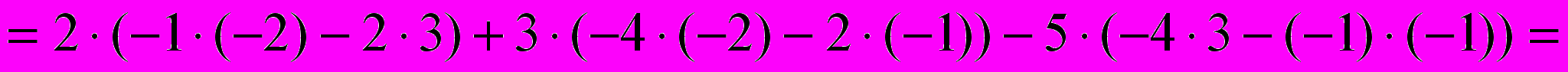
Ответ: 87.


З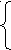адача 4.1.б. Решить систему уравнений методом Гаусса:


ax + by = ,

cx + dy = .

Сначала решите самостоятельно!

Решение:

Решим систему, используя элементарные преобразования над строками расширенной матрицы.










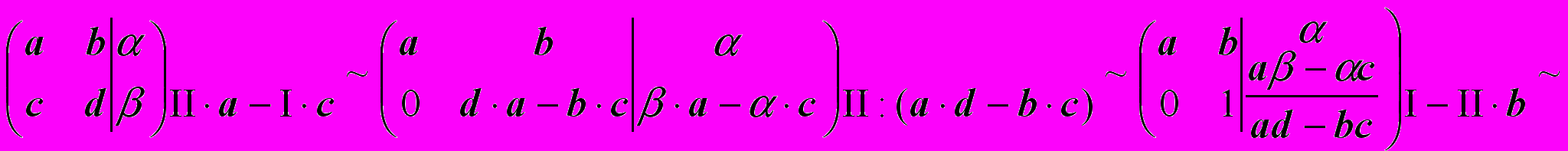
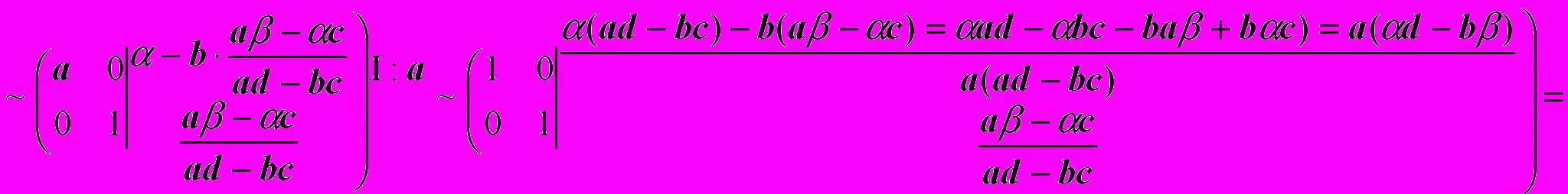
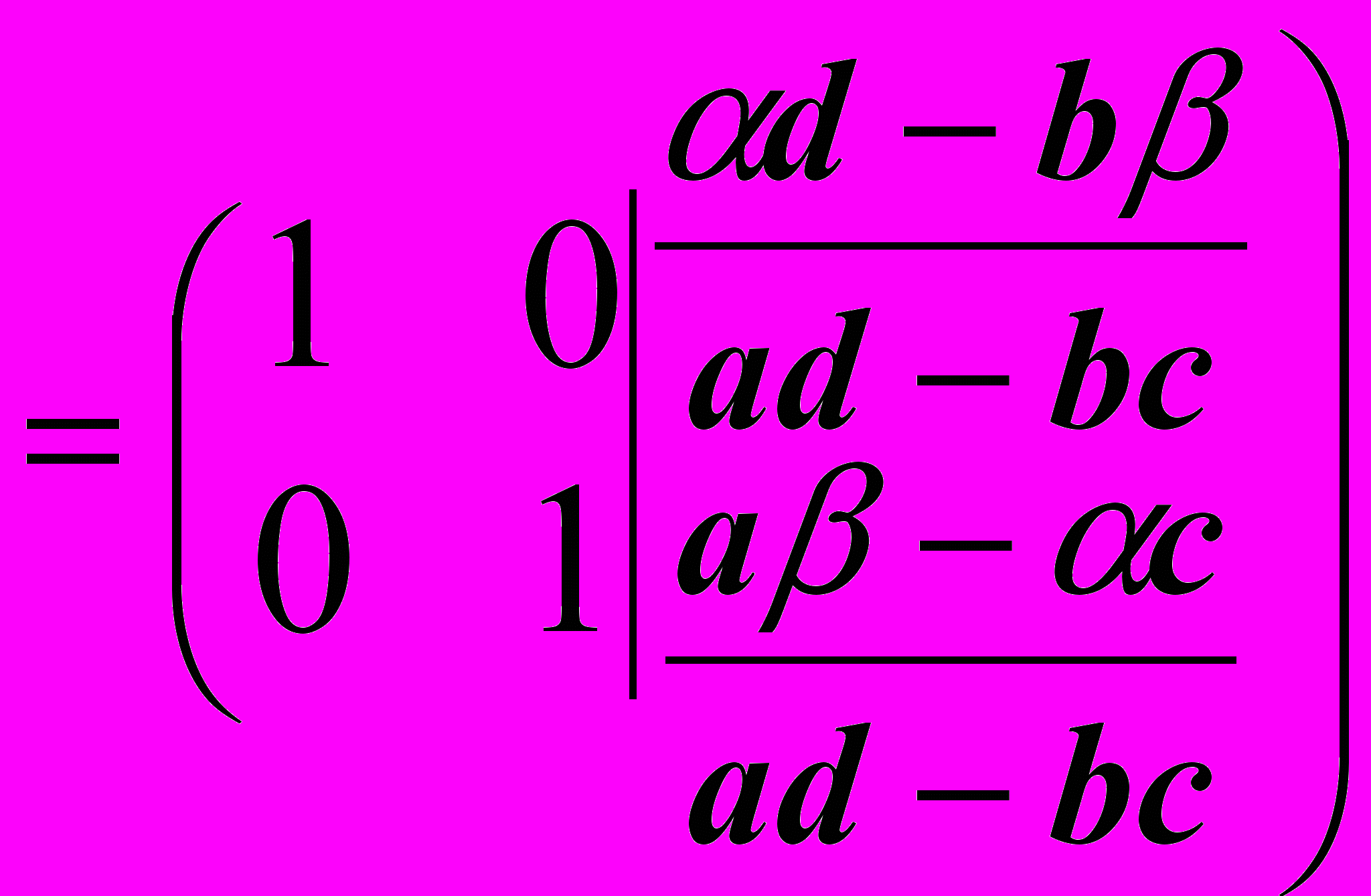
Ответ: Решением системы является упорядоченная пара чисел:





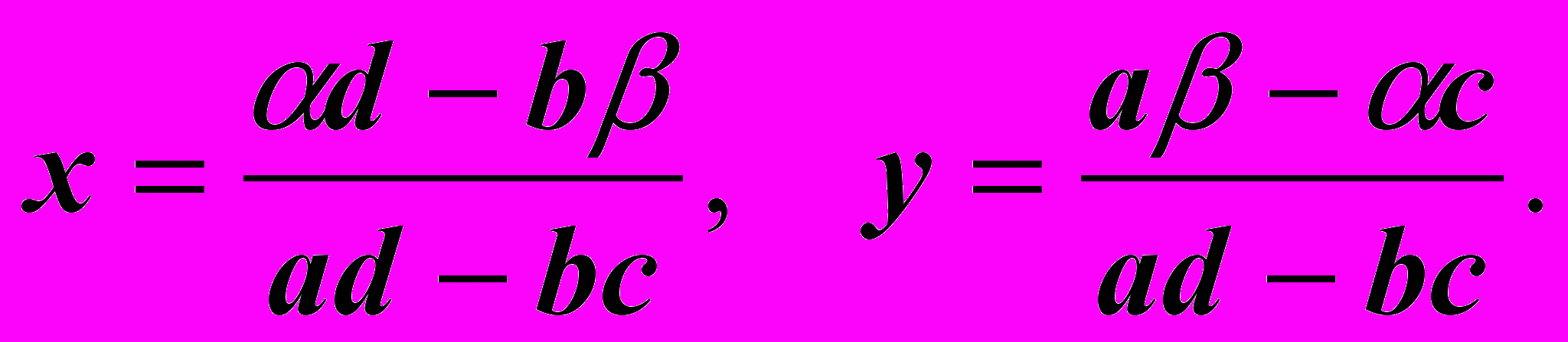
Теперь некоторые комментарии к решению.


Запишем систему в виде матричного уравнения




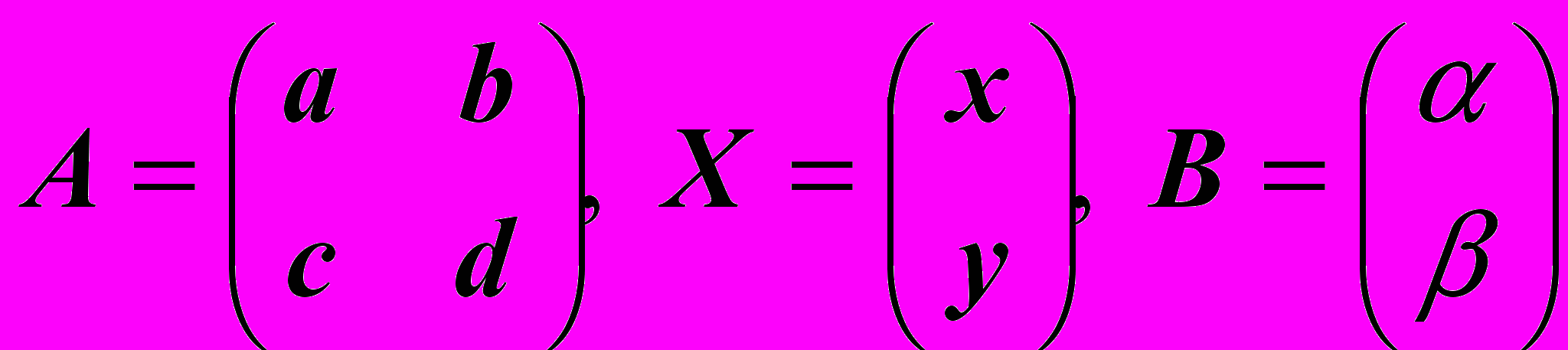
AX = B, где


Тогда расширенная матрица исходной системы имеет вид (A|B), а полученная в результате последовательности элементарных преобразований расширенная матрица эквивалентной системы имеет вид (E|A^-1B), где слева от вертикальной черты расположена единичная матрица E, а справа расположена матрица-столбец X = A^-1B, т.е. решение матричного уравнения.


? Вопрос: Можно ли использовать похожий алгоритм для нахождения, например, матрицы, обратной к матрице А?


Задача 4.3. Найти матрицу A^-1, обратную к матрице




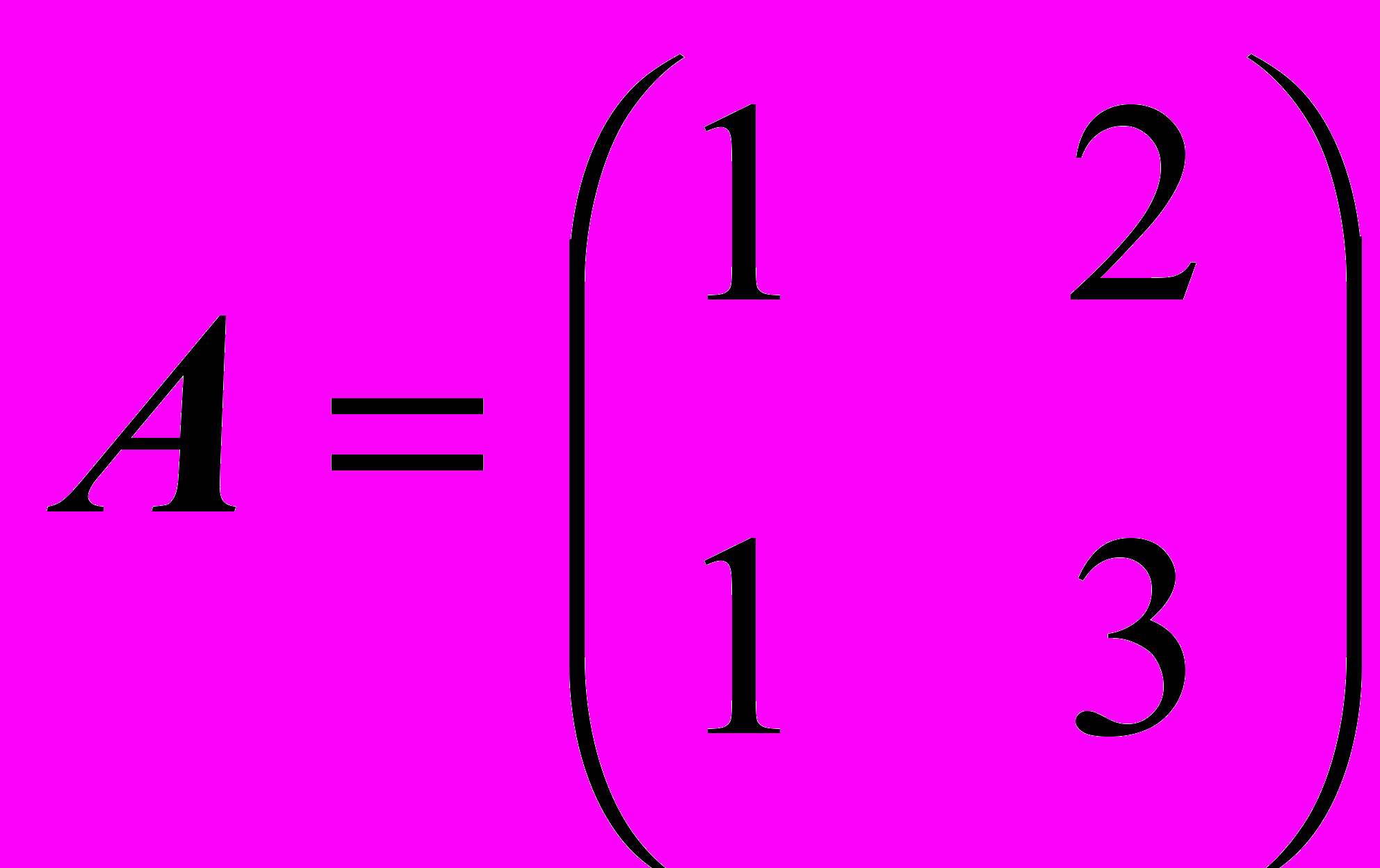
Решение:

Запишем две матрицы, разделенные вертикальной чертой: слева - матрицу A, справа - матрицу E. Используя элементарные преобразования над строками этой двойной матрицы, приведем матрицу слева к единичной матрице E, тогда справа окажется матрица - решение исходного матричного уравнения AX = E, т.е. матрица A^-1!




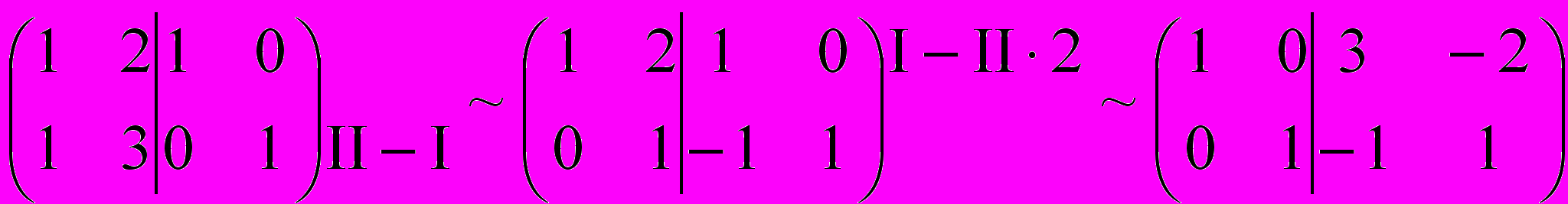
Как видим (естественно, после обязательной проверки), в самом деле получилась матрица A^-1, обратная к матрице А.

О

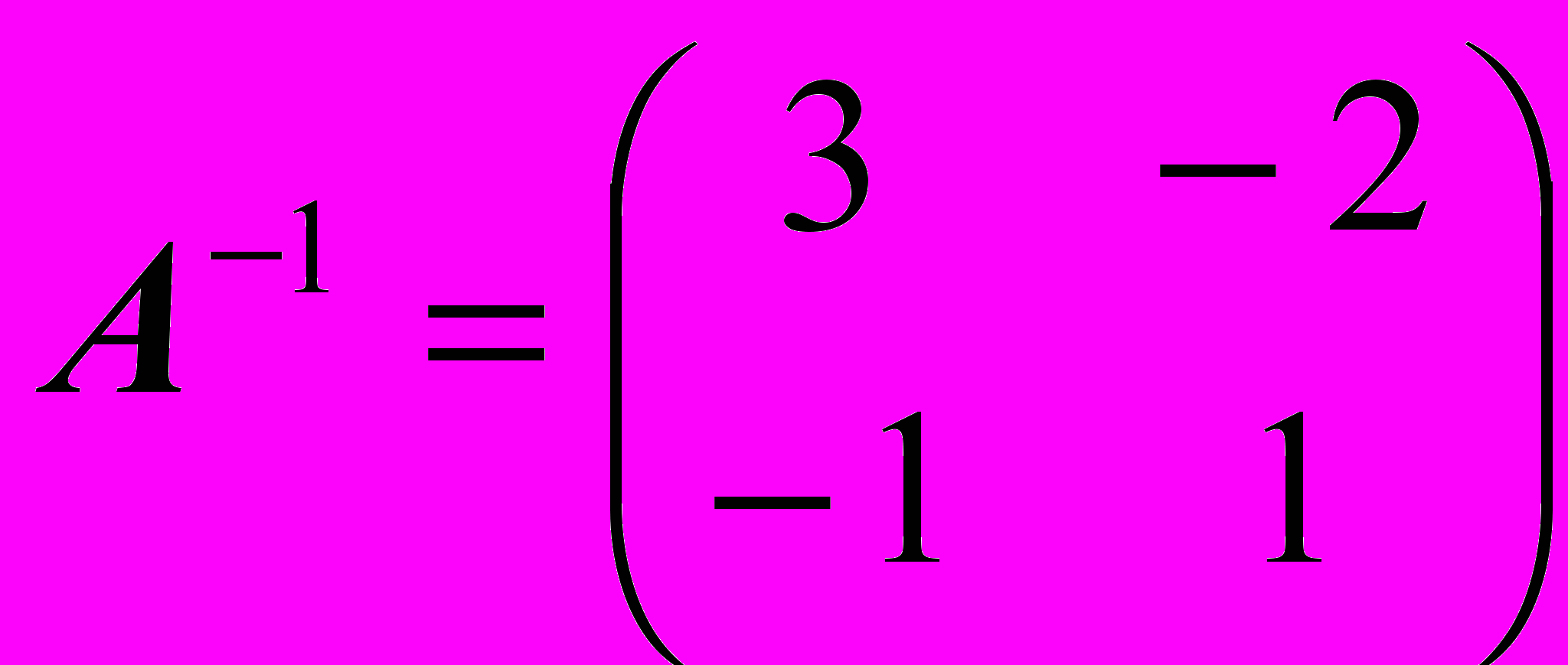
твет:


Итак, мы освоили способ нахождения обратной матрицы, который называется методом Гаусса-Жордана.


Задача 4.4. Найти матрицу A^-1, обратную к матрице




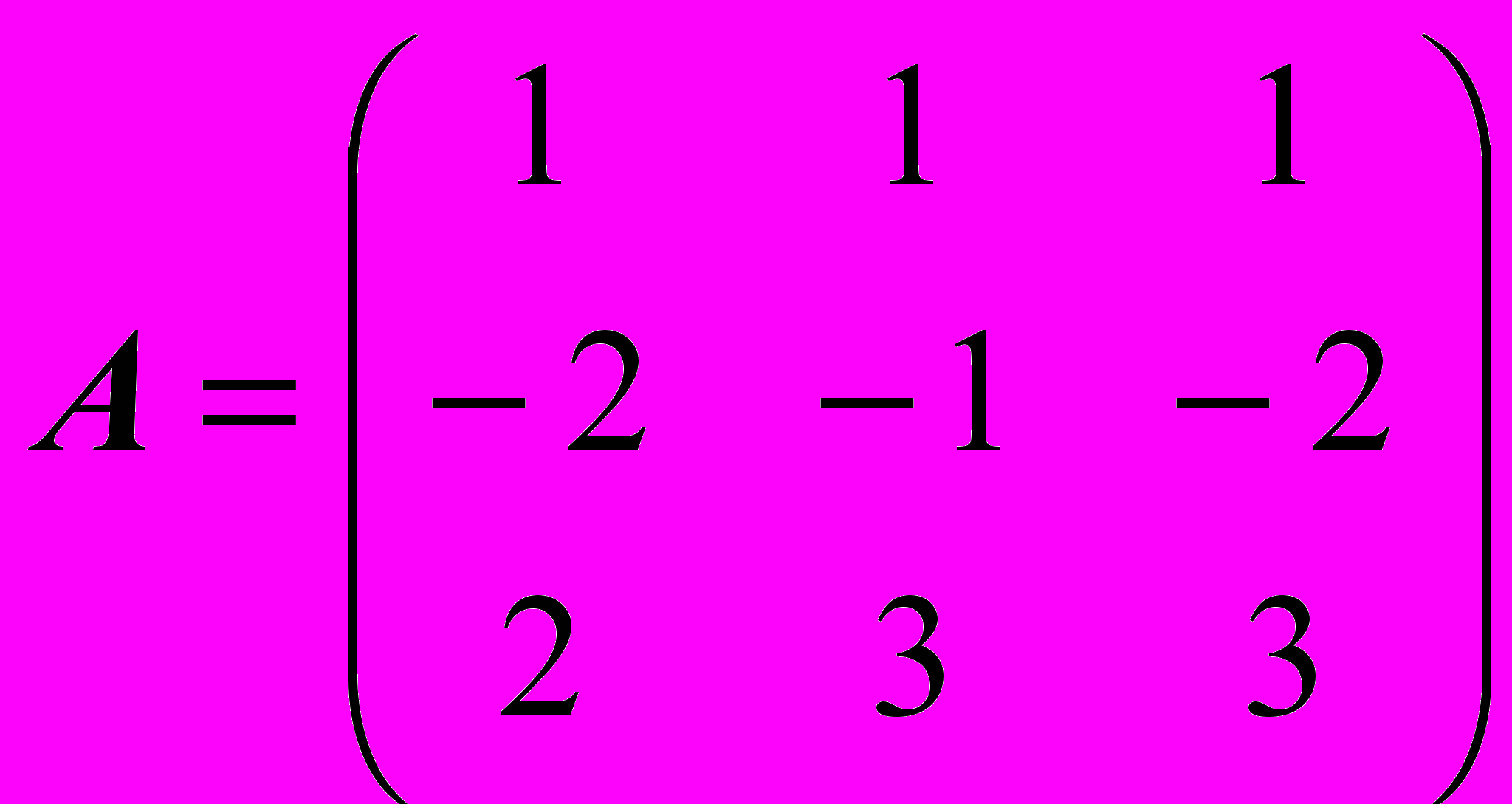
Решение:







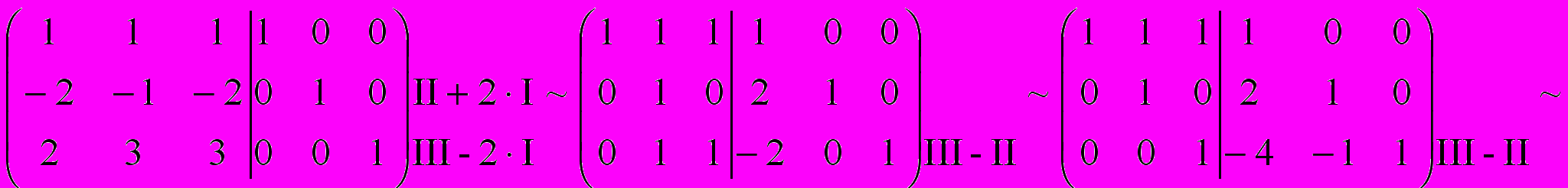
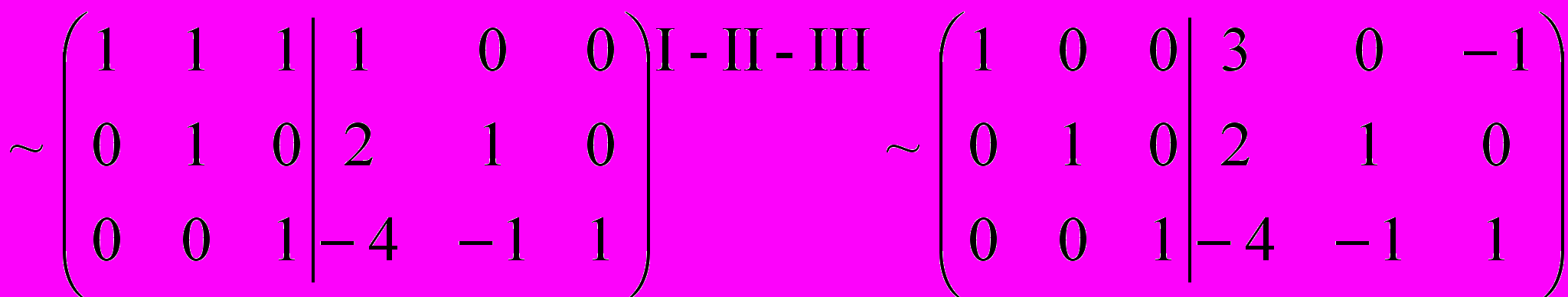
ПРОВЕРКА! (Проделайте самостоятельно)

О

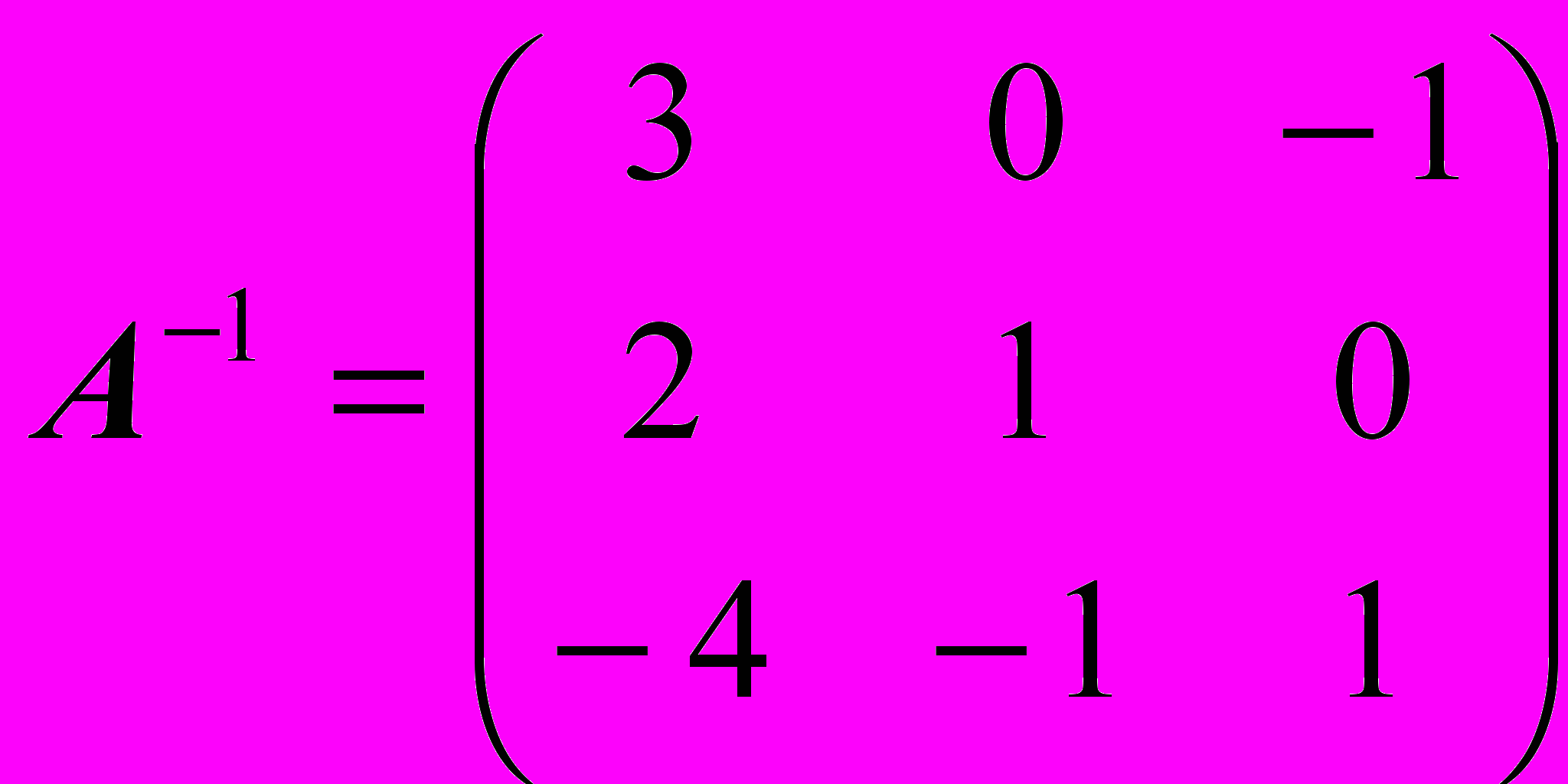
твет: