Тема: Програмування. Основні етапи розробки прикладних програм
| Вид материала | Документы |
- Текст програми це набір інструкцій (команд), які можуть бути виконані комп'ютером., 221.57kb.
- Тема: Робота в середовищі програмування. Запуск програм на виконання, 202.65kb.
- 1. Мови програмування (процедурні, візуальні, специфікацій). Концепція інструментального, 757.76kb.
- Програма Комплексного вступного іспиту на окр «Спеціаліст», 814.3kb.
- Називається комплекс програмних та мовних засобів, які використовуються для створення, 149.17kb.
- План лекції Тема І основні питання. Актуальність теми Лекційний матеріал Педіатрія, 473.4kb.
- Тема. Основні етапи розв’язування прикладної задачі з використанням комп’ютера. Інформаційна, 85.92kb.
- Розробка програми (робочого плану) моніторингу світового ринку готельних та ресторанних, 33.83kb.
- Структуризація програми. Поле, метод, класс, файл, проект. Об’єктне програмування., 327.95kb.
- Рекомендації з розробки навчальних та робочих програм (зі змінами І доповненнями) львів, 500.26kb.
Можна будувати відповідні вказівні типи. Застосування вказівників дозволяє оперувати із динамічними об’єктами. Використання саме динамічних об’єктів є зручним у тих випадках, коли структура цих об’єктів і реалізація їх поведінки є достатньо громісткою, а отже код у пам'яті виявиться великим.
В статичній пам'яті не вдасться розмістити достатню кількість таких об’єктів, при цьому можуть бути задачі, в яких кількість об’єктів не є фіксованою, тобто вони постійно утворюються і знищуються.
Оголошення динамічних об’єктів здійснюється за звичайним правилом побудови вказівних типів.
TYPE
POINT=object
... ... ...
END;
CIRCLE=object(POINT)
... ... ...
END;
PPOINT=POINT;
PCIRCLE:=CIRCLE;
VAR
a:POINT;
b:CIRCLE;
pa:PPOINT;
pb:PCIRCLE;
Так оголошені вказівники на об’єкти класів є статичними змінними – це чотирибайтні числа-адреси у пам'яті.
Створюються динамічні об’єкти явним викликом
New(pa);
New(pb);
При цьому в динамічній пам'яті відводиться ділянка відповідного розміру, що відповідає структурі об’єкта.
Задати стан чи реалізувати поведінку через вказівник на динамічний об’єкт можна таким чином:
pa.SETCOORD(100,100);
pa.SETCOL(5);
pa.ON;
Використання процедури New для створення динамічного об’єкту має одну особливість від використання у випадках інших динамічних змінних. Якщо об’єкт має метод конструктор, то цей метод може бути виконаний одночасно із створенням динамічного об’єкта, при цьому ідентифікатор методу вказується другим параметром процедури New.
New(pa,INIT);
New(pb,INIT);
Використання конструктора в якості другого параметру не обов’язково.
Знищуються динамічні об’єкти явним чином.
Dispose(pa);
Dispose(pb);
При цьому відповідні вказівники звільняються від своїх значень і відповідні ділянки пам'яті звільняються від відповідних об’єктів.
Якщо динамічний об’єкт має методи-деструктори, то їх можна одночасно викликати із знищенням динамічного об’єкта, при цьому в якості другого параметру процедури Dispose використовується ідентифікатор деструктора.
Dispose(pa,DONE);
Dispose(pb,DONE);
Тема: Особливості операції присвоєння між динамічними об’єктами.
Між динамічними об’єктами як і між статичними можна виконувати присвоєння, при цьому присвоєння можливе між обертами одного класу та між об’єктами різних класів, що пов’язані принципом наслідування і лише від нащадка до предка, проте операція присвоєння у випадку динамічних об’єктів повинна виконуватися з певною обережністю. Взагалі присвоєння копіює стан і реалізацію поведінки між об’єктами. Якщо операція присвоєння виконується між вказівниками, то про ніяке копіювання стану немає мови.
VAR
pa1,pa2:PPOINT;
pb1,pb2:PCIRCLE;
BEGIN
New(pa1);
New(pa2);
pa2.SETCOORD(100,100);
pa2.SETCOL(5);
pa2.ON;
pa1:=pa2;
Присвоєння виду в даному випадку не скопіює стан і поведінку другого об’єкта до першого, а надасть другому об’єкту два вказівники.
Перший об’єкт втратить свій вказівник і перетвориться у „сміття” у пам'яті. Така ситуація називається структурною невизначеністю, оскільки деякі маніпуляції з двома об’єктами можна буде виконати через вказівник ра1. хоча коди всіх методів другого об’єкта пов’язані з вказівником ра2.
Для того, щоб за допомогою операції присвоєння скопіювати стан потрібно використовувати операцію розіменування вказівника.
Тема: Методи розробки алгоритмів і програм.
Зрозуміло, що багато прикладних задач можна розв’язати різними способами. Вибір методу розв'язку визначається із:
- постановки задачі;
- наявними програмними ресурсами;
- вимогами по швидкодії, використанням ресурсів ЕОМ.
Останній пункт означає, що обраний варіант програмування задачі повинен реалізувати її за найменший час або якомога менше використовувати ресурси оперативної та зовнішньої пам'яті. Зрозуміло, що час роботи програми в часових одиницях не є критерієм ефективності, оскільки він ще суттєво залежить від архітектури ЕОМ, тому цей варіант оцінювання ефективності проводять за кількістю так званих важких операцій даної задачі.
Враховуючи багатоманіття способів розв'язку конкретної задачі, потрібно володіти основними методами побудови алгоритмів та способами оцінювання їх ефективності. Окрім розглянутої часової ефективності це може бути критерій стійкості розв'язку, повноти розв'язку, оптимальності.
Тема: Метод повного перебору.
Застосовується так званих задачах вибору оптимального варіанту. Полягає у наступному: перебираються всі можливі варіанти розв'язку і для кожного з них визначається деяка цільова функція, яка має набувати
Переваги: простота методу як в алгоритмічному варіанті, так і в програмній реалізації.
Недоліки: в більшості випадків надзвичайно великий об’єм обчислень, що суттєво збільшує час роботи програми.
Наприклад. Пошук мінімального (максимального) елемента у масиві. Для п-елементів є величина порядку о(п). Для даної задачі чи не єдиний алгоритм розв'язку.
Задача „Комівояжер”. Дано п-пунктів, між якими є шляхи сполучення. Відомі вартості всіх сполучень, потрібно побудувати такий маршрут, що сполучає всі пункти лише по одному разу, при якому витрати будуть мінімальними.
Згідно з МПП перебираються всі можливі варіанти маршруту, для кожного з яких встановлюється цільова функція. В якості розв'язку буде той варіант, де функція мінімальна.
При програмуванні даної задачі за цим методом використовується п вкладених циклів по всіх можливих пунктах.
for i1=1 to n do
begin
f:=0;
for i2:=1 to n do
if i2<>i1 then
begin
f:=f+a[i1,i2]
for i3:=1 to n do
if i3<>i2 then
begin
... ... ... ...
if in<>in-1 then
f:=f+a[in-1,in]
end; ... end;
if f
end;
Даний фрагмент програми передбачає перебір всіх можливих значень величини f для різних варіантів маршрутів, змінна і має бути достатньо велике значення.
Цей варіант передбачає наявність всіх шляхів сполучень, тому у випадку відсутності частини шляхів сполучень потрібно передбачити вилучення тих варіантів, які не можливі за умовою.
Тема: Метод „розділяй і володарюй”.
Ідея методу полягає по розділені складної задачі на декілька окремих під задач, що має цілісну структуру. Такий поділ дозволяє отримати декілька простіших задач, кожну з яких можна окремо розв’язати. Остаточний розв'язок є об'єднанням всіх часткових розв’язків. Метод РІВ передбачає адитивний поділ. Кожна під задача має той самий характер, що і основна задача. Об'єднання часткових розв’язків виконується не комбінуванням а сумуванням.
Якщо ж поділ дає різноманітні задачі, метод виділення під цілей.
Наприклад. Обчислення площі п-кутника, що заданий координатами вершин.
п-кутник розбивається діагоналями на п-2 трикутники.
Зауваження. В розглянутому прикладі діагоналі проводяться з однієї вершини. Якщо многокутник опуклий, то вибір такої вершини для поділу на трикутники є довільним. У випадку не опуклого п-кутника в якості вершини поділу вибирається не опукла вершина. Якщо таких вершин буде декілька, то за методом РІВ п-кутник поділяється на к- та т-кутники між двома не опуклими вершинами.
Для перевірки не опуклості вершин можна скористатися одним з двох способів:
- Якщо вершина і опукла, то пряма, проведена через вершини і та і+1 або і-1 та і матиме всі вершини лише по оду сторону, якщо ж вершина і є не опуклою, то відносно такої прямої решта вершин розмістяться по різні сторони. В програмній реалізації цього факту можна скористатися рівнянням прямої, що проходить через дві точки.
.
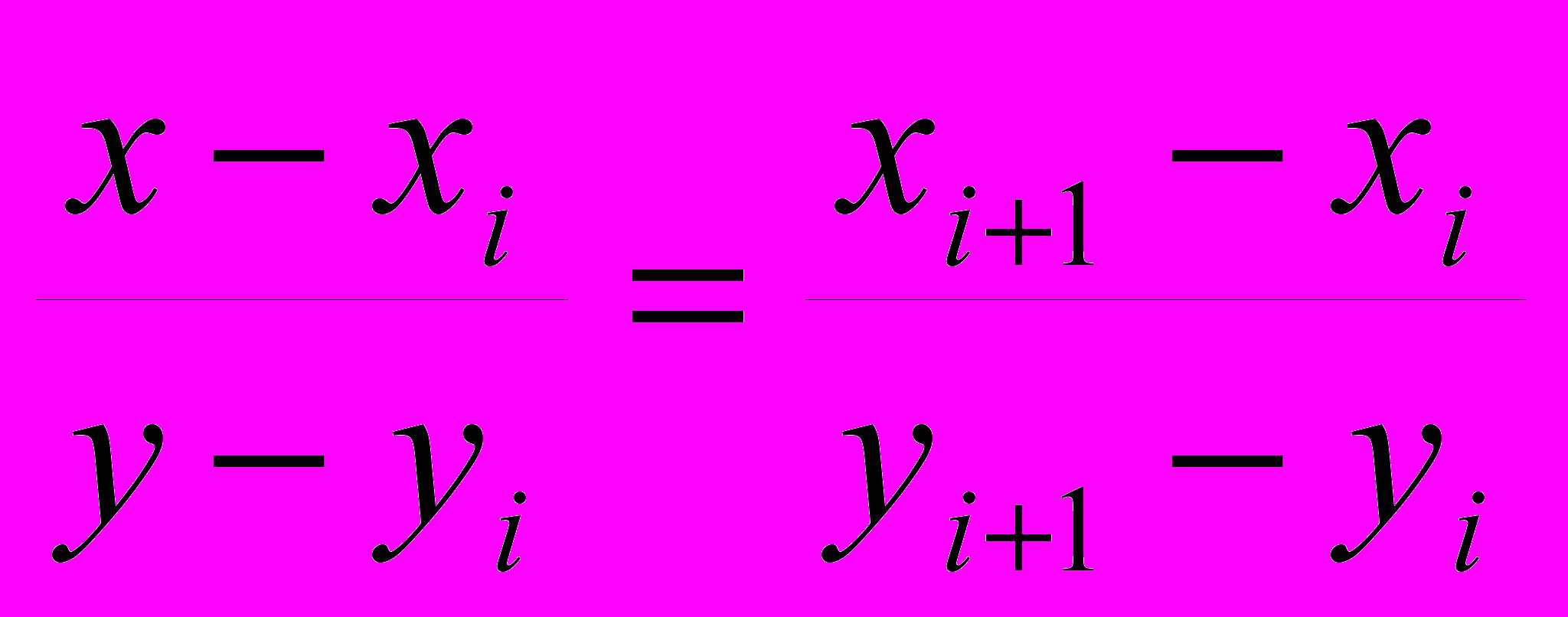Якщо підстановка замість вільних змінних по у та х координати решти вершин
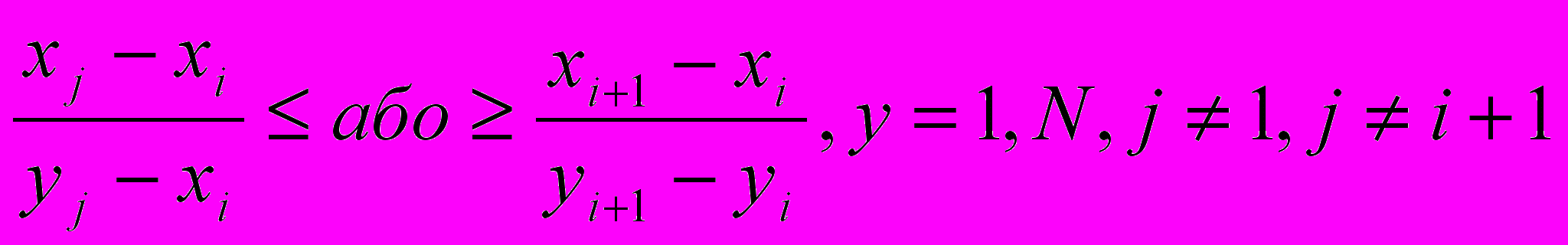даватиме один і той же знак, то відповідна вершина буде опуклою.Сортування масиву. Розділення його на частини, по окремим впорядкуванням їх та наступним злиттям частин.
Виявляється дешевше сортувати два під масиви і об’єднати їх у впорядкований, а ніж сортувати весь масив вцілому.
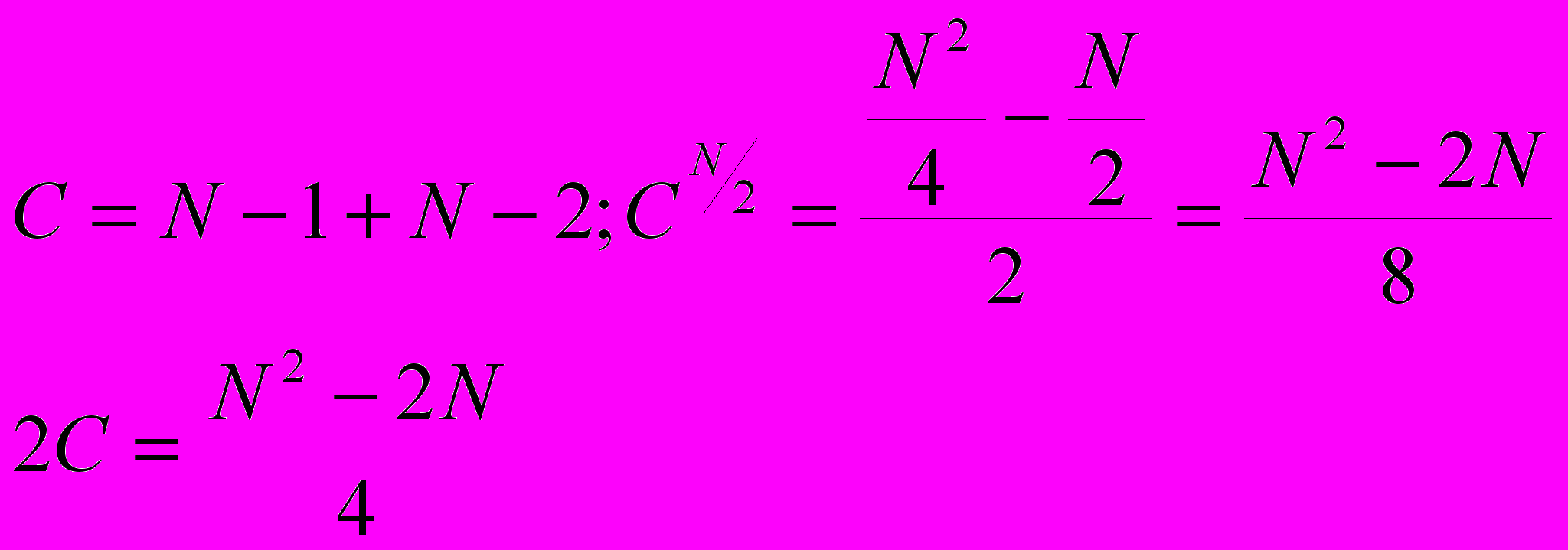
Злиття
.
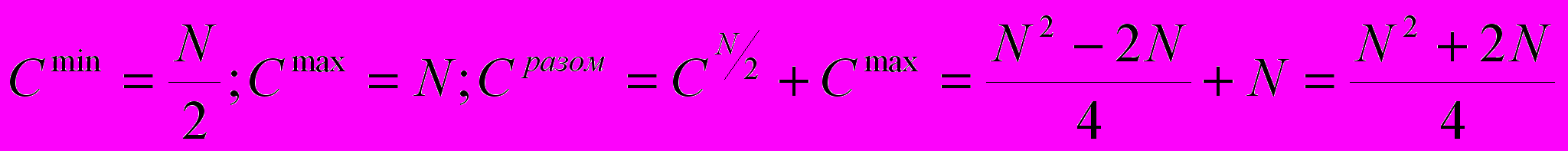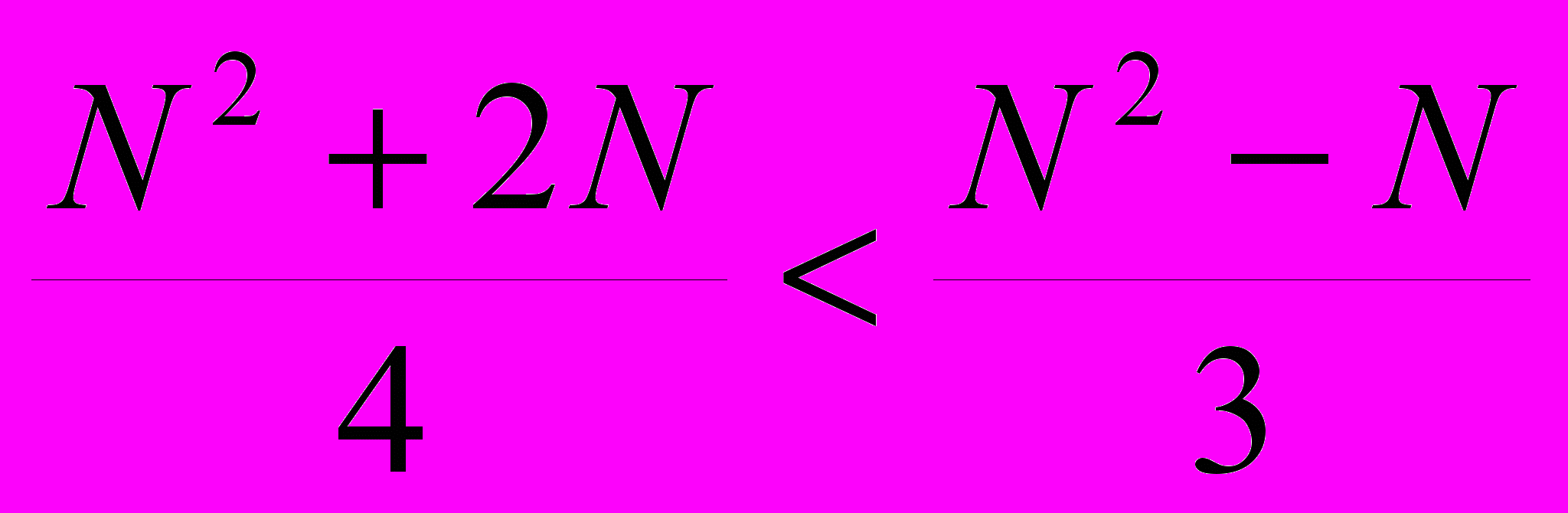.Фрагмент підпрограми має вигляд:
i:=1;
j:=1;
k:=1;
while (i<=N)and(j<=M)do
if a[i]
begin
i:=i+1;
k:=k+1
end
else
begin
c[k]:=b[j];
j:=j+1;
k:=k+1;
end;
while i<=N do
begin
c[k]:=a[i];
i:=i+1;
j:=k+1
end;
while j<=M do
begin
c[k]:=b[j];
j:=j+1;
k:=k+1;
end;
Тема: Метод послідовних наближень.
В ряді випадків розв’язок задачі не може бути знайдений абсолютно точно. Це може мати місце лише, якщо вхідні дані задачі визначені не точно. В процесі обчислення виконується округлення або взагалі задача немає точного розв'язку. В таких випадках користуються методом послідовних наближень, при цьому вибирається або довільним чином, або за певною умовою початкове наближення розв'язку, потім будується деякий алгоритм, який дозволяє за кожним попереднім наближенням розв'язку отримати наступне наближення. Такий процес уточнень продовжується до тих пір, поки буде досягнута необхідна точність результату.
Оскільки точний розв'язок в принципі є невідомим, то користуються наступною умовою припущення уточнень
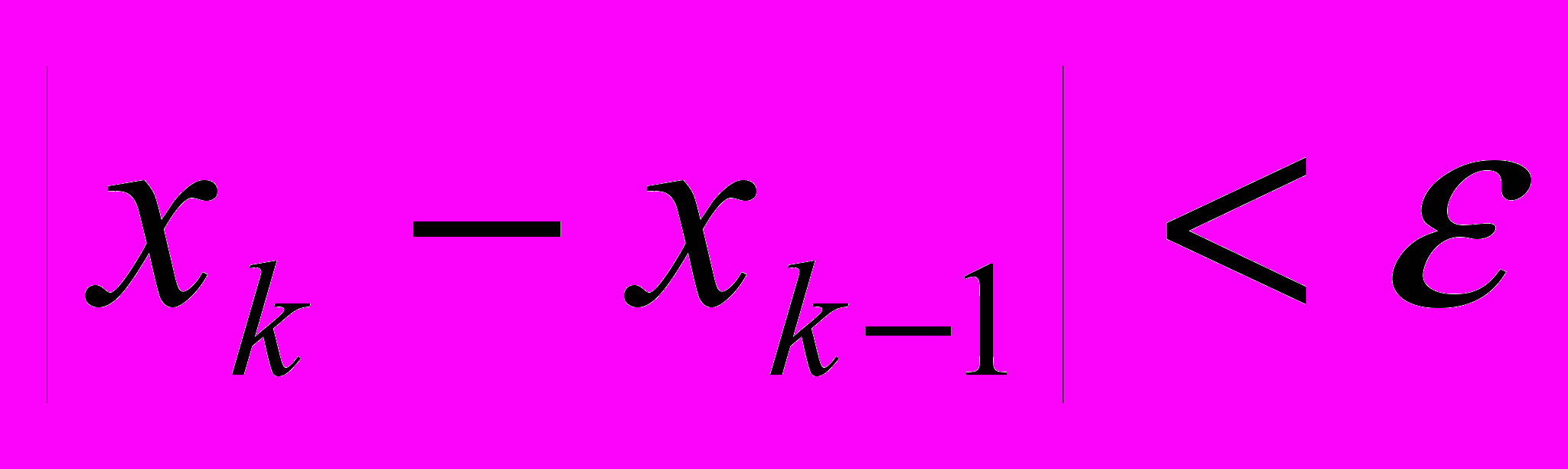.Наприклад. Формула Ньютона-Рафоса для обчислення кореня квадратного для невід’ємного числа.
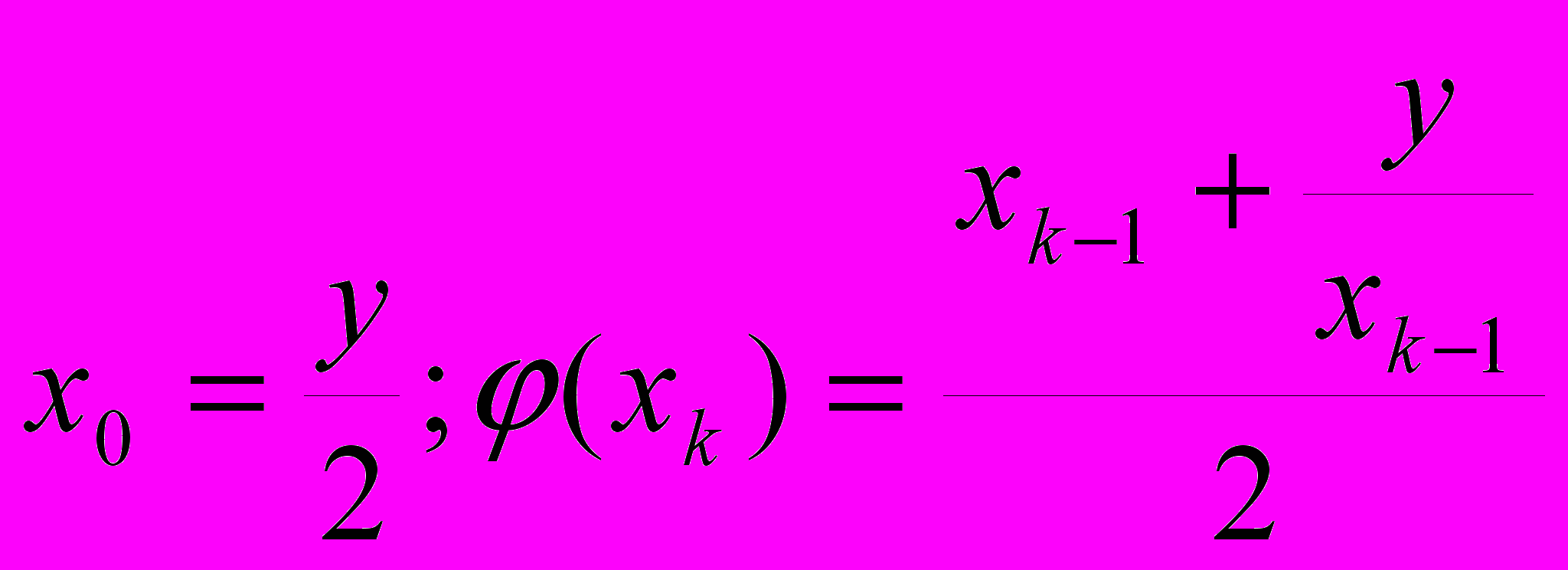;алгоритм Ньютона-Рафоса закладений в реалізацію функцій sqr, sqrt.
Обчислення значень функції за розкладом у ряд.
Для всіх неперервних функцій існує розклад у ряд по степеням аргументу.
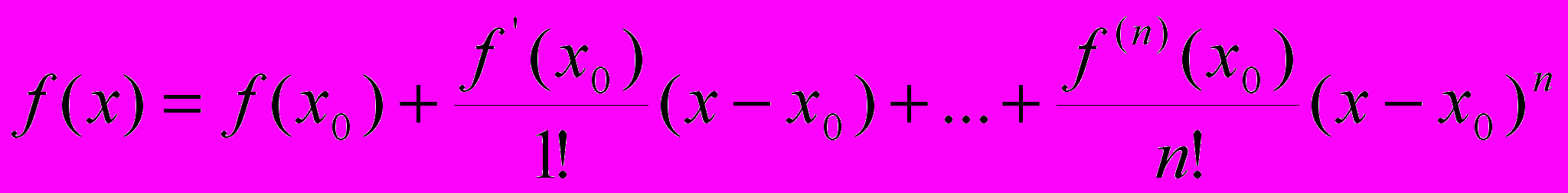.Всі стандартні функції мов програмування обчислюються саме через розклад в ряд, оскільки в цьому випадку операція зводиться до додавання і множення. Умова зупинки процесу обчислень
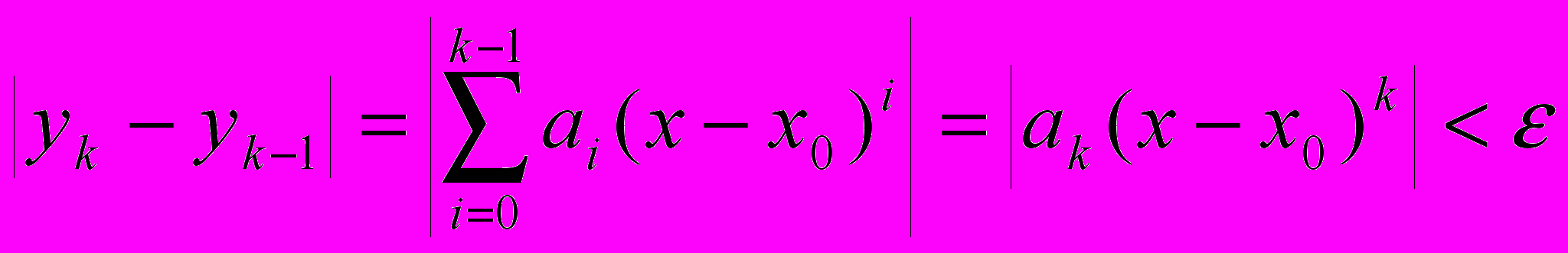.Обчислення визначеного інтегралу.
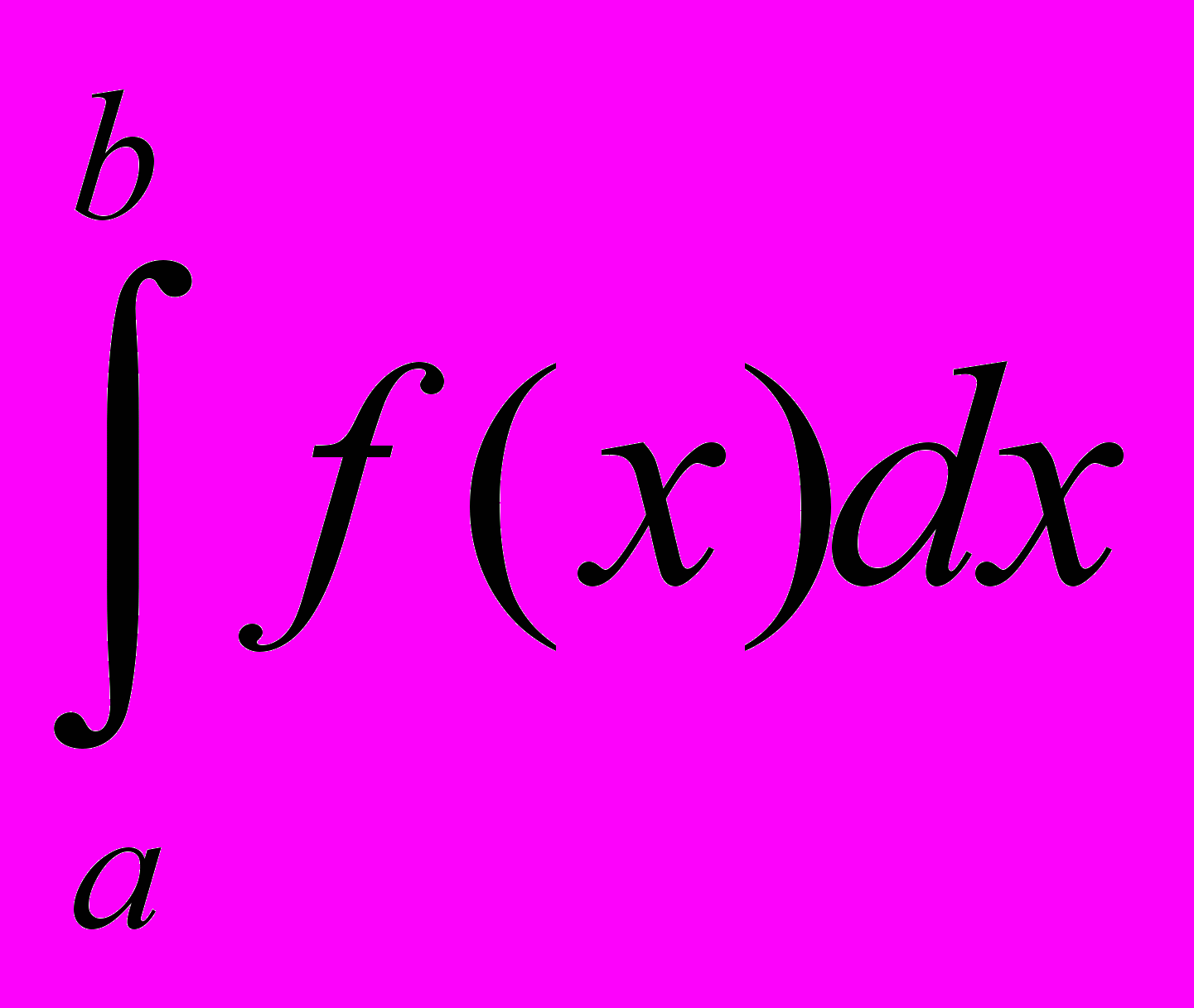замінюється інтегральною сумою з відповідним набором вагових коефіцієнтів. В залежності від вибору квадратних формул вагові коефіцієнти будуть такими: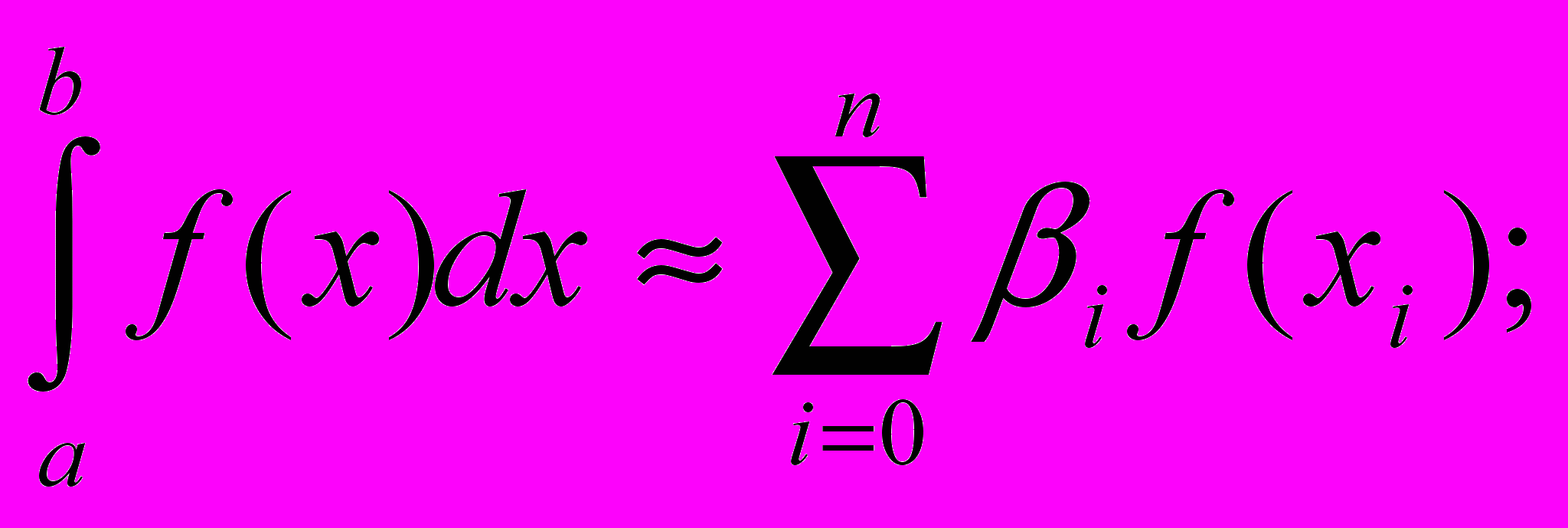
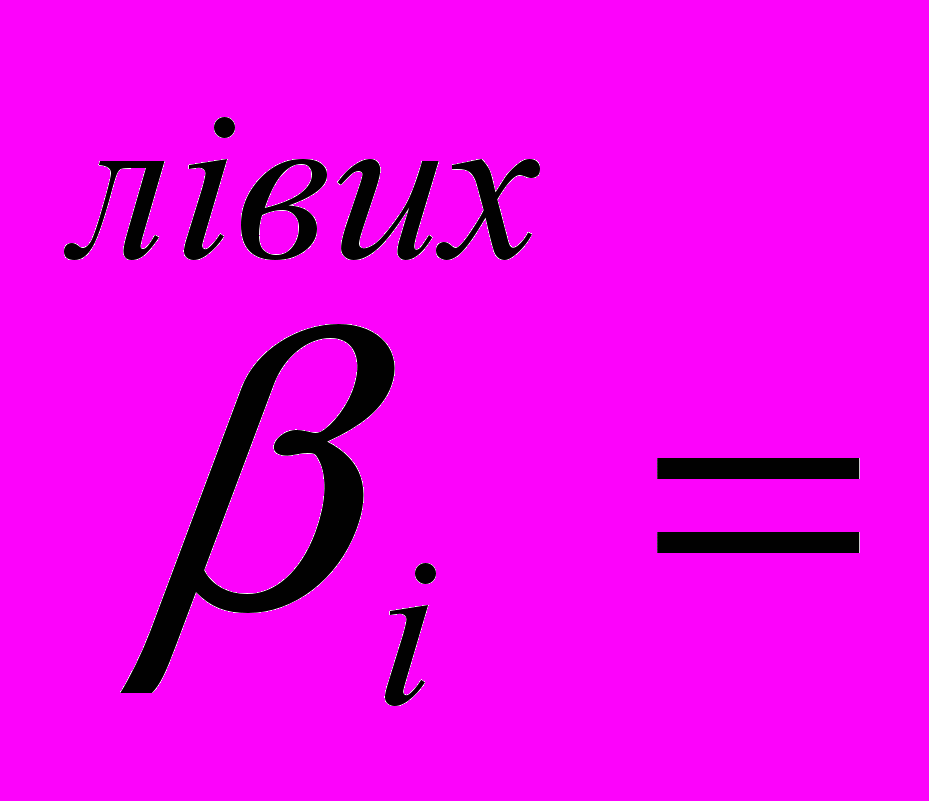h, коли і=0,...,п-1 і 0, коли і=п;
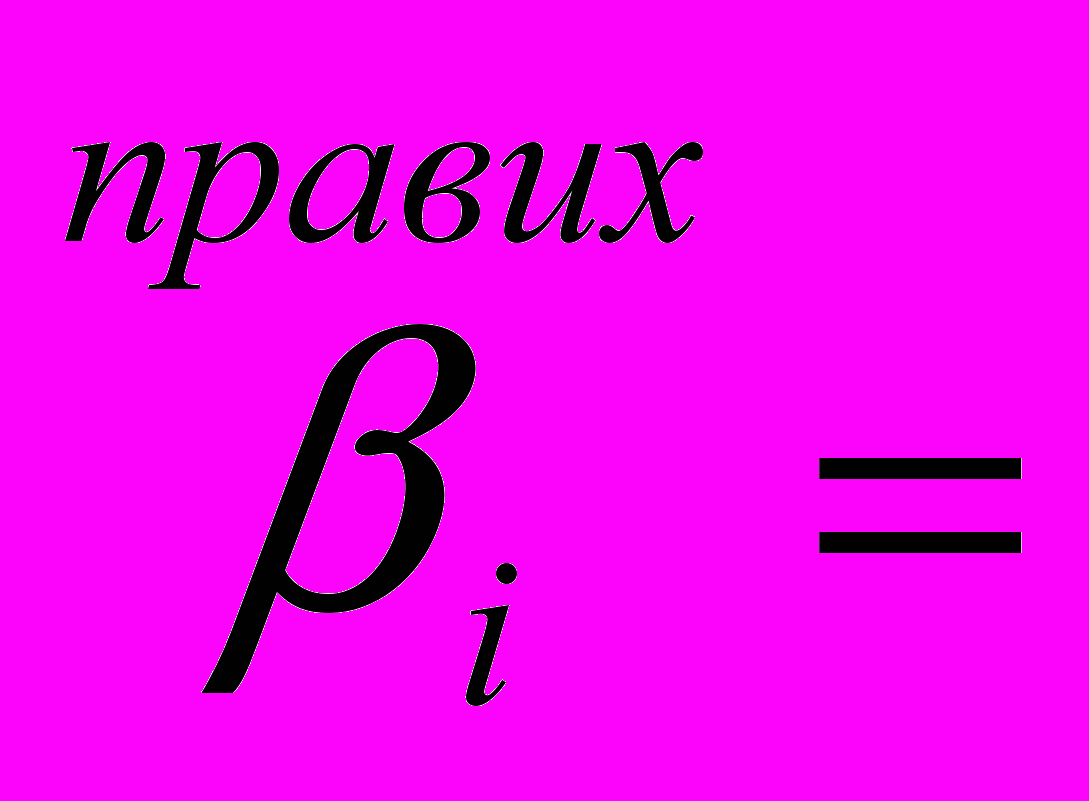h, коли і=1,...,п і 0, коли і=0;
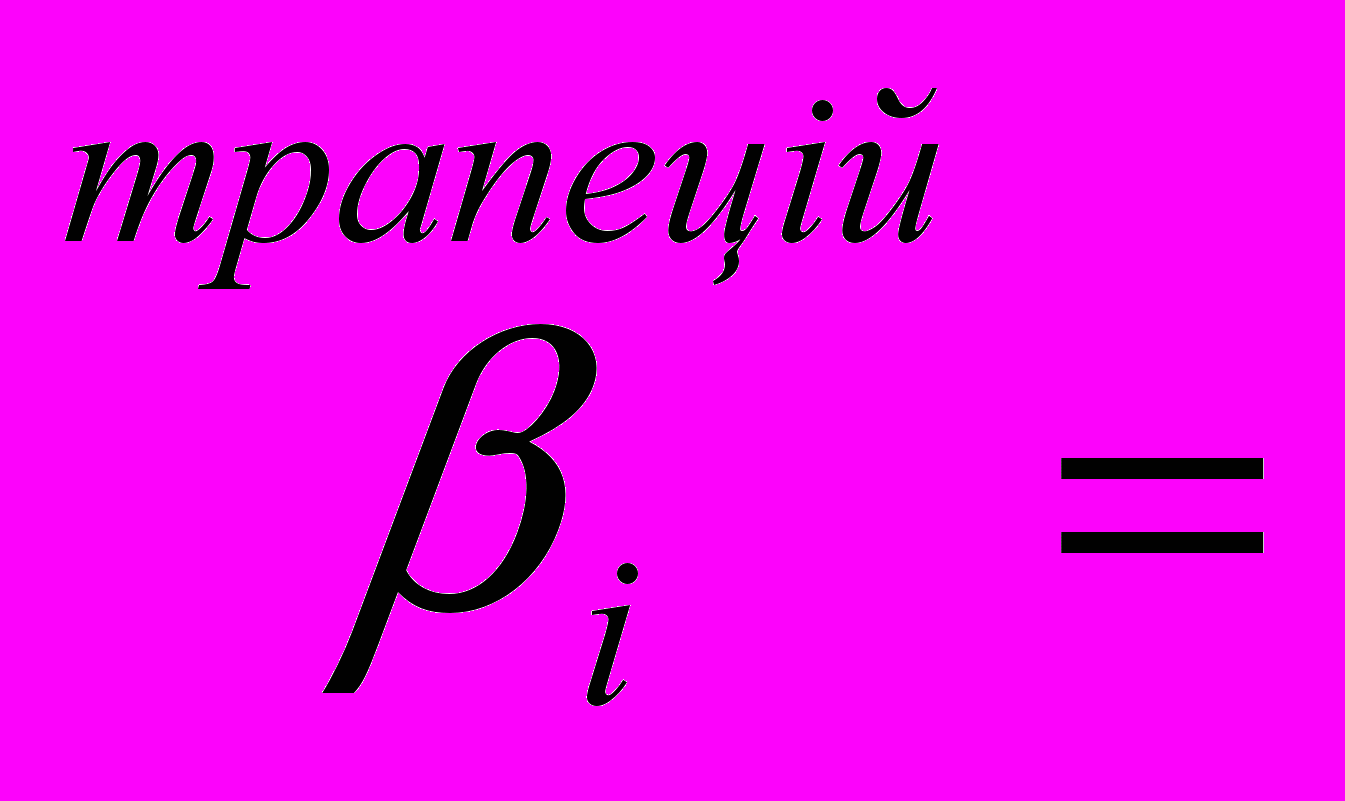h/2, коли і=0, і=п і h, коли і=1,...,п-1;
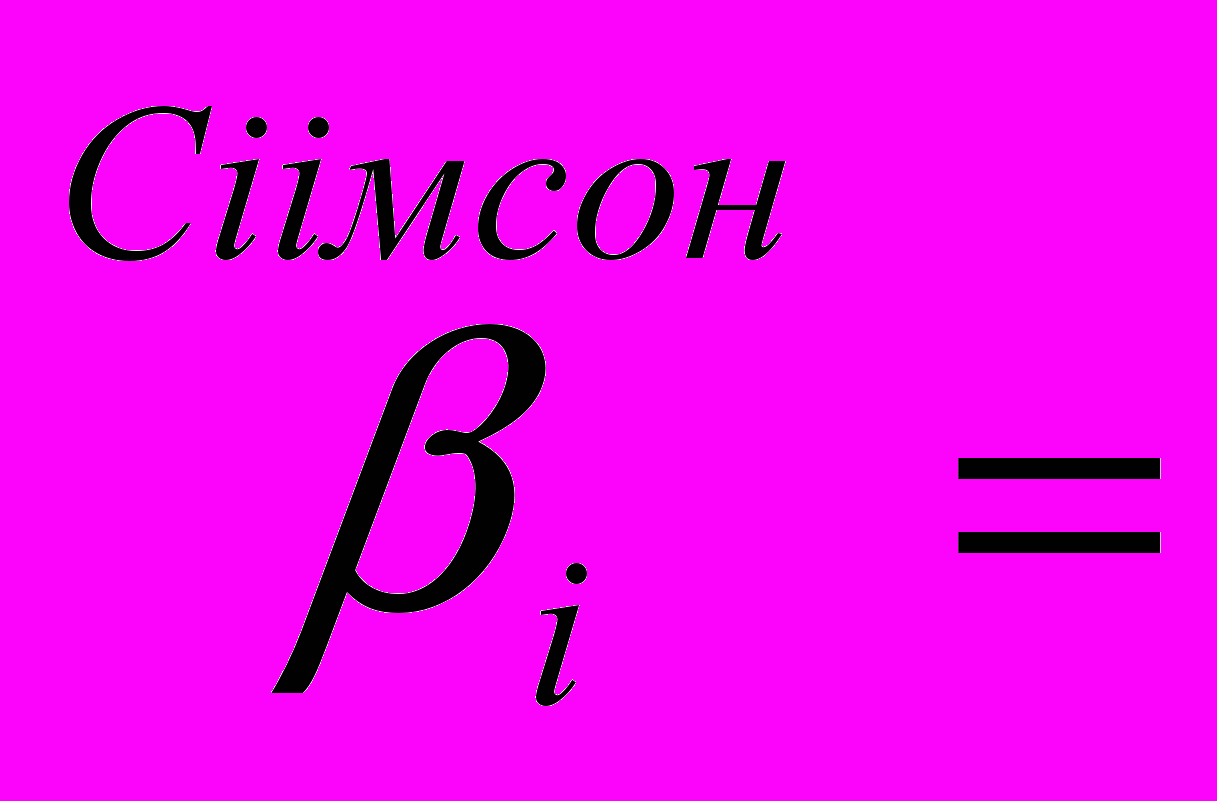h/3, коли і=0,і=2к,2к=п і 2h/3, коли i=2j, j=1,…,n-1 i 4h/3, коли i=2j+1, j=0,…,n-1.Обчислення інтеграла з заданою точністю можна проводити за таким алгоритмом: спочатку вибирається невелике число з п кількістю інтервалів розбиття, при заданому значенні обчислюється початкове наближення інтегралу за відповідною квадратичною формулою.
Тема: Метод найшвидшого „градієнтного” спуску.
В ряді випадків задач розв'язок легко отримати, роблячи щоразу черговий крок алгоритму в напрямі досягнення мети, при цьому встановлюється деякий порядок пріоритетів ходів. На кожному кроці наступний крок алгоритму встановлюється у певному у певному порядку, по-порядку пріоритетів ходів, який можливий на даному, тому цей метод називають найшвидшим спуском з аналізом пріоритетів напряму.