Geum.ru

А. Н. Туполева утверждаю: Проректор по учебной и методической работе И. К. Насыров 2007 г. Программа дисциплины

Вид материалаПрограмма дисциплины

Содержание


Требования к оформлению РГР.
Базовая СРС
Подобный материал:
1   2   3   4

ПРИЛОЖЕНИЕ 2


Требования к оформлению РГР.

Пояснительная записка РГР должна содержать выданное студенту индивидуальное задание и подробное описание выполненных им разделов в следующем порядке:

-построение математической модели оптимизации предложенного в задании объекта в виде задачи линейного программирования (ЗЛП);

-приведение поставленной ЗЛП к канонической форме с односторонними ограничениями;

-построение начального опорного плана ЗЛП;

-решение исходной ЗЛП первым и вторым алгоритмами симплекс-метода;

-исследование двойственной задачи, сопряжённой с исходной ЗЛП .

Нумерация страниц отчета сквозная, первой страницей является титульный лист, второй – содержание и т.д. Разделы пояснительной записки нумеруются арабскими цифрами. Номер подраздела состоит из номера раздела и номера подраздела, разделенных точкой. Таблицы также нумеруются и снабжаются содержательными заголовками. Формулы, на которые имеются ссылки в тексте, нумеруются в пределах раздела. Номер формулы состоит из номера раздела и порядкового номера формулы, заключенных в круглые скобки.

В конце отчета приводится список использованной литературы с указанием фамилии и инициалов автора, заглавия книги, издательства и года издания.


ПРИЛОЖЕНИЕ 3.


Варианты заданий для проведения контрольных аттестаций


Задание №1

1. Пусть -унимодальная на функция и . Оценить точность определения минимального значения и точки минимума функции методом перебора в результате вычислений функции .

2. Найти минимальное значение константы Липшица для функции на отрезке

3. Повысится или замедлится сходимость метода ломаных с увеличением значения константы Липшица. Ответ пояснить рисунком.

4. Найти классическим методом минимум функции .


5. Найти минимум функции методом Ньютона из начальной точки .

6. Дать определение градиента функции многих переменных; каким свойством обладает вектор градиента; как ориентирован относительно него любой вектор, задающий направление убывания; как осуществляется исчерпывающий спуск.

7. Для функции построить векторы , , с началом в точке (2;2). Установить, какие из них задают направление убывания в точке (2;2) и выполнить по одному из них исчерпывающий спуск.


Задание №2

  1. Дать классификацию задач математического программирования.
  2. Классическим методом решить задачу

при условии .
  1. Привести к канонической форме ЗЛП


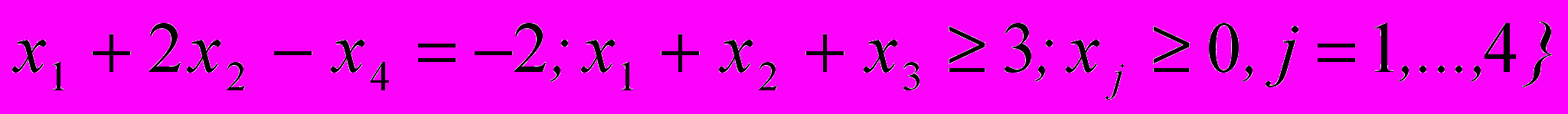
  1. Построить угловую точку множества планов, заданного ограничениями:
  2. Проверить, являются ли векторы опорными планами

множества планов, заданного ограничениями:



и если являются, то какими, вырожденными или невырожденными.

6. Решить графическим методом ЗЛП

.


Задание №3


1. Перечислить основные методы оптимизации при наличии ограничений.

2. Какова специфика МСП и для решения каких задач его применение предпочтительно?

3. Перечислить основные алгоритмы МСП.

4. Что является критерием останова в МСП ?

5. Какие задачи решаются МШФ и какова основная идея этого метода ?

6. Дать определение выпуклой функции и указать её основное экстремальное свойство

на выпуклом множестве .

7. Дать математическую постановку ЗВП .

8. Какие направления в точке называются возможными ?

9. Что означает отсутствие в точке подходящих направлений ?

10. Кратко описать принципиальный алгоритм метода возможных направлений.

11. Кратко описать правило выбора длины шага в методе возможных направлений.

12. Построить графически конус подходящих направлений в точке (3;1) допустимой

области следующей ЗВП

.




ПРИЛОЖЕНИЕ 4.


Рекомендуемый список контрольных вопросов по курсу:


Методы одномерной оптимизации
  1. Дать математическую постановку задачи одномерной оптимизации.
  2. Дать определения точки локального минимума и точки глобального минимума функции одной переменной.
  3. В чем заключается классический метод минимизации?
  4. Пояснить достоинства и недостатки прямых методов минимизации.
  5. Перечислить основные методы одномерного поиска.
  6. Назвать основные методы, использующие производные; указать их достоинства и недостатки.


Методы безусловной минимизации функции многих переменных
  1. Дать математическую постановку задачи безусловной минимизации функций многих переменных.
  2. Описать классический метод ее решения.
  3. Назвать основные прямые методы безусловной минимизации и указать их достоинства и недостатки.
  4. Пояснить метод деформируемого многогранника.
  5. Дать определение градиента функции многих переменных; как ориентирован относительно него любой вектор, задающий направление убывания функции?
  6. Как осуществляется исчерпывающий спуск в направлении убывания?
  7. Перечислить основные градиентные методы и пояснить их общую идею .
  8. Описать итерационную процедуру метода наискорейшего спуска.


Методы оптимизации при наличии ограничений
  1. Дать постановку общей задачи математического программирования (ЗМП).
  2. Пояснить классификацию ЗМП.
  3. Дать постановку задачи линейного программирования (ЗЛП) и описать ее каноническую форму.
  4. Пояснить понятия плана ЗЛП и оптимального плана ЗЛП.
  5. Что такое множество планов ЗЛП, какими свойствами оно обладает?
  6. Описать графический метод решения ЗЛП.
  7. Пояснить основную идею симплекс-метода решения ЗЛП.
  8. Сформулировать признак оптимальности опорного плана.
  9. Перечислить основные алгоритмы метода случайного поиска (МСП), описать их общую идею и отличительные особенности.
  10. В каких случаях применение МСП предпочтительно?
  11. Какой шаг в МСП считается удачным ?
  12. Как формируется критерий останова в МСП ?
  13. Какова основная идея методов последовательной безусловной оптимизации(МПБО)?
  14. Перечислить основные алгоритмы МПБО и пояснить их отличительные особенности.
  15. Дать постановку задачи выпуклого программирования (ЗВП).
  16. Какие функции называются выпуклыми и какими экстремальными свойствами они обладают?
  17. Дать определения возможного направления и подходящего направления.
  18. Описать общую схему метода возможных направлений.
  19. Как осуществляется в методе возможных направлений выбор подходящего направления в заданной точке допустимой области ЗВП?
  20. Как вычисляется длина шага в подходящем направлении при решении ЗВП методом возможных направлений?
  21. Как оценивается в методе возможных направлений погрешность приближенного решения ЗВП?


Оптимизация в функциональных пространствах
  1. Дать определение функционала.
  2. Что называется функциями сравнения?
  3. Дать определение абсолютного и относительного экстремумов функционала.
  4. Сформулировать простейшую вариационную задачу с фиксированными границами.
  5. Пояснить основную идею метода вариаций.
  6. Что представляет собой уравнение Эйлера?
  7. Каково правило решения простейшей вариационной задачи?


ПРИЛОЖЕНИЕ 5 к программе дисциплины Методы оптимизации

Распределение и содержание заданий на самостоятельную работу

№№

п/п
Курс, семестр
Наименование учебной работы
Раздел, тема
Объем

СРС

(в часах)
Форма изучения
Информационно- методическое обеспечение
Форма кон-троля выпол-нения СРС
Баллы в

БРС

Базовая СРС

1
3 к.,

5 сем.
Проработка

теоретического материала лекций

Темы 1…9

10
Проработка и

изучение учебного материала. Подготовка к аттестации
Электронный

конспект

лекций,

стр.1-55.

Контрольные мероприятия в рамках БРС


15

2
3 к.,

5 сем.
Проработка

теоретического материала лекций

Темы

10-13

7
Проработка и изучение учебного материала. Подготовка к аттестации
Электронный

конспект

лекций,

стр. 55…99.


Контрольные мероприятия в рамках БРС


15

3
3 к.,

5 сем.
Проработка

теоретического материала лекций

Темы

14-20

10
Проработка и изучение учебного материала. Подготовка к аттестации
Электронный

конспект

лекций,

стр.99-128.

Контрольные мероприятия в рамках БРС


15

4
3 к.,

5 сем.
подготовка к лаборат.

работам
Темы

5,8,

14,15


9
Обработка результа-тов эксперимента и оформление отчёта.

Подготовка к защи-те лаб. работ
Лабораторный. практикум «Численные методы оптимизации». [3]

Защита

лабораторных работ.


15







Итого по базовой СРС



36









60

Дополнительная СРС

5
3 к.,

5 сем.
Расчётно-графическая

работа

Темы

11,13

17
Изучение метод.ма-

териалов. Выполне-ние расчётов и схем. Оформлен. записки.
Методическое пособие по РГР «Линейное программирование»
Защита курсового проекта.
Отдельная

оценка

6
3 к.,

5 сем.
Экзамен
Темы

1-20
36
Повторение учебн. материала.
Электронный кон-спект лекций
Письменная и устная
40







Итого по дополн. СРС



53


















Всего СРС



89









100