То схо­ди­мость ите­ра­ци­он­ного про­цесса может быть зна­чи­тельно уве­ли­че­на, если использовать сле­­ду­ю­­щий алгоритм

• Уголовный процесс, 1106.99kb.
• Не был на квн, но думаю, что почти во всем согласился бы с Сережей. Кроме одной фразы:, 30.84kb.
• Конспект лекции 14. Алгоритм деятельности по разрешению конфликта «17 шагов» (по, 19.85kb.
• Компьютер сочиняет, 32.66kb.
• 1. общие положения планируемые расходы на приобретение Предмета лизинга, размер и порядок, 238.77kb.
• Секция “Философская онтология”, 38.57kb.
• Чный ответ, демонстрирующий хорошее знание текста произведения, умение использовать, 243.63kb.
• -, 309.11kb.
• В основных направлениях экономического и социаль­ного развития СССР на 1986-1990, 974.56kb.
• «Основы проблемного обучения в начальной школе», 404.27kb.

Матрицей называется прямоугольная таб­ли­ца из чи­­сел, содержащая некоторое количество m строк и n столбцов, при этом числа m и n на­зываются порядками мат­ри­цы. Если m = n, мат­­рица на­зывается квадратной, а число m = n - ее по­­рядком. Для записи матриц ис­пользуются сле­ду­ю­щие обо­зна­че­ния:

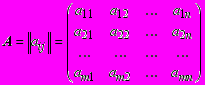, (1.33)

где числа a_ij называются элементами матрицы A. В слу­чае, если m = n и определитель матрицы detA  0, мат­ри­ца A на­зывается невырожденной и для нее можно найти об­рат­ную мат­ри­цу. Обратной по от­но­шению к дан­ной мат­ри­це A называется матрица A^-1, которая, бу­ду­чи умно­женной как справа, так и сле­ва на A, дает еди­­ничную матрицу:

.

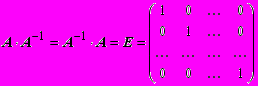Матрица A^T, полученная перестановкой строк со столб­ца­ми в мат­­ри­це A, называется транс­по­ни­ро­ван­ной. Квад­ратная мат­ри­ца A на­зы­ва­ет­ся сим­мет­рич­еской, если A^T = A, и ор­то­го­наль­ной, если A^T A = E.

Характеристическим уравнением матрицы A на­­зы­ва­ет­ся матричное уравнение ||A - E|| = 0, в ко­тором _i - соб­ст­вен­ные (или ха­рак­те­рис­ти­чес­кие) числа (или зна­че­ния) мат­­рицы A. Соб­ст­вен­ным вектором, отвечающим соб­ст­вен­­ному чис­лу _i, называется вектор

,

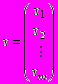который удов­летворяет матричному уравнению Ax =_i x. Ког­­да говорят о вычислении собст­вен­ных чисел, то раз­ли­ча­ют полную и частичную проблему собст­венных чисел. В пол­ной проблеме вы­чис­ля­ют все собственные числа и со­от­­ветст­ву­ю­щие им собственные векторы матриц, а под час­тич­­­ной про­блемой обычно понимают задачу на­хо­ж­де­ния од­­ного или нескольких собственных чи­сел и со­от­ветс­т­ву­ющих им собственных век­то­ров.

В настоящем параграфе рассматривается не­сколь­­ко эф­фек­тивных алгоритмов, реализующих как операции над мат­­рицами, так и задачи ре­ше­ния полной про­бле­мы соб­ст­вен­ных значений.

Задача определения собственных значений и собст­вен­ных векторов матриц имеет большое зна­че­ние при ре­ше­нии очень широкого спектра за­дач. Методы ре­ше­ния ука­занной за­дачи по типу примененной вы­чис­ли­тельной схе­мы мож­но разделить на пря­мые (точные) и ит­е­ра­ци­он­ные (при­бли­женные).

В прямых методах по не­ко­то­ро­му правилу вы­чис­ля­ют­ся коэффициенты матрицы с заранее из­­вестными свой­ст­ва­ми, а затем собственные зна­че­ния находятся как корни ха­­рак­теристического мно­го­­члена по какому-ли­бо из­вест­но­­му чис­­­лен­ному методу. После этого опре­де­ляются собс­т­­вен­ные векторы, что считается не очень слож­ной за­да­чей.

В итерационных методах коэффициенты ха­рак­те­рис­ти­ческого уравнения не вычисляют, а составляют не­ко­то­рые итерационные по­сле­до­ва­тель­нос­ти, поз­во­ля­ю­щие най­ти одно или несколько, а иног­да и все соб­ст­вен­ные зна­че­ния исходной ма­три­цы А. Ите­­ра­ци­онные ме­то­ды почти всег­­да бо­лее тру­до­ем­кие, од­на­ко они на­деж­нее прямых ме­то­­­дов, так как менее чув­ст­вительны к ошиб­кам округ­ле­ния.

К прямым можно отнести методы Кры­лова, Да­ни­лев­с­ко­го, Самуэльсона и др., а к ите­рационным - сте­пен­ной и ме­­тод Якоби, или, как его еще на­зы­ва­ют, ме­тод вращений. По­­след­ний метод считается на­и­более эф­фек­тивным из всех известных [Kpылов и др., 1972].

4.1. ВЫЧИСЛЕНИЕ СОБСТВЕННЫХ ВЕКТОРОВ И СОБСТВЕННЫХ ЗНАЧЕНИЙ МАТРИЦ ПО МЕТОДУ КРЫЛОВА

Пусть А - некоторая квадратная матрица ||а_ij|| по­рядка n. Рассмотрим связанное с ней уравнение ||А -Е|| = 0, определитель которого есть ал­геб­ра­и­ческий многочлен степени n от :

||А -Е|| = (-1)ⁿ (ⁿ - P₁^{n -1} P_{n -1}P_n . (1.34)

Кор­нями этого многочлена являются собственные зна­че­ния (собственные числа) матрицы А. Эта сис­тема име­ет ненулевое решение тогда и только тог­да, когда ___n.

А.Н.Крылов¹ предложил эффективный ме­тод по­стро­е­ния характеристического мно­го­чле­на, ос­но­­ван­­­ный на при­ме­нении ми­ни­маль­но­го мно­го­чле­на мат­ри­цы, ан­ну­ли­ру­ю­ще­го за­дан­ный вектор.

Возьмем произвольный вектор с⁽⁰⁾  0, раз­мер­­нос­ти n и составим по­сле­до­ва­тель­ность ли­ней­но не­за­висимых век­то­ров по правилу

с⁽¹⁾ = А с⁽⁰⁾; c⁽²⁾ = A c⁽¹⁾; ...; c⁽ⁿ⁾ = A c^{(n -1)} .

Очевидно, что c⁽ⁿ⁾ бу­дет являться линейной ком­би­на­ци­ей пре­ды­ду­щих линейно независимых век­то­ров.

Рас­писав полученную на последнем шаге си­с­те­му

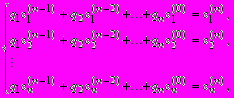(1.35)

где с_i - соответствующие координаты вектора с⁽ⁱ⁾, а q_i - не­оп­ределенные коэффициенты, по­лу­чим не­од­но­род­ную сис­те­му из n алгебраических урав­нений. Опре­де­литель этой сис­темы



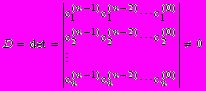
будет отличен от нуля тогда и только тогда, ког­да с⁽ⁱ⁾ об­ра­зу­ют систему линейно независимых век­то­ров [Кры­лов и др., 1972]. Полученные зна­че­ния q_i бу­­дут ра­в­ны р_i - ко­эф­фи­ци­ентам ха­ра­к­те­рис­ти­чес­ко­го урав­­нения мат­рицы А (1.34).

Для определения q_i систему (1.35) решают ме­то­дом Га­усса (с обязательной проверкой). Если сис­те­му не удается привести в ходе решения к тре­у­голь­но­му виду, то говорят о зависимости по­стро­ен­ной сис­те­­мы век­торов, и тогда мож­но записать толь­ко де­ли­­тель ха­рак­те­рис­тического мно­­го­чле­на мат­p­ицы. Сам многочлен ре­ша­ется одним из из­­вест­­ных ме­то­дов решения линейных ал­­геб­ра­и­чес­­ких урав­нений.

После того как найдены собственные зна­че­ния _i мат­­ри­цы А, ищут собственные векторы мат­ри­цы А, что при­во­дит к решению следующей од­но­род­­­ной сис­те­­мы ли­ней­ных ал­­гебраических урав­не­ний:

(A -  E)х = 0. (1.36)

Так как _i являются корнями ми­ни­маль­но­го ан­ну­ли­рующего вектора с⁽⁰⁾ многочлена (1.34), то ре­ше­ния сис­темы (1.36) представляют в ви­де линейной ком­би­нации не­за­висимых ве­к­то­ров с⁽ⁱ⁾

x^(k) =_i1 c^{(n -1)} + _i2 c^{(n -2)} + ... + _in c⁽⁰⁾,

где коэффициенты _ij удовлетворяют ус­ло­вию Ax⁽ⁿ⁾=_k x⁽ⁿ⁾. Умножая x⁽ⁿ⁾ на А и учитывая, что с^(j)=Ас^(j-1), по­лучают

_i(_i1c^(n-1)+_i2c^(n-2)+...+_inc⁽⁰⁾) =

= _i1 c⁽ⁿ⁾ + _i2 c^(n-1) + ... + _in c⁽¹⁾.

Если же учесть, что A)c⁽ⁿ⁾ º 0, то после приведения по­доб­ных (с учетом формул 1.35) последнее ра­вен­ст­во мож­но переписать в виде

(q_n _i1 - _i _in)c⁽⁰⁾ + (q_n-1 _i1 + _in - _i _in-1)c⁽¹⁾ +

+ (q_n-2_i1 + _in-1 - _i_in)c⁽²⁾ + ... + (q₁_i1 + _i2 - _i_i1)c^(n-1) = 0.