4. Методы расчёта сложных электрических цепей

4.1. Эквивалентные преобразования цепей

Анализ процессов в электрических цепях во многих случаях может быть существенно упрощен за счёт использования различных преобразований, в результате которых отдельные участки цепей заменяются участками с более простой топологией или участками, более удобными для анализа.

Два участка цепи называются эквивалентными, если при замене одного из этих участков другим токи и напряжения остальной части цепи не меняются.

Эквивалентные преобразования электрических цепей основаны на эквивалентных преобразованиях соответствующих систем уравнений электрического равновесия.

Эквивалентное преобразование участка цепи с последовательным соединением элементов

Рассмотрим неразветвленную электрическую цепь (рис. 4.1), содержащую N сопротивлений, М емкостей, К индуктивностей и Р неуправляемых источников напряжения (обобщенная одноконтурная цепь).

R₁ R_N

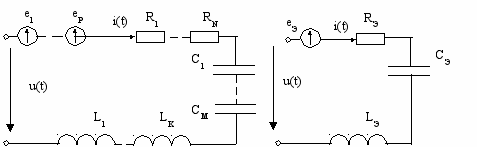
а б

Рис. 4.1. Преобразование участка цепи с последовательным соединением элементов

Так как через все элементы цепи протекает один и тот же ток i, то уравнение электрического равновесия, составленное на основе второго закона Кирхгофа и компонентных уравнений, может быть записано в следующей форме:

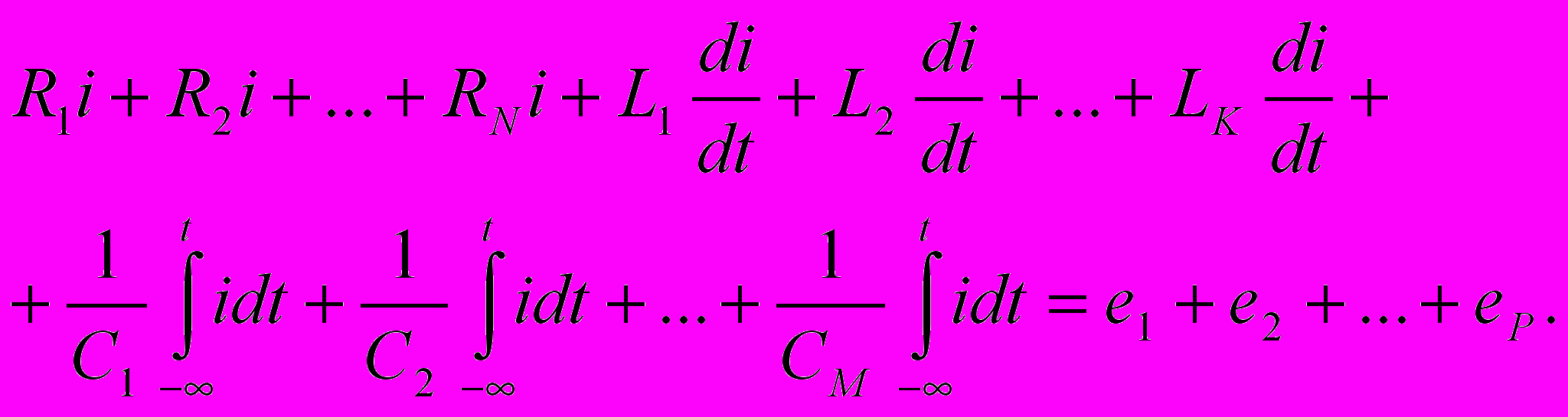
(4.1)

После преобразований получим

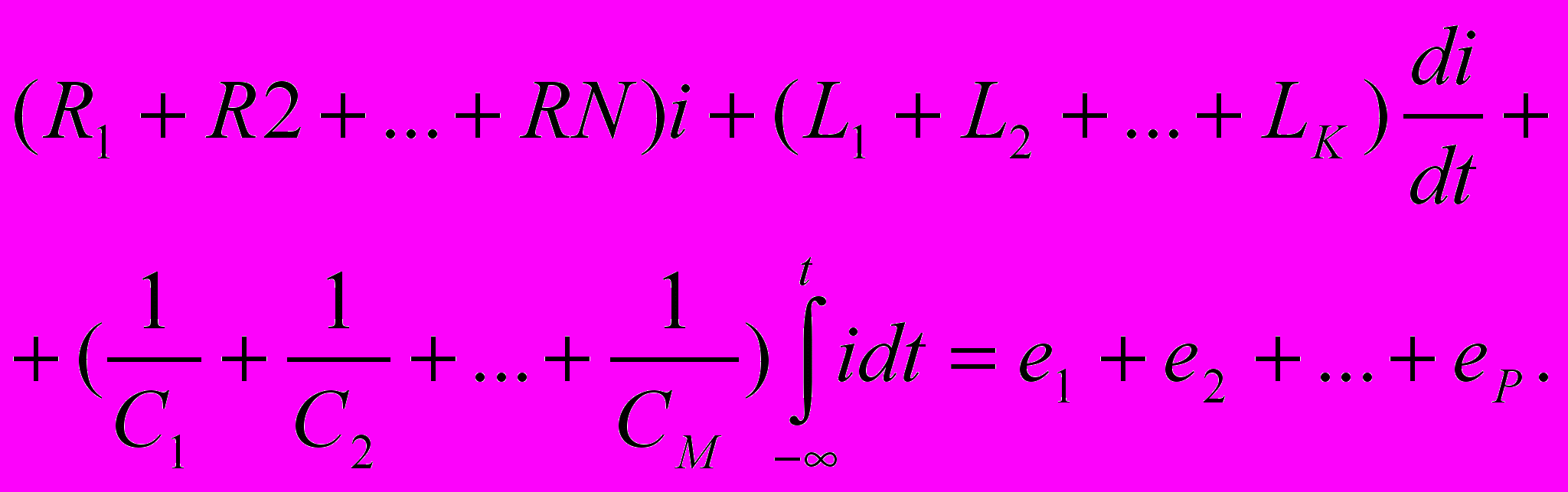
(4. 2)

или

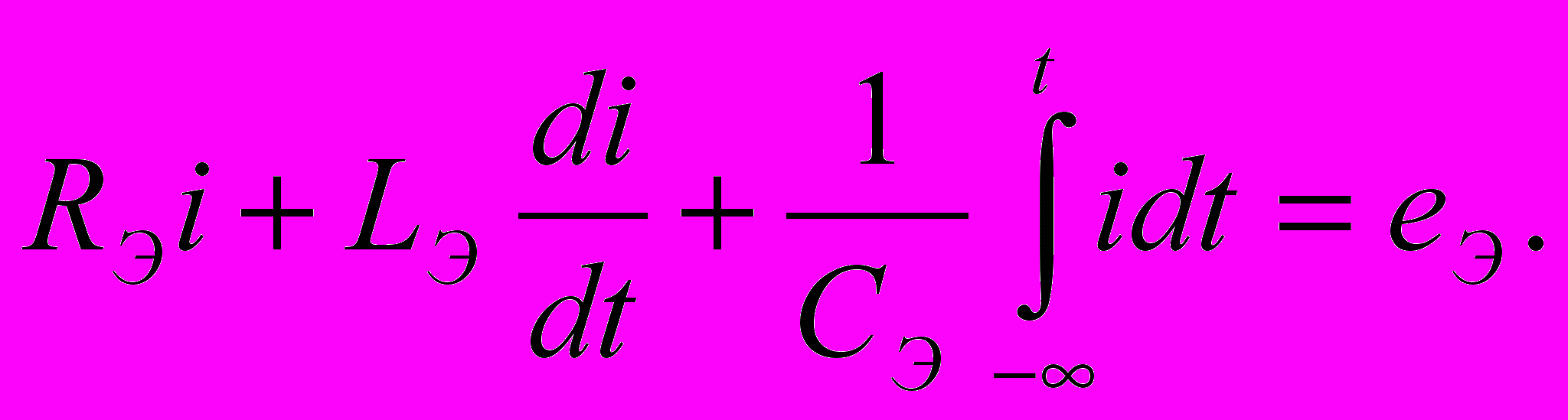
(4. 3)

Уравнению (4.3) соответствует преобразованная цепь, схема которой изображена на рис. 4.1, б. Таким образом, ток и напряжение на зажимах обобщенной одноконтурной цепи не изменятся, если каждую из групп последовательно включенных однотипных элементов заменить одним эквивалентным элементом R_Э, С_Э. L_Э и е_Э(t):

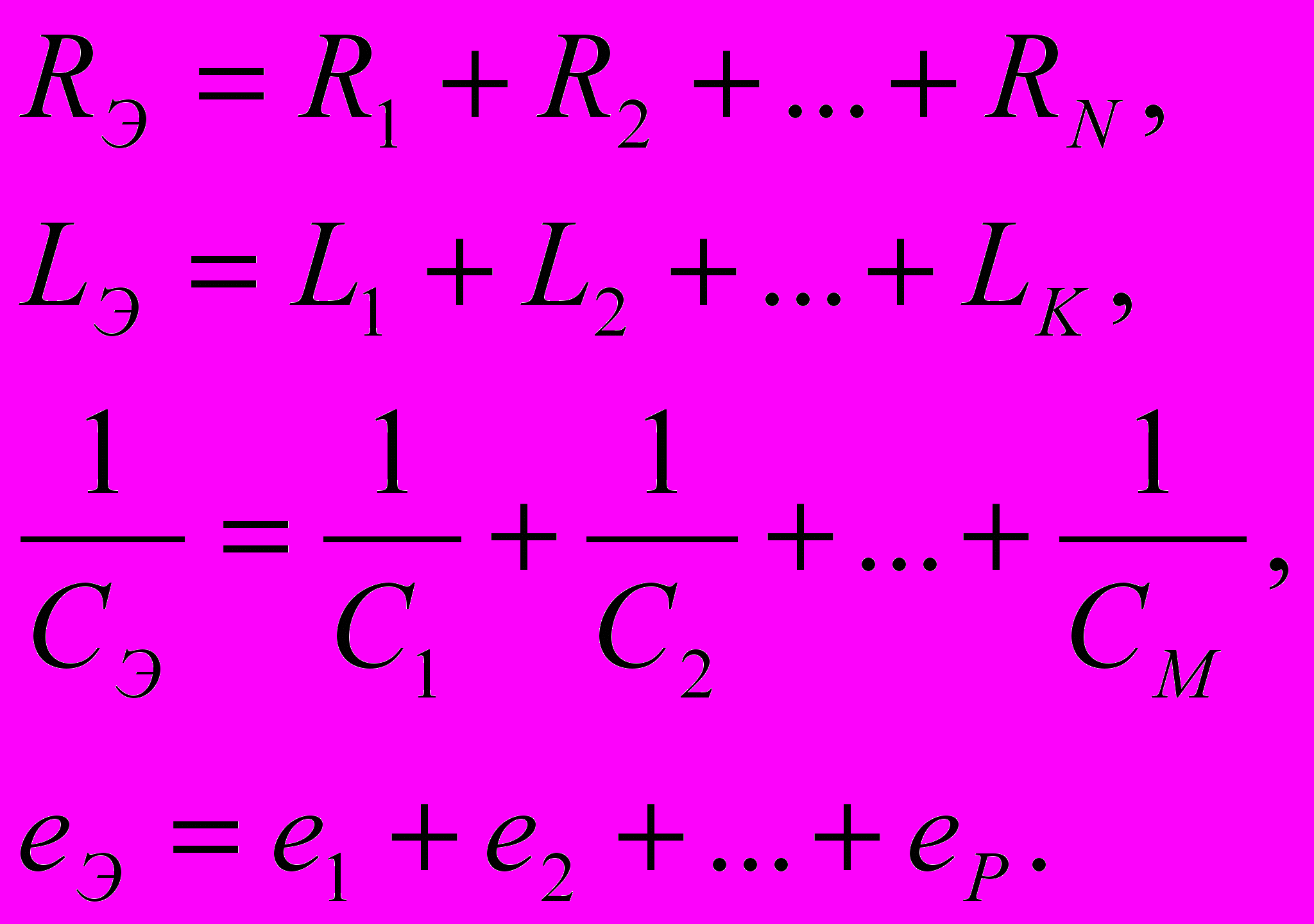
(4. 4)

Из выражения (4.4) следует, что при последовательном включении сопротивлений, индуктивностей и источников напряжения параметры эквивалентного элемента равны сумме параметров последовательно включенных элементов соответствующего типа. При этом суммирование ЭДС источников напряжения производится алгебраически, с учетом их знаков. При последовательном включении емкостей значение величины, обратной Сэ, определяется как сумма обратных значений всех последовательно включенных емкостей, причем эквивалентная емкость Сэ меньше, чем любая из последовательно включенных емкостей.

Подобное эквивалентное преобразование справедливо для цепей при гармоническом воздействии: комплексное сопротивление цепи равно сумме комплексных сопротивлений последовательно соединённых участков.

Эквивалентное преобразование участка цепи с параллельным соединением элементов

Пусть электрическая цепь (рис. 4.2, а) состоит из параллельно соединенных N сопротивлений, М емкостей, К индуктивностей и Р неуправляемых источников тока (обобщенная двухузловая цепь).

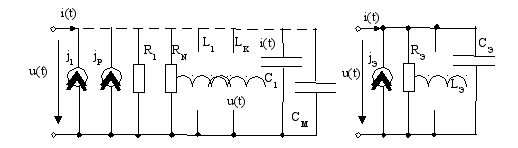
а б

Рис. 4.2. Преобразование участка цепи с последовательным соединением элементов

Все элементы цепи находятся под одним и тем же напряжением и, поэтому уравнение электрического равновесия, составленное на основании первого закона Кирхгофа, может быть записано в форме

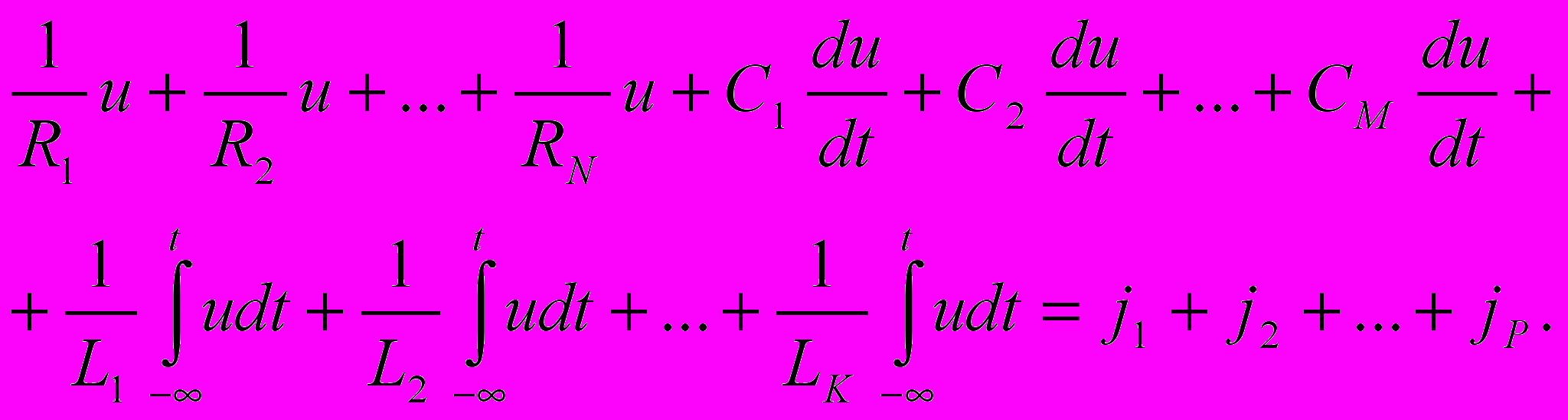
(4. 5)

После приведения подобных членов получаем:

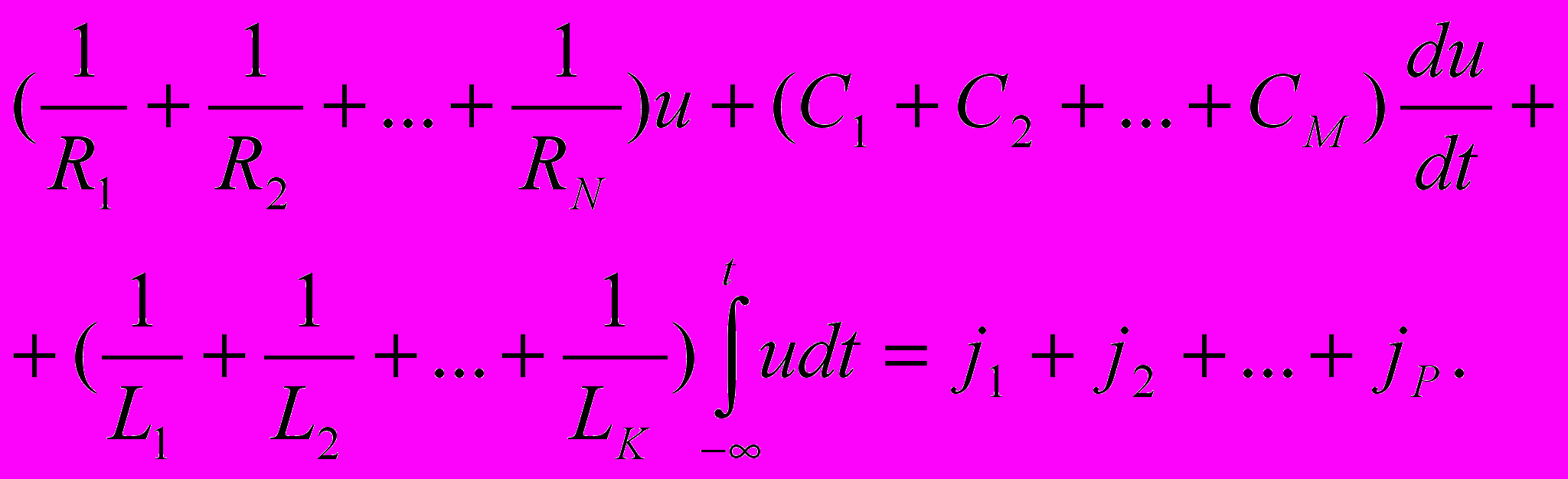
(4. 6)

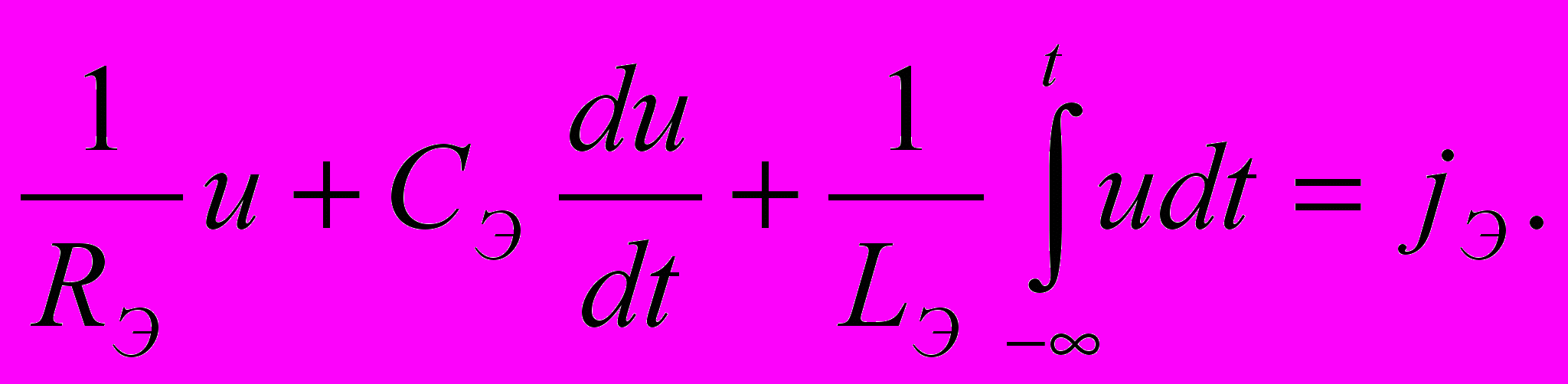
(4. 7)

Уравнению (4.7) соответствует преобразованная цепь, схема которой приведена на рис. 4.2, б. Видно, что ток и напряжение на зажимах обобщенной двухузловой цепи не изменятся, если каждую из групп параллельно включенных однотипных элементов заменить одним эквивалентным элементом, параметры которого

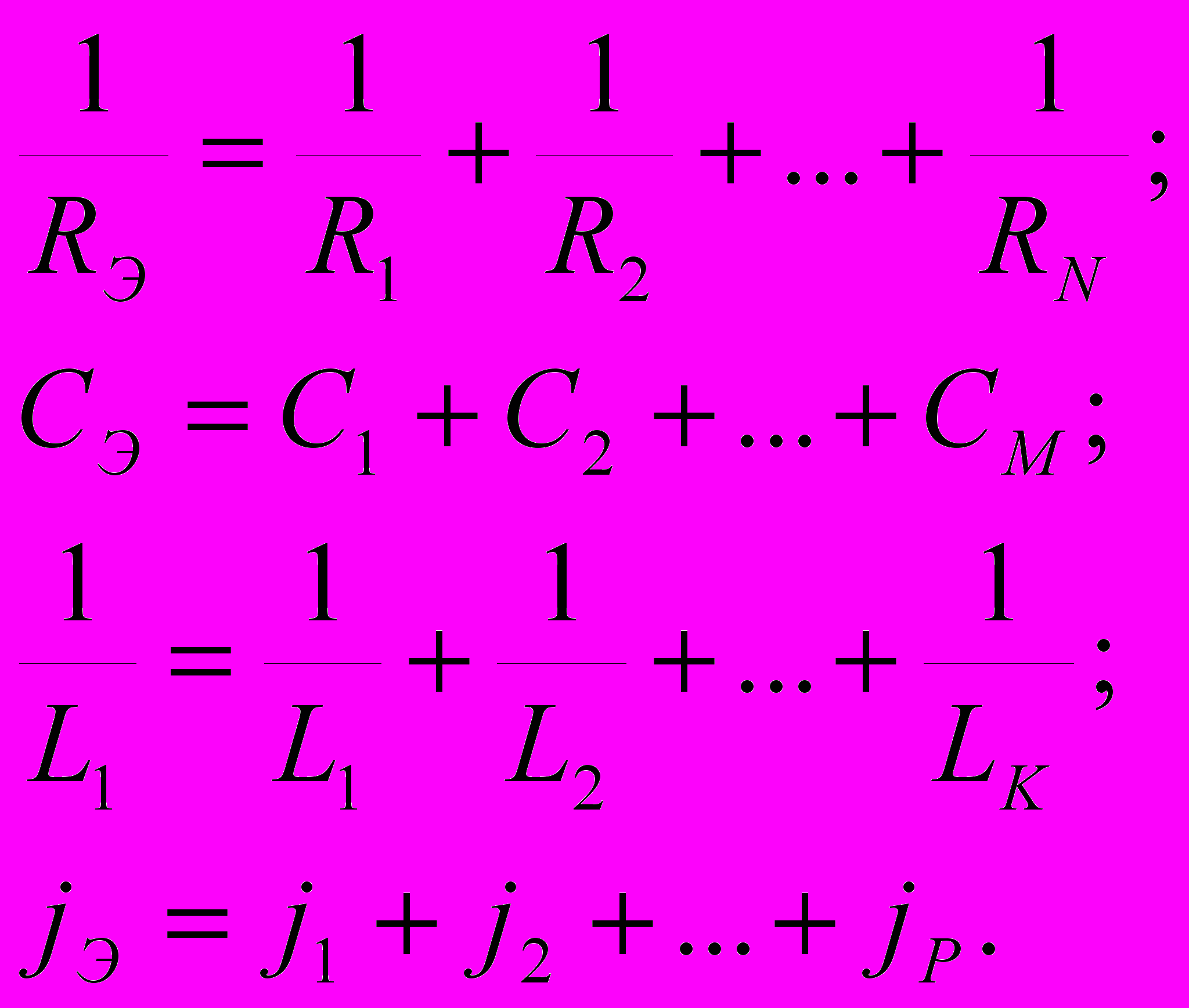
(4. 8)

Из выражения (4.8) следует, что при параллельном включении емкостей и источников тока параметры эквивалентного элемента равны сумме параметров параллельно включенных элементов соответствующего типа. При этом суммирование токов источников тока производится алгебраически с учетом их знаков, определяемых ориентацией источников относительно узла, для которого составляется уравнение (4.6).

При параллельном включении сопротивлений или индуктивностей значения величин, обратных Rэ и Lэ, будут определяться как сумма обратных значений этих сопротивлений или индуктивностей. Значения Rэ и Lэ будут меньше, чем сопротивление или индуктивность любого из параллельно включенных элементов соответствующего типа.

Участки цепей со смешанным соединением элементов

Правила преобразования участков цепей с параллельным или последовательным соединением элементов могут быть применены и для преобразования пассивных участков цепей со смешанным соединение элементов. Преобразование таких участков, представляющих собой сочетание групп параллельно или последовательно включенных элементов, обычно производят в несколько этапов, на каждом из которых группу параллельно включенных элементов заменяют одним двухполюсником, комплексная проводимость которого равна сумме комплексных проводимостей параллельно включенных элементов, а группу последовательно включенных элементов — одним двухполюсником, комплексное сопротивление которого равно сумме комплексных сопротивлений всех последовательно включенных элементов.

Подобное эквивалентное преобразование справедливо для цепей при гармоническом воздействии: комплексная проводимость цепи равна сумме комплексных проводимостей параллельно соединённых участков.

Эквивалентное преобразование треугольника сопротивлений в звезду и обратное преобразование

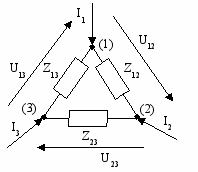
Найдем условия эквивалентности двух участков электрической цепи (рис. 4.3, а, б), которые представляют собой соединение пассивных идеализированных двухполюсников треугольником и звездой. По определению, эти участки цепи эквивалентны, если при замене одного участка другим токи выводов и напряжения между выводами останутся неизменными.

I₁

(1)

Z₁

U₁₂

U₁₃

Z₂

Z₃

(2)

(3)

I₂

I₃

U₂₃

а б

Рис. 4.3. Преобразование треугольник - звезда и звезда – треугольник

Для эквивалентности треугольника сопротивлений звезде достаточно потребовать, чтобы любая пара из трех напряжений между выводами одной цепи была равна соответствующей паре напряжений другой цепи (при одинаковых значениях токов внешних выводов).

Рассчитав сопротивления Z₁, Z₂, Z₃ по заданным Z₁₂, Z₁₃, Z₂₃, можно осуществить эквивалентную замену треугольника сопротивлений звездой (преобразование треугольник — звезда):

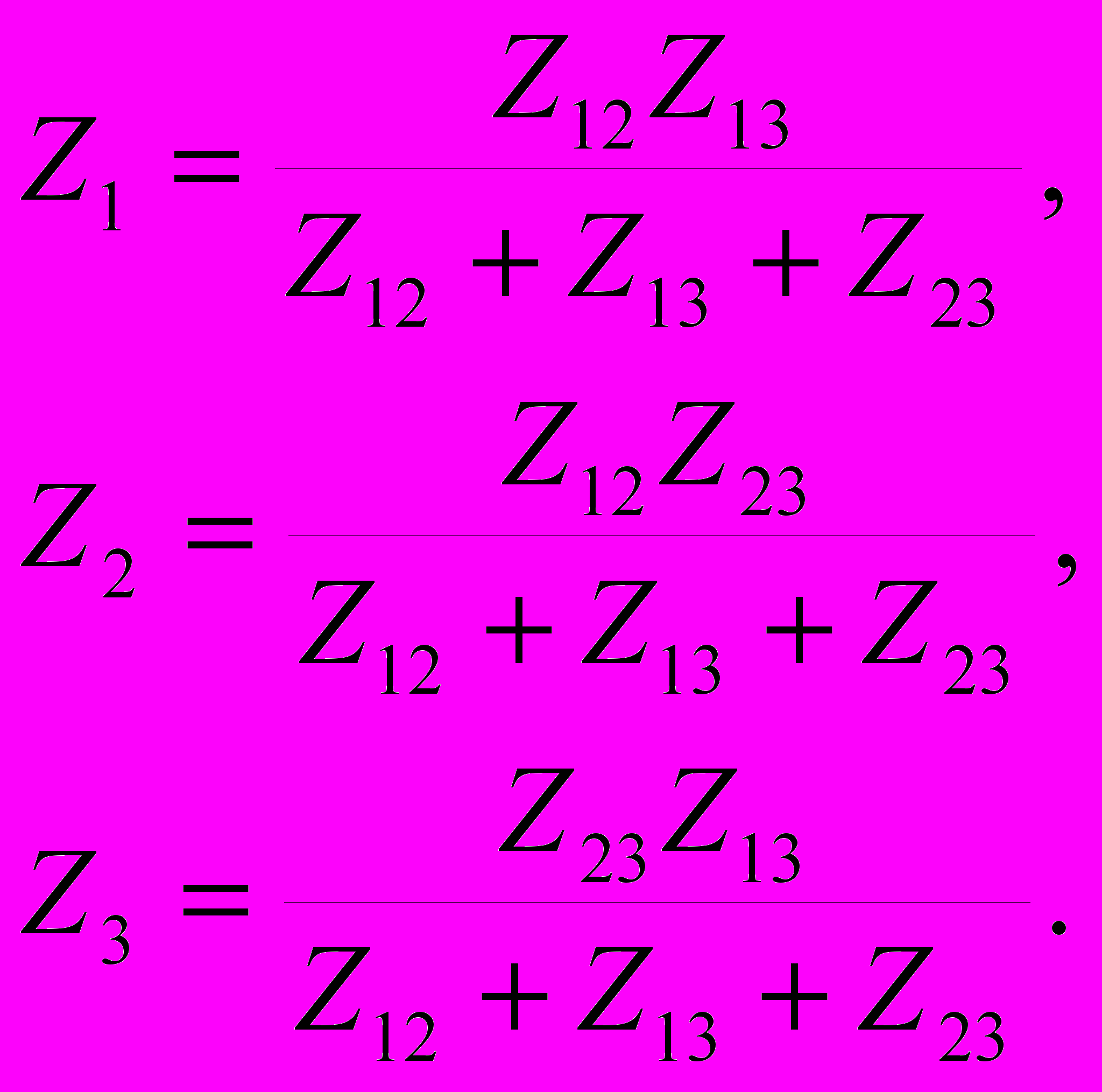
(4.9)

Из рис. 4.3 видно, что при этом преобразовании из цепи устраняется контур, образуемый сопротивлениями Z₁₂, Z₁₃, Z₂₃,и появляется новый узел — место соединения сопротивлений Z₁, Z₂, Z_3.

Решая систему уравнений (4.9) относительно Z₁₂, Z₁₃, Z₂₃, получим соотношения, позволяющие производить эквивалентную замену звезды сопротивлений треугольником (преобразование звезда—треугольник):

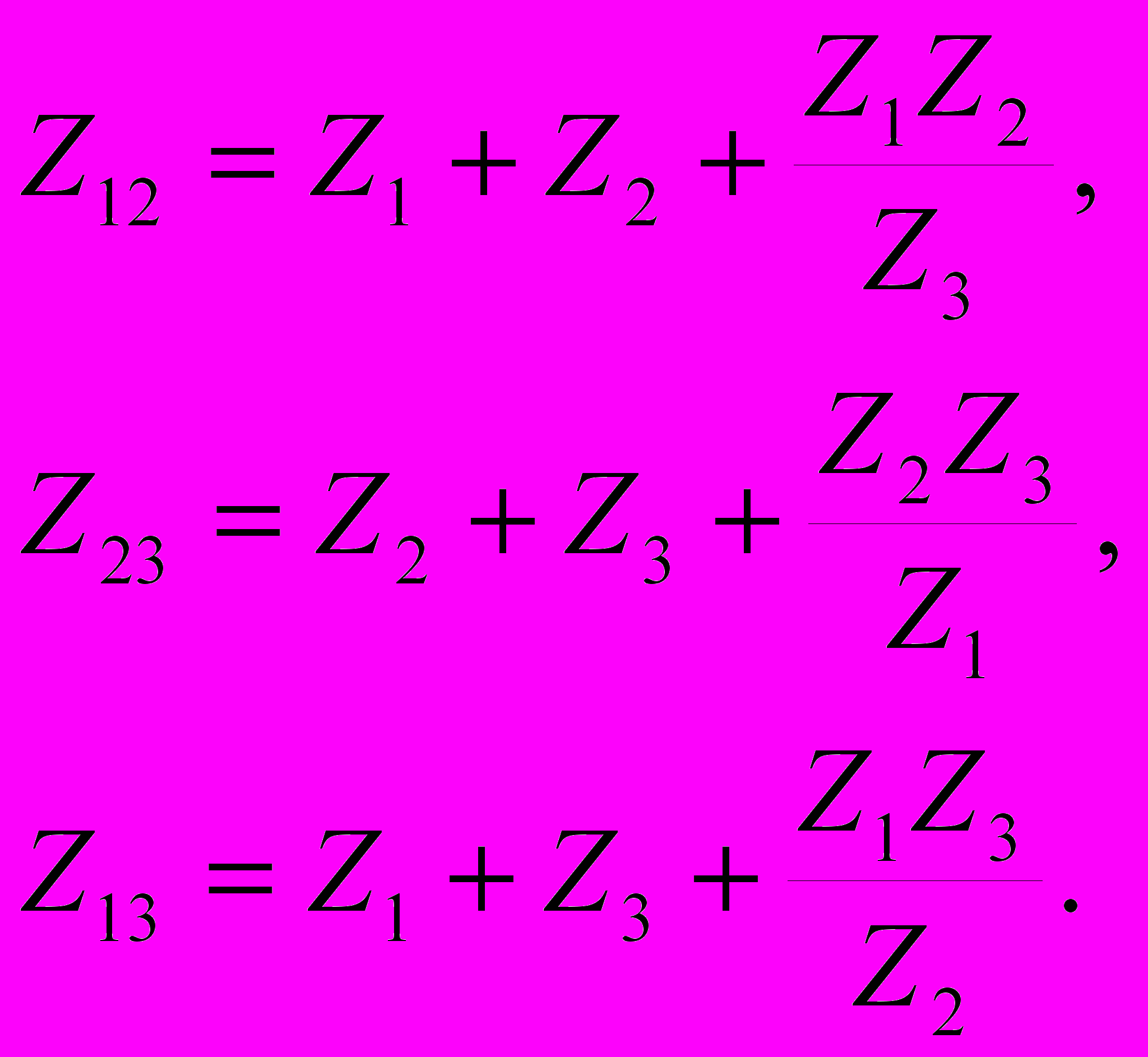
(4.10)

Преобразование звезда-треугольник приводит к уменьшению числа узлов преобразуемой цепи (за счет устранения узла, являющегося местом соединения сопротивлений Z₁, Z₂, Z₃), однако при этом появляется новый контур, образуемый сопротивлениями Z₁₂, Z₁₃, Z₂₃

Заменим в выражениях (4.10) комплексные сопротивления элементов их проводимостями. Проведя преобразования, установим, что выражения для комплексных проводимостей элементов, образующих стороны треугольника, имеют такую же структуру, как и выражения для комплексных сопротивлений, входящих в лучи звезды (4.9):

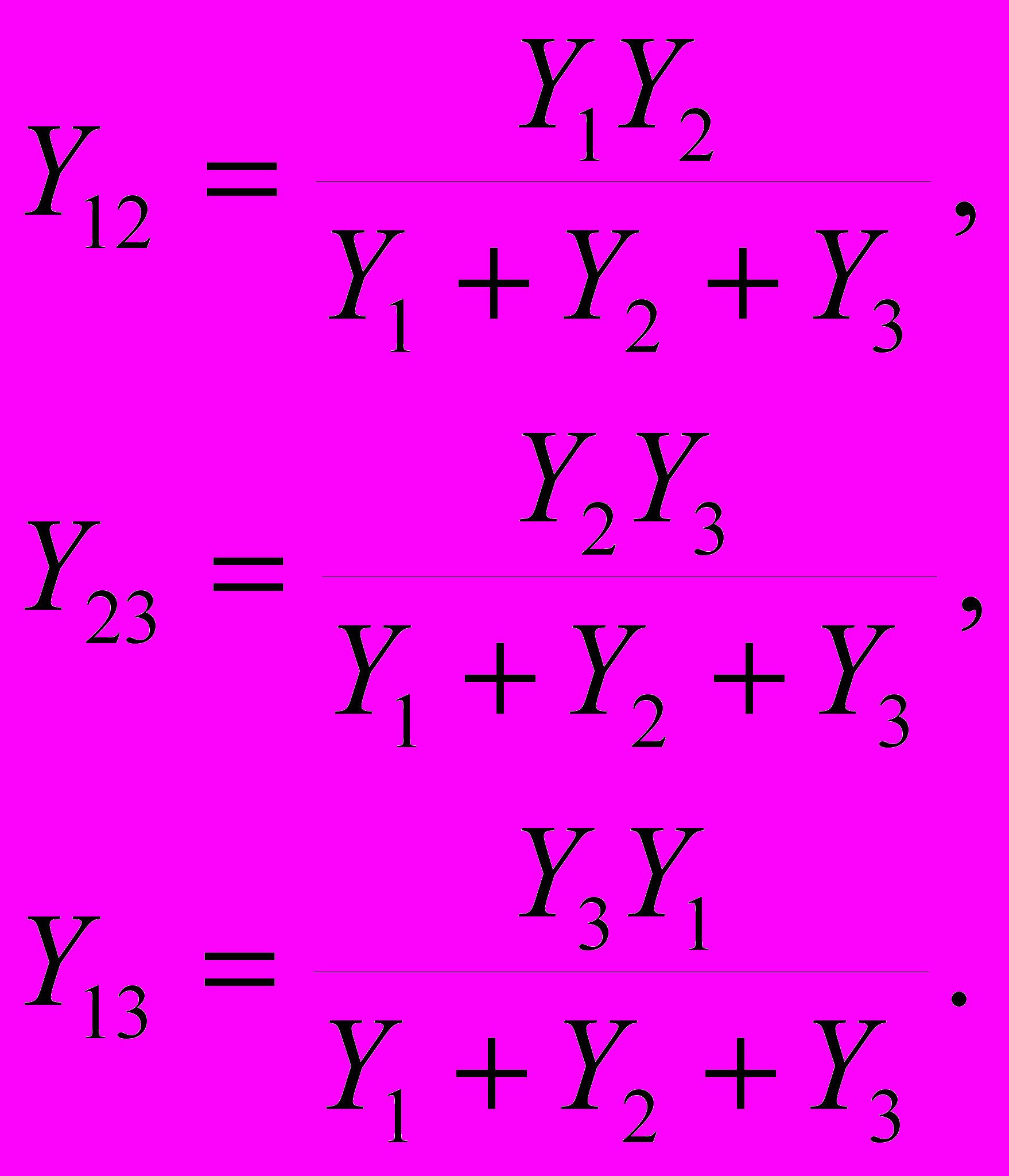
Применение преобразований треугольник—звезда и звезда—треугольник в ряде случаев позволяет существенно упростить анализ цепей, в частности иногда с помощью этих преобразований удается приводить сложные участки цепей к более простым (параллельное, последовательное или смешанное соединение элементов).

Комплексные схемы замещения источников энергии

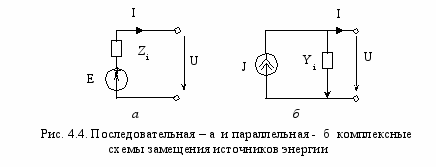
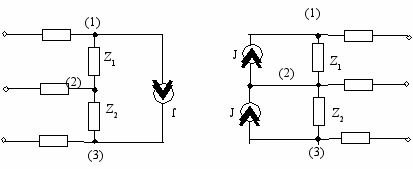
Ранее были рассмотрены последовательная и параллельная схемы замещения линеаризованных источников постоянного тока и напряжения и получены соотношения для их взаимного преобразования (2.28), (2.29). Аналогичные соотношения выполняются и для линеаризованных источников гармонических токов и напряжений, т. е. для источников, комплексные схемы замещения которых содержат идеальный источник напряжения Е и комплексное внутреннее сопротивление Z_i(рис. 4.4, а) или идеальный источник тока J и комплексную внутреннюю проводимость Y_i (рис. 4.4, б).

Формулы перехода от последовательной схемы замещения к параллельной

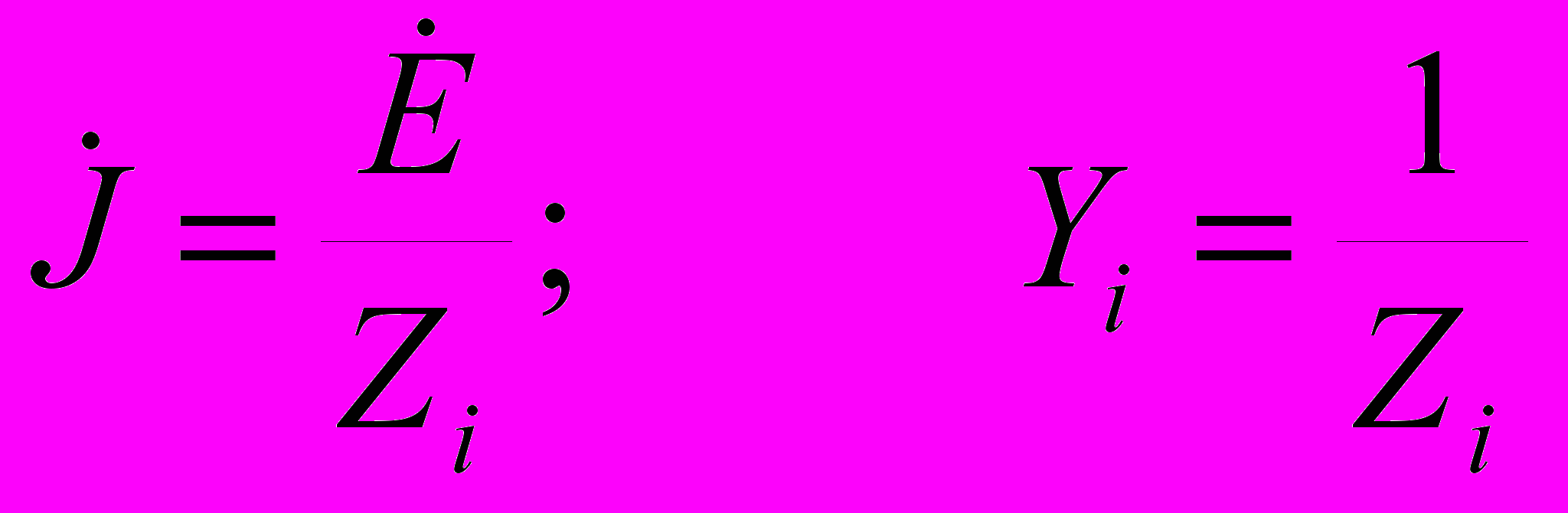(4.11)

и от параллельной схемы к последовательной

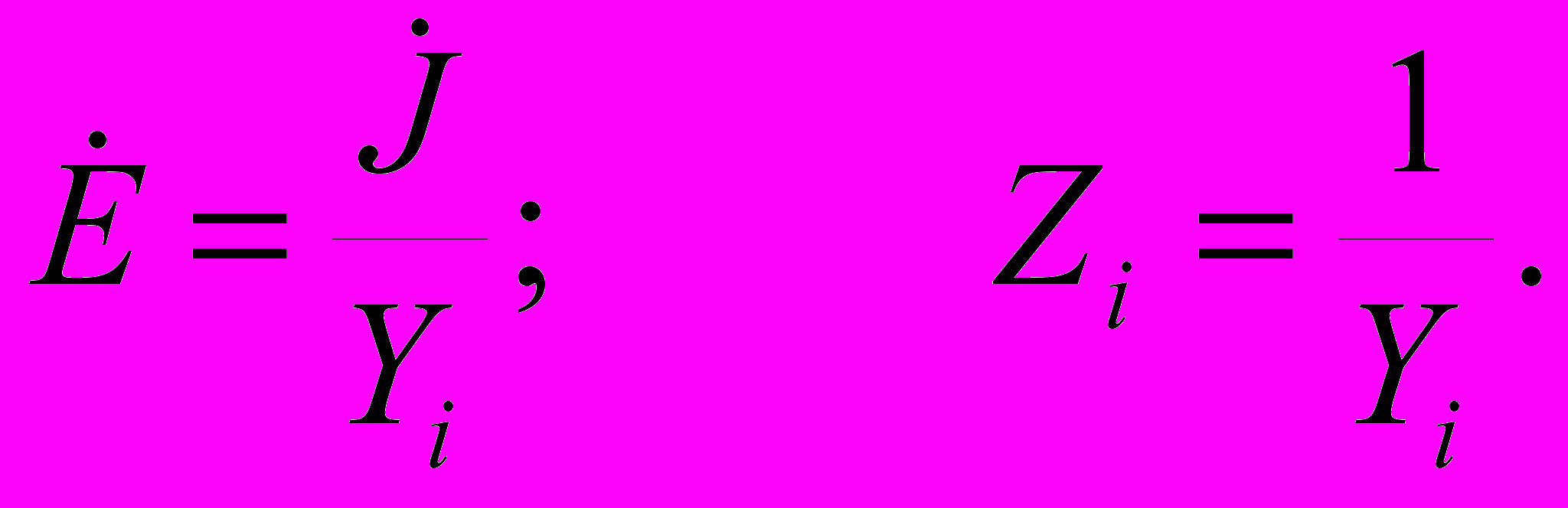(4.12)

В ряде случаев при анализе цепей возникает необходимость преобразовывать источники, т. е. заменять идеализированный источник одного типа другим. Для линеаризованных источников с конечным внутренним сопротивлением (проводимостью) эта задача решается путем преобразования последовательной схемы замещения источника в параллельную или обратно с помощью выражений (4.12). Если в эквивалентной схеме реального источника содержится только идеальный источник напряжения, однако в цепи, внешней по отношению к нему, имеется произвольный пассивный двухполюсник, включенный последовательно с источником, то его комплексное сопротивление Z можно рассматривать как внутреннее сопротивление линеаризованного источника Z_i, что дает возможность воспользоваться для преобразования источника выражениями (4.12). Аналогично, если параллельно идеальному источнику тока включена любая ветвь, составленная из пассивных элементов, то ее комплексную проводимость У можно рассматривать как внутреннюю проводимость линеаризованного источника Уi. Идеальные источники тока и напряжения, которые могут быть преобразованы один в другой таким образом, называются невырожденными.

Формулами (4.12), (4.13) можно воспользоваться и для взаимного преобразования невырожденных управляемых источников тока и напряжения. Разумеется, при этом характер управляющего воздействия (ток или напряжение) не изменяется.

Если в анализируемую цепь включены идеальный источник напряжения и последовательно с ним нет элементов, сопротивление которых можно рассматривать как внутреннее сопротивление линеаризованного источника, или идеальный источник тока, параллельно которому нет ветвей, проводимость которых можно трактовать как внутреннюю проводимость соответствующего источника, то такие источники называют вырожденными. Вырожденные источники напряжения и тока не могут быть преобразованы один в другой непосредственно с помощью выражений (4.12), (4.13), однако они могут быть устранены из рассматриваемой цепи с помощью преобразований, получивших название переноса источников.

Перенос источников

Рассмотрим участок идеализированной электрической цепи, содержащий вырожденный источник напряжения (рис. 2.41, а). Данный участок цепи может быть заменен одним из эквивалентных ему участков цепей, не содержащим вырожденных источников.

Идеальный источник напряжения Е из ветви, подключенной между узлами (6) и (7) (рис. 4.5, а), можно перенести во все ветви, подключенные к узлу (6) (рис. 4.5, б) или во все ветви, подключенные к узлу (7) (рис. 4.5, в).

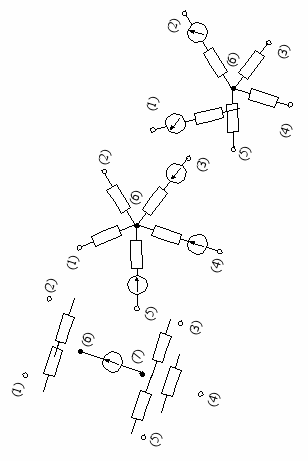
а б в

Рис. 4.5. Перенос источника ЭДС

В обоих случаях перенос источника напряжения произведен без изменения ЭДС источника и его ориентации относительно направлений обхода контуров 1 и 4. Ветвь, ранее содержавшая источник Е, после преобразования исчезает, причем узлы (6) и (7), к которым она была подключена, объединяются в один узел. Процессы во всех трех идеализированных цепях описываются решениями одной и той же системы уравнений электрического равновесия, составленной на основании законов Кирхгофа.

Вырожденный источник тока, включенный между узлами (k) и (n) произвольной электрической цепи, может быть заменен несколькими источниками тока, включенными параллельно любым ветвям электрической цепи, образующим путь между узлами (k) и (n). Например, вырожденный источник тока J, включенный между узлами (1) и (2) электрической цепи (рис. 4.6, а), может быть заменен двумя источниками тока, подключенными параллельно ветвям с комплексными сопротивлениями Z₁ и Z₂, образующими путь между этими же узлами (рис. 4.6, б). Источник тока переносится без изменения тока источника J и его ориентации относительно узлов. Эквивалентность цепей следует из того, что процессы в них описываются одной и той же системой уравнений электрического равновесия, составленной на основании законов Кирхгофа.

а б

Рис. 4.6. Перенос источника тока

В общем случае в результате переноса источника тока вырожденный источник заменяется несколькими невырожденными источниками, которые при необходимости могут быть преобразованы в источники напряжения. Ветвь, ранее содержавшая вырожденный источник тока, после переноса источника исчезает.

4.2. Метод контурных токов

Метод контурных токов основан на важной топологической особенности электрических цепей: токи всех ветвей цепи могут быть выражены через токи главных ветвей.

Для определения токов главных ветвей (контурных токов) составляют систему из р — р_ит — q + 1 уравнений, называемых контурными уравнениями.

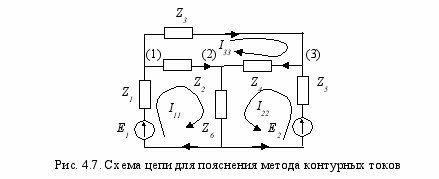Рассмотрим методику формирования контурных уравнений на примере простой цепи, не содержащей источников тока, схема которой приведена на рис. 4.7.

Токи всех ветвей цепи могут быть выражены через контурные токи этой цепи. Например, для рассматриваемого примера

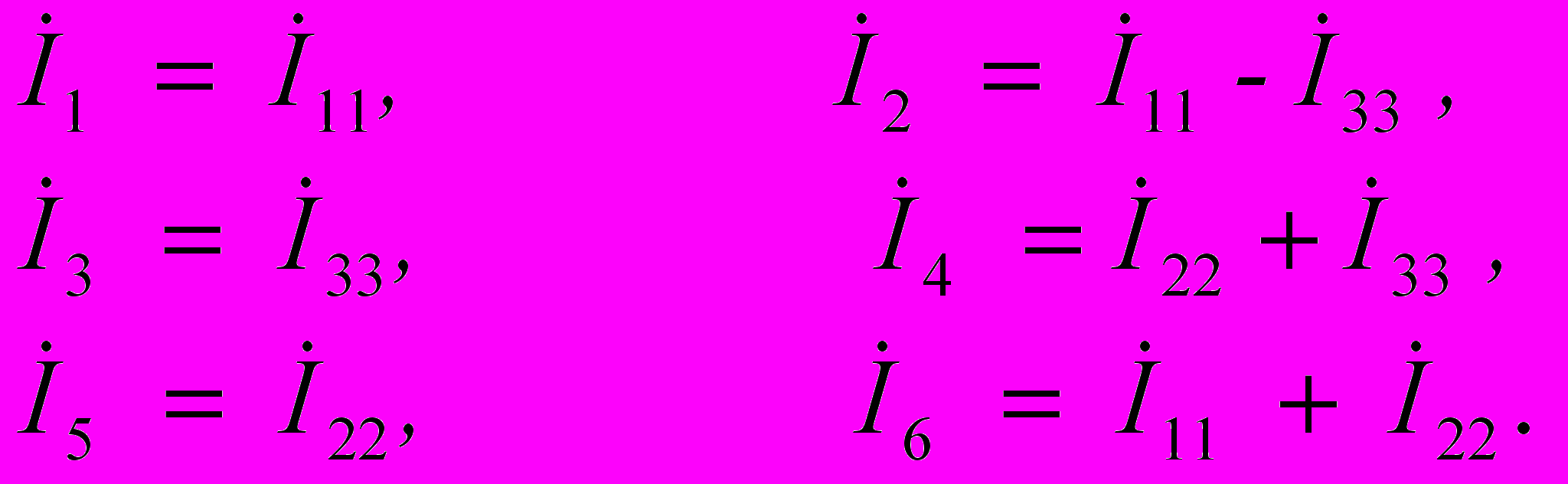
(4.13)

Для определения токов воспользуемся уравнениями, составленными на основании второго закона Кирхгофа,

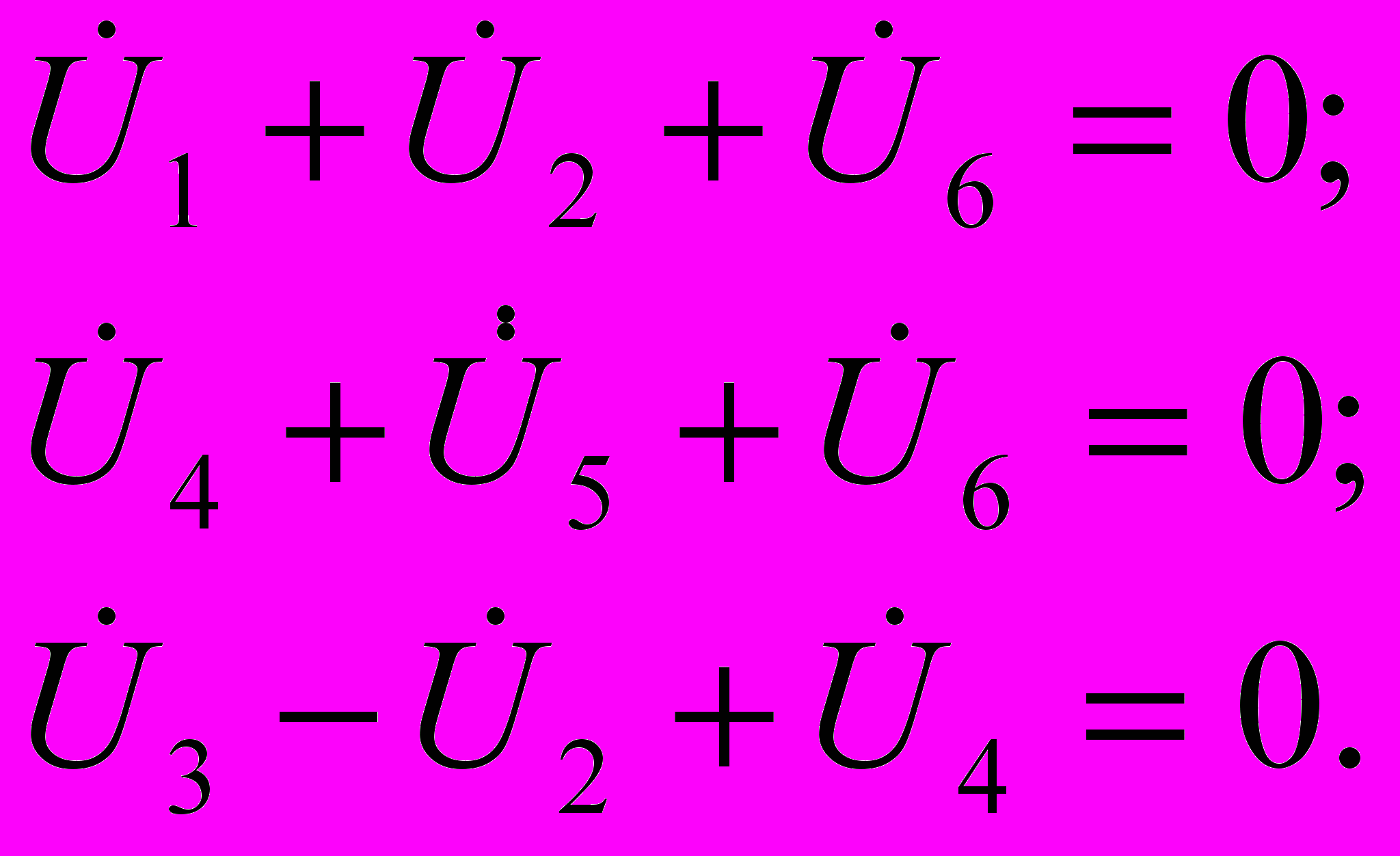
(4.14)

выразив входящие в них напряжения ветвей через токи ветвей.

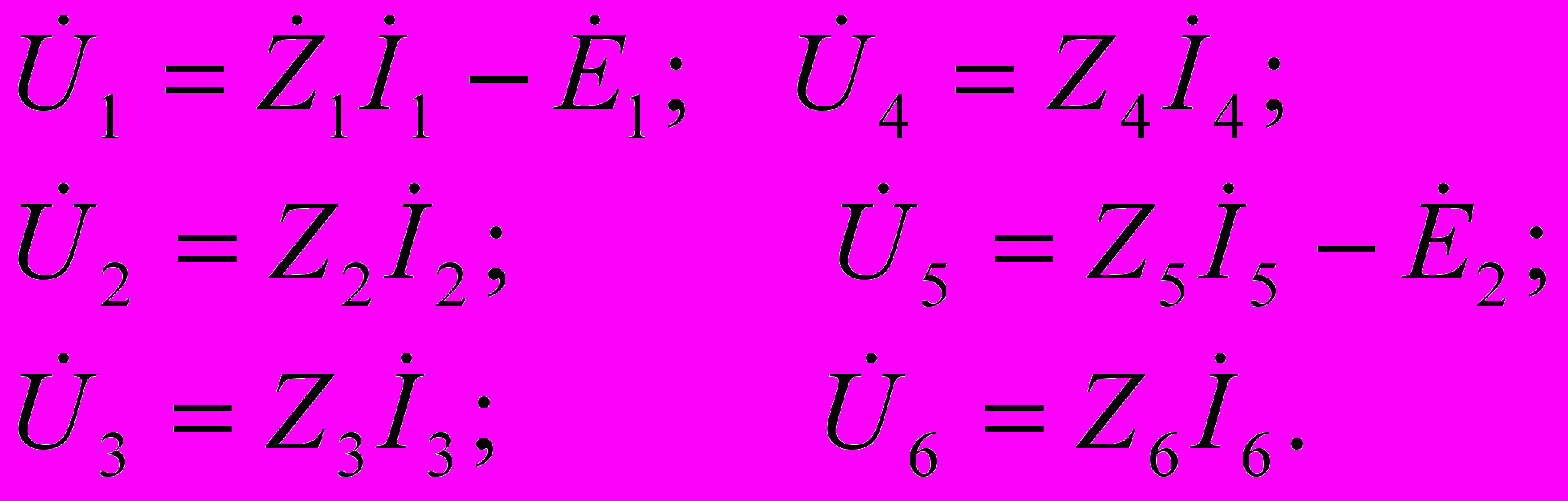
(4.15)

Подставляя (4.14), (4.15) в уравнение (4.13), получаем:

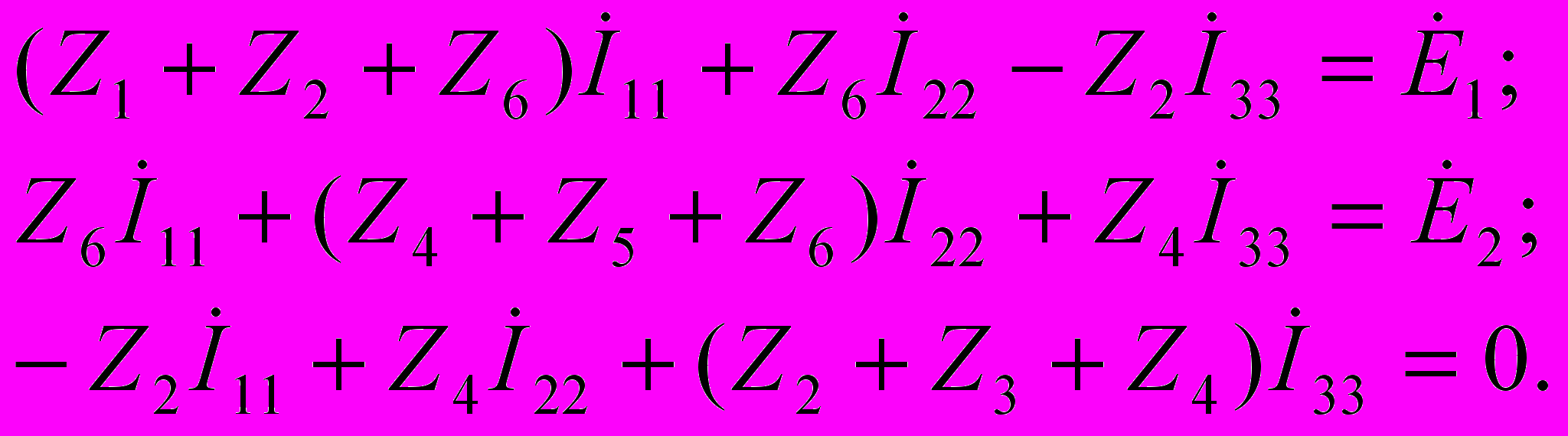
(4.16)

На практике контурные уравнения формируют не прибегая к составлению основной системы уравнений электрического равновесия, поэтому применение этого метода позволяет упростить и составление, и решение уравнений электрического равновесия цепи.

В матричной форме система уравнений вида (4.16) запишется в следующем виде:

(4.17)

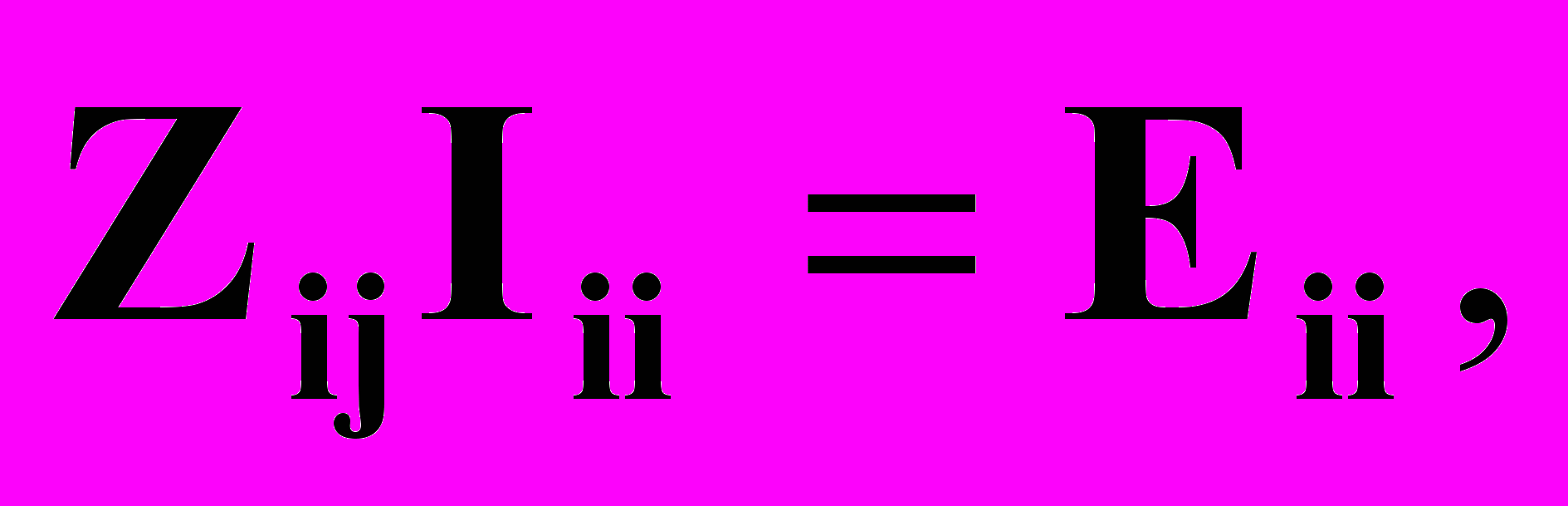
где Z_ij – матрица сопротивлений контуров,

I_ii – матрица контурных токов,

Е_ii– матрица контурных ЭДС.

Для рассматриваемого примера

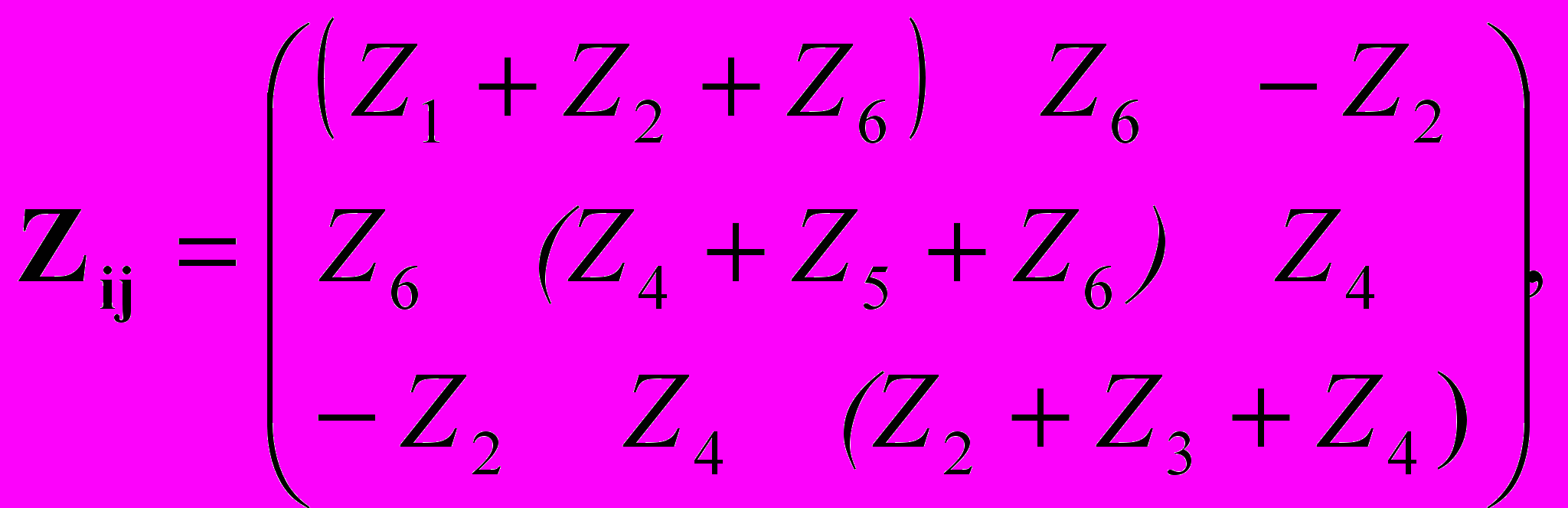
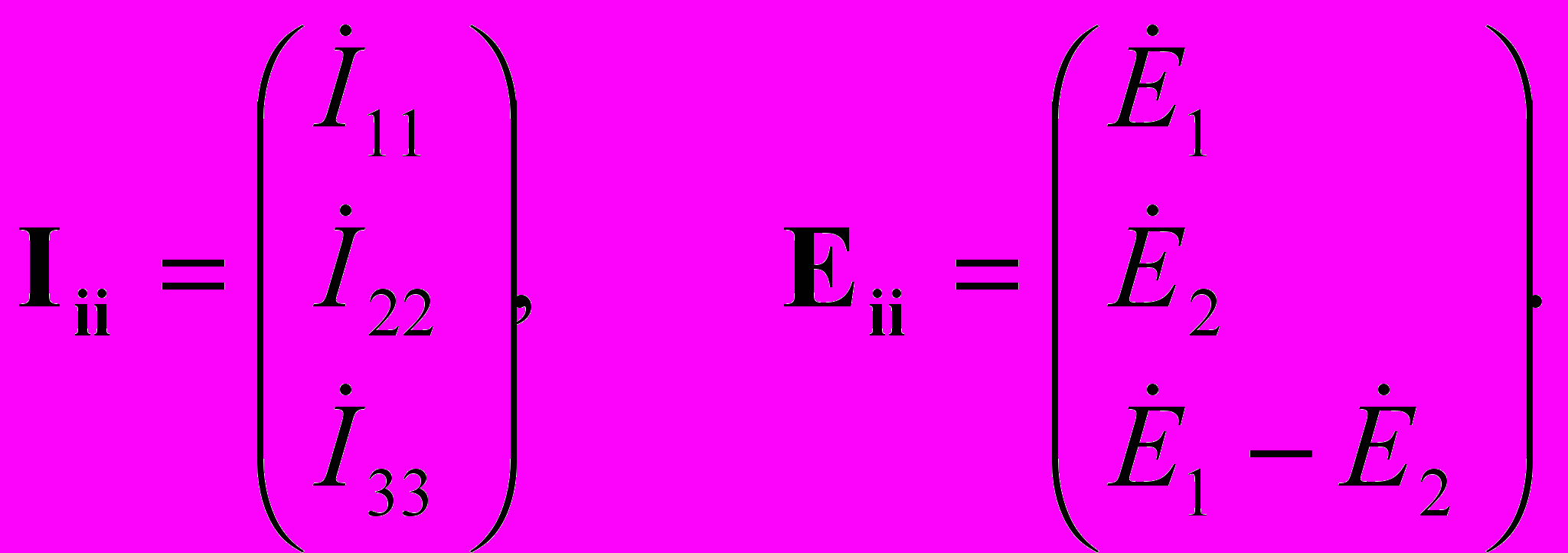
Сформулируем правила составления контурных уравнений.

1. Формирование Z_ij.

Собственным сопротивлением Z_ii i-гo контура называется сумма сопротивлений всех ветвей, входящих в этот контур. В цепи (см. рис. 4.7) выделено три независимых контура, их собственные сопротивления:

Z₁₁=Z₁+Z₂+Z₆, Z₂₂=Z₄+Z₅+Z₆, Z₃₃=Z₂+Z₃+Z₄.

Взаимным, или общим, сопротивлением i-гo и j-го контуров называется сопротивление Z_ij, равное сумме сопротивлений ветвей, общих для этих контуров. Взаимное сопротивление берется со знаком плюс, если контурные токи рассматриваемых контуров протекают через общие для этих контуров ветви в одинаковом направлении; если контурные токи в общих ветвях имеют противоположные направления, то взаимное сопротивление берут со знаком минус. Если рассматриваемые контуры не имеют общих ветвей, то их взаимное сопротивление равно нулю. Взаимные сопротивления контуров цепи (см. рис. 4.7):

Z₁₂=Z₂₁=Z₆, Z₁₃=Z₃₁= -Z₂, Z₂₃=Z₃₂= Z₄.

Для линейных цепей, составленных только из сопротивлений, емкостей, индуктивностей и независимых источников напряжения, матрица контурных сопротивлений квадратная и симметричная относительно главной диагонали.

2. Формирование I_ii.

Это матрица-столбец неизвестных контурных токов.

3. Формирование Е_ii.

Контурная ЭДС Е_ii i-гo контура – это алгебраическая сумма ЭДС всех идеализированных источников напряжения, входящих в данный контур. Если направление ЭДС какого-либо источника, входящего в i-й контур, совпадает с направлением контурного тока этого контура, то соответствующая ЭДС входит в E_ii со знаком плюс, в противном случае — со знаком минус. Контурные ЭДС рассматриваемой цепи:

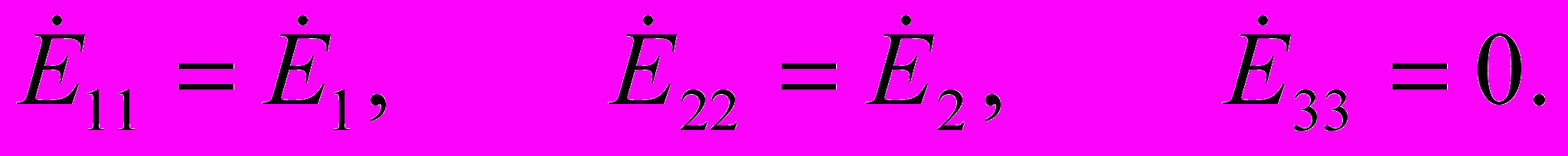
Решая систему уравнений (4.17) любым из методов, можно найти все неизвестные контурные токи цепи.

Например, выражение для контурного тока kk-го контура при использовании формулы Крамера:

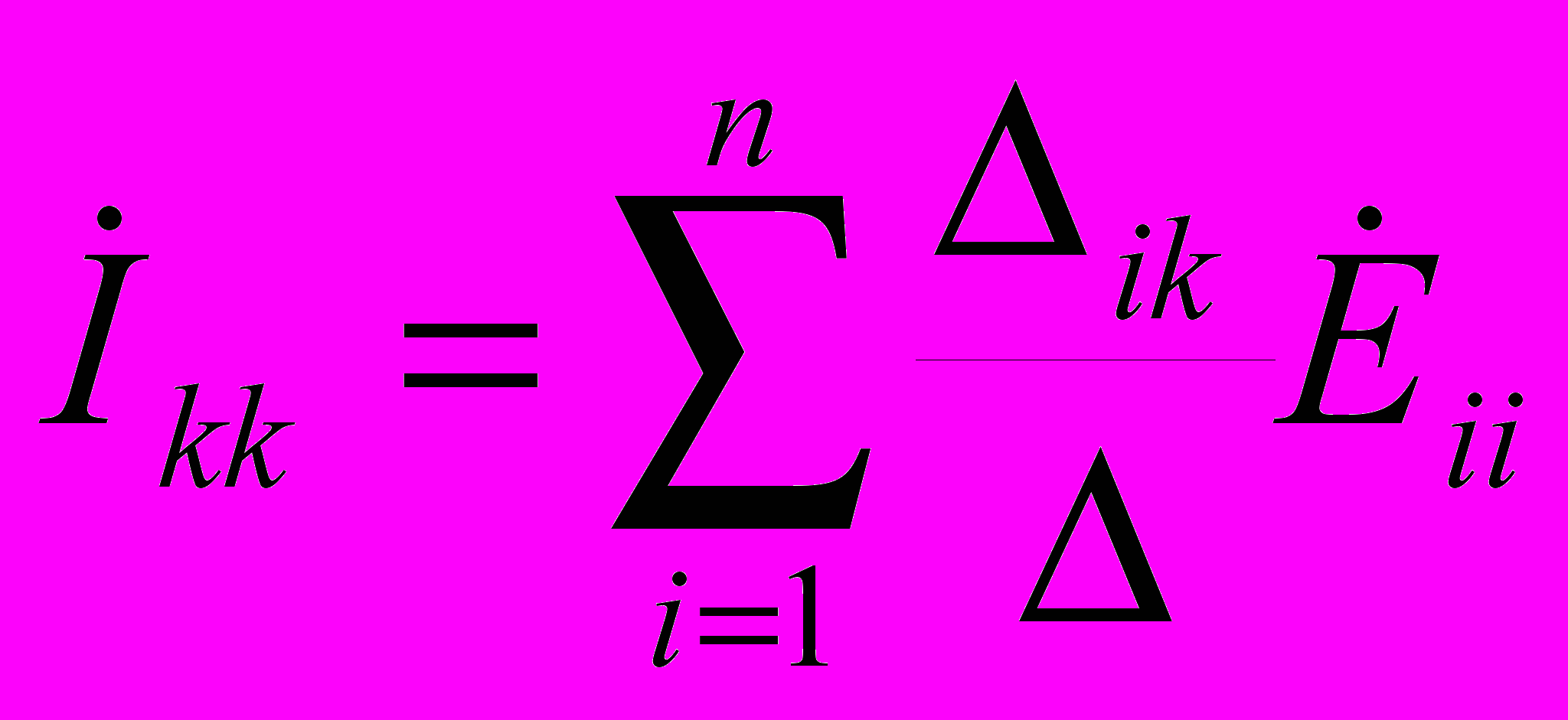
(4.18)

где — определитель системы уравнений (4.17); _ij— алгебраическое дополнение элемента Z_ij этого определителя. В аналогичной форме могут быть записаны выражения для контурных токов всех остальных контуров. На практике обычно используют более экономичные методы, такие, как метод исключения Гаусса.

При составлении контурных уравнений планарных цепей в качестве независимых удобно выбирать контуры, соответствующие ячейкам.

Если электрическая цепь содержит независимые источники тока, то следует:

заменить источники тока независимыми источниками напряжения с помощью эквивалентных преобразований,

либо

выбрать контуры таким образом, чтобы по ветви с источником тока протекал только один контурный ток. Количество неизвестных контурных токов сокращается при этом на число независимых источников тока. Матрица контурных сопротивлений в этом случае будет не квадратной: число столбцов будет равно числу независимых контуров, а число строк — числу неизвестных контурных токов.

Метод контурных токов можно использовать и для составления уравнений электрического равновесия цепей со связанными индуктивностями, однако алгоритм формирования матрицы контурных сопротивлений при этом усложняется.

4.3. Метод узловых напряжений

Напряжения всех ветвей электрической цепи могут быть выражены через узловые напряжения этой цепи т.е. через напряжения независимых узлов рассматриваемой цепи относительно базисного. Напряжение некоторой ветви, включенной между i-м и базисным узлами, равно узловому напряжению i-гo узла U_i₀, взятого со знаком плюс или минус в зависимости от направления напряжения этой ветви, а напряжение ветви, включенной между i-м и j-м узлами (рис. 4.8), — разности узловых напряжений этих узлов U_i₀-U_j₀.

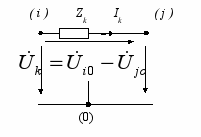
Рис. 4.8. К определению понятия узлового напряжения

Метод формирования уравнений электрического равновесия цепи, в котором в качестве независимых переменных используются неизвестные напряжения независимых узлов относительно базисного, называется методом узловых напряжений.

Рассмотрим метод формирования узловых уравнений на примере цепи, не содержащей источников напряжения (рис. 4.9). Данная цепь получена из цепи, схема которой изображена на рис. 4.7, путем преобразования источников напряжения в источники тока и замены комплексных сопротивлений ветвей их комплексными проводимостями.

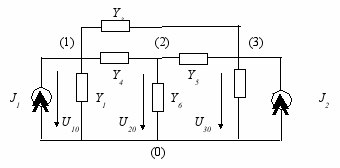
Рис. 4.9. К составлению уравнений электрического равновесия методом узловых напряжений

Цепь имеет три независимых узла, для которых можно составить уравнения баланса токов:

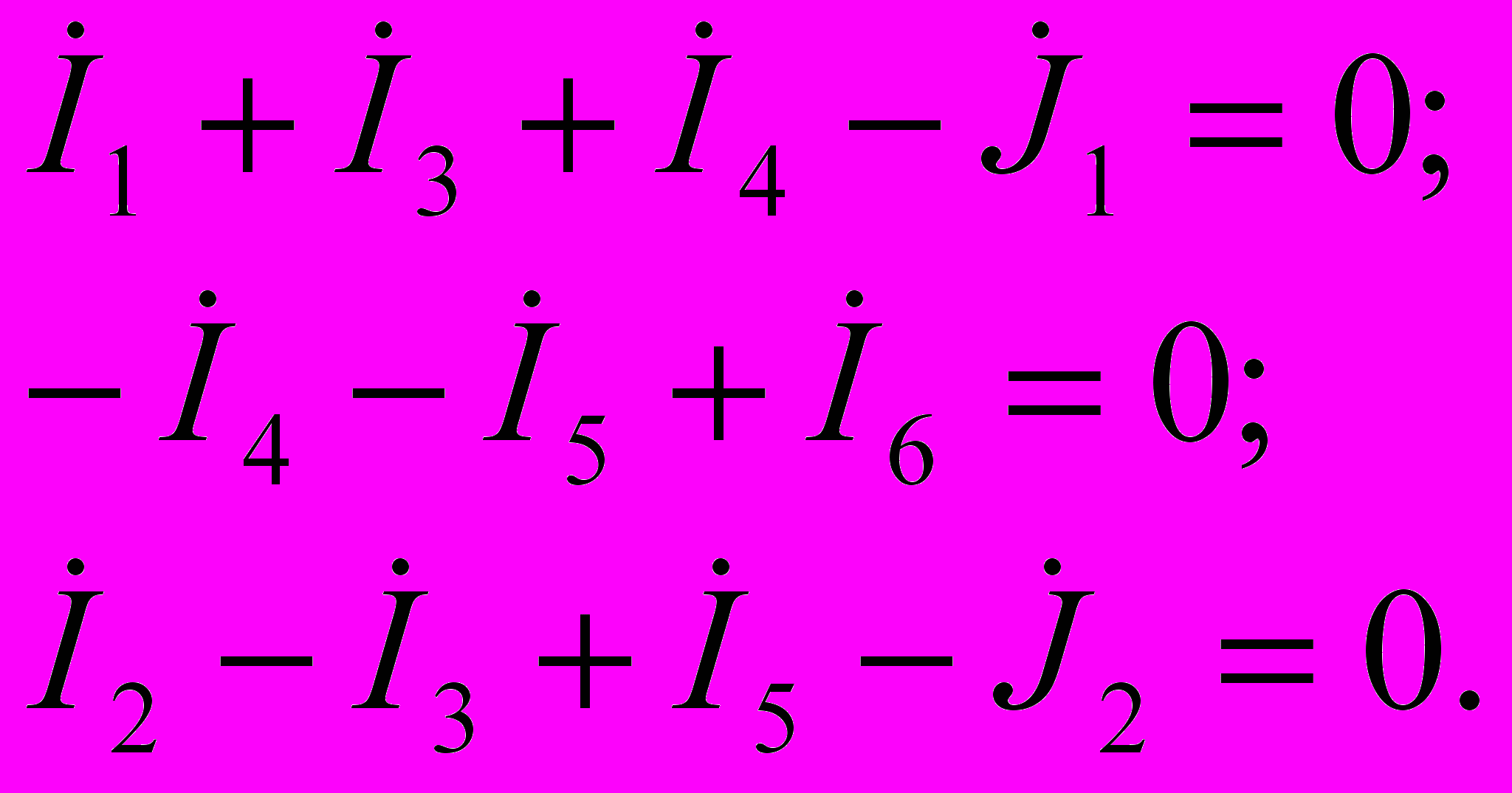
(4.19)

Выразим неизвестные токи ветвей цепи через напряжения этих ветвей, а напряжения ветвей — через соответствующие узловые напряжения:

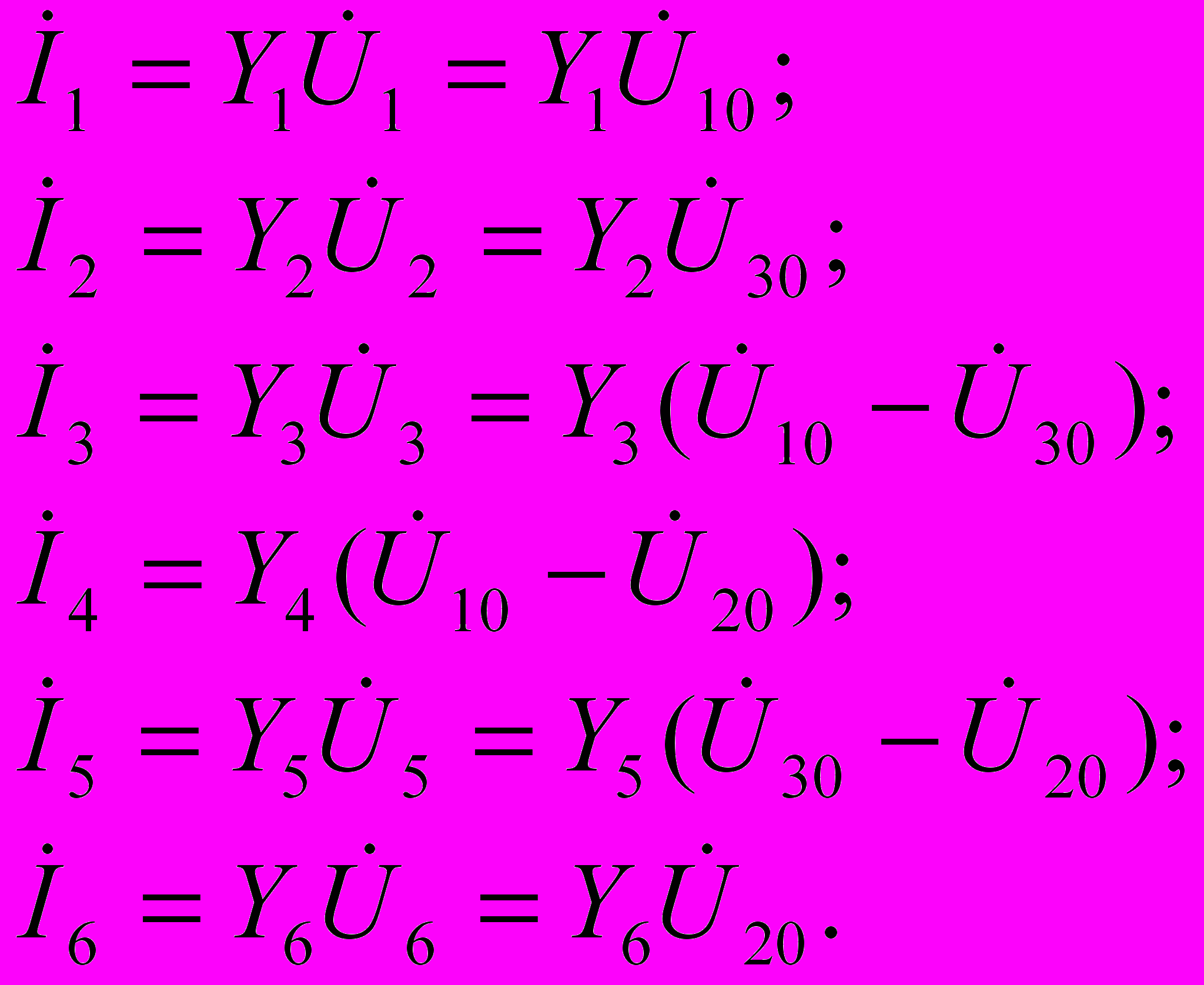
(4.20)

Подставляя выражения (4.20) в (4.19), получим систему уравнений для определения трех неизвестных узловых напряжений:

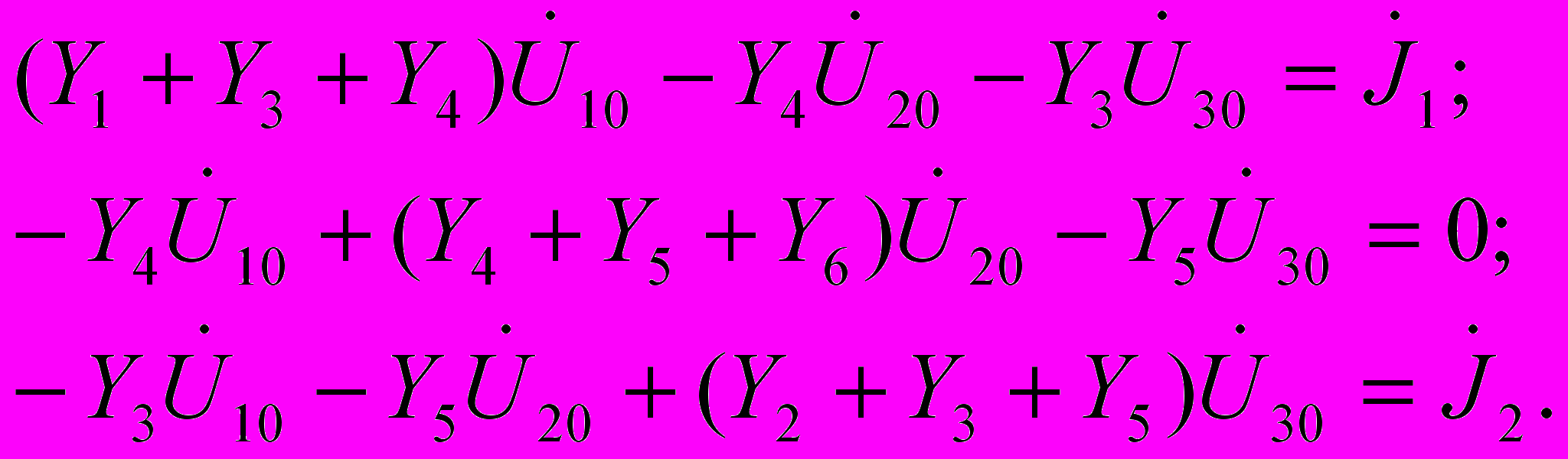
(4.21)

На практике узловые уравнения формируют не прибегая к составлению основной системы уравнений электрического равновесия, поэтому применение этого метода позволяет упростить и составление, и решение уравнений электрического равновесия цепи.

В матричной форме система уравнений вида (4.21) запишется в следующем виде:

(4.22)

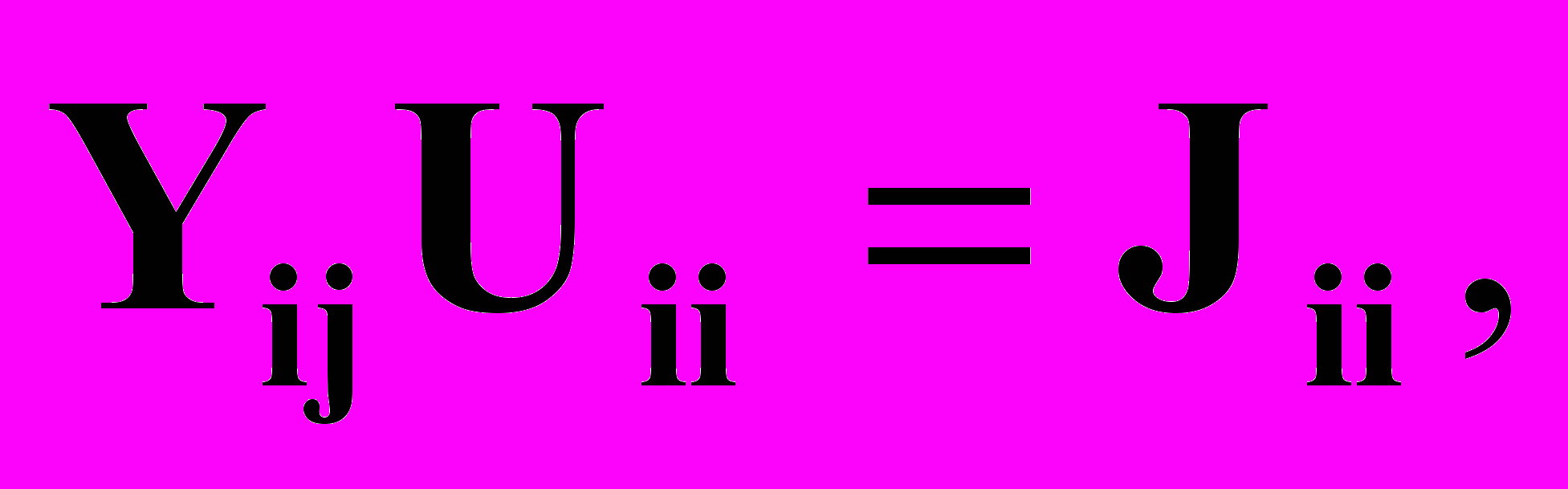
где Y_ij – матрица проводимостей узлов,

U_i₀ – матрица напряжений узлов,

J_i₀– матрица узловых токов.

Для рассматриваемого примера

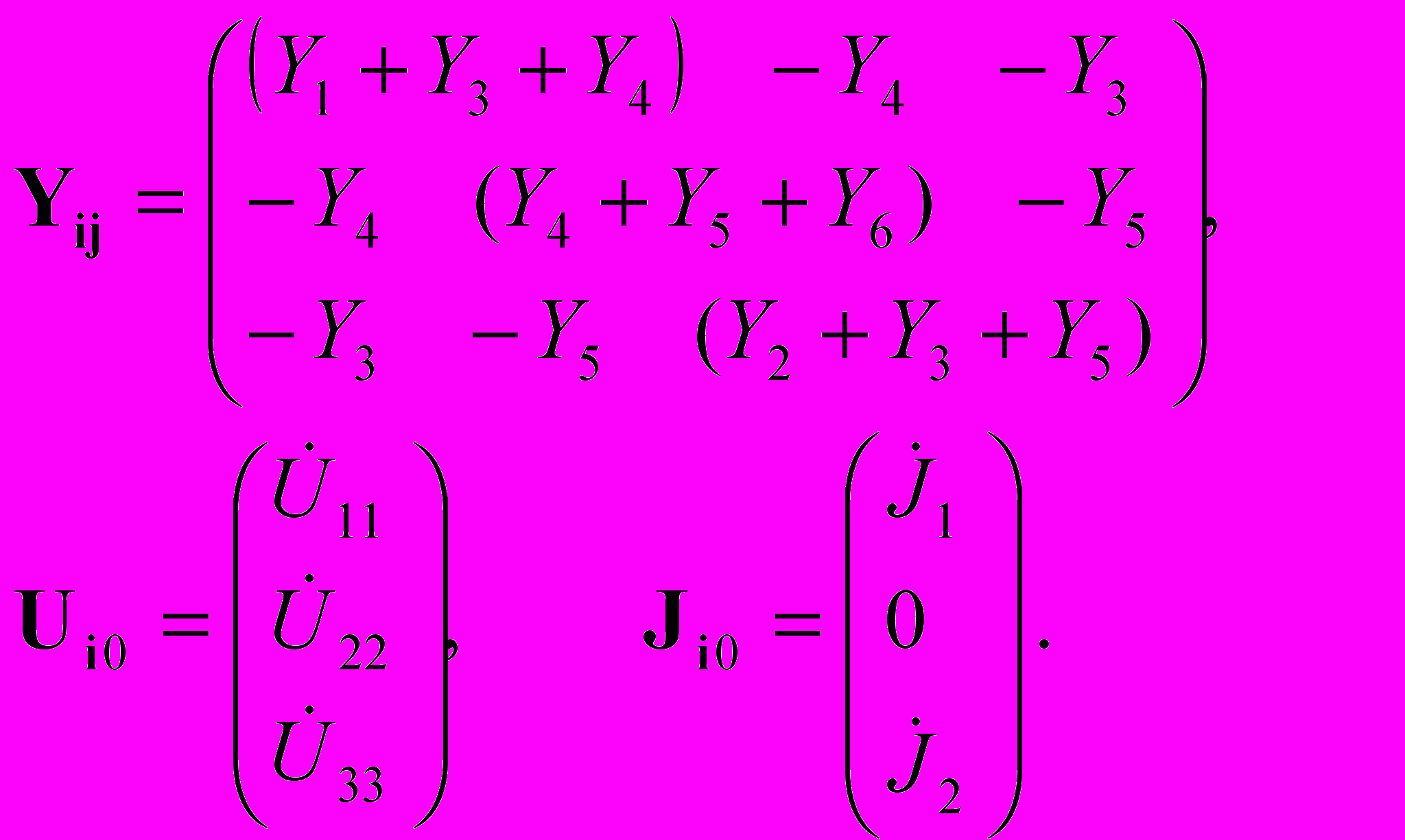
Сформулируем правила составления узловых уравнений.

Формирование Y_ij.

Собственная проводимость Y_ii i-гo узла - это сумма проводимостей всех ветвей, подключенных к данному узлу. Для рассматриваемой цепи

Y₁₁ = Y₁+Y₃+Y₄; Y₂₂ = Y₄+Y₅+Y₆; Y₃₃ = Y₂+Y₃+Y₅.

Взаимная проводимость i-гo и j-го узлов — это сумма проводимостей всех ветвей, включенных непосредственно между этими узлами, взятая с противоположным знаком. Если в цепи отсутствуют ветви, включенные непосредственно между i-м и j-м узлами, то Y_ij = 0. Для цепи, схема которой приведена на рис. 3.3,

Y₁₂ = Y₂₁ = -Y₄, Y₂₃ = Y₃₂ = -Y₅, Y₁₃ = Y₃₁ = -Y₃.

Для линейной электрической цепи состоящей только из сопротивлений, емкостей, индуктивностей и независимых источников тока, матрица узловых проводимостей квадратная и симметричная относительно главной диагонали.

Формирование U_i₀.

Это матрица-столбец неизвестных напряжений узлов.

2. Формирование J_i₀.

Узловым током J_i₀ i-го узла называется алгебраическая сумма токов всех источников тока, подключенных к данному узлу. Если ток какого-либо источника тока направлен к i-му узлу, то он входит в J_i₀ со знаком плюс, если ток направлен от i-го узла, то он входит со знаком минус. Для рассматриваемой цепи

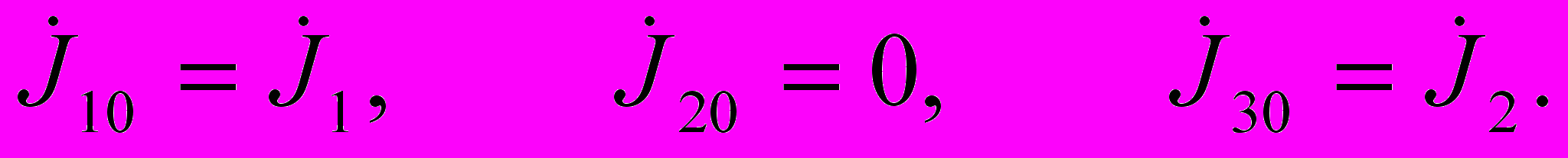
Решая систему уравнений (3.10) любым из методов, можно найти все неизвестные узловые напряжения цепи.

Например, выражение для напряжения k-го узла при использовании формулы Крамера

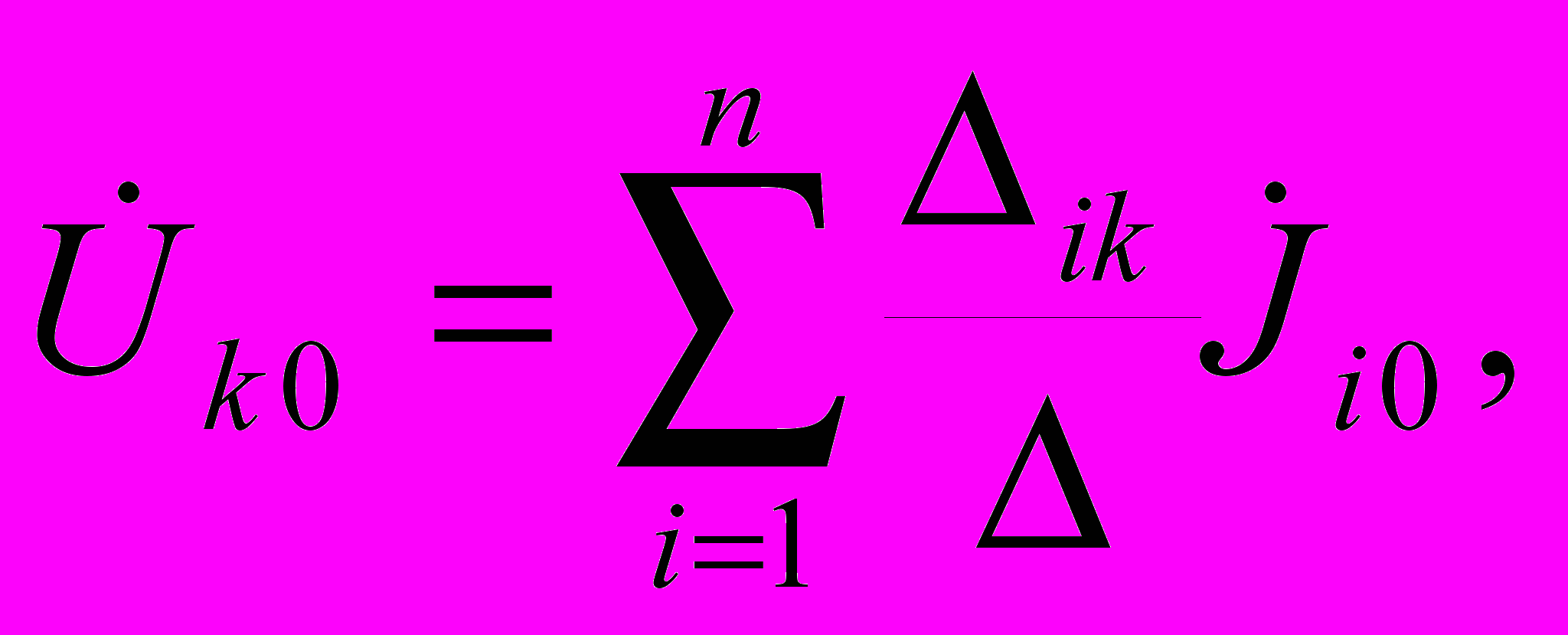
(4.23)

где — определитель системы уравнений (4.22);

_ij— алгебраическое дополнение элемента Y_ij этого определителя.

В аналогичной форме могут быть записаны выражения для напряжений всех остальных узлов.

Если цепь содержит независимые источники напряжения, то следует:

заменить источники напряжения независимыми источниками тока с помощью эквивалентных преобразований,

либо

составить систему узловых уравнений с учётом того, что не все узловые напряжения будут независимы: узловые напряжения двух узлов, между которыми включён источник напряжения, будут отличаться только на напряжение этого источника. Количество неизвестных узловых напряжений сокращается при этом на число независимых источников напряжения. Матрица контурных проводимостей в этом случае будет не квадратной: число столбцов будет равно числу независимых узлов, а число строк — числу неизвестных независимых узловых напряжений. Следует, по возможности, выбирать в качестве базисного тот узел, к которому подключён источник напряжения.

Метод узловых напряжений применим для анализа цепей любой топологии. Нецелесообразно применять его для анализа цепей со связанными индуктивностями, так как существенно усложняется алгоритм формирования узловых уравнений.

4.4. Метод эквивалентного источника

Автономный двухполюсник – двухполюсник, напряжение холостого хода или ток короткого замыкания которого не равны нулю.

Теорема об эквивалентном источнике (эквивалентном генераторе) (теорема Тевенина)

Ток произвольной ветви линейной электрической цепи не изменится, если автономный двухполюсник, к которому подключена данная ветвь, заменить эквивалентным линеаризованным источником энергии, который может быть представлен последовательной или параллельной схемой замещения. ЭДС идеального источника напряжения в последовательной схеме замещения равна напряжению холостого хода автономного двухполюсника, ток идеального источника тока в параллельной схеме замещения равен току короткого замыкания автономного двухполюсника, а внутреннее сопротивление и внутренняя проводимость эквивалентного источника равны соответственно комплексному входному сопротивлению и комплексной входной проводимости автономного двухполюсника.

Эта теорема позволяет существенно упростить анализ цепей в тех случаях, когда требуется определить ток или напряжение только одной ветви сложной цепи. В связи с тем, что параметры элементов последовательной и параллельной схем замещения активного двухполюсника легко поддаются измерениям, выполняемым на внешних зажимах, теорему об эквивалентном источнике применяют и для построения эквивалентных схем активных двухполюсников по результатам их экспериментального исследования.

Пример 4.1. Используя теорему об эквивалентном источнике, определим ток

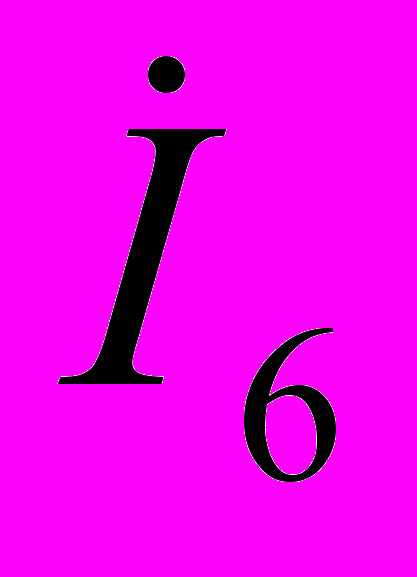в цепи, схема которой приведена на рис. 4.10, а.

Выделим из рассматриваемой цепи ветвь, содержащую сопротивление Z₆, и представим остальную часть цепи последовательной схемой замещения (рис. 4.10, а).

ЭДС источника напряжения

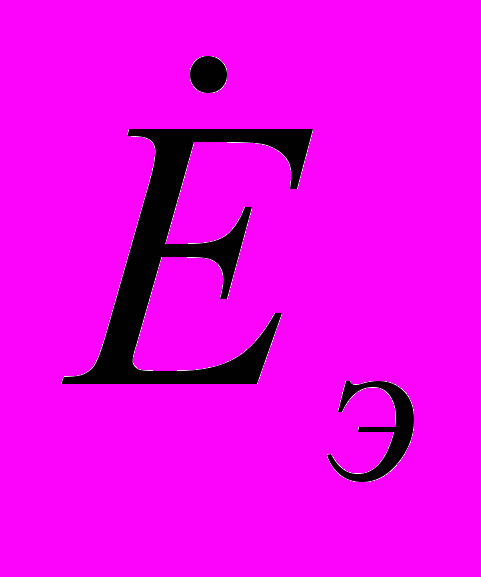определяется как напряжение холостого хода на зажимах автономного двухполюсника, схема которого приведена на рис. 4.10, в: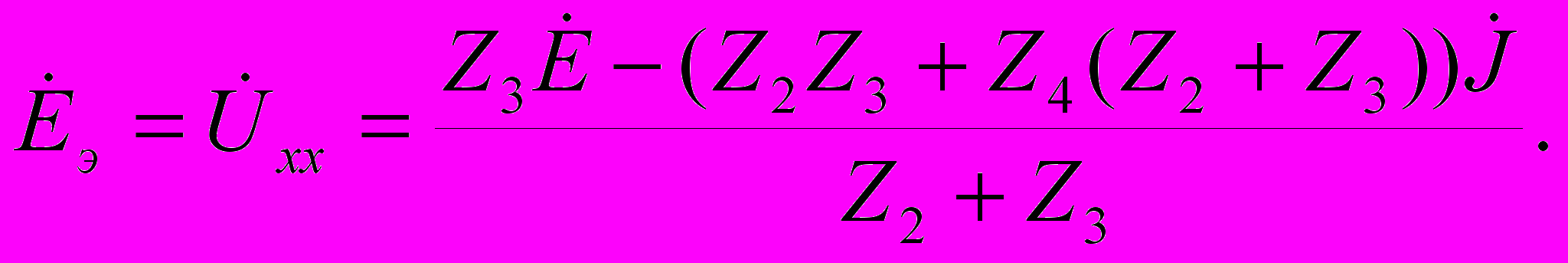

а) б) в)

Рис. 4.10. К примеру 4.1

Внутреннее сопротивление эквивалентного источника равно входному сопротивлению неавтономного двухполюсника (рис. 4.10, г)

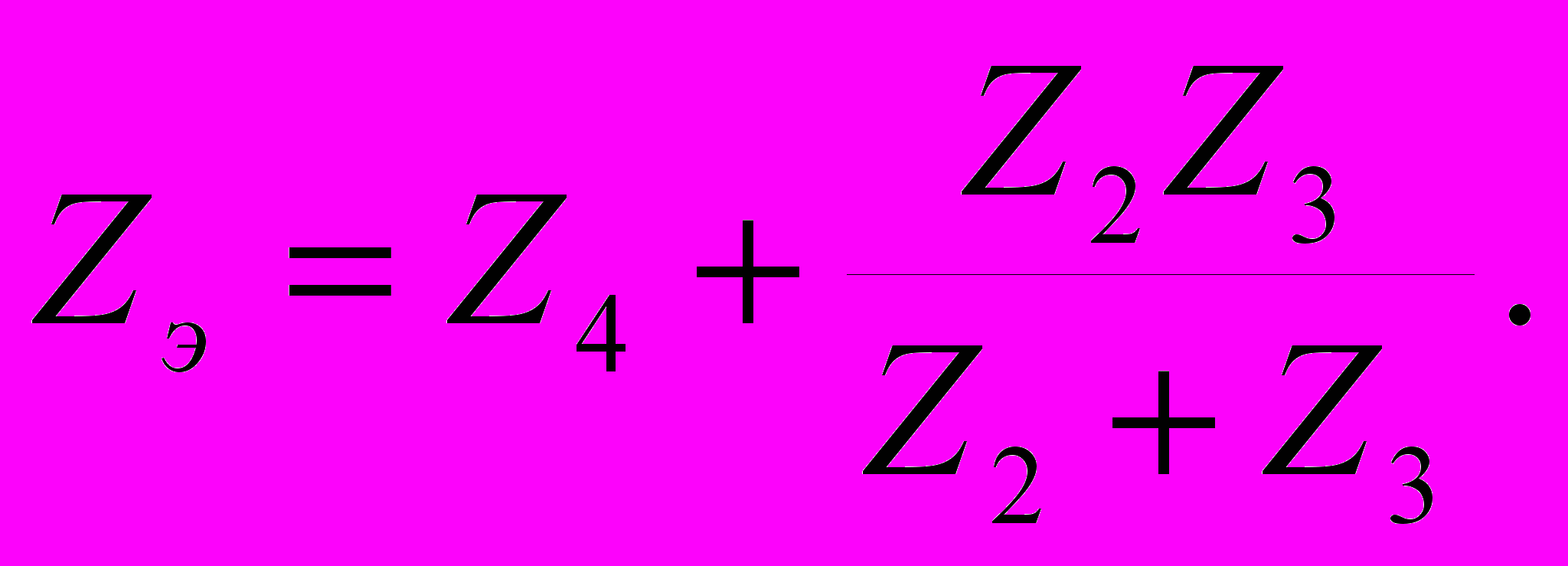
Используя преобразованную схему рассматриваемой цепи (рис. 3.9, а), находим искомый ток:

.

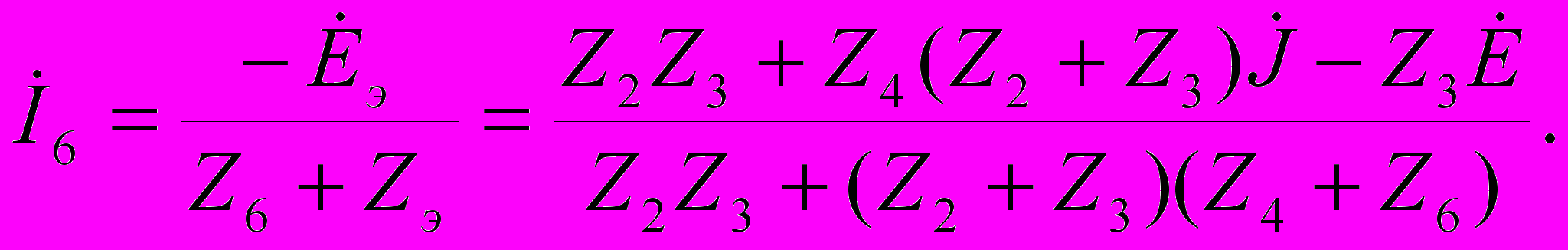Воспользовавшись теоремой об эквивалентном источнике, можно найти последовательную или параллельную схемы замещения любого сколь угодно сложного линейного активного двухполюсника.

Blog

4. Методы расчёта сложных электрических цепей

Содержание