Курс: 1 семестр 2 дисциплина: Инженерная графика задания для самостоятельной работы

Вид материала

Самостоятельная работа

Содержание Расстояние от точки до плоскости определяется перпендикуляром, опущенным из заданной точки S Содержание работы

Подобный материал:

• Аннотация примерной программы дисциплины «Инженерная и компьютерная графика» Рекомендуется, 412.89kb.
• Отчет о выполнении 1 этапа проекта кафедры «Инженерная графика и дизайн», 95.62kb.
• Аннотации дисциплин, 456.29kb.
• Учебно-методический комплекс по дисциплине «Начертательная геометрия. Инженерная графика», 977.22kb.
• И. М. Губкина а. В. Бочарова, Т. П. Коротаева инженерная графика точка, прямая плоскость, 413.16kb.
• Рабочая учебная программа предмета инженерная графика по специальности Автоматизация, 192.78kb.
• Рабочая программа По дисциплине «Инженерная и компьютерная графика» По специальности, 412.76kb.
• Рабочая программа По дисциплине «Инженерная графика» По специальности 230102-Автоматизированные, 269.94kb.
• Донской Г. М. Задания для самостоятельной работы по истории средних веков:, 209.22kb.
•      В основе периодизации средневековой культуры этапы развития ее социально-экономического, 1200.34kb.

Графическая работа 2

Тема: Способы преобразования чертежа

Содержание работы: По заданным координатам точек пирамиды SABC определить:

Задача 1. Натуральную величину основания АВС (способом перемены плоскостей проекций);

Задача 2. Расстояние от вершины S до основания АВС (способом перемены плоскостей проекций);

Задача 3. Кратчайшее расстояние между ребрами SС и АВ (способом перемены плоскостей проекций);

Задача 4. Величину двухгранного угла при ребре АВ (способом плоскопараллельного перемещения).

Указания:

• Задание выполнить на двух листах формата А3 (420х297);
  

• Масштаб 1:1;
  
• Композиция эпюра горизонтальная.
  

Примеры решения задач

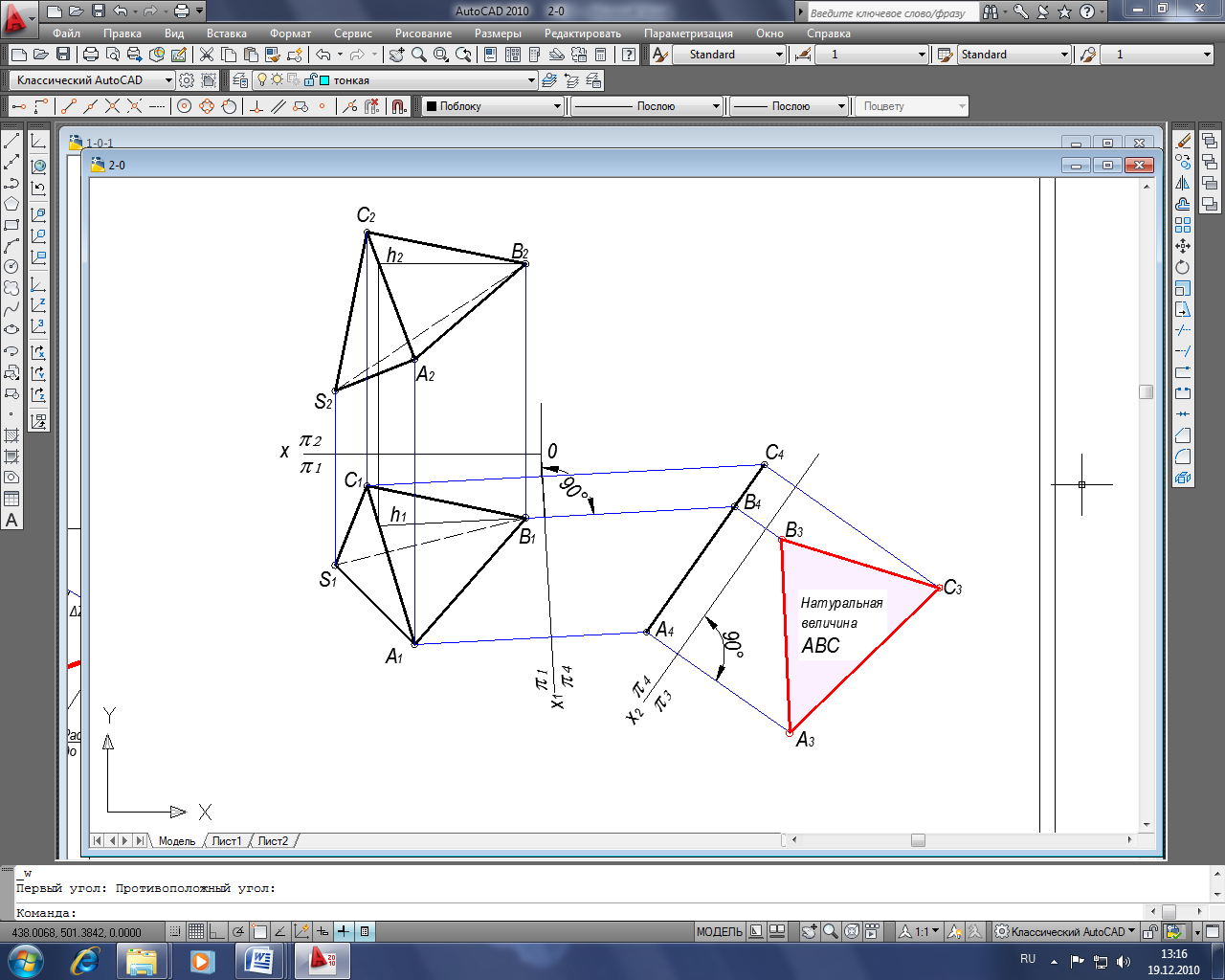
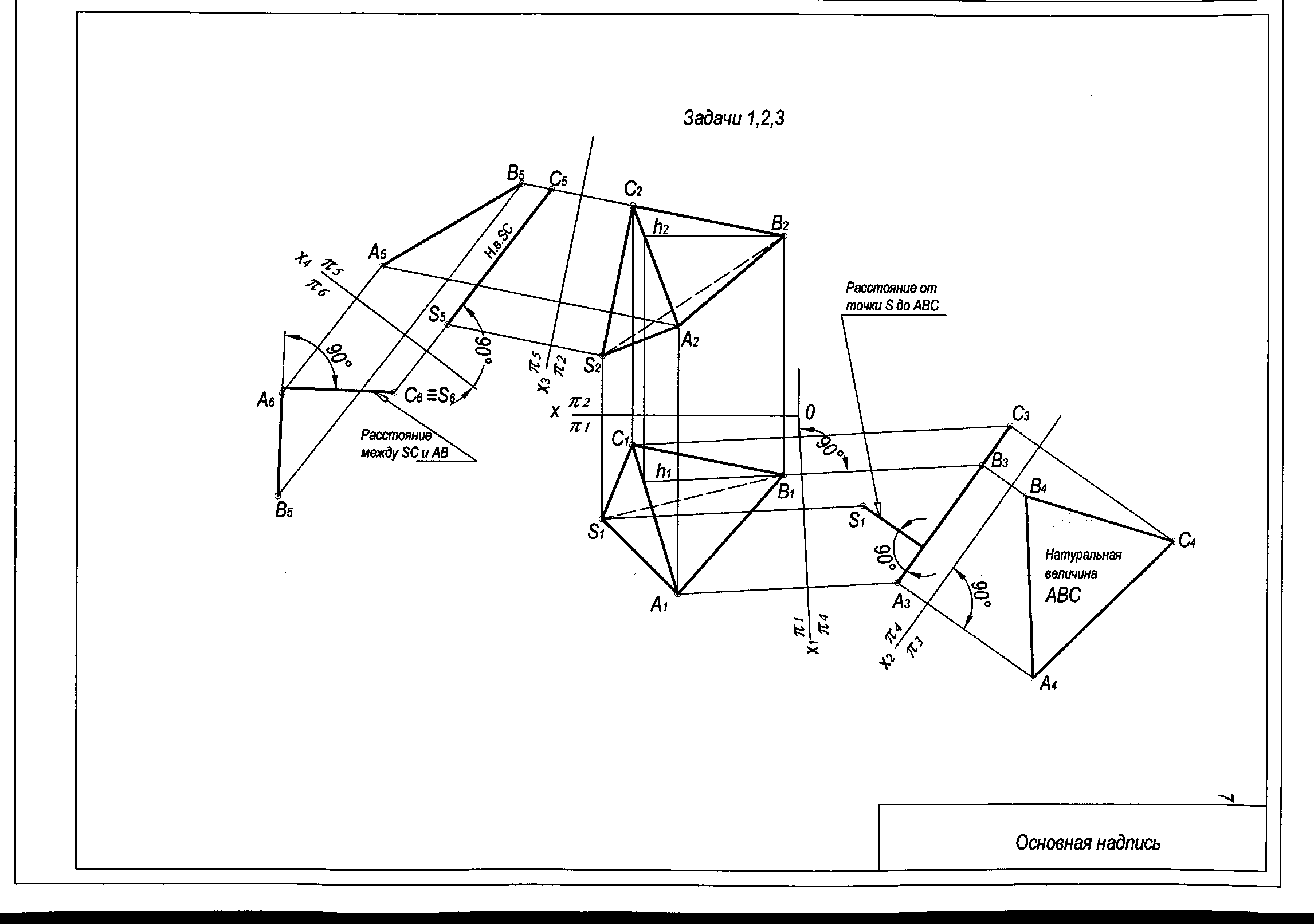
Задача 1. Построить натуральную величину основания АВС (способом перемены плоскостей проекций).


Для решения задачи необходимо выполнить два преобразования. Первое – когда плоскость примет положение проецирующее (в прямую линию), второе – параллельное (в натуральную величину).


Последовательность построения:

1. Проводим горизонталь h;
   
2. Проводим ох перпендикулярно h₁, получаем систему плоскостей ₁/₄, где ₄ новая фронтальная плоскость;
   
3. Проецируем все точки на плоскость ₄, для этого проводим линии связи из точек А₁В₁С₁ перпендикулярные оси ох₁;
   
4. На линиях связи откладываем расстояния от оси ох₁ равные до соответствующих проекций точек взятые на ₂ от оси ох;
   
5. На новую плоскость проекций ₄ заданная плоскость АВС проецируется в виде отрезка прямой линии А₄В₄С₄;
   
6. Проводим ось ох₂ параллельно проекции плоскости А₄В₄С₄ , получаем систему плоскостей ₄/₃. где ₃ новая горизонтальная плоскость;
   
7. Проецируем все точки на новую плоскость проекций ₃ , для чего проводим линии связи из точек А₄В₄С₄ перпендикулярные оси ох₂
   
8. На них (линиях связи) от новой оси ох₂ откладываем расстояния равные до соответствующих проекций точек, взятые на плоскости ₁ от оси ох_1.
   
9. Получаем новое положение точек А₃В₃С₃, натуральную величину треугольника АВС.
   

Задача 2. Построить расстояние от вершины S до основания АВС (способом перемены плоскостей проекций).

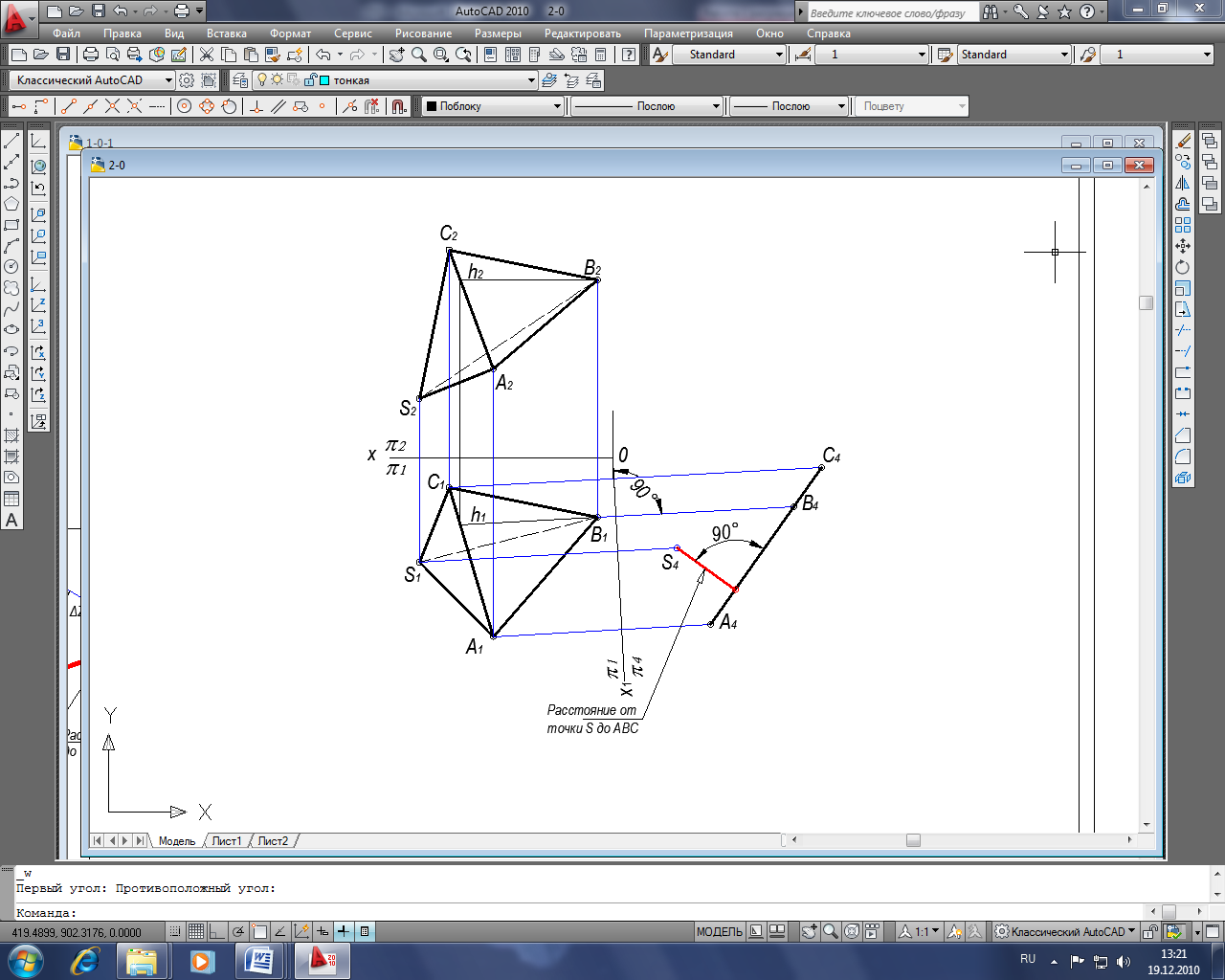
Расстояние от точки до плоскости определяется перпендикуляром, опущенным из заданной точки S₄ на прямую А₄В₄С₄, в которую проецируется заданная плоскость.


Последовательность построения:

1. Проводим горизонталь h;
   
2. Проводим ох перпендикулярно h₁, получаем систему плоскостей ₁/₄, где ₄ новая фронтальная плоскость;
   
3. Проецируем все точки на плоскость ₄, для этого проводим линии связи из точек А_1,В_1,С₁ , S₁ перпендикулярные оси ох₁;
   
4. На линиях связи откладываем расстояния от оси ох₁ равные до соответствующих проекций точек взятые на ₂ от оси ох;
   
5. На новую плоскость проекций ₄ заданная плоскость АВС проецируется в виде отрезка прямой линии А₄В₄С₄;
   
6. Из нового положения точки S₄ проводим перпендикуляр на полученную прямую- это и есть расстояние от точки S до плоскости АВС.
   

Задача 3. Построить кратчайшее расстояние между ребрами SС и АВ (способом перемены плоскостей проекций)

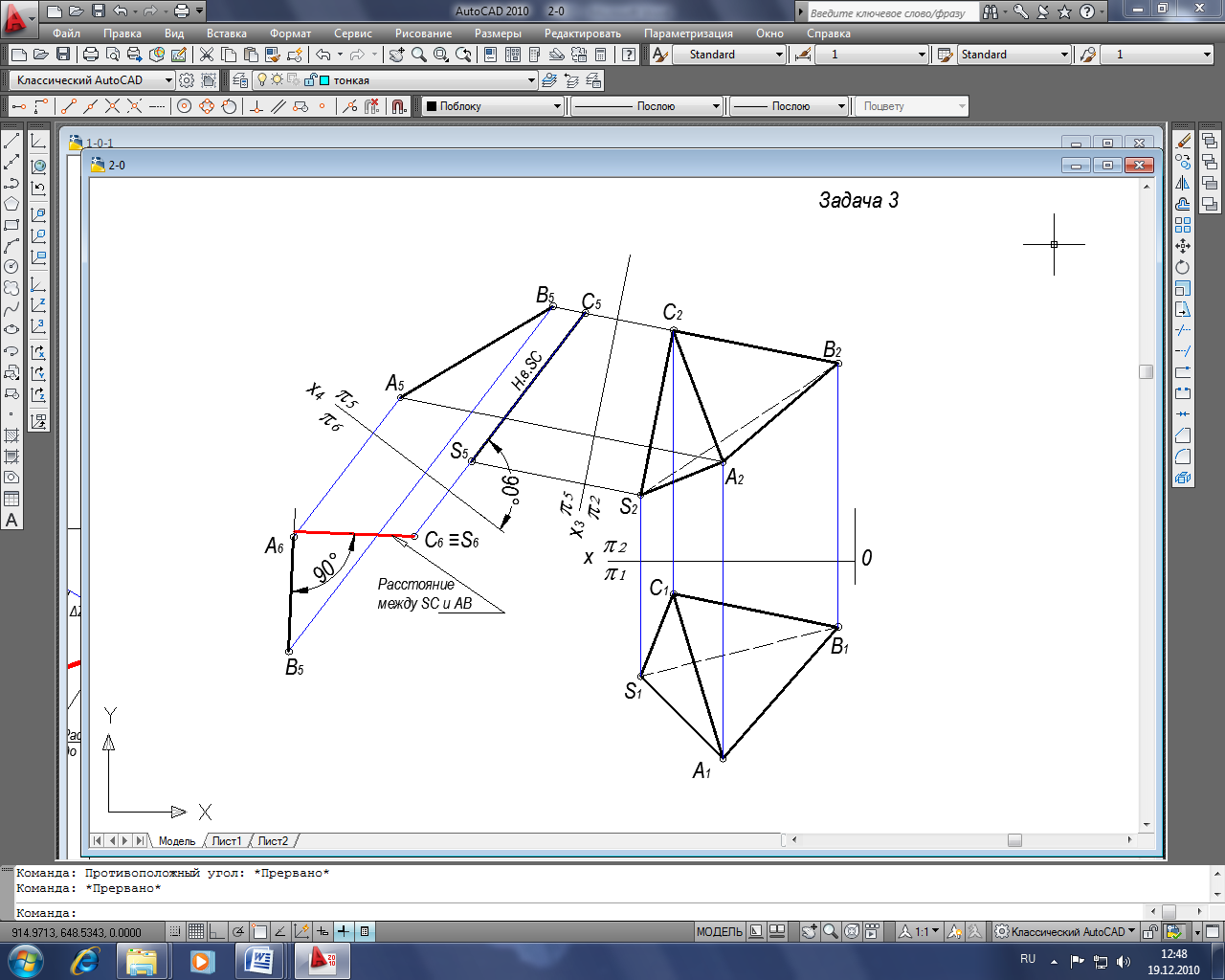
Кратчайшее расстояние между скрещивающимися прямыми определяется как расстояние между точкой, в которую проецируется одна из прямых, и плоскостью, в которую заключается другая.


Последовательность построения:

1. Проводим ох₃ параллельно проекции прямой S₂C_2, получаем систему плоскостей проекций ₅/₂ , где ₅ новая горизонтальная плоскость;
   
2. Проецируем все точки на плоскость _5, для чего из точек А₂,В₂,С₂ , S₂ проводим линии связи перпендикулярные оси ох₃;
   
3. На этих линиях связи от новой оси ох₃ откладываем расстояния равные до соответствующих проекций точек взятые на плоскости ₁ от оси ох, получаем проекции точек А₅,В₅,С₅ , S₅, где S₅C₅ проецируется в натуральную величину;
   
4. Проводим ох₄ перпендикулярно S₅C₅ , получаем систему плоскостей проекций ₅/_6, где ₆ новая фронтальная плоскость:
   
5. Проецируем все точки на плоскость проекций ₆, для чего из точек А₅,В₅,С₅ , S₅ проводим линии связи перпендикулярно оси ох_4;
   
6. На этих линиях связи от новой оси ох₄ откладываем расстояния равные до соответствующих проекций точек взятые на плоскости ₂ от оси ох₃, получаем проекции точек А₆,В₆,С₆ , S₆, где S₆C₆ проецируется в точку;
   
7. Из точки S₆ ≡C₆ опускаем перпендикуляр на прямую А₆В₆, получаем расстояние иежду скрещивающимися прямыми АВ и SC.
   

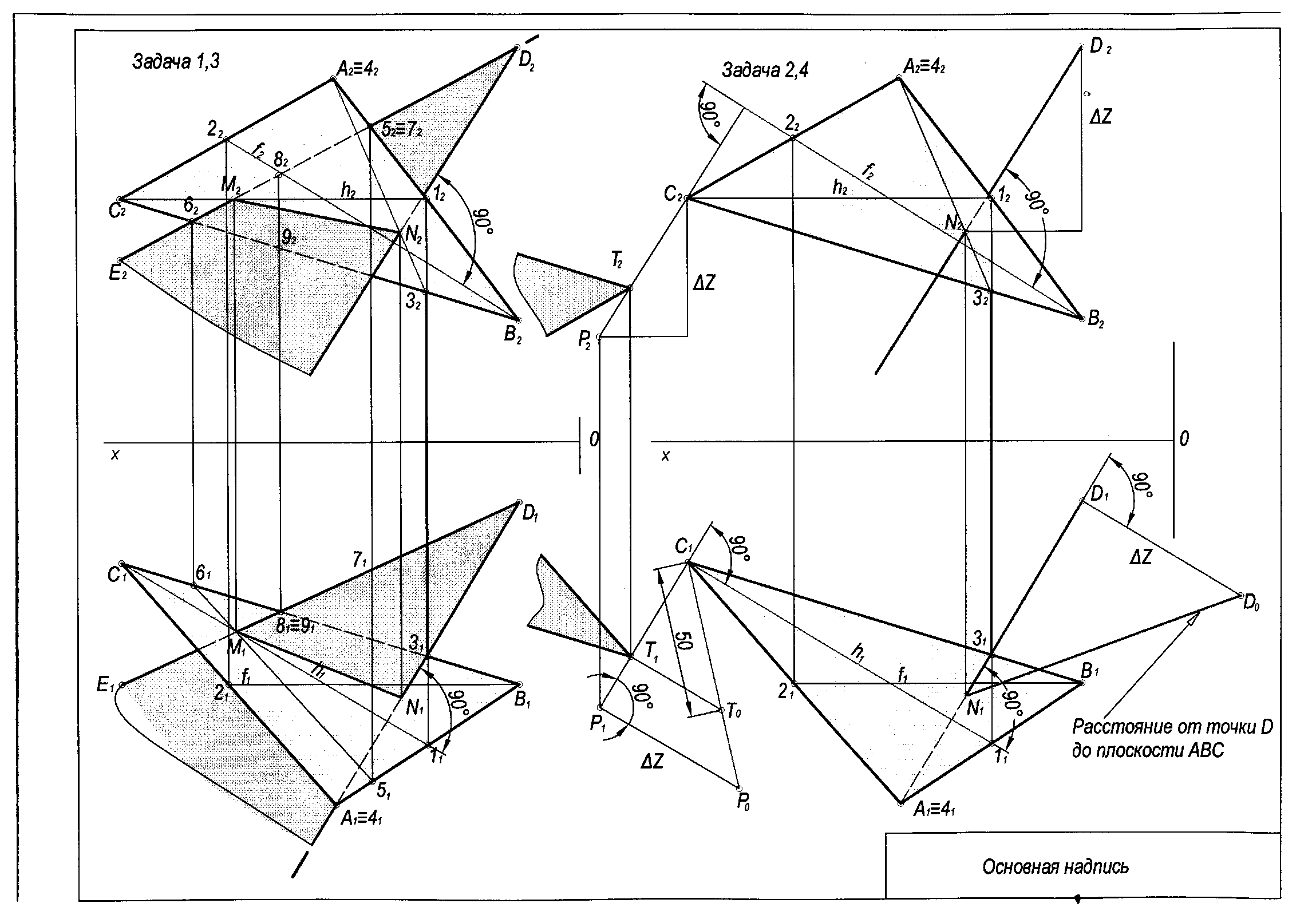
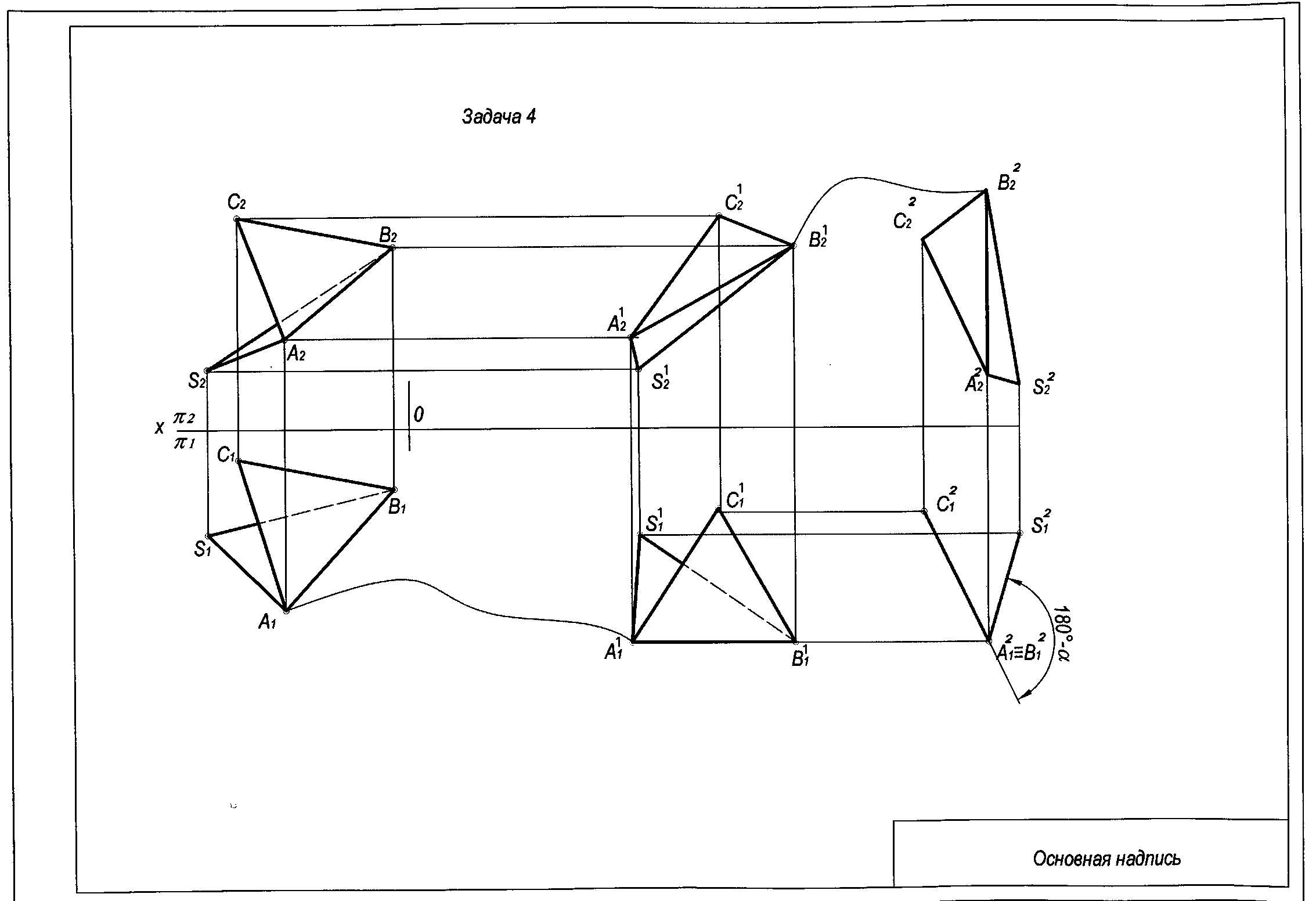
Задача 4. Построить величину двухгранного угла при ребре АВ (способом плоскопараллельного перемещения).

Для решения задачи необходимо, чтобы ребро при двухгранном угле проецировалось сначала в натуральную величину, а затем в точку. Тогда двухгранный угол проецируется в линейный угол, значение которого является искомым.




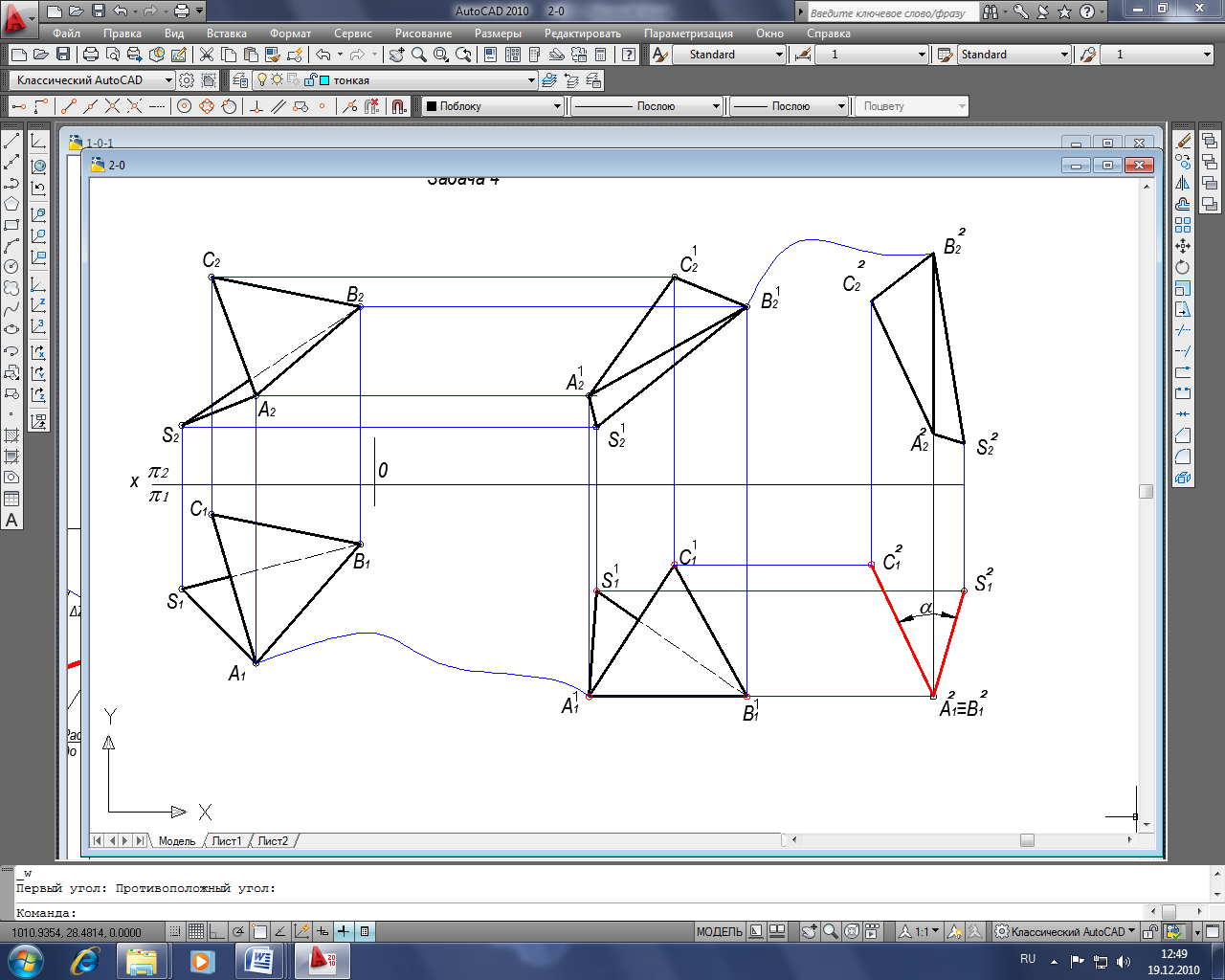
Последовательность построения:

1. Перемещаем горизонтальную проекцию двухгранного угла А₁В₁С₁ S₁ в положение, когда ребро АВ займет положение параллельное оси ох (при этом траектория движения точек произвольная кривая линия);
   
2. Проекции точек А₂,В₂,С₂ , S₂ перемещаем по прямым линиям параллельным оси ох;
   
3. В пересечении линий связи, проведенных из горизонтальных проекций точек А¹₁В¹₁С¹₁ S¹₁, получим новое положение двухгранного угла А¹₂В¹₂С¹₂ S¹₂, где ребро А¹₂В¹₂ проецируется в натуральную величину;
   
4. Перемещаем фронтальную проекцию двухгранного угла А¹₂В¹₂С¹₂ S¹₂ в положение, когда ребро А¹₂В¹₂ займет положение перпендикулярное оси ох (при этом траектория движения точек произвольная кривая линия);
   
5. Проекции точек А¹₁В¹₁С¹₁ S¹₁ перемещаем по прямым линиям параллельным оси ох;
   
6. В пересечении линий связи, проведенных из фронтальных проекций точек А²₂В²₂С²₂ S²₂, получим новое положение двухгранного угла А²₁В²₁С²₁S²₁, где ребро А²₁В²₁ проецируется в точку, а двухгранный угол в линейный. Величина этого линейного угла α и является величиной двухгранного.
   

Графическая работа 3

Тема: Поверхности. Сечение поверхностей плоскостями

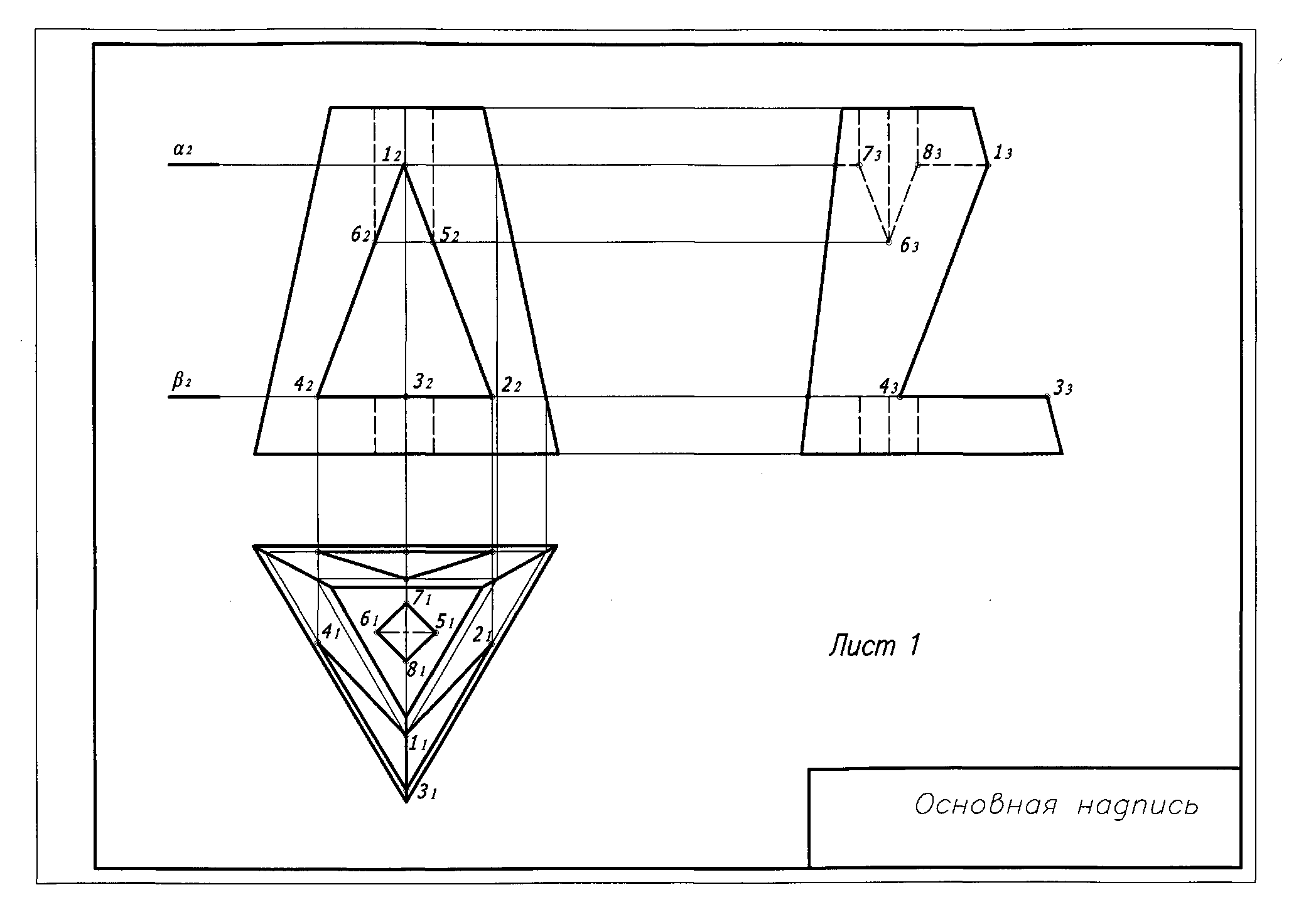
Содержание работы: по заданным проекциям многогранника (усеченной пирамиды или призмы) и сферы со сквозными отверстиями (окнами) в трех проекциях построить пирамиду и сферу.

Указания:

• Задание выполнить на двух листах формата А3 (420х297);
  
• Масштаб 1:1;
  
• Композиция эпюра горизонтальная;
  

Последовательность построения чертежа:

1. Построить три проекции заданных фигур;
   
2. Обозначить все характерные точки окон на фронтальной проекции;
   
3. Построить вспомогательные плоскости через характерные точки;
   
4. Построить проекции вспомогательных плоскостей на горизонтальной и профильной проекции фигуры;
   
5. По линиям связи построить проекции характерных точек на вспомогательных плоскостях;
   
6. Определить видимость;
   
7. Отметить видимость: видимые линии - сплошной, невидимые – штриховой.
   

Графическая работа 4

Тема: Поверхности. Взаимное пересечение поверхностей

Содержание работы:Построить линию пересечения поверхностей заданных непрозрачных фигур

Задача 1. Построить линию пересечения поверхностей методом секущих плоскостей;

Задача2. Построить линию пересечения поверхностей методом концентрических сфер.

Указания:

• Задание выполнить наформате А3 (420х297);
  
• Масштаб 1:1;
  
• Композиция эпюра горизонтальная;
  
• Задачу 1 расположить на листе слева, задачу 2 – справа.
  

Задача 1.Построить линию пересечения поверхностей методом секущих плоскостей.



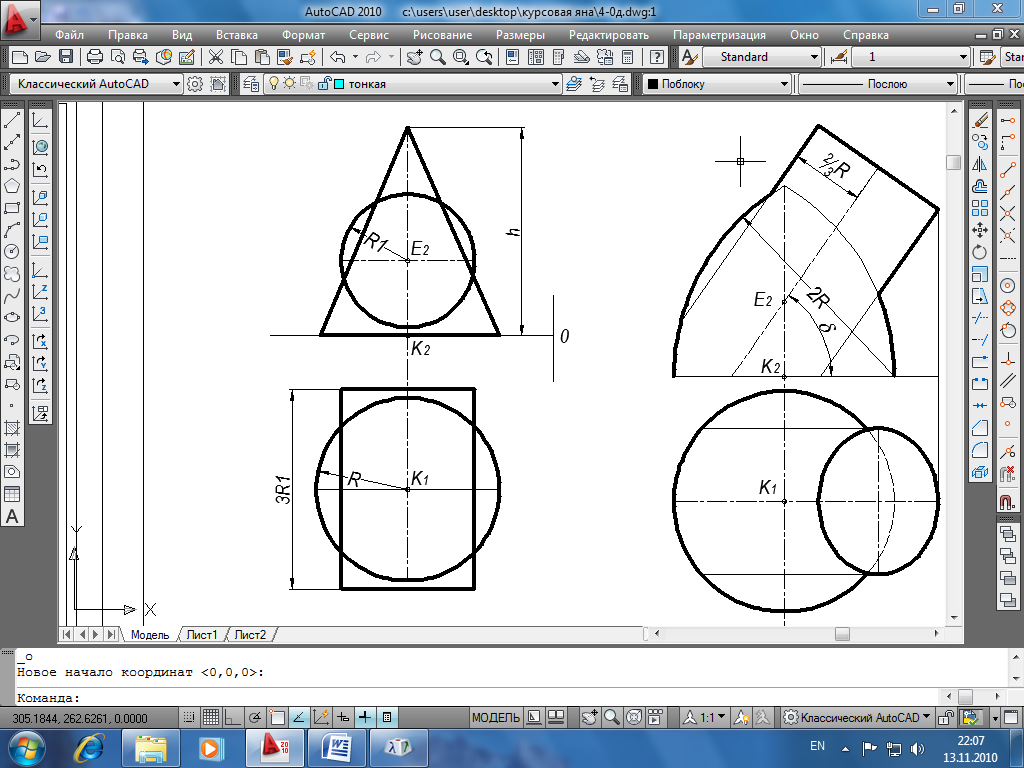
Последовательность построения чертежа:

(метод вспомогательных секущих плоскостей)

1. Построить две проекции заданных фигур, расположив их, слева на листе;
   
2. Определить и обозначить опорные точки;
   
3. Построить на горизонтальной плоскости проекции опорных точек;
   
4. Между опорными точками провести вспомогательную секущую плоскость;
   
5. Построить линии пересечения вспомогательной плоскости с заданными поверхностями;
   
6. Пункты 4,5 повторить несколько раз (3-4);
   
7. Полученные точки соединить между собой последовательно;
   
8. Определить видимость линии пересечения и очерков заданных поверхностей;
   
9. Обозначить видимость: видимые линии – сплошной, невидимые – штриховой.
   

Задача2. Построить линию пересечения поверхностей методом концентрических сфер.



Последовательность построения чертежа:

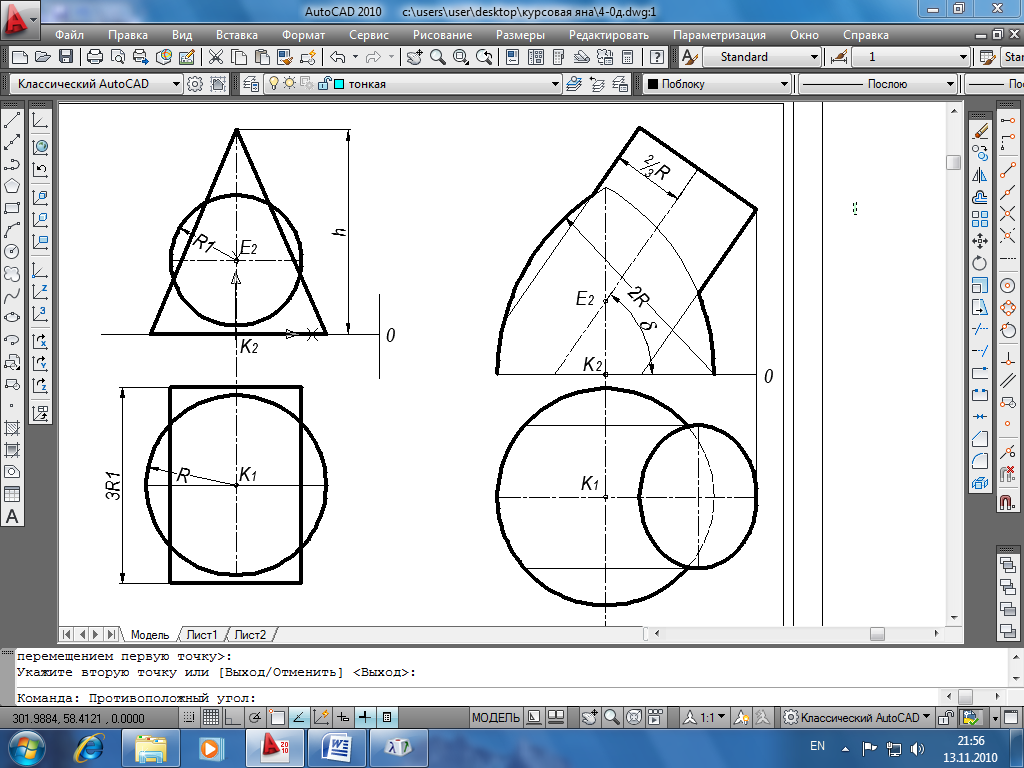
(метод вспомогательных концентрических сфер)

1. Построить две проекции заданных фигур, расположив их, справа на листе;
   
2. Определить и обозначить опорные точки;
   
3. Определить центр вспомогательных секущих сфер;
   
4. Определить радиусы maxи minсферы;
   
5. Провести первую вспомогательную секущую сферу;
   
6. Построить две линии пересечения (окружности) вспомогательной сферы с заданными поверхностями;
   
7. В пересечении построенных линий отметить точки искомой линии пересечения;
   
8. Для получения достаточного количества точек линии пересечения двух поверхностей, ввести несколько сфер посредников, с радиусами R_max>R>R_min и пункты 5.6.7 повторить;
   
9. Недостающие проекции точек линии пересечения найти из условия их принадлежности одной из поверхностей;
   
10. Одноименные проекции точек последовательно соединить плавной кривой линией;
    
11. Определить видимость в проекциях;
    
12. Отметить видимые линии – сплошной, невидимые – штриховой.
    

ПРИЛОЖЕНИЕ 3.

Образец графической работы 1.


Образец графической работы 2.








Образец графической работы 3.







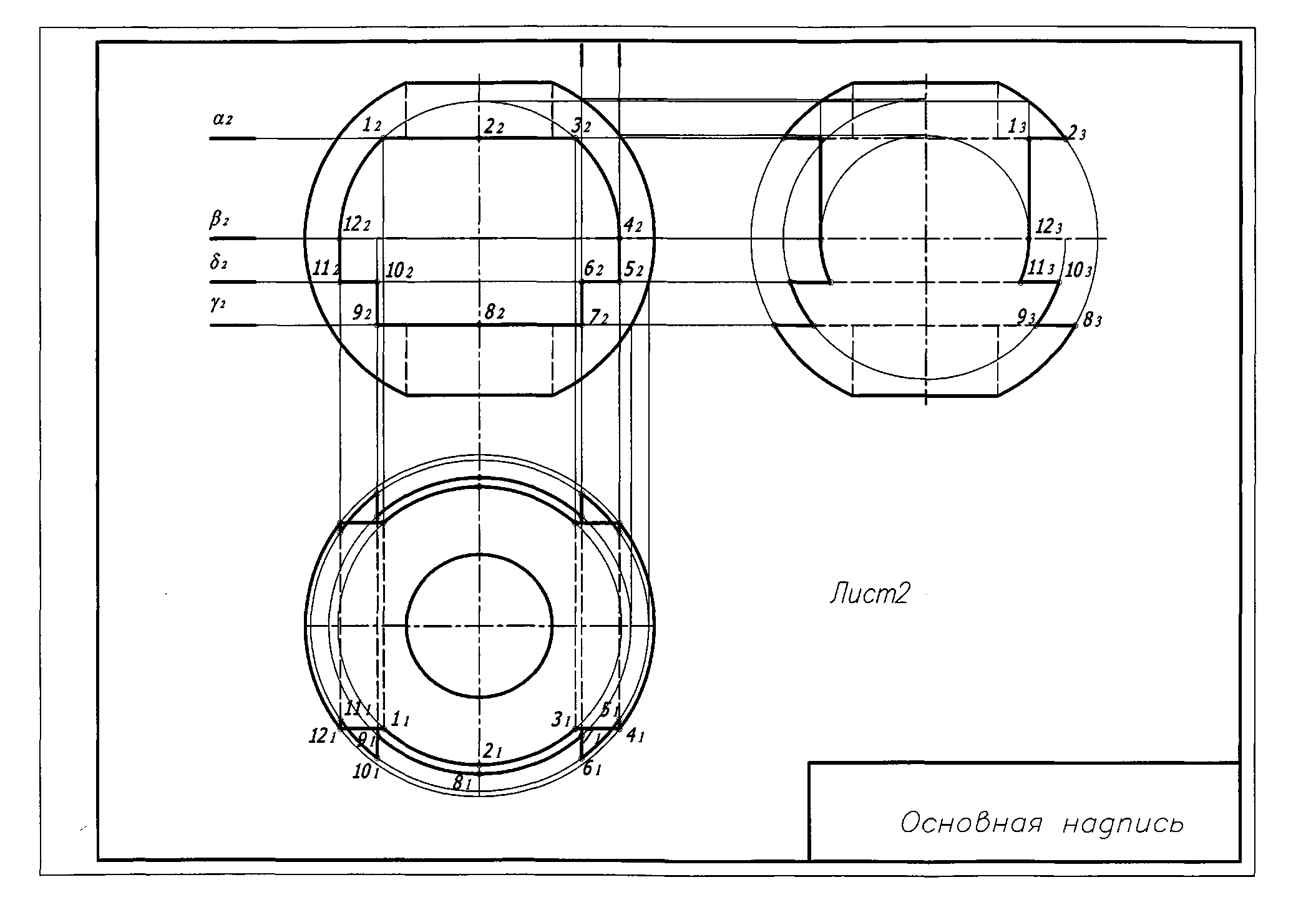
Образец графической работы 4.