Geum.ru

Курс: 1 семестр 2 дисциплина: Инженерная графика задания для самостоятельной работы

Вид материалаСамостоятельная работа

Содержание


Содержание работы
Графическая работа №4
Таблица 4. (метод вспомогательных секущих плоскостей)
На чертеже в качестве пересекающихся прямых принимают горизонталь и фронталь. Поэтому фронтальную проекцию перпендикуляра провод
Для решения задачи задаем плоскость
Подобный материал:
1   2   3   4



Графическая работа №2

Формат А-3 (297х420) , 2листа

Содержание работы: По заданным координатам вершин пирамиды SABC определить:

1. Натуральную величину основания АВС (перемены плоскостей проекций);

2 Расстояние от вершины S до основания АВС (методом перемены плоскостей проекций);

3. Кратчайшее расстояние между ребрами SС и АВ(методом перемены плоскостей проекций);

4. Величину двухгранного угла при ребре АВ (плоскопараллельным перемещением)

Указания:. Данные взять из таб.2

Таблица 2

Вариант
Точки
Координаты, мм
Вариант
Точки
Координаты, мм

Х
У
Z
X
Y
Z

1,

17
S
20
50
45
9,

25
S
75
50
65

A
10
20
10
A
40
55
5

B
55
50
19
B
0
20
50

C
80
0
60
C
65
0
25

2,

18
S
70
20
20
10,

26
S
80
65
50

A
5
30
60
A
45
5
55

B
5
10
20
B
5
45
10

C
60
65
40
C
70
20
0

3,

19
S
65
15
40
11,

27
S
5
60
50

A
40
25
60
А
40
5
55

B
0
15
20
B
80
45
10

C
60
70
25
C
15
20
0

4,

20
S
75
65
50
12,

28
S
0
55
60

A
40
5
55
A
35
55
5

B
0
50
10
B
75
20
50

C
65
25
0
C
10
0
25

5,

21
S
80
65
50
13,

29
S
0
25
15

A
45
5
55
A
25
60
25

B
5
45
10
B
65
20
5

C
70
20
0
C
5
10
60

6,

22
S
20
45
50
14,

30
S
5
25
25

A
10
10
20
A
30
60
30

B
50
10
50
B
70
20
10

C
80
60
0
C
15
10
65

7,

23
S
70
20
20
15,

31
S
70
40
45

A
45
60
30
A
80
10
20

B
5
20
20
B
35
10
50

C
50
30
65
C
10
60
0

8,

24
S
65
20
15
16,

32
S
10
55
50

A
55
65
20
A
45
10
55

B
0
20
5
B
80
45
10

C
50
25
60
C
15
20
0



Формат А-3 (297х420) , 2листа

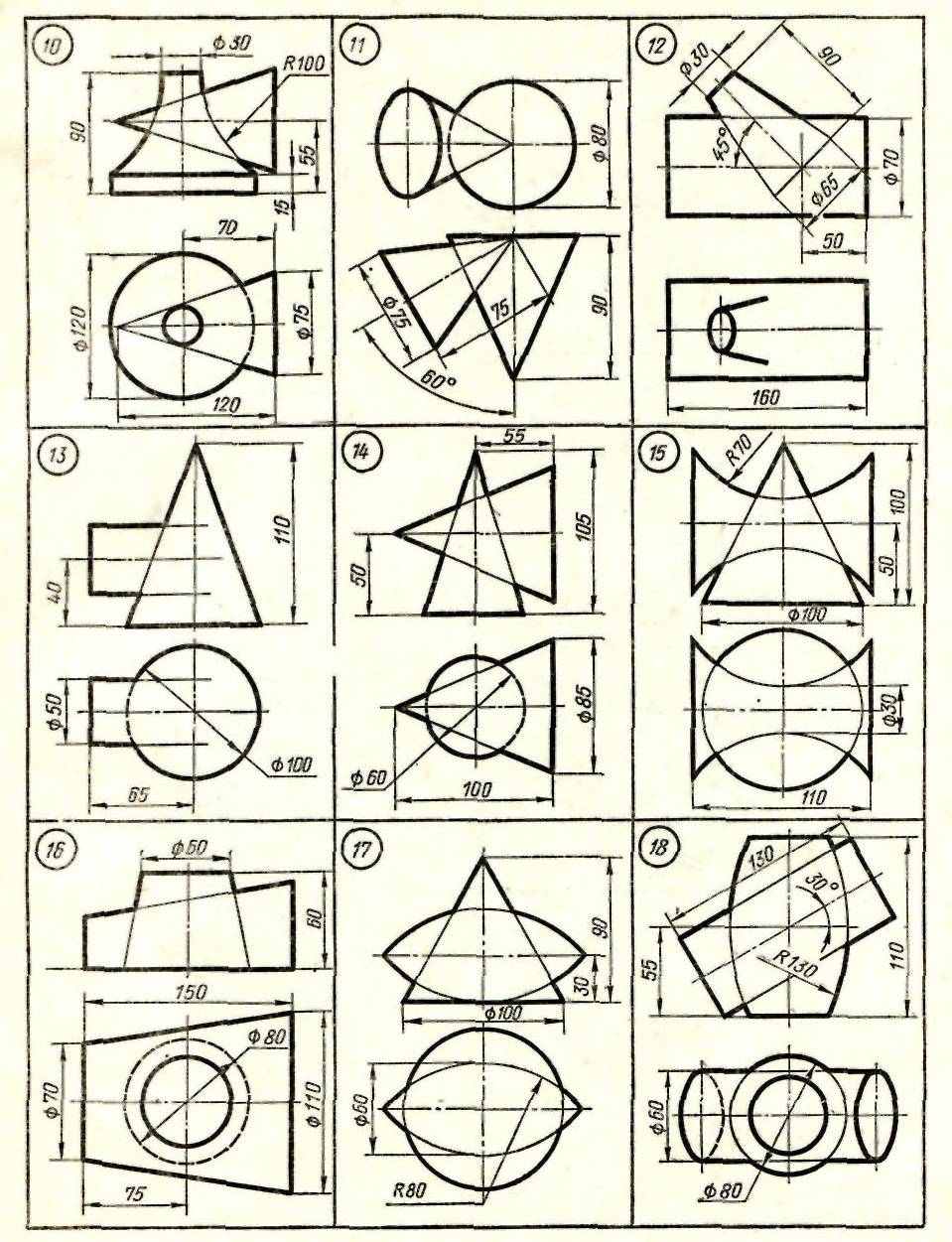
Содержание работы: по заданным проекциям многогранника (усеченной пирамиды или призмы) и сферы со сквозными отверстиями (окнами) в масштабе 1: 1 в трех проекциях построить пирамиду и сферу.

Данные взять из таблицы 3.

Вариант 1,12

Таблица3.







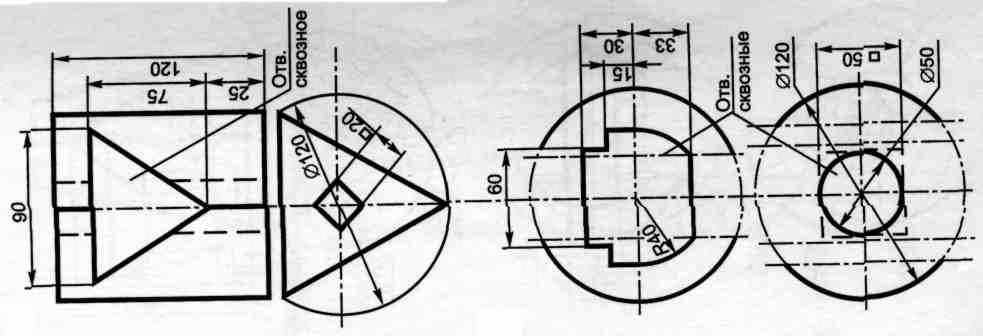
Вариант 2,13




Вариант 3,14




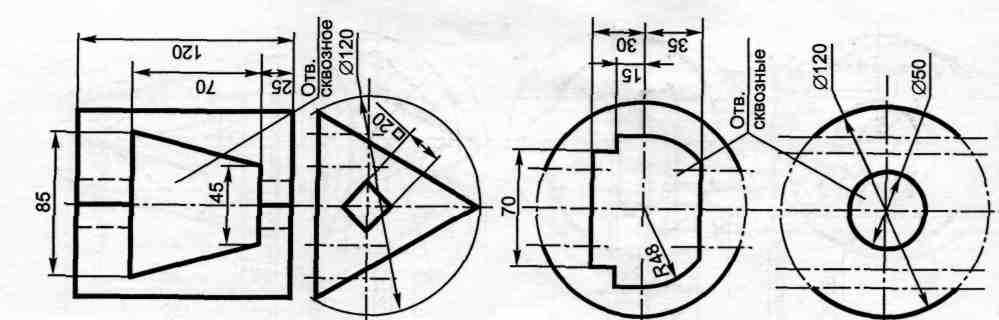
Вариант 4,15


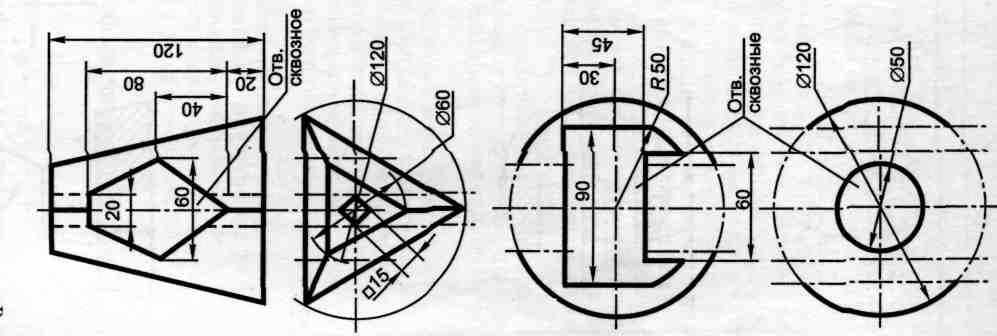
Вариант 5,16




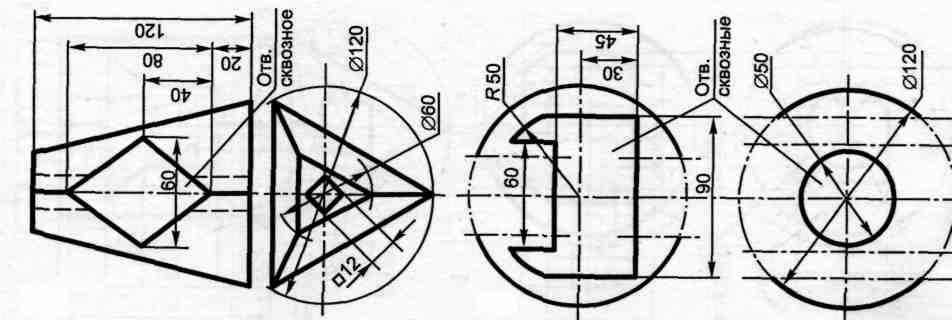
Вариант 6,17




Вариант 7,18




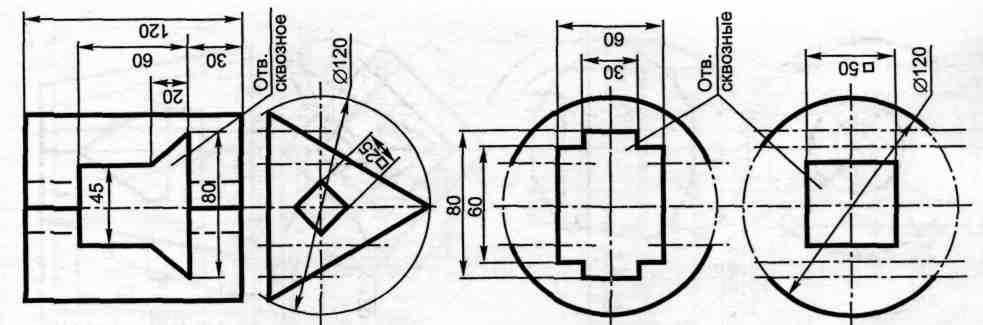
Вариант 8,19


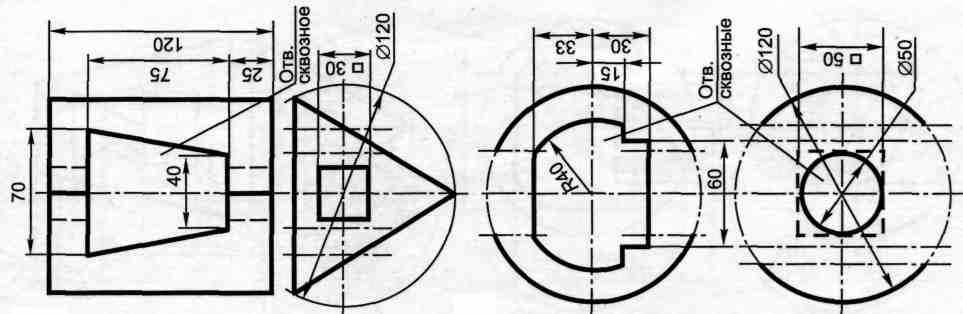
Вариант 9,20


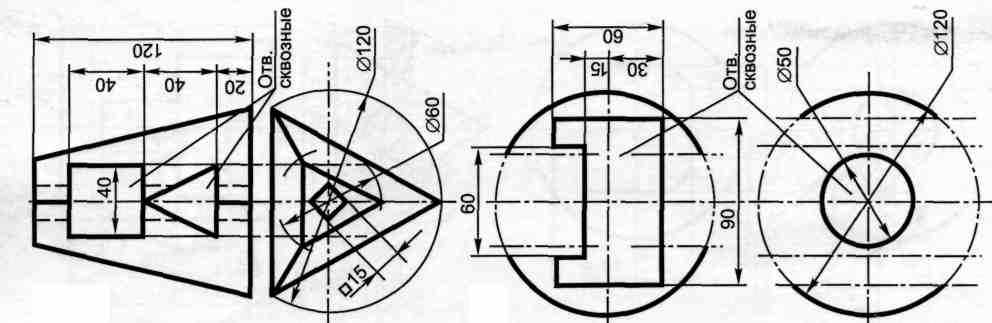
Вариант 10,21




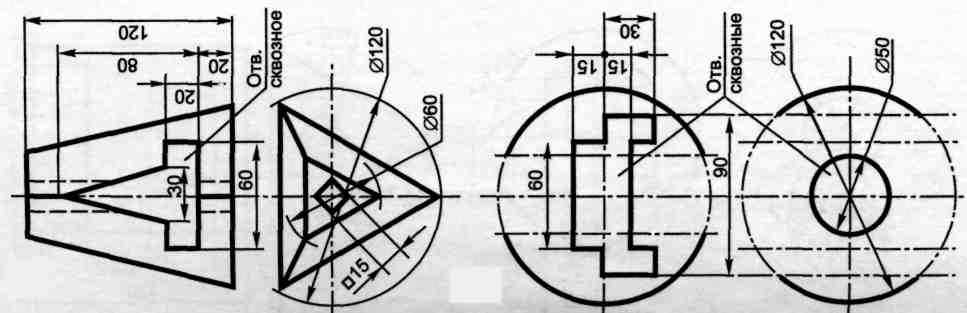
Вариант 12,22




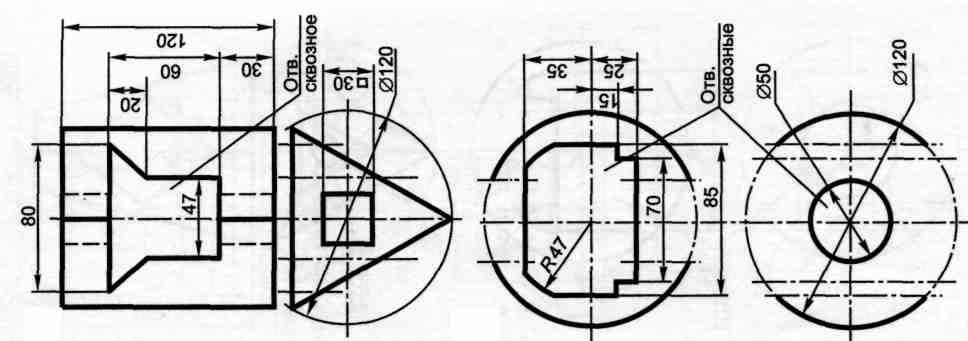
Графическая работа №4

Формат А-3 (297х420) , 1лист

Содержание работы: Построить линию пересечения поверхностей заданных непрозрачных фигур

Указания: По заданным изображениям построить проекции пересекающихся поверхностей, Линии пересечения построить методом вспомогательных секущих плоскостей и методом концентрических сфер.

Варианты заданий таблица 4, 5.


Таблица 4. (метод вспомогательных секущих плоскостей)





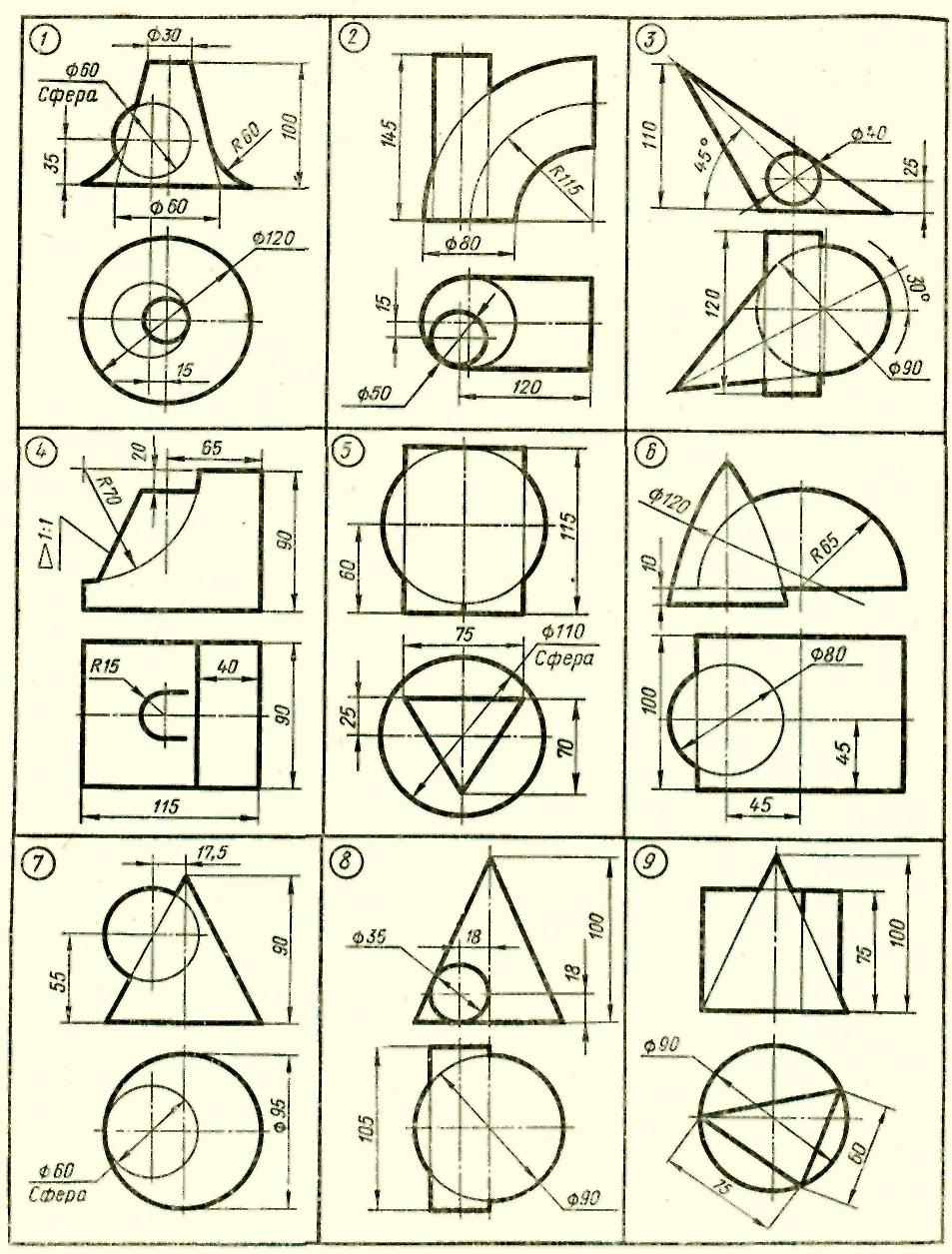
Продолжение таблицы 4







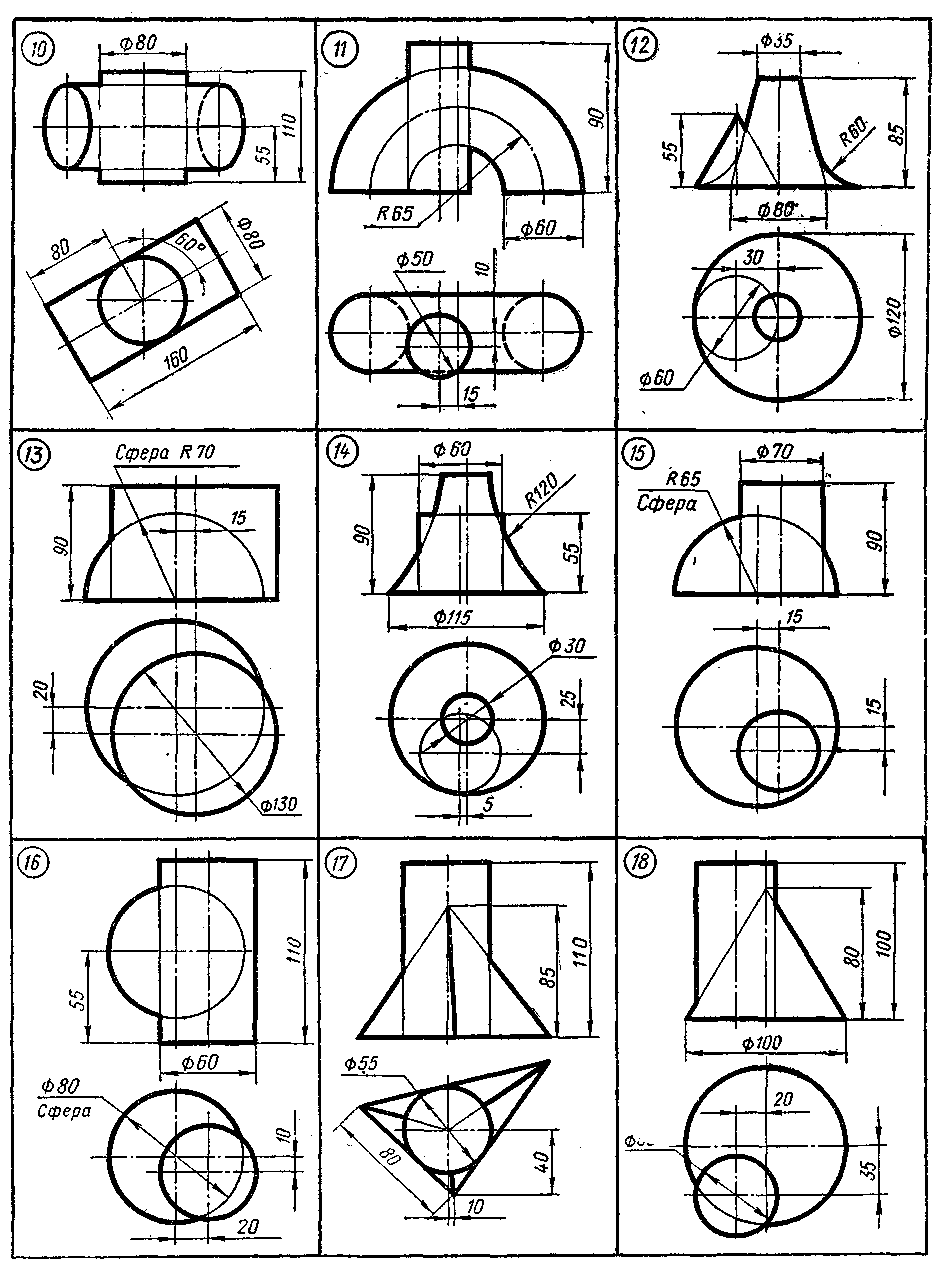
Таблица 5 (Метод концентрических плоскостей)




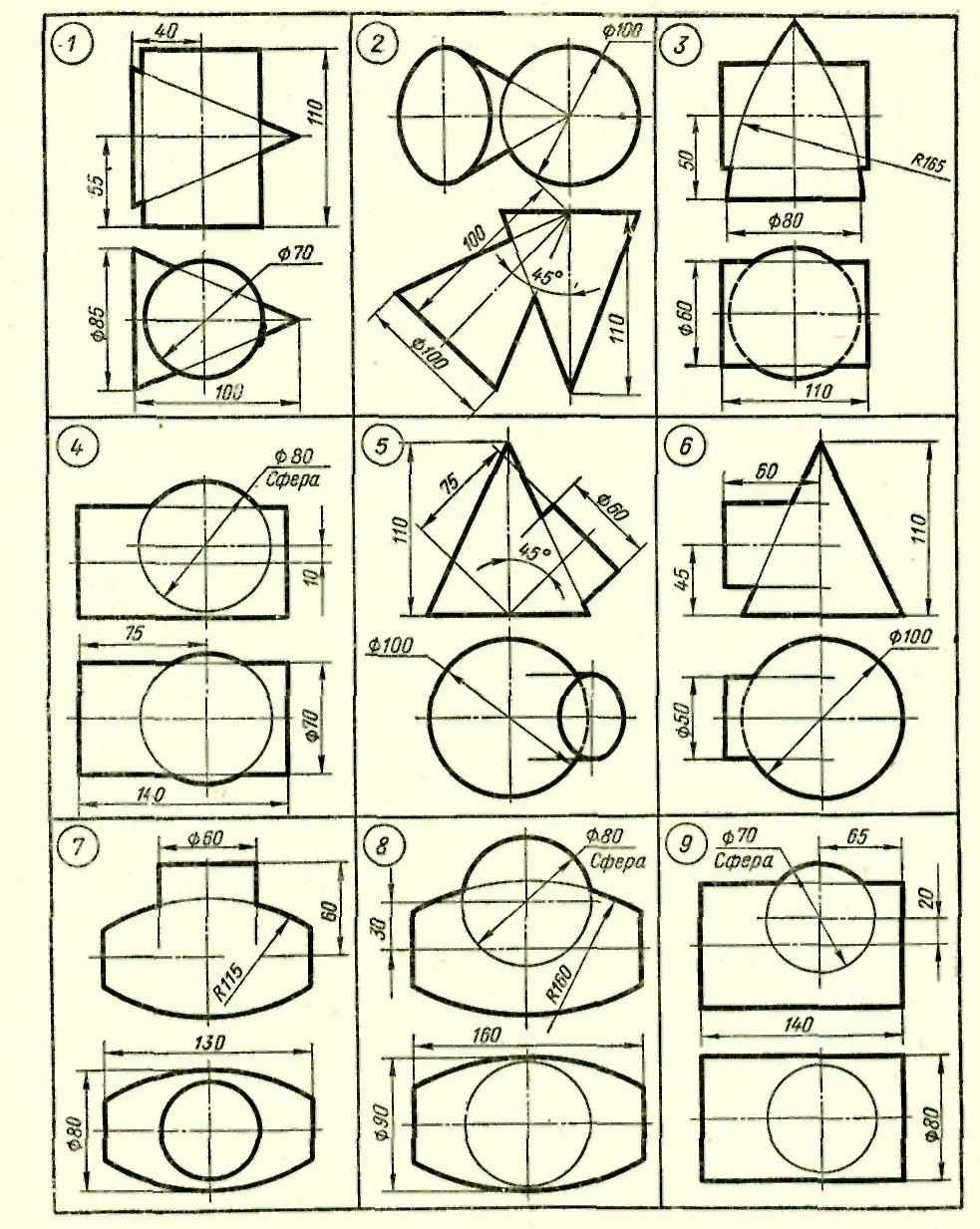
Продолжение таблицы 5.







ПРИЛОЖЕНИЕ 2


Графическая работа 1

Тема: Точка, прямая, плоскость

Содержание работы: По заданным координатам точек ABCDEF выполнить четыре задачи:

Задача 1. Построить точку пересечения прямой DE c плоскостью, заданной треугольником АВС;

Задача 2. Определить расстояние от точки D до плоскости;

Задача 3. Через прямую DЕ провести плоскость, перпендикулярную плоскости АВС, и построить линию пересечения этих плоскостей, определить видимость;

Задача 4. Построить плоскость, параллельную плоскости, заданной треугольником АВС, и отстоящую от нее на 50мм.

Указания:
  • Задание выполнить на формате А3 (420х297);
  • Масштаб 1:1;
  • Композиция эпюра горизонтальная;
  • Точку начала координат нужно взять левее середины листа, задачи 1и 3 совместить на одном чертеже и расположить слева, задачи 2 и 4 расположить справа.

Примеры построения задач:

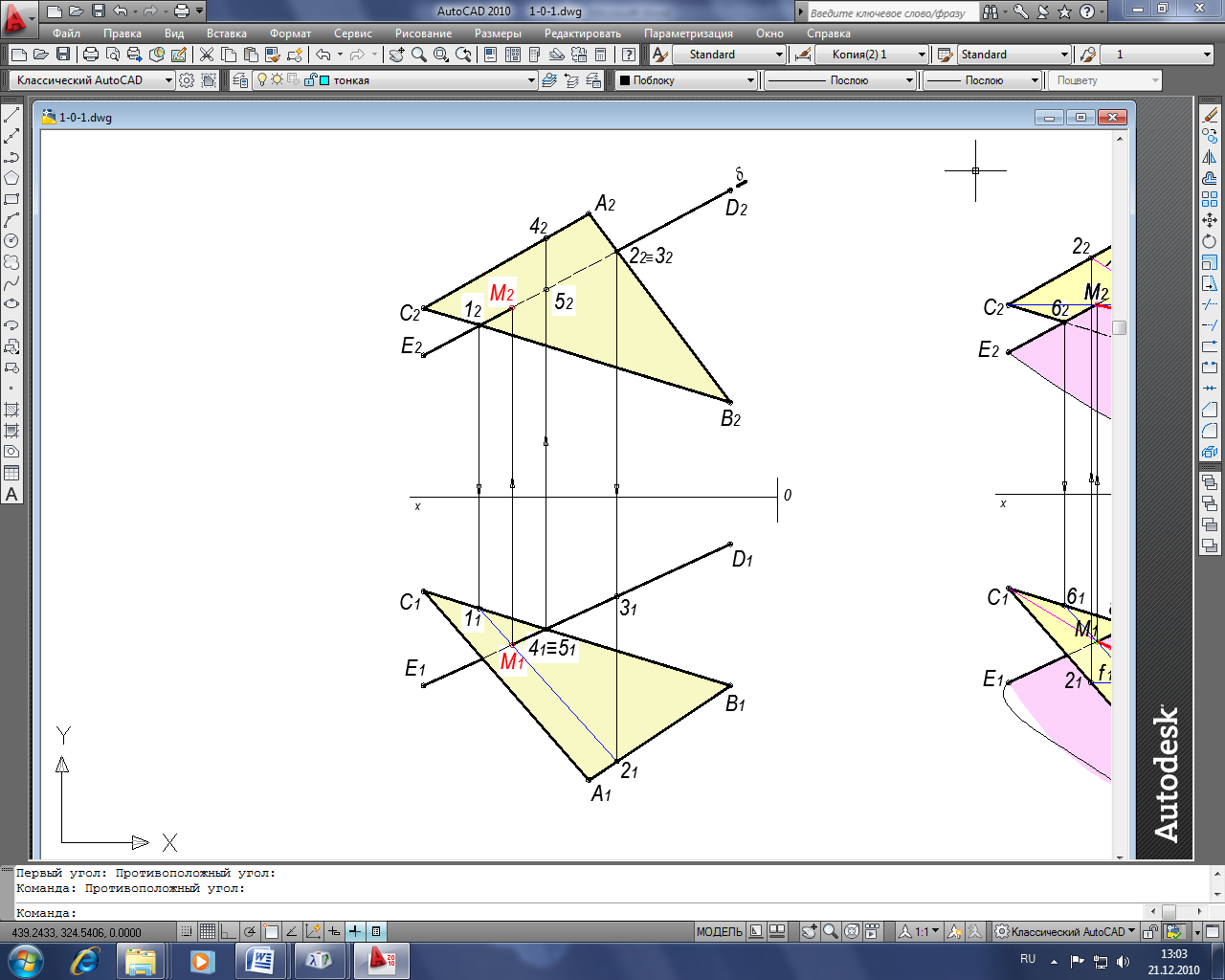
Задача 1. Построить точку пересечения прямой DE c плоскостью, заданной треугольником АВС


Последовательность построения:

  1. Заключаем DE во вспомогательную плоскость  2;
  2. Отмечаем линию пересечения (12 – 22) двух плоскостей α(АВС) ∩;
  3. По линиям связи строим (11–21);
  4. В пересечении полученной прямой (11–21) и заданной D1E1 отмечаем точку М1 - горизонтальную проекцию точки пересечения DE c плоскостью α(АВС);
  5. М2 – по линии связи;
  6. Для построения видимости прямой с плоскостью, сравниваем положение конкурирующих точек 41≡51 на 2 и 22≡32 на 1;
  7. Отмечаем видимость.



Задача 2. Определить расстояние от точки D до плоскости α(АВС).


Расстояние от точки до плоскости определяется величиной перпендикуляра опущенного из заданной точки на плоскость.

На чертеже в качестве пересекающихся прямых принимают горизонталь и фронталь. Поэтому фронтальную проекцию перпендикуляра проводят под углом 90  к фронтальной проекции фронтали, а горизонтальную проекцию перпендикуляра под углом 90к горизонтальной проекции горизонтали.





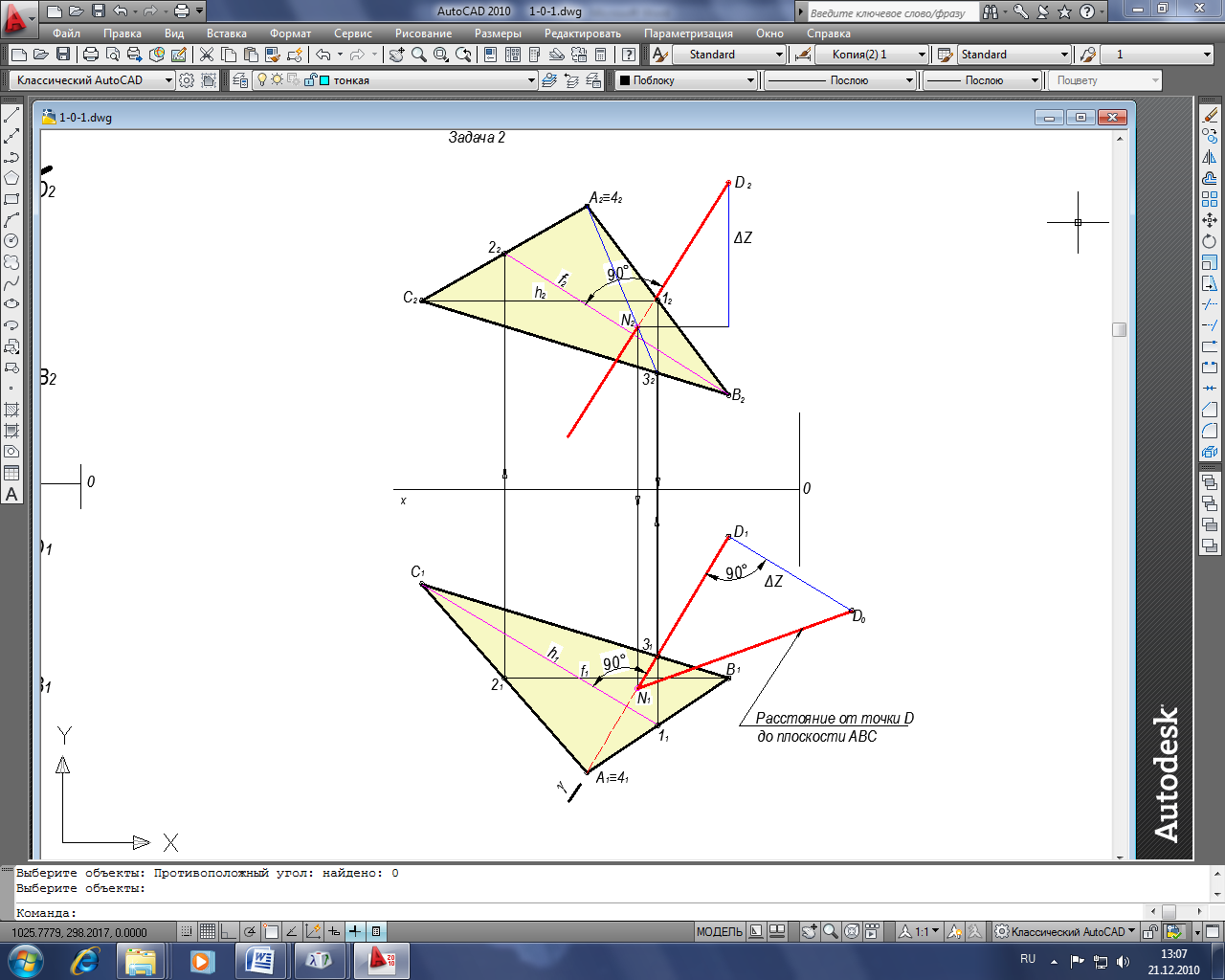
Последовательность построения:


1. В плоскости α(АВС) проводим горизонталь h;

2. В плоскости α(АВС) проводим фронталь f;

3. Из точки D1 проводим прямую

(D1 …) h1;

4. Из точки D2 проводим прямую (D2…) f2;

Строим точку пересечения перпендикуляра (D…)с плоскостью α(АВС), для чего:

5. Заключаем перпендикуляр (D…)во вспомогательную плоскость  1;

6. Отмечаем (11-21) прямую пересечения двух плоскостей - заданной α(АВС) и вспомогательной;

7. По линиям связи строим (12-22);

8. На 2 в пересечении (12-22) и (D2 …)отмечаем точку N2 – точку пересечения перпендикуляра с плоскостью;

9. По линии связи строим горизонтальную проекцию точки N1;

Построенная прямая D N является прямой общего положения, поэтому натуральную величину отрезка D N необходимо построить методом прямоугольного треугольника:

10. Из точки D1 проводим прямую перпендикулярную D1 N 1;

11. На 2 строим ΔZ= ΔZD – ΔZN

12. Отмечаем точку Dо, где D1Dо= ΔZ

13. Получаем Dо N1 равную натуральной величине D N , то есть расстояние точки D до плоскости α(АВС).


Задача 3. Через прямую DЕ провести плоскость β, перпендикулярную плоскости α (АВС), и построить линию пересечения этих плоскостей, определить видимость

При построении взаимно перпендикулярных плоскостей используют свойство: плоскости перпендикулярны, если прямая, принадлежащая одной плоскости, перпендикулярна другой плоскости.

Плоскость β перпендикулярная плоскости α может быть построена через прямую линию перпендикулярную к плоскости α. Плоскость β задается двумя пересекающимися прямыми (D…) и DЕ. При этом плоскость β содержит прямую (D…) перпендикулярную плоскости α(АВС). В качестве пересекающихся прямых на плоскости α взяты горизонталь и фронталь этой плоскости.



Последовательность построения:

Из точки D проводим прямую перпендикулярную плоскости α(АВС)
  1. В плоскости α(АВС) проводим горизонталь h;
  2. В плоскости α(АВС) проводим фронталь f;
  3. Из точки D 1 проводим прямую (D 1…) h1;
  4. Из точки D 2 проводим прямую (D 2…) f2;

Получили плоскость β заданную двумя пересекающимися прямыми (D…) и DЕ. Плоскость β содержит прямую (D…)перпендикулярную α(АВС);

Строим линию пересечения двух плоскостей α (АВС) и β(D…) ∩DЕ, для чего сводим задачу на построение точек пересечения двух прямых (D…) ,DЕ с плоскостью α (АВС):
  1. Заключаем (D 1…) во вспомогательную плоскость  1;
  2. Отмечаем (31-41) прямую пересечения двух плоскостей - заданной α(АВС) и вспомогательной;
  1. По линиям связи строим (32-42);
  2. На 2 в пересечении (32-42) и (D2 …)отмечаем точку N2 – точку пересечения перпендикуляра с плоскостью;
  3. По линии связи строим горизонтальную проекцию точки N1; получили первую точку линии пересечения плоскостей α∩ β ;

Для построения второй общей точки М плоскостей α∩ β заключаем DE во вспомогательную плоскость δ 2;
  1. Отмечаем линию пересечения (52 – 62) двух плоскостей α(АВС) ∩ δ;
  2. По линиям связи строим (51–61);
  3. В пересечении полученной прямой (51–61) и заданной D1E1 отмечаем точку М1 - горизонтальную проекцию точки пересечения DE c плоскостью α(АВС);
  4. М2 – по линии связи; получили вторую точку линии пересечения плоскостей α∩ β ;
  5. Строим проекции М N на 1 и 2.
  6. Определяем видимость плоскостей для чего сравниваем положение конкурирующих точек 5≡7 на 1 и 8≡9 на 2;
  7. Отмечаем видимость: видимые части плоскостей – сплошной толстой линией, невидимые – штриховой.



Задача 4. Построить плоскость параллельную плоскости, заданной треугольником α(АВС), и отстоящую от нее на 50мм

При построении взаимно параллельных плоскостей используют свойство: если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то плоскости параллельны.

Для решения задачи задаем плоскость двумя пересекающимися прямыми q и t, в качестве точки пересечения выбираем точку Т удаленную от плоскости α(АВС) на расстояние 50мм.

Последовательность построения:

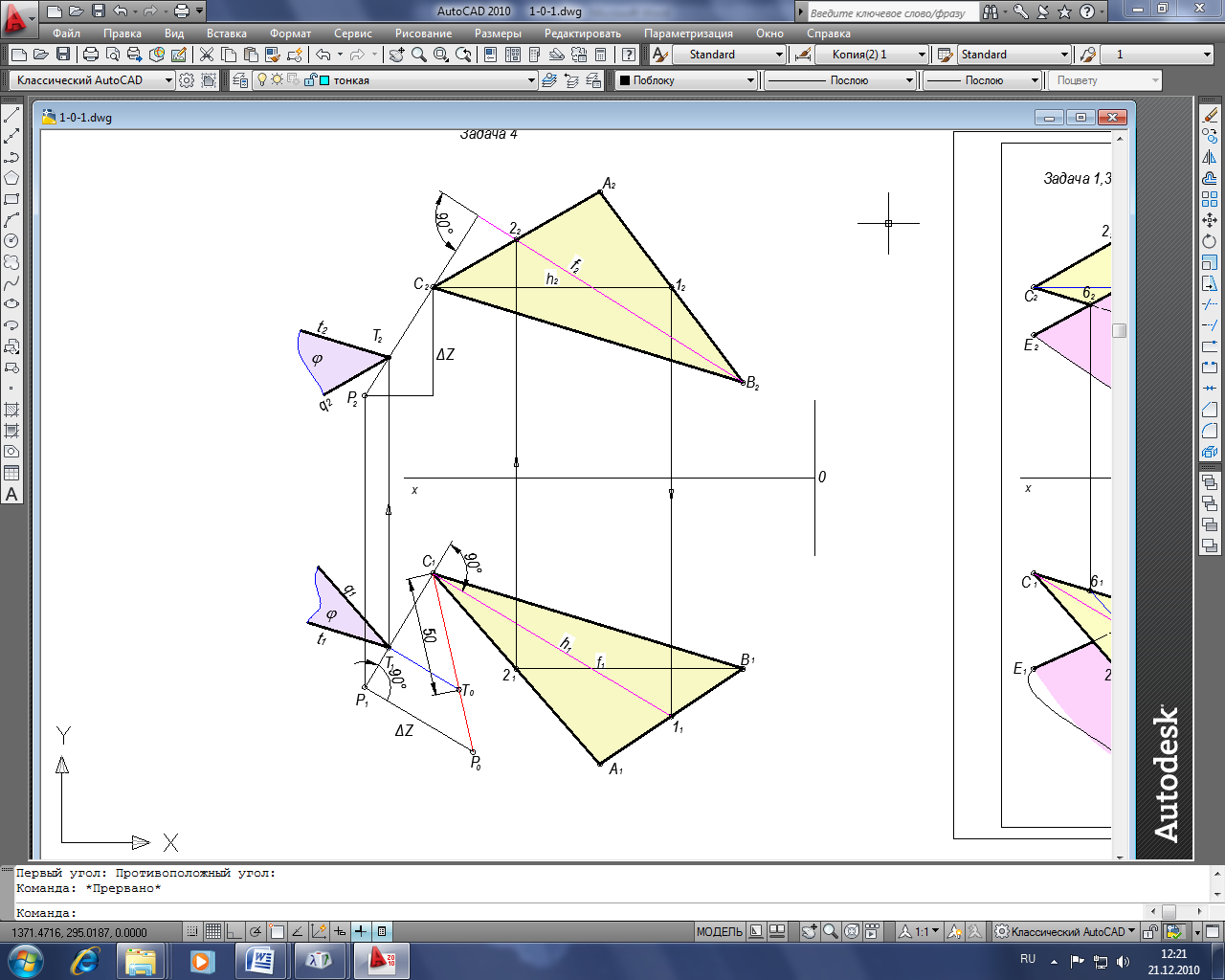
  1. В плоскости α(АВС) проводим горизонталь h;
  2. В плоскости α(АВС) проводим фронталь f;
  3. Из точки С 1 проводим прямую (С1…) h1;
  4. Из точки С 2 проводим прямую (С2…) f2;
  5. На перпендикуляре (С…) берем произвольную точку Р;

Находим натуральную величину расстояния от точки Р до плоскости α(АВС), где РС прямая общего положения.
  1. Проводим (Р 1…)  Р1С1;
  2. На плоскости 2 определяем разность концов отрезка Р2С2 равную ΔZ= ΔZс – ΔZр;
  3. Получаем Ро С1 равную натуральной величине РС , то есть расстояние точки Р до плоскости α(АВС);
  4. По условию задачи плоскость должна быть удалена от плоскости α(АВС) на расстояние 50мм, поэтому на Ро С1 отмечаем точку То, где отрезок То С1 равен 50мм;
  5. Строим горизонтальную проекцию точки Т1, гдеТо Т1 Р1С1;
  6. По линии связи строим Т2;
  7. Задаем плоскость двумя пересекающимися прямыми q и t в тоске Т, проекции которых соответственно параллельны одноименным проекциям прямых АС и ВС плоскости α(АВС).