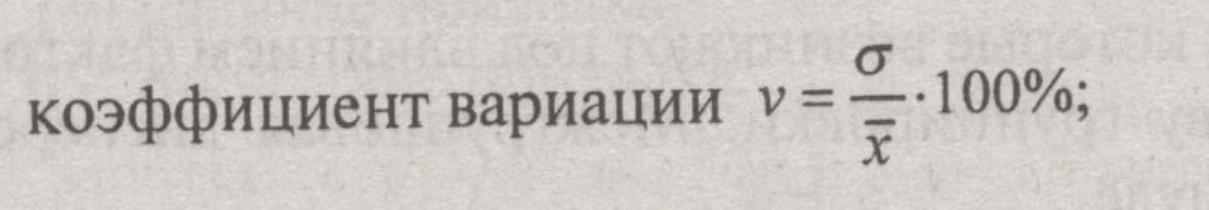Статистика Предмет, метод и задачи статистики. Источники статистической информации
| Вид материала | Документы |
- Общая теория статистики, 25.3kb.
- С. В. Щедроткина 2009 г. Дисциплина: Статистика Специальность: 080106 Финансы (по отраслям), 46.43kb.
- Темы лекционных занятий: Предмет, метод и задачи статистического исследования Современная, 25.16kb.
- Методические указания к контрольной работе по курсу: «Статистика», для студентов очно-заочного, 76.42kb.
- Задачи современной статистики. Статистика и ее роль в познании общественных явлений, 408.08kb.
- Программа курса Тема I. Предмет, метод и задачи статистики Тема, 1602.61kb.
- Лекция №1 «Предмет и метод статистики», 80.82kb.
- План Статистика як наука. Предмет, метод І задачі статистики Предмет статистики, 83.56kb.
- Понятие, значение и задачи статистики. Основные понятия и категории статистики, 38.18kb.
- 1. Предмет и задачи статистики, 1075.66kb.
Статистика
1. Предмет, метод и задачи статистики. Источники статистической информации.
Статистика (С) – это вид деятельности, направленной на получение, обработку и анализ информации, характеризующей количественные закономерности жизни общества во всем их многообразии (технико-экономические, социально-политические явления, культура) в неразрывной связи с ее качественным содержанием. Таким образом, под С понимается сбор цифровых данных, их обобщение и обработка.
В более узком смысле С рассматривается как совокупность данных о каком-либо явлении или процессе (например, когда говорят о С выборов).
Под предметом С понимается количественная сторона массовых общественных явления в постоянной связи с их содержанием или количественной стороной, а также количественное выражение закономерности общественного развития в конкретных условиях места и времени.
С опирается на общие положения социально-экономической теории. Вместе с тем у нее свои специфические методы цифрового освещения явления, то есть совокупность приемов, применяемых в процессе статистического исследования. Это наглядно проявляется в том, через какие 3 характерных этапа проходит статистическое исследование: 1) осуществление массового научного организованного наблюдения для получения первичной информации об отдельных единицах явления; 2) группировка и сводка материалов, как распределение всей массы случаев на однородные группы, подсчет характеризующих эти группы количественных показателей и оформление их в виде таблицы; 3) обработка статистических показателей и анализ результатов для получения общих выводов о состоянии явления.
В составе С как науки выделяют отделено общую теорию С и производные от нее экономическую С и социальную С. Общая теория С разрабатывает основополагающие принципы и методы статистического исследования общественных явлений, занимается самыми общими категориями С. Экономическая С обеспечивает систематическое количественное описание всех основных сторон экономического процесса и экономики в целом. К ее основным задачам относят: 1) предоставление информации общеэкономического характера органам гос. управления для принятия стратегических решений; 2) предоставление сведений коммерчески значимого характера предпринимателям для правильной организации своей деятельности; 3) информирование общественности страны об актуальных социально-экономических явления.
Экономическая С пользуется в России различными источниками данных, все их можно отнести либо к внутренним, которые организует и собирает Федеральная служба государственной статистики (отчетность предприятий, регистр предприятий, переписи и обследования), либо к внешним, организуемые другими ведомствами (административные источники, денежная и банковская статистика, таможенная С и т.д.)
2. Статистическое наблюдение (СН), сводка и группировка.
На первом этапе статистического исследования, т.е. на стадии массового научно-организационного наблюдения, решается ключевая задача создания необходимой информационной базы. СН – это систематический научно обоснованный сбор информации о социально-экономических явлениях и процессах. Цель наблюдения определяет объект статистического наблюдения. Под ним понимается определенное явление, которое подлежит наблюдению. Объект статистического наблюдения также есть статистическая совокупность. Под ней понимается множество единиц обладающих некоторыми общими свойствами, существенными для их характеристики
СН классифицируется по различным признакам: 1) по охвату единиц совокупности: 1. сплошное (по всем без исключения единицам совокупности); 2. несплошное (например, выборочным); 2) по времени проведения СН бывает: 1) непрерывным (текущим), с систематической регистрацией фактов 2) единовременным (разовое сплошное обследование по мере необходимости) 3) периодическим (например, инвентаризация).
На втором этапе статистического исследования прибегают к группировке и сводке.
Под группировкой понимается расчленение единиц статистической совокупности на группы, однородные в каком-либо существенном отношении. Признак, по которому единицы совокупности подразделяются на группы именуется группировочным признаком или основанием группировки.
Группировка, выполняемая по 1 признаку, называется простой, а по нескольким – комбинированной.
Группировочные признаки бывают атрибутивными (в виде текстовой записи) и количественными (имеющими цифровое выражение).
После проведения группировки осуществляется обобщение данных наблюдения по выделенным частям и целому по средствам статистической сводки – подсчета числа единиц в подгруппах и группах выделенных при группировке, и подведения количественных итогов.
Результаты группировки и сводки оформляются в виде статистических таблиц. В таблице 2 основных элемента: 1. Подлежащее (обычно в первой вертикальной или горизонтальной графе), перечень единиц или групп; 2) сказуемое (цифры, характеризующие эти единицы и группы).
Таблицы бывают простыми (части подлежащего не являются группами одинакового качества; групповыми (подлежащее образовано в результате группировки единиц по одному какому-то признаку); комбинационными (подлежащее образовано по двум и более признакам).
3. Статистическая совокупность, единицы совокупности и наблюдения.
На этапе статистического исследования, т.е. на стадии массового научно-организационного наблюдения, решается ключевая задача создания необходимой информационной базы. Систематический научно обоснованный сбор информации о социально-экономических явлениях и процессах, то есть статистическое наблюдение. Цель наблюдения определяет объект статистического наблюдения.
Единица наблюдения – единица, о которой записываются данные, составляющие программы статистического изучения. В каждом конкретном статистическом исследовании объектов наблюдения, а также в зависимости от тех задач, которые нужно разрешить в процессе наблюдения, определяется, сколько единиц наблюдения должно быть обследовано (одно или несколько). При переписи населения, например, единицей наблюдения является человек; если же изучению подлежат также и семьи, то устанавливаются две единицы наблюдения: отдельный человек и семья. Правильное определение единицы наблюдения имеет существенное значение не только для проведения самого наблюдения, но и для последующих стадий статистического исследования.
От единицы наблюдения следует отличать единицу совокупности, т.е. первичный элемент объекта статистического наблюдения, признаки которого подлежат регистрации и который является основой ведущегося счета. Например, при учете племенного скота единицей наблюдения является каждое сельскохозяйственное предприятие (фермерское хозяйство, коллективное хозяйство и т.п.), а единицей совокупности – каждое животное; при переписи оборудования единицей наблюдения является каждое предприятие, а единицей совокупности – станок и т.д.
Следует отметить, что единица совокупности и единица наблюдения могут совпадать.
4. Статистический признак и показатель; случайная величина.
Понятия статистический признак и статистический показатель взаимосвязаны и в ряде случаев употребляются как тождественные. Показатель выражает единство количественной стороны явления (его меру), признак – отличительные особенности или сходство объектов статистической совокупности.
Статистические признаки могут быть количественными (возраст, рос человека) и качественными (пол человека, его профессия). Признаки, систематически принимающие различные значения у отдельных единиц совокупности, называются варьирующими признаками (размеры одежды и обуви). Признаки бывают первичными и вторичными. Первичные признаки лежат в основе программы сбора первичным статистических материалов. Вторичные признаки – это признаки, характеризуемые в процессе обработки и анализа данных. Так, группа предприятий по эффективности капитальных вложение основана на вторичных признаках, ибо для эффективности необходимо знать первичные признаки предприятий – размер капитальных вложений, уровень себестоимости и др.
Статический показатель – обобщенная количественная характеристика явлений и процессов в единстве с их качественной определенностью. Примером статистического показателя служат: численность населения; количество индивидуальных частных предприятий в общем количестве торговых предприятий; удельный вес работающих граждан в общей численности населения; удельный вес менеджеров, имеющих специальное управленческое образование, от их общего количества и т.п. В статистической практике термин «показатель»употребляется и в более узком смысле как конкретное значение размеров явления в условиях конкретного места и времени: определенный процент норм выработки рабочими по предприятию, группе предприятий и т.п.
Статистические показатели называются натуральными, когда они выражены в единицах счета или различных физических единицах измерения (в мерах линейных, площади, объема, веса, мощности и т.д.), и денежными, или стоимостными, когда они представляют денежную оценку экономических объектов или их элементов.
Статистические показатели также условно делятся на объемные и качественные. К первым относятся показатели, связанные с изменением величины совокупности объектов (элементов), например, численности рабочих на предприятии, компании или фирме, объем основных фондов и т.п. К группе качественных статистических показателей относят признаки уровня развития явления, например себестоимости единицы изделия. Такие показатели полнее и ярче характеризуют качественные особенности явлений, закономерности их развития.
Под случайной величиной понимается переменная, которая может принимать любое значение из данного множества с определенной относительной частотой и вероятностью.
(Из лекции. Статистический признак представляет собой конкретное свойство, качество единицы наблюдения. Признаки бывают количественные (возраст, рост человека) и качественные (пол человека). Количественные признаки описываются в С случайными величинами.
Статистический показатель является количественно-качественной характеристикой явлений и процессов. У статистического показателя 4 необходимых параметра: качественный, пространственный, временной, количественный.)
5. Абсолютные величины (АВ). Их виды.
АВ характеризуют численность совокупности и объем (размер) изучаемого социально-экономического явления в определенных границах времени и места. Они являются всегда именованными числами, т.е. имеют какую-либо единицу измерения. Единицы измерения могут быть натуральные, условно-натуральные, стоимостные (денежные) и трудовые. Выбор единицы измерения зависит от сущности изучаемого явления и конкретных задач исследования.
АВ подразделяются на две группы
1. АВ, характеризующие объем явления на определенную дату (например, стоимость основного капитала предприятия на 1 января). Эти величины имеют особенности: если они характеризуют объем явления на определенную дату по нескольким единицам (например, стоимость основного капитала по предприятиям фирмы). То их можно суммировать и получить общий объем явления. Если данные характеризуют объем явления по одной единице на несколько моментов (например, стоимость основного капитала на начало каждого квартала), то эти АВ суммировать нельзя.
2. АВ, характеризующие объем явления за определенный период времени – результат процесса (например, выпуск продукции предприятием за месяц или за год). В это случает позволительно суммировать данные, как за один и тот же период по нескольким единицами, получая общий для них итог, так и за несколько периодов по одной единице, получая итог за боле длительный период.
АВ могут быть получены путем суммирования данных статистического наблюдения или расчетным путем. Например, численность населения страны определяется по результатам сводки данных единовременного наблюдения. При определении стоимостных показателей объема продукции АВ получают расчетным путем.
6. Относительные величины (ОВ). Их классификация; основные виды.
ОВ получаются в результате сопоставления двух статистических показателей и дают цифровую меру их соотношения. Она получается путем деления сравниваемого показателя на другой показатель, принимаемый за базу сравнения.
ОВ подразделяются две группы: 1. ОВ, полученные в результате соотношения одноименных статистических показателей (ОВ динамики, планового задания, выполнения плана, структуры, координации, наглядности) и выражаются или коэффициентом, т.е. показателем того, во сколько раз сравниваемая величина больше или меньше базисной или в процентах; 2) дргие получаются в результате разноименных статистических показателей (так называемые ОВ интенсивности, например, показатель производства продукции на душу населения) и выражаются именованными числами, показывая итог числителя в расчете на 1,10,100 и т.д. единиц знаменателя.
ОВ динамики характеризуют изменение явления во времени. Они показывают, во сколько раз увеличился (или уменьшился) объем явления за определенный период времени.
ОВ планового задания, выражаются отношением величины показателя по плану к фактической величине показателя в предшествующем периоде.
ОВ выполнения плана характеризуется отношением фактической величины показателя в определенном периоде к плановому заданию на тот же период.
ОВы структуры (так называемый удельный вес) показывают долю отдельных частей в общем объеме совокупности.
ОВы координации выражаются соотношением численности двух частей единого целого, показывая сколько единицы одной группы приходится в среднем на 1, 10, 100 и т.д. единиц другой группы совокупности.
ОВы наглядности характеризуются сопоставлением одноименных показателей по одному и тому же моменту или периоду времени, но по разным объекта.
Показатель производства продукции на душу населения характеризуется отношением выпуска определенного вида продукции в натуральном выражении за года к среднегодовой численности селения.
7. Средние величины (СВ). Средние арифметические. Мода и медиана.
Под СВ понимается обобщающий показатель типичного уровня варьирующего количественного признака на единицу совокупности в определенном месте и в определенное время. СВ обязательно является именованной. СВ бывают двух видов: 1) степенные – представляют собой абстрактные характеристики совокупности (средняя арифметическая, средняя гармоническая, средняя квадратическая и средняя геометрическая); 2) структурные выражаются конкретными величинами, совпадающими в какими-то определенными вариантами совокупности (мода, медиана).
Средняя арифметическая и средняя гармоническая наиболее распространенные виды средней, получивших широкое применение в плановых расчетах, при расчете общей средне из средних групповых, а также при выявлении взаимосвязи между признаками с помощью группировок. Выбор средней арифметической и средней гармоничской определяется характером имеющей в распоряжении исследователя информации.
Средняя квадратическая применяется для расчета среднего квадратического отклонения, являющегося показателем вариации признаков, а также в технике (например, при сооружении трубопроводов).
Средняя геометрическая (простая) используется при вычислении среднего коэффициента роста (темпа) в рядах динамики, если промежутки времени, к которым относятся коэффициенты роста, одинковы. Если средние коэффициенты роста относятся к периодам различной продолжительности, то общий средний коэффициент роста за весь период определяется по формуле средней геометрической взвешенной.

Структурные средние – мода и медиана – в отличие от степенных выступают как конкретные величины, совпадающие с вполне определенными вариантами совокупности. Это делает их незаменимыми при решения ряда практических задач.
Модой называется значение признака, которое наиболее часто встречается в совокупности (в статистическом ряду).
Медианой называется значение признака, которое лежит в середине ранжированного ряда и делит этот ряд на две равные по численности части.
Ранжированный ряд – ряд, расположенный в порядке возрастания или убывания значений признака.
Для определения медианы сначала определяют ее место в ряду, используя формулу
n+1
NMe = -------, где n – число членов ряда.
2
Если ряд состоит из четного числа членов, то за медиану условно принимают среднюю арифметическую из двух срединных значений.
8. Вариационный ряд (ВР) и его изучение. Построение ряда. Виды рядов.
Различия индивидуальных значений признака у единиц совокупности называют вариацией признака. Изучение вариации в переделах однородной группы предполагает использование следующих приемов: построение ВР (ряда распределения); его графическое изображение, исчисление основных характеристик распределения.
Построение ВР сводится к созданию групповой таблицы, построенной по количественному признаку, в сказуемом которой показывается число единиц в каждой группе. Тем самым такая таблица фактически представляет собой совокупность сочетания вариантов и соответствующим им частот. Различие индивидуальных значений признака у единицы совокупности называются вариацией признака.
По характеру вариации значений признака различают: 1) Признаки с прерывным изменением (дискретные); 2) признаки с непрерывным изменением (непрерывные)
Признаки с прерывным изменением могут принимать лишь конечное число определенных значений. Для них применяется построение дискретного ряда. В первой графе ряда указываются конкретные значения каждого индивидуального значения признака, во второй графе – численность единиц с определенным значением признака.
Для признака, имеющего непрерывное изменение, строится интервальный ВР, состоящий также как дискретный ряд, из двух граф (варианты и частоты). При его построении в первой графе отдельные значения признака указываются в интервале «от – до», во второй графе – число единицы, входящих в интервал. Интервалы образуются, как правило, равные и закрытые.
9. Графическое изображение вариационных рядов. Полигон и гистограмма.
Одним из этапов изучения вариационного ряда является его графическое изображение. Дискретный вариационный ряд изображается в виде так называемого полигона, или многоугольника распределения частот, являющегося разновидностью статистических ломаных. Для изображения интервального ряда применяются полигон распределения частот и гистограмма частот.
Строятся графики в прямоугольной системе координат. При построении полигона частот на оси абсцисс в одинаково масштабе откладываются направо в порядке возрастания значения признака (для дискретного характера) или центральные значения интервалов (для интервальных рядов); по оси ординат наносится шкала для выражения величин частот. Из точек на оси абсцисс, соответствующих величине признака, восстанавливаются перпендикуляры высотой, соответствующей частоте; вершины перпендикуляров соединяются отрезками прямой. Крайние точки полученной ломаной соединяются с лежащими на оси абсцисс следующими (меньшими и большими) возможными, но фактически не наблюдающимися значениями признака, частота которых, очевидно, равна 0. Замкнутая с осью абсцисс ломаная линия представляет полигон распределения частот.
Для построения гистограммы по оси абсцисс откладываются величины интервалов, а частоты изображаются прямоугольниками, построенными на интервалах с высотой в масштабе оси ординат.
10. Основные характеристики вариационных рядов. Показатели центра распределения.
Исчисление основных характеристик распределения происходит по 3 группам показателей: 1. центра распределения; 2. степени вариации; 3. формы распределения.
Для характеристики центра распределения в вариационном ряду применяются: средняя арифметическая, медиана, мода.
Средняя арифметическая для дискретного ряда распределения исчисляется по формуле:
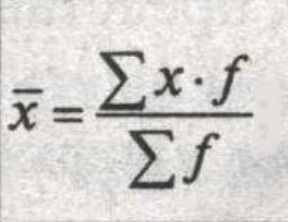
где x - варианты значений признака; f- частота повторения данного варианта.
Средняя арифметическая для интервального ряда распределения:
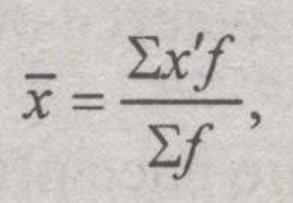
где х' — середина соответствующего интервала значения признака; вычисляется как средняя из значений границ интервала.
Структурные средние – мода и медиана – в отличие от степенных выступают как конкретные величины, совпадающие с вполне определенными вариантами совокупности. Это делает их незаменимыми при решения ряда практических задач.
Модой (Мо) называется значение признака, которое наиболее часто встречается в совокупности (в статистическом ряду).
Медианой (Ме) называется значение признака, которое лежит в середине ранжированного ряда и делит этот ряд на две равные по численности части.
Ранжированный ряд – ряд, расположенный в порядке возрастания или убывания значений признака.
11. Показатели вариации ряда распределения. Дисперсия; коэффициент вариации.
Показателями степени вариации бывают абсолютные: размах колебаний, среднее линейное отклонение, среднее квадратическое отклонение, дисперсия; и относительными: коэффициент вариации.
Дисперсия исчисляет так:

Наиболее часто применяется коэффициент вариации. Его применяют не только для сравнительной оценки вариации, но и для характеристики однородности совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 33% (для распределений, близких к нормальному)