Geum.ru

Лекция Кинематика атмосферных движений. 1

Вид материалаЛекция

Содержание


Кинематика скалярных полей.
D(x,y). Если этого не происходит, центр будет существовать. Если окажется, что D(x,y=0
Подобный материал:



- -

Лекция 3. Кинематика атмосферных движений. 1


Атмосфера как сплошная среда с точки зрения динамической метеорологии описывается набором полей физических величин, таких, например, как плотность воздуха, его температура, скорость ветра, сила тяжести, сила внутреннего трения. Эти физические величины математически представляют собой различные объекты: плотность и температура – это скалярные величины. Скорость ветра и сила тяжести – это векторные величины. Сила внутреннего трения – это матричная величина, причем особого вида, который называется тензором. Исследование свойств атмосферы требует умения производить над любым из этих объектов операции математического анализа – дифференцирование и интегрирование. Выполнение этих операций изучается в курсе высшей математики и гидромеханики, но некоторые особенно важные для динамической метеорологии понятия рекомендуется повторить с помощью приложения 3, где. приведена сводка операций над векторами, полезных для получения важнейших формул динамической метеорологии. Применение векторной записи позволяет существенно сократить математическую запись этих формул.

Кинематика скалярных полей.


Как задать нужное скалярное поле. Скалярное поле f математически нельзя задать в неявной форме потому, что такая запись допускает неоднозначность функции в точке, что не соответствует определению понятия поля. Поэтому любая скалярная метеорологическая характеристика f может быть записана в виде явной функции от пространственных координат и времени 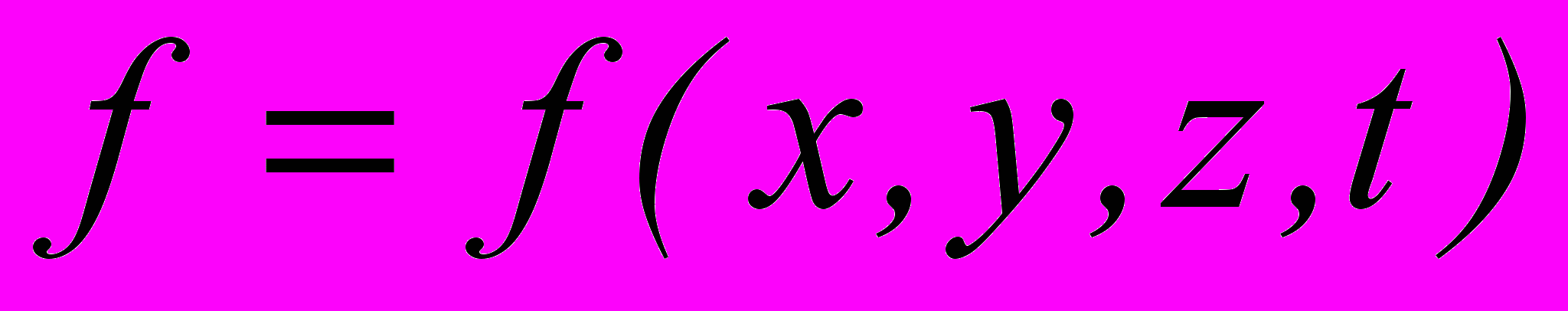. Такая запись означает, что в данной точке пространства r(x,y,z) в момент времени t существует только одно значение характеристики f. Следует помнить, что поверхность одинаковых значений функции f (эквискалярная поверхность) задается уравнением 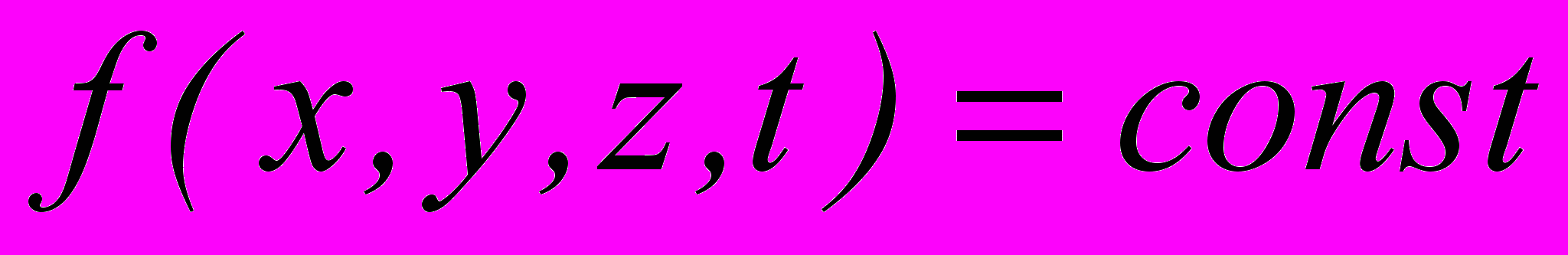, которое может связывать координаты точки неявной зависимостью.

Все метеорологические характеристики зависят от высоты сильнее, чем от горизонтальных координат. Поэтому принято изображать их на картах, отнесенных к одной и той же высоте z = const . Поэтому метеорологические карты какой-либо метеорологической характеристики можно считать графическим заданием скалярной функции от горизонтальных координат и времени .

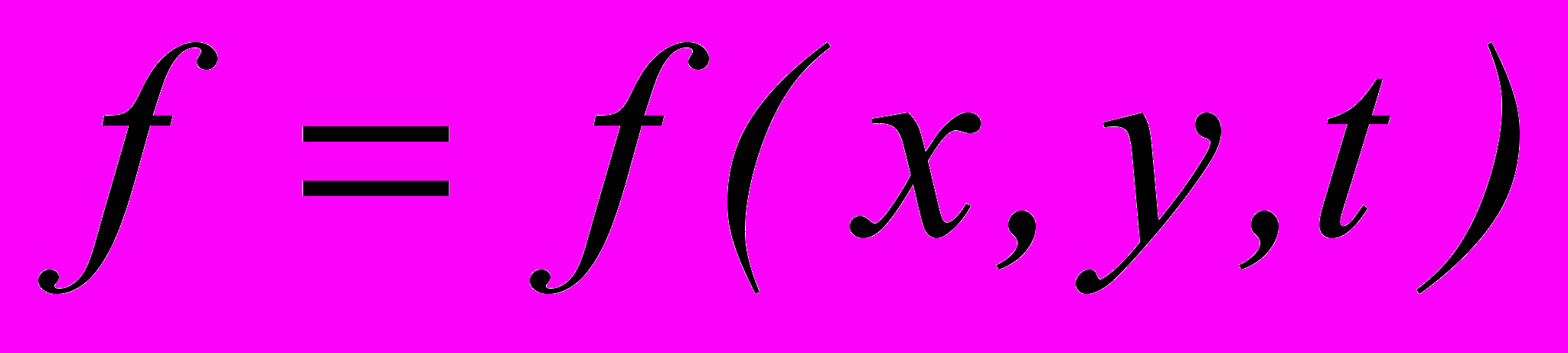Изолиния – это множество точек, на котором значение функции одинаково, поэтому уравнение изолинии в некоторый момент t=t1 имеет вид 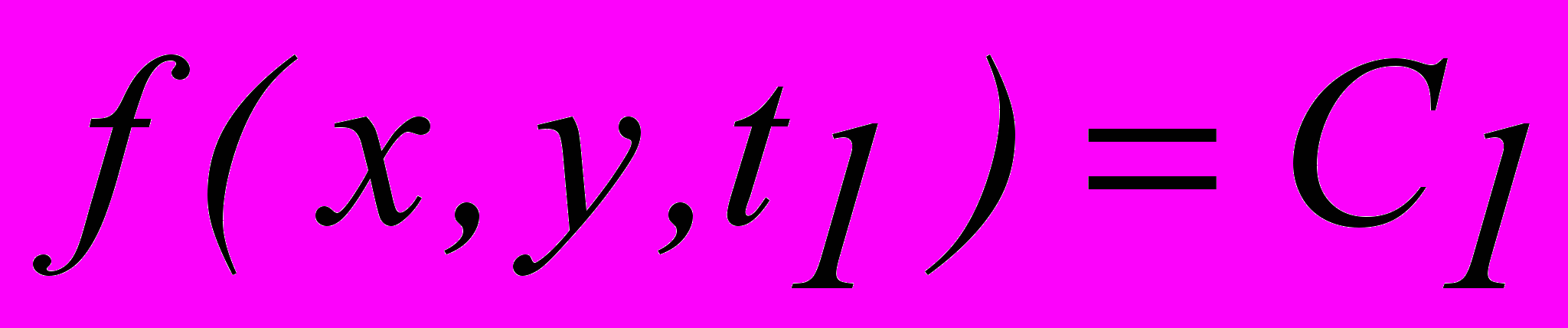. В момент t=t2 нестационарная характеристика будет иметь другое значение 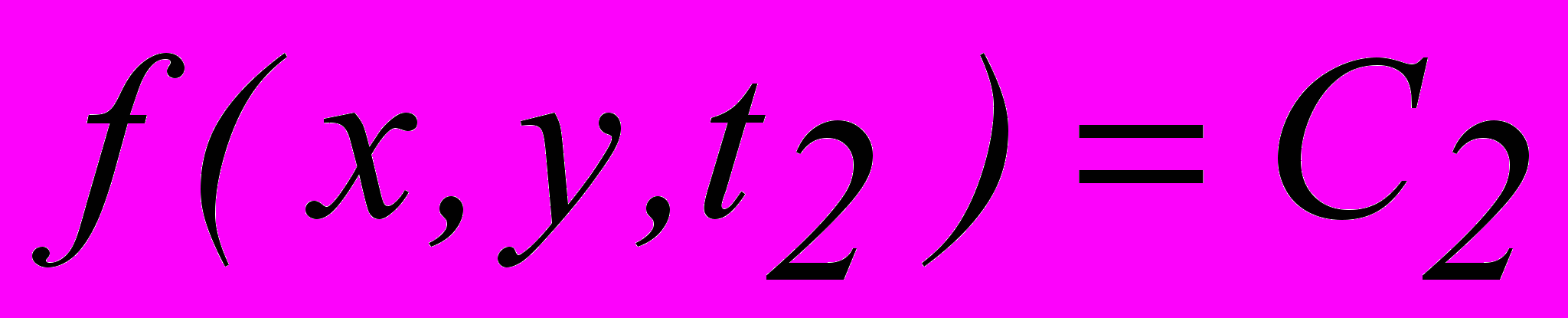, то есть через точку (x,y) пройдет другая изолиния. Если необходимо следить за точками, принадлежащими первой изолинии, то ее уравнение будет иметь вид 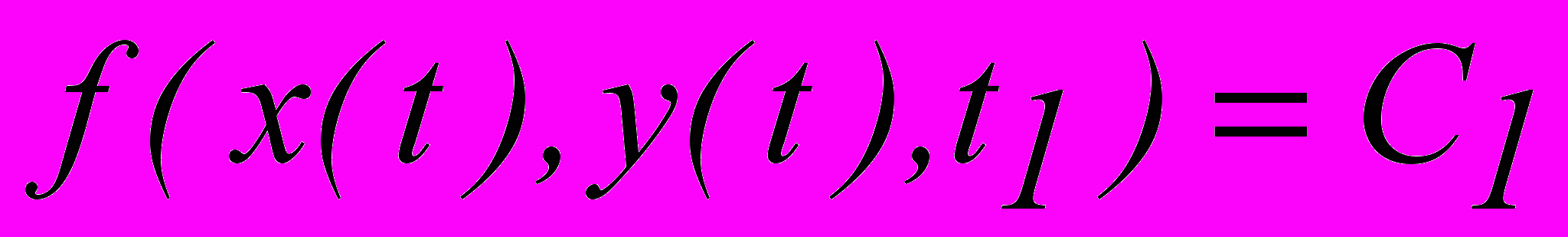. Для пояснения можно решить задачу 1.

Пусть формула, определяющая скалярное поле с круговыми изолиниями имеет вид 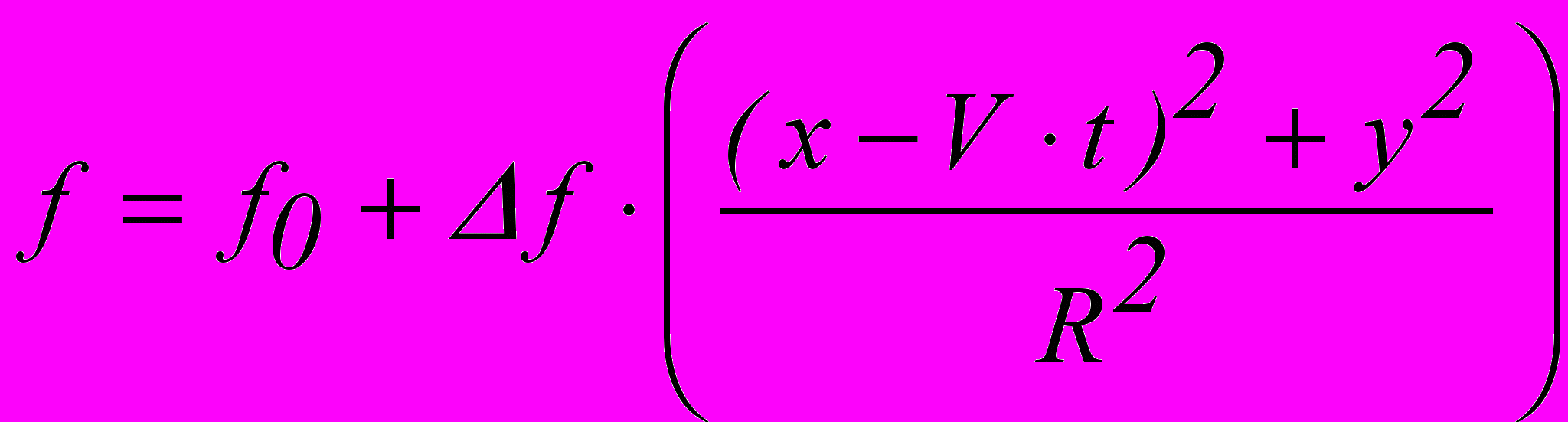, причем параметры f0, Δf , R, V –имеют постоянные значения. Записать уравнения изолиний, проходящих через точку x1,y1 в моменты t1 и t2 соответственно. Оценить, как измениться первая из этих изолиний к моменту t2.


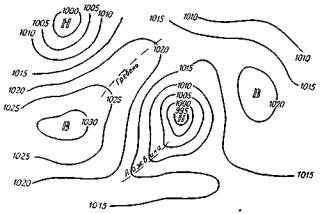Изолинии скалярного поля приземного (z=0) давления P(x,y,t) называются изобарами, а само это поле имеет структуру изобар, представленную на рис.3.1. Важно помнить, что реальные поля давления сильно не отличаются от среднего климатического значения P0 =1013 гПа. Элементами структуры скалярного поля такого вида являются центры ΔPk, , каждый из которых может быть представлен виде множества близких к эллиптическим изобар. Таким образом, почти любое поле давление в ограниченном районе можно описать формулами

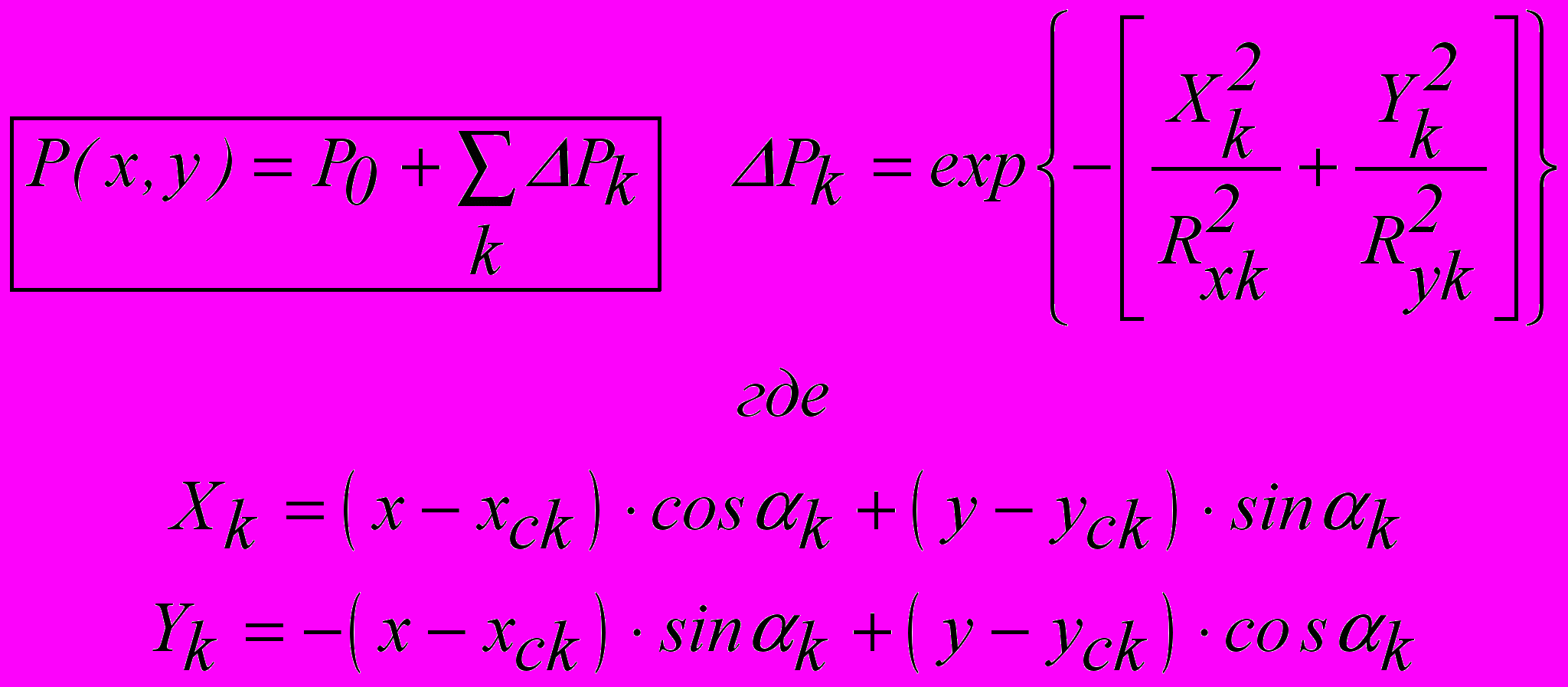(3.1)

В них обозначены: x , y – координаты точки, для которой производится расчет значения давления (они меняются от точки к точке); P0 –одинаковое для всех точек значение среднего давления; ΔPk – разность давления в центре с номером k и среднего давления P0 (положительна, если центр с номером k является антициклоном, и отрицательна для циклона); xck , yck – координаты центра с номером k ; αk –угол наклона главной оси эллиптичности центра с номером k относительно оси OX исходной системы координат.

Полезно отметить, что использованные в (3.1) отклонения поля давления ΔPk от климатического, если их прологарифмировать, будут параболоидами. Однако использовать полиномиальные функции для описания метеорологических полей нельзя, так как они неограниченны.

С помощью формулы (3.1) можно построить сложные метеорологические поля. Для достижения полной ясности рекомендуется решить задачу 2. Построить поле давления в области, где х меняется от -25 до 25 (шаг по х принять равным 1), у меняется от -25 до 25 (шаг по у принять равным 1). Среднее давление P0 принять равным 1013 гПа. Предположить, что отклонения от среднего давления ΔPk формируются двумя центрами (k=1,2), причем центр 1 является антициклоном с давлением в центре 1030 гПа, центр 2 является циклоном с давлением в центре 970 гПа. Координаты центров (хс1=-18, ус1=18); (хс2=8, ус1=-10). Угол наклона главной оси эллиптичности для антициклона α1 = 0.7, для циклона α2 = 2 (значения в радианах). Полудиаметры осей: для антициклона Rx1= 12.2, Ry1= 6.5, для циклона Rx2= 6.2, Ry2= 5.0.

Характеристики скалярного поля. Одним из важнейших векторов при описании скалярного поля f является градиент этой скалярной величины (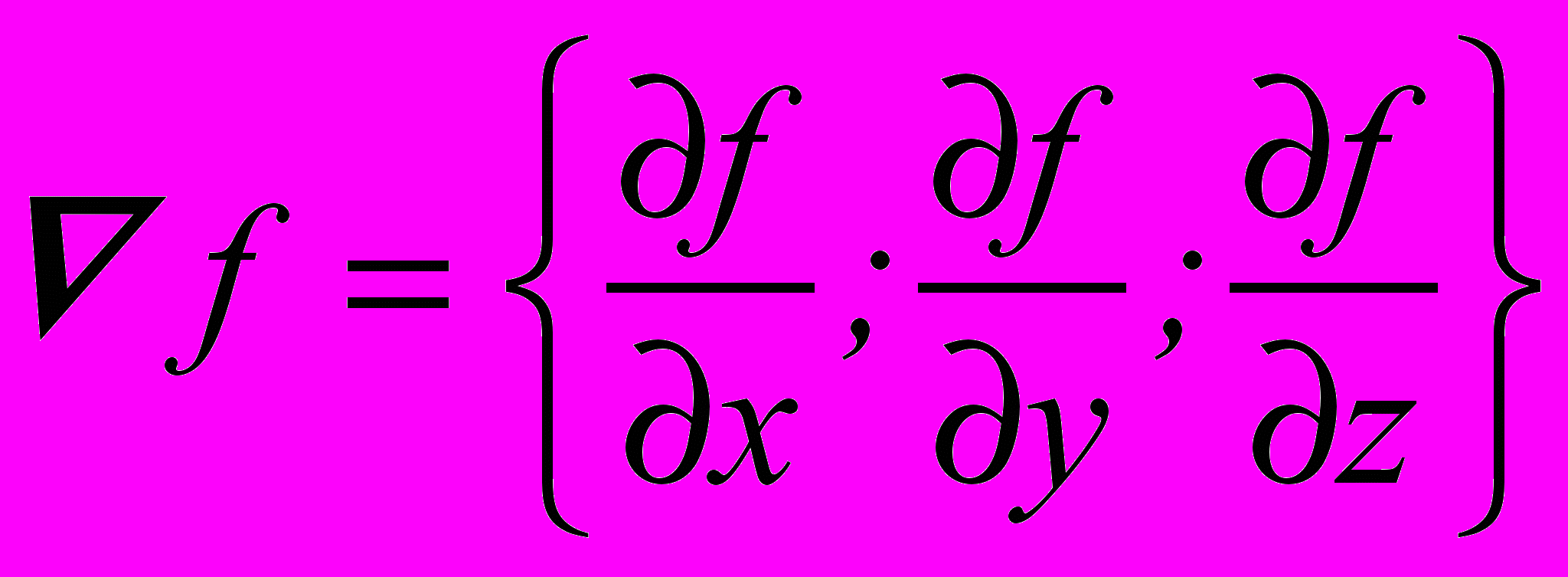)в заданной точке. Градиент – это производная по направлению наиболее быстрого изменения скалярной величины. Через него можно вычислить производную в любом заданном направлении 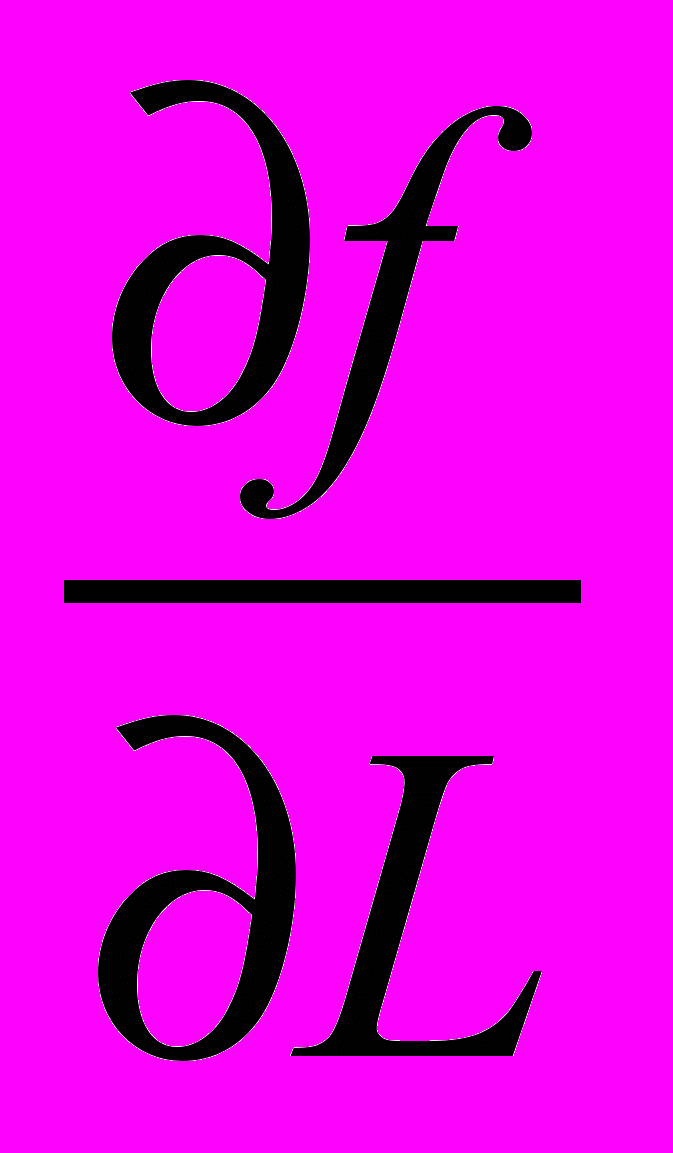путем применения соотношения

(3.2)

В нем L – вектор, компонентами которого являются косинусы углов между направляющей прямой и осями координат (OX, OY, OZ).

Кроме градиента, часто бывает необходимо вычислить лапласиан и кривизну K изолинии или радиус кривизны изолинии Rk в заданной точке. Для этого можно воспользоваться формулами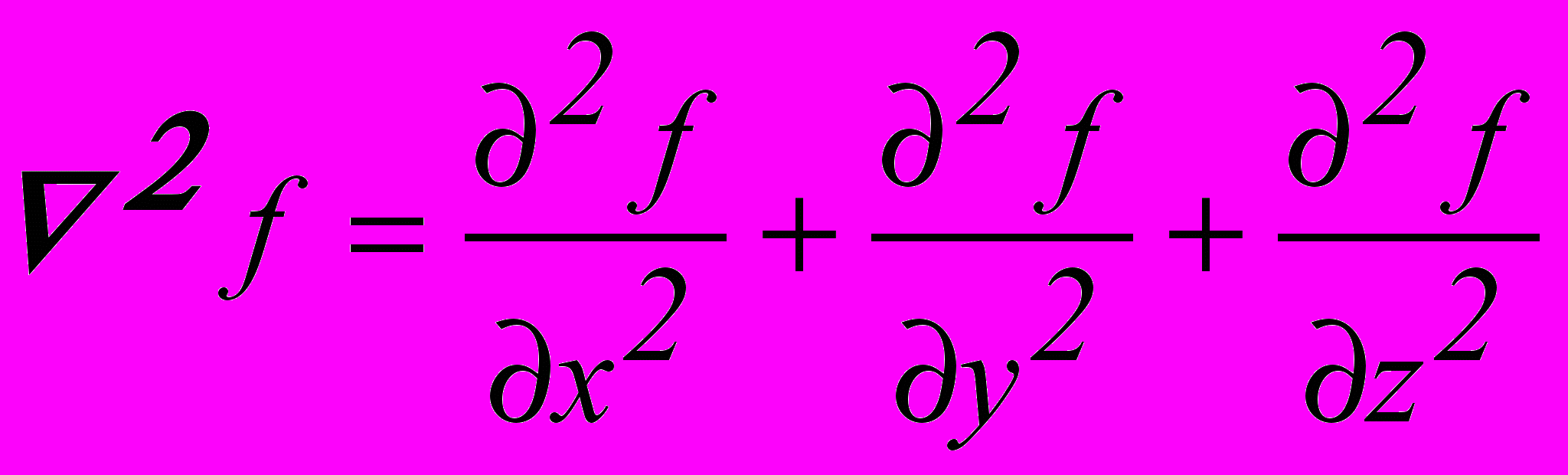

(3.3)

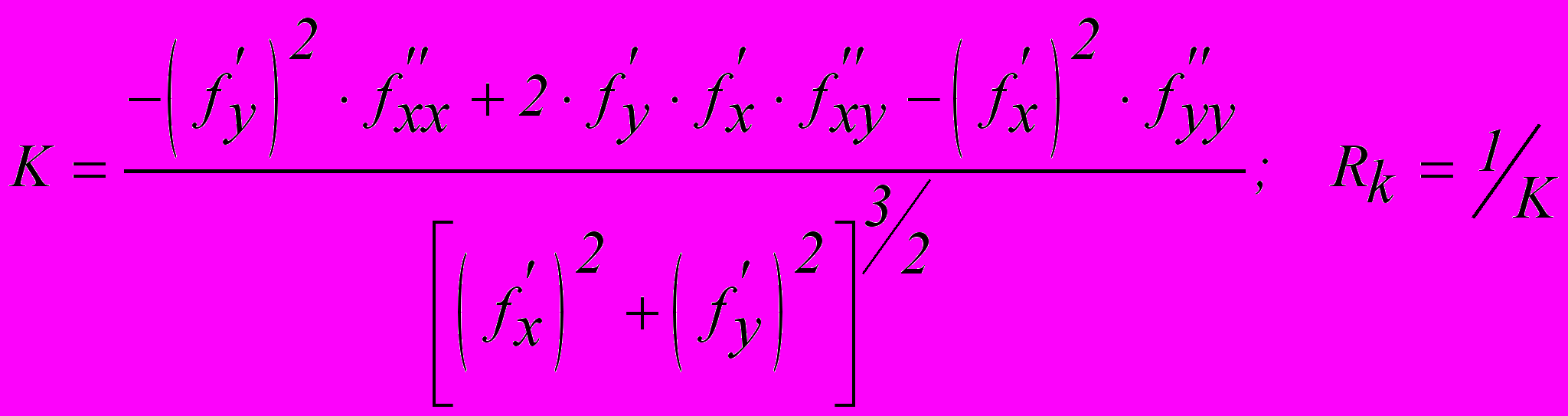(3.4)

Положительное значение лапласиана или кривизны изолинии скалярного поля в точке показывает, что в этой точке форма поля вогнута. Отрицательное значение указывает на выпуклую форму поля.

Значение градиента обращается в нуль в точках экстремума скалярного поля. Это значит, например, что экстремальные значения на метеорологических картах располагаются там, где выполняются условия

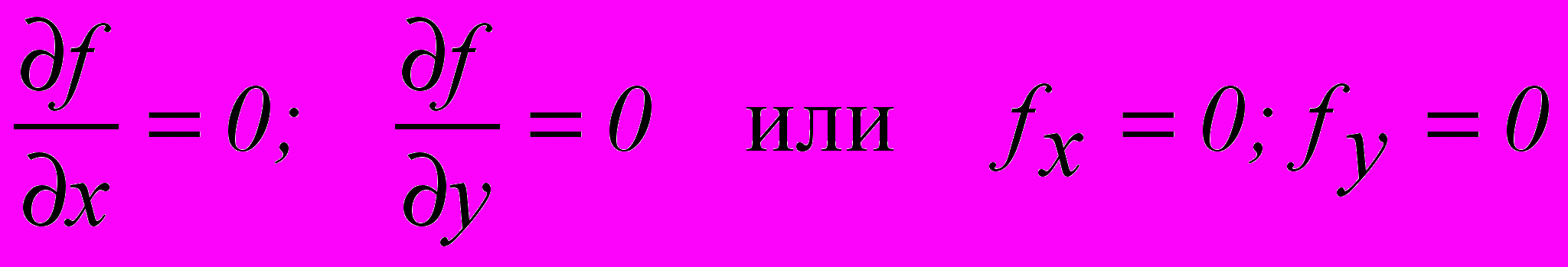(3.5)

Точки экстремума определяют структуру скалярного поля. Для изучения условий их существования полезно получить формулы скорости их перемещения. В движущейся точке экстремума уравнения (3.5) выполняются все время. Поэтому, находя индивидуальные производные от этих уравнений, получим

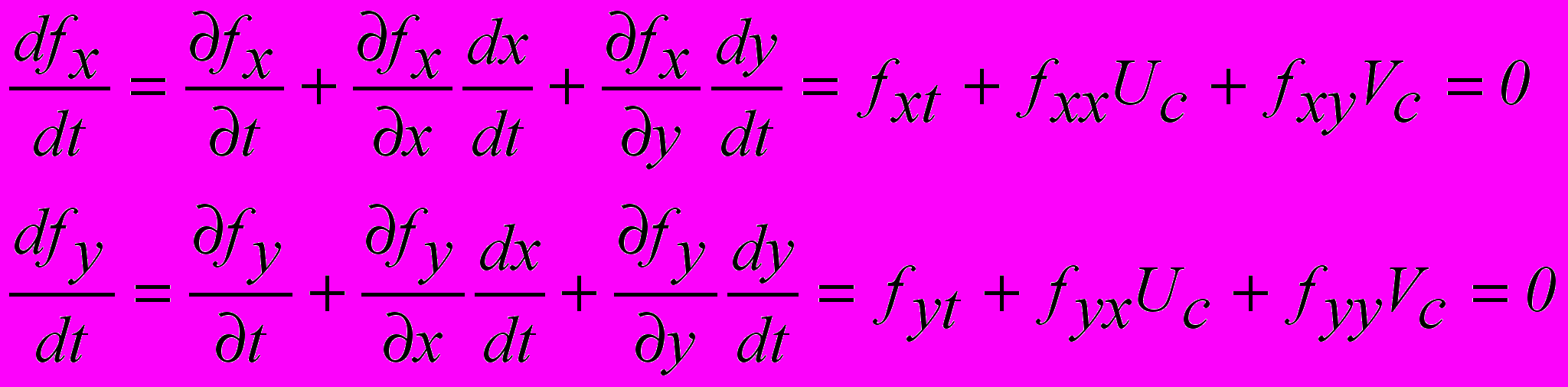(3.6)

В этих уравнениях величины 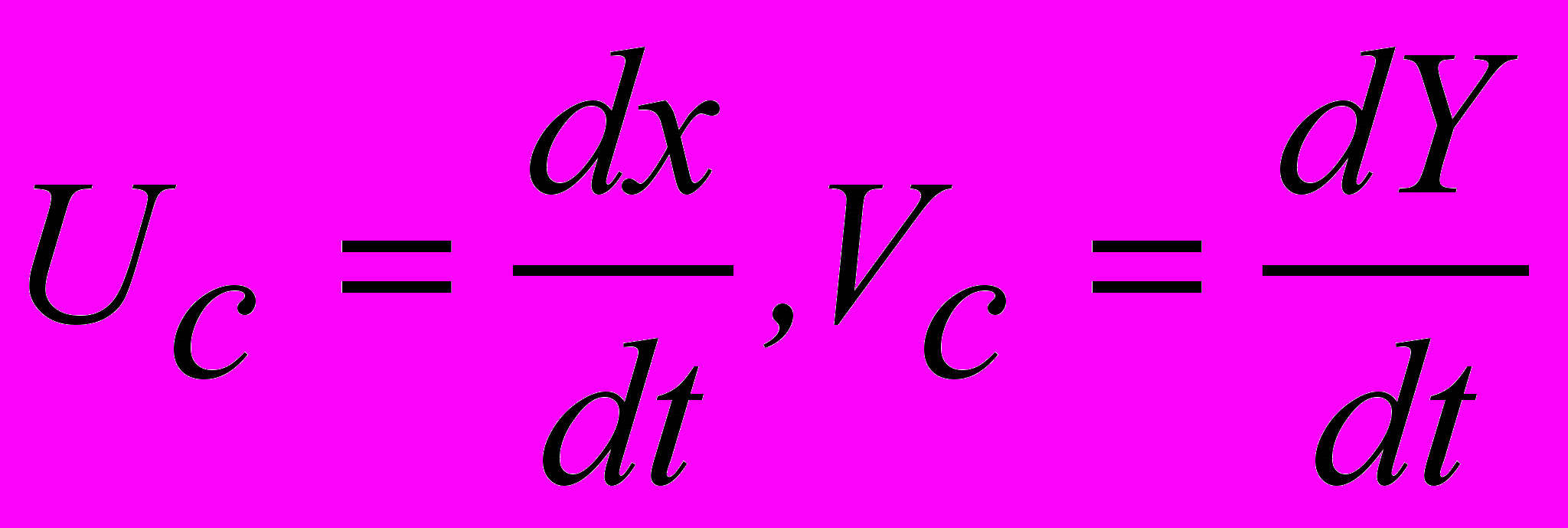являются составляющими вектора скорости перемещения центра, а представляют собой вторые частные производные скалярного поля, вычисленные в точке экстремума и должны считаться известными, так как поле f(x,y,t) задано. Решая уравнения (3.6) относительно неизвестных 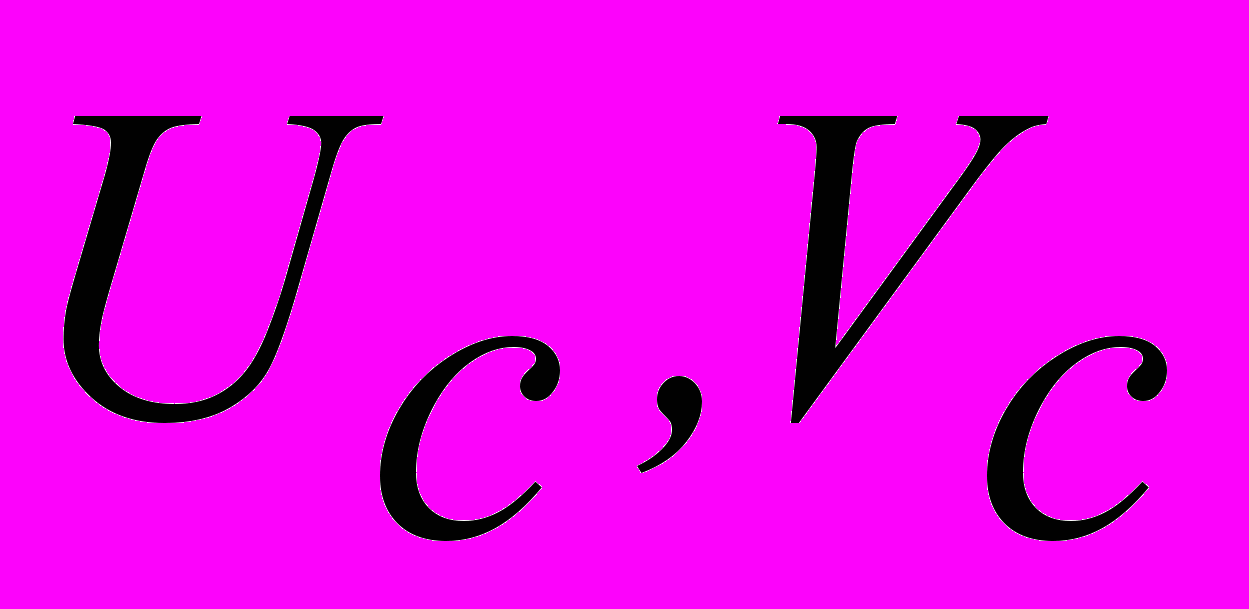, получим формулы для определения скорости перемещения изучаемого центра

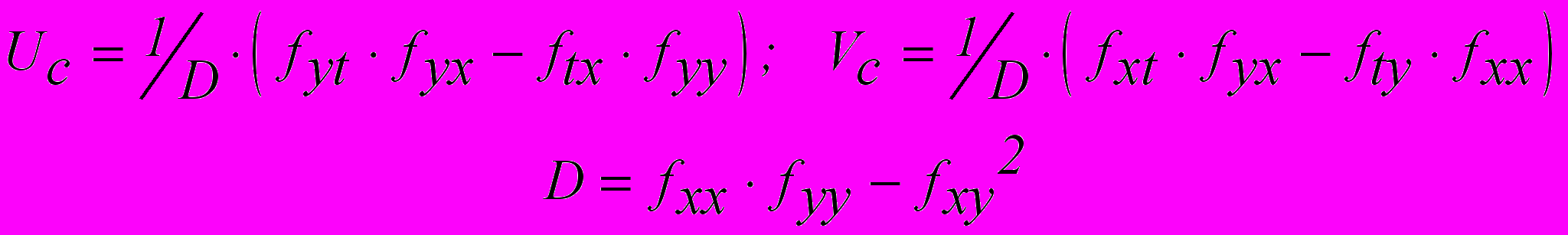(3.7)

Эти формулы показывают, что перемещение центра зависит от того, обращается ли в данной точке в нуль определитель D(x,y). Если этого не происходит, центр будет существовать. Если окажется, что D(x,y=0, то либо имевшийся центр разрушится, либо возникнет новый, ранее не существовавший центр. Это значит, что изменится структура рассматриваемого поля.

Значение функции D(x,y) еще и в том, что при отрицательных ее значениях в скалярном поле не могут существовать центры, и оно может иметь только характер седловины. Таким образом нулевая изолиния функция D(x,y) разбивает скалярное поле на области. Там, где D(x,y)>0 могут существовать центры, там, где D(x,y<0) проходят области перевалов. На самой линии границы D(x,y=0) центры возникают или исчезают, если эту линию пересекают одновременно линии fx (x,y,t)=0 и fy (x,y,t)=0.

В метеорологических расчетах часто требуется определить направление нормали к эквискалярной поверхности 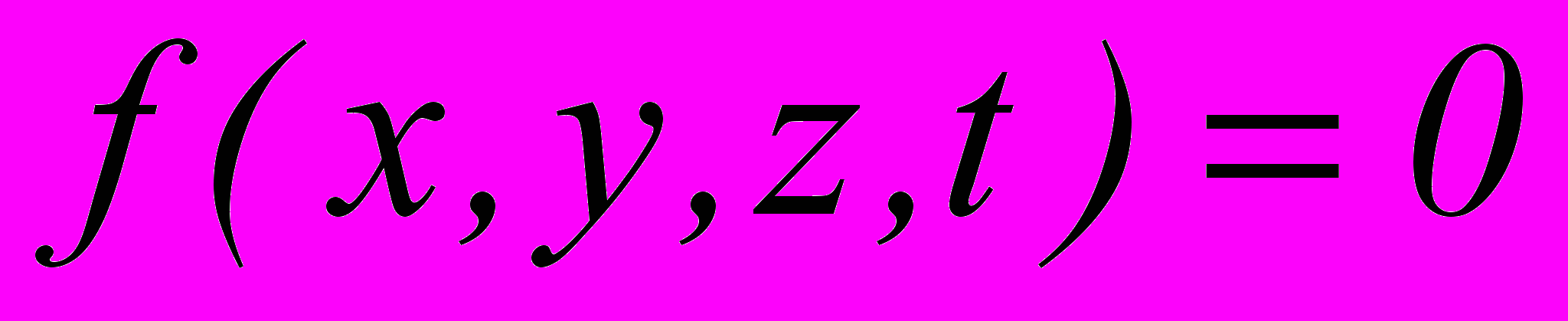. Это можно сделать на основе определения единичного вектора нормали и градиента скалярного поля в заданной точке по формулам:

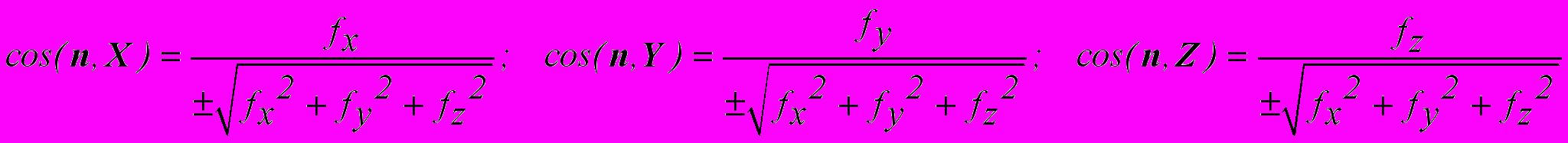(3.8)

Знак плюс соответствует внешнему направлению вектора нормали n к поверхности f , (X,Y,Z) – обозначения нормалей к соответствующим координатным поверхностям. (Нормаль Z, например, определяет координатную плоскость XOY !).

Часто требуется оценить угол наклона касательной плоскости к стационарной эквискалярной поверхности 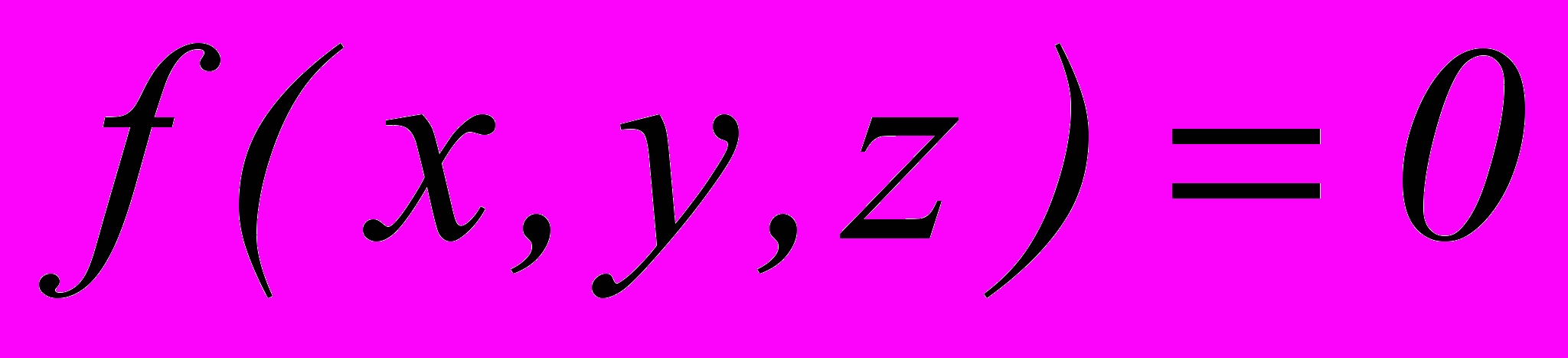. Это можно сделать, записав уравнение касательной плоскости к заданной эквискалярной поверхности:

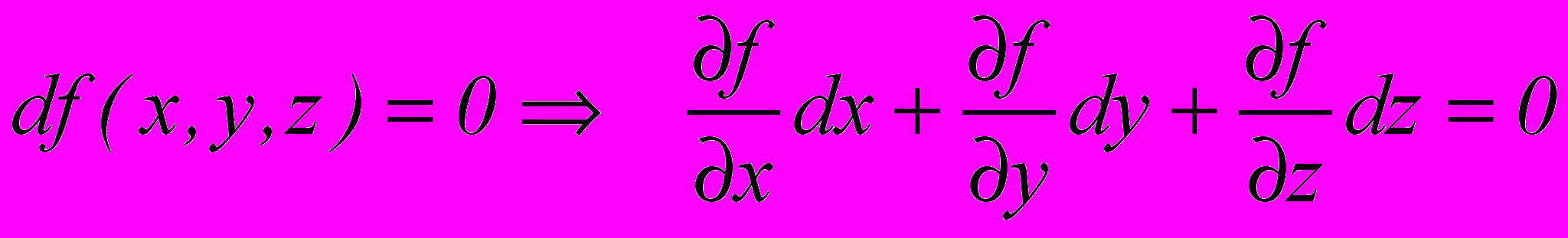(3.9)

Если направить ось абсцисс по касательной к изолинии, то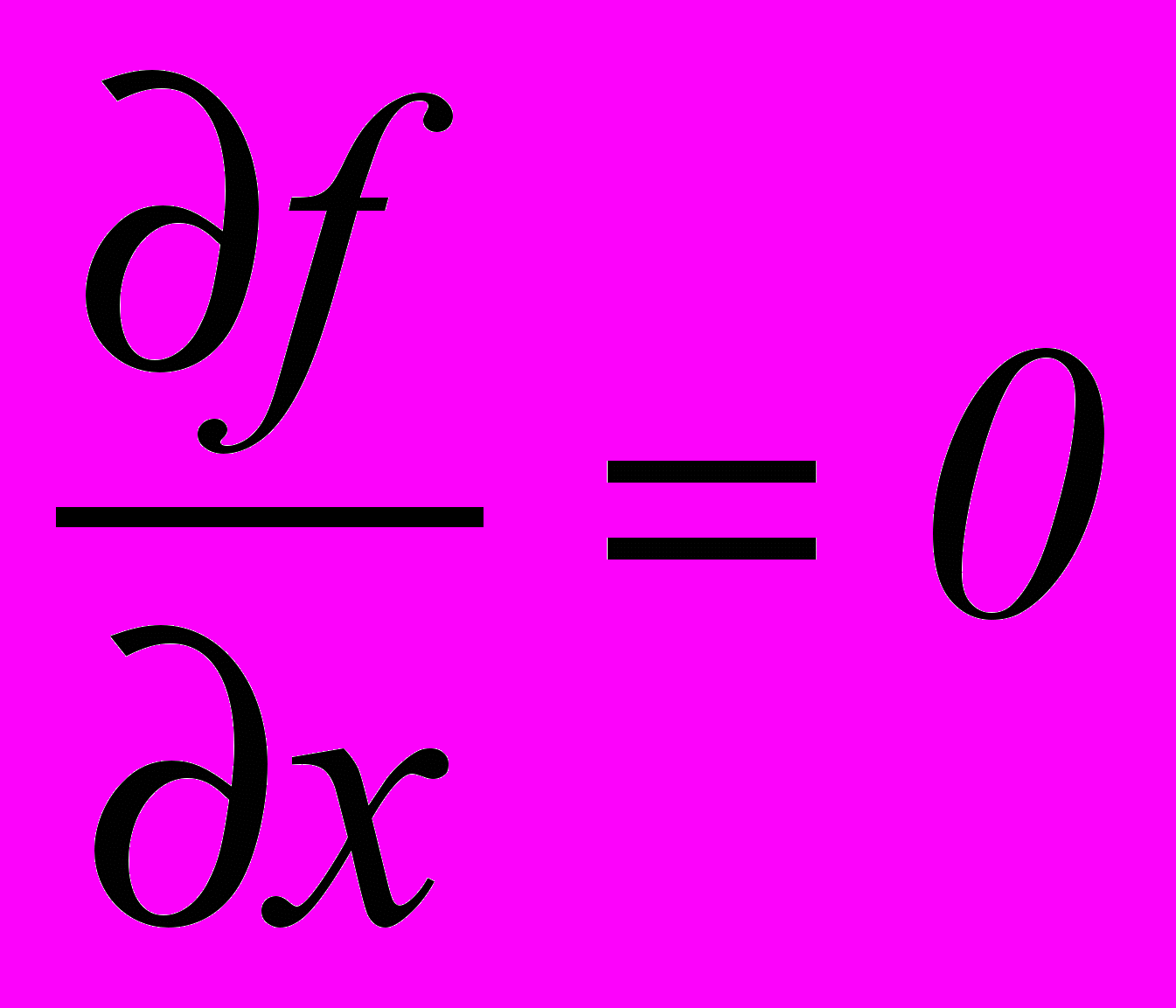. Отсюда следует выражение для тангенса угла наклона α касательной плоскости по нормали (y) к изолинии:

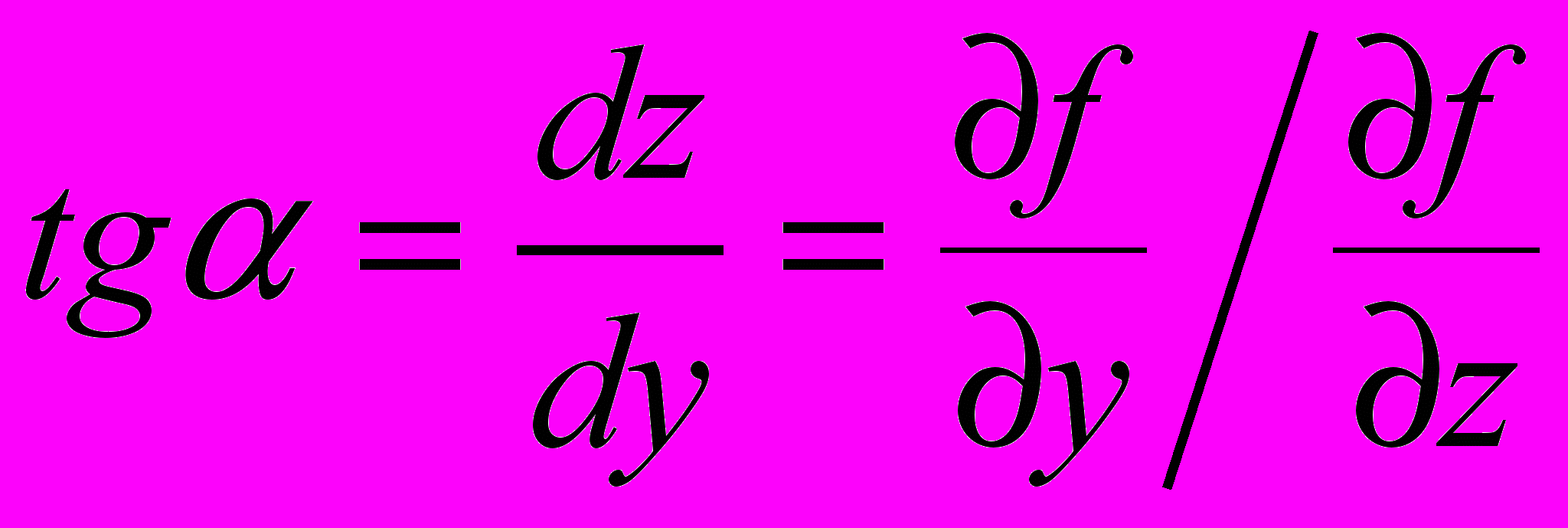(3.10)

Полезно иметь в виду, что метеорологические скалярные поля гораздо сильнее изменяются по вертикали, чем по горизонтали, поэтому угла наклона их эквискалярных поверхностей очень малы. Например, для поля давления характерное значение горизонтального градиента составляет около 1 гПа/100 км, а барическая ступень (изменение высоты, необходимое для изменения давления на 1 гПа), составляет примерно 10 метров. Поэтому угол наклона изобарических поверхностей к горизонту приблизительно равен 10-4 радиана или около 3 угловых минут.

Добавить кинематику ПОВЕРХНОСТЕЙ РАЗРЫВА и ИНВЕРСИИ