Задачи повышенной сложности по дисциплине «начертательная геометрия» Методические рекомендации для самостоятельной работы студентов

Вид материала

Методические рекомендации

Содержание 1 Геометрические места точек Задача №16 Задача №17 Задача №19 Решение задачи №14 Решение задачи №19 Левина надежда сергеевна светлова

Подобный материал:

• Ло» в учебный процесс по дисциплине «Графика» внедрена рабочая тетрадь по разделу «Начертательная, 34.69kb.
• Методика рейтингового контроля знаний студентов специальности «Промышленное и гражданское, 58.63kb.
• Методические рекомендации для самостоятельной работы студентов по дисциплине «Социальная, 367.42kb.
• Учебно-методический комплекс по дисциплине опд. Ф. 01. 01 «Начертательная геометрия., 480.75kb.
• Методические рекомендации по организации самостоятельной работы, 458.16kb.
• Данное пособие может быть использовано в качестве рабочей тетради. Печатается в соответствии, 383.85kb.
• Методические рекомендации для организации самостоятельной работы студентов учебной, 419.88kb.
• Учебно-методический комплекс по дисциплине «Начертательная геометрия. Инженерная графика», 977.22kb.
• Методические указания по выполнению самостоятельной работы студентов Павлодар, 142.95kb.
• Методические рекомендации к выполнению самостоятельной работы для студентов, обучающихся, 597.82kb.

Федеральное агентство по образованию Российской Федерации


Бийский технологический институт (филиал)

государственного образовательного учреждения высшего профессионального образования «Алтайский государственный технический университет

имени И.И. Ползунова»


Э.А. Алексеева, Н.С. Левина, О.Р. Светлова, Г.Д. Леонова


ЗАДАЧИ ПОВЫШЕННОЙ СЛОЖНОСТИ

ПО ДИСЦИПЛИНЕ «НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ»


Методические рекомендации для самостоятельной работы студентов

механических специальностей


Бийск 2010

УДК 744.4 (076)

С17


Рецензент: Климонова Н.М., кафедра «Технической механики»


Алексеева, Э.А. Задачи повышенной сложности по дисциплине «Начертательная геометрия»: методические рекомендации для самостоятельной работы студентов механических специальностей / Н.С. Левина, О.Р. Светлова, Г.Д. Леонова

Алт. гос. техн. ун-т, БТИ. – Бийск:

Изд-во Алт. гос. техн. ун-та, 2010. – 38 с.


Данные методические рекомендации предназначены для индивидуальной работы студентов, углубленно изучающих курс начертательной геометрии.


УДК 744.4 (076)

С17


Рассмотрены и рекомендованы к изданию

на заседании кафедры «Техническая графика».

Протокол №63 от 20 сентября 2010 г.


 Э.А. Алексеева, Н.С. Левина, О.Р. Светлова, Г.Д. Леонова, 2010

БТИ АлтГТУ, 2010

СОДЕРЖАНИЕ

ВВЕДЕНИЕ	4
1 ГЕОМЕТРИЧЕСКИЕ МЕСТА ТОЧЕК	4
2 УСЛОВИЯ ЗАДАЧ	5
3 РЕШЕНИЯ ЗАДАЧ	17
СПИСОК ЛИТЕРАТУРЫ	37

ВВЕДЕНИЕ


Данный сборник задач соответствует программе курса начертательной геометрии для машиностроительных, механико-технологических специальностей. Однако ограничение курса начертательной геометрии в часах и его односеместровое прохождение обусловливают и программное ограничение круга рассматриваемых на занятиях вопросов.

Особенностью данных рекомендаций является повышенный уровень сложности, представленных в нем задач, это позволяет адресовать его для индивидуальной работы студентам, претендующим на высокие значения баллов модульно-рейтинговой системы, а также для подготовки к олимпиадам по начертательной геометрии.

В первой части методических рекомендаций приведены правила нахождения геометрических мест (множеств точек), используемые при решении многих из приведенных во второй части сборника задач.

Каждая задача решается сначала в пространстве, чтобы представить форму и расположение геометрических элементов и установить последовательный порядок построений, при помощи которых находятся искомые элементы задачи. Только после этого можно переходить к графическому решению.

В третьей части методических рекомендаций приведены ответы к задачам в текстовой и графической форме, а также указания к решению некоторых из них.


1 ГЕОМЕТРИЧЕСКИЕ МЕСТА ТОЧЕК


1. Геометрическим местом точек (ГМТ), равноудаленных от заданной точки на расстоянии l, является сфера радиусом l.

2. ГМТ, равноудаленных от двух заданных точек на расстоянии l, является плоскость, перпендикулярная отрезку и проходящая через его середину.

3. ГМТ, равноудаленных от трех заданных точек на расстоянии l, является прямая, проходящая из центра описанной окружности и перпендикулярная плоскости, заданной этими точками.

4. ГМТ, равноудаленных от заданной прямой на расстоянии l, является цилиндр радиусом l.

5. ГМТ, равноудаленных от двух пересекающихся прямых на расстоянии l, является биссекторная плоскость плоского угла.

6. ГМТ, равноудаленных от двух параллельных прямых, является плоскость, перпендикулярная отрезку, которым измеряется расстояние между прямыми, и проходящая через его середину.

7. ГМТ прямых, проходящих через данную точку (вершину конуса) и наклоненных к данной плоскости под углом , является поверхность конуса вращения, образующие которого наклонены к основанию конуса под углом .

8. ГМТ прямых, проходящих через точку А и удаленных от другой точки В на заданное расстояние l, является конус с вершиной в точке А, поверхность которого касается сферы с центром в точке В радиусом l.


2 УСЛОВИЯ ЗАДАЧ


Задача №1


Построить проекции прямого кругового конуса, ось которого лежит на прямой SM, а точка А принадлежит окружности его основания.




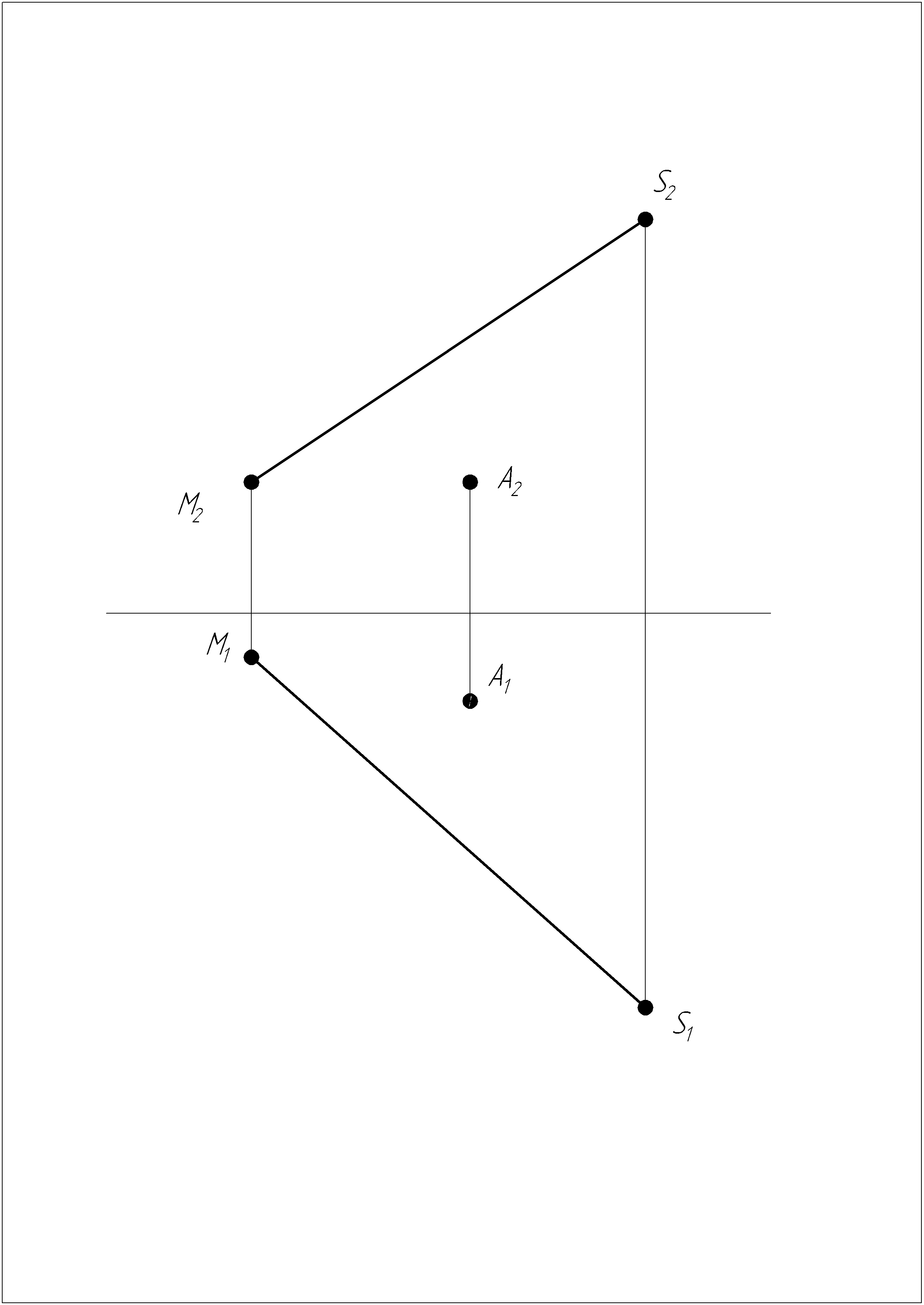
Задача №2


Найти на внешней прямой АВ точку, равноудаленную от фронтали f и горизонтали h плоскости Р.




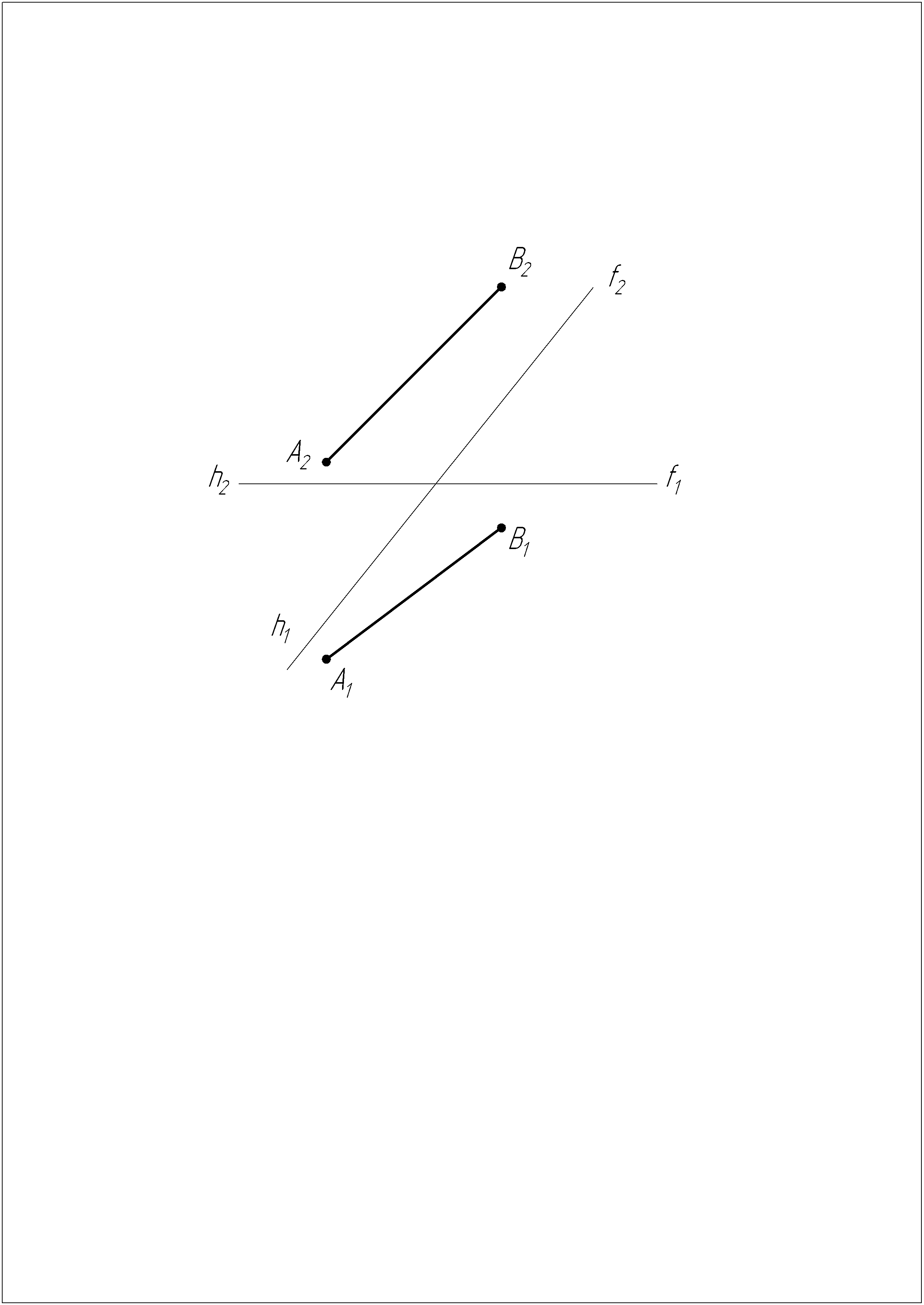
Задача №3


Построить проекции конуса вращения с вершиной в данной точке А и радиусом основания, равным высоте конуса, если основание его лежит в плоскости 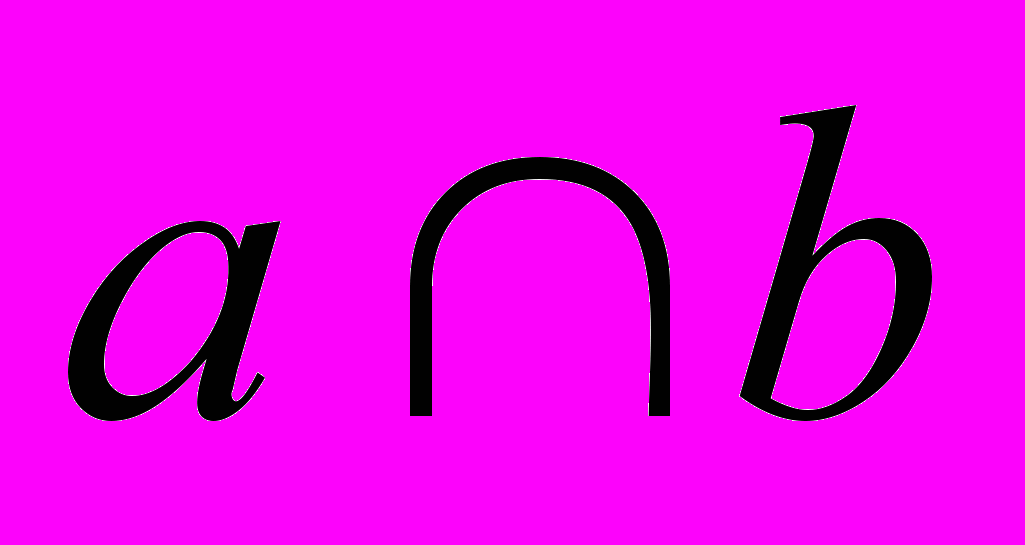 () общего положения.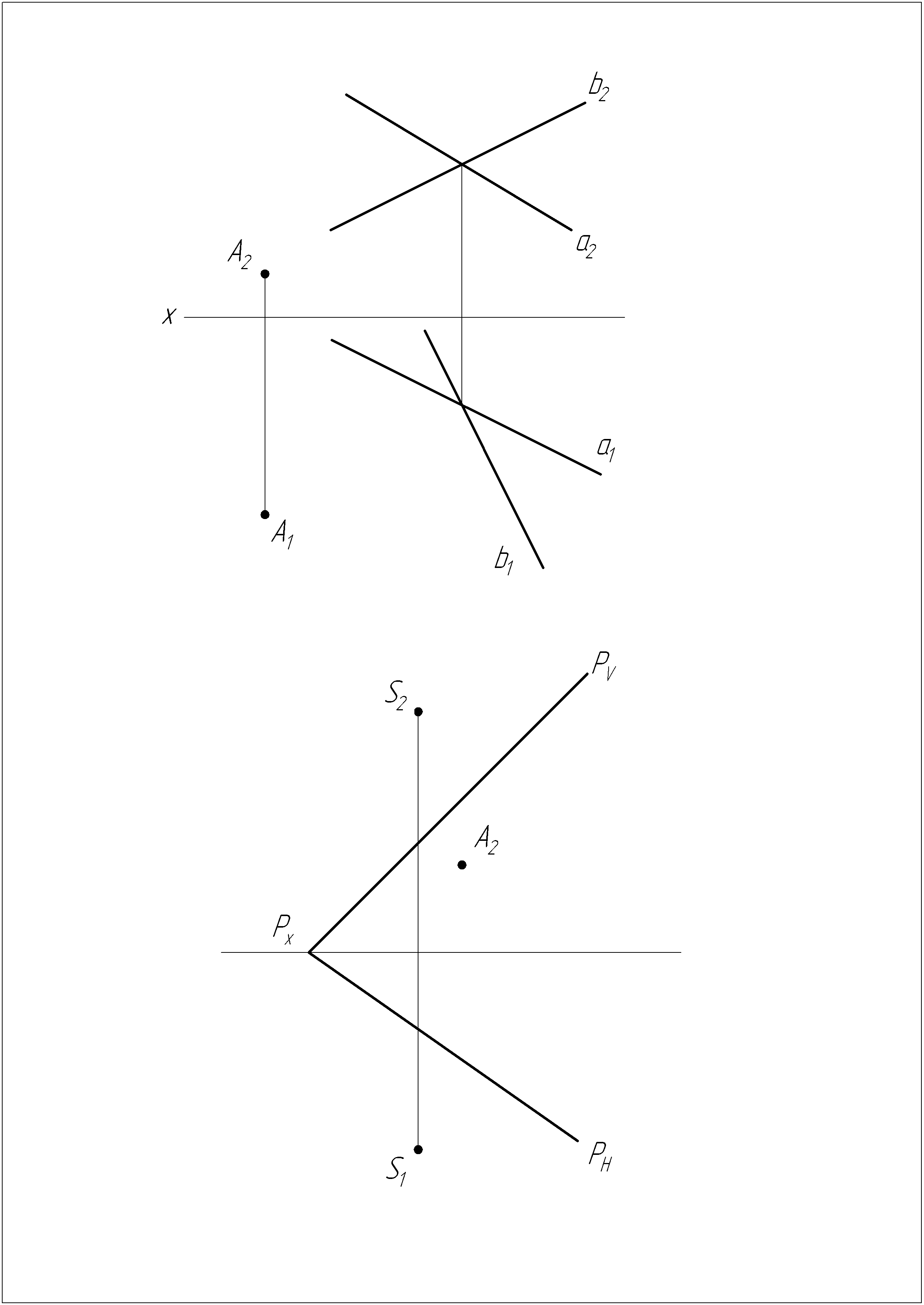




Задача №4


Построить на плоскости ABC точку, отстоящую от прямых l и AB на расстоянии 20 мм и 15 мм соответственно.





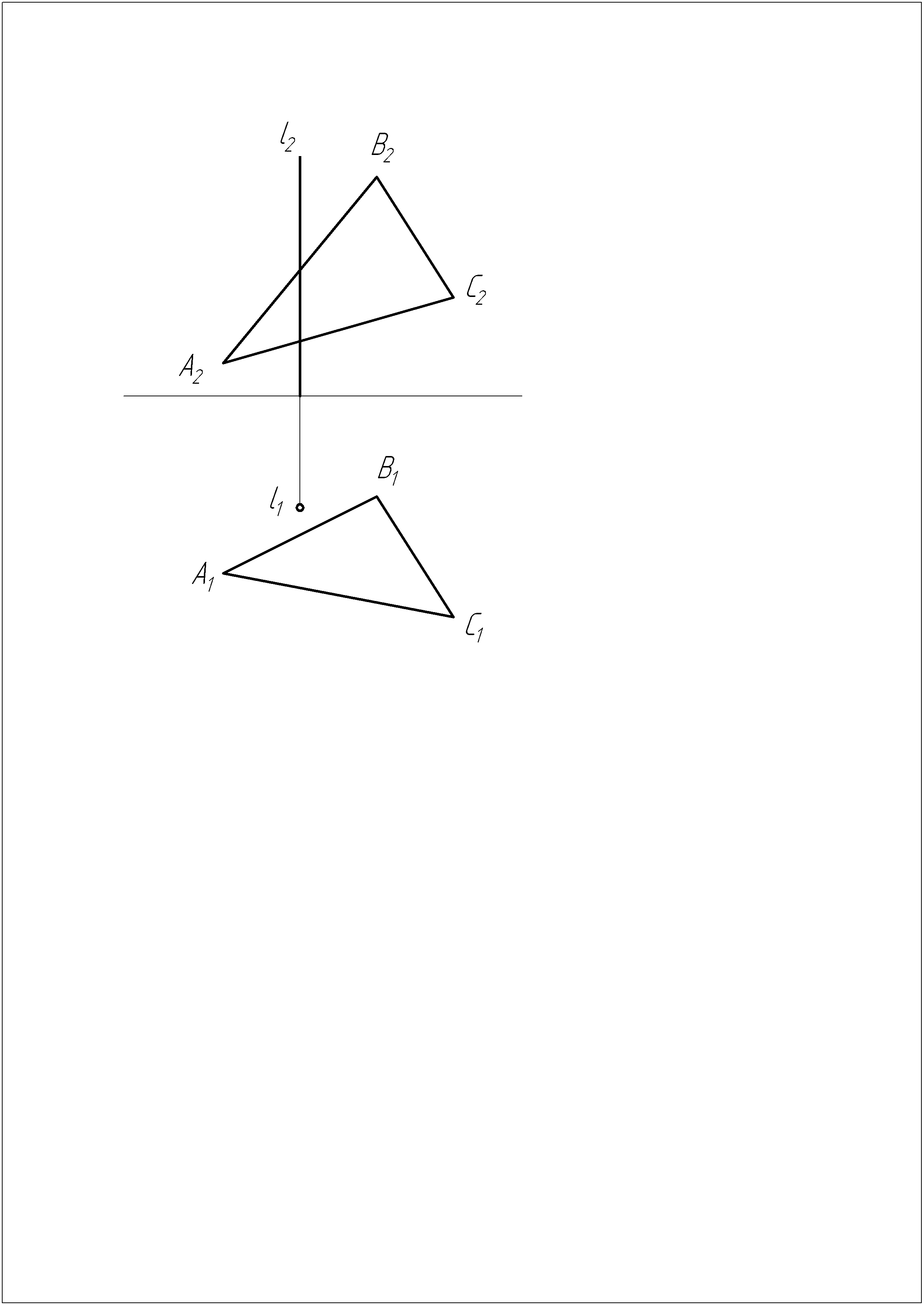
Задача №5


Найти на плоскости Р (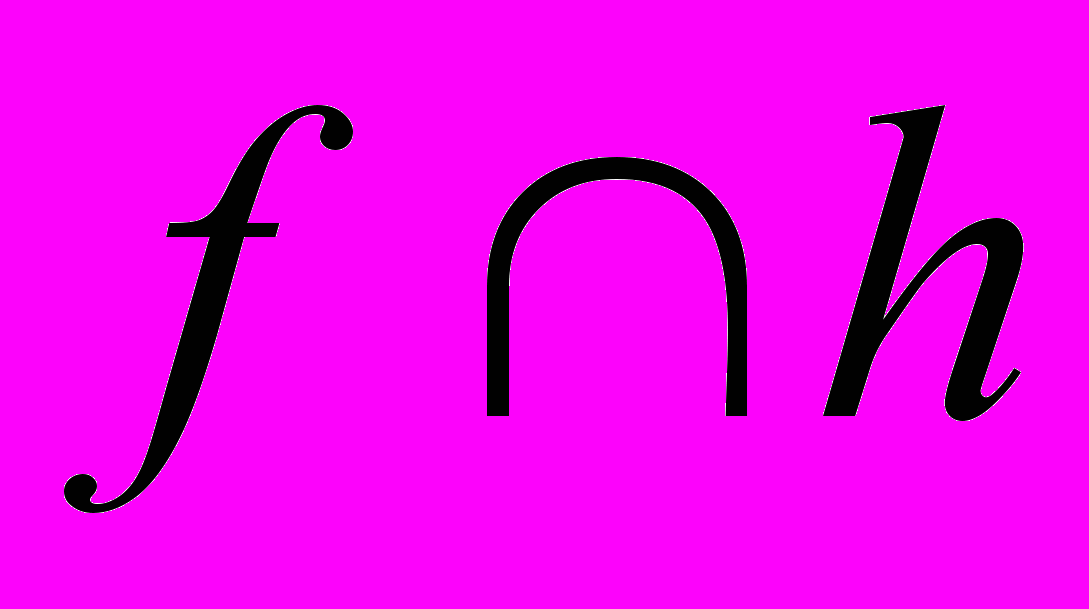) точку, удаленную от точки С этой плоскости на 15 мм и от внешней точки А на 30 мм.





Задача №6


Построить множество окружностей радиуса R 20 мм, центры которых принадлежат прямой общего положения, a их плоскости перпендикулярны к этой прямой.





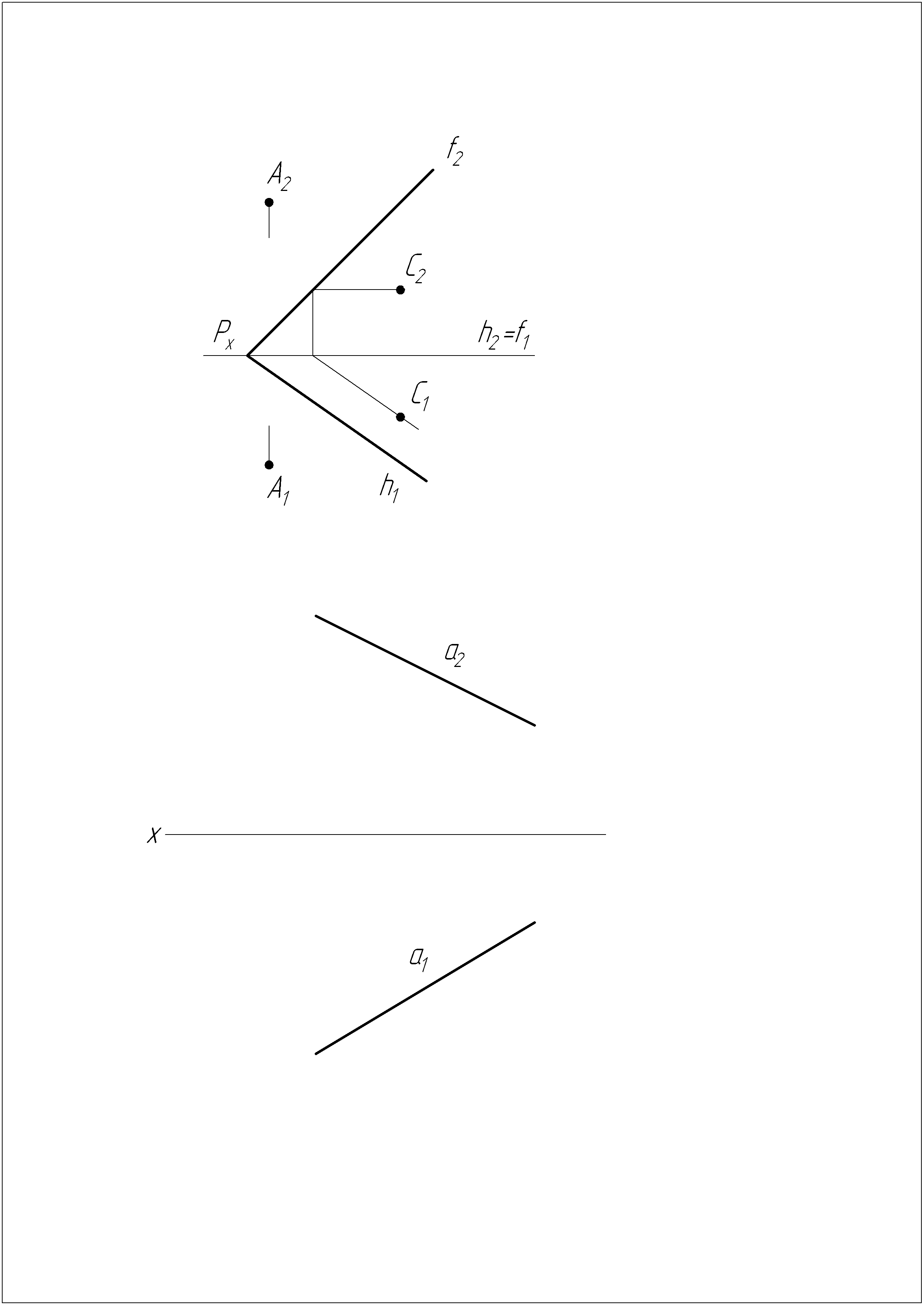
Задача №7


Построить линию пересечения заданных поверхностей вращения.





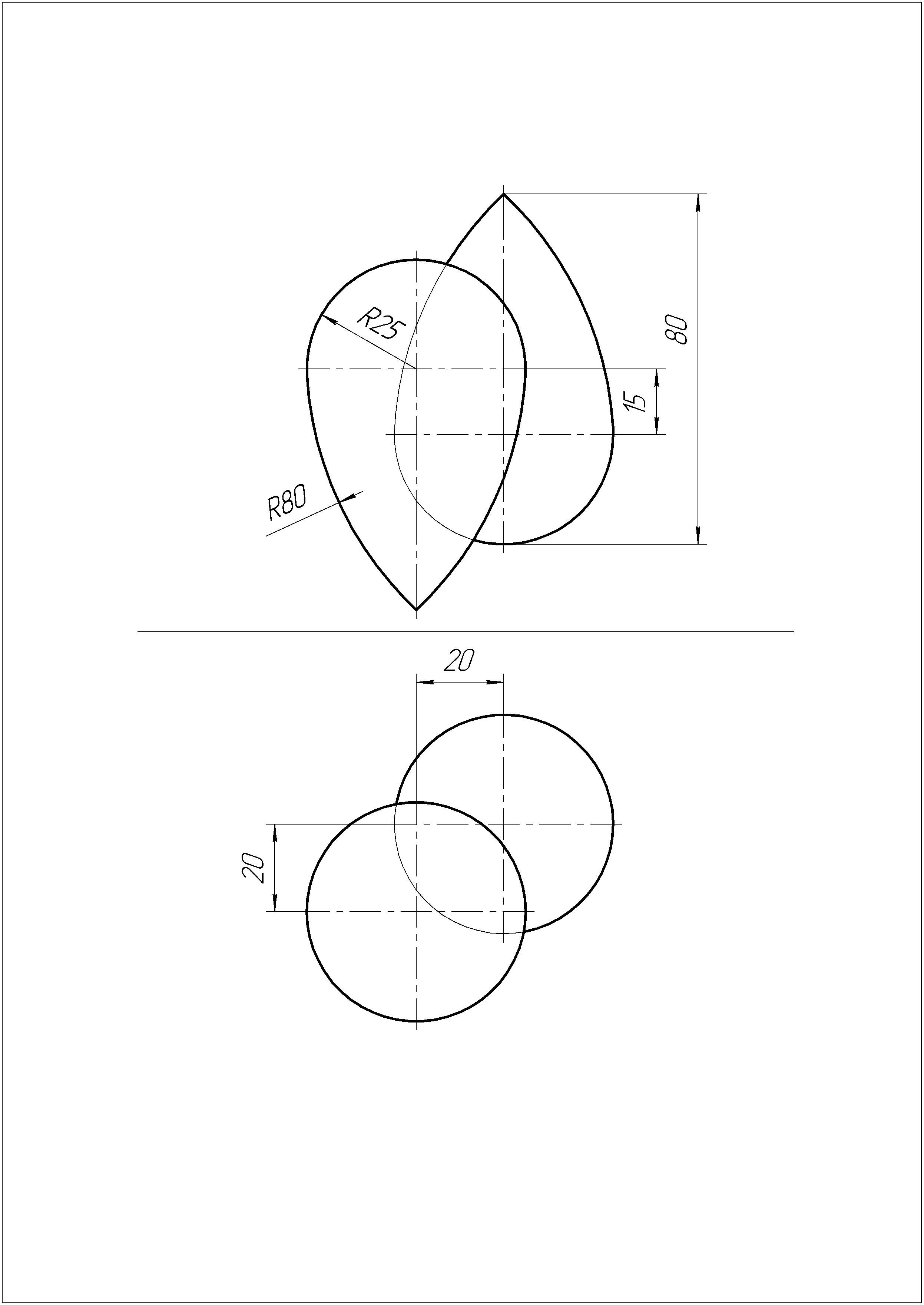
Задача №8


Через точку А, провести прямые, пересекающие прямую CD в точках, отстоящих от точки В на расстояние в 17 мм.





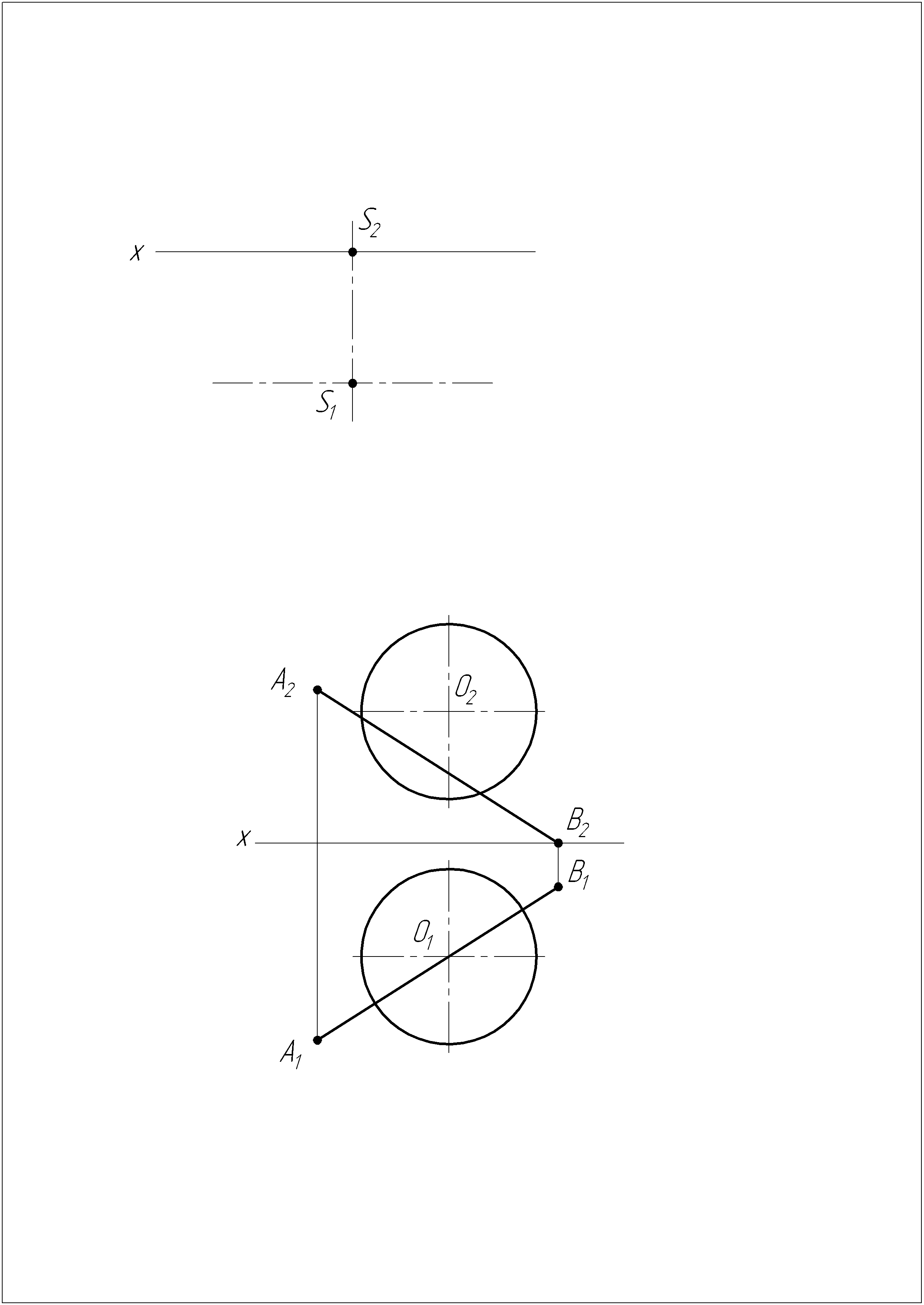
Задача №9


Построить проекции прямой, проходящей через точку S, принадлежащую горизонтальной плоскости проекций, под углом 30° к плоскости П₁ и под углом 45° к плоскости П₂.





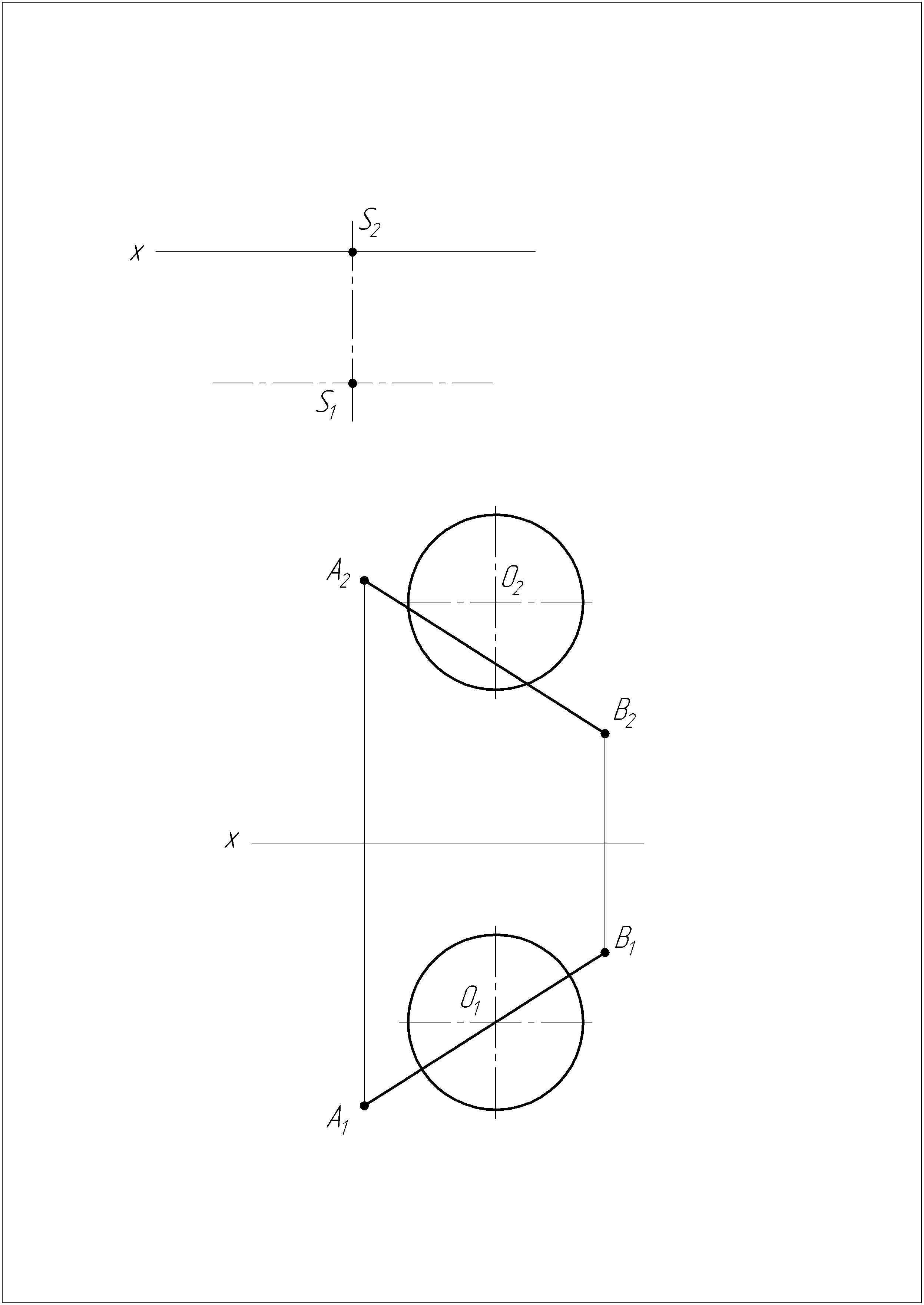
Задача №10


На поверхности сферы построить геометрическое место точек, равноудаленных от прямой АВ на расстояние в 25 мм.





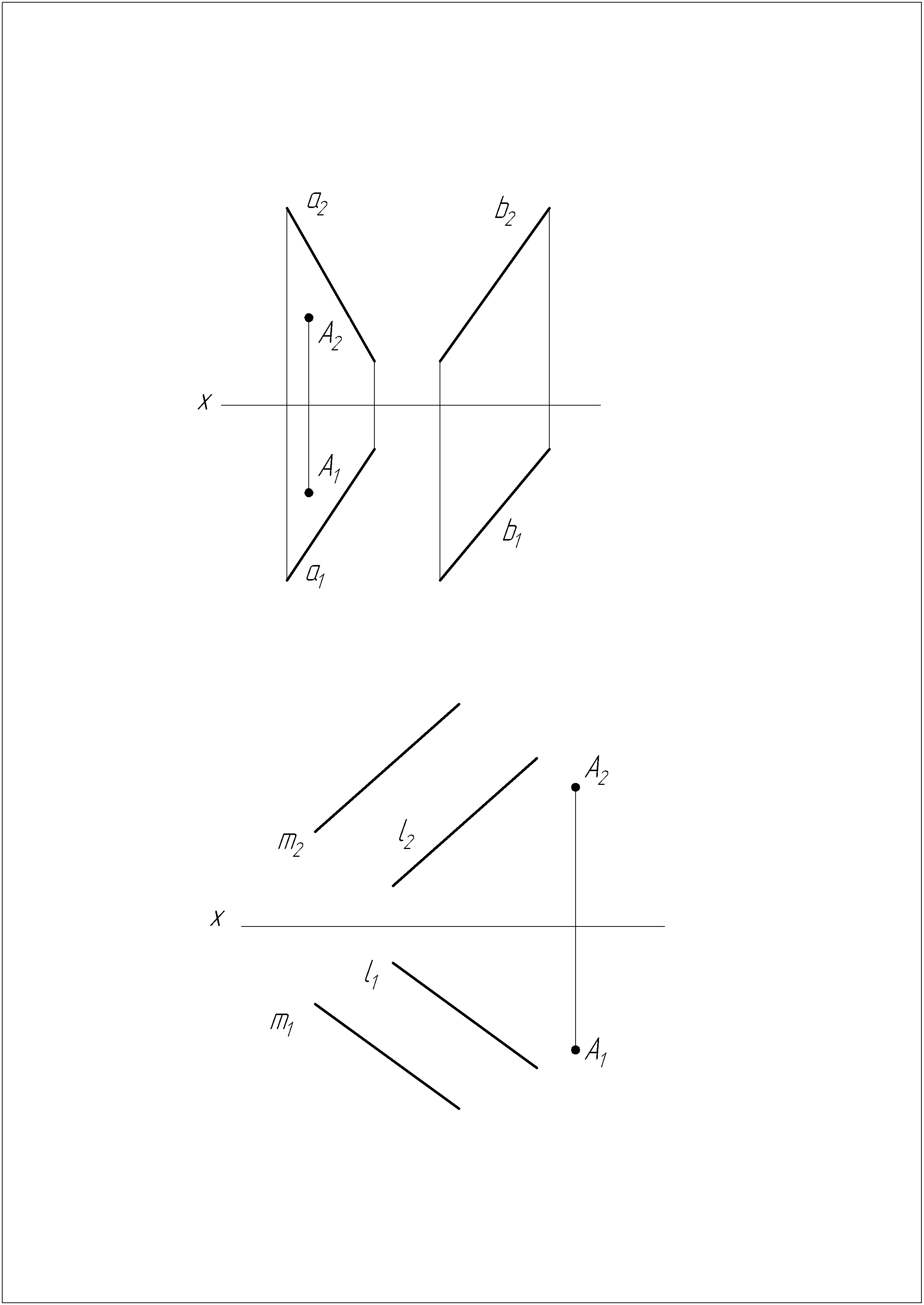
Задача №11


На гипаре (гиперболическом параболоиде) (a; b; П₂) построить множество точек, равноудаленных от точки А на расстояние 20 мм.





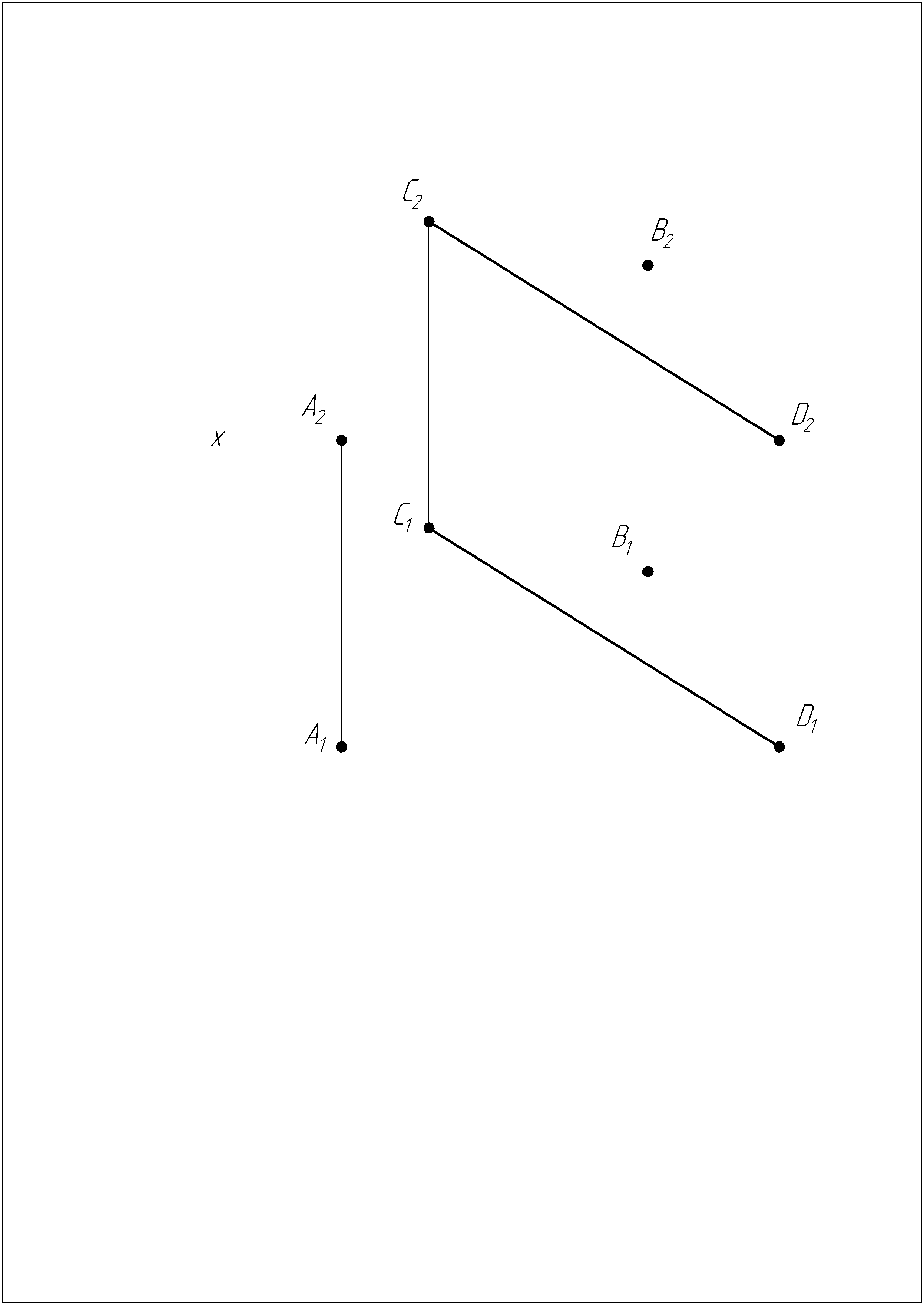
Задача №12


Построить проекции правильной треугольной призмы, два ребра которой совпадают с данными прямыми m и l. Нижнее основание призмы лежит в плоскости , проходящей через точку А. Высота призмы 50 мм.





Задача №13


Построить проекции шара, касающегося заданных прямых а, b, с, если касание с прямой а происходит в точке А.





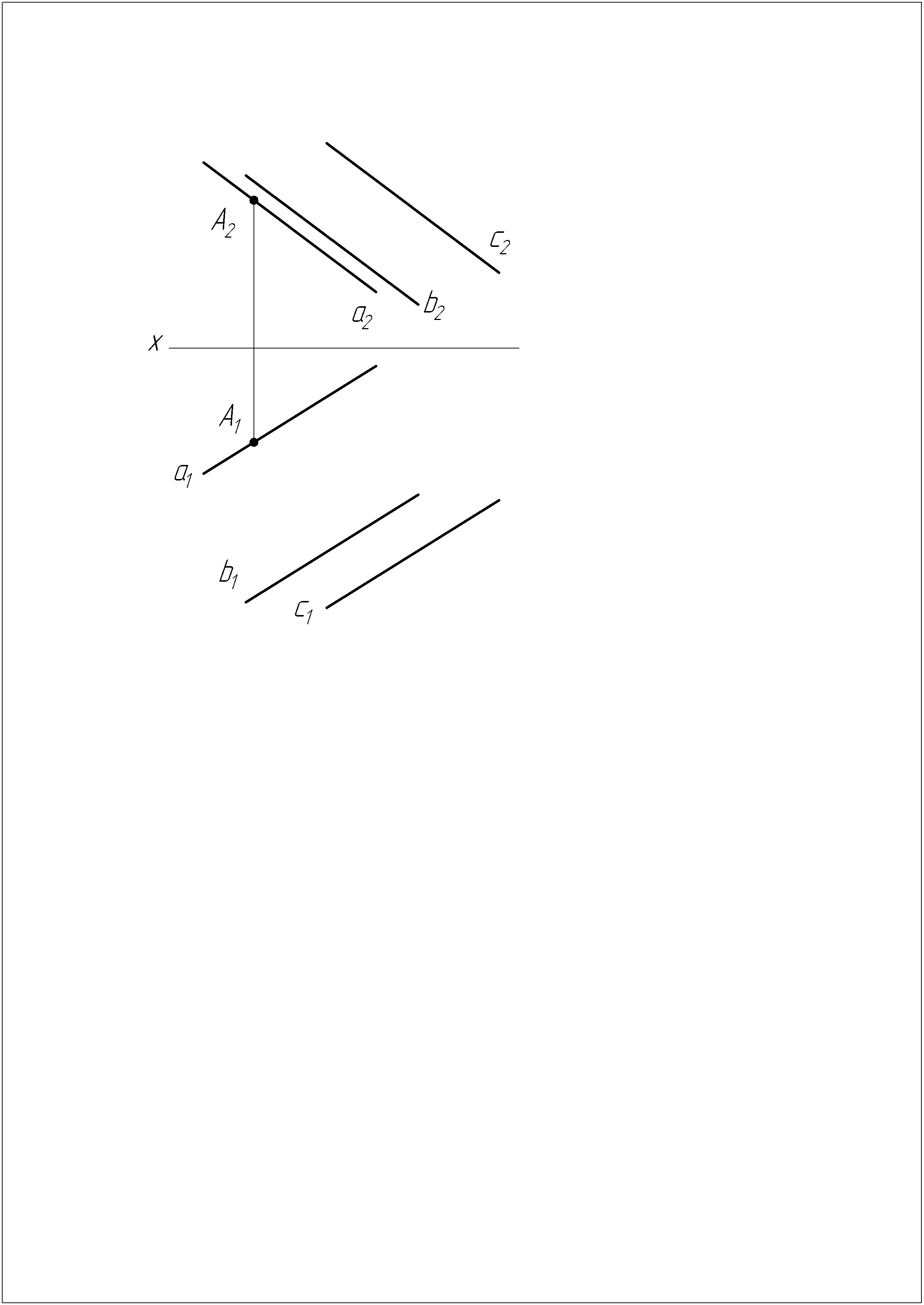
Задача №14


Найти на плоскости Р точку, удаленную от внешних точек А и В соответственно на 30 мм и 50 мм.




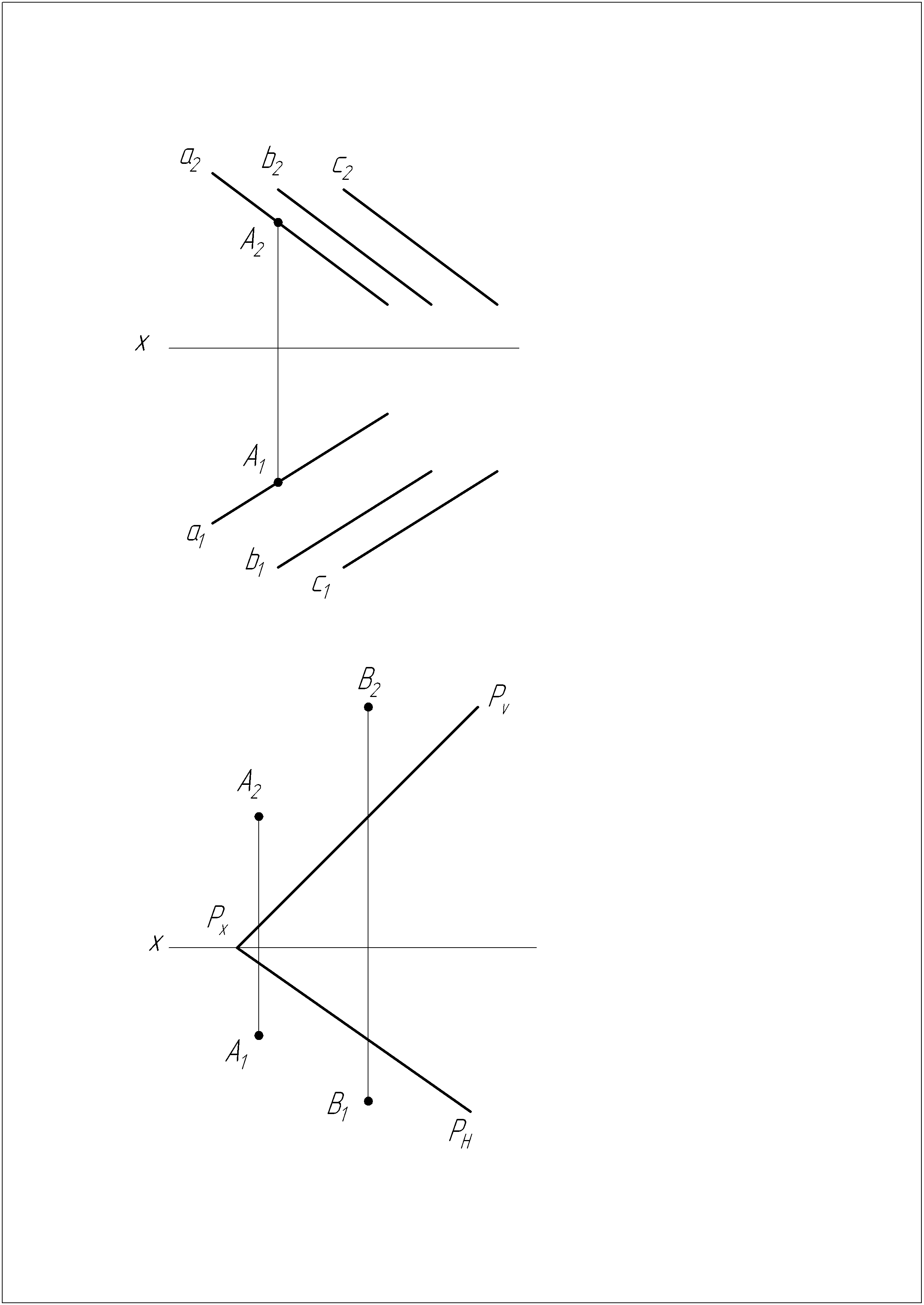
Задача №15


Построить параллелограмм ABCD, ВС принадлежит m, AB=1,25/АK/. Точка K – основание перпендикуляра, опущенного из точки А на ВС, и делит ВС в отношении .





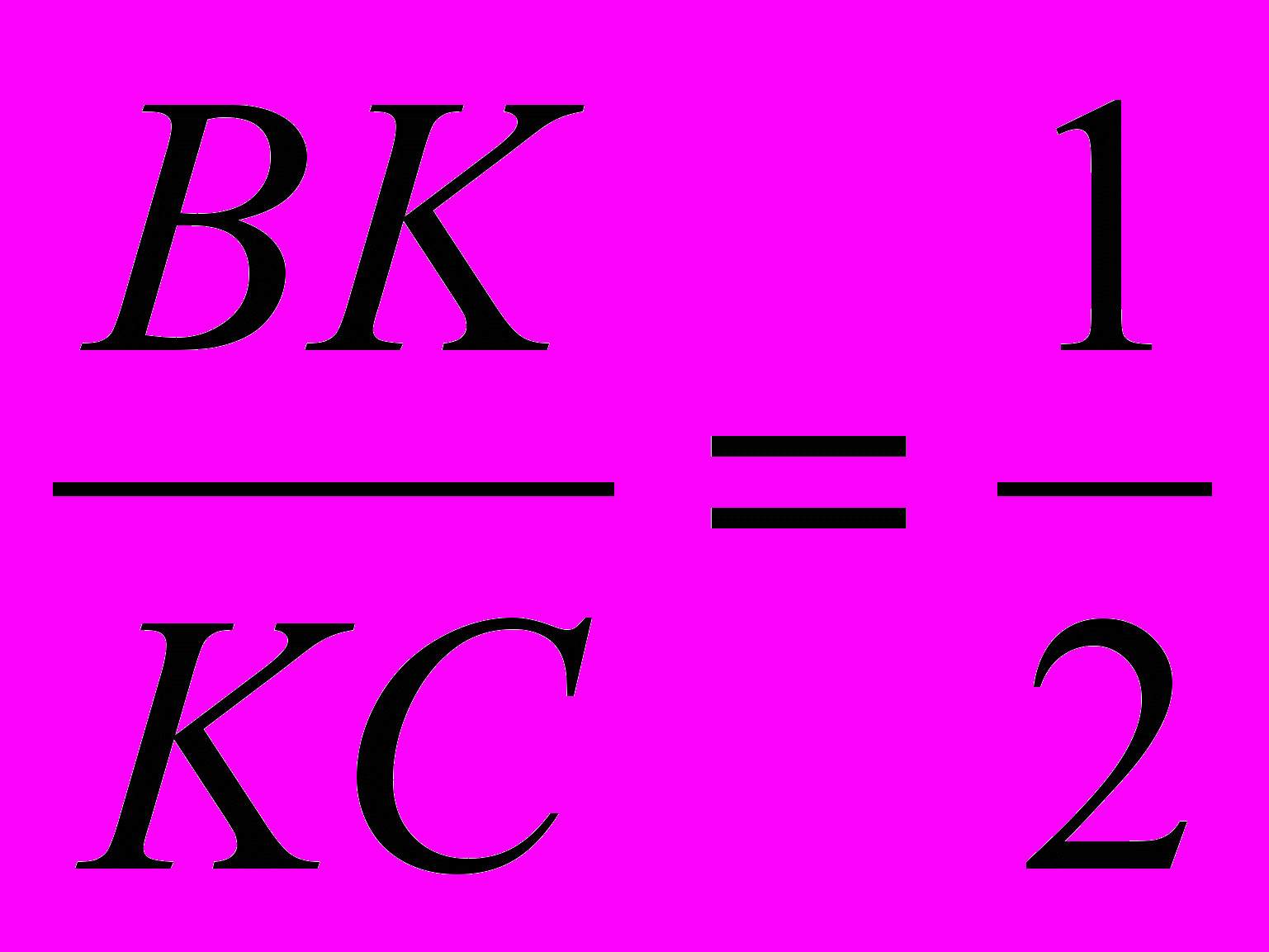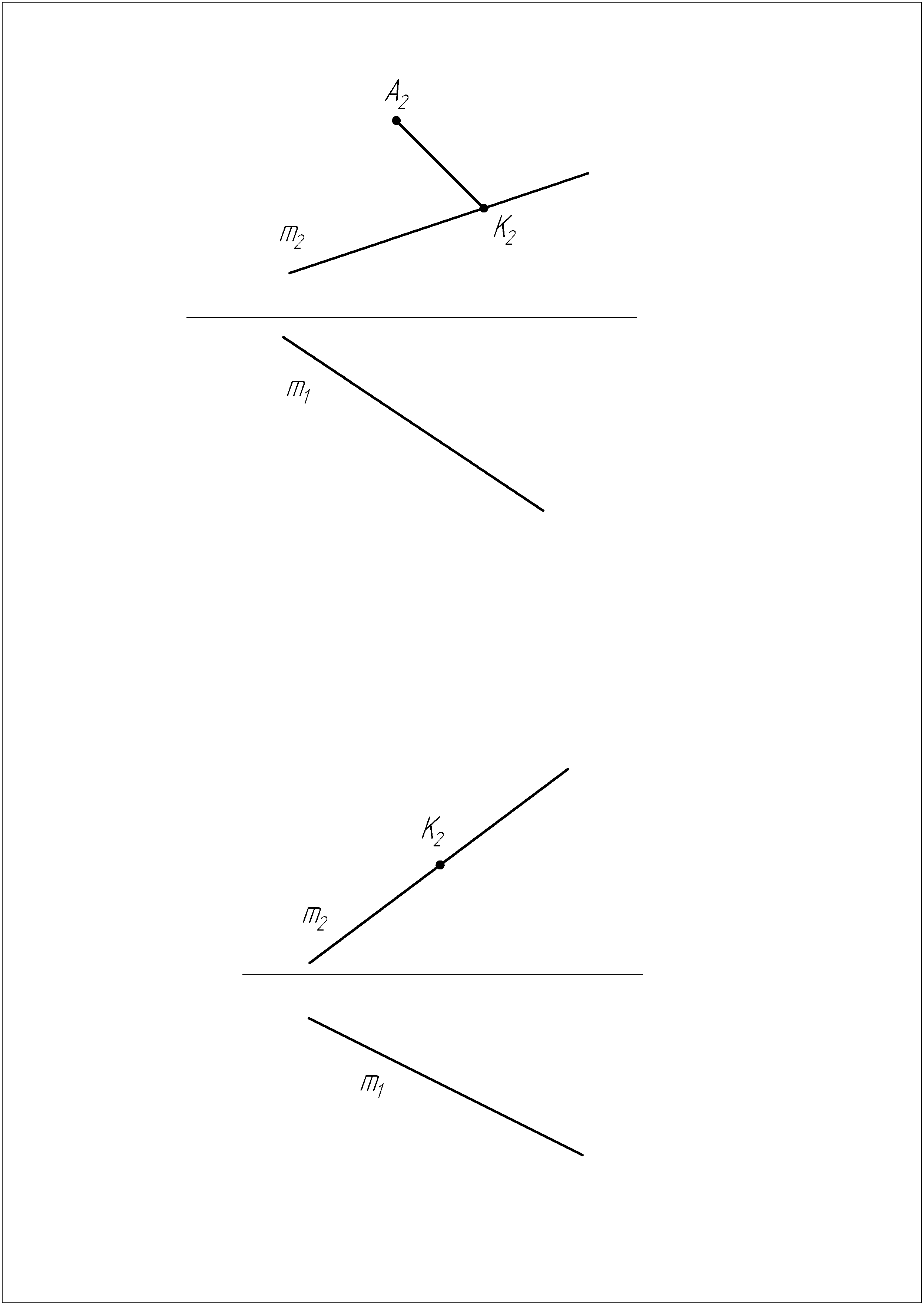
Задача №16


Построить проекции квадрата ABCD с диагональю BD на прямой m, исходя из условия, что А принадлежит V и удалена от Н на 15 мм. Точка K – точка пересечения диагоналей.




Задача №17


Построить центр сферы, вписанной в заданную пирамиду. А (80;70;10), B (10;25;10), C (10;85;10), D (50;25;80).


Задача №18


Пирамида SABC имеет цилиндрический вырез, касательный к грани SAB, ось цилиндра перпендикулярна плоскости V и проходит через точку K, лежащую на средине SC. Построить три проекции пирамиды с вырезом.





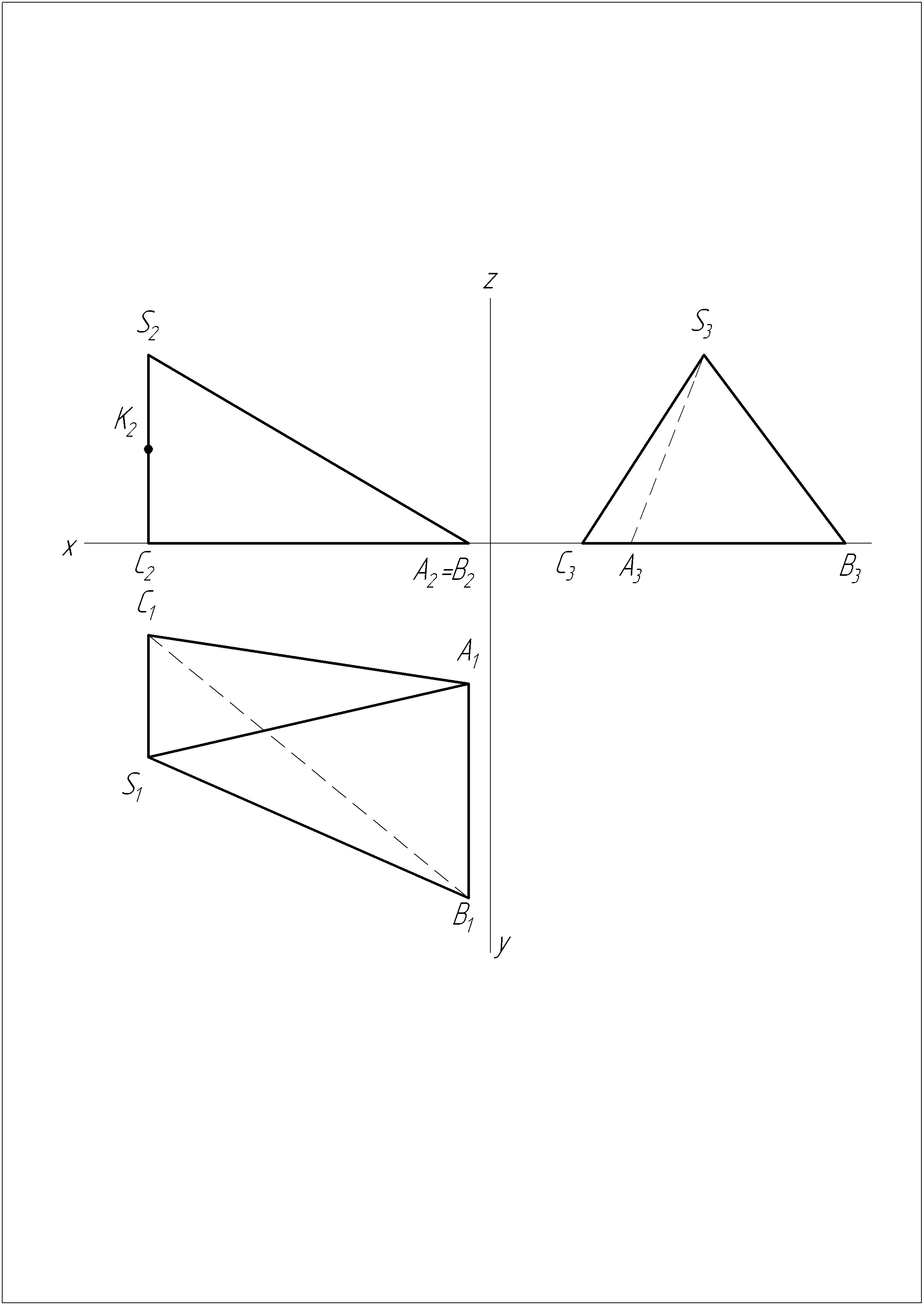
Задача №19


По заданным координатам вершин построить проекции пирамиды. Найти положение центра описанной вокруг пирамиды сферы. А (80;70;30), B (10;25;30), C (10;85;30), D (50;25;100).


Задача №20


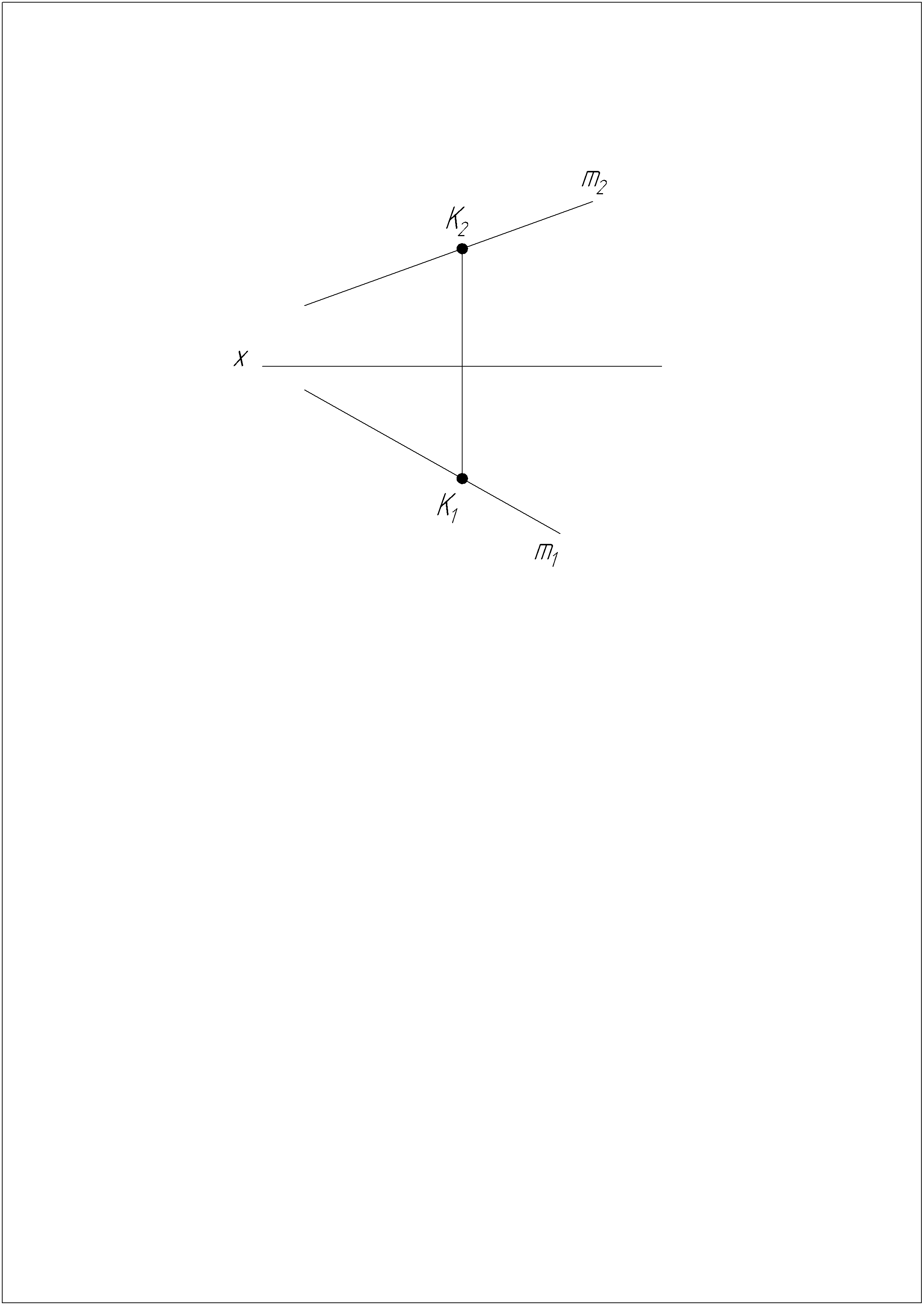
Построить проекции ромба АВCD с меньшей диагональю BD на прямой m, исходя из условия, что вершина А принадлежит оси х, а отношение диагоналей равно 2. Точка K – точка пересечения диагоналей ромба (без преобразования).





3 РЕШЕНИЯ ЗАДАЧ


Решение задачи №1




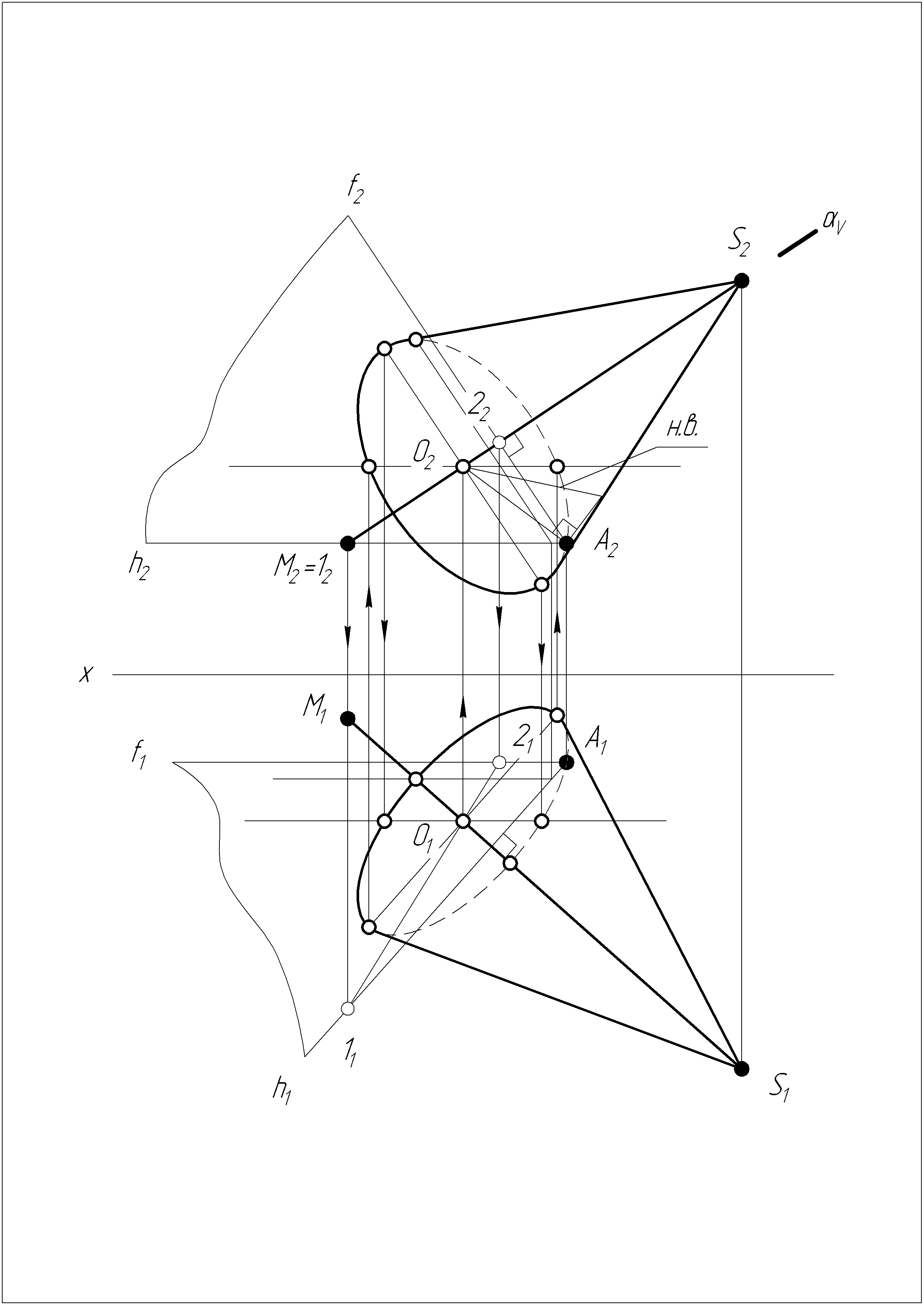
1. Через точку А проводим плоскость перпендикулярную прямой MS.

2. Находим точку О – точку пересечения MS с перпендикулярной плоскостью (hf).

3. Находим натуральную величину радиуса окружности основания конуса, т.е. натуральную величину отрезка ОА.

4. Находим большую и малую оси эллипса и ряд дополнительных точек, принадлежащих основанию.

5. Соединяем точки для получения эллипсов и из точки S проводим касательные (очерковые образующие).

6. Определяем видимость основния.


Решение задачи №2





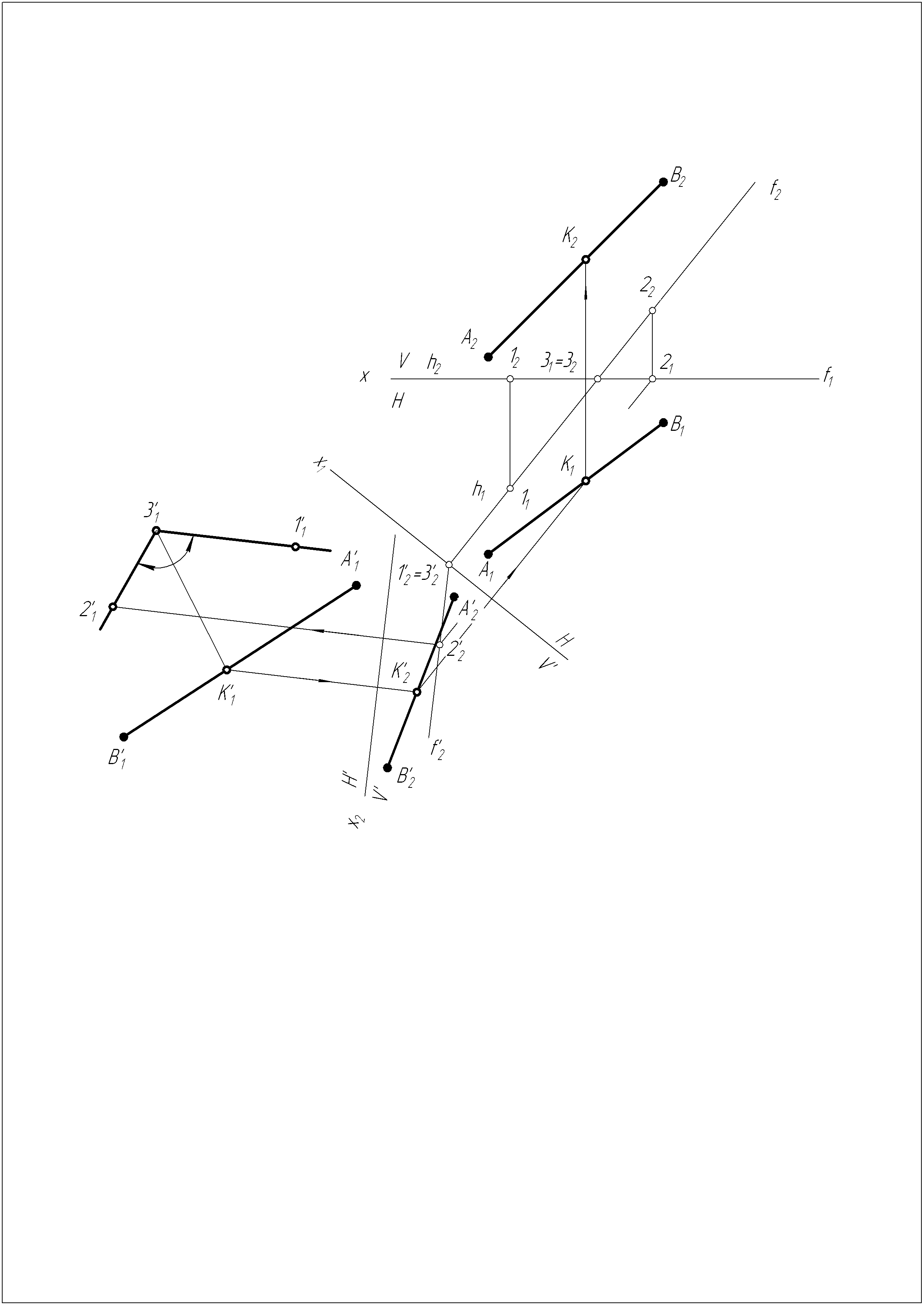
Производим преобразование чертежа методом замены плоскостей проекций. Плоскость hf из плоскости общего положения преобразуем в проецирующую, а затем в плоскость уровня.

Проводим биссектрису угла 2₁3₁1₁, таким образом определяем положение точки K.


Решение задачи №3





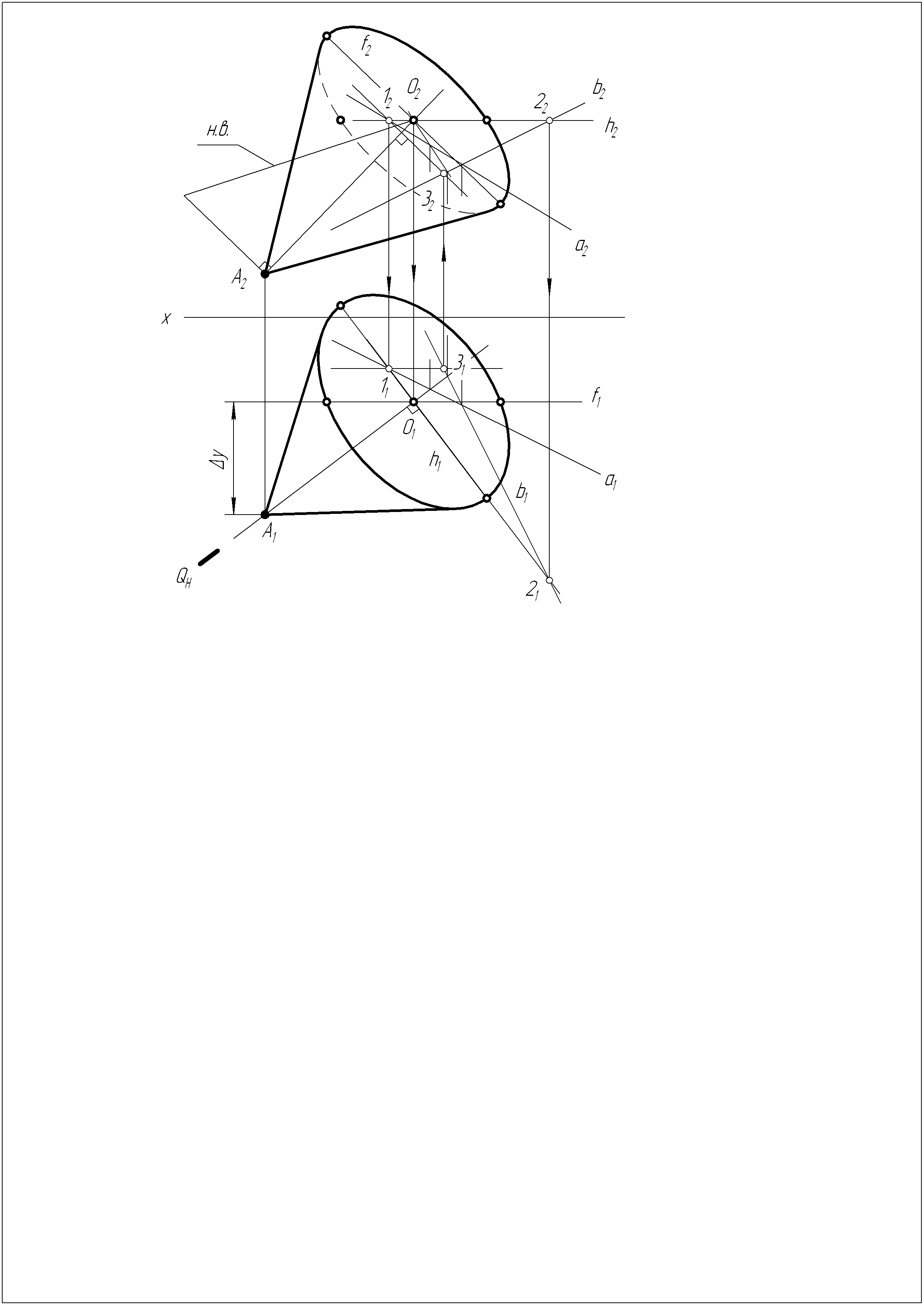
1. В плоскости, заданной пересекающимися прямыми a и b, проводим линии уровня.

2. Из точки А опускаем перпендикуляр на заданную плоскость.

3. Находим точку О – точку пересечения перпендикуляра с плоскостью ab.

4. Находим натуральную величину высоты конуса ОА.

5. Находим точки, определяющие основание конуса, большую и малую оси, исходя из условия, что диаметр основания конуса равен высоте.

6. Соединяем точки для получения эллипсов и из точки А проводим касательные (очерковые образующие).

7. Определяем видимость основания.


Решение задачи №4





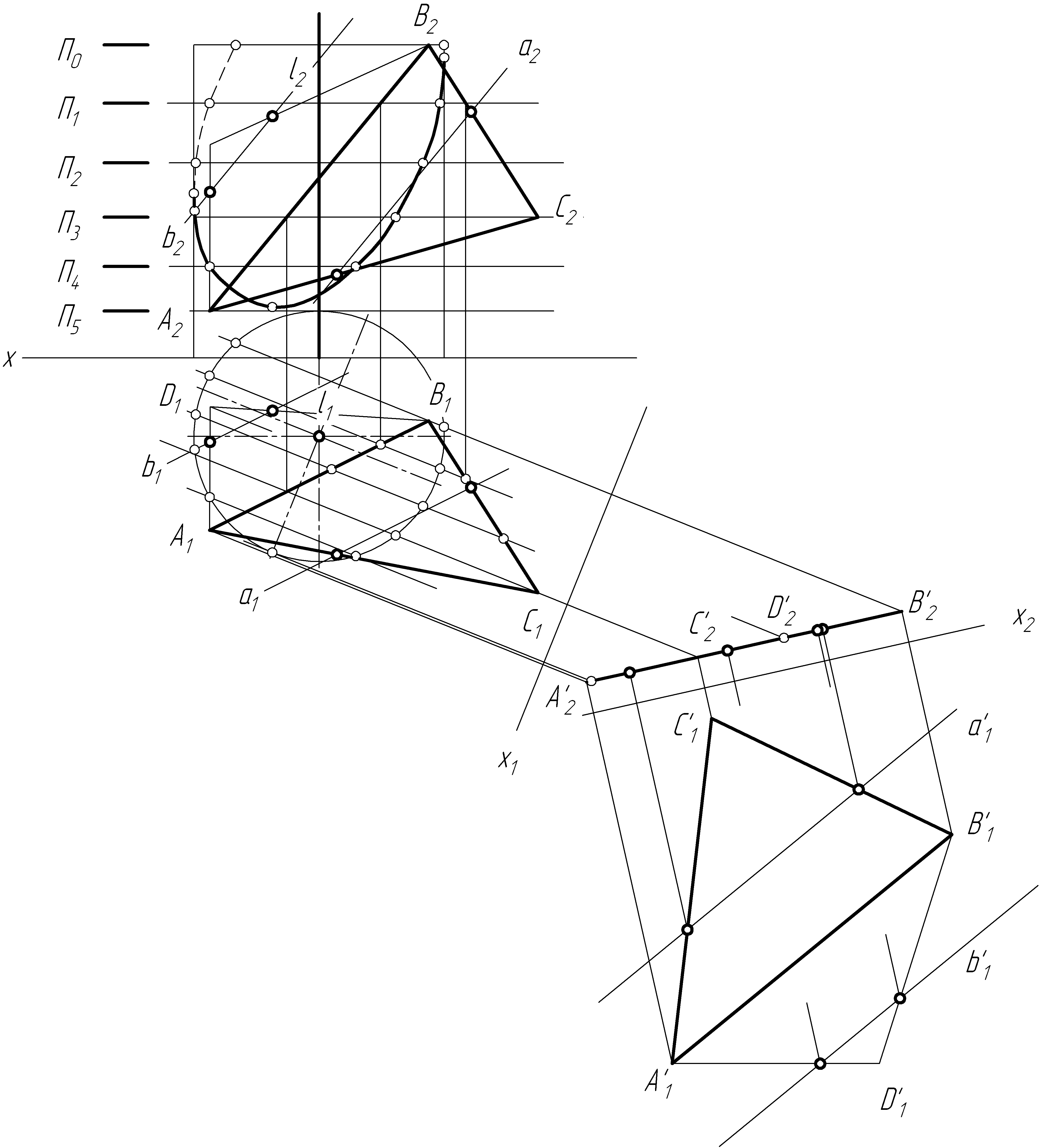
Решение задачи №5





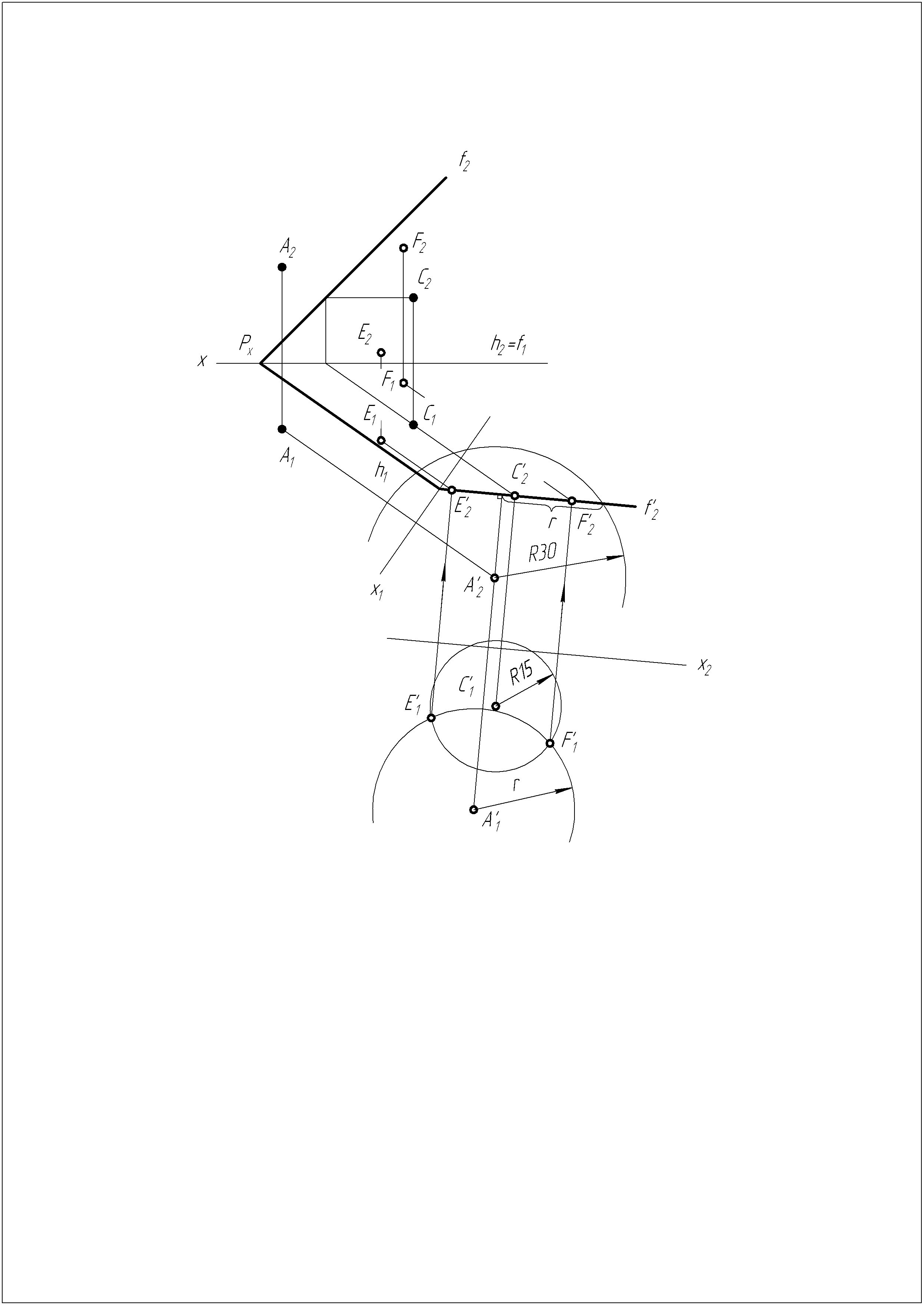
Производим преобразование чертежа. Плоскость hf из плоскости общего положения преобразуем в проецирующую, которая пересекает сферу с центром в точке А и радиусом 30 мм по окружности радиуса r.

Вторым преобразованием, окружности радиусами R15 и r проецируются в натуральную величину. На пересечении этих окружностей получаем точки Е и F.

Находим проекции точкек Е и F на незамененных плоскостях проекций.

Решение задачи №6





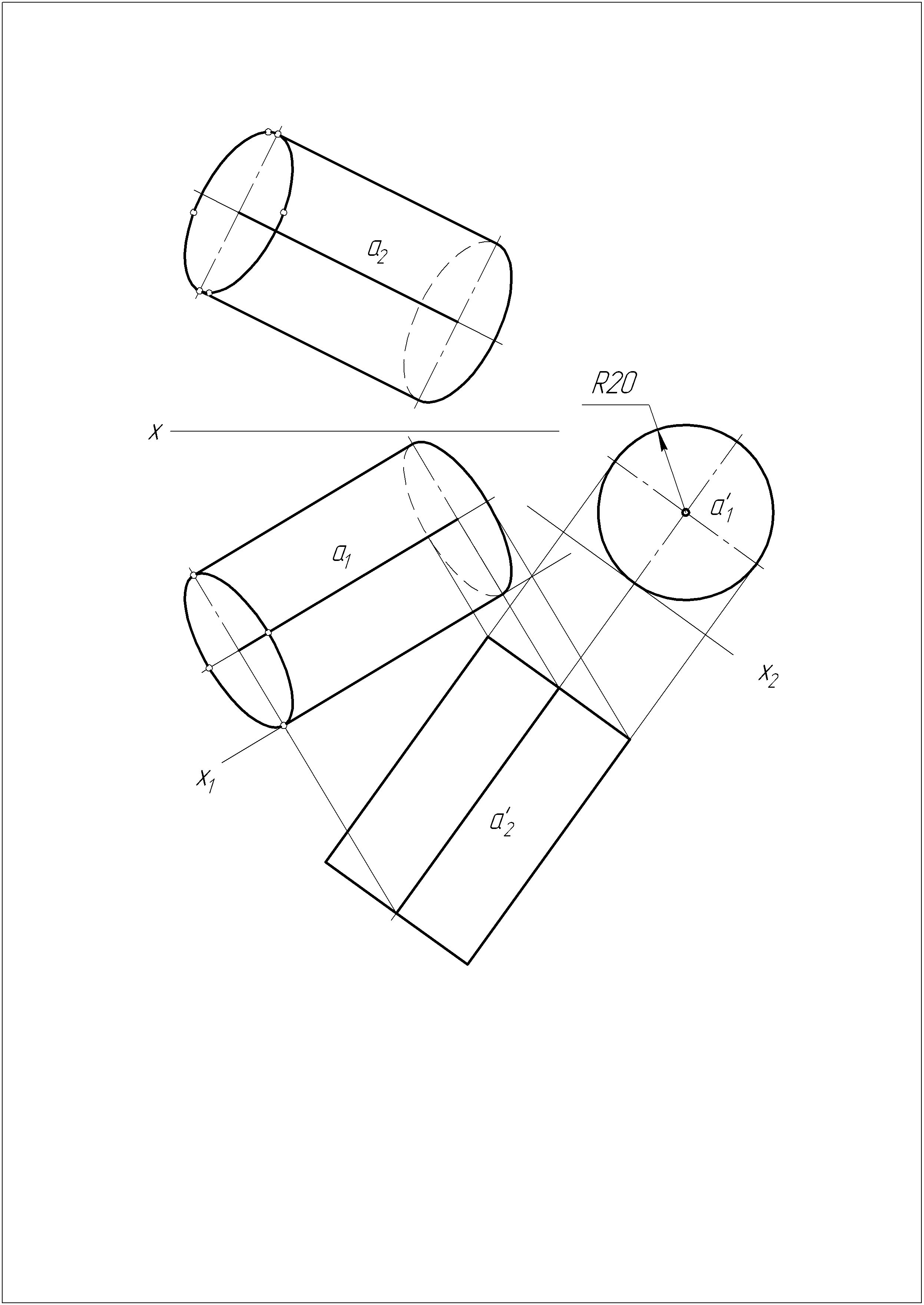
Производим преобразование чертежа. Прямую а общего положения преобразуем в прямую уровня, а затем в проецирующую.

Проводим окружность радиуса R20. Множеством окружностей перпендикулярных прямой а является цилиндр. Строим его проекции на незамененных плоскостях проекций.


Решение задачи №7





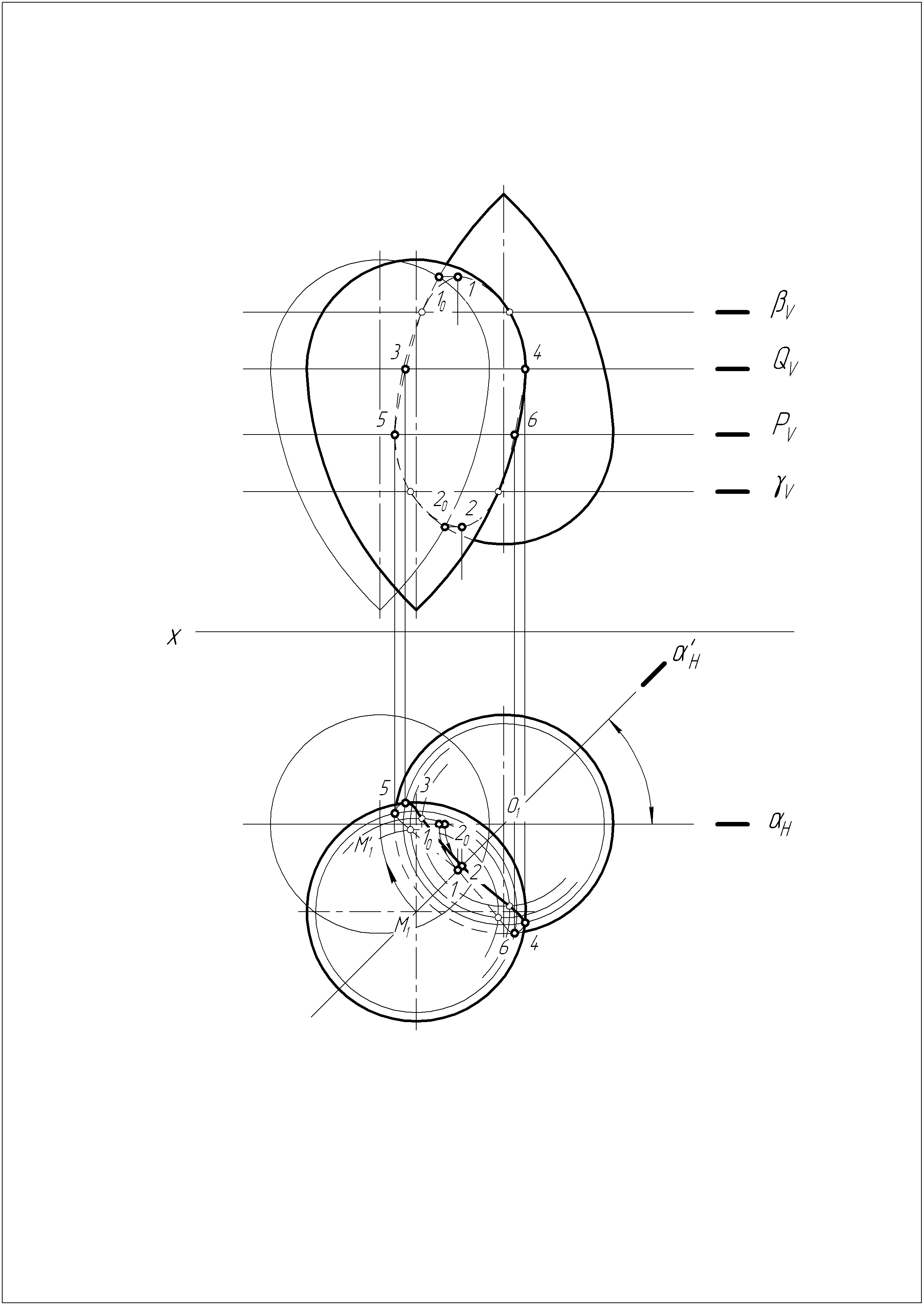
1. Построить высшую и низшую точки линии пересечения, используя плоскость .

2. Построить точки, принадлежащие экваторам одной и второй поверхности вращения (плоскости Q и P).

3. Построить промежуточные точки, принадлежащие линии пересечения (плоскости  и ).

4. Соединяем полученные точки, определяем видимость.


Решение задачи №8





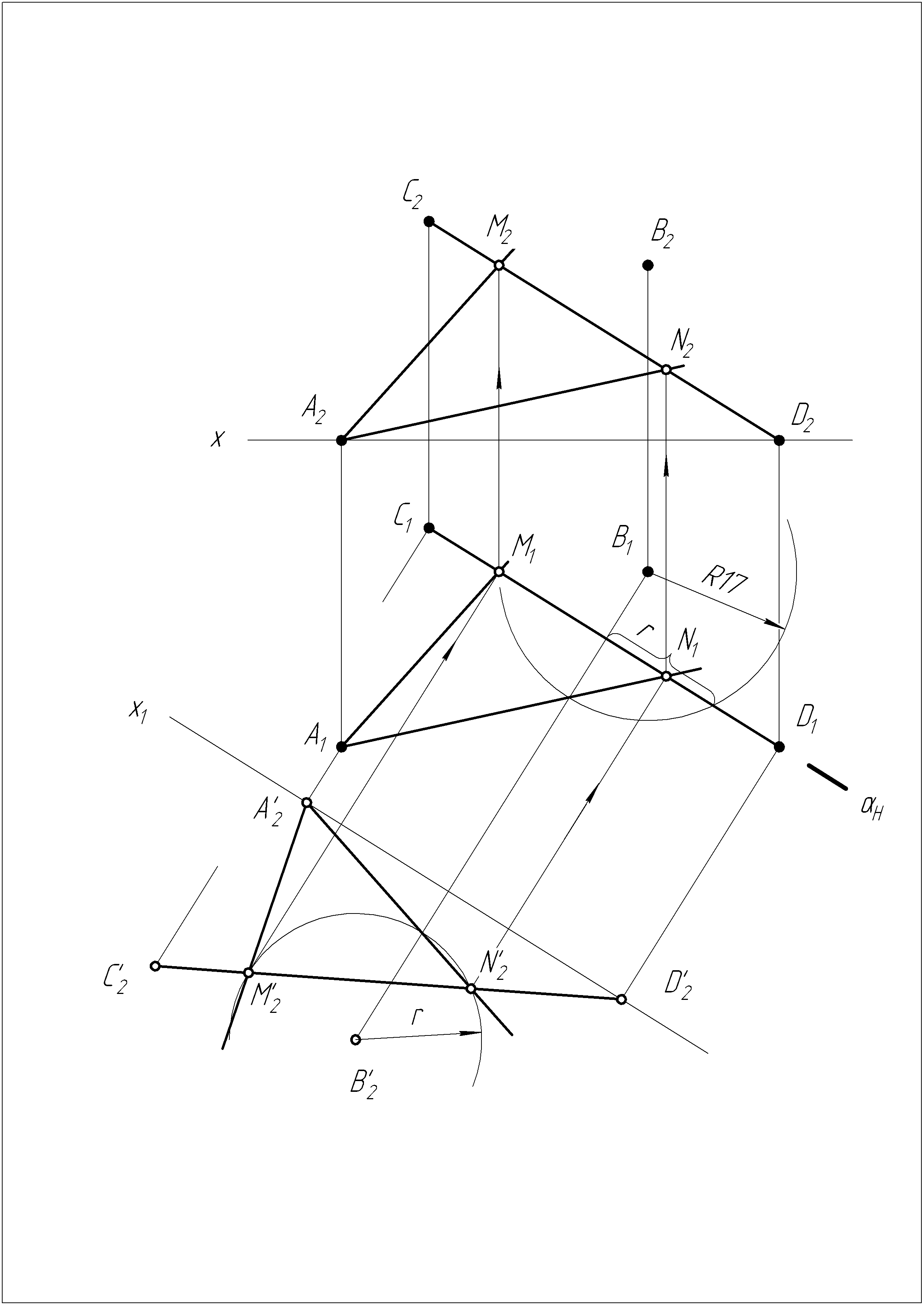
Определяем точки пересечения прямой CD с поверхностью сферы с центром в точке В и заданного радиуса R17 (M и N).

Искомые прямые АМ и AN.


Решение задачи №9





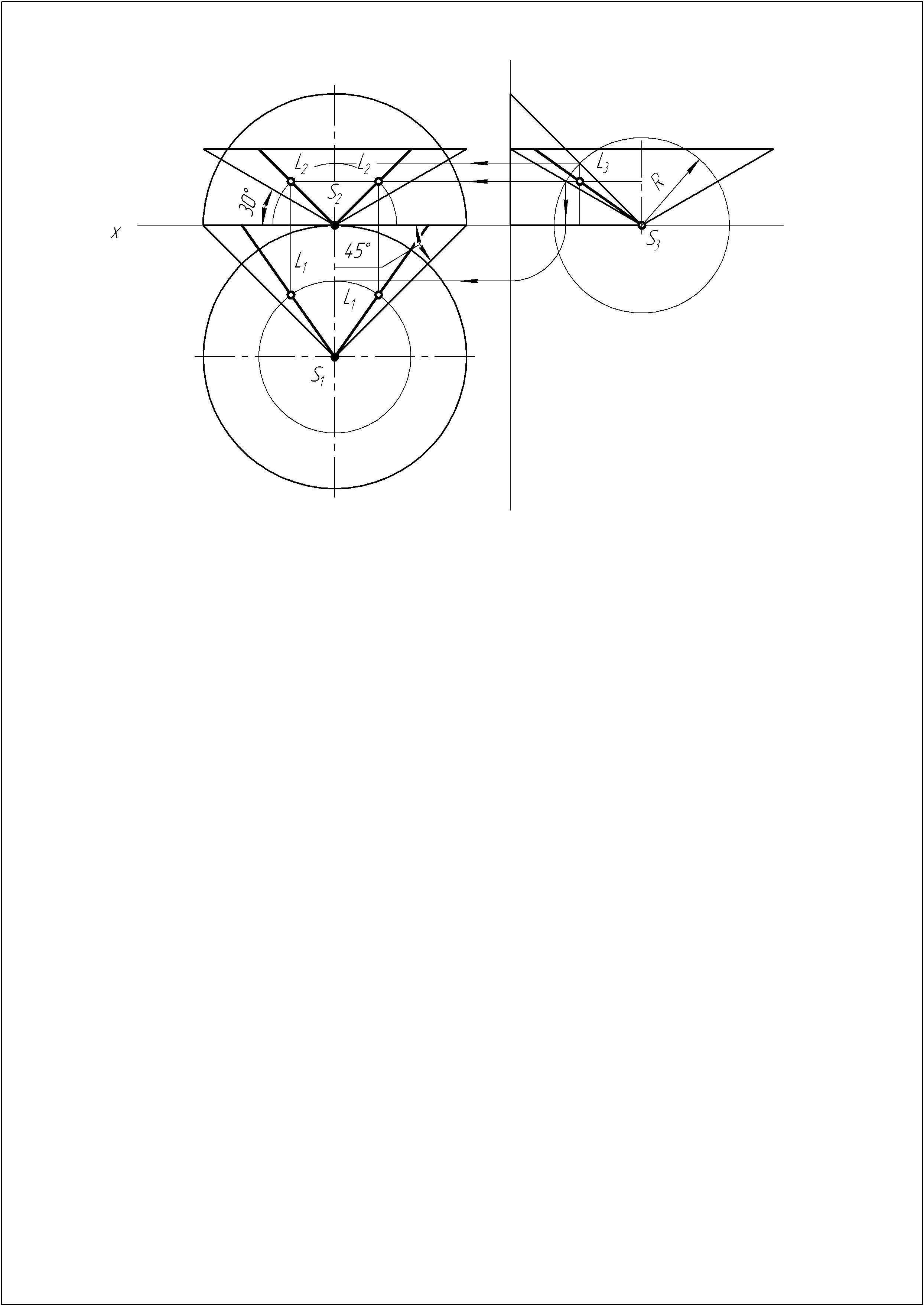
Из точки S строим одну коническую поверхность, ось которой перпендикулярна П₂, а образующие расположены под углом 45 к плоскости П₂, и вторую коническую поверхность ось которой перпендикулярна П₁, а образующие расположены под углом 30 к плоскости П₁.

Строим линии пересечения этих конусов (образующие SL).


Решение задачи №10





ГМТ удаленных от прямой AB на расстояние в 25 мм является цилиндрическая поверхность.

Находим линию пересечения цилиндра и сферы. Сначала определяем положение характерных точек M, N и K, а затем дополнительных 1 и 2.

Полученная линия является решением задачи.


Решение задачи №11





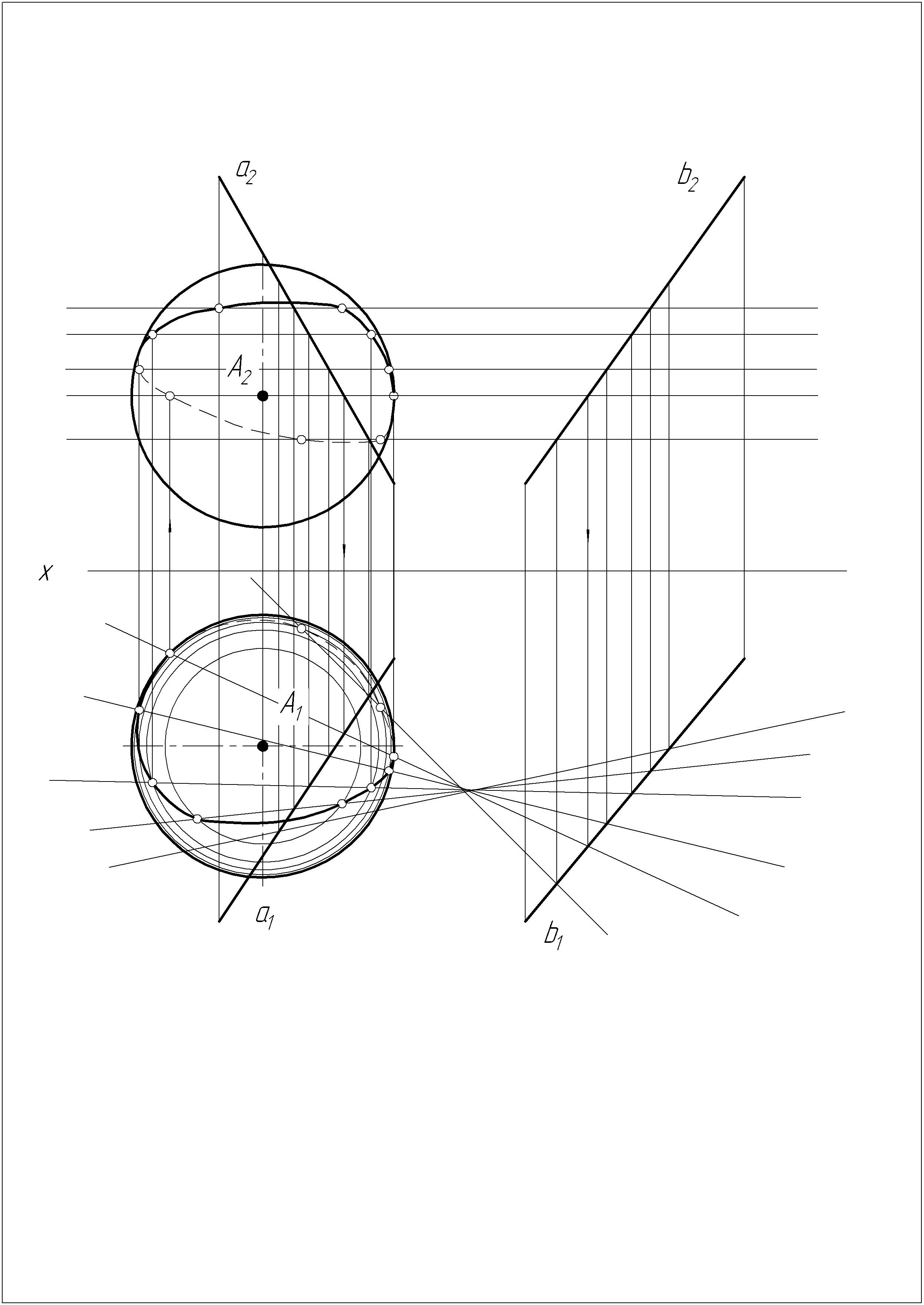
1. Строим сферу радиусом R20, с центром в точке A.

2. Строим каркас косой плоскости (гиперболического параболоида) и определяем их линию пересечения.


Решение задачи №12





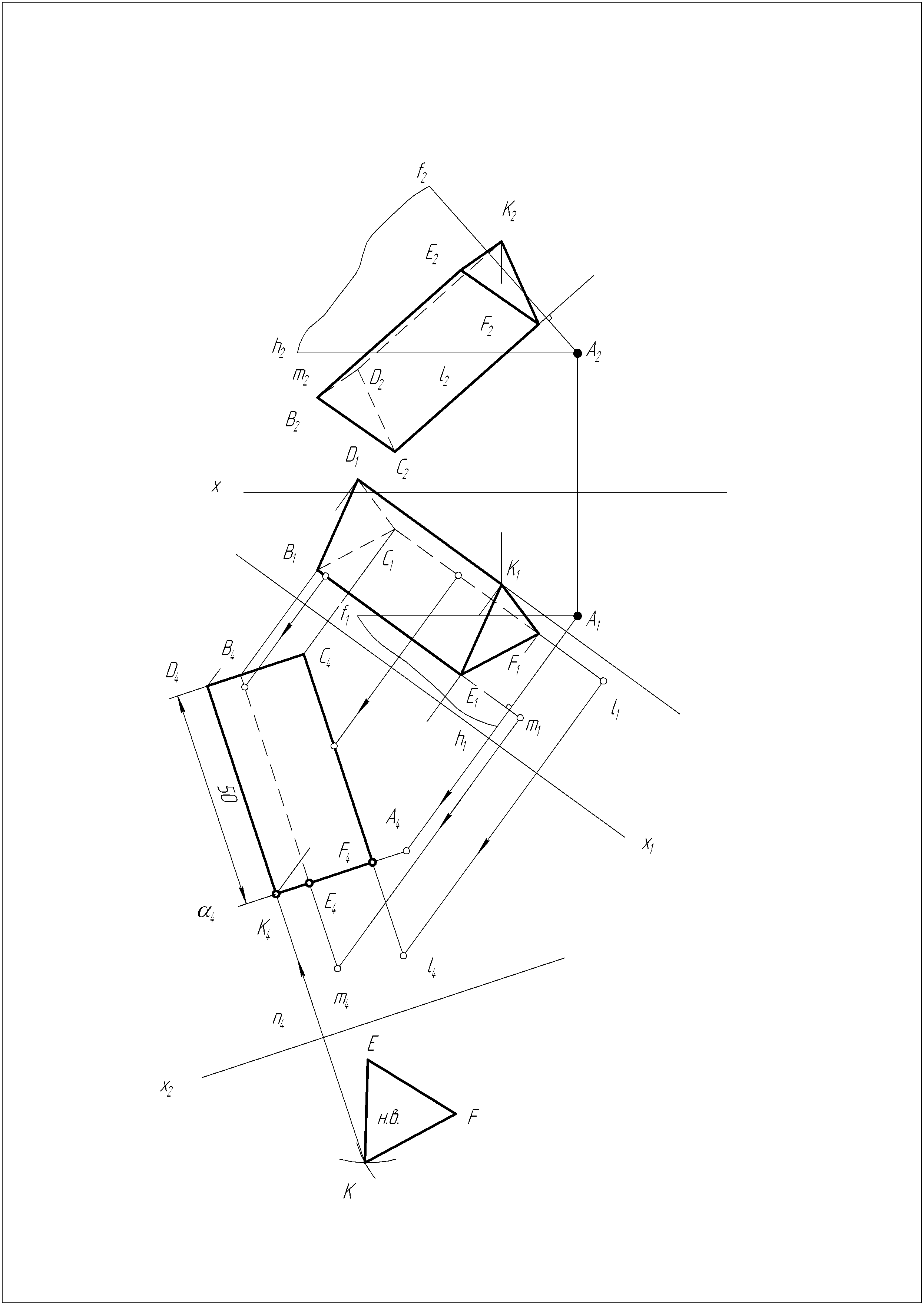
Решение задачи №13





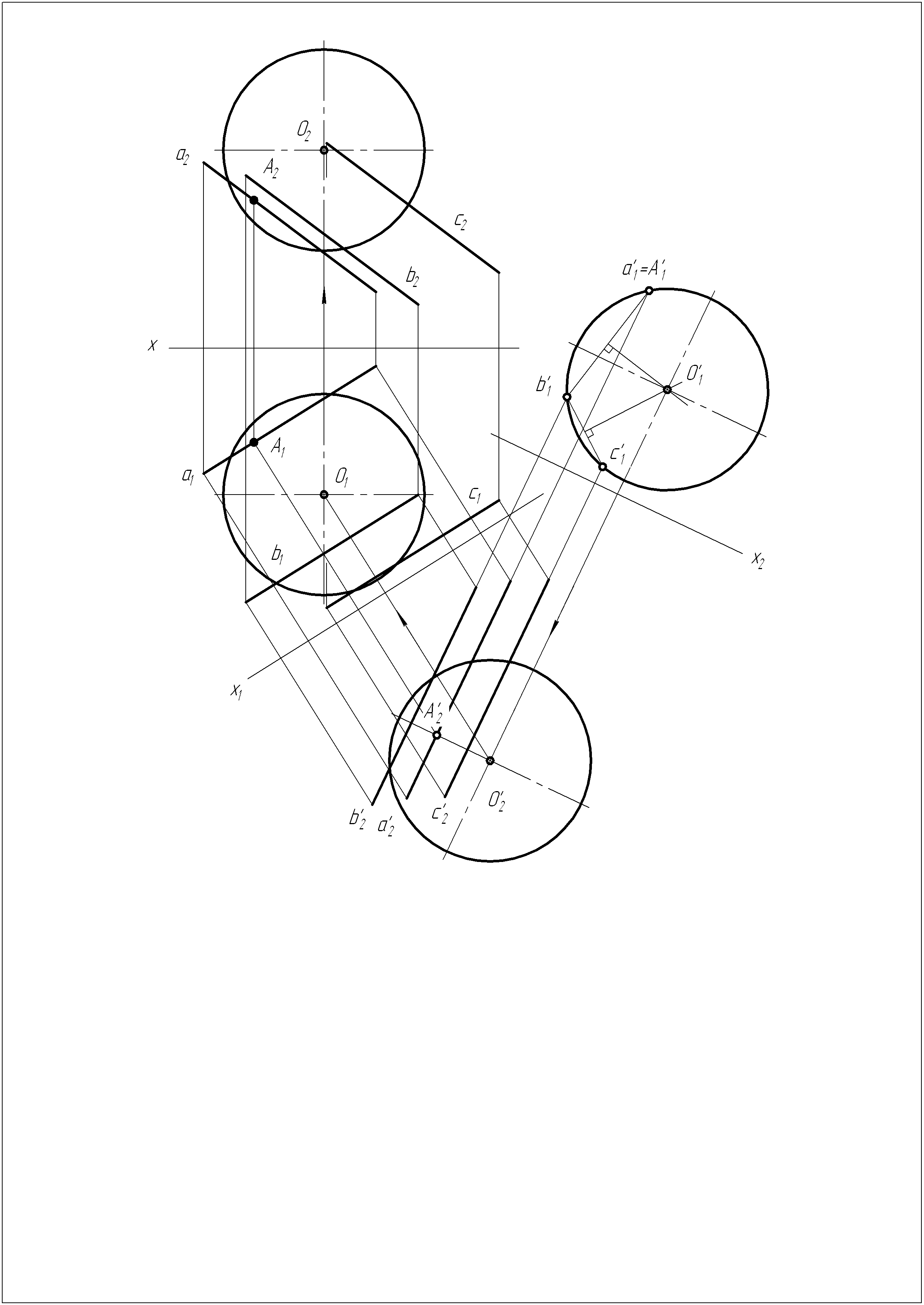
Решение задачи №14





Решение задачи №15





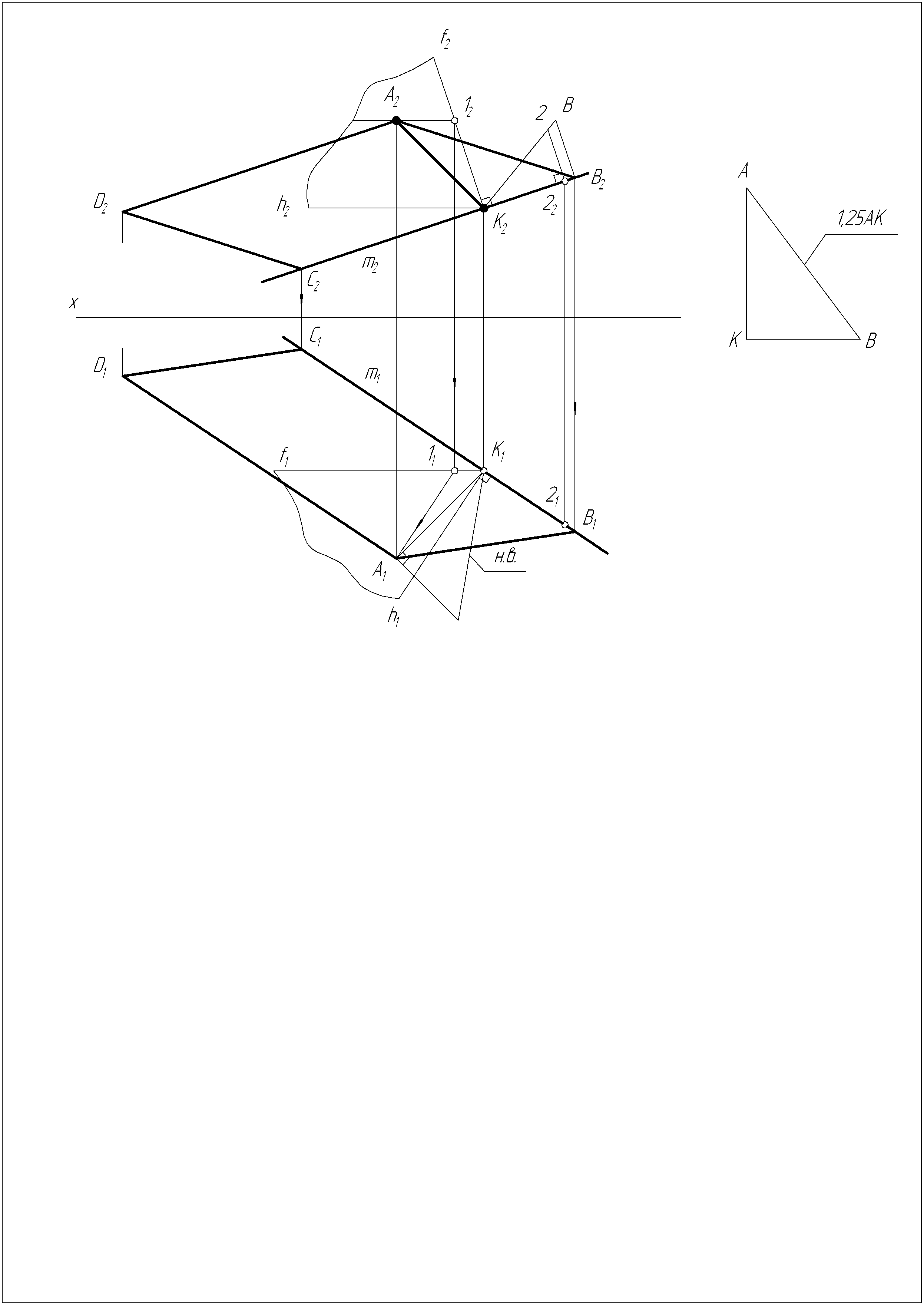
Решение задачи №16





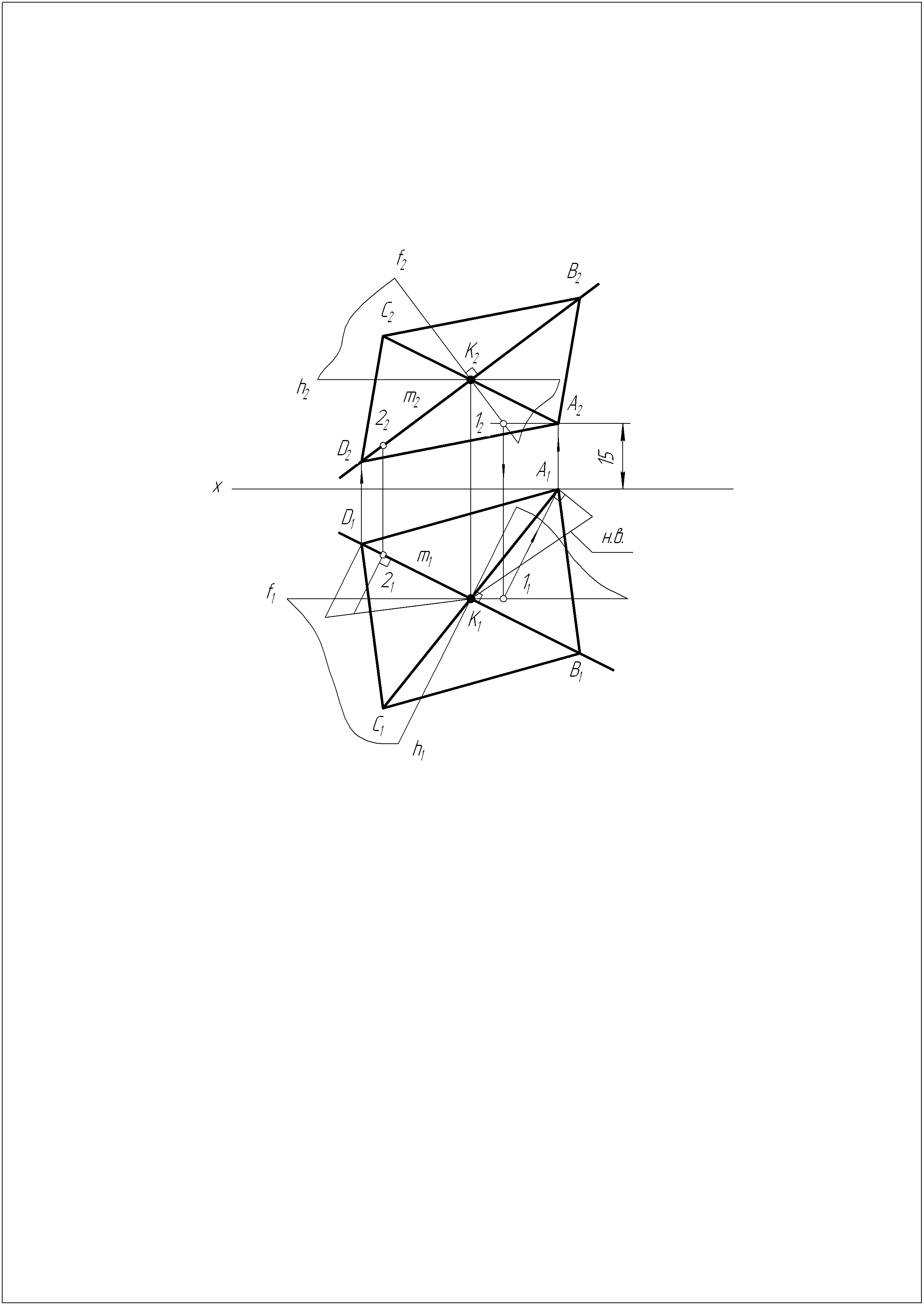
Решение задачи №17




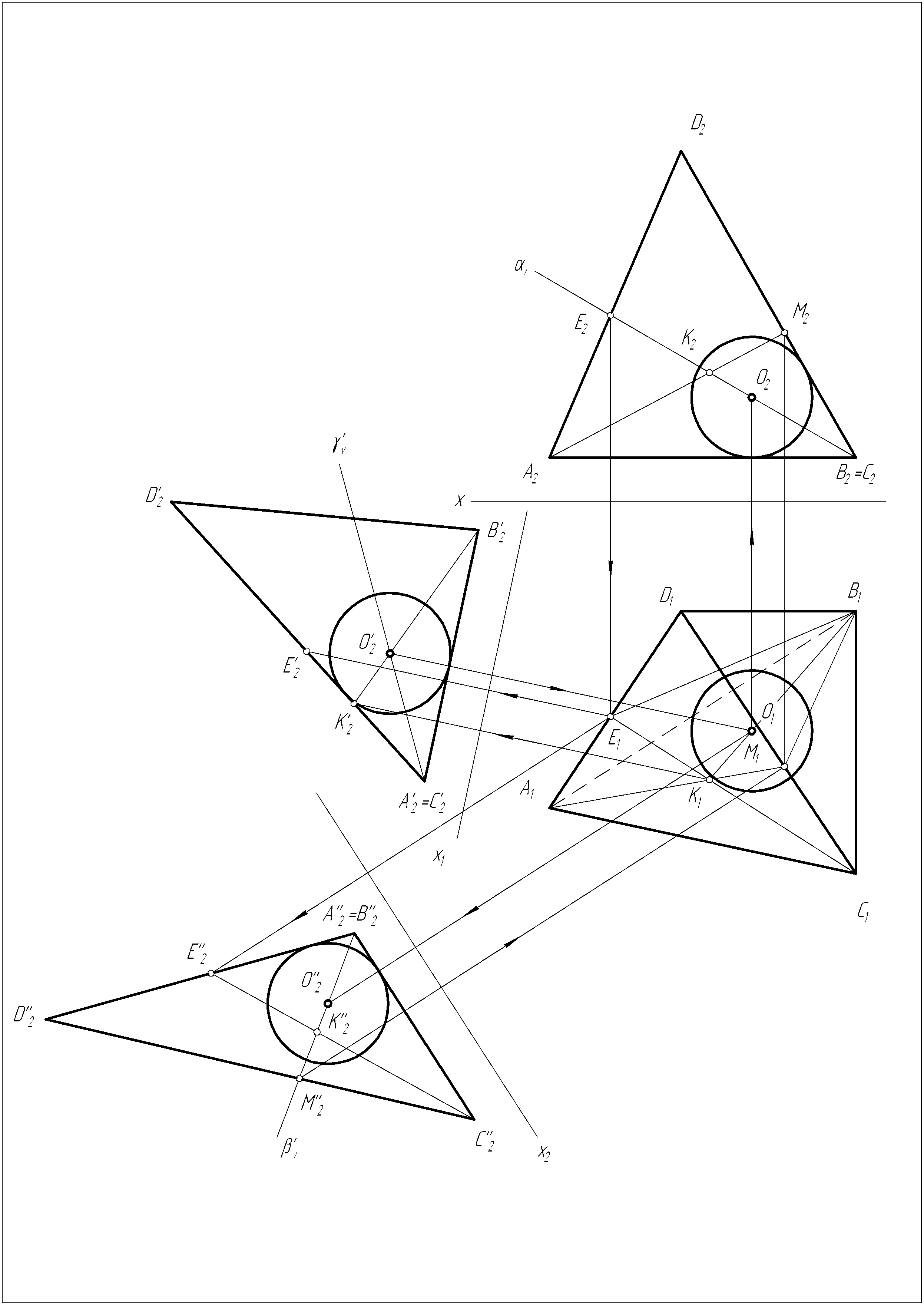
1. Строим биссекторную плоскость двугранного угла при ребре ВС (плоскость ).

2. Строим биссекторную плоскость двугранного угла при ребре АВ (плоскость ).

3. Строим линию пересечения плоскостей  и  (KB).

4. Строим биссекторную плоскость двугранного угла при ребре АС (плоскость ).

5. Строим точку пересечения плоскости  с прямой KB, т.е. точку О – центр вписанной сферы.

Решение задачи №18





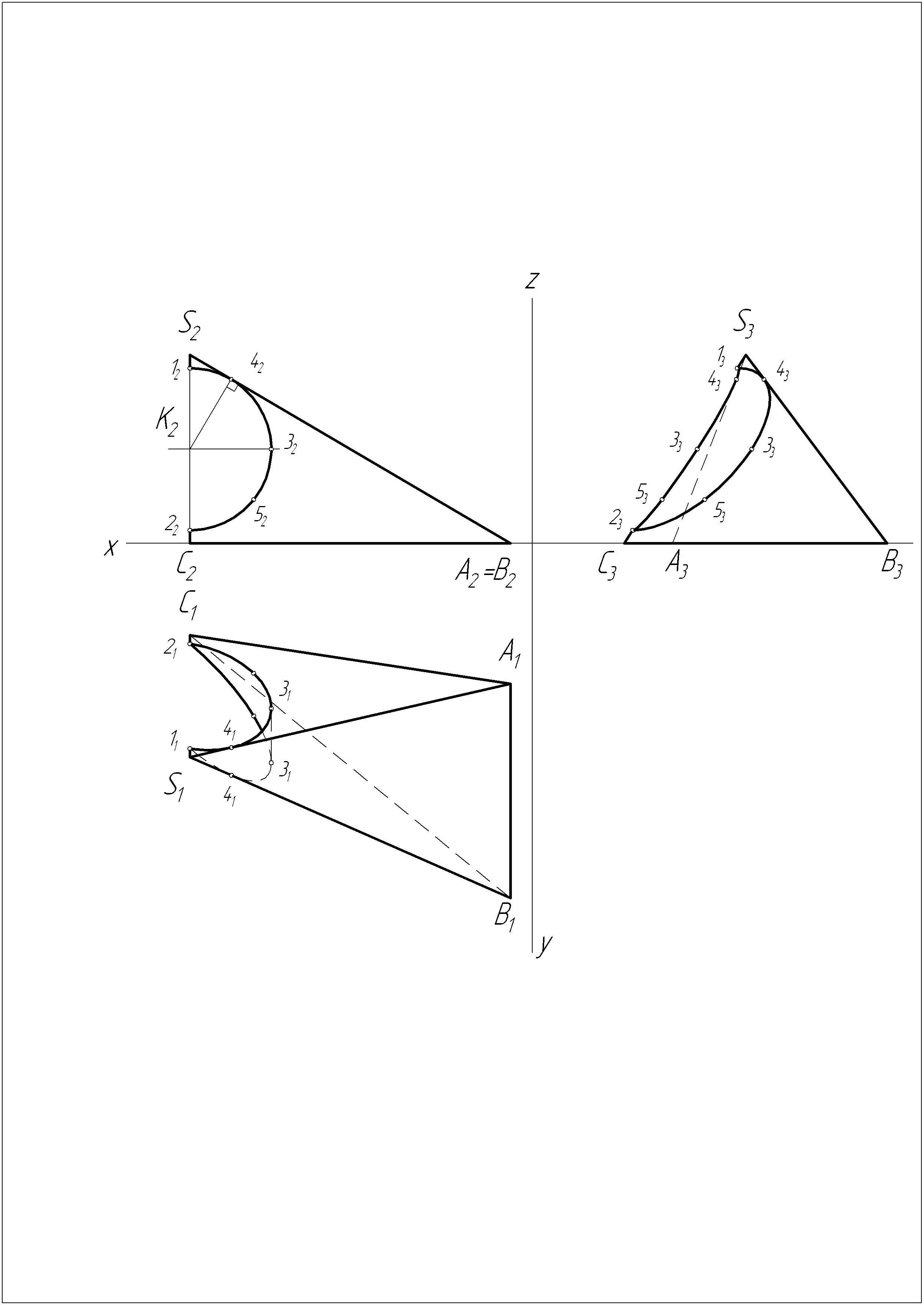
Решение задачи №19





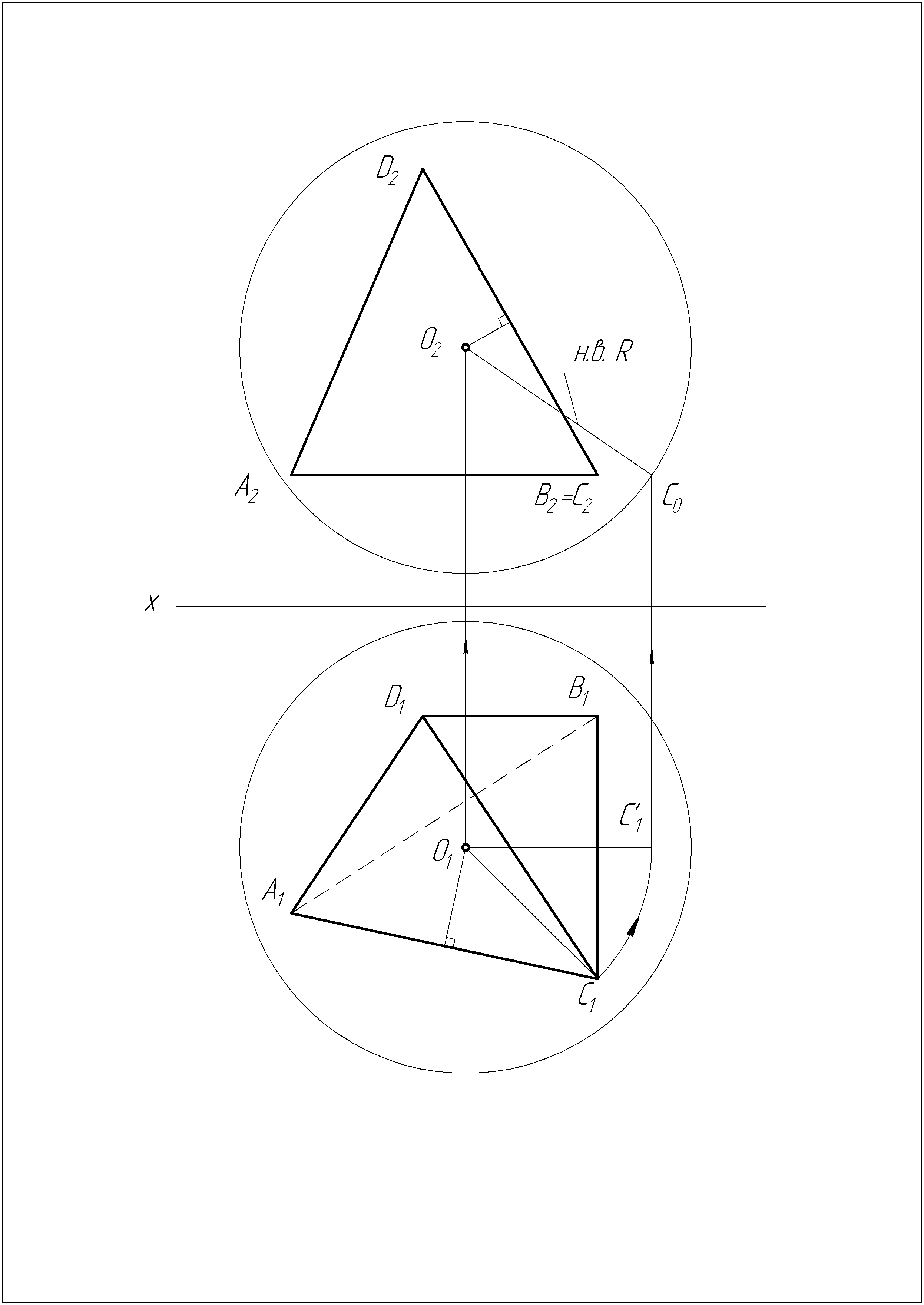
Точка О находится на пересечении перпендикуляров, восстановленных из центров описанных окружностей треугольников граней пирамиды.


Решение задачи №20





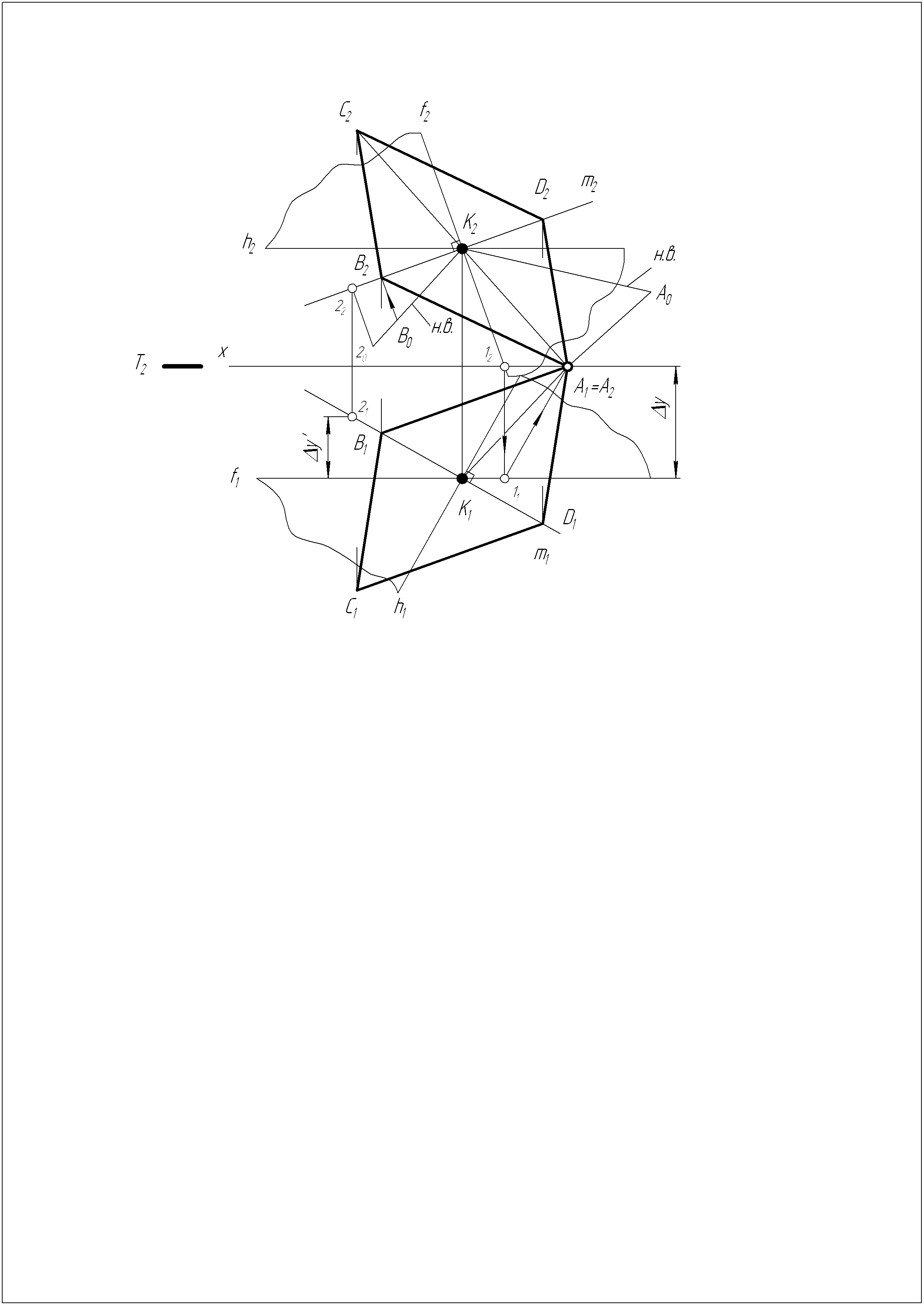
1. Проводим плоскость, перпендикулярную к прямой m.

2. Находим положение точки А как точки пересечения перпендикулярной плоскости с осью х.

3. Определяем натуральную величину большей диагонали (АK).

4. Находим положение точек для меньшей диагонали (АK=2ВK).

5. Строим проекции ромба.


СПИСОК ЛИТЕРАТУРЫ


1. Гордон, В.О. Курс начертательной геометрии / В.О. Гордон, М.А. Семенцов-Огиевский; под ред. В.О. Гордона. – 25-е изд., стер. – М.: Высшая школа, 2003.

2. Гордон, В.О. Сборник задач по курсу начертательной геометрии / В.О. Гордон, Ю.Б. Иванов, Т.Е. Солнцева; под ред. В.О. Гордона. – 9-е изд., стер. – М.: Высшая школа, 2003.

3. Курс начертательной геометрии / под ред. В.О. Гордона. – 24-е изд., стер. – М.: Высшая школа, 2002.

4. Начертательная геометрия / под ред. Н.Н. Крылова. – 7-е изд., перераб. и доп. – М.: Высшая школа, 2000.

5. Начертательная геометрия. Инженерная и машинная графика: программа, контрольные задания и методические указания для студентов-заочников инженерно-технических и педагогических специальностей вузов / А.А. Чекмарев, А.В. Верховский, А.А. Пузиков; под ред. А.А. Чекмарева. – Изд. 2-е, испр. – М.: Высшая школа, 2001.

6. Фролов, С.А. Начертательная геометрия / С.А. Фролов. – М.: Машиностроение, 1978.

7. Начертательная геометрия: учебник для вузов / Н.Н. Крылов, Г.С. Иконникова, В.Л. Николаев, Н.М. Лаврухина; под ред. Н.Н. Крылова. – 6-е изд., перераб. и доп. – М.: Высшая школа, 1990. – 240 с.: ил.


Учебное издание


АЛЕКСЕЕВА ЭМИЛИЯ АНТОНОВНА

ЛЕВИНА НАДЕЖДА СЕРГЕЕВНА

СВЕТЛОВА ОЛЬГА РАФАИЛОВНА

ЛЕОНОВА ГАЛИНА ДМИТРИЕВНА


ЗАДАЧИ ПОВЫШЕННОЙ СЛОЖНОСТИ

ПО ДИСЦИПЛИНЕ

«НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ»


Методические рекомендации для самостоятельной работы студентов

механических специальностей


Редактор

Технический редактор Сазонова В.П.

Подписано в печать 05.03.2010. Формат 6084/8

Усл. п. л. 5,5. Уч.-изд. л. 5,12

Печать – ризография, множительно-копировальный

аппарат «RISO EZ300»


Тираж 30 экз. Заказ 2010–39

Издательство Алтайского государственного

технического университета

656038, г. Барнаул, пр-т Ленина, 46


Оригинал-макет подготовлен ИИО БТИ АлтГТУ

Отпечатано в ИИО БТИ АлтГТУ

659305, г. Бийск, ул. Трофимова, 27