Общая характеристика работы

Вид материала

Документы

Подобный материал:

• Содержание лекций  Модели местного самоуправления в России  Местное самоуправление:, 786.51kb.
• Общая характеристика работы актуальность работы, 336.09kb.
• Общая характеристика работы актуальность работы, 236.99kb.
• Общая характеристика работы актуальность работы, 227.87kb.
• Общая характеристика работы актуальность работы, 227.87kb.
• Задачи физического воспитания детей дошкольного возраста. Общая характеристика средств, 34.6kb.
• Реферат по курсу: экология на тему: Общая характеристика экосистем, как, 726.64kb.
• Научная работа студентов, 2153.55kb.
• Научная работа студентов, 2114.42kb.
• Общая характеристика работы актуальность работы, 487.01kb.

p газообразного радиатора ИВЧ, то после того, как пройден черенковский порог для электронов с минимальной энергии в пучке, интенсивность ИВЧ в некотором диапазоне давлений начинает зависеть от p линейно. В точке пересечения экстраполированной прямой зависимости интенсивности ИВЧ от давления газа с фоновым значением интенсивности определяется показатель преломления газа n^*. Величина 1/n^* соответствует средней скорости частиц пучка в единицах скорости света.

Метод использовали для определения средней скорости пучка электронов микротрона. Ширина распределения пучка с помощью магнитной фокусирующей системы, установленной перед камерой с газом - радиатором, была снижена до ± 4 кэВ по сравнению с ± 50 кэВ на выходе микротрона. Имелся очень короткий нелинейный участок по n из-за дополнительной немонохроматичности пучка, которая была обусловлена рядом причин, в том числе, потерями энергии во входном окне и в газе – радиаторе. Чтобы снизить влияние дисперсии света в радиаторе, перед фотоумножителем был установлен фильтр с полосой пропускания 10 нм. В работе (Jennings et al., 1960) было сделано важное усовершенствование: показатель преломления находили не по давлению газа, как в работе 1958 г., а непосредственно контролировали встроенным интерферометром Жамена.

На возможность определения распределения частиц по скоростям по участку нелинейной зависимости интенсивности излучения от давления, авторы упомянутых работ не обратили внимания. В работе (De Almeida et al., 1974), в которой спустя полтора десятилетия был предложен тот же метод для определения распределения скорости (энергии) электронов на выходе ускорителей медицинского назначения, но без ссылок на работы (Bhidey et al., 1958, Jennings et al., 1960), наличие нелинейного участка даже не отмечено.

В 4.2 рассматривается метод нахождения спектра скорости частиц в пучке по зависимости интенсивности ИВЧ в оптическом диапазоне от показателя преломления радиатора.

В работах (Trukhanov et al., 1977, Вайнер, Труханов, 1979, Труханов, 1990, Trukhanov, Shvedunov, 2004, Trukhanov, Poliektov, Shvedunov 2004) соискателя и др. было показано, что именно нелинейный участок зависимости интенсивности ИВЧ в координатах I(n^-2) позволяет находить уже не среднюю скорость частиц в пучке, а их распределение по скорости. Если потребовать, чтобы оптическая система собирала на фотоприемник одну и ту же долю ИВЧ, испускаемую частицами независимо от места и направления их пролета через радиатор, то спектр по скорости можно найти даже в случае произвольного и неизвестного углового распределения частиц, что совершенно исключено в других методах.

При измерении спектра пучка ускорителя указанное выше условие светособирания выполняется элементарно. В случае произвольного углового распределения частиц оно реализуется, например, в шаровом черенковском детекторе.

Рассмотрим случай оптического диапазона. Если показатель преломления равен n(ν), то число фотонов N_ph частоты ν в единичном частотном диапазоне, достигающих фотоприемника (фотоумножителя), можно записать как (Труханов, 1990):

(4.1),

где f(β) - распределение частиц в пучке по скорости, m – длина пути частицы в радиаторе, g – некоторый множитель. Уравнение (4.1) представляет по отношению к интересующей функции f(β) интегральное уравнение Вольтерра первого рода, правая часть которого задана с погрешностью. Его решение относится к так называемым некорректно поставленным (или плохо-обусловленным) задачам. Однако в последние десятилетия были развиты новые эффективные подходы к ним, позволяющие получать устойчивые решения.

Преобразуем уравнение (4.1) в уравнение типа свертки (Труханов, 1990). Введем переменные:

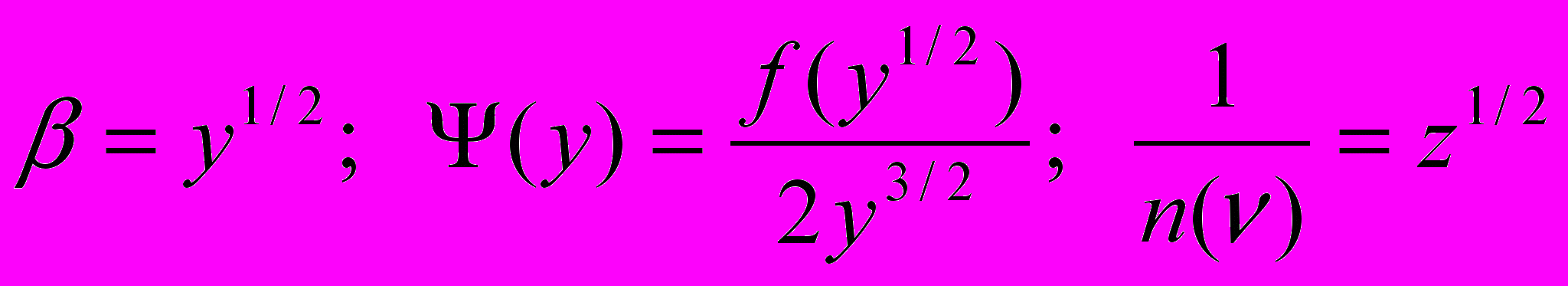
(4.2)

Имеем:

(4.3)

Последовательно дифференцируя (4.3), получим решение:

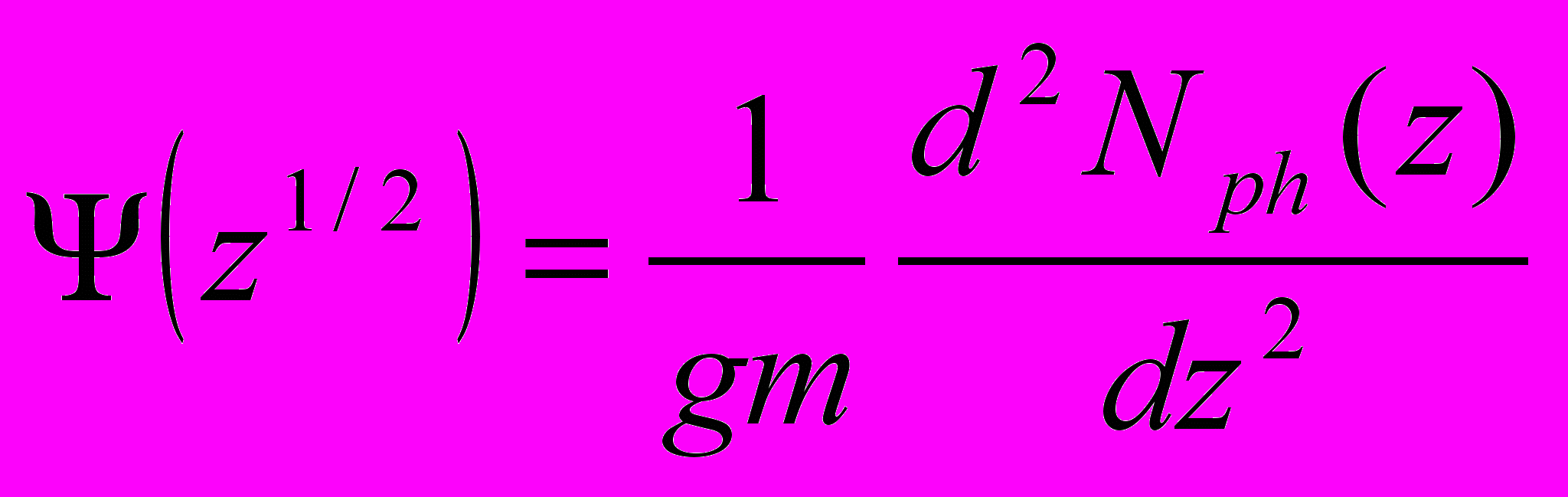. (4.4)

В работах (Trukhanov et al., 1977, Вайнер, Труханов, 1979, Труханов, 1990) решение уравнения (4.1) было выражено через первую и вторую производные интенсивности ИВЧ. В п. 4.2 обращается внимание также на то, что уравнение (4.1) было записано в работе (Труханов, 1990) не для числа фотонов, а для интенсивности. Запись через число фотонов в наших последующих работах (Trukhanov, Shvedunov, 2004а, Trukhanov, Poliektov, Shvedunov 2004б) и в настоящей работе более соответствует специфике фотоприемников.

По измерениям I(n) при 1/n < β _min , т.е. по линейному участку зависимости I(1/n²), найти вид спектра нельзя. Действительно, преобразуем уравнение (4.1), считая, что функция f(β) нормирована к 1:

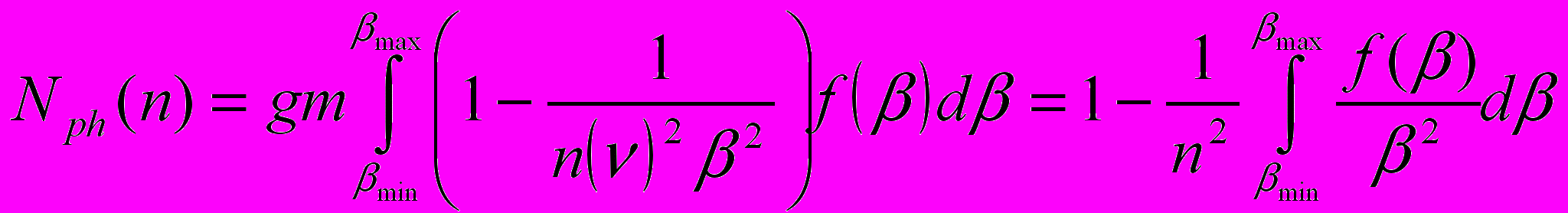(4.1а)


Уравнению (4.1а) могут удовлетворять самые различные функции f(β). Правая часть этого уравнения является прямой в координатах N _ph (n), 1/n². Из уравнения (4.1а) также следует, что линейная экстраполяция I(n) к нулю по n, которую использовали авторы работ (Bhidey et al., 1958, Jennings et al., 1960), справедлива лишь при n ~ 1.

Первая производная уравнения (4.3) представляет собой интегральный спектр, т.е. число частиц со скоростью (энергией), равной или большей нижнего предела интеграла.Такая возможность также необычна, так как если чувствительность порогового детектора зависит от энергии, получить интегральный спектр, измеряя отклик в интересующей точке, как правило, не удается.

Детектор, основанный на нахождении первой производной функции I(n^-2), может быть использован на выходе ускорителя как пороговый датчик, сигнализирующий о превышении некоторой регламентированной предельной энергии (например, выше которой может наводиться радиоактивность в облучаемом продукте). Это позволит следить за режимом ускорения и управлять им.

Уравнение (4.1) может быть решено и другими методами. Однако сведение интегрального уравнения Вольтерра первого рода к уравнению второго рода дифференцированием здесь нерационален. Действительно, поскольку ядро уравнения (4.1) обращается в нуль в точке β =1/n, то требуется продифференцировать (4.1) дважды. В результате получим интегральное уравнение Вольтерра второго рода, но с правой частью, содержащую вторую производную, которая уже является решением нашей задачи. Поэтому решение полученного уравнения Вольтерра второго рода является излишним. Могут быть применены также аналоговые способы для получения второй производной в эксперименте.

В п. 4.2 рассматриваются некоторые практические вопросы создания спектрометров для ускорителей.

Предпочтительно выбирать одноатомные газы, чтобы избежать трудностей, связанных с возможной диссоциацией молекул в пучке. Если ширина распределения электронов по энергии мала, что характерно, например, для микротронов и некоторых других ускорителей, то требуемое изменение давления не превышает нескольких процентов. Нагрев газа-радиатора не должен влиять на характеристики спектрометра, если корпус обладает достаточной прочностью и жесткостью. Нагрев в импульсе тоже несущественен, если длительность импульса мала. Непосредственное определение коэффициента преломления газа и его изменений в процессе измерений и наличие узкополосного фильтра перед фотоумножителем снизят погрешности эксперимента, обусловленные дисперсией. Поток фотонов ИВЧ вблизи порога для большинства ускорителей по оценкам более чем достаточен для надежной его регистрации. Интенсивность переходного излучения (ПИ), возникающего на различных граничных поверхностях (входное окно и т.п.), не меняется сколько-нибудь заметно при изменении давления (т.е. показателя преломления среды) и, следовательно, практически не влияет на результаты измерения. Фон ПИ может быть снижен, например, уменьшением апертуры перед фотодетектором. Действительно, ИВЧ вблизи порога испускается в узком конусе под углом θ_ЧИ = arccos (1/nβ), который, например, в газе при энергиях до ~ 20 МэВ значительно меньше, чем угол, под которым испускается ПИ: θ_ПИ = 1/γ, где γ – релятивистский фактор.

При оценке разрешающей способности предложенного монитора энергетического распределения в пучке необходимо принимать во внимание ионизационные и радиационные потери в нем и их флуктуации. Если энергетические потери и их флуктуации по предварительной оценке могут внести заметный вклад в спектр частиц, то на следующей стадии необходимо уточнить найденный предложенным методом спектр, решая уже известную в литературе задачу о восстановлении первичного спектра по спектру частиц, прошедших слой вещества.

Метод опробован на линейном ускорителе электронов с одновременным контролем результатов с помощью магнитного спектрометра на выходе (Вайнер и др., 1983) и на разрезном микротроне НИИЯФ МГУ (Trukhanov, Poliektov, Shvedunov 2004б).

В п. 4.3 рассматривается метод определения скорости частиц пучка, основанный на использовании дисперсии света в радиаторе.

Зависимость показателя преломления радиатора (и, соответственно, порога ИВЧ) от длины волны приводит к некоторым трудностям в рассмотренном выше методе измерения распределения энергии электронов в пучке ускорителя. Например, для повышения точности измерения характеристик пучков с малой шириной распределения частиц по скорости необходима установка узкополосного фильтра перед фотоприемником и т.п. Дисперсия вообще вызывает сложности в технике черенковских счетчиков и спектрометров, вынуждая прибегать к ахроматизации оптических систем и т.д.

Однако это явление оказывается «дружественным» в другом предложенном нами методе определения скорости частиц пучка (Trukhanov, Shvedunov, 2004а, Trukhanov, Poliektov, Shvedunov 2004б). В нем впервые используются спектральные свойства ИВЧ. Спектральный прибор, расположенный после черенковского детектора, разлагает ИВЧ, возникающее в радиаторе, в спектр. Поскольку показатель преломления зависит от длины волны, порог ИВЧ также оказывается ее функцией. Таким образом, измерение числа фотонов с разной длиной волны эквивалентно описанному выше методу измерения распределения частиц в пучке по энергии при изменении давления газа в мониторе или измерениям с большим числом пороговых счетчиков. Число фотонов (или же интенсивность ИВЧ) на разных длинах волн регистрируется с помощью линейки фотодетекторов

В оптическом диапазоне показатель преломления с увеличением длины волны убывает. Учитывая такой характер кривой дисперсии и то, что порог ИВЧ на длине волны λ определяется в данном случае соотношением 1/β_λ = n(λ), отмечаем: чем выше скорость электрона, тем большей длине волны соответствует порог ИВЧ. Таким образом, для данной кривой дисперсии порог различен для различных участков спектра частиц по скорости (энергии). При энергии частицы, равной черенковскому порогу, число фотонов (или интенсивность) ИВЧ равна нулю, но растет с убыванием длины волны, на которой регистрируется ИВЧ от данной частицы.

Число фотонов ИВЧ с длиной волны λ в единичном интервале, которые испускаются электронами с распределением по скоростям f(β), можно записать как:

(4.5)

Используя в данном случае соотношение для порога ИВЧ 1/β_λ = n(λ), перепишем (4.5): 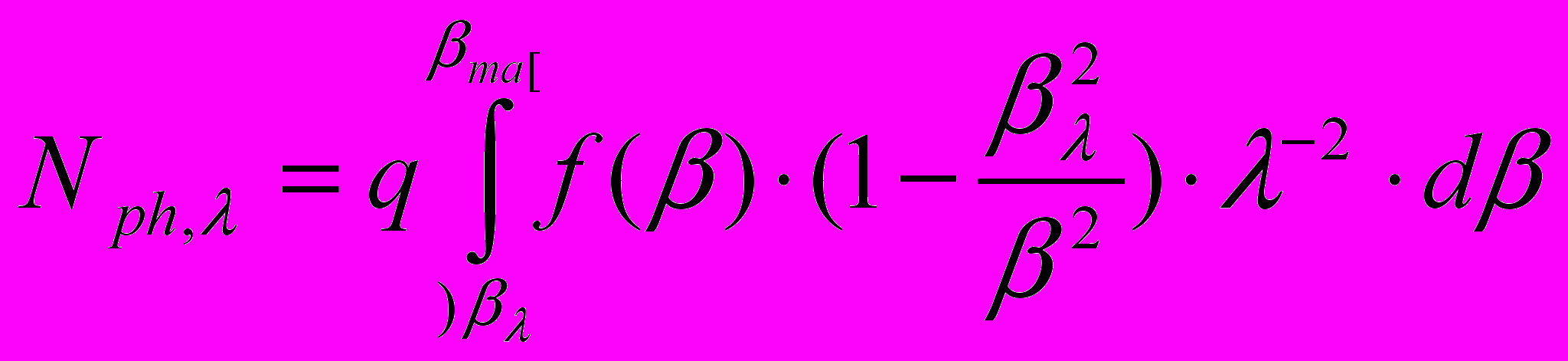(4.6)

Прибегая к известной формуле Коши для дисперсии (4.7), найдем: (4.8)

Преобразуем (4.6), дифференцируем по β_λ, опять преобразуем, снова дифференцируем, еще раз преобразуем и получаем:

(4.9)

Таким образом, решение задачи о распределении частиц по скорости в пучке ускорителя в данном случае сводится в принципе к определению числа фотонов ИВЧ в соответствующих участках оптического спектра и нахождению их первых и вторых производных по длинам волн.

Как уже отмечалось выше, нахождение производных по данным, содержащим погрешность, принадлежит к некорректным или плохо поставленным задачам. Поэтому здесь также необходимо использование соответствующих известных методов. Разумеется, можно и непосредственное решать интегральное уравнение Вольтерра первого рода (4.6), что также приводит к плохо поставленной задаче. В любом случае возможен выбор между двумя и более способами решения. Возможно, что еще более надежно использовать несколько способов, сопоставляя результаты между собой. Заметим, что решение через производные позволяет более удобно проводить модельные расчеты.

Предложенный метод может быть особенно удобен для непрерывного мониторинга пучков ускорителей с узким спектром. Например, при энергии 30 МэВ и ширине спектра 0,2-0,25 МэВ необходимый спектральный диапазон ИВЧ в случае ксенона, как радиатора, лежит от 400 до 600 нм. В принципе метод позволяет находить распределение частиц по скорости в единственном импульсе ускорителя, а если быстродействие фотоприемников или встроенного перед ними оптического затвора велико – то и внутри импульса. При высоких энергиях метод является практически неразрушающим. По-видимому, его можно применять не только для мониторинга пучков электронных ускорителей, но и ускорителей тяжелых частиц.

В заключение кратко в главе 4 рассмотрены возможности измерения спектра скоростей ускоренных тяжелых ионов с помощью предложенных методов. При скорости частиц β = 0,9÷0,95; и ширине распределения 10^-3 и меньше показатель преломления радиатора должен быть порядка 1,1, а его изменения должны составлять 10^-3 и меньше от этой величины. Здесь возможны варианты. Один из них – использование в качестве радиатора известного фторорганического соединения перфтор-3-бутилтетрагидрофурана (коммерческое название FC-75), при температуре порядка 240⁰ С и давлении около 1,4÷1,8 МПа. На ускорителях с существенно более высокими энергиями проблемы с выбором радиаторов упрощаются.

С использованием зависимости интенсивности ИВЧ от показателя преломления радиатора (в том числе, явления дисперсии) оказывается возможным создавать эффективные устройства для измерения параметров потоков частиц. Пороговый характер излучения упрощает регистрацию при наличии фона, практическая безынерционность позволяет регистрировать процессы с высоким временным разрешением, линейность дает возможность работать в широком диапазоне изменения плотности потока, причем при больших плотностях можно использовать достаточно тонкие радиаторы. При работе в оптическом диапазоне упрощается борьба с помехами и наводками.


ВЫВОДЫ


1. Для обеспечения радиационной безопасности космических кораблей при будущих межпланетных полетах может быть применена магнитная защита обитаемого отсека от галактических космических лучей и заряженных частиц солнечных событий.

2. Разработаны теоретические методы определения в первом приближении требуемых для защиты магнитных полей без учета ослабления потоков ГКЛ и СКЛ в веществе корабля и элементах (сверхпроводник, силовая конструкция и т.д.) магнитной защиты.

3. Разработан обратный траекторный метод расчета ослабления потоков ГКЛ и СКЛ магнитной защитой и определения доз в фантоме за ней с учетом взаимодействия заряженных частиц с веществом корабля и элементами магнитной защиты (комбинированная защита полем и веществом). Он основан на расчетах траекторий частиц, стартующих из интересующего микрообъема фантома во внешнее пространство и набирающих энергию в веществе до момента их выхода из защиты с последующим «сшиванием со спектром частиц в космосе при учете возможности захвата частиц магнитным полем из-за ионизационных потерь.

4. На основе обратного траекторного метода в параметрическом виде определены энергии отсечки частиц ГКЛ для снижения доз до предполагаемых в межпланетном полете. При полете к Марсу энергия отсечки должна составлять не менее (0,6 ÷ 0,8) ГэВ/нуклон. При этом устраняется радиационная опасность от СКЛ, что позволит осуществлять будущие межпланетные полеты независимо от солнечной активности.

5. Предложены варианты специальных магнитных систем для создания искусственного геомагнитного поля при межпланетном полете и при работах на лунной базе. Показано, что такие системы будут обладать сравнительно небольшой массой и энергопотреблением.

6. Поддержание постоянства в обитаемом объеме величины модуля магнитного поля с помощью магнитных систем, управляемых магнитометром, должно способствовать устранению нежелательных эффектов воздействия на экипажи околоземных объектов вариаций уровня ГМП на борту. Выбраны оптимальные режимы питания магнитных систем для орбит с разными углами наклона.

7. Широкополосный фон ЭМП на борту межпланетных кораблей и на лунной базе следует рассматривать как множество виртуальных источников и соответственно его нормировать. Распространенное мнение, что если электромагнитное поле удовлетворяет требованиям электромагнитной совместимости аппаратуры, то для человека оно тем более не превышает предельно допустимый уровень, оказывается в условиях широкополосного фона некорректным, что показано на примере аппаратуры, поставляемой на Российский Сегмент МКС. Необходим пересмотр требований к испытаниям и допуску аппаратуры на борт, а также к бортовой аппаратуре для измерений и мониторинга электромагнитного поля на борту.

8. В связи с положительным опытом использования радиотермометрии для исследования воздействия моделируемых факторов космического полета, необходима дальнейшая разработка методов и аппаратуры радио - и акустотермометрии для продолжения исследований, для использования их в отборе, при тренировках и в качестве бортовой аппаратуры контроля состояния членов экипажа, особенно, в условиях межпланетного полета и работ на Луне.

9. Разработаны применительно к радиобиологическим и радиационно-физическим экспериментам в целях обеспечения радиационной безопасности человека в космосе методы определения распределения скоростей частиц в пучках ускорителей, основанные на использовании зависимости интенсивности излучения Вавилова-Черенкова от показателя преломления радиатора. Они практически не разрушают пучок, позволяют контролировать и изменять его параметры в процессе облучения объекта и проводить измерения в пучках с неизвестным угловым распределением. С их помощью станет возможным неразрушающим способом определять распределение по скоростям (по энергии) частиц даже в одиночном сгустке частиц и внутри этого сгустка. Таких возможностей другие методы пока не имеют.


Список работ, опубликованных по теме диссертации


1 Вайнберг Б.Р. Об одном методе расчета потоков частиц в системах магнитной защиты / Вайнберг Б.Р., Егоров Ю.В., Труханов К.А., Шлапак В.Н //. Вопросы дозиметрии и защиты – М.: МИФИ, 1978. - Вып. 17. - С. 149 – 154.

2 Вайнер Е.А. О возможности измерения некоторых характеристик пучков заряженных частиц на выходе ускорителей / Вайнер Е.А., Труханов К.А. // Доклады 3-го Всесоюзного совещания по применению ускорителей в народном хозяйстве – Ленинград. 26-28.06.1979. -Т.3. - С. 345-350.

3 Вайнер Е.А. Использование излучения Вавилова-Черенкова для измерения спектра ускоренных электронов / Вайнер Е.А., Труханов К.А., Пономарев В.Н., Филин Л.Н.// Вопросы атомной науки и техники. Серия: техн. физич. эксперимента.- Харьков. - ХФТИ АН.- 1983. - Вып. 2/14. - С. 70.

4 Васин А. Л. Оценка вклада широкополосного квазинепрерывного электромагнитного фона в дозовую нагрузку / Васин А. Л., Труханов К. А.// Радиац. биология. Радиоэкология - М., 2003. -Т. 43.- В.5. - С. 590-593.

5 Григорьев Ю.Г. Избранные вопросы теории биологического действия электромагнитных полей / Григорьев Ю.Г., Труханов К.А., Васин А.Л // Глава 7 монографии «Электромагнитные поля и здоровье человека; под ред. Ю.Г. Григорьева – М.: Изд-во РУДН. - 2002. - С. 124- 140

6 Зак П.П. О возможном механизме зрительных фосфенов, возникающих у космонавтов под действием тяжелых заряженных частиц / Зак П.П., Труханов К.А., Бриндикова Т.А., Лебедев В.М., Спасский А.В., Федорович И.Б., Островский М.А.// Труды II-го Международного Симпозиума и II-х Сисакяновских чтений. Москва – Дубна 29.05-1.06.01. -Дубна. Изд-во ОИЯИ. - Т. I. - С. 216-219.

7 Мацнев Э.И. Использование метода радиотермометрии (РТМ) при моделировании воздействия экстремальных факторов на организм человека. / Мацнев Э.И., Труханов К.А., Яковлева И.Я.// В сб. тезисов 1-го Международного Конгресса “Слабые и сверхслабые поля и излучения в биологии и медицине” - С-Пб. 16-19.06.1997. - С. 19.

8 Труханов К.А. Корреляционная радиотермометрия / Труханов К.А.// Там же. - С. 89-90.

9 Труханов К.А. О возможной роли эффекта Ааронова - Бома в биологическом действии магнитного поля / Труханов К.А. //Косм. биол. и мед. (Авиакосм. и экол. медицина). 1978. - № 3. - С.82-83.

10 Труханов К.А. Возможности пассивного определения некоторых характеристик биологической среды на основе радиометрии / Труханов К.А. // В сборнике докладов 2-й Международной Конференции «Радиоэлектроника в медицинской диагностике: оценка функций и состояния организма». Москва. 23-26.09.1997. - С. 32-35.

11 Труханов К.А. Измерение глубинной температуры методом радиотермометрии при моделировании воздействия некоторых экстремальных факторов на организм человека / Труханов К.А. // Там же. - С. 78-80.