Удк 631. 6 Обоснование водных мелиораций агроландшафтов (на примере московской области)

Вид материала

Автореферат диссертации

Содержание Н - полный напор почвенной влаги; C OY, справа - осью симметрии, проходящей через середину элювиального элементарного ландшафта. Сверху область ограничена осью OX W - объемная влажность почвы; Ψ Нi,к - напор в блоке с координатами (i,k) Глава 4. Экспериментальная проверка математической модели

Подобный материал:

• Удк (631. 527+631. 531): 635. 34 Научное обоснование и разработка системы методов селекции, 1105.12kb.
• Удк 635. 649:(631. 52+631. 53) Теоретическое обоснование и практическое использование, 946.29kb.
• Удк 631. 468: 631. 81 Гаврилюк В. А., к с. г н.,, 157.57kb.
• Н. И. Вавилова удк 631. 44. 5; 631. 58; 631. 674 № в государственной регистрации 81047036, 351.52kb.
• Удк [631. 6: 628. 3]: 631. 22+504., 114.95kb.
• Удк 338. 43: 631. 15: 631., 86.96kb.
• Московской области, 301.82kb.
• Отчет о реализации «Основных направлений развития архивного дела в Московской области», 202.87kb.
• Удк 581. 1: 631. 811: 631. 445, 23.49kb.
• Закон московской области, 1654.03kb.

Глава 3. Разработка математической модели

для прогнозирования передвижения влаги в ландшафтах


В третьей главе представлены вопросы разработки двумерной математической модели для расчета процесса передвижения влаги в почвах и грунтах ландшафтных катен.

Для более полного учета свойств компонентов ландшафтов и ландшафтообразующих факторов необходима разработка более совершенных методов расчета водного режима почв и грунтов природных и антропогенных ландшафтов, наиболее полно учитывающих факторы, влияющие на процесс перераспределения подземных вод. Перспективными в этом отношении являются методы моделирования передвижения влаги в почвах и грунтах, основанные на теории массопереноса в ненасыщенных и насыщенных пористых средах. Они характеризуются возможностью более адекватного отображения реальных условий поступления и перераспределения влаги в почвах. В основе этих методов лежат аналитические или численные решения дифференциальных уравнений влагопереноса, полученных на основе изучения состояния и передвижения почвенной влаги.

Возрастающие требования к точности прогноза водного режима агроландшафтов и выбора мелиоративных режимов вызывают необходимость количест­венную оценку процесса передвижения влаги выполнять с помощью двумерных математических моделей нестационарного влагопереноса. В связи с силь­ной нелинейностью двумерные дифференциальные уравнения влагопе­реноса не имеют в настоящее время точных аналитических решений и решаются, как правило, численными методами с использованием вычислительной техники. Анализ имеющихся математических моделей и алгоритмов показал необходи­мость их дальнейшего развития и приспособления к особенностям решаемых задач. В расчетах необходимо учитывать рельеф поверхности земли природных и антропогенных ландшафтов, климатические характеристики, испарение и отбор влаги растительным покровом, переменную мощность корнеобитаемой зоны растений, природную и привнесенную человеком слоистость и неоднородность свойств почвы и подстилающих горизонтов, влияние мелиоративных и агромелиоративных мероприятий, водообмен с нижележащими горизонтами.

Основное дифференциальное уравнение, описывающее движение воды в двумерной области можно записать следующим образом:

, (3)

где Н - полный напор почвенной влаги; C_W - коэффициент дифференциальной влагоемкости; K_Wx, K_Wy коэффициен­ты влагопроводности почвы в горизонтальном и вертикальном на­правлениях соответственно; е(x,y,t) - интенсивность отбора влаги кор­нями растений; W- объемная влаж­ность почвы; х, у - пространственные координаты; t - время.

Рассматриваемая двумерная область Ω {(x,y): x[0, B], y[0, L]} слева ограничена осью OY, справа - осью симметрии, проходящей через середину элювиального элементарного ландшафта. Сверху область ограничена осью OX, совпадающей с поверхностью земли, снизу - линией, совпадающей с границей подстилающего пласта (как частный случай - водоупора). Для учета рельефа поверхности земли выполнялось преобразование координат центров блоков расчетной схемы.

Для полного математического описания решаемой задачи кроме уравнения процесса задавались условия однознач­ности (начальные и граничные условия, распределение параметров), выделяющие конкретную задачу из рассматриваемого процесса. Начальным условием при решении исходного уравнения является распределение почвенной влажности или полного напора.

Граничные условия на поверхности земли могут быть различны­ми в зависимости от физической постановки задачи. При поливе, вы­падении осадков без образования слоя воды и наличии испарения задается поток влаги через поверхность почвы - граничное условие 2-го рода. При выпадении больших дождей или при поливе может создавать­ся слой воды, и на поверхности почвы задается гра­ничное условие 1-го рода. На нижней границе рассматриваемой области возможно несколько видов граничных условий 2-го рода. В случае если ниж­ней границей является водоупор, поток через нижнюю границу задается равным нулю. Более общим является случай, когда существует поток через нижнюю границу, вызванный дренирующим действием более глубокой гидрографической сети или наличием напорного подпитывания. На правой границе горизонталь­ный поток влаги принимается равным нулю - граничное условие 2-го рода. На левой границе при задании граничных условий вы­деляли три зоны. От поверхности земли до уровня воды в водном объекте горизонтальный по­ток принимался равным нулю - граничное условие 2-го рода. На отрезке, равном слою воды в водном объекте могут задаваться граничные условия 1-го или 2-го рода. На отрезке, равном расстоянию от дна водного объекта до нижней грани­цы рассматриваемой области, горизонтальный поток принимался равным нулю - граничное условие 2-го рода.

Для аппроксимации зависимости влажности почвы от капиллярного на­пора была использована формула следующего вида (Голованов А.И., Ведерников В.В., Зейлигер А.М.)

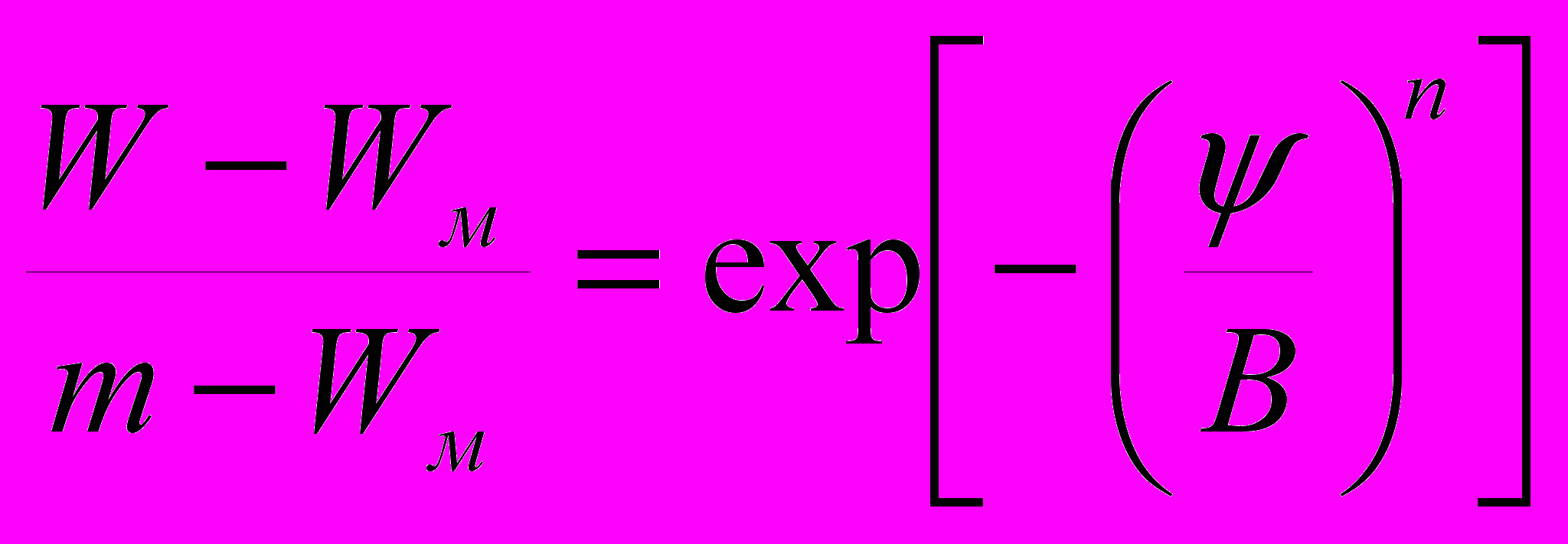, (4)

где W - объемная влажность почвы; Ψ - капиллярный напор; W_м - максималь­ная гигроскопичность; т – пористость почвы; В, п - безразмерные эмпирические коэффициенты.

Важной гидрофизической характеристикой почв является зави­симость коэффициента влагопроводности от объемной влажности почвы. В разработанной двумерной математической модели влагопереноса была использована следующая формула (Аверьянов С.Ф., Голованов А.И.)

, (5)

где k_w - коэффициент влагопроводности почвы; k - коэффициент филь­трации почвы; n – показатель степени.

Рассматриваемое двумерное уравнение влагопереноса относится к нелинейным параболическим урав­нениям в частных производных с параметрами, зависящими от иско­мой функции и со сложными начальными и изменяющимися во времени граничными условиями, учет которых является необходимым при опи­сании специфических особенностей формирования водного режима мелиорируемых агроландшафтов. Аналитических решений этого уравнения в опи­санной выше постановке в настоящее время нет, решить его можно численными методами с использованием вычислительной техники. Для решения данного уравнения нами был использован метод конечных разностей и составлена разностная схема, описывающая данное дифференциальное уравнение.

Для этого область непрерыв­ного изменения аргумента была заменена областью дискретного его изменения и дифференциальные операторы были заменены конечно-разностными операторами, то есть была осуществлена аппроксима­ция пространства решений дифференциального уравнения пространством сеточных функций.

Уравнение представлялось в конечно-разностной форме по неявной схеме и записывалось в следующем виде:




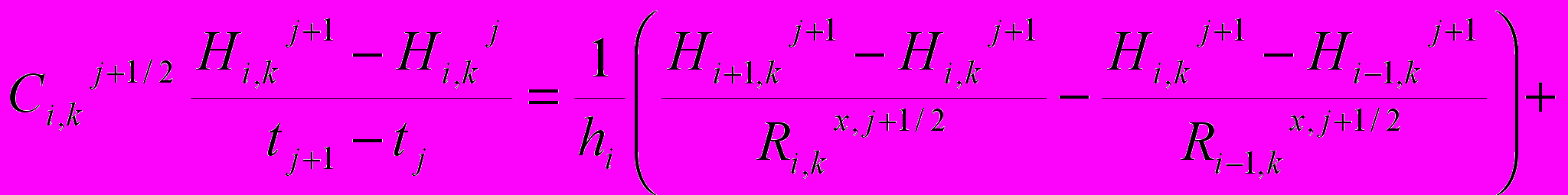
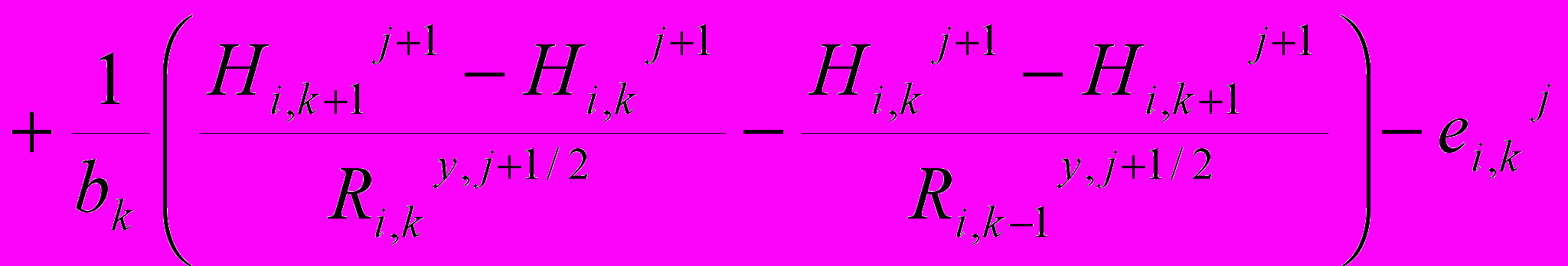(6)


i = 1, 2...N; k = I, 2 ... M; j = 0, 1, 2 ...G где i,k,j - номера шагов по вертикальной, горизонтальной и вре­менной координате соответственно; N,M,G - общее число шагов сетки по вертикальной, горизонтальной и временной координате соответственно; h_I - величина i-го шага пространственной сет­ки по вертикальной координате; b_k - величина k-го шага про­странственной сетки по горизонтальной координате; H_i,k^J ; H_i,k^J+1 - напоры в центре блока с координатами ( i, k ) на моменты времени j и j+1 соответственно; c^j+1/2_i,k - коэффициент влагоемкости блока с координатами (i,k) на момент времени j+1/2; R^x,j+1/2_i,k - сопротив­ление передвижению влаги из блока с координатами (i, k) в блок с координатами ( i + 1, k ) в момент времени j+ 1/2 ; R^y,j+1/2_i,k - сопротивление передвижению влаги из блока с координатами ( i , k ) в блок с координатами ( i , k+1 ) в момент вре­мени J+ 1/2 ; е^j_i,к - средняя удельная интенсивность массоизменения влаги (отбора корнями растений) за время л tj в блоке с координатами ( i , k ).

Сопротивления передвижению влаги из блока в блок определя­лись следующим образом:

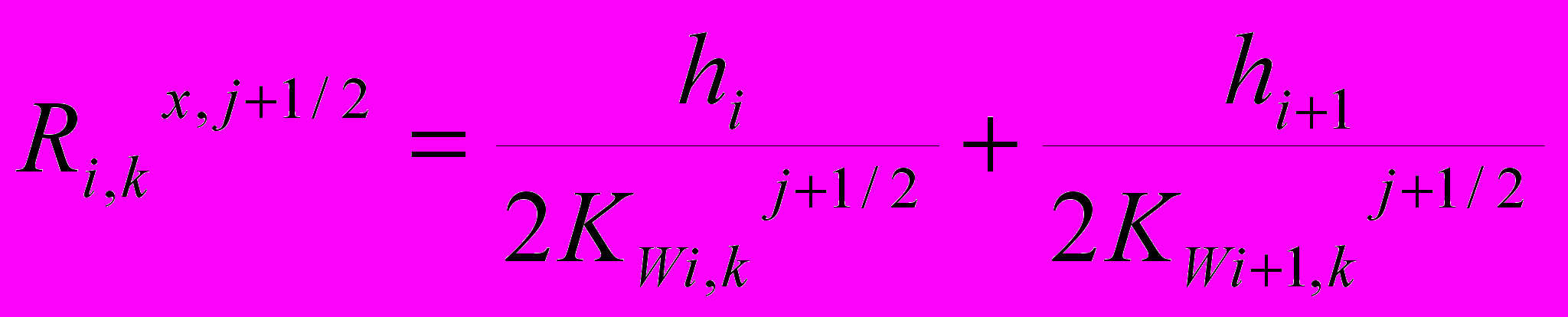(7)

(8)

где K^j+1/2_wi,k - коэффициент влагопроводности блока с координатами (i,к) при влажности W^j+1/2_i,k .

Конечно-разностное уравнение (6) решалось методом переменных направлений со средней аппроксимацией коэффи­циентов, для чего оно заменялось следующей системой:





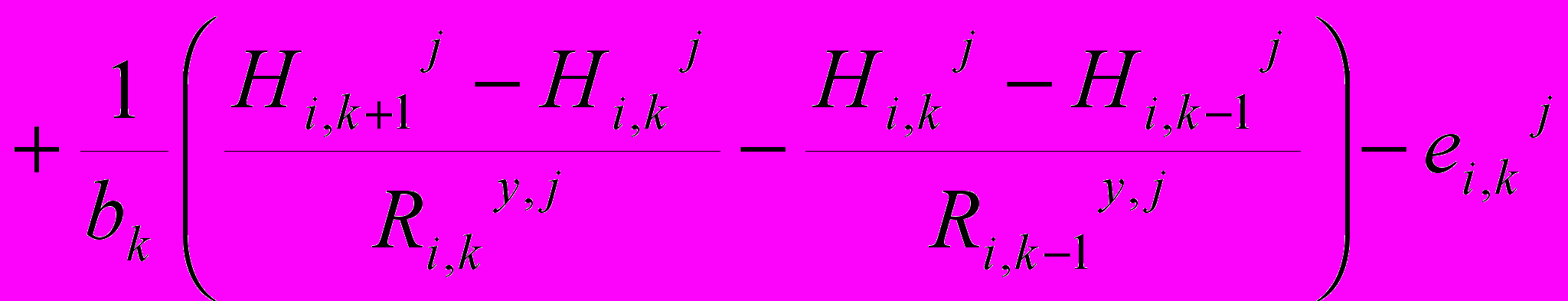
(9)






Для расчетов по каждому направлению был использован метод прогонки, для чего система уравнений приводилась к следующему виду:



(10)



где








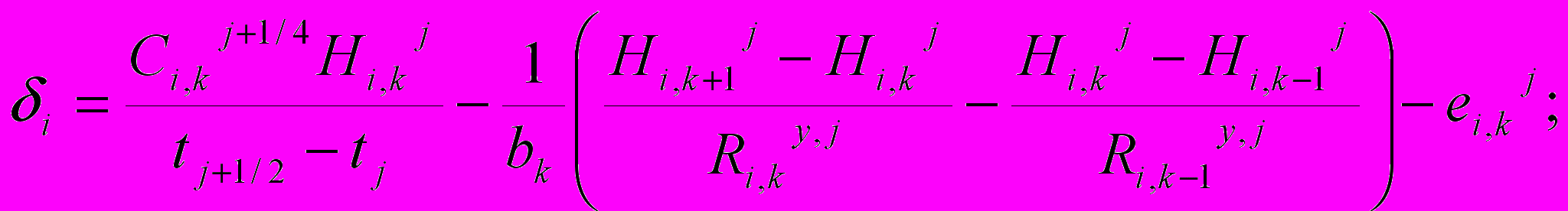
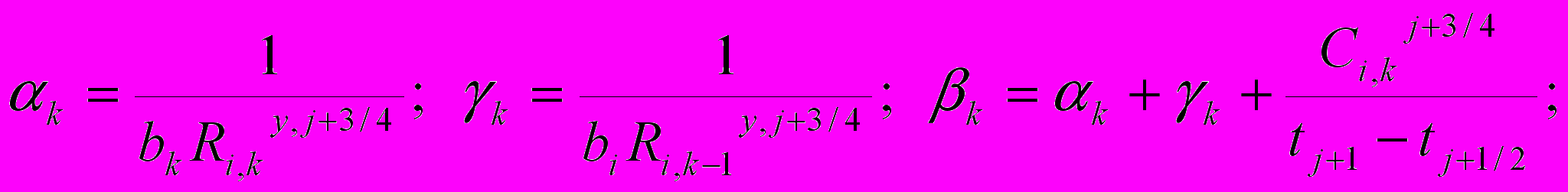
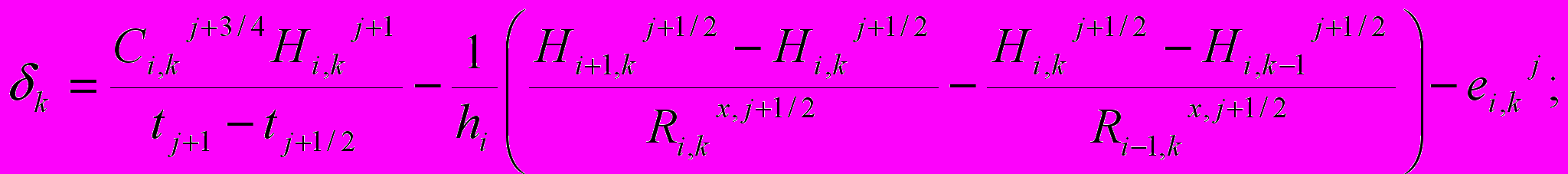
При прямой прогонке определялись прогоночные коэффициенты по рекуррентным формулам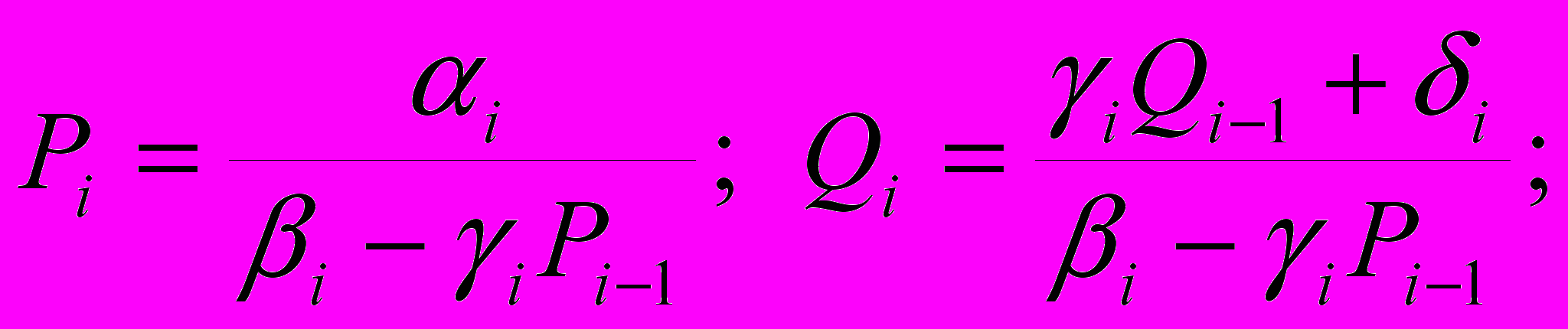



(11)



При обратной прогонке определялись сеточные функции, то есть напоры в узлах сетки



(12)



Прогоночные коэффициенты и напоры в крайних блоках находились из граничных условий.

Таким образом, в результате решения двумерного уравнения с помощью приведенного алгоритма на любой момент времени рассчи­тывается распределение напоров в пространстве ландшафтной катены. С по­мощью зависимости (4) осуществлялся переход от на­поров к влажностям, и вычислялось распределение влажности почвы по глубине и по ширине двумерной области.

При расчете коэффициентов влагоемкости и сопротивлений ис­пользовался метод итераций на каждом интервале временного шага. Итерации прекращались после выполнения следующего условия схо­димости


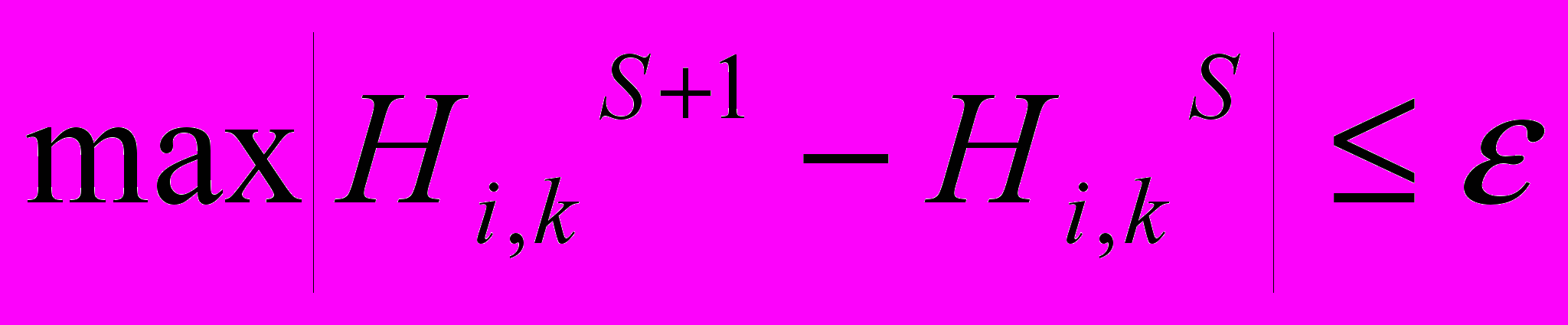(13)

где Нi,к - напор в блоке с координатами (i,k); 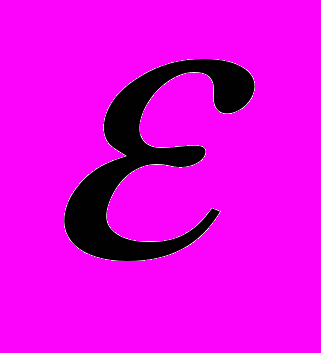- задан­ная погрешность вычислений; S = 0, 1, 2 ... N - номер итерации.

Для повышения точности расчетов в численном алгоритме ис­пользовался переменный шаг по пространственным координатам.

Для расчетов с помощью приведенного алгоритма нами была разработана программа на алгоритмическом языке Фортран. Про­грамма не предъявляет специальных требований к операционной системе и может быть реализована на персональном компьютере с процессором типа Р-4, и имеющем объем оперативной памяти порядка 512 Мб.

На основе разработанного метода расчета передвижения влаги в элементарных ландшафтах пространства ландшафтной катены можно решать многоцелевые практичес­кие задачи, и в частности:

1. Рассчитывать динамику напоров, влажностей, влагозапасов и уровней грунтовых вод в пространстве элементарных ландшафтов ландшафтной катены в естественных условиях.

2. Рассчитывать все составляющие водного баланса элементарных ландшафтов и всей ландшафтной катены в целом: эффективные осадки, эвапотранспирация, водообмен между элементарными ландшафтами (приток и отток воды), а также между ландшафтной катеной и водным объектом.

3. Рассчитывать водообмен между почвенным слоем и нижележащими горизонтами.

4. Производить количественную оценку влияния мелиоративных мероприятий (орошение, осушение) и агромелиоративных мероприятий на функционирование агроландшафтов.

5. Рассчитывать оптимальные мелиоративные режимы и параметры мелиоративных воздействий (орошение, осушение) в агроландшафтах для проектируемых мелиоративных систем.

Для прогнозирования влияния мелиоративных мероприятий, таких как орошение и осушение, на функционирование агроландшафтов в методике был предусмотрен блок расчета продуктивности агрофитоценозов по апробированной для территории страны модели продуктивности Шабанова В.В.


Глава 4. Экспериментальная проверка математической модели

передвижения влаги в почвах и грунтах ландшафтных катен


В четвертой главе представлены результаты экспериментальной проверки разработанной двумерной математической модели для расчета процесса передвижения влаги в почвах и грунтах ландшафтных катен.

Количественная оценка правильности расчетов по математической модели в первую очередь выполнялась путем вычисления невязки баланса влаги во всей рассматриваемой области (ландшафтной катене) и в подобластях (элементарных ландшафтах ландшафтных катен: супераквальном, трансаккумулятивном, трансэлювиальном, элювиальном) на каждом временном шаге. Программа расчетов составлена таким обра­зом, что за каждый расчетный промежуток времени вычисляются все составляющие водного баланса для всей рассматриваемой двумерной об­ласти и ее подобластей, и рассчитывается невязка водного баланса. Уравнение вод­ного баланса для всей рассматриваемой двумерной области (ландшафтной катены) имеет вид:

Oc - e_f - e_k – D - R + G + m - ∆W = 0 , (14)

где Ос - количество выпавших осадков; e_f и e_K - величина физического испарения и транспирации соответственно; D - величина дренажного стока; R – отток воды в водный объект (реку); G - вели­чина водообмена, вызванного напорным питанием; т - количество поливной воды; ∆W - изменение влагозапасов за расчетный период.

Соблюдение материального баланса в двумерной области может служить одним из критериев точности расчетов по математической модели влагопереноса. Как показали проведенные вычисления, не­вязка водного баланса в результате расчетов не превышала 0,001% от исходной величины влагозапасов, что говорит о высокой точности расчетов.

Важным этапом математического моделирования является выполнение проверочных расчетов и сопоставление результа­тов расчетов с экспериментальными данными. Если совпадение с данными полевых исследований получается достаточно удовлетворительным, это дает основание ис­пользовать модель в прикладных инженерных расчетах водного режи­ма мелиорируемых земель, что в свою очередь открывает большие возможности при проектировании инженерно-мелиоративных мероприя­тий.

Проверка разработанной модели данными экспериментальных исследований проводилась нами в два этапа. На первом этапе было выполнено сравнение результатов расчетов по модели с результатами полевых исследований, выполненных нами на опытном участке МГУП. Эти полевые исследования включали в себя изучение водного режима осушаемых почв по методике локальных полевых исследований, позволяющей получать характеристики водного режима почв и подстилающих грунтов в пределах водосборной площади отдельного регулирующего элемента - дрены.

На втором этапе было выполнено сравнение результатов расчетов по разработанной математической модели с опубликованными результатами полевых исследований водного режима почв ландшафтных катен, выполненных другими исследователями в Московской области.

Передвижение влаги в почвах является пространственным нестационарным процессом, ис­следование которого с учетом всех воздействующих природных факто­ров невозможно в лабораторных условиях. В лабораторных экспери­ментах не представляется возможным воспроизвести естественное сложение и естественную слоистость почв, влияние растительного покрова на расход влаги, водообмен с нижележащими горизонтами, динамику метеорологических характеристик и другие факторы. Поэ­тому для исследования процесса передвижения влаги в почвах требуется постановка полевых экспериментов, позволяющих изучать процесс в природных условиях с соблюдением естественно­го масштаба времени и пространства.

В зависимости от хода метеорологических элементов на одном и том же участке эффекты изучаемых в полевом опыте факторов мо­гут сильно колебаться по годам. Для получения достаточно надежных результатов требуется повторение опыта в разных погодно-климатических условиях. Поэто­му для проверки разработанной модели мы на первом этапе использовали результаты наших натурных исследований, выполненных в течение нескольких веге­тационных периодов (1979...1982 гг.), различавшихся между собой по условиям естественной влагообеспеченности.

Весь комплекс полевых исследований проводился на опытном участке МГУП, расположенном в Калязинском районе Тверской области. Тверская область граничит с Московской областью и по своему экономическому облику и экономическим связям относится к группе центральных областей Российской Федерации. Геологическое строение и геологическая история территории области в основных чертах сходны с геологическим строением и геологической историей соседних областей: Московской, Новгород­ской, Псковской. В области почти всюду с поверхности залегают отложе­ния четвертичного периода, лежащие под ними коренные породы об­нажаются лишь кое-где, преимущественно по берегам рек. В основном почвенный покров области представлен дер­ново-подзолистыми почвами, которые составляют 95,6% от общей площади пашни. В области распространены различные по степени оподзоленности почвы: слабо-, средне- и сильноподзолистые. Сопоставление величин испаряемос­ти и атмосферных осадков показывает, что Тверская область находится в зоне избыточного увлажнения, однако вегетационные периоды неко­торых лет характеризуются недостатком влаги.

Опытный участок имеет плоский рельеф и геоморфологи­чески приурочен к моренной равнине, местами прикрытой маломощ­ным прерывистый слоем песков, которая в этом районе замещает об­ширное зандровое пространство - Кимрско-Калязинскую зандровую низину. В геологическом строении принимают участие лед­никовые отложения Калининского горизонта, перекрытые покровны­ми отложениями. Литологически ледниковые отложения представлены средними и легкими суглинками. В моренной суглинистой толще по­всеместно отмечаются включения гравия, гальки и валунов. Водное питание массива, на котором расположен опытный участок, осуществляется за счет выпадения и застаивания атмос­ферных осадков. Этот тип водного питания характерен для право­бережья р. Волги между г. Кимры и г. Калязин, где преобладают верховые болота атмосферного питания, образовавшиеся вследствие близкого залегания водоупорного горизонта при незначительной дренированности плоских междуречий и обширных пойменных террас. Проведенные на опытном участке пьезометрические измере­ния показали, что на участке отсутствует грунтово-напорное пи­тание.

Для понижения уровня почвенно-грунтовых вод на участке был построен горизонтальный дренаж в виде системы закрытых дрен, впадающих непосредственно в ограждающие откры­тые каналы. Водоприемником служит ручей, впадающий в реку Сабля. В вертикальной плоскости закрытый дренаж запроектирован из ус­ловия обеспечения минимального уклона дрен 0,003. Устройство траншей для дрен осуществлено экскаватором ЭТЦ-202; параметры траншей: ширина по дну - 0,5 м, заложение откосов - 0,0. Дрены выполнены из гончарных трубок с внутренним диаметром 0,05 м, длина дрен составляет в среднем 160 м. Закрытый дренаж построен на опытном участке с несколькими вариантами междренных расстояний. Глубина закладки дрен на вариантах составляет 1,0 м.

Почвы опытного участ­ка относятся к освоенным дерново-среднеподзолистым среднепахотным поверхностно оглеенным почвам, по механическому составу – к легким суглинкам. Анализы меха­нического состава почвы опытного участка проводились с исполь­зованием анализатора размеров частиц (седиграфа), который обес­печивает высокую воспроизводимость результатов, что считается критерием объективности данного метода.

Моделирование процессов передвижения почвенной влаги, поз­воляющее количественно оценить состояние среды обитания расте­ний, требует всестороннего учета водно-физических свойств поч­вы. Поэтому были проведены лабораторные исследова­ния с целью изучения физических и водно-физических свойств почвы опытного участка.

Плотность почвы определяли радиоизотопным методом при помощи поверхностно-глубинного плотномера ППГР-1, принцип дей­ствия которого основан на явлениях ослабления, рассеяния и отра­жения гамма-излучения почвенной толщей. При определении плотнос­ти почвы гамма-плотномером необходимо вводить поправку, учиты­вающую влияние почвенной влаги на процесс ослабления гамма-из­лучения. Для этого параллельно с измерениями плотности проводи­ли замеры влажности почвы радиоизотопным поверхностно-глубин­ным влагомером ВПГР-1.

Плотность твердой фазы почвы опытного участка определялась пикнометрическим методом с применением дистиллированной воды. Значения плотности почвы и плотности твердой фазы исполь­зовались для расчета общей пористости почвы. Максимальную гигроскопичность определяли методом Николаева А.В. Максимальную молекулярную влагоемкость почвы опытного участка определяли методом Долгова С.И. Коэффициент фильтрации почвы опытного участка определяли по методу Канараке.

Для того чтобы проводить расчеты вод­ного режима зоны аэрации с помощью математического моделирова­ния необходимо экспериментально определить также две гидрофизические характеристики почвы: зависимость коэффициента влагопроводнос­ти от влажности почвы и зависимость капиллярного напора от влажности почвы (основную гидрофизическую характеристику).

С целью получения более представительных данных об основной гидрофизичес­кой характеристике почвы опытного участка ее определение было проведено нами несколькими методами: методом капилляриметра; экспресс-методом (Жернов И.Е., Дзекунов Н.Е., Файбишенко Б.А.); методом сенсоров. Это дало возможность более дифференцированно подходить к оценке водоудерживающей способности дерново-подзолистых почв опытного участка при проведении прогнозных расчетов.

Годы проведения наследований значительно различалась между собой по условиям естественной влагообеспеченности. Расчеты показали, что вегетационные периоды в годы про­ведения исследований имели различные обеспеченности величин климатического дефицита увлажнения, то есть исследованиями были охвачены различные годы - от очень влажного (1980 г.) до среднего (1981 г.).

Влажность почвы является важнейшей характеристикой условий влагообеспеченности сельскохозяйственных культур, правильное определение которой необходимо также для расчета влагозапасов почвы. В основу методики полевых исследований были положены наблюдения за влажностью почвы в течение периодов вегетации при помощи влагомера ВПГР-1 по стационарным скважинам, армиро­ванным тонкостенными дюралюминиевыми трубами марки Д1Т с внутренним диаметром 38 мм.

Наблюдения за влажностью почвы проводи­лись по схеме локальных полевых исследований, позволяю­щей получать характеристики работы отдельной дрены в пределах ее водосборной площади. В 1979...1980 годах сеть наблюдательных скважин охва­тывала вариант дренажа с междренными расстояниями 24 м. Наблюдательные скважины располагались по створам, пер­пендикулярным к дренажным линиям, на разном расстоянии от дрен, что позволяло изучать характерные особенности формирования вод­ного режима почвы в междренном пространстве. Схема расположения наблюдательных скважин давала воз­можность контролировать влажность почвы на расстояниях 1 м от дрены, В/4 и В/2 (где В - междренное расстояние). За­меры влажности почвы проводились с частотой – 1 раз в 5... 10 дней. По вертикаль­ному профилю почвы была принята следующая схема измерений по скважинам: первое измерение выполнялось на глубине 10 см, ос­тальные - через каждые 20 см, а при необходимости - более часто (через 10 см) до глубины 1,0 м. Параллельно с измерениями влажности почвы проводили за­меры уровня грунтовых вод по наблюдательным скважинам, располо­женным вблизи от скважин для влагометрии.

Для проверки разработанной двумерной математической модели нестационарного влагопереноса было выполнено сопоставле­ние результатов расчетов по разработанной компьютерной программе с результатами полевых наблю­дений, выполненных на опытном участке в период 1979...1982 гг. Были использованы данные полевых наблюдений за влажностью почвы и уровнями грунтовых вод, осредненные по шести наблюдательным точкам, расположенным в середине междренья и по шести наблюдательным точкам, расположенным на расстоянии 1 м от дрены. Результаты расчетов по модели положения уровней грунтовых вод и влагозапасов в слое 0,0...0,75 м для варианта с междренным расстоянием 24 м сравнивались с данными полевых наблюдений. Анализ результатов показал достаточно хорошее совпадение рассчитанных ха­рактеристик с опытными данными. Максимальное отклонение экспериментальных значений от рассчитанных не превышает для уровня грунтовых вод 10%, для влагозапасов - 5%. Коэффициент корреляции рассчитанных и измеренных значений составляет более 0,97.

Второй этап проверки разработанной математической модели включал сопоставление результатов расчетов с опубликованными результатами полевых исследований водного режима почв ландшафтных катен (Зайдельман Ф.Р., 1969, 1975) на Рузском и Мещерском почвенно-мелиоративных стационарах, расположенных в Московской области. В этих основополагающих работах Зайдельманом Ф.Р. освещен важный вопрос взаимодействия и совместного развития геоморфологических и почвенных процессов, исследован водный режим ландшафтных катен Московской области.

Почвообразующими породами почв Рузского стационара являются тяжелосуглинистые и глинистые лессовидные (покровные) бескарбонатные отложения, подстилаемые на глубине 2…3 м днепровской суглинистой мореной, которая в свою очередь покоится на глинах юры. На литологическом разрезе Рузского стационара были выделены следующие почвы: дерново-подзолистая суглинистая, дерново-подзолистая суглинистая глубокооглеенная, дерново-подзолистая глееватая и дерново-глеевая тяжелосуглинистые почвы (Зайдельман Ф.Р., 1975). Эти почвы расположены соответственно: на вершине холма и склонах с уклонами 2-3⁰, нижней трети склона с уклонами 2⁰, плоском основании склона, в понижении. Таким образом, была дана морфологическая характеристика почв характерных элементарных ландшафтов ландшафтно-геохимической катены: элювиального, трансэлювиального, трансаккумулятивного, супераквального.

Вертикальная расчлененность рельефа составляет 11,0 м, ширина ландшафтного разреза составляет 700 м, средняя мощность почв и подстилающих грунтов (до юрских глин) составляет 18,0 м.

Расчеты по модели значений влагозапасов почвы в слое мощностью 0-70 см и сопоставление результатов с результатами полевых исследований выполнялись для разных участков ландшафтной катены - вершины холма, нижней трети склона, плоского основания склона.

Для проверки разработанной математической модели нами были использованы также опубликованные материалы полевых исследований, проведенных Зайдельманом Ф.Р. на Мещерском почвенно-мелиоративном стационаре, расположенном в Московской области в пределах зандровой равнины Клязьминско-Москворецкого междуречья (Зайдельман Ф.Р., 1969, 1975). Вертикальная расчлененность рельефа составляет 4,0 м, ширина ландшафтной катены составляет 342 м, средняя мощность почв и подстилающих грунтов (до юрских глин) составляет 14,0 м.

Почвообразующими породами являются песчаные флювиогляциальные отложения мощностью 6-12 м, покоящиеся на суглинисто-супесчаной морене, в основании которой залегают юрские глины. На литологическом разрезе Мещерского стационара были выделены следующие почвы: дерново-слабоподзолистая супесчаная, дерново-подзолистая супесчаная глубокооглеенная, дерново-подзолистая глееватая супесчаная, дерново-подзолистая глеевая супесчаная, торфянисто-глеевая (Зайдельман Ф.Р., 1969, 1975). Эти почвы расположены соответственно: на вершине плоского холма, на пологом склоне, на плоском основании склона, в депрессии у основания склона.

Проверка модели проводилась путем сопоставления рассчитанных влагозапасов в расчетном слое почвы 0-70 см и полученных во время полевых исследований. Анализ результатов расчетов показал, что математическая модель адекватно воспроизводит наблюдавшуюся динамику влагозапасов почвы для разных участков ландшафтных катен рассмотренных стационаров. Максимальное отклонение экспериментальных значений от рассчитанных влагозапасов не превысило 10%. Коэффициент корреляции рассчитанных и измеренных значений составляет более 0,97.

Выполненные расчеты и сопоставление их результатов с результатами полевых исследований позволяют говорить о том, что разработанная математическая модель достаточно адекватно описывает динамику влагозапасов в почвах и грунтах с различным геоморфологическим положением, и может быть применена для прогнозов водного режима сопряженных элементарных ландшафтов ландшафтных катен.