Правила симметрии в записи информации в ДНК международный проект "Геном человека" 1990-2003 г г

Вид материала

Документы

Содержание Рис. 1. Cпираль Уотсона-Крика 1. Противоположная полярность цепей ДНК. Симметрия пар оснований Таблица 1 Геном человека Симметрия троек оснований. Количество кодонов в хромосоме 6 генома человека 2. Одинаковая полярность цепей ДНК. С 3. Генерация случайных последовательностей с симметриями обеих видов.

Подобный материал:

• Н. К. Янковский Тема лекции: «Геном человека: наука и жизнь», 17.62kb.
• Роль вирусов в жизни человека, 476.23kb.
• Определение: генетический код это система записи информации о последовательности расположения, 51.8kb.
• И. Э. Лалаянц геном человека, 126.67kb.
• Лекция «Генная инженерия», 240.12kb.
• Пупов Данил Владимирович Раздел Введение. Строение молекулы ДНК. История доказательства, 86.42kb.
• Реферат на тему : «Многообразие симметрии в жизни», 122.91kb.
• Репарация ДНК (Часть, 391.42kb.
• Днк наномеханические роботы и вычислительные устройства, 1331.95kb.
• «Кошки и гены», 784.32kb.

ПРАВИЛА СИММЕТРИИ В ЗАПИСИ ИНФОРМАЦИИ В ДНК

Международный проект “Геном человека” – 1990-2003 г.г.

(6 млрд.$). Стартовал проект ENCODE (энциклопедия кодирующих элементов генома). Геном человека состоит из 3-х млрд. пар оснований. Фрагмент записи последовательности (1 млн. страниц текста).

CCTCATTTAGCTCTAGCCCAGTAGAACCACGGCAGAGACTCCCAACA

В ДНК содержится примерно 20-25 тысяч генов, около половины ДНК – многократно повторяющиеся последовательности, кодирующие участки (экзоны) – 2%, интроны – 23%, 75% - межгенная ДНК.

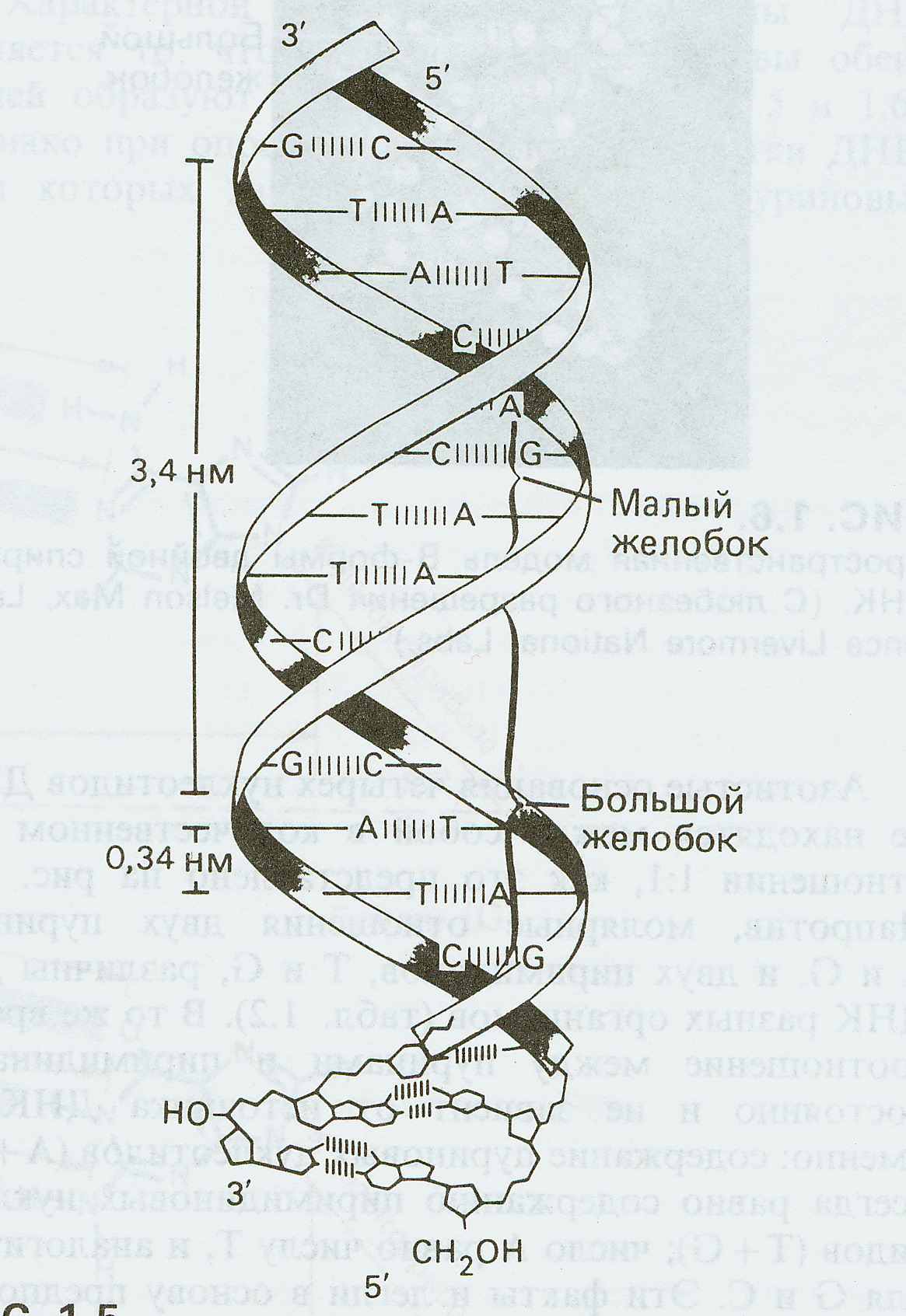Рис. 1. Cпираль Уотсона-Крика

ДНК имеет форму двойной спирали, информация записана в 4-х буквенном алфавите A, C, G, T оснований, C – G, A – T – комплементарные пары оснований.

Исследовались геномы: человека, шимпанзе, мыши, крысы, курицы, рыбы Tetraodon, растения Arabidopsis, C.elegans, дрожжей,

60 бактерий, 30 вирусов.





1. Противоположная полярность цепей ДНК. Запись и считывание оснований на первой нити выполняется слева направо в направлении 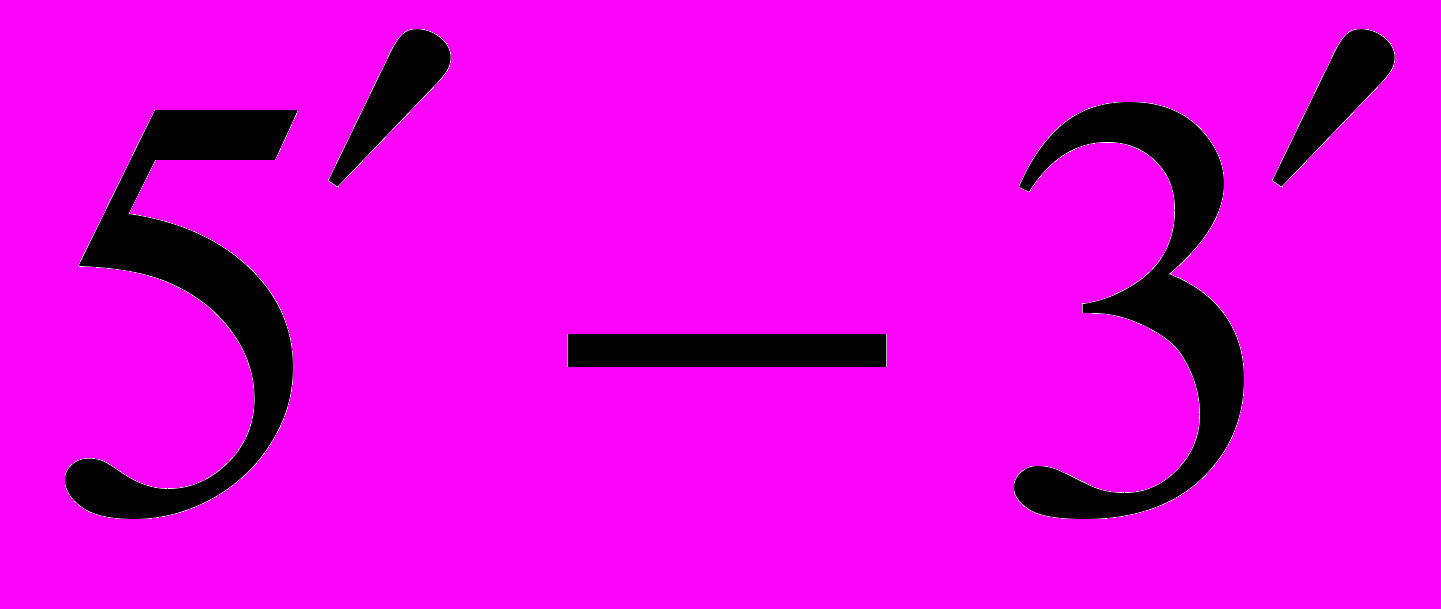, а на комплементарной нити в направлении 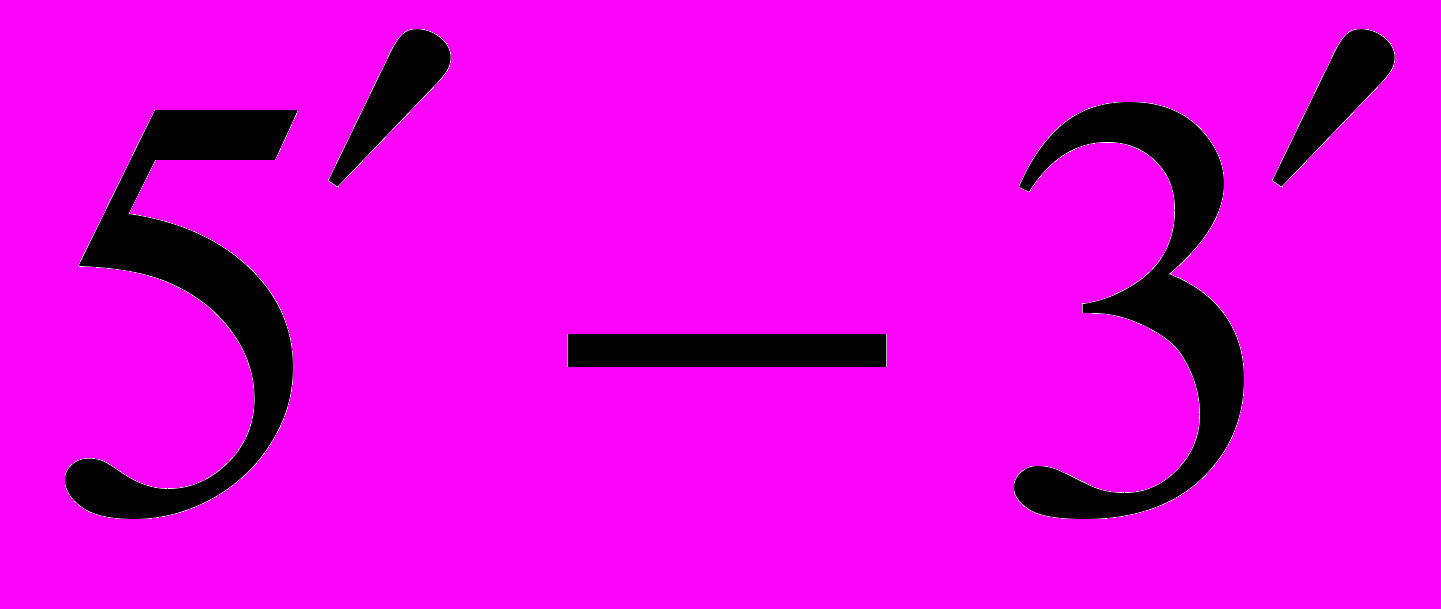справа налево (рис.2).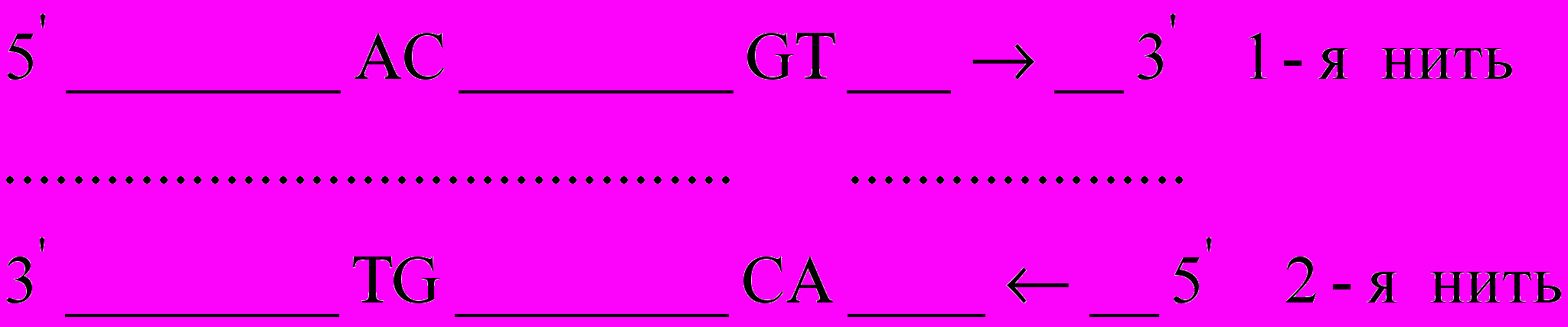





Рис. 2. Условная запись двух нитей хромосомы (модель Уотсона-Крика)

Симметрия оснований. На одной нити ДНК выполняются соотношения

n(A) = n (T), n(C) = n(G). (1)


n(i, 1 н.)= n(i, 2 н.), 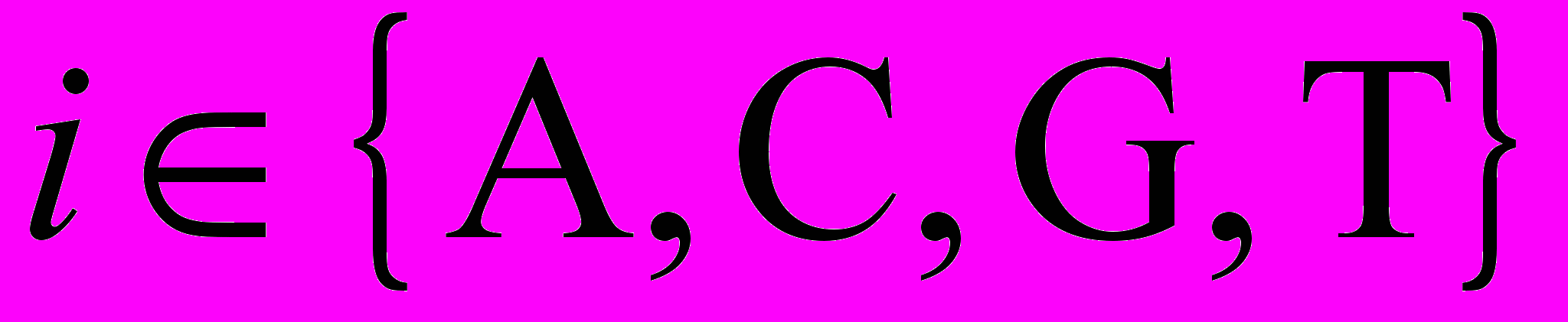. (2)


Вывод: веса двух нитей совпадают.

Симметрия пар оснований из соотношений

n(AC) = n(GT), n(AG) = n(CT)

n(TC) = n(GA), n(TC) = n(CA) (3)

n(AA) = n(TT), n(CC) = n(GG),


или в виде формулы

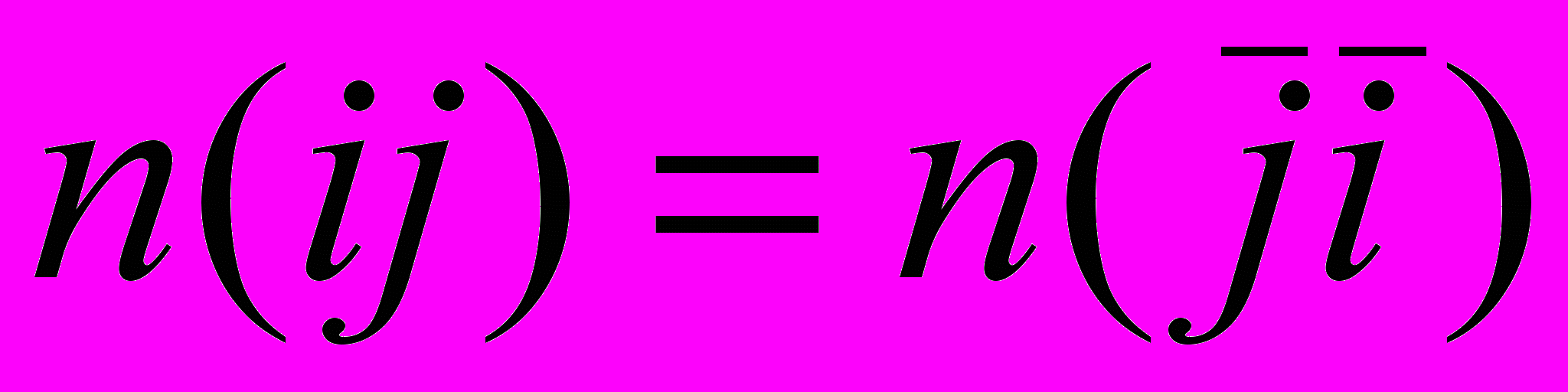, (4)


, .

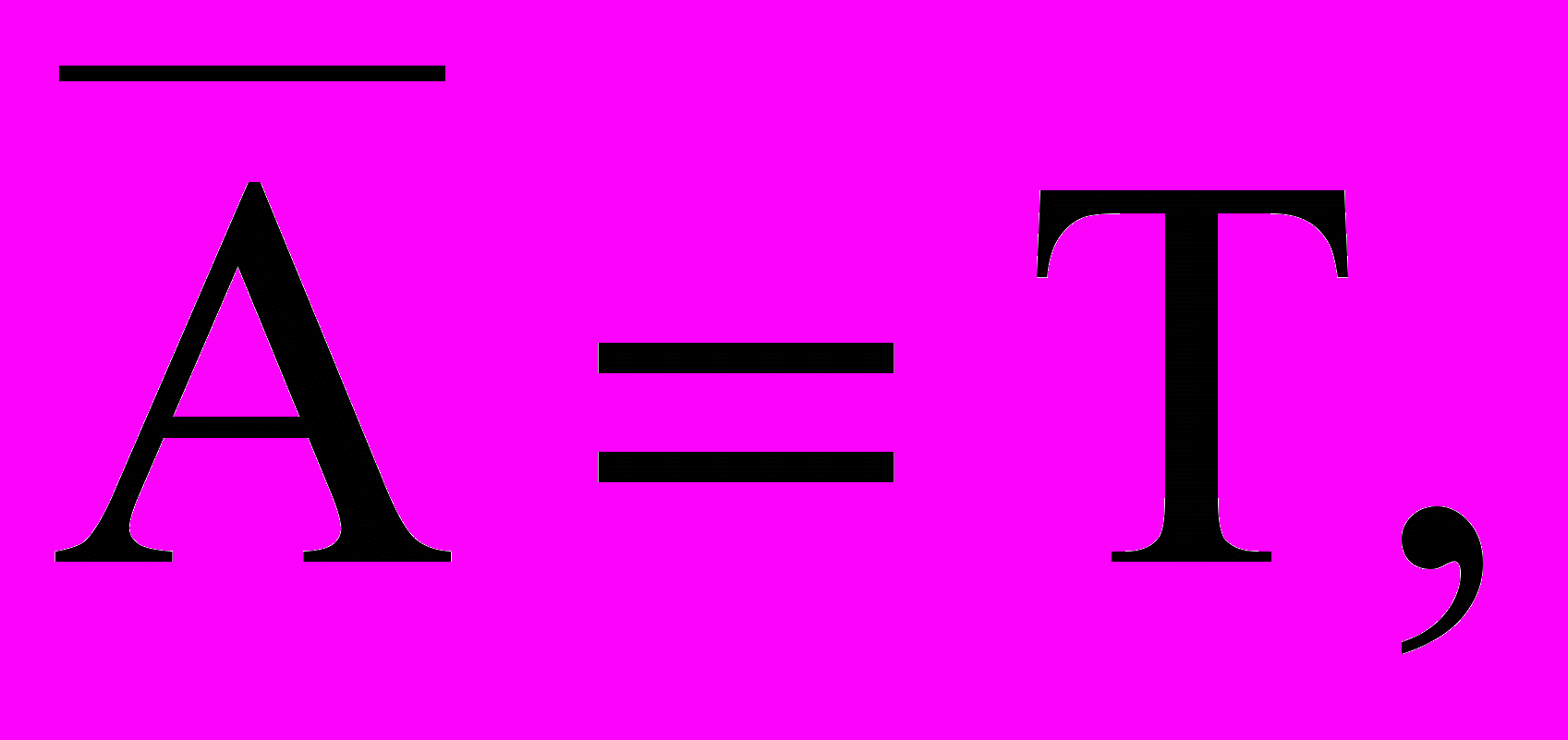
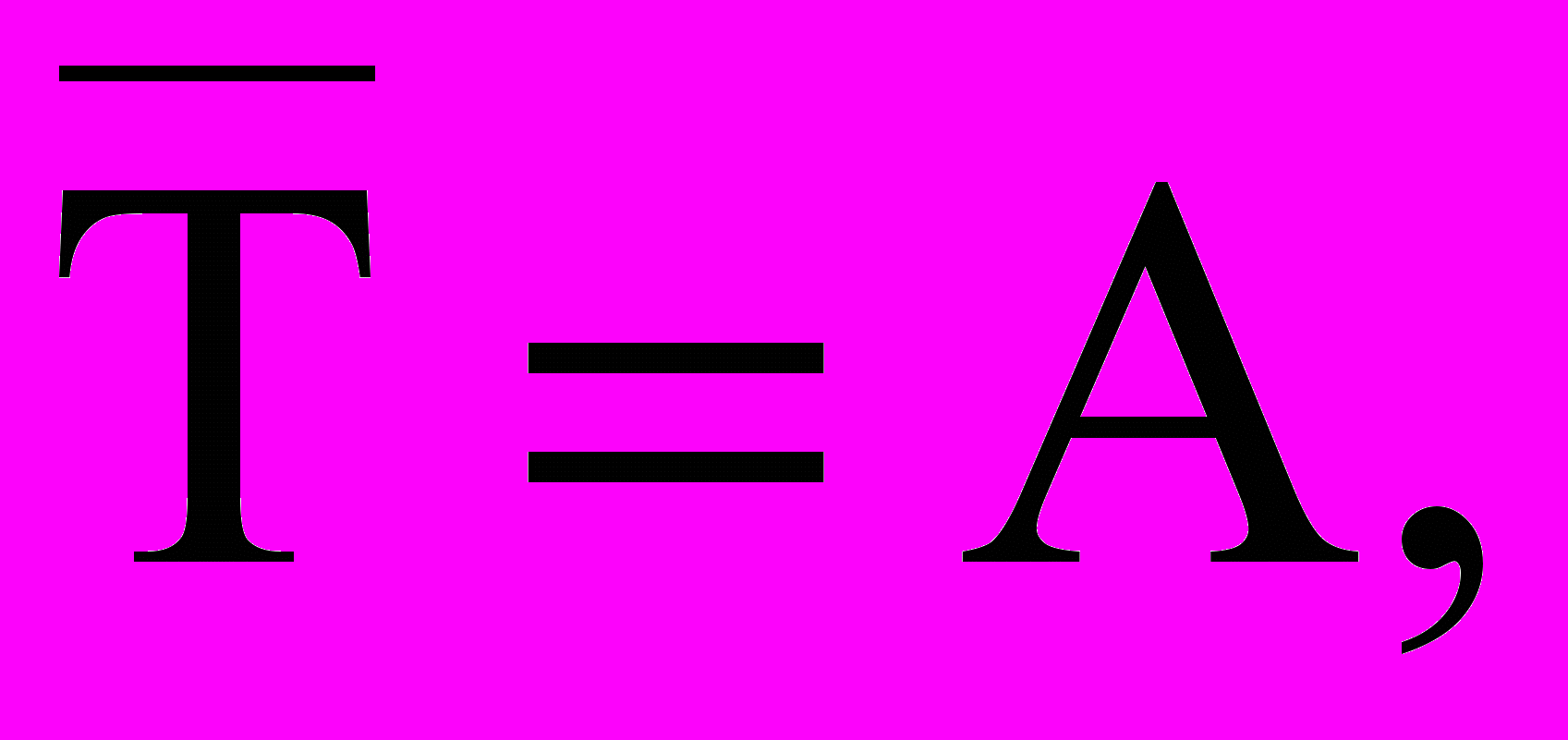
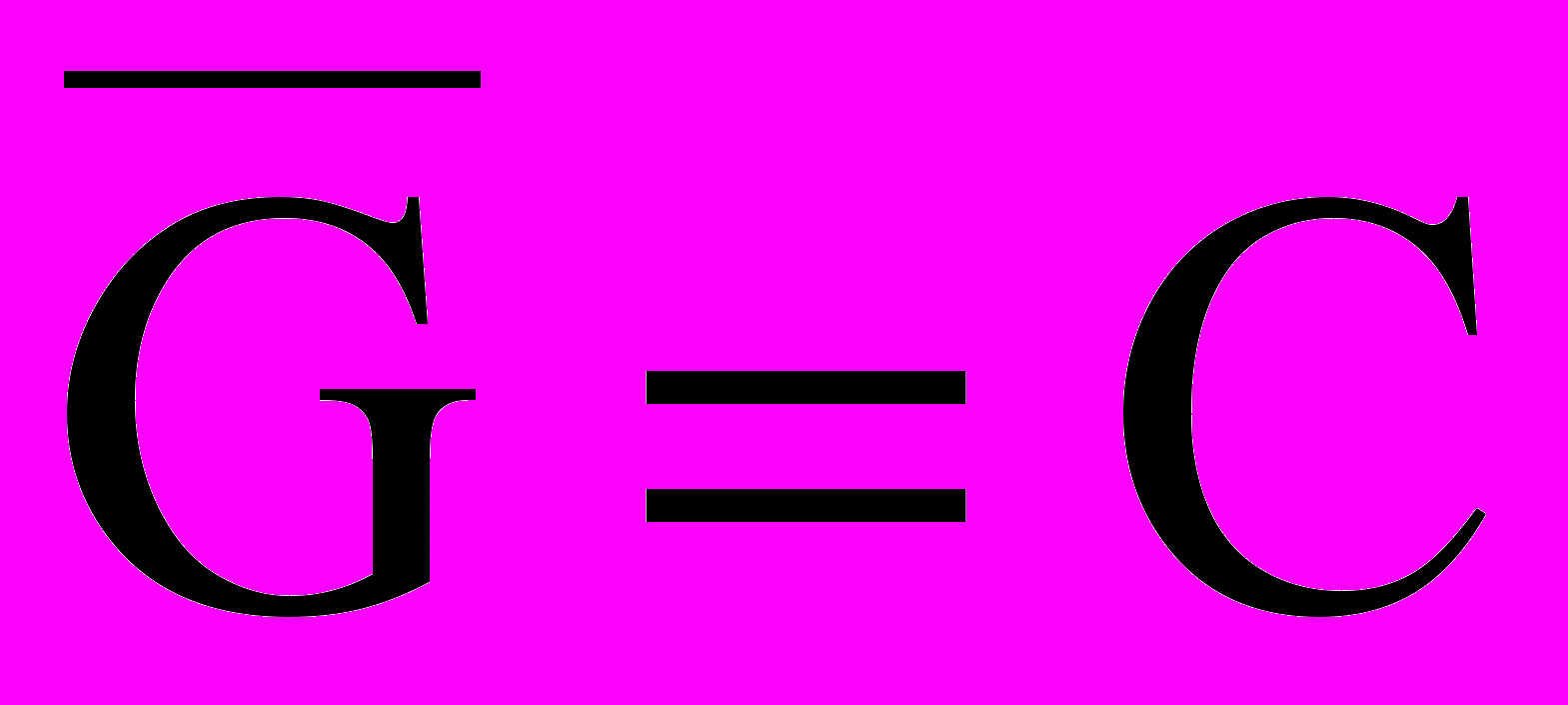Пары AT, TA, CG и GC отсутствуют в (3), поскольку они приводят к тавтологии.


n(ij, 1 н.)= n(ij, 2 н.). (5)

Таблица 1

Геном человека

Пары букв	Хромосома 1	Хромосома 3	Хромосома 6	Хромосома 10	Хромосома 18
AA	21 191 409	19 746 023	17 083 089	12 607 303	7 553 856
TT	21 245 312	19 772 366	17 080 492	12 628 305	7 560 778
AC	11 189 673	9 791 735	8 417 550	6 641 892	3 762 190
GT	11 209 763	9 798 222	8 411 037	6 651 425	3 776 890
AG	15 878 823	13 482 539	11 543 173	9 275 834	5 136 579
CT	15 904 404	13 478 613	11 532 563	9 286 062	5 138 944
CA	16 200 299	13 972 734	11 983 646	9 656 789	5 382 301
TG	16 226 750	13 970 283	11 984 196	9 667 666	5 401993
CC	12 132 633	9 518 322	8 128 472	7 073 095	3 640 163
GG	12 121 539	9 520 091	8 140 958	7 062 604	3 647 384
GA	13 313 713	11 472 583	9 879 809	7 851 856	4 411 285
TC	13 322 934	11 477 596	9 862 177	7 860 740	4 408 666
AT	16 615 348	15 646 889	13 495 077	9 896 788	6 012 563
TA	14 169 829	13 466 193	11 592 344	8 305 870	5 117 737
CG	2 256 627	1 620 941	1 473 327	1 353 534	677 210
GC	9 838 754	7 836 943	6 709 818	5 793 769	3 027 601

Для любой последовательности без пропусков букв с точностью до единицы выполняются соотношения

n(Ai) + n(Ci) + n(Gi) + n(Ti) =


= n(iA) + n(iC) + n(iG) + n(iT), (6)

где .


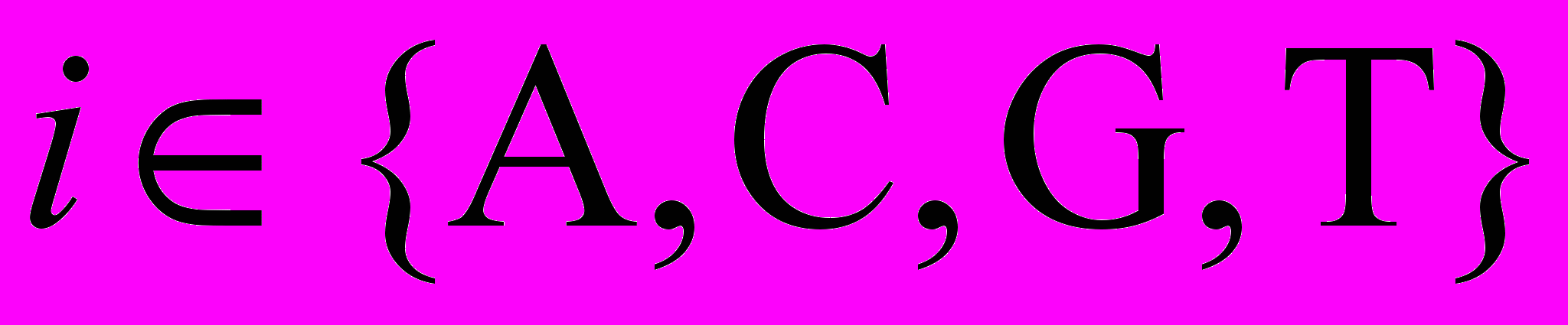Для пар AT, TA получаем связывающее ограничение

n(CA) + n(GA) + n(TA) = n(AC) + n(AG) + n(AT). (7)

Для пар CG и GC – соотношение


n(AC) + n(GC) + n(TC) = n(CA) + n(CG) + n(CT). (8)


Утверждение 1. Из симметрии пар оснований вытекает симметрия оснований.

Симметрия троек оснований. Кодоны (тройки оснований) связаны следующими соотношениями:

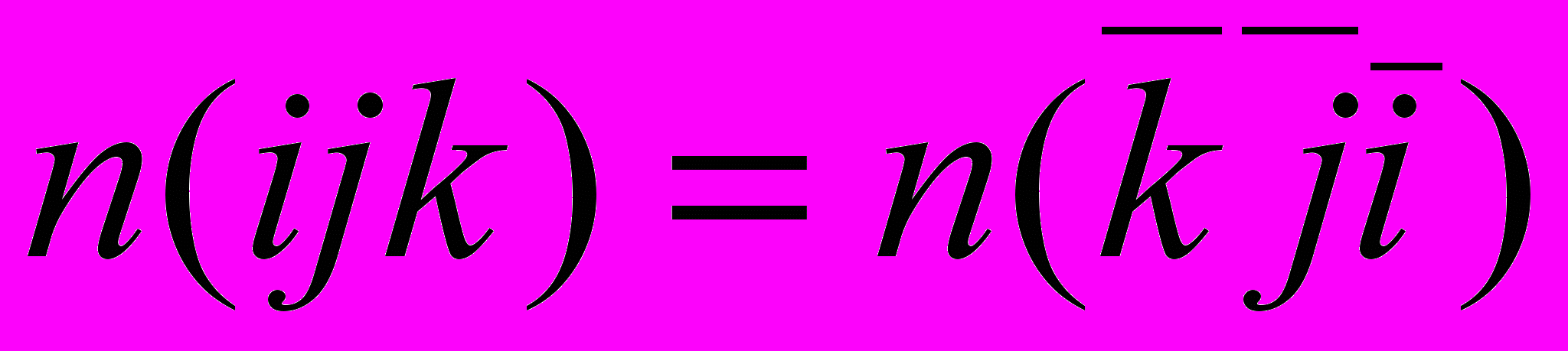, (9)

где 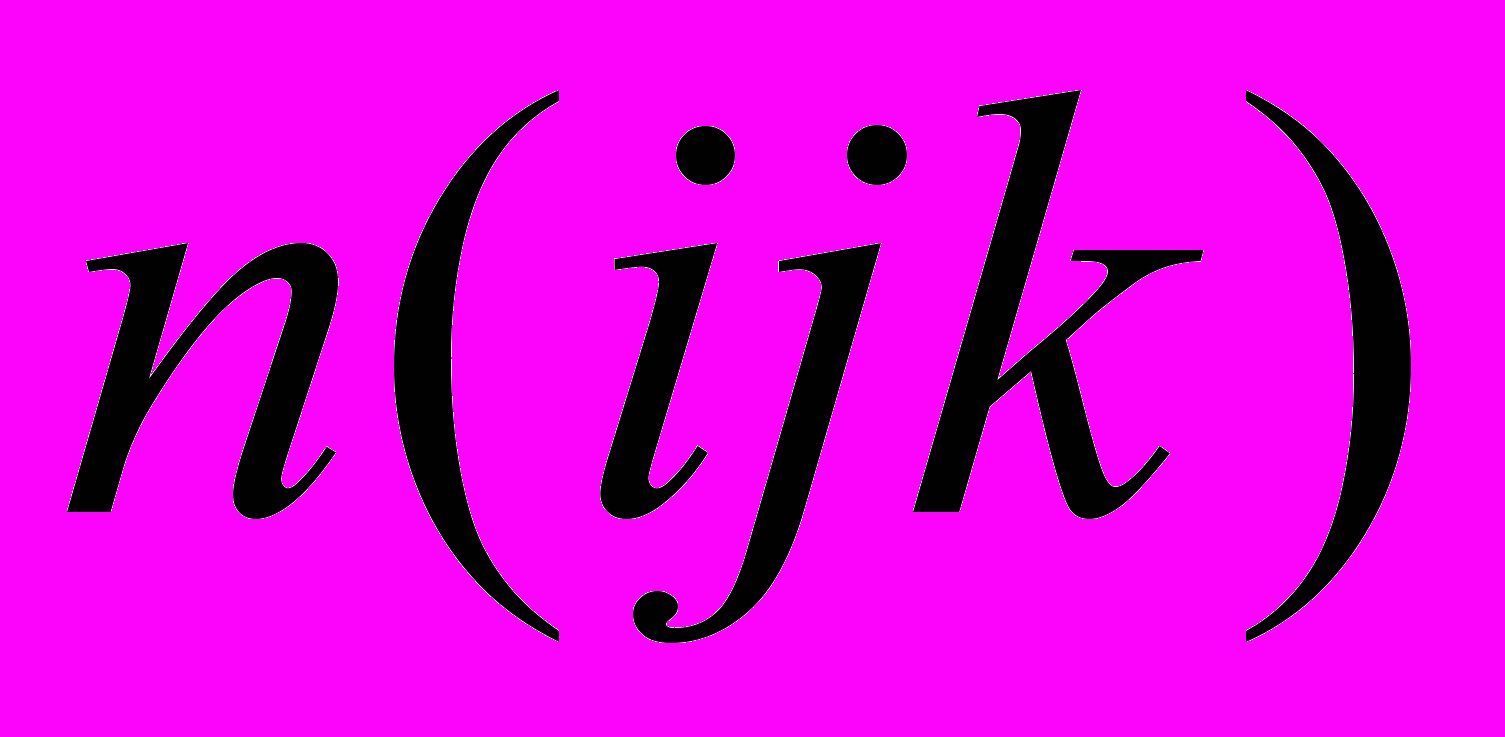– число троек оснований 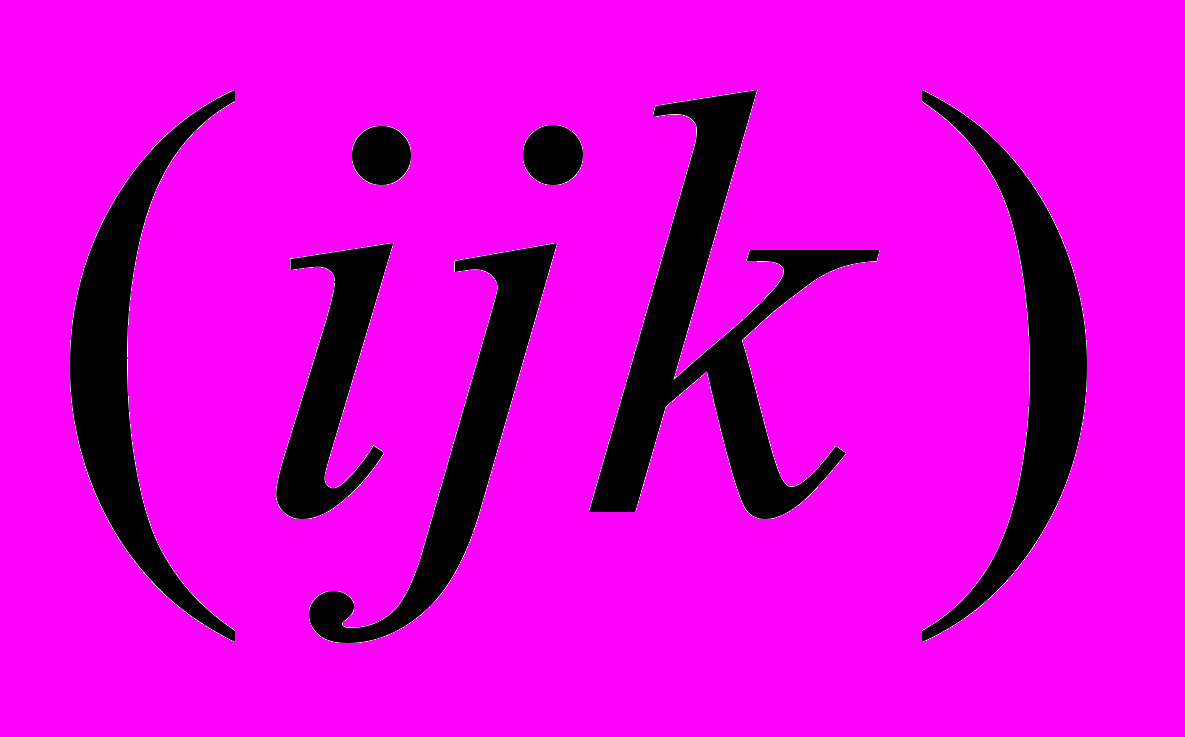, , 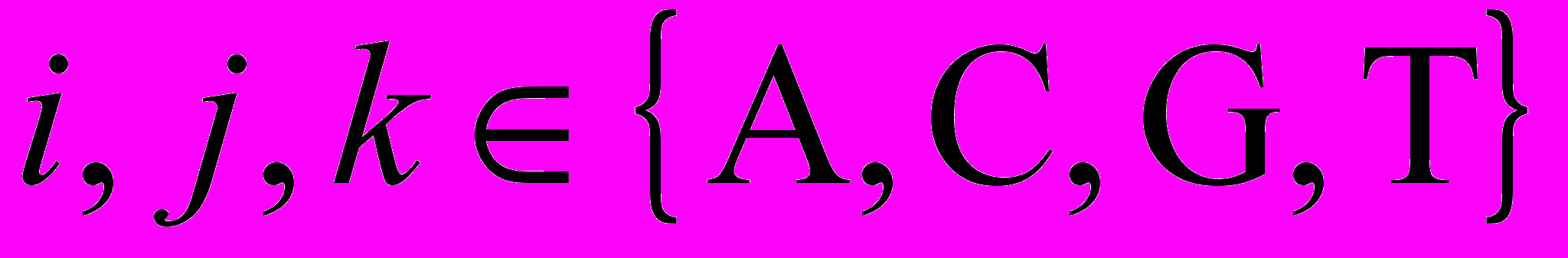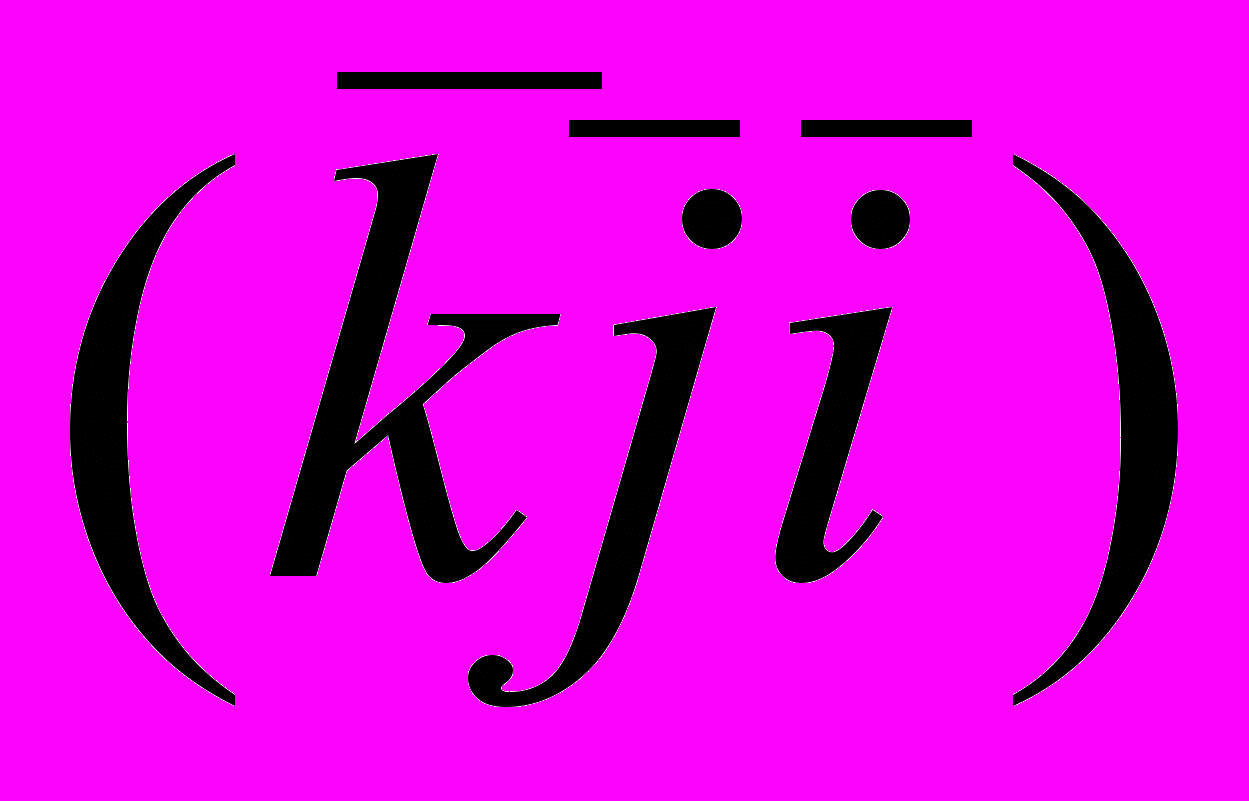– антикодон кодона .

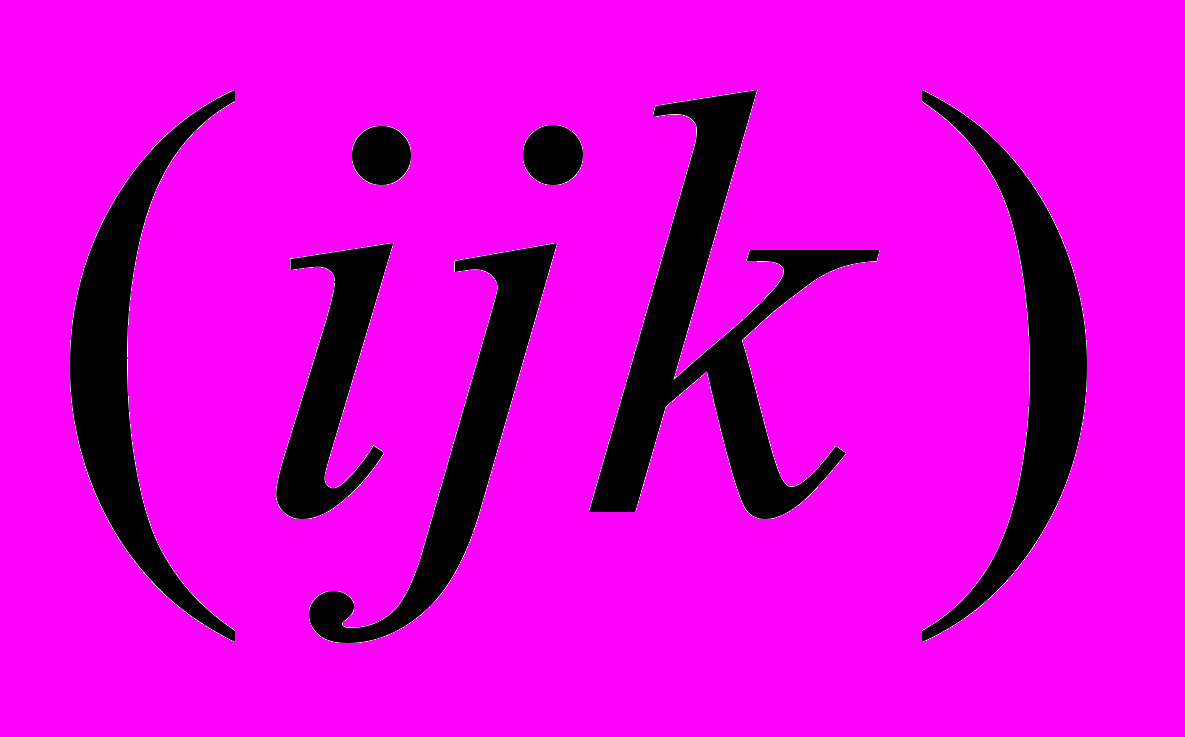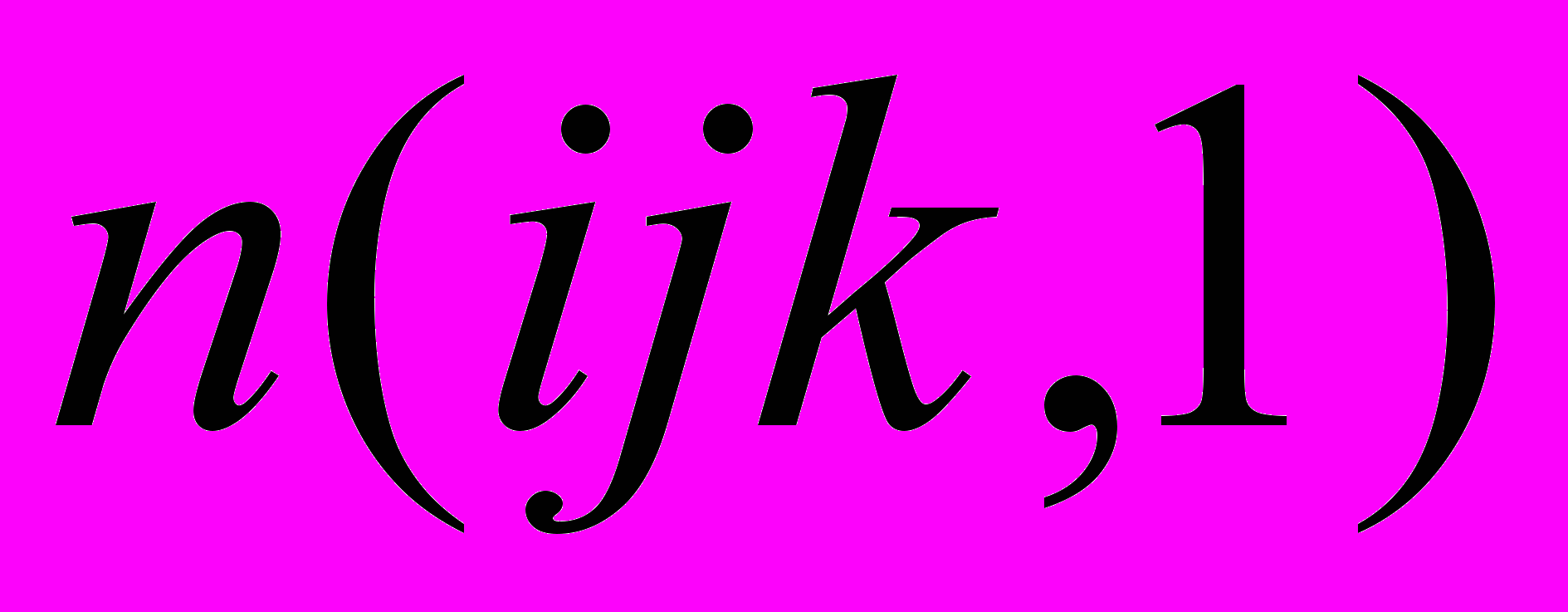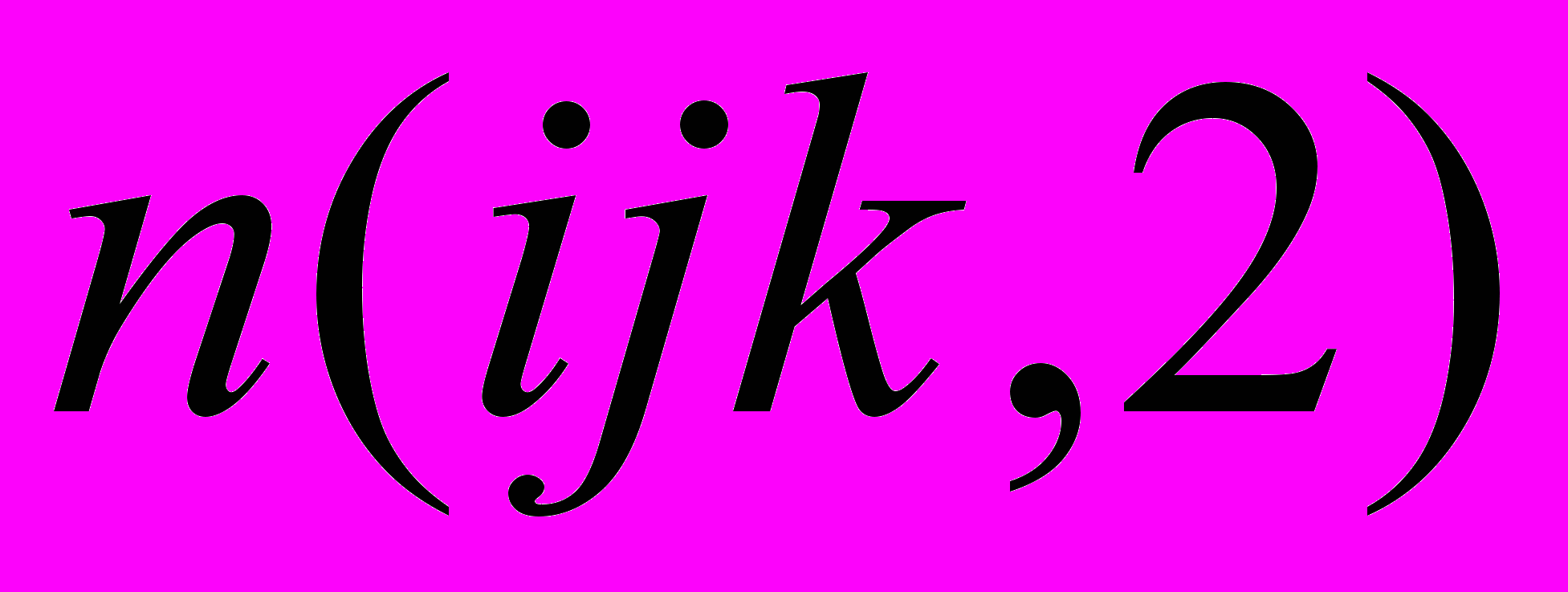= , (10)

Таблица 2

Количество кодонов в хромосоме 6 генома человека
кодон	число	кодон	число	кодон	число	кодон	число
AAA	6 742 017	TTT	6 744 661	CAG	3 216 761	CTG	3 217 346
AAC	2 509 339	GTT	2 507 886	CCA	2 932 409	TGG	2 932 367
AAG	3 412 539	CTT	3 407 422	CCC	1 980 135	GGG	1 986 846
AAT	4 419 198	ATT	4 420 523	CCG	394 680	CGG	396 760
ACA	3 417 383	TGT	3 417 331	CGA	341 096	TCG	340 572
ACC	1 872 766	GGT	1 869 465	CGC	345 302	GCG	346 653
ACG	391 422	GGT	390 169	CTA	2 226 977	TAG	2 227 635
ACT	2 735 979	AGT	2 734 072	CTC	2 680 818	GAG	2 686 241
AGA	3 741 389	TCT	3 735 896	GAA	3 394 901	TTC	3 388 807
AGC	2 242 727	GCT	2 239 440	GAC	1 533 503	GTC	1 532 047
AGG	2 824 985	CCT	2 821 248	GCA	2 330 699	TGC	2 327 157
ATA	3 684 661	TAT	3 682 369	GCC	1 793 026	GGC	1 794 632
ATC	2 260 505	GAT	2 265 164	GGA	2 490 014	TCC	2 482 545
ATG	3 129 388	CAT	3 128 346	GTA	1 962 626	TAC	1 966 011
CAA	3 229 842	TTG	3 228 944	TAA	3 716 329	TTA	3 718 080
CAC	2 408 697	GTG	2 408 478	TCA	3 303 155	TGA	3 307 301

Для шести пар (3) 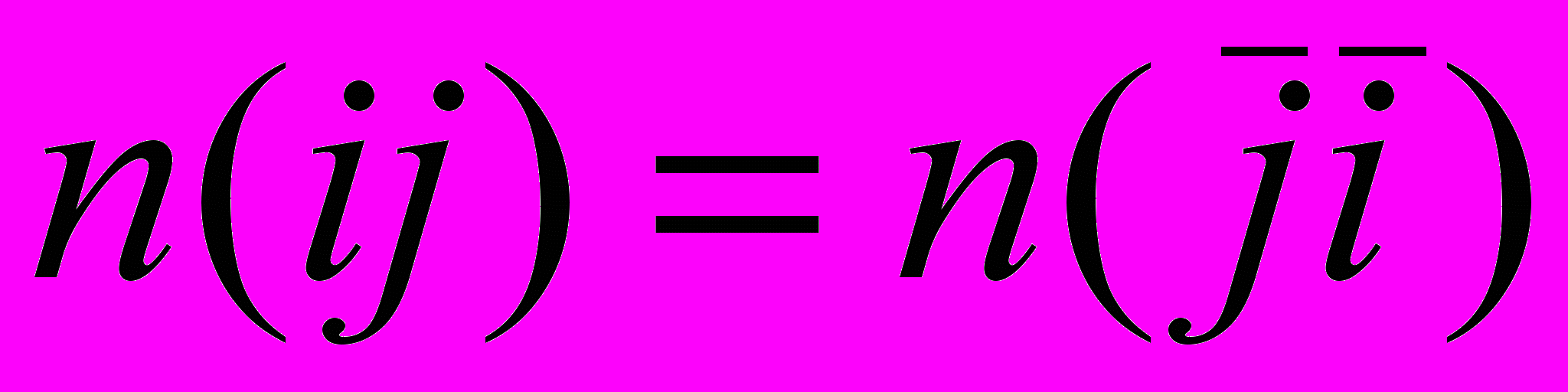получаем связывающие ограничения для троек оснований


n(AAC) + n(AAG) + n(AAT) = n(CAA) + n(GAA) + n(TAA), (11)


n(ACA)+n(ACC)+n(ACG)+n(ACT)=n(AAC)+n(CAC)+n(GAC)+ n(TAC), (12)


n(AGA)+n(AGC)+n(AGG)+n(AGT)=n(AAG)+n(CAC)+n(GAC)+ n(TAC), (13)


n(CAA)+n(CAC)+n(CAG)+n(CAT)=n(ACA)+n(CCA)+n(GCA)+ n(TCA), (14)


n(CCA) + n(CCG) + n(CCT) = n(ACC) + n(GCC) + n(TCC), (15)


n(GAA)+n(GAC)+n(GAG)+n(GAT)=n(AGA)+n(CGA)+n(GGA)+ n(TGA), (16)


Утверждение 2. Из симметрии троек оснований вытекает симметрия пар оснований.

Из симметрии последовательностей оснований по индукции вытекает симметрия коротких последовательностей.

Поскольку симметрия в записи оснований по нитям в ДНК обнаружена эмпирически и в настоящее время не существует объяснения этого феномена в природе, то важно найти такую модель, которая будет подтверждать симметрию последовательностей оснований на основе симметрии коротких последовательностей.

Утверждение 3. Для модели однородной цепи Маркова симметрия троек оснований вытекает из симметрии оснований и симметрии пар оснований.

Для однородной цепи Маркова оценки вероятностей троек основани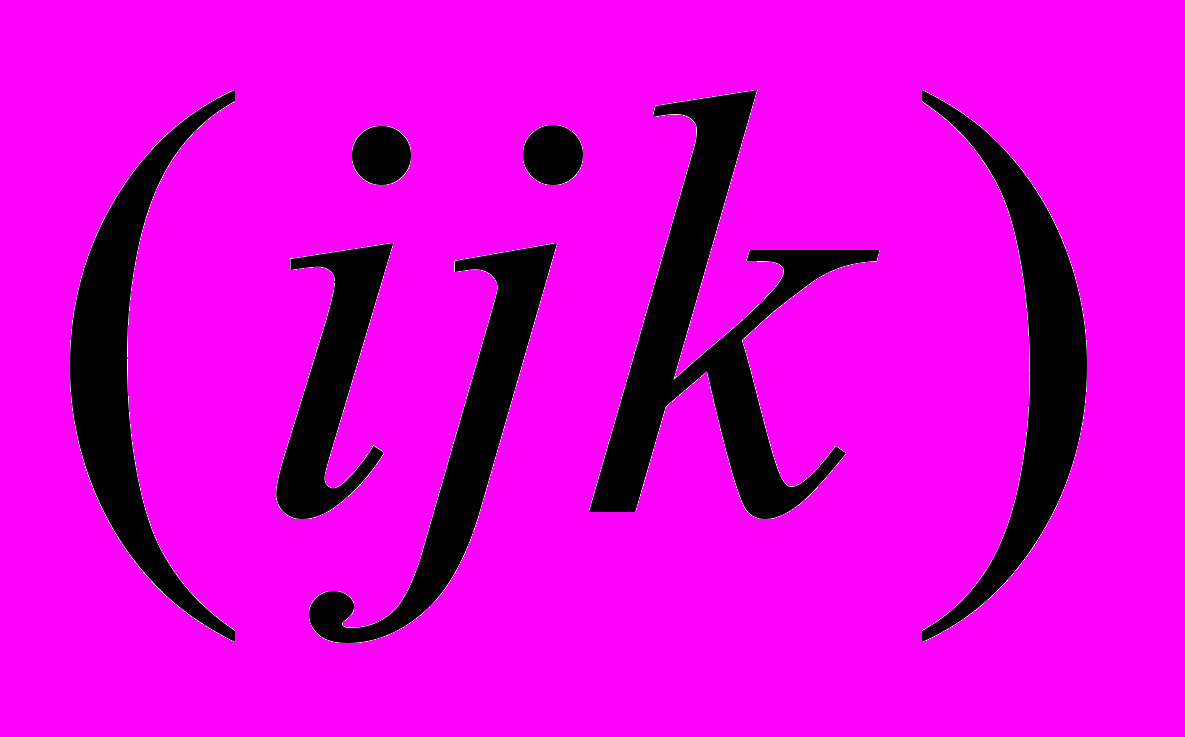й и 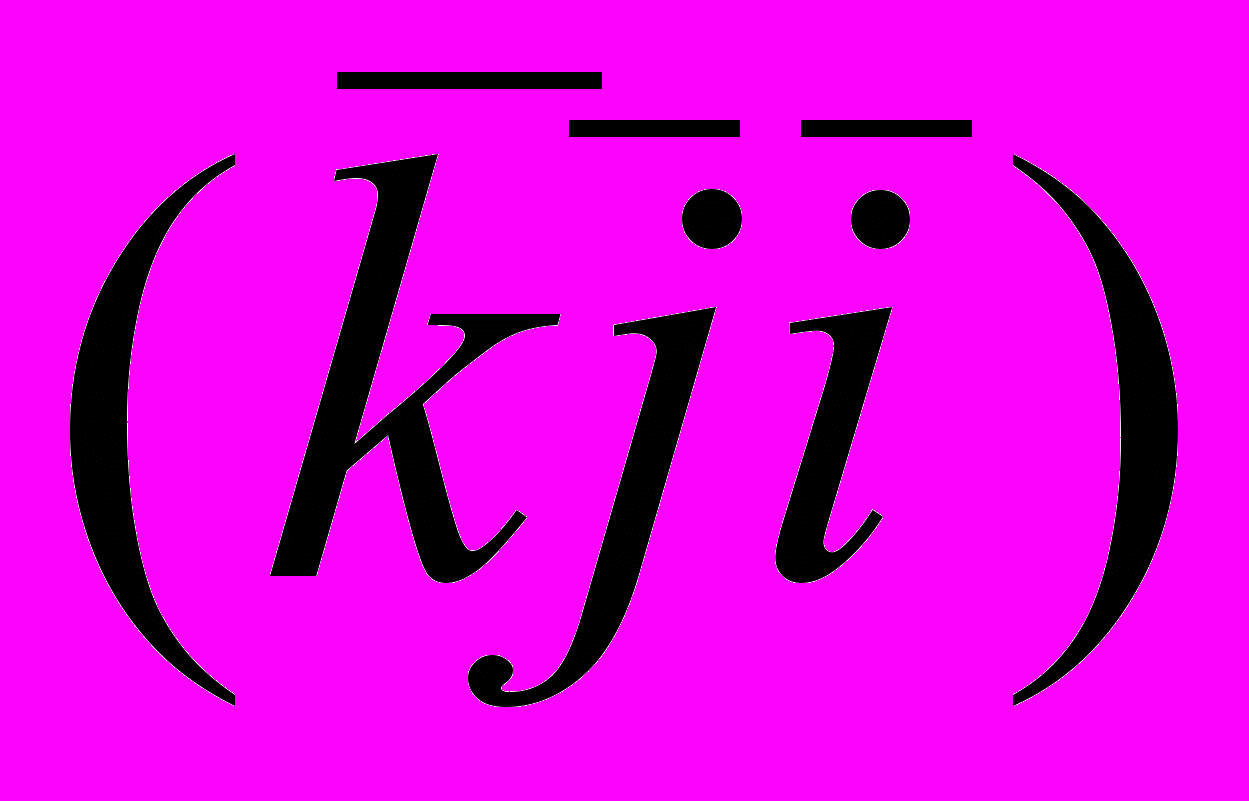совпадают

= ,

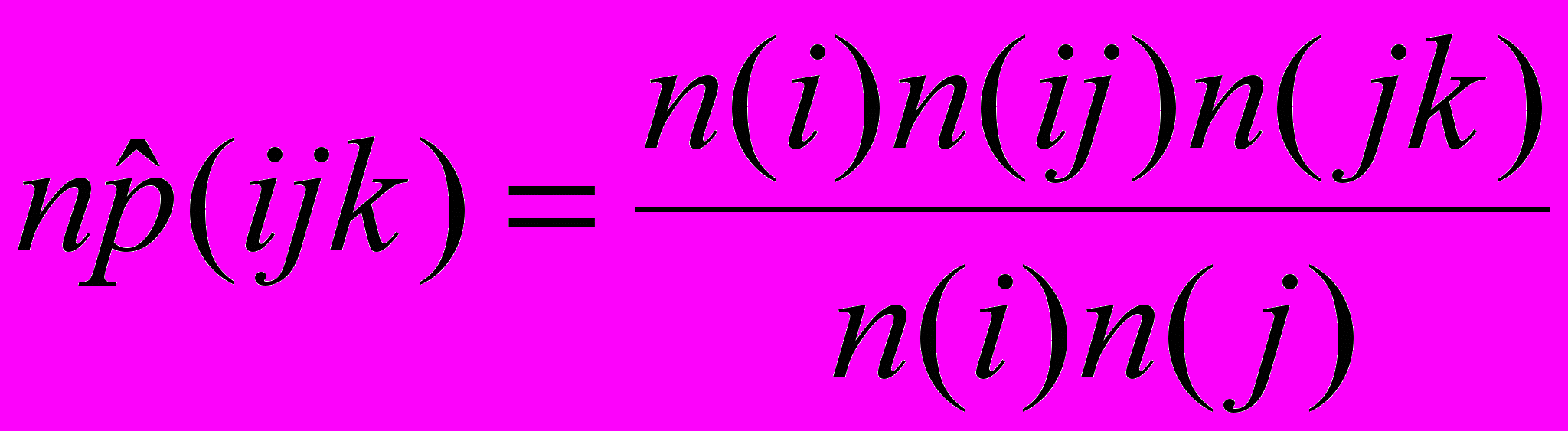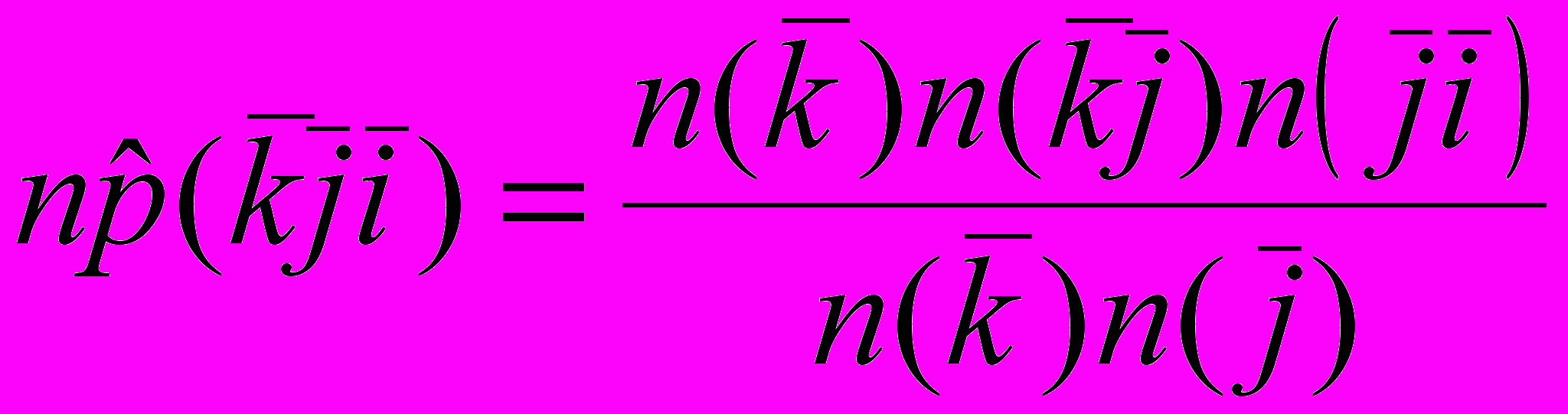где 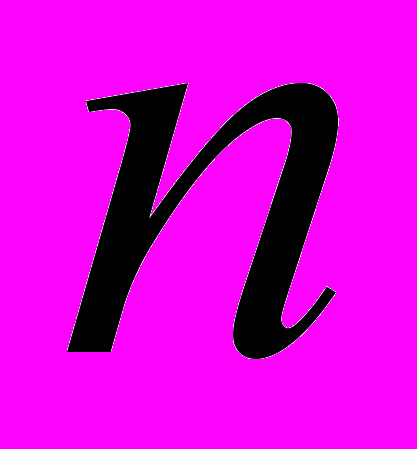– длина хромосомы, т.е. ожидаемое число повторов троек основани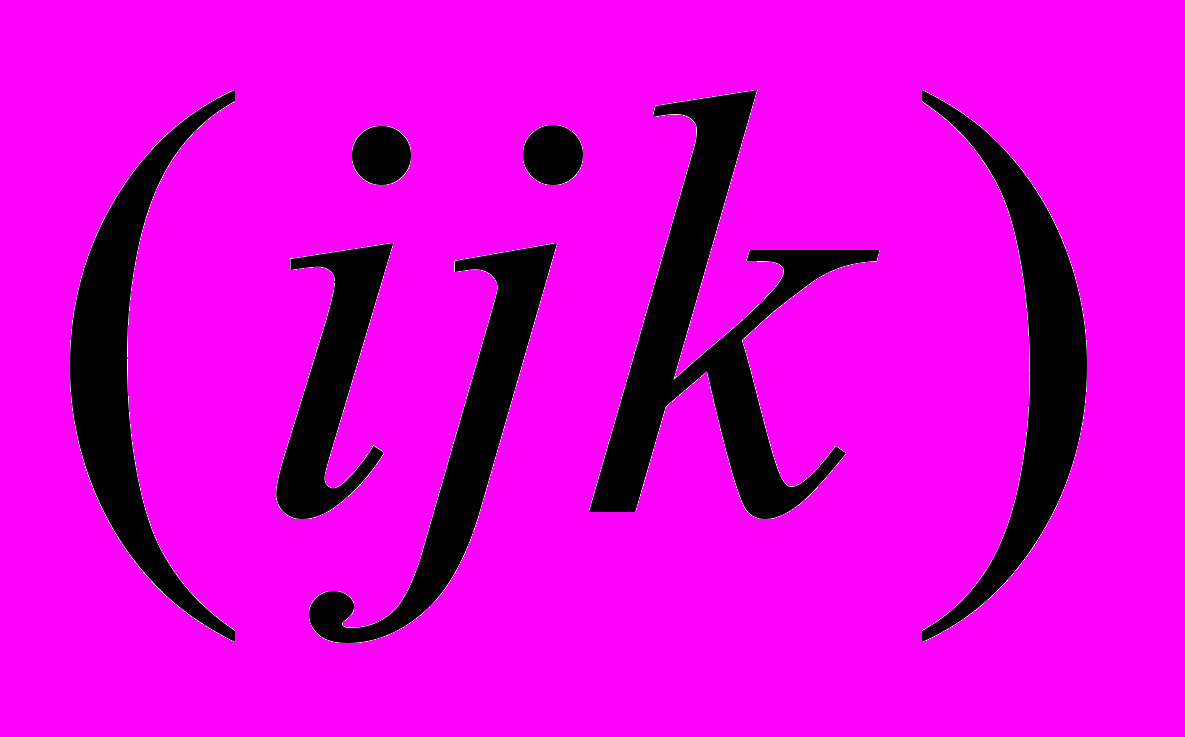й и 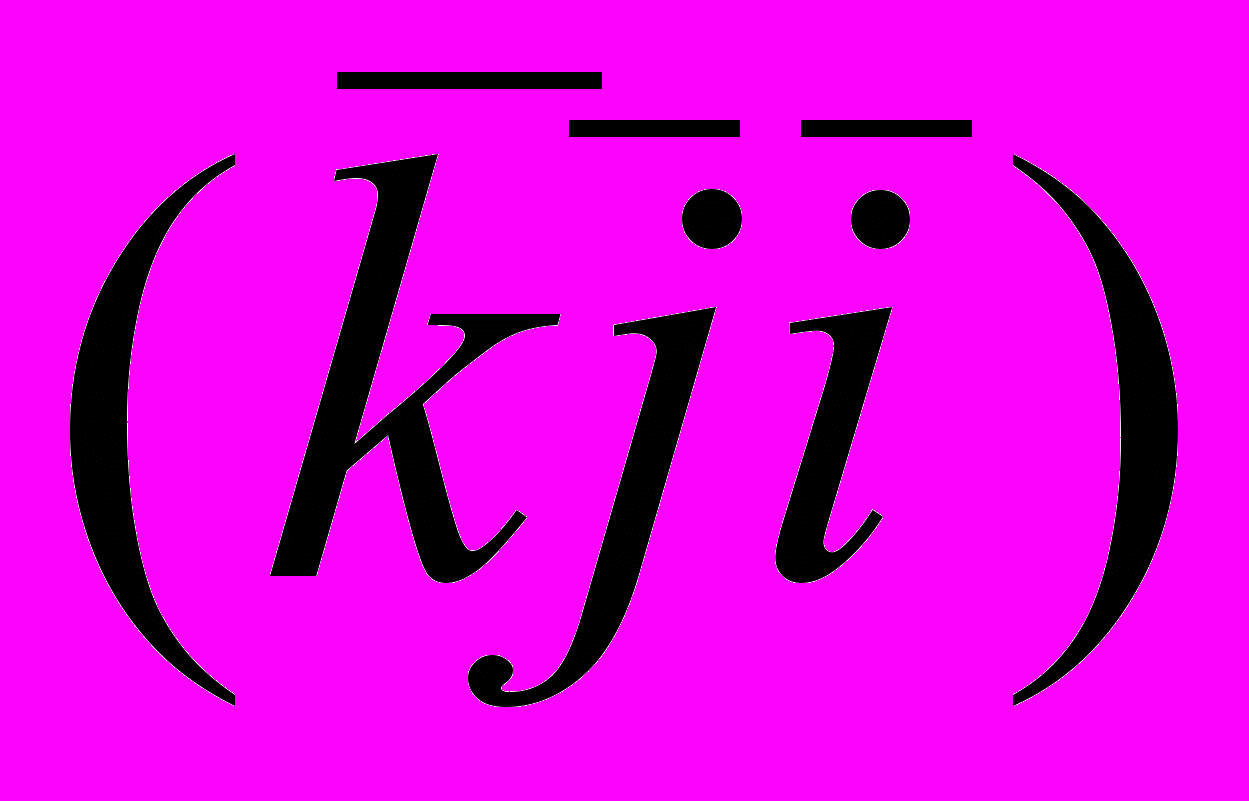совпадают.

Симметрия для последовательностей оснований подтверждается для модели однородной цепи Маркова и вытекает из симметрии пар оснований.

Утверждение 4. Оценка вероятности последовательности 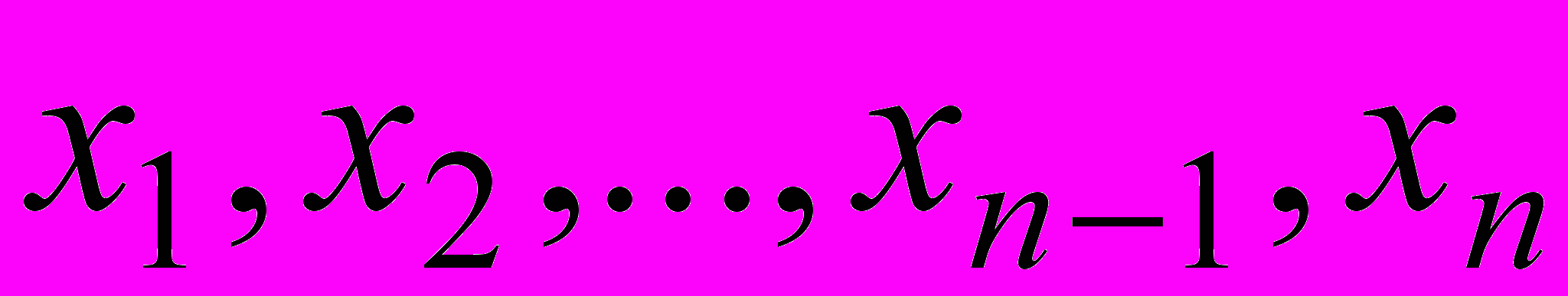совпадает с оценкой вероятности последовательности , т.е.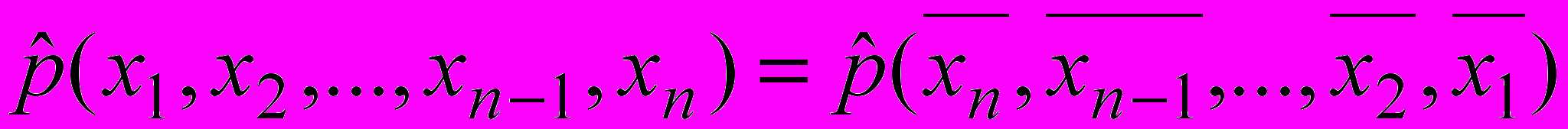


. (17)


2. Одинаковая полярность цепей ДНК. Симметрия оснований 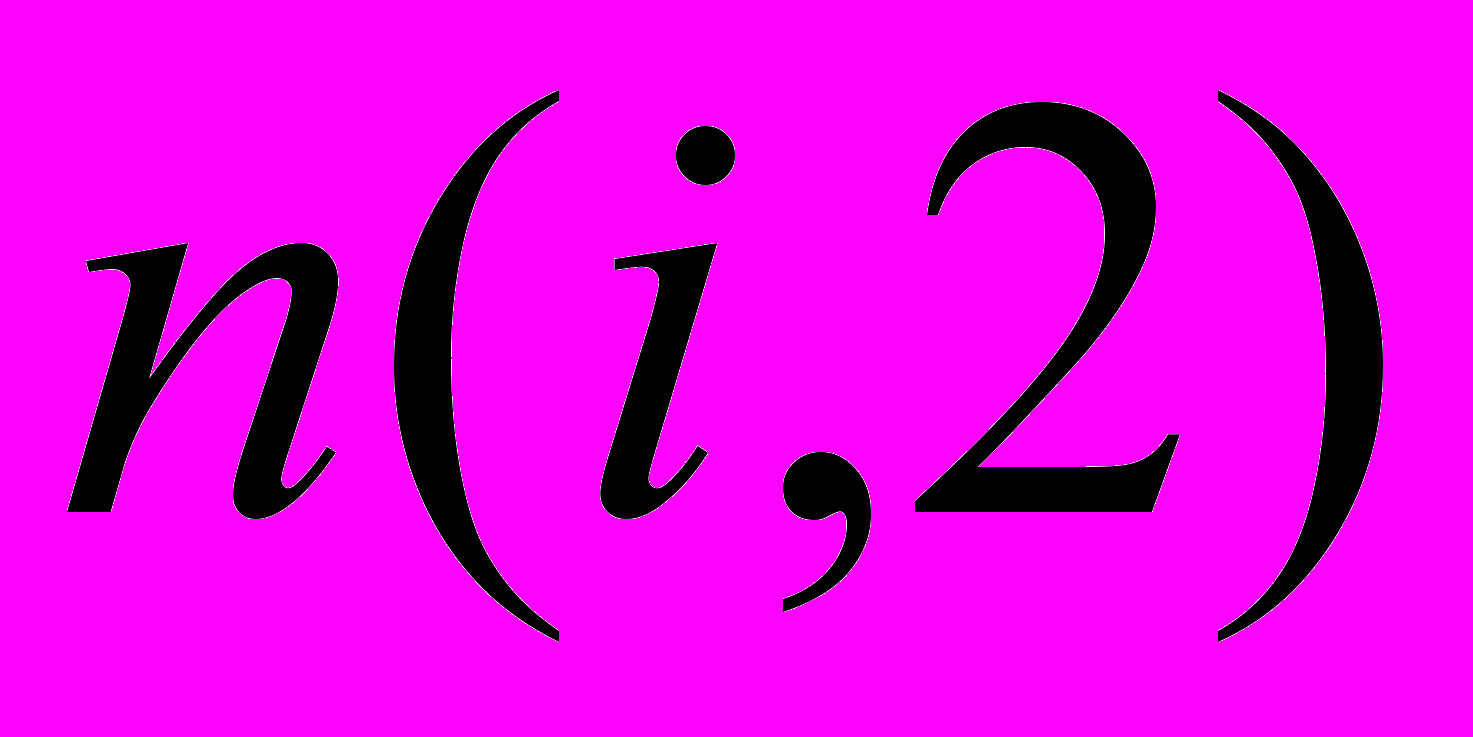, 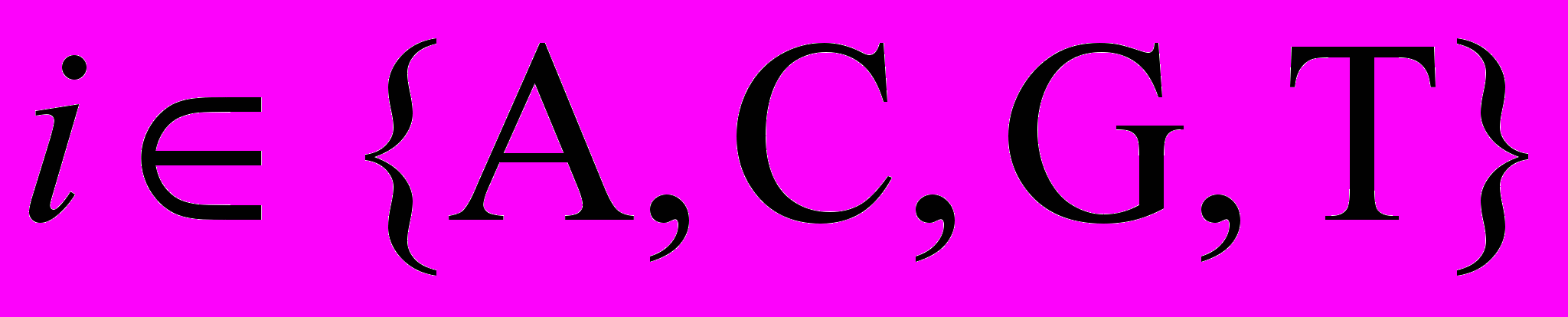может выполняться и в том случае, когда обе комплементарные нити ДНК имеют одинаковые направления записи и считывания оснований (рис.3). Однако в природе такой вид симметрии отсутствует.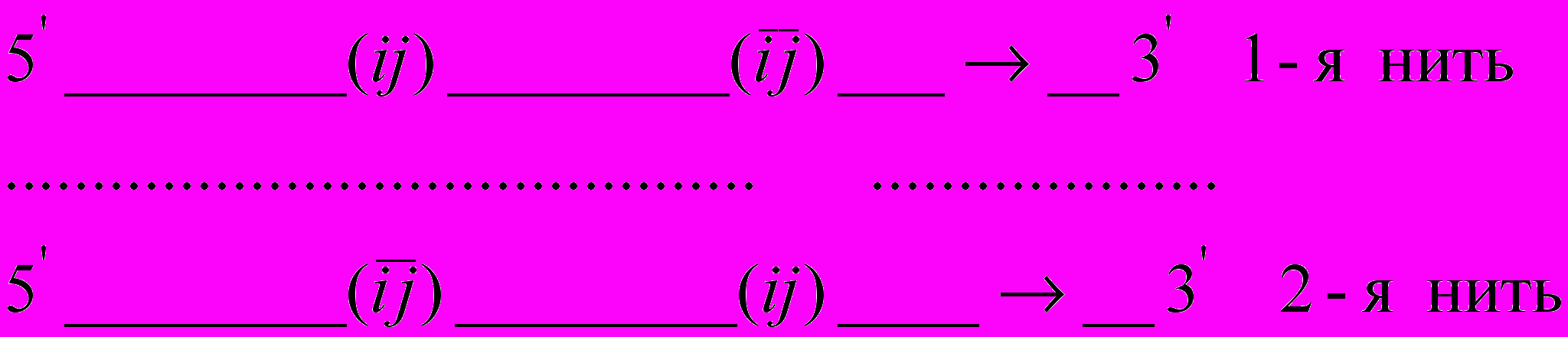





Рис 3. Одинаковая полярность нитей ДНК


Поэтому из симметрии оснований нельзя вывести симметрию пар оснований.

Симметрия пар оснований 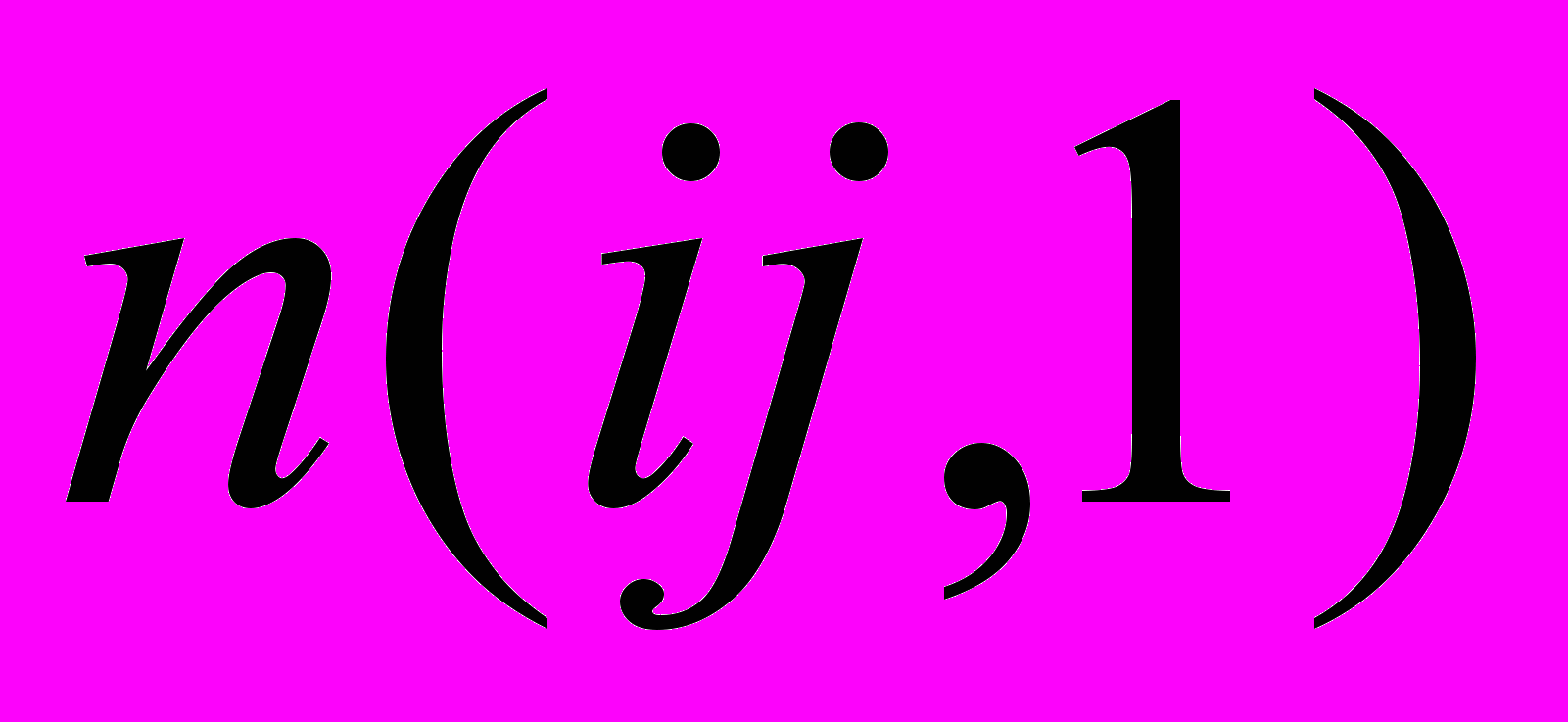= 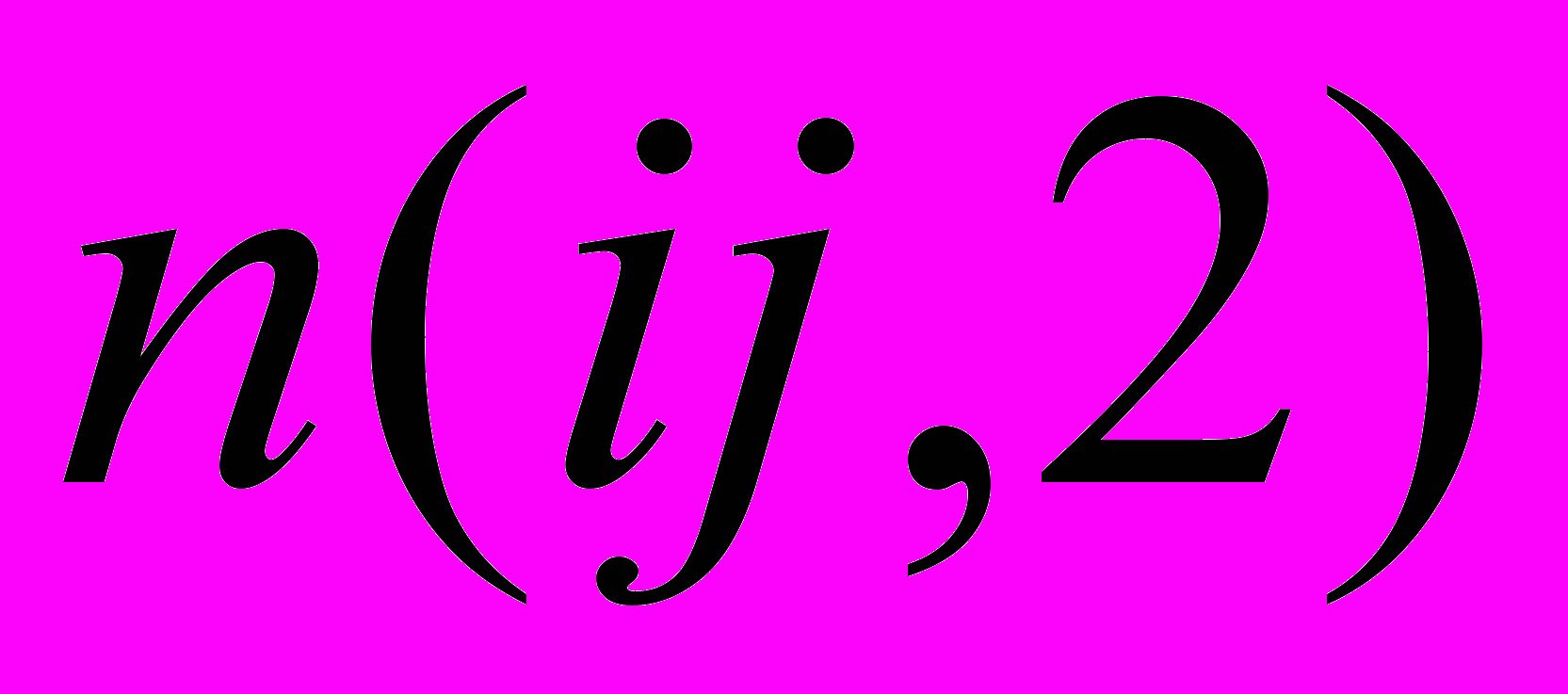вытекает из соотношений

n(AA)= n(TT), n(CC)= n(GG),


n(AC)= n(TG), n(CA) = n(GT), (18)

n(AG)= n(TC), n(CG) = n(GC),


n(AT)= n(TA), n(CT) = n(GA),


или в виде

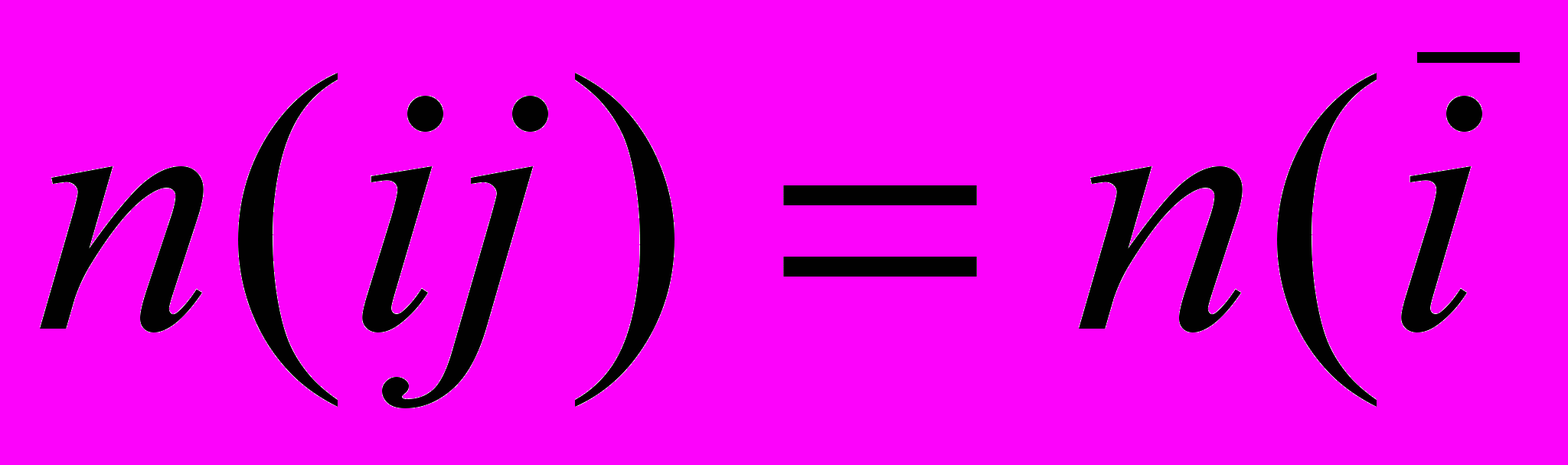
. (19)


Для симметрии (19) два ограничения (7), (8) с учетом (19) трансформируются в одно ограничение


n(CA) + n(GA) = n(AC) + n(AG) . (20)


Симметрия троек оснований 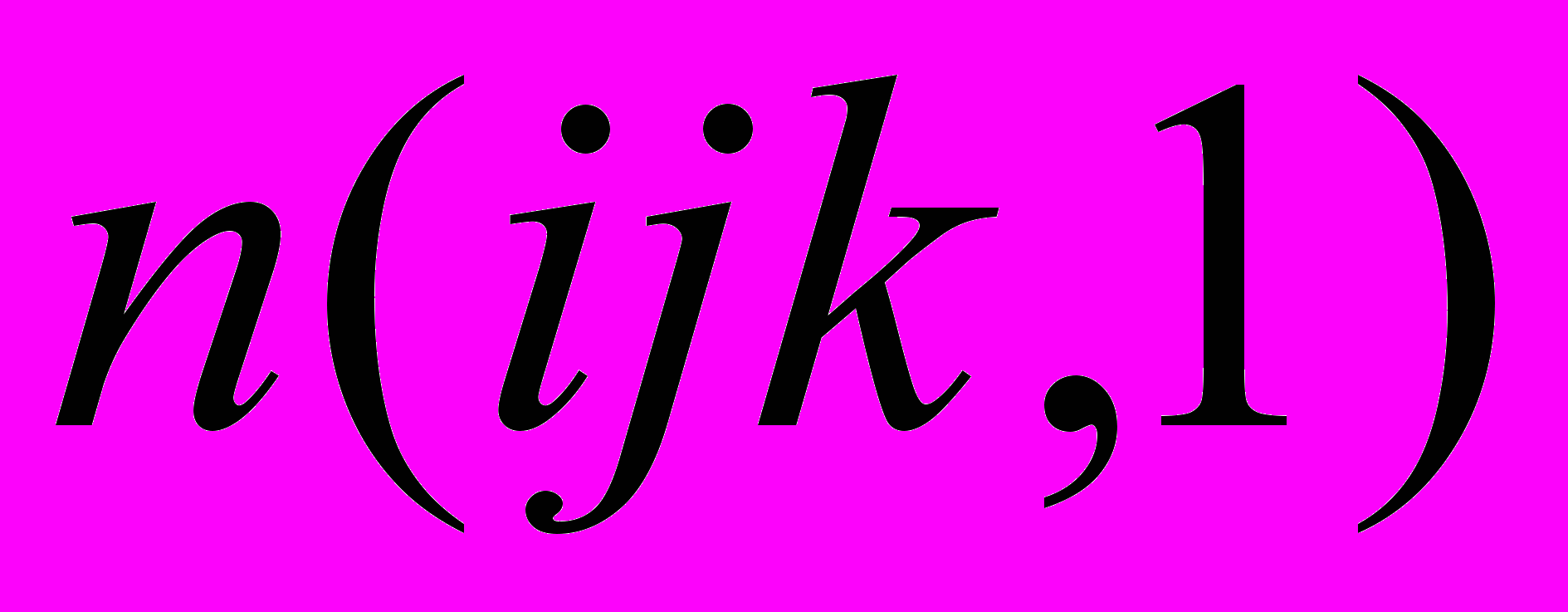= 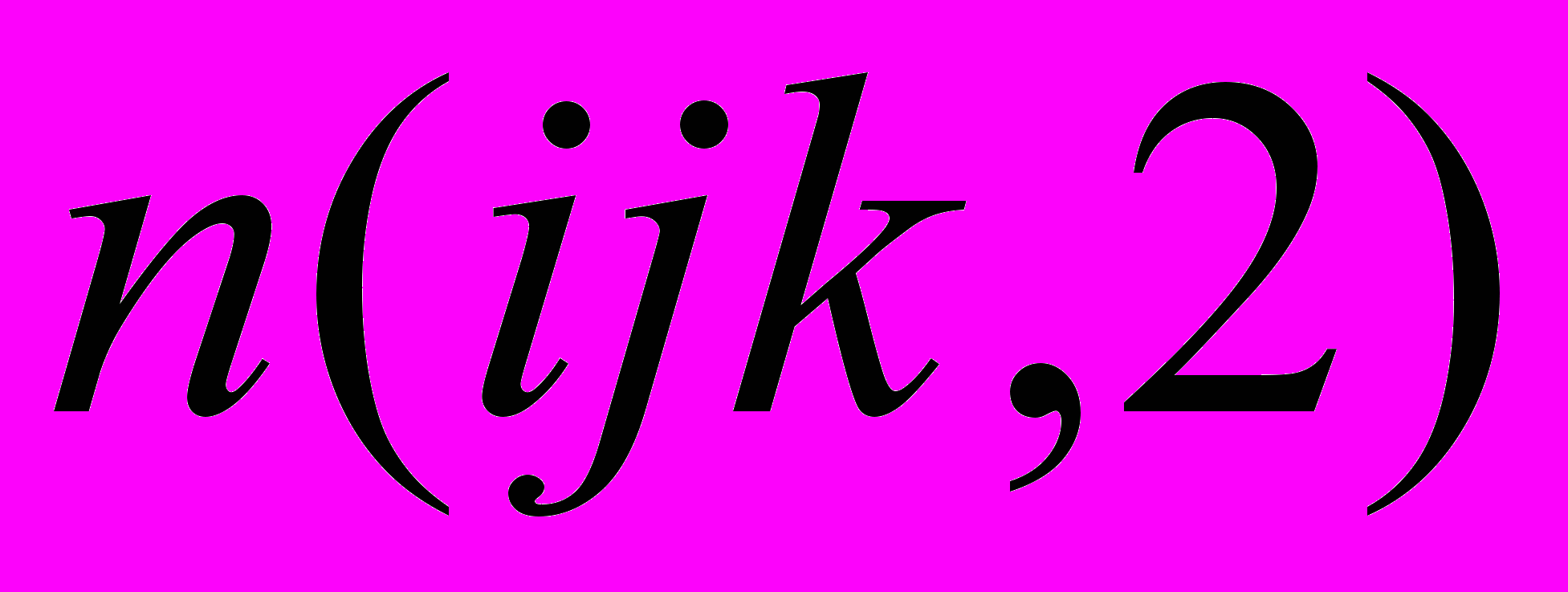вытекает из соотношений

. (21)


Для симметрии (21) к шести ограничениям (11)–(16) добавляются два ограничения


n(ATC) + n(ATG) + n(ATT) = n(AAT) + n(CAT) + n(GAT), (22)

n(CGA) + n(CGC) + n(CGT) = n(ACG) + n(CCG) + n(TCG). (23)


Для симметрии с одинаковой полярностью нитей ДНК справедливы рассмотренные выше утверждения 1–3.

Для однородной цепи Маркова оценки вероятностей троек основани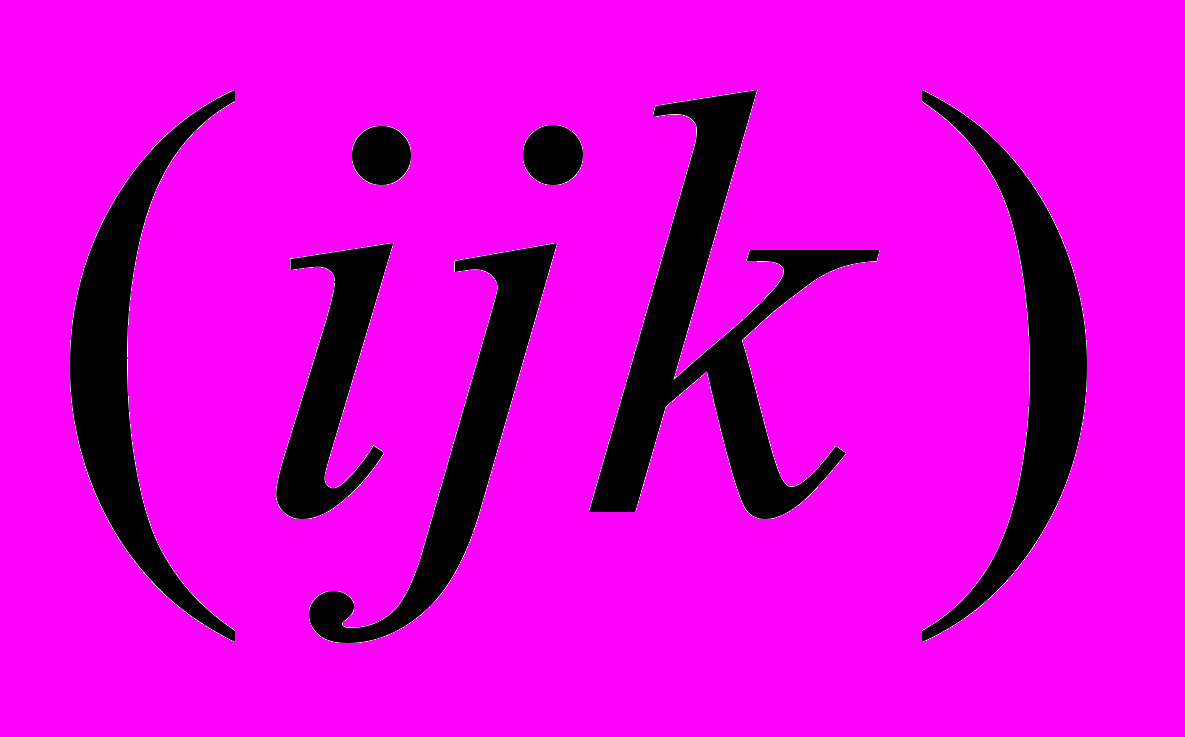й и 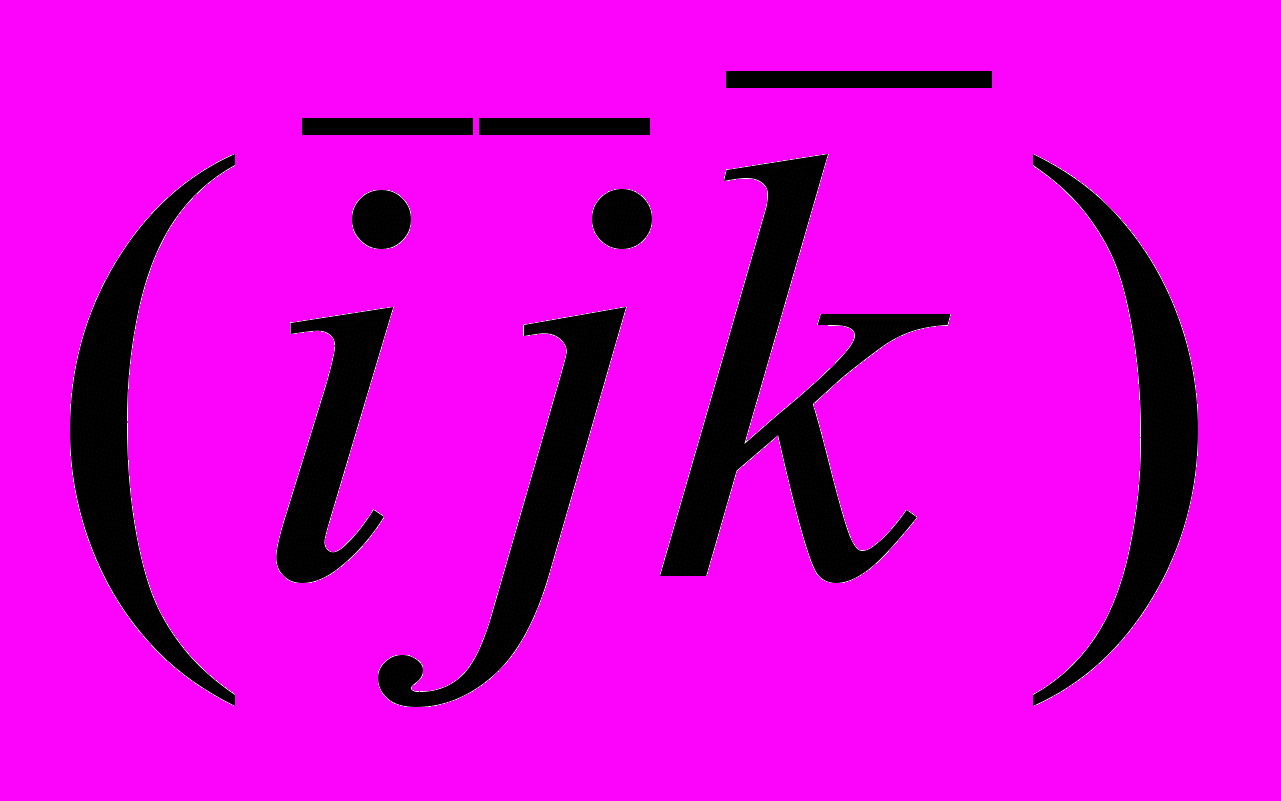совпадают

= .

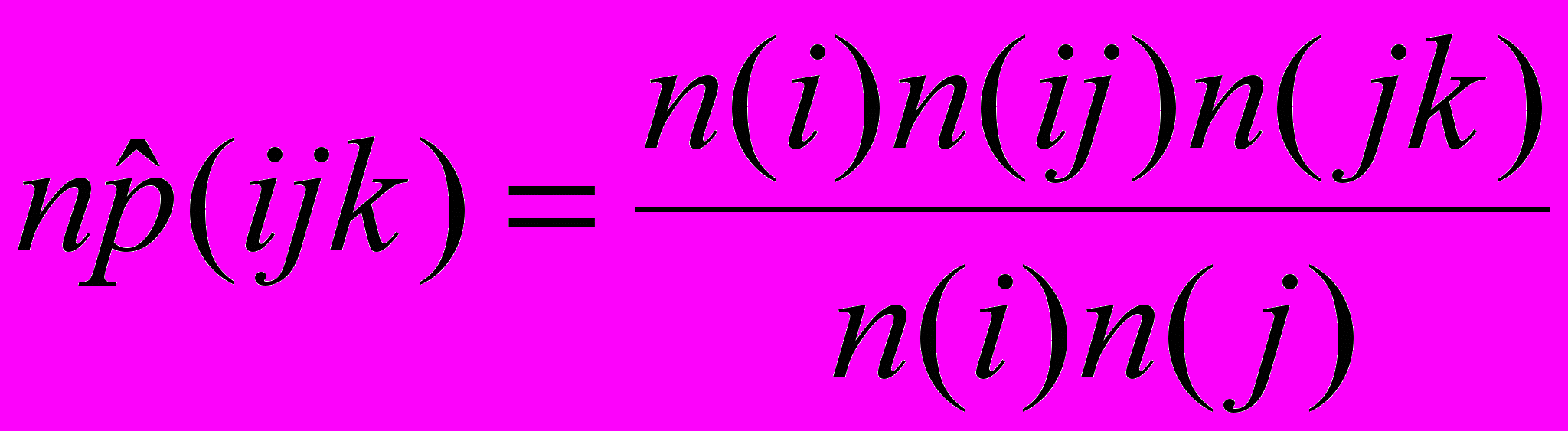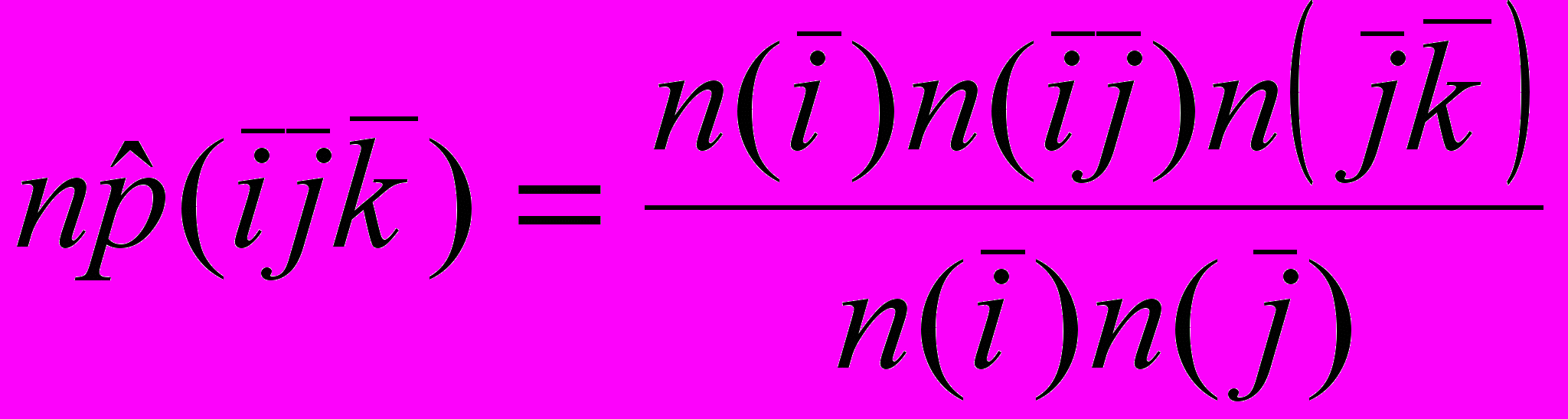Утверждение 4 записывается следующим образом.

Утверждение . Оценка вероятности последовательности 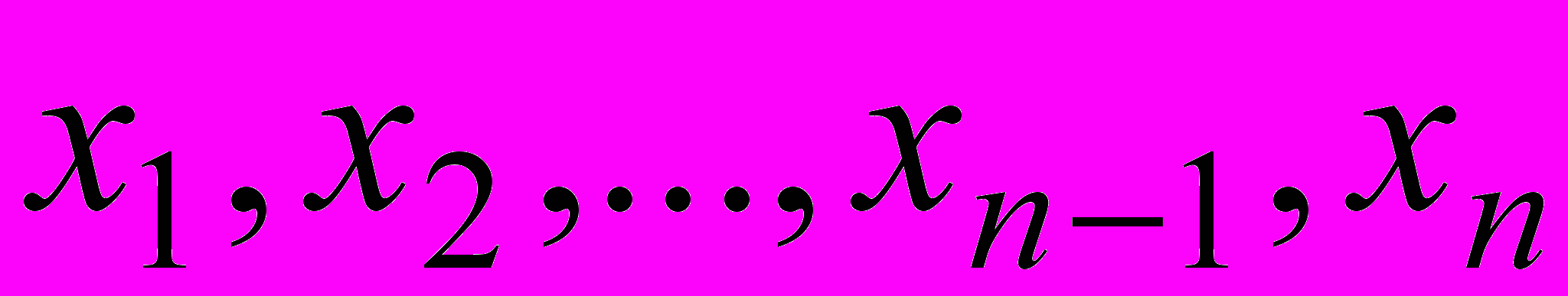совпадает с оценкой вероятности последовательности 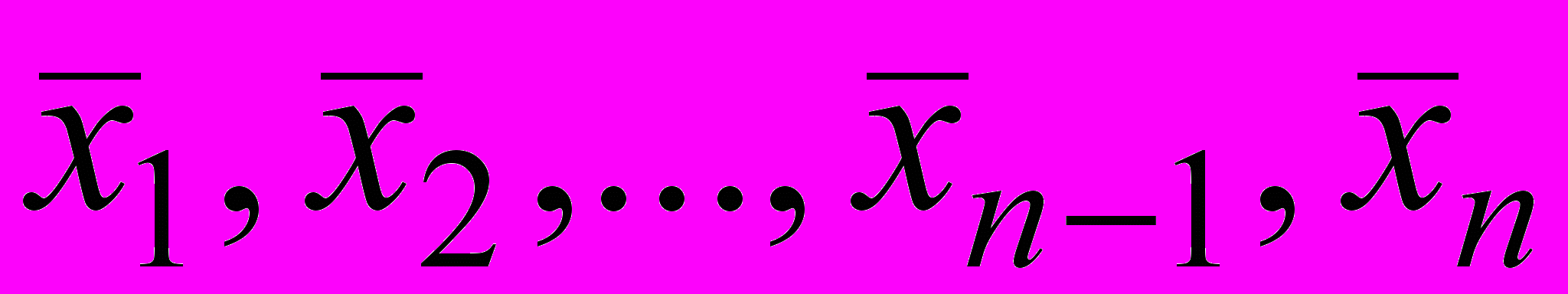, т.е.


. (26)


Симметрия вида 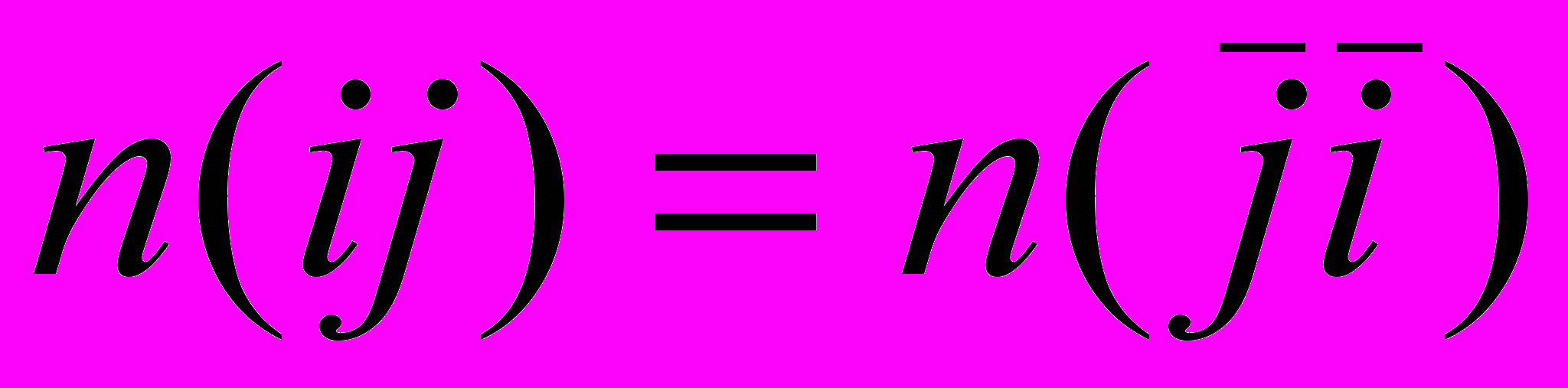имеет 8 связывающих ограничений для пар оснований, а симметрия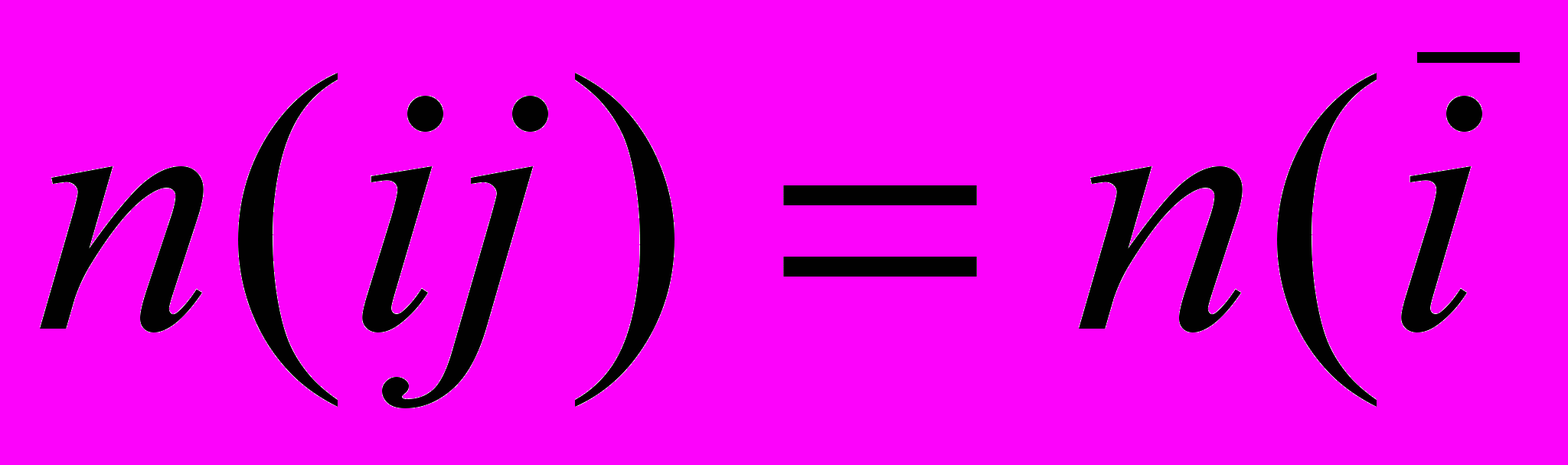 содержит 9 ограничений (20), (22). Для троек оснований у симметрии вида на 2 ограничения больше, чем у симметрии .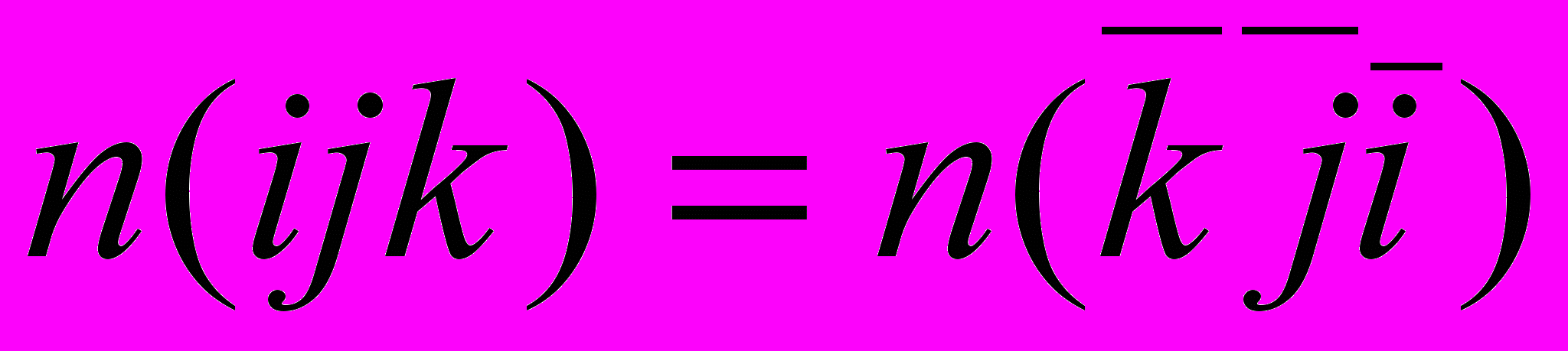

Поэтому у ДНК с противоположной полярностью нитей больше степеней свободы, чем у ДНК с одинаковой полярностью, т.е. с точки зрения теории информации модель Уотсона-Крика более эффективна.


3. Генерация случайных последовательностей с симметриями обеих видов. С помощью модели цепей Маркова можно легко сгенерировать случайную последовательность, для которой будет выполняться симметрия вида 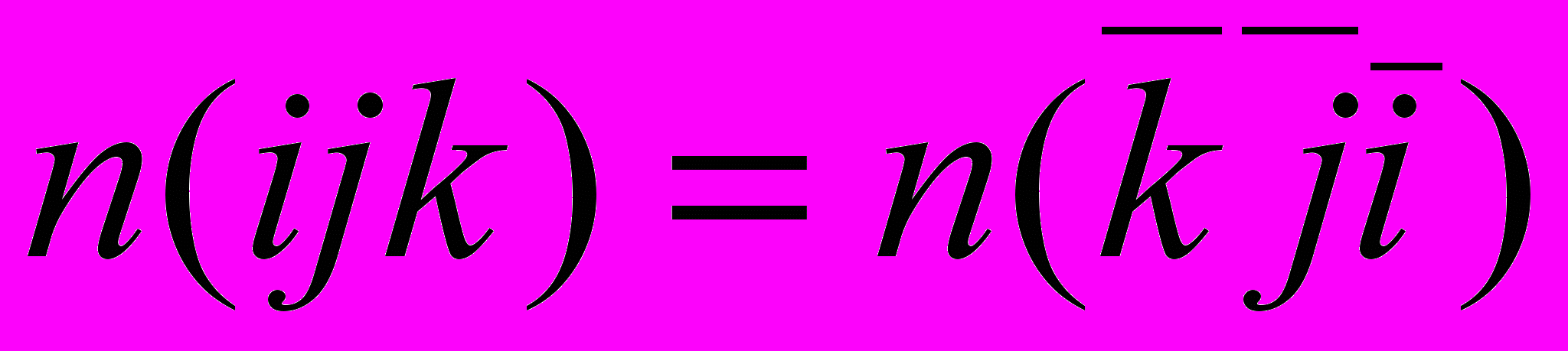. На основе оценок переходных вероятностей, таблицы 1 и датчика псевдослучайных чисел строится случайная последовательность оснований, совпадающая по длине с хромосомой человека.

Первое основание	Второе основание
	A	C	G	T
A	0,3266	0,1725	0,2448	0,2561
C	0,3484	0,2610	0,0485	0,3421
G	0,2864	0,2117	0,2608	0,2412
T	0,2181	0,2051	0,2498	0,3270

Таблица 1: Переходные вероятности в цепочках оснований

ijk		n(ijk)			ijk		n(ijk)		
aaa	ttt	6931319	6953141	0,31%	cag	ctg	3968104	3971877	0,09%
aac	gtt	3659367	3667685	0,23%	cca	tgg	4231496	4232443	0,02%
aag	ctt	5196124	5202925	0,13%	ccc	ggg	3166451	3163597	0,09%
aat	att	5430603	5437075	0,12%	ccg	cgg	588979	587592	0,24%
aca	tgt	3906403	3915530	0,23%	cga	tcg	647493	646673	0,13%
acc	ggt	2921470	2925418	0,13%	cgc	gcg	478028	477042	0,21%
acg	cgt	543435	543016	0,08%	cta	tag	3472066	3470901	0,03%
act	agt	3830137	3833597	0,09%	ctc	gag	3261613	3263830	0,07%
aga	tct	4554218	4560669	0,14%	gaa	ttc	4353459	4362550	0,21%
agc	gct	3365393	3365564	0,01%	gac	gtc	2298885	2301870	0,13%
agg	cct	4145751	4152111	0,15%	gca	tgc	3432455	3435791	0,10%
ata	tat	3627798	3630628	0,08%	gcc	ggc	2570998	2566847	0,16%
atc	gat	3408799	3411769	0,09%	gga	tcc	3473521	3480118	0,19%
atg	cat	4152825	4153497	0,02%	gta	tac	2447121	2445778	0,05%
caa	ttg	5298710	5310889	0,23%	taa	tta	4633924	4634246	0,01%
cac	gtg	2797415	2800885	0,12%	tca	tga	4647372	4652712	0,11%

Таблица 2: Статистика по тройкам оснований для цепочек длины 22310⁶ оснований

Количество оснований	Минимальное отклонение	Максимальное отклонение	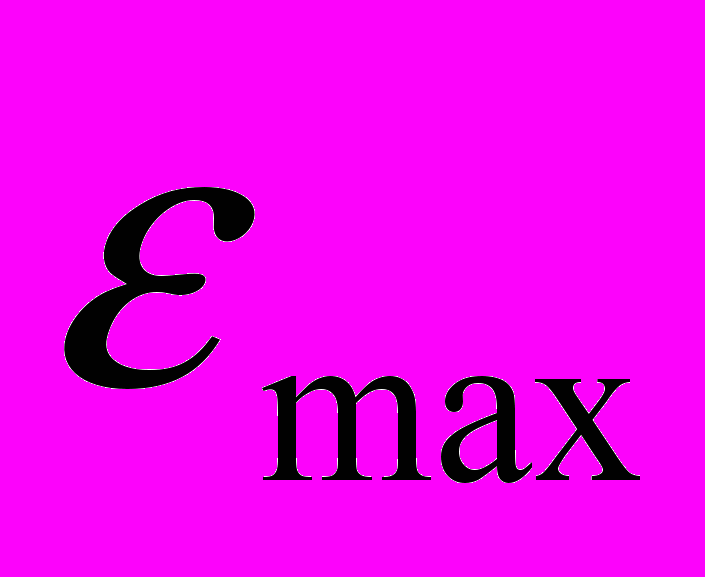Среднее отклонение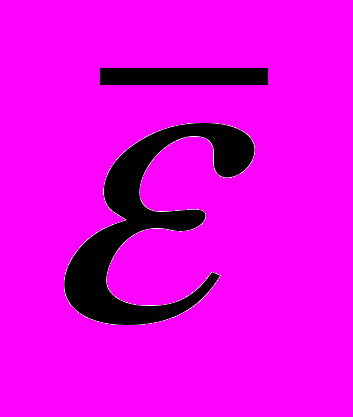
20000	0,13%	10,39%	2,86%
50000	0,03%	2,86%	1,14%
200000	0,05%	2,27%	0,81%
106	0,02%	0,91%	0,29%
5106	0,01%	0,40%	0,18%
223106	5,110-3%	0,31%	0,13%

Таблица 3: Статистка по относительной разности числа комплементарных оснований

Первое основание	Второе основание
	A	C	G	T
A	0,3266	0,1725	0,2448	0,2561
C	0,3689	0,2763	0,0514	0,3034
G	0,3031	0,0514	0,2760	0,3695
T	0,2557	0,2448	0,1725	0,3270

Таблица 4: Новые переходные вероятности в цепочках оснований

ijk		n(ijk)			ijk		n(ijk)		
aaa	ttt	7341532	7359207	0,24%	caa	gtt	5149990	5154109	0,08%
aac	ttg	3875183	3882096	0,18%	cac	gtg	2720083	2720158	0,00%
aag	ttc	5502305	5511508	0,17%	cag	gtc	3856752	3859271	0,07%
aat	tta	5752239	5752431	0,00%	cat	gta	4034677	4036244	0,04%
aca	tgt	4379729	4386669	0,16%	cca	ggt	4354970	4352330	0,06%
acc	tgg	3275634	3274232	0,04%	ccc	ggg	3259661	3253668	0,18%
acg	tgc	609760	611086	0,22%	ccg	ggc	605309	603964	0,22%
act	tga	3597609	3602725	0,14%	cct	gga	3575644	3569488	0,17%
aga	tct	5104466	5112922	0,17%	cga	gct	665943	664977	0,15%
agc	tcg	865613	865745	0,02%	cgc	gcg	112966	112580	0,34%
agg	tcc	4647487	4654703	0,16%	cgg	gcc	604063	605586	0,25%
agt	tca	6220361	6216317	0,07%	cgt	gca	810422	810486	0,01%
ata	tat	4503685	4506729	0,07%	cta	gat	3311569	3313749	0,07%
atc	tag	4308309	4308723	0,01%	ctc	gag	3170599	3170147	0,01%
atg	tac	3039110	3035319	0,12%	ctg	gac	2233348	2232147	0,05%
att	taa	5756291	5753158	0,05%	ctt	gaa	4235636	4226579	0,21%

Таблица 5: Статистика по тройкам оснований для нового типа симметрии в цепочке длиной 22310⁶ оснований

Количество оснований	Минимальное отклонение	Максимальное отклонение	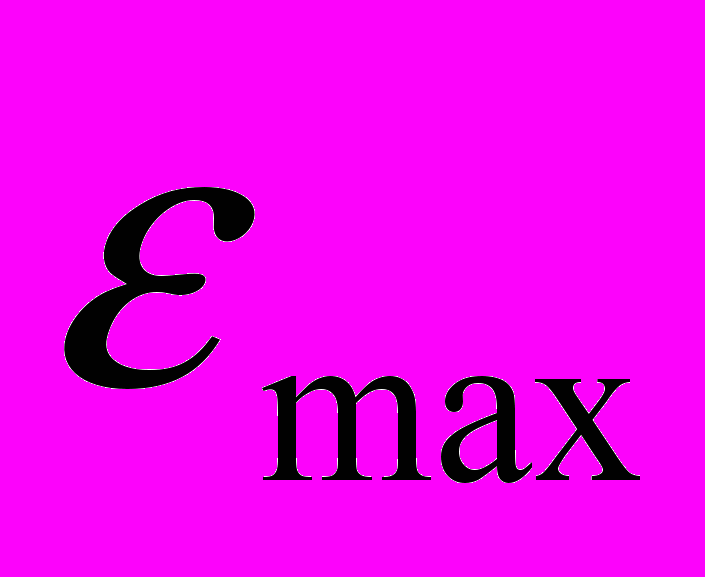Среднее отклонение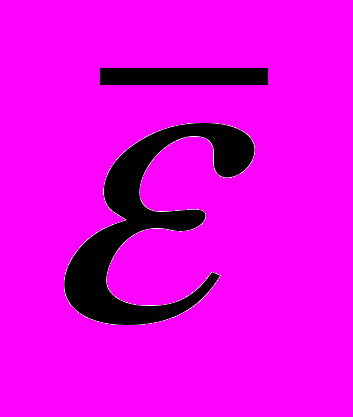
20000	0,08%	5,30%	1,95%
50000	0,02%	5,64%	1,50%
200000	0,03%	3,15%	0,69%
106	0,01%	1,35%	0,31%
5106	410-3%	0,50%	0,23%
223106	310-3%	0,34%	0,12%

Таблица 6: Статистка по относительной разности числа комплементарных оснований для нового типа симметрии