Тема Введение: научное мировоззрение, инженерный подход

Вид материала

Конспект

Содержание Определения информации и сообщения. Органы чувств. Вероятностная теория информации: Кодирование и интерпретация сообщений, мера Величайшее литературное произведение — в принципе не что иное, как Поезд, который сходит с рельсов, заведомо имеет большую информационную ценность, чем поезд, прибывающий по расписанию." В.2.2. Количество информации Н называют средним количеством информации на знак, информацией на знак I. — Я. В общем случае связь между средней длиной слов Ь Тема 8. Гносеологические модели процедур разработки информационных систем. Каскадная, итерационная и спиральная гносеологические модели процесса проектирования ИС

Подобный материал:

• Тема философия ее предмет и место в культуре человечества, 269.16kb.
• Нестареющий парадокс психофизических явлений: инженерный подход, 1446.38kb.
• Тема: статья, 36.51kb.
• Семинару № Тема: Предмет, структура и функции философии, 27.82kb.
• Тематика лекций для аспирантов, по специальности Химия Введение (4 ч.), 99.04kb.
• Тесты для самопроверки знаний раздел I. Что такое философия? Тема Философия в системе, 1997.45kb.
• Темы Тема Раздел I. Что такое философия?, 1476.9kb.
• О. В. Белова Новосибирск: Научно-учебный центр психологии нгу, 1996 Введение Тема Тема, 1006.61kb.
• О. В. Белова Новосибирск: Научно-учебный центр психологии нгу, 1996 Введение Тема Тема, 1005.33kb.
• Аннотация дисциплины «инженерный анализ», 37.1kb.

Тема 4. Информация и сообщение. Теория информации Шеннона.

Определения информации и сообщения. Органы чувств. Вероятностная теория информации: Кодирование и интерпретация сообщений, мера информации (энтропия) информации.


Вероятностная теория информации

„ Величайшее литературное произведение — в принципе не что иное, как _;разбросанный в беспорядке алфавит."

Жан Кокто'

'В.2.1. Шенноновские сообщения

„Тот факт, что зло всё ещё имеет более высокую информационную ценность, чем добро,— неплохой признак. Он доказывает, что добро по-прежнему является правилом, а зло, напротив, исключением."
Нильс Ионсон

„ Поезд, который сходит с рельсов, заведомо имеет большую информационную ценность, чем поезд, прибывающий по расписанию."

Гастон Лакур

Содержащаяся в сообщении информация может существенно зависеть от того момента времени, в который сообщение достигает приёмника. Задержка такого сообщения одновременно изменяет его характер. Примерами могут служить лотерейный билет, прогноз погоды и штормовое предупреждение. Предельным является случай, когда вся информация, которую несёт сообщение, определяется временем прибытия (заранее обусловленного) сигнала. Тогда говорят об извещении или тревоге. Примерами служат пожарный сигнал, звон колокола, бой часов или сигнал сирены.

Существуют, однако, сообщения, информация которых не зависит от времени. Такие сообщения часто можно рассматривать как последовательности отдельных сообщений, которые посылаются друг за другом во времени: в момент времени t₀ — первое сообщение, в момент t₁ — второе и т. д. Так как нас не интересует дальнейшая внутренняя структура отдельных сообщений, мы можем считать их знаками. Эти знаки считаются выбранными с некоторыми не зависящими от времени вероятностями из заранее заданного конечного или бесконечного набора знаков. Здесь нас особо интересует случай, имеющий место, например, при бросании кубика, когда вероятность встретить некоторый знак Z, в произвольный момент времени t совпадает с относительной частотой знака Z во всей последовательности знаков. Последовательности знаков с таким свойством называются шенноневскими сообщениями, а порождающий их отправитель — источником сообщений или шенноновским источником. С математической точки зрения источник сообщений — это стационарный случайный процесс.

Поскольку сами знаки и содержащаяся в них информация известны заранее, существенный момент при поступлении некоторого знака состоит в самом факте, какой именно из заданных знаков получен, т. е. какой из знаков был „выбран". Эти „выборы" исследуются теорией информации Шеннона. К. Шеннон в 1948 г. ввёл в связи с этим математическое понятие количества информации. Это в существенном мера тех затрат, которые необходимы для того, чтобы расклассифицировать („разобрать") переданные знаки. Слово „информация" употребляется здесь, очевидно, в некотором специальном смысле, не совпадающем с тем, в котором оно использовалось нами ранее.

В.2.2. Количество информации

Шенноновская теория информации, точнее количества ин­формации, исходит из элементарного альтернативного выбора между двумя знаками (битами) О и 1_. Такой выбор соответствует приёму сообщения, состоящего из одного двоичного зна­ка. По определению количество информации, содержащееся в таком сообщении, принимается за единицу и также называется битом.

Если выбор состоит в том, что некоторый знак выбирается из множества п знаков, где 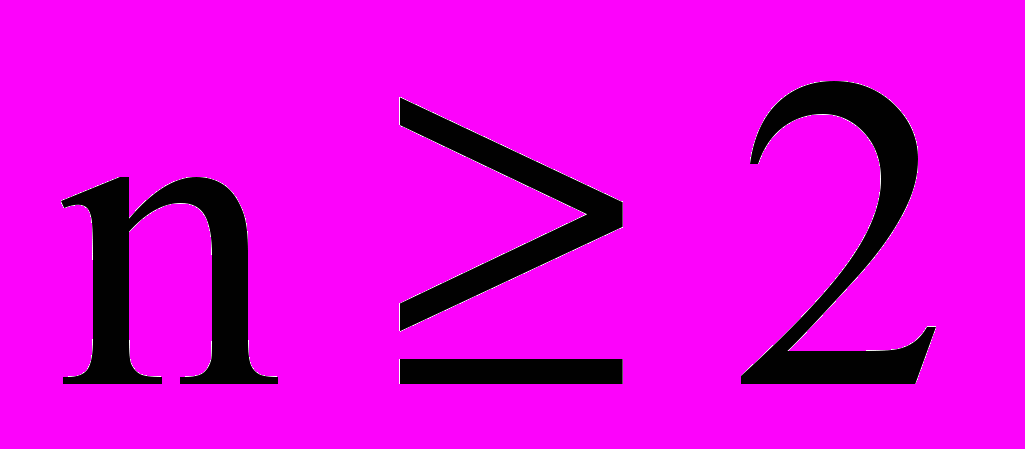то это можно сделать посредством конечного числа следующих друг за другом альтернативных выборов в форме выборочного каскада: данное множество из п знаков разбивается на два (непустых) подмножества, каждое из которых точно так же разбивается дальше, пока мы не получим одноэлементные подмножества.

При заданном выборочном каскаде нас интересует теперь, сколько потребуется альтернативных выборов для выбора какого-нибудь определённого знака. На рис. 1 приведён пример: чтобы выбрать а или е, нужны два альтернативных выбора (количество информации составляет 2 бита); чтобы выбрать b, с или f, необходимы три альтернативных выбора, и т. д.

Если некоторый знак встречается часто, то, естественно, количество выборов, требующихся для его опознавания, стремятся сделать возможно меньшим. Соответственно для опознавания более редких знаков приходится использовать большее число альтернативных выборов. Другими словами, часто встречающиеся знаки содержат малое, а редкие знаки — большое количество информации. Поэтому представляется разумным разбивать исходное множество знаков не на равновеликие, а на равновероятные подмножества, т. е. так, чтобы при каждом разбиении на два подмножества суммы вероятностей для знаков одного и для знаков другого подмножества были близки друг к другу, насколько это возможно. Ради простоты будем считать сначала, что заданные вероятности позволяют получить точное равенство. Тогда если i-й знак выделяется после k_i альтернативных выборов, то вероятность его появления р_i равна 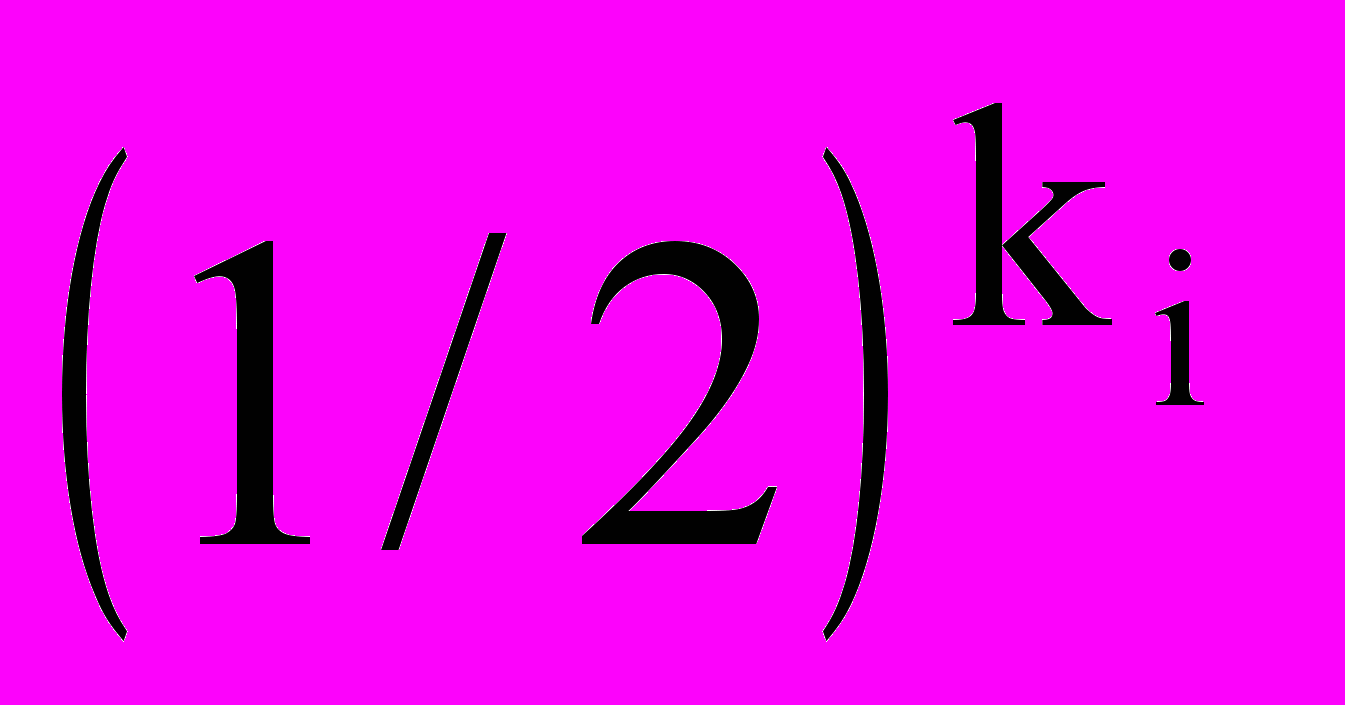. Обратно, для выбора знака, который встречается с вероятностью р_i требуется k_i = ld(1/р_i) альтернативных выборов. Исходя из сказанного мы определим количество информации, содержащейся в знаке, задаваемое частотой появления такого знака, как 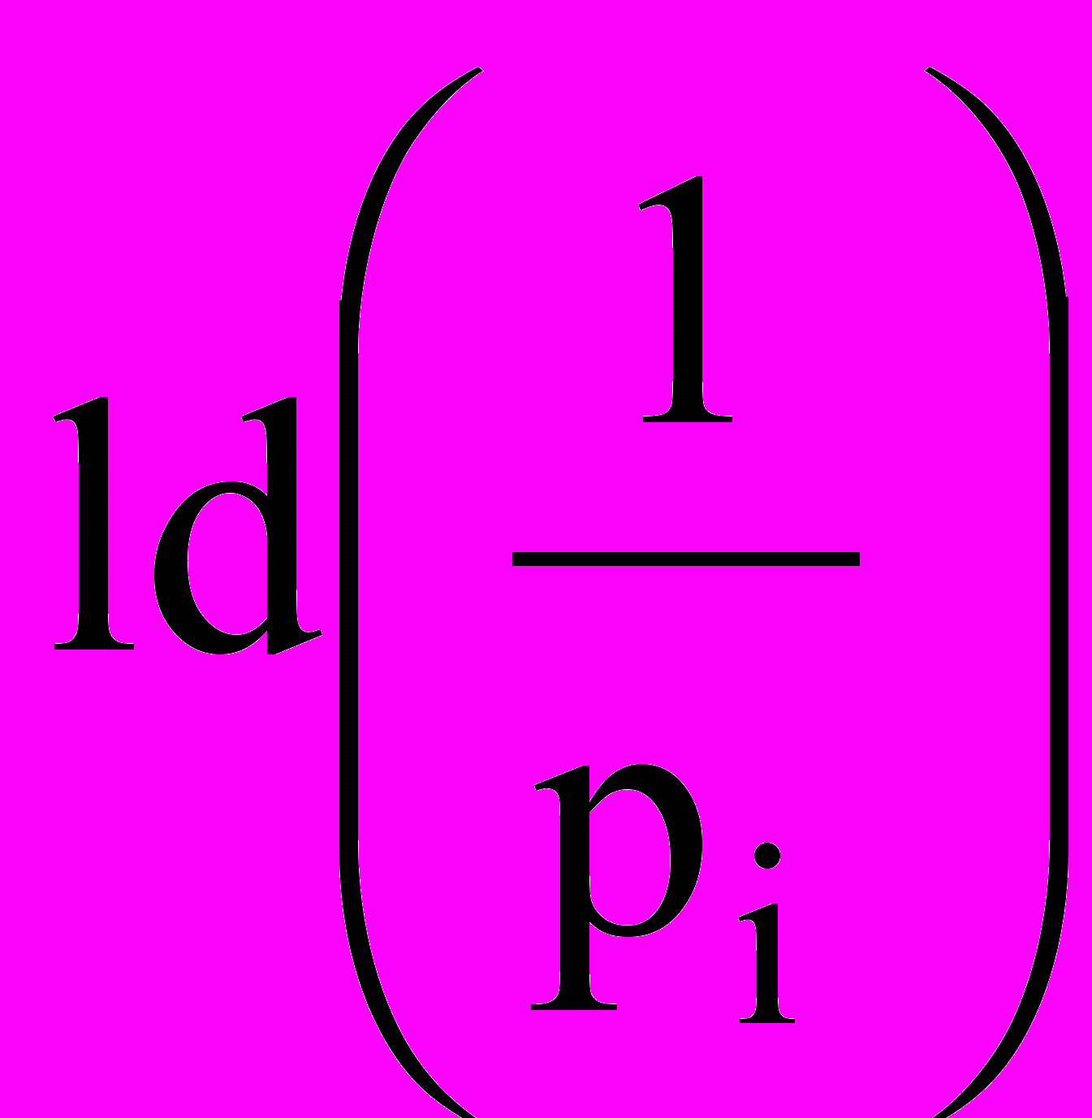(бит).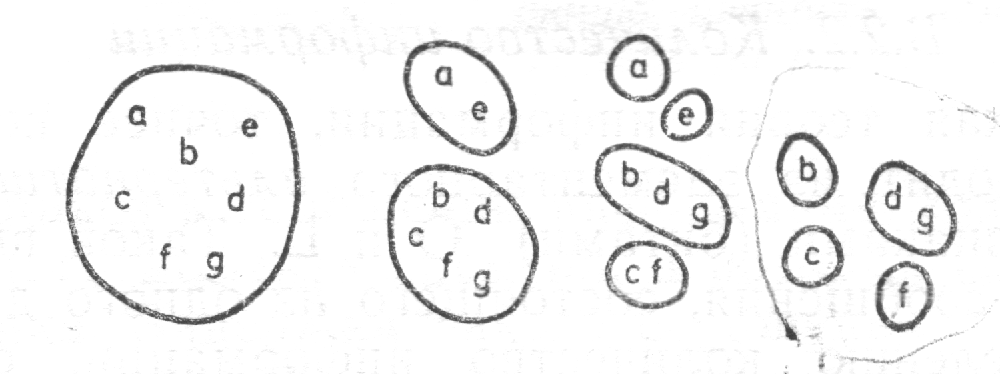



Рис.1. Выборочный каскад.


Тогда среднее количество информации, приходящейся на один произвольный знак, будет равно 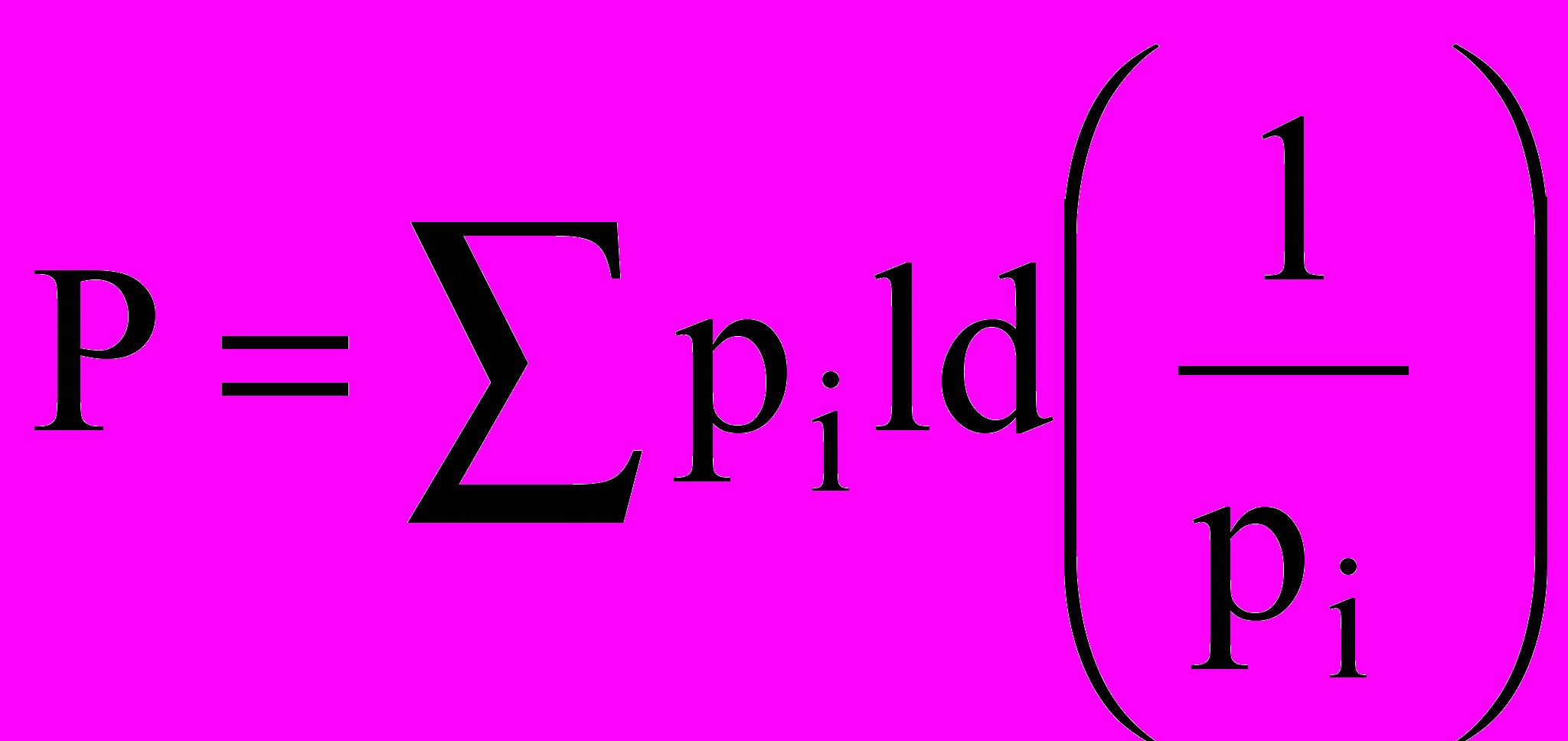(бит).


Это — основное определение теории информации Шеннона. Величину Н называют средним количеством информации на знак, информацией на знак или энтропией источника сообщений.

Результат одного отдельного альтернативного выбора может быть представлен как О или L. Тогда выбору всякого знака соответствует некоторая последовательность двоичных знаков О и L, т. е. двоичное слово. Мы назовем это двоичное слово кодировкой знака, а множество кодировок всех знаков источника со­общений — кодированием источника сообщений. Получающиеся двоичные слова имеют, вообще говоря, разную длину: знаку, вероятность которого р_i, соответствует слово длины N_i = ld(1/р_i). Однако условие Фано (см. 1.4.3) при этом выполняется автоматически.

Таким образом, Н является еще и средней длиной двоичных слов, используемых при двоичном кодировании источника сообщений. На рис. 2 показано, как производится кодирование для примера, приведённого на рис. 1.

Буква		Кодирование
a	1/4	00
e	1/4	01
f	1/8	100
c	1/8	101
b	1/8	110
d	1/16	1110
g	1/16	1111

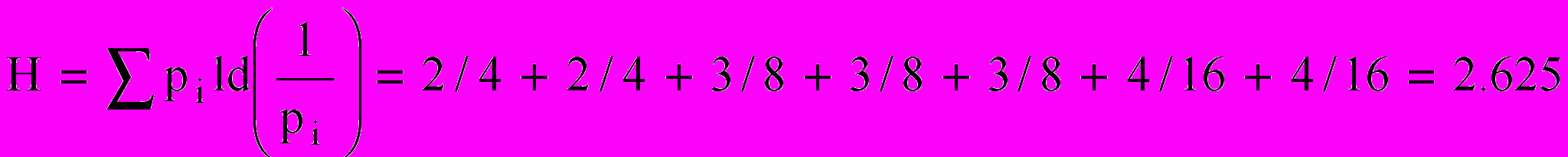Рис.2. Оптимальное кодирование.


Если количество знаков представляет собой степень двойки, п = 2^N и все знаки равновероятны, p_i=(1/2)^N, то все двоичные слова имеют длину N и

H=N=ldn

Легко показать, что для источника сообщений с п знаками и произвольными значениями p_i.



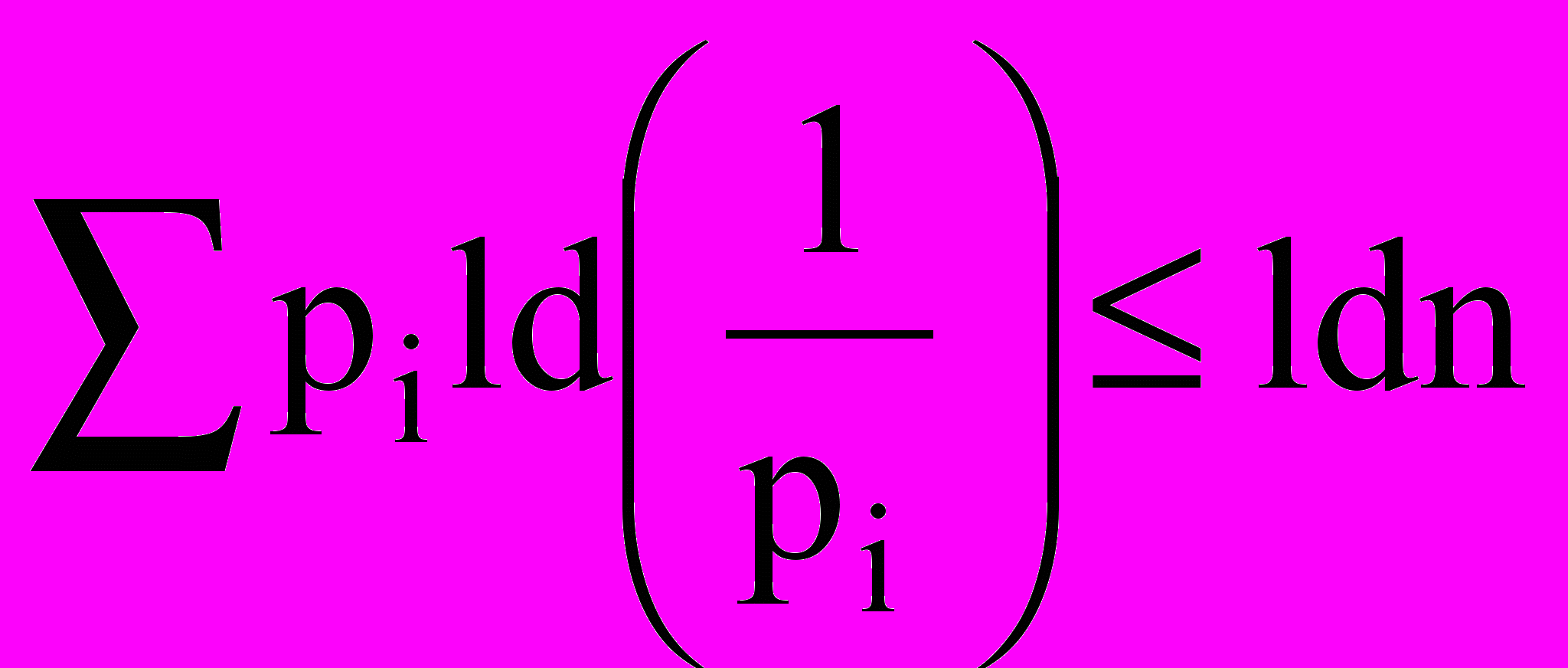
Равенство достигается в случае равновероятных знаков. Но даже в этом случае ldп — это, вообще говоря, не целое число. Это значит, что ldп не может быть (одинаковым для всех знаков) количеством необходимых альтернативных выборов. Тем не менее выбор из п знаков всегда можно осуществить с помощью N альтернативных выборов, где



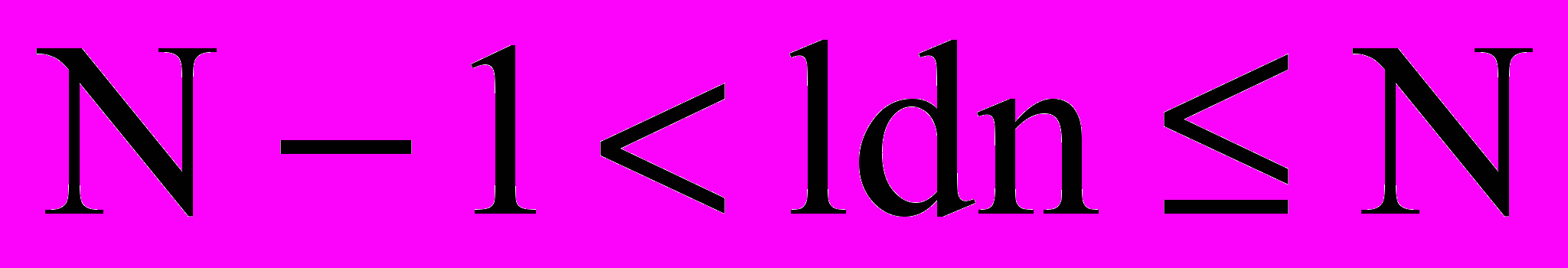
Для этого достаточно разбивать всякое множество знаков так, чтобы количества знаков в двух получающихся подмножествах различались не более чем на 1. Таким образом, для источника с п знаками всегда существует кодирование словами длины N, где .

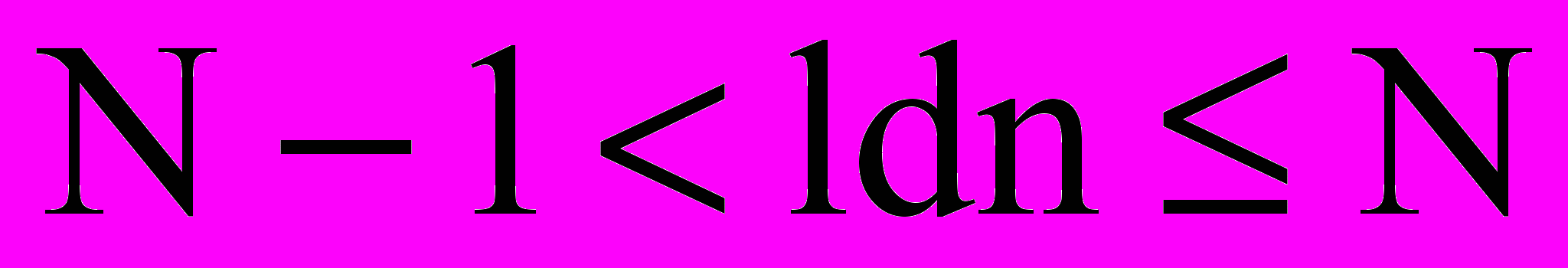Несмотря на сказанное, имеет смысл использовать основное определение количества информации, содержащейся в знаке, и тогда, когда вероятности не являются целочисленными (отрицательными) степенями двойки или когда нельзя произвести точного разбиения на равновероятные подмножества.

Если при некотором кодировании источника сообщений i-й знак имеет длину N_i то средняя длина слов равна



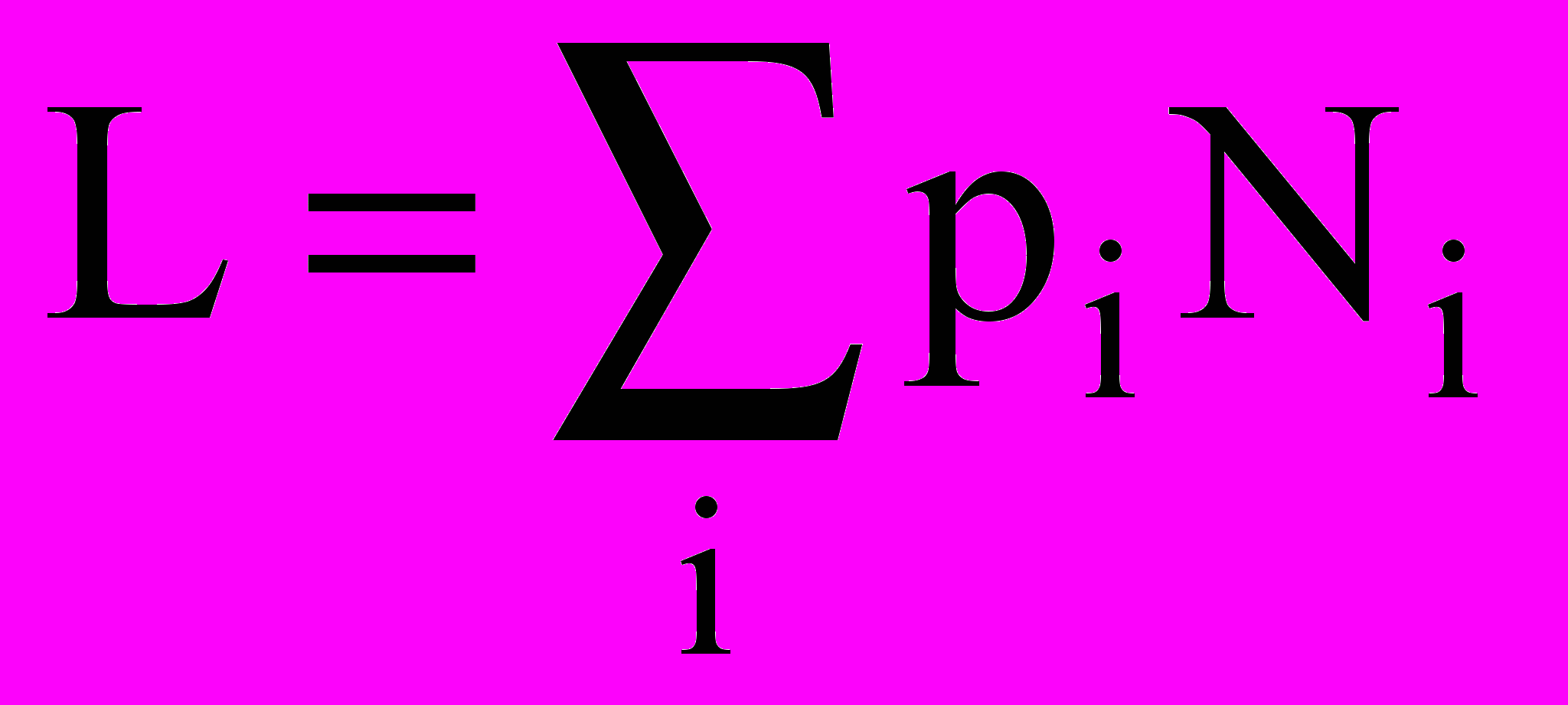
Наложив на набор знаков то ограничение, что его можно раз­бить на точно равновероятные подмножества, мы установили выше, что I. — Я. В общем случае связь между средней длиной слов Ь и энтропией Н источника сообщений даёт следующая

Теорема кодирования Шеннона (Шеннон, 1948г.).

1. Имеет место неравенство

.

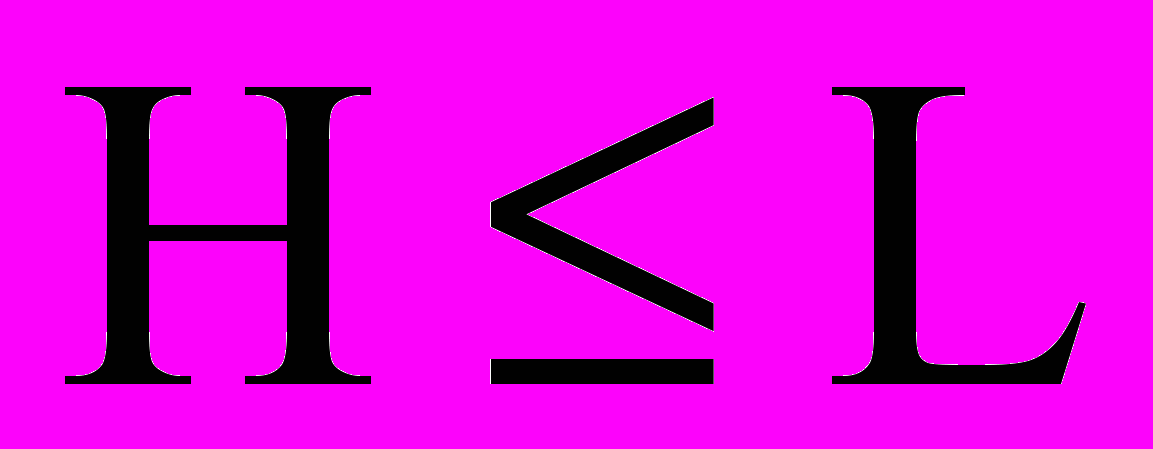2. Всякий источник сообщений можно закодировать так, что разность L — Н будет как угодно мала.

Чтобы получить кодирования, о которых говорится в пункте 2 теоремы, следует не просто кодировать каждый знак по отдель­ности, а рассматривать вместо этого двоичные кодирования для п^k групп по и знаков. Тогда длина кода i-го знака Z_i вычисляется так:

N_i=(средняя длина всех кодовых групп, содержащих Z_i) / k .

Чем больше берётся k, тем точнее можно приблизиться к разбиению на равновероятные подмножества. Часто уже при k=2 или k=3 достигается практически приемлемое приближение.

Именно теорема кодирования является оправданием для оп­ределения энтропии по формуле 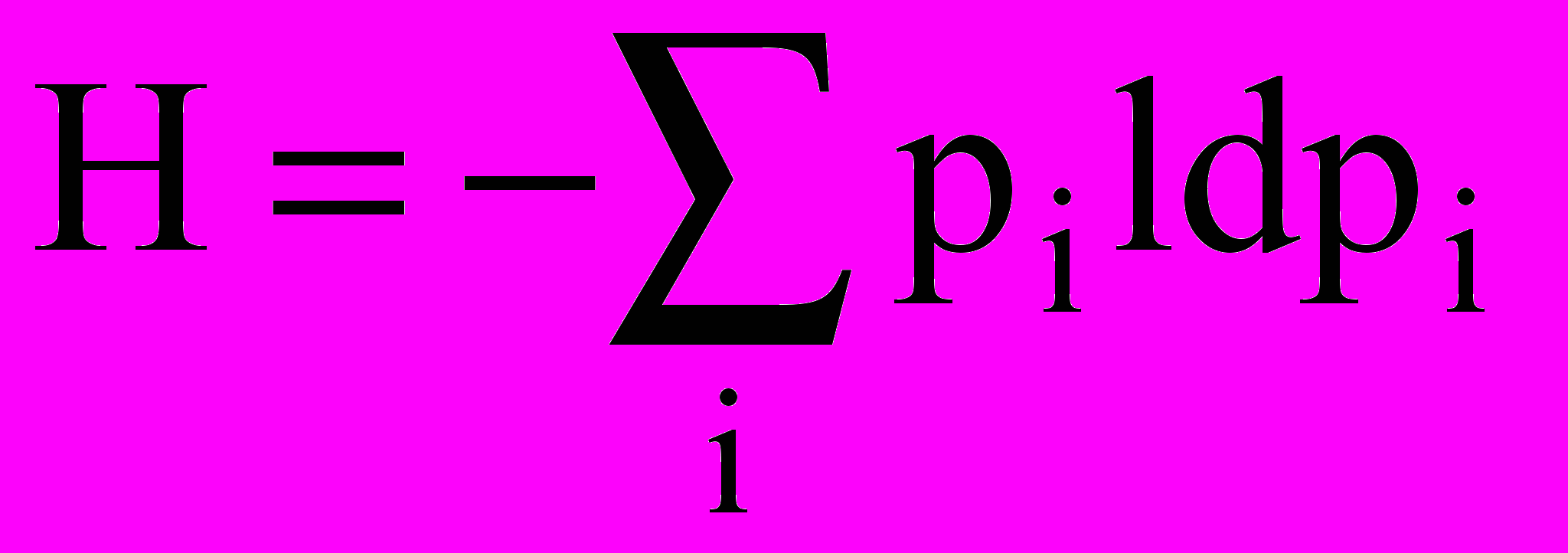; действительно,

Н — это нижняя граница для количества затрачиваемых альтер­нативных выборов при наилучшем возможном кодировании.

Разность L — H называют избыточностью кода, а 1—(H/L) — относительной избыточностью кода. Последняя задаётся обычно в процентах.

Избыточность — это мера бесполезно совершаемых альтернативных выборов. Так как в практических случаях отдельные знаки почти никогда не встречаются одинаково часто, то кодирование с постоянной длиной кодовых слов в большинстве случаев избыточно. Несмотря на это, такое кодирование применяют довольно часто, руководствуясь техническими соображениями, в частности возможностью параллельной и мультиплексной передачи.


Тема 8. Гносеологические модели процедур разработки информационных систем.

Обобщенная структура предмета научной деятельности. Методы исследования: анализ (дедукция), инверсный анализ, научные исследования (индукция), инженерное проектирование. Каскадная, итерационная и спиральная гносеологические модели процесса проектирования ИС.


Представив модель проектирования как научно-творческий процесс (рис.1.3), рассмотрим сущность инженерного подхода в EDA-технологи с позиций теории познания.



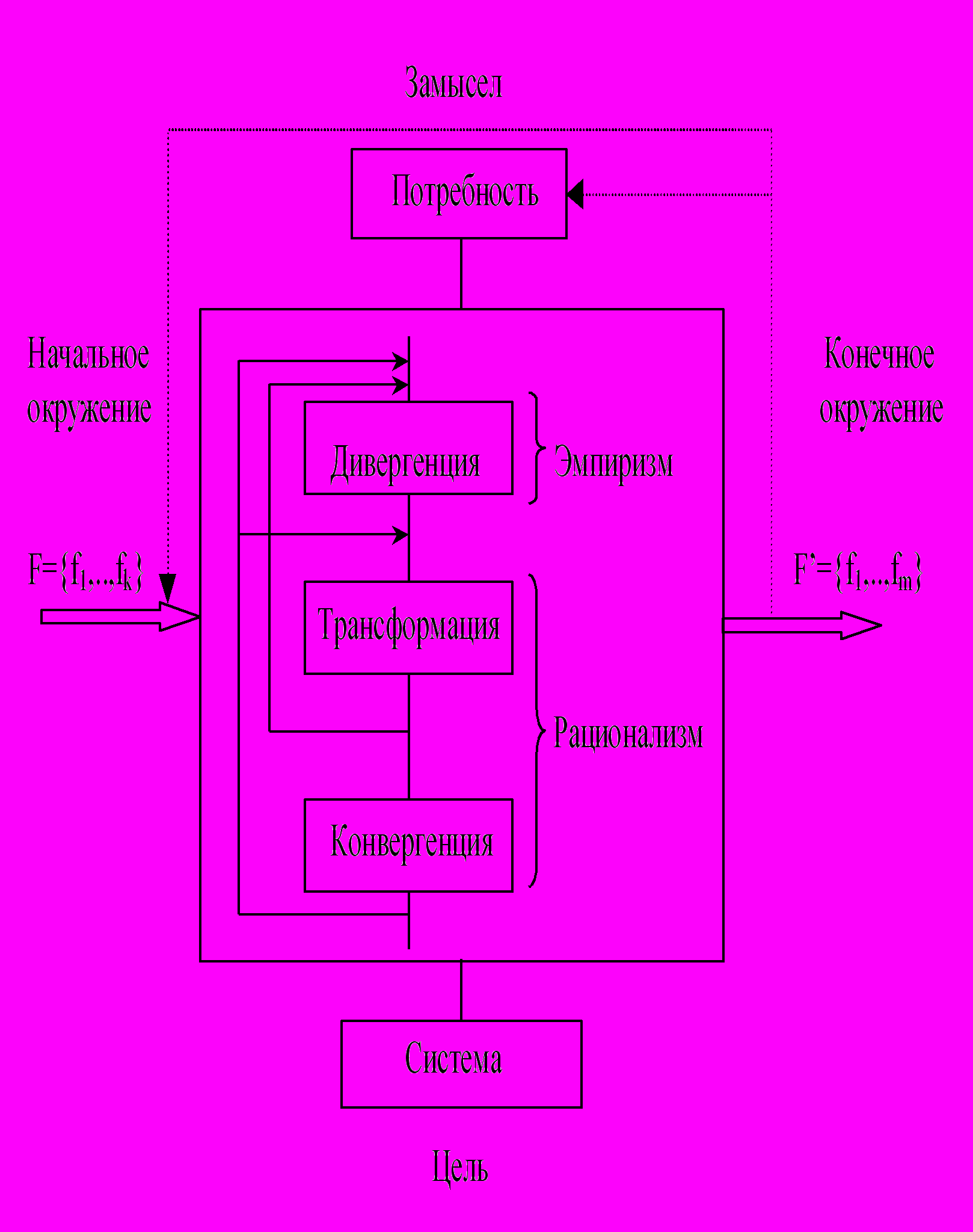
Рис.1.3. Модель проектирования, как научно-творческого процесса.


Инженерное проектирование начинается с возникновения замысла и формирования потребностей на основе факторов начального окружения F (факторы не определяющие функциональные или физические требования к системе, но воздействующие на сам процесс – орудия разработки: модели представления, инструментальные средства; организационное строение компании и др.). На выходе проектирования имеем разработанную систему и конечное окружение в виде множества факторов F’. Конечное окружение оказывает непосредственное воздействие на эволюцию дальнейшего процесса инженерного проектирования. Множество факторов F’ рекурсивно переходит во множество факторов F начального окружения на каждом новом цикле (см. пунктирную линию рис.1.3).

Будем выделять три ступени познания инженерного проектирования EDA-технологии:

• Дивергенция. Ступень расширения границ проектной ситуации в целях обеспечения достаточного пространства для поиска решений. Стадия, позволяющая говорить об изобретательстве как процессе получения ряда инвариантов.
  
• Трансформация. Эту ступень будем сопоставлять с такими процессами как исследование и создание принципов и концепций, когда формируется концептуальная схема проектируемого объекта, выбирается формальный аппарат анализа в виде множества моделей представления. Часто, эта ступень рассматривается как инженерный анализ – детальное изучение одного из вариантов.
  
• Конвергенция. Стадия окончательного выбора варианта технического решения, в основе которой лежат положения теории принятия решений – выбор одного из числа имеющихся вариантов, полученных в результате проведения модельных экспериментов.
  

Первой ступени присущи закономерности исследования, основанные на эмпирических подходах и эвристических методах, затрагивающих стремление ученых найти соответствующую модель проектировщика, как особого рода организованной «системы». Вторая и третья ступень описываются рациональными законами, и позволяют говорить о возможности разработки формальных схем и математических моделей представления, как самого процесса проектирования, так и обоснования принятия проектных решений. Будем трактовать эти ступени (трансформацию и конвергенцию) как исследования с присущими им методами на основе уже определенных критериев и целей проектирования.


Объединение присущих им формальных методов в обобщенную схему возьмем за основу структуры «инженерного проектирования» (рис.1.4).




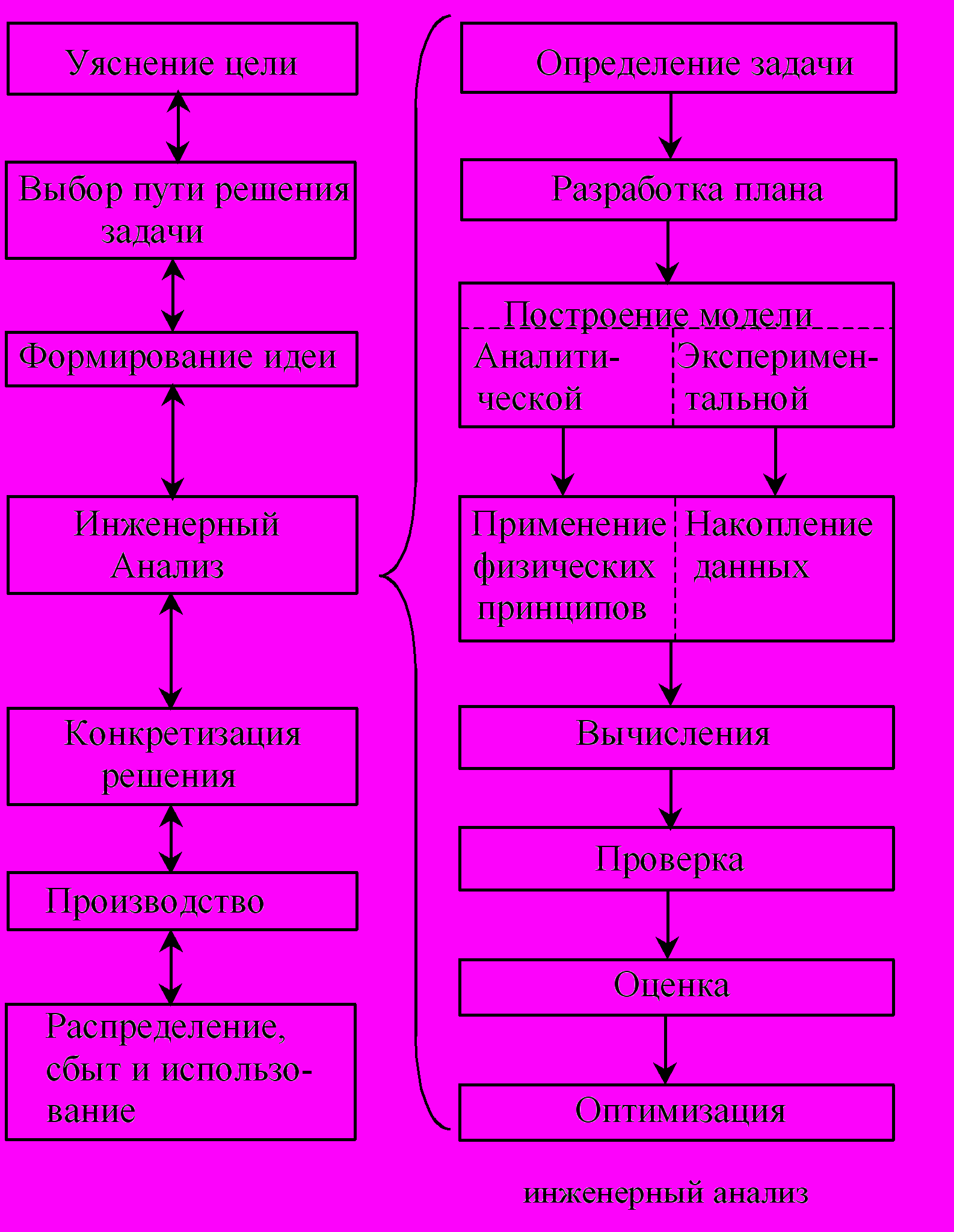
Рис.1.4. Структура этапов инженерного проектирования EDA-технологии.


Учитывая циклический и многоступенчатый характер научно-творческого процесса инженерного проектирования, и в качестве первичной попытки классификации мыслительной деятельности с позиций прагматической методологии, используем определение стратегии проектирования, как последовательности этапов, на каждом из которых применяется тот или иной метод моделирования. С этих позиций определим следующие виды стратегий, которые должна поддерживать информационная технология (ИТ): линейные, циклические, разветвленные, адаптивные, случайного поиска. Определим концепцию инженерного проектирования как один из методов исследования.


Обобщенная структура предмета научной деятельности.

Признаки системной классификации методов исследования (рис.1.5.б) зададим через обобщение структуры предмета научной деятельности EDA-технологии (рис.1.5.а).





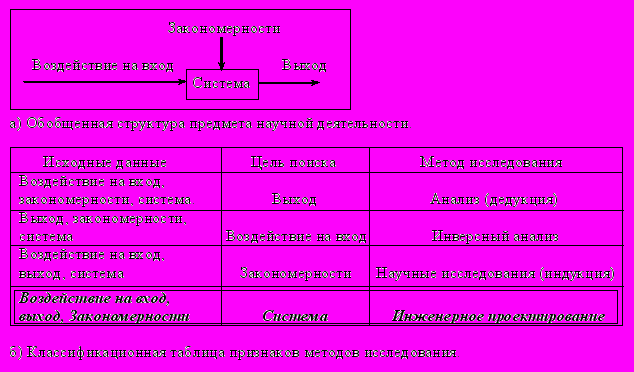
Рис.1.5. Научные методы исследования.


За методологическую основу формирования информационной технологии возьмем следующее определение системы :

Система - есть множество предметов вместе со связями между предметами и между их признаками. Предметы – суть просто части или компоненты системы. Признаки – свойства предметов. Окружение системы – есть множество всех предметов вне системы: изменение признаков, которых влияет на систему, признаки которых изменяются вследствие поведения системы.

Такое определение системы позволяет сформулировать в ИТ с прагматической точки зрения трактовку объекта как системы. Трактовка объекта как системы означает подбор элементов системы как носителей определенных свойств для реализации требуемых связей или же наоборот, - подбор элементов как носителей связей с учетом определенных свойств объектов как единого целого. Данные связи (свойства) образуют структуру, которая в информационной форме представляет абстрактную систему, а в энергоматериальной форме - реальную систему.

Исходя из выше изложенного, определим: результатом инженерного проектирования информационных систем является не сам объект, а идея этого объекта – объект предписание, объект рецепт, в общем, объект – практическая модель, указывающая, что именно, в какой последовательности, в каком количестве и каким образом должно быть взято и сделано, чтобы получить материально-технический объект.

Каскадная, итерационная и спиральная гносеологические модели процесса проектирования ИС

За годы эволюции процесса инженерного проектирования программных систем явно выделяются три скачка в идеологии классификации подходов (П) к технологии разработки ПС (порядок исполнения этапов в ходе разработки, а также критерии перехода от этапа к этапу):

1. Каскадный (П^к) - предполагает переход на следующий этап после полного окончания работ по предыдущему этапу. Процесс инженерного проектирования разбивается на заранее регламентированные временные промежутки «от и до» - стадии проектирования, в рамках которых, действия разработчиков нормированы скрупулезными методиками и инструкциями. Действует негласный тезис: «любая переделка с возвратом к предыдущему этапу – брак разработчика, чем меньше возвратов, тем корректнее технология проектирования». Основная идеологическая идея – непогрешимость выработанных методик и указаний. Каскадный период характеризуется так называемой технологической линейностью и отсутствием учета диалектического развития средств поддержки и эффективен в применении при небольших объемах и сроках разработки (в рамках первых трех витков спирали объективирования, см. гл.2).

2. Итерационный (П^и)- предполагает межэтапные корректировки с циклами обратной связи. Сохраняется идея разбиения на этапы, но не с учетом времени технологического выполнения и методической поддержки, а с учетом классификации проектных работ по средствам формализованного описания. Средства формального описания делят на уровни определенности: концептуальный, логический, физический. Действует принцип: «отдельная специальность – отдельный формальный аппарат – отдельный этап». Системный аналитик – постановщик и проектировщик системы, специалист по алгоритмам, кодировщик алгоритмов, документалист и пр. На этом этапе учитываются диалектические изменения в методической поддержке каждого этапа. Методическая поддержка имеет рекомендательную форму эпистемологического характера. Конкретные инструкции конкретных этапов зависят от множества системотехнических факторов, изменяющихся в процессе разработки ПС, в том числе - от фактора старения методик. Итерационный подход эффективен при большой сложности проектируемой системы, но при небольших сроках разработки, т.е. когда достигается предел уровня абстрагирования и осуществляется учет третей и четвертой спирали объективирования (см. гл.2).

3. Спиральный (П^с) - делает упор на анализе целей проекта, разработке спецификаций. Отсутствуют регламентированные этапы, технологическая поддержка принимает эпистемологическую форму. Процесс разработки ПС представляет собой набор спиралей, где каждый виток спиралей соответствует поэтапной модели создания фрагмента или версии программного изделия, на нем уточняются цели и характеристики проекта, определяется его качество, планируются работы следующего витка спирали. На базе моделей проверяется и обосновывается реализуемость технических решений путем создания прототипов. Спиральный подход ориентирован на решение больших и сложных ПС и являет собой некую научно обоснованную системологическую надконцепцию, в основе которой лежит накопление и повторное использование моделей и прототипов, ориентация на развитие и модификацию программных систем, анализ риска и издержек в процессе инженерного проектирования.