Семинар №6 Тема: Машины Тьюринга
| Вид материала | Семинар |
- Базовые программы для машины тьюринга реферат по дисциплине «Дискретная математика», 52.31kb.
- Сложность вычислений, 29.79kb.
- Понятие алгоритма и вычислимой функции. Частично рекурсивные функции. Тезис Черча., 17.86kb.
- Задача об остановке произвольной машины Тпри обработке произвольного слова t алгорифмически, 97kb.
- Разработка программы с использованием машины Поста (машины Тьюринга). Анализ современных, 17.6kb.
- Учебно-методический комплекс Специальность 010400 Информационные технологии, 135.47kb.
- Программа вступительного экзамена в магистратуру по специальности 6М080600 аграрная, 36kb.
- Программа дисциплины по кафедре "Cтроительные и дорожные машины " cпасательная техника, 440.32kb.
- Программа дисциплины по кафедре "Cтроительные и дорожные машины " машины и оборудование, 292.86kb.
- Задача точного определения понятия алгоритма была полностью решена в 30-х годах, 519.73kb.
Семинар №6
Тема: Машины Тьюринга.
Задачи: 1. Освоить понятие примитивно-рекурсивной функции.
2. Научиться доказывать пр.рекурсивность функций.
Время: 1 пара (2x45 мин).
Место проведения: НГУ, ауд.307а.
Метод: семинар.
Ход семинара:
| Учебные вопросы, время | Действия семинариста | Действия обучаемых |
| 0. проверяю дом. задание (10 мин) | Необходимый разбор домашнего задания. Коллоквиум? Контрольная работа. | Вопросы. |
| 1. определение примитивной рекурсии (10 мин) | Определение простейших функций. Получение примитивно-рекурсивных функций из простейших. | Вспоминают лекции, записывают. Вопросы. |
| 2. примеры п.р.ф. (40 мин) | Доказать, что перечисленные функции являются п.р.ф. Доказать, что перечисленные функции не могут быть получены из O и 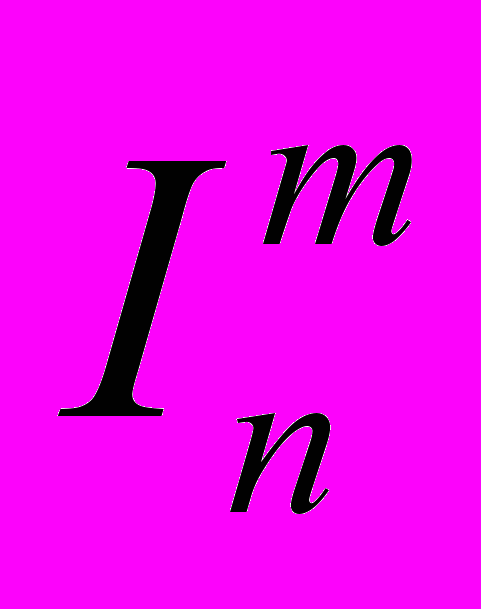 операторами S и R. операторами S и R. | |
| 3. п.р. предикаты (15 мин) | Конъюнкция, дизъюнкция, отрицание предикатов. Оператор ограниченной минимизации. | |
| 4. Окончание (5 мин) | Записываю на доске д/з: 1-4. Объявляю о теме следующего семинара: Оператор минимизации. Частично-рекурсивные функции. | Записывают задачи на дом. |
.
Конспект:
Примитивно рекурсивные функции.
Базовые функции:
- s(x) := x+1;
- 0 – нульместная функция;
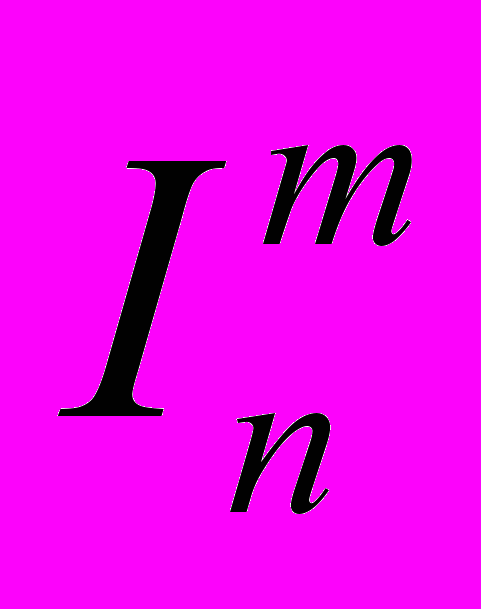 (x1,…,xn) := xm, (mn)
(x1,…,xn) := xm, (mn)
Операторы:
- Суперпозиция
 ;
;
- Примитивная рекурсия
 ;
;
- Ограниченная минимизация ;
- Минимизация.
Рекурсивные предикаты.


Задачи:
