Сложность вычислений

Вид материала

Документы

Содержание II. Классы сложности.

Подобный материал:

• Параллельные алгоритмы решения трехмерных упруго-пластических задач, 98.53kb.
• Краткая история развития, 58.89kb.
• Построение и анализ комбинаторных алгоритмов, 62.76kb.
• Ений (Soft Computing) состоит в том, что в отличие от традиционных, жестких вычислений,, 160.09kb.
• Основатель научной школы параллельных вычислений мгту им. Н. Э. Баумана, 203.21kb.
• Решение по итогам заседания рго от 09. 11. 10 Как перевести тему «облачных вычислений», 99.27kb.
• Методические указания к курсу «Основы молекулярных вычислений», 140.04kb.
• Муниципальное общеобразовательное учреждение, 266.77kb.
• Реферат на тему «История развития вычислительной техники», 409.19kb.
• Облачные услуги различного уровня, ведущие мировые фирмы по ит-технологиями разрабатывают, 127.18kb.

СЛОЖНОСТЬ ВЫЧИСЛЕНИЙ

доц. В.Н. Крупский

1/2 года

I. Модели вычислений.

1. Многоленточные машины Тьюринга. Время и зона вычисления, связь между ними. Другие варианты машин Тьюринга.

2. Упрощения многоленточной модели, их цена. Моделирование произвольного ленточного алфавита двухбуквенным. Моделирование нескольких лент одной.

3. Универсальная машина Тьюринга. Теоремы об иерархии по времени и по зоне.

4. Машины с неограниченными регистрами (RAM) и ядро языка BASIC. Универсальная машина Тьюринга для BASIC-программ, оценка её времени работы и зоны. Практика получения верхних оценок сложности конкретных задач, основанная на таком моделировании.

5. Булевы схемы и схемная сложность. Универсальная машина Тьюринга для булевых схем, оценка её времени работы и зоны.

II. Классы сложности.

1. Класс P, его (относительная) независимость от выбора модели вычислений. Примеры задач из класса P: целочисленная арифметика, арифметика остатков, сложение и умножение матриц над кольцом вычетов по модулю n, связность в графе.

2. Распознавание языков последовательностями булевых схем и неравномерный класс P/Poly. Включение P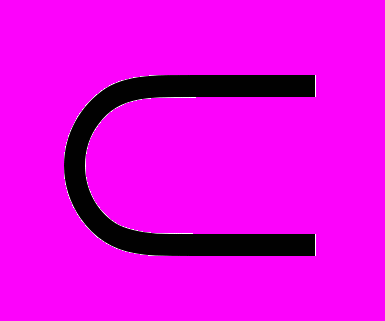P/Poly.

3. Доказательство принадлежности языку предъявлением ''свидетеля''. Класс NP. Примеры задач из класса NP: проблема выполнимости булевых формул (SAT), краевая задача полимино, проблема существования гамильтонова цикла, задача о клике (CLIQUE), целочисленное линейное программирование. Связь с недетерминированными машинами Тьюринга. Гипотеза P ≠ NP.

4. Упорядочение по трудности задач внутри NP. Полиномиально ограниченная по времени много-однозначная сводимость (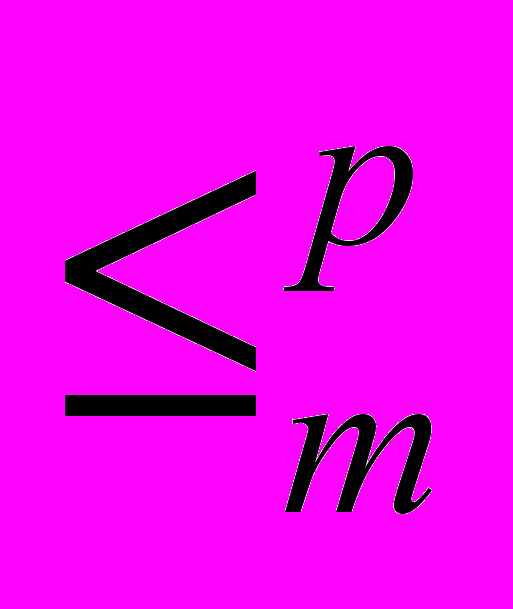, сводимость Карпа). Понятие NP-полной задачи. NP-полнота задач SAT, CLIQUE, задачи целочисленного линейного программирования.

5. Вероятностные вычисления с полиномиальным ограничением по времени. Класс BPP. Включение BPP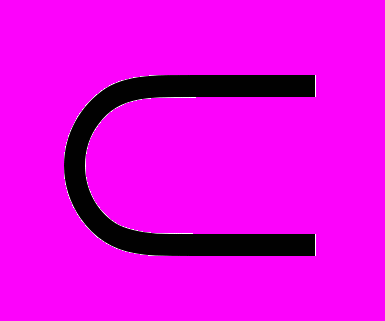P/Poly. Вероятностный алгоритм распознавания простых чисел. Полиномиальная иерархия (PH). Конечные детерминированные игры с полиномиальным ограничением по времени. Запись условия существования выигрышной стратегии с помощью полиномиально ограниченных кванторов, классы полиномиальной иерархии ( 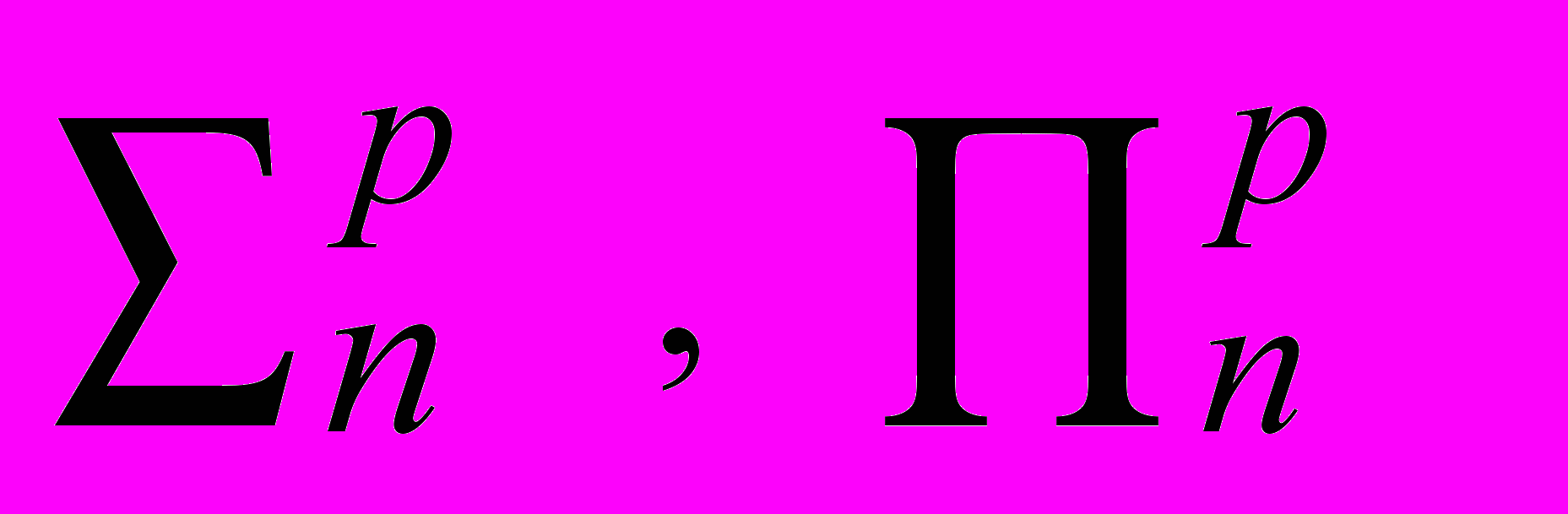). Включение BPP.

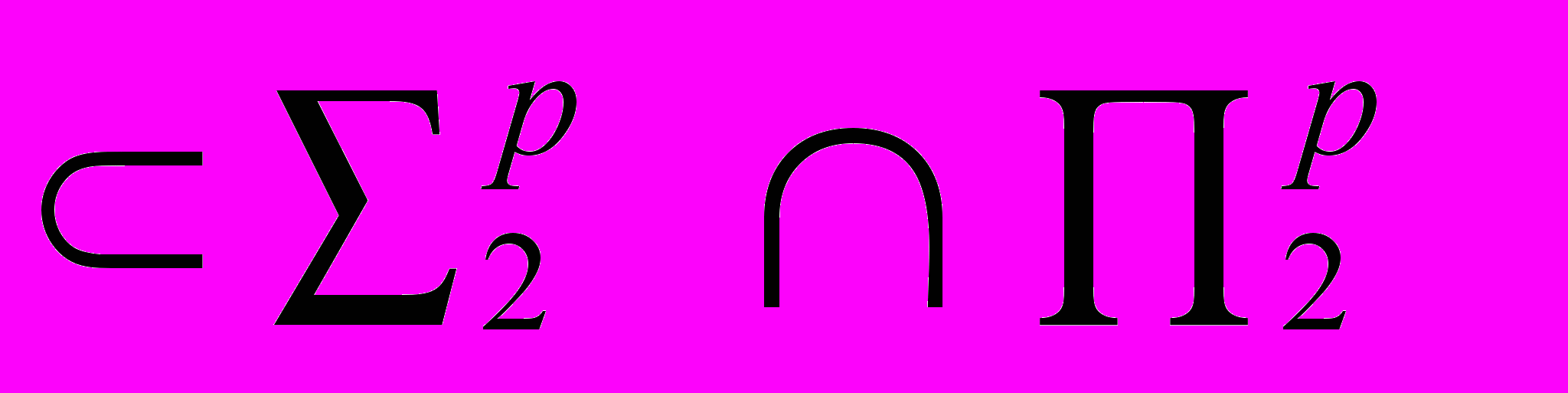6. Класс PSPACE и его игровая характеризация. Включение PH 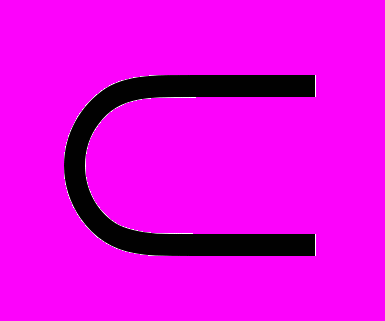PSPACE.

7. Варианты проблемы выполнимости квантифицированных булевых формул в качестве примеров полных задач для классов полиномиальной иерархии и класса PSPACE.


Литература

1. Крупский В.Н. Сложность вычислений. Конспект лекций. 2001.

.msu.ru/Complexity/input/t2.php

2. Ахо А., Хопкрофт Дж., Ульман Дж. Построение и анализ вычислительных алгоритмов. М., Мир, 1979.

3. Китаев А., Шень А., Вялый М. Классические и квантовые вычисления. М., МЦНМО, ЧеРо, 1999.

Дополнительная литература

1. Гэри М., Джонсон Д. Вычислительные машины и труднорешаемые задачи. М., Мир, 1982.

2. Gacs P., Lovasz L. Complexity of Algorithms. 1999.

le.edu/HTML/YALE/CS/HyPlans/lovasz/complex.ps