A. 13. O. Использование решений фирмы ni в автоматизированной системе контроля оптических деталей

Вид материала

Документы

Содержание 2. Результаты работы 5 закрепляются в специальной регулировочной оправе, состоящей из фторопластового основания a 4. Преимущество технологии National Instruments

Подобный материал:

• Положение об автоматизированной информационной системе учета и контроля лиц, транспортных, 712.89kb.
• О защите информации в автоматизированной банковской системе, 77.06kb.
• Программа учебной дисциплины «Теория и практика принятия управленческих решений» для, 1260.31kb.
• Ской деятельности фирмы, методы и способы его организации и использования, а также, 168.36kb.
• Моделирование и динамическая стабилизация нановыглаживания прецизионных поверхностей, 151.88kb.
• Введение Курс "Методы и средства измерений, испытаний и контроля", 172.41kb.
• Щелканов Виктор Владимирович Разработка общесистемных функциональных решений для автоматизированной, 522.67kb.
• 9. организация выполнения управленческих решений как стадия менеджмента, 1738.31kb.
• 1. основные положения, 349.47kb.
• Основные принципы управления персоналом в организации, 242.97kb.

A.13.O. ИСПОЛЬЗОВАНИЕ РЕШЕНИЙ ФИРМЫ NI В АВТОМАТИЗИРОВАННОЙ СИСТЕМЕ КОНТРОЛЯ ОПТИЧЕСКИХ ДЕТАЛЕЙ.


Махов В.Е., Потапов А.И., Кацан И.Ф.


Северо-Западный заочный государственный университет, Миллионная 5, СПб, 312-86-96, mahov@nwpi.ru


1. Введение

При производстве оптических деталей для контроля их формы поверхностей традиционно используется интерференционный способ ее сравнения с пробной высокоточной деталью (кольца Ньютона). Хотя такой способ относится к косвенным методам контроля (сравнения с длиной волны света), он положен в основу стандартов качественного контроля для оптической промышленности. В производственном обиходе наблюдаемую интерференционную картину называют «цветом», так как при освещении белым светом наблюдаемые линии интерференционных полос имеют радужную (цветную) окраску. Физика явления колец Ньютона достаточно хорошо описывается интерференцией света в тонких пленках [1].

Метод контроля по кольцам Ньютона имеет высокую чувствительность (в достаточно узком диапазоне), но достаточно высокую относительную погрешность. Высокая погрешность контроля, прежде всего, связана с тем, что из анализа картины интерференции, не представляется возможным достаточно точно произвести оценку периода интерференционных полос, в данном случае в полярной системе координат. В то же время расширить диапазон измерений (например, уменьшить набор пробных деталей) возможно, если уменьшить погрешность определения периода интерференционных полос.

Трудности автоматизации процесса контроля заключаются в низком контрасте и месте локализации интерференционных полос с одной стороны, с другой в реализации механической системы прижима и сканирования места контакта по поверхности детали. Необходимо также учитывать, что большая часть информация заложена в цвете интерференционных полос, который неадекватно воспринимается сенсорами изображения (по отношению к длине волны). Использование монохроматического, но некогерентного излучения, также не позволяет повысить контраст и порядок наблюдаемой интерференции (малая длина когерентности), а использование когерентных источников приводит к значительному спекл шуму (хаотическая интерференция на апертуре оптической системы) [2]. В любом случае, трудно ожидать уменьшения погрешности контроля при построении автоматизированной системе контроля.

Матричные фотоприемники, используемые для регистрации оптического изображения, имеют сравнительно невысокое разрешение. Увеличение числа элементов матрицы (N) не приводит к пропорциональному увеличению линейного разрешения (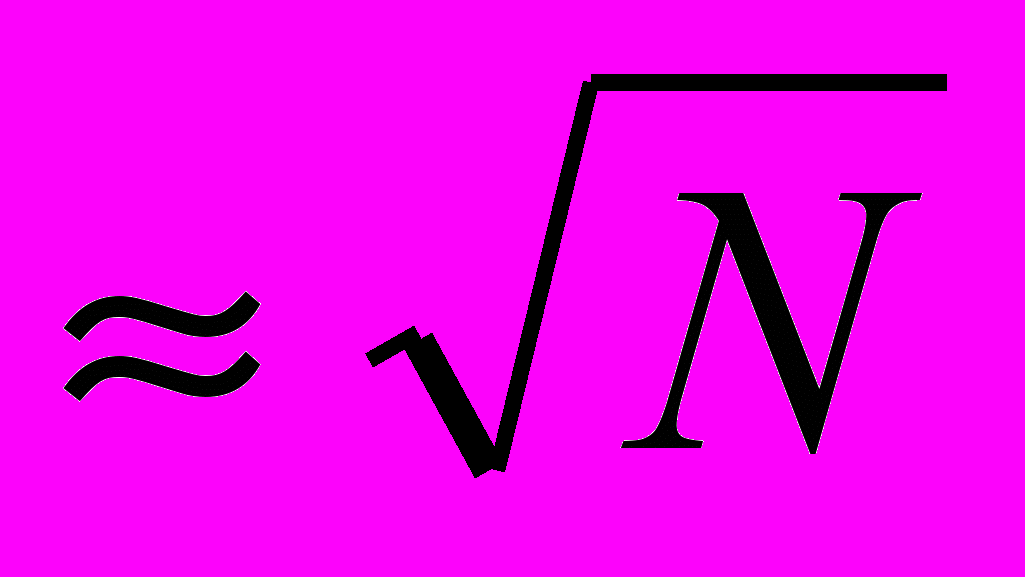). Ранее нами было показано [3, 4], что повысить точность технологического контроля в интерференционных схемах можно при помощи гетеродинно-растрового (ГР) метода обработки получаемой информации, в том числе с использованием матричных фотоприемников [3]. Физическая основа ГР метода близка к оптическому гетеродинированию интерференционной картины в схеме с двумя пучками лучей с очень близкими длинами волн ₁ (₁) и ₂ (₂), как в методе голографической гетеродинной интерферометрии [2], при котором картина интерференции перемещается в плоскости двух неподвижных фотоприемников, регистрирующих разностную частоту (₁-₂ ). По разности фаз, регистрируемых сигналов, удается определить период интерференции, причем спекл шум оказывает косвенное влияние. При ГР методе картина интерференции неподвижна, перемещается растровая структура с пространственным периодом близким картине интерференции. При этом происходит суперпозиция распределения освещенности с растром на апертуре фотоприемника.

Суть повышения точности контроля при использовании ГР метода заключается, во-первых, в том, что получаемая информация отображается в некоторый заранее выбранный и сконструированный параметр (критерий), который выбирается адекватным контролируемому параметру [3], и во-вторых в измерительный процесс вводиться временная координата, которая обеспечивает усреднение получаемых данных по выбранному критерию. Увеличивая время измерения, мы увеличиваем точность, усредняя временные факторы шума. В силу этих особенностей класс ГР методов обладает высокой помехозащищенностью по отношению к внешним воздействиям шума и изменению в позиционировании объекта контроля, что обеспечивает высокоточный технологический контроль.

Как было показано ранее [3,4], класс ГР методов описывается интегральным уравнением Фредгольма второго рода:

,

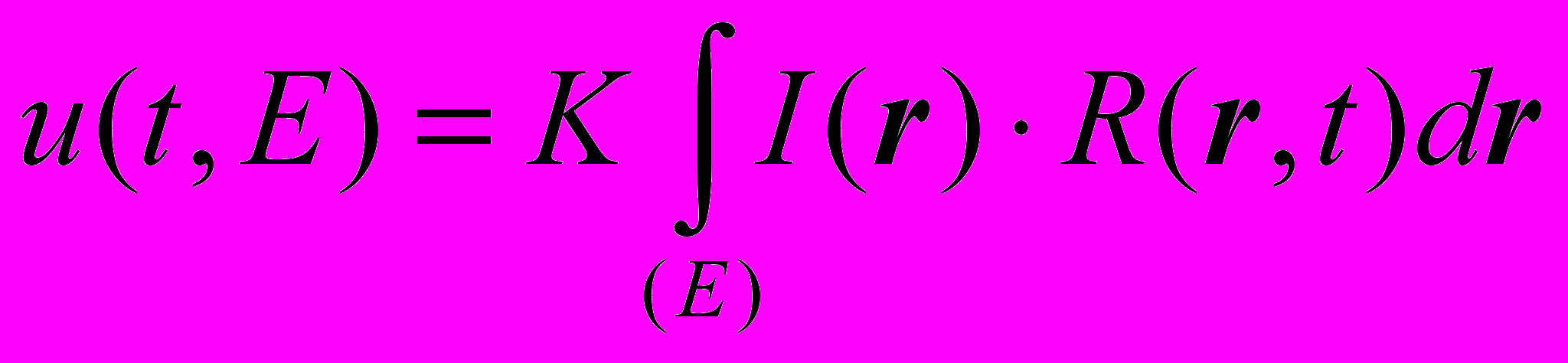где R(r,t) – пространственно-временная функция растра, (E) – апертура фотоприемника, I(r) – распределение освещенности (информационное поле).

Заданной особенностью ядра R(r,t) данного интегрального уравнения ГР метода является его строгая периодичность по времени (период T), можно рассматривать также пространственную периодичность по r (период T_R), что можно записать следующим образом:

, .

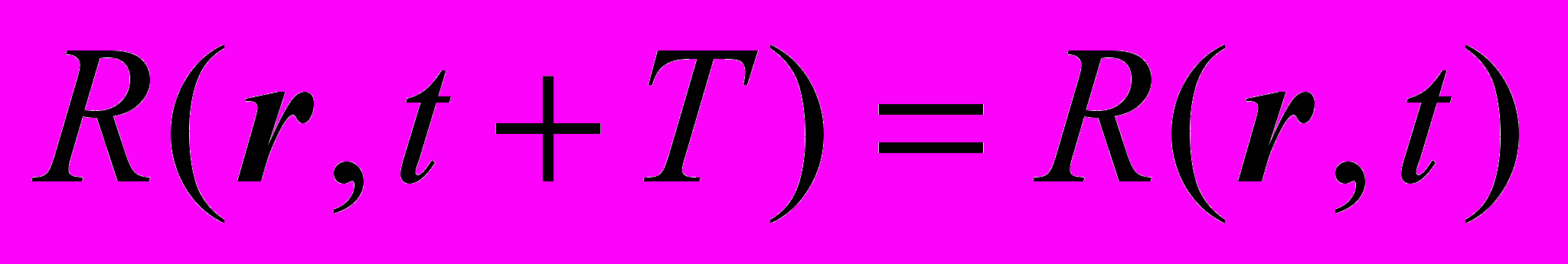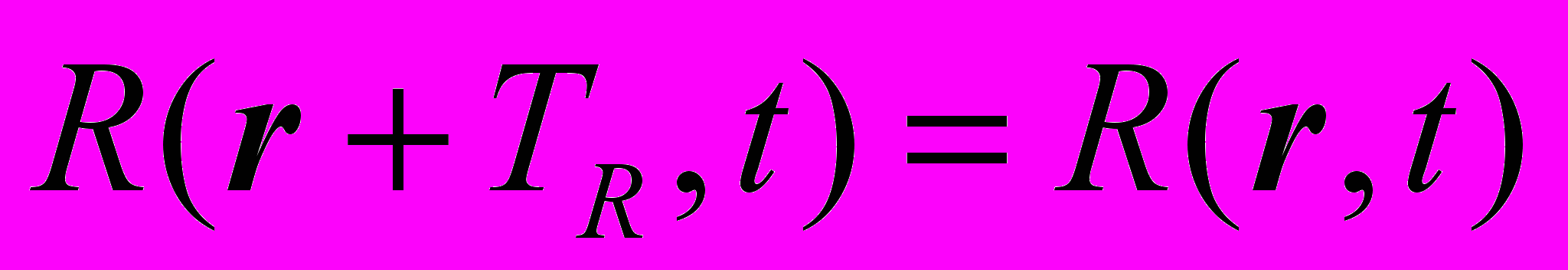Временная периодичность ядра интегрального уравнения определяет временную периодичность получаемого выходного сигнала u(t,E)=u(t+T,E) при любом 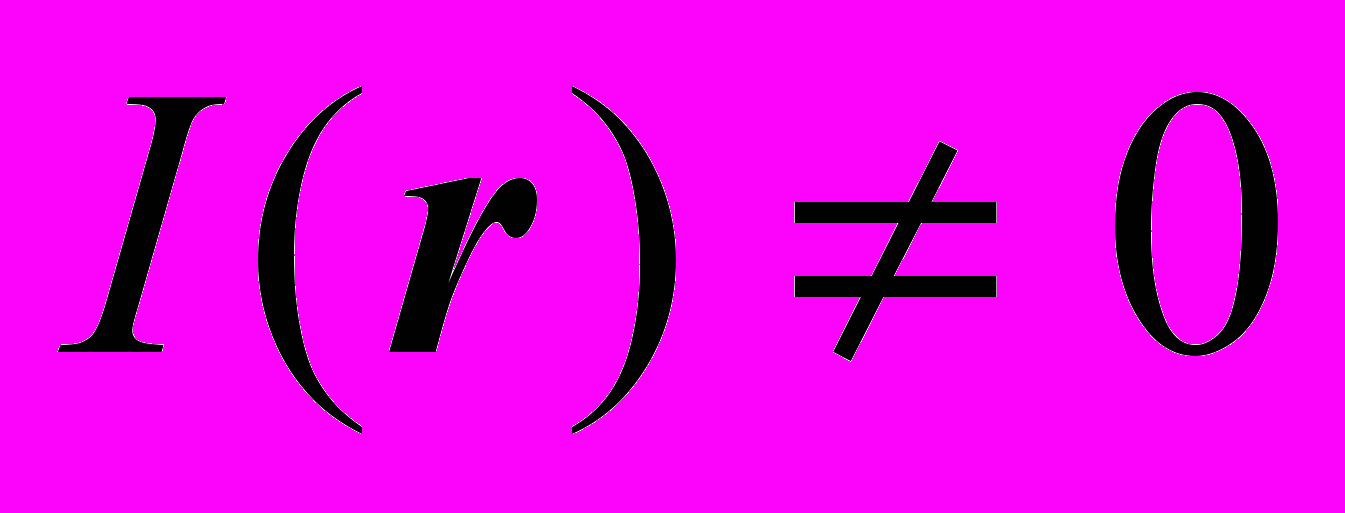. Сохранение формы функции растра позволяет отождествлять его временное изменение с пространственным перемещением во времени его структуры и определяет в общем случае пространственно временную инвариантность (изопластичность) системы ГР преобразования информации. В силу временной и пространственной периодичности функции растра, ее можно представить в следующем виде:

.

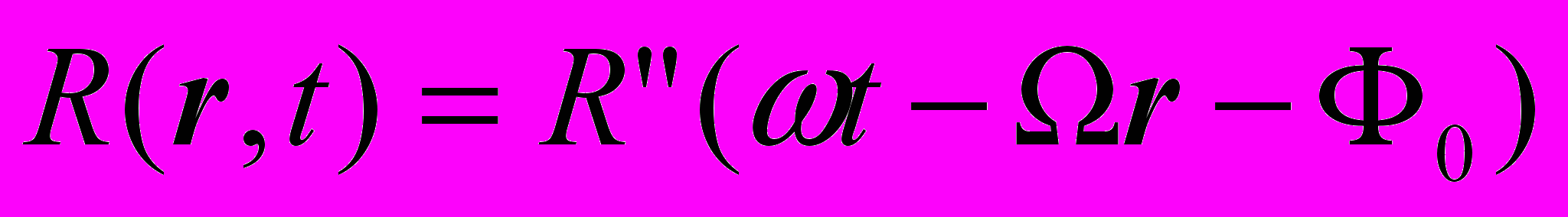Основное уравнение ГР преобразования с учетом наложенных условий пространственно временной периодичности функции растра может быть записано в следующем виде:



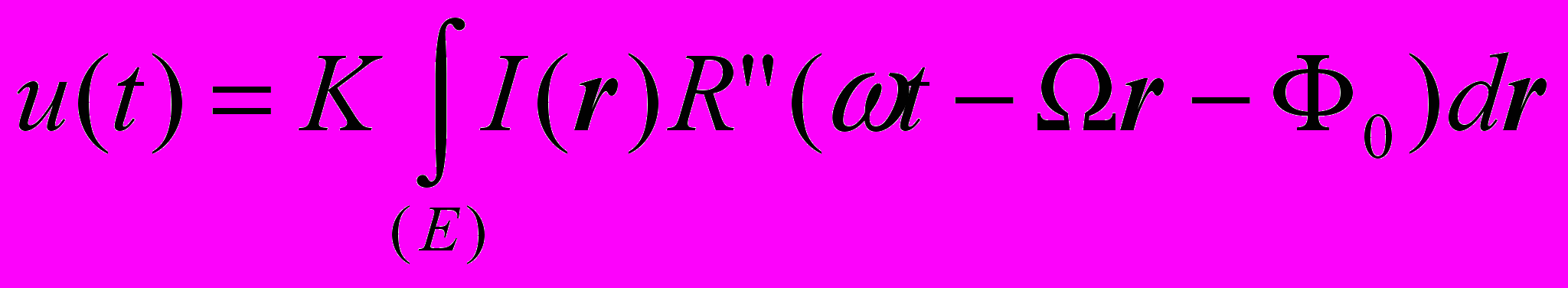
Исходя из прикладного характера решаемых задач для дальнейшего анализа математической модели ГР метода целесообразно использовать методы спектрального анализа. В этом случае правую часть уравнения можно представить как свертку функций I (r) и R”( r, t) [5], для функции I_E(r), расширенной по всей области определения 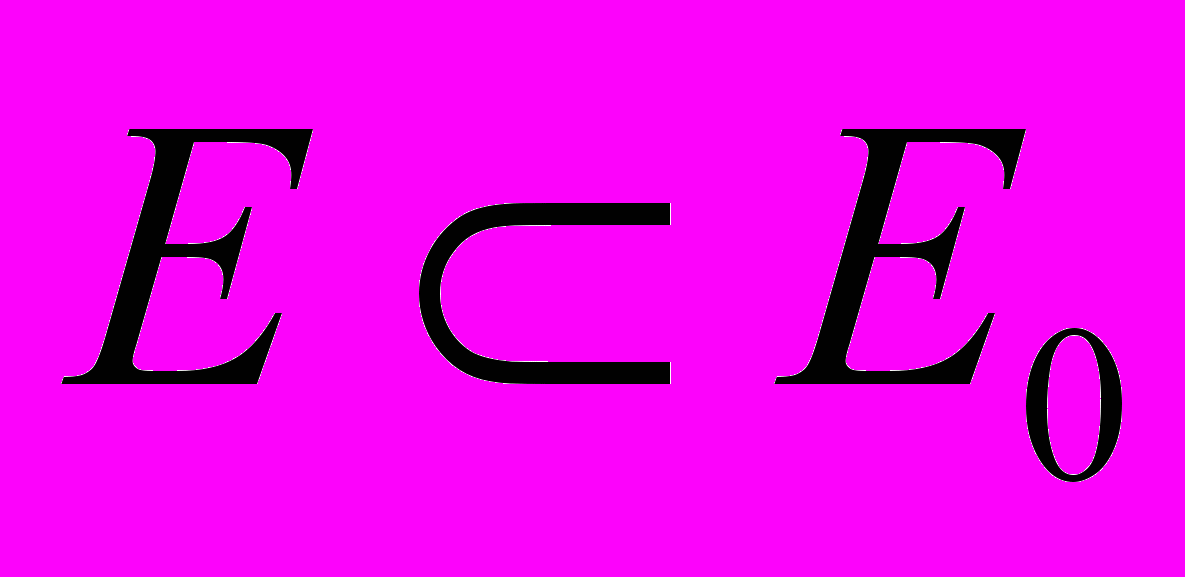: I_E(r) =0 (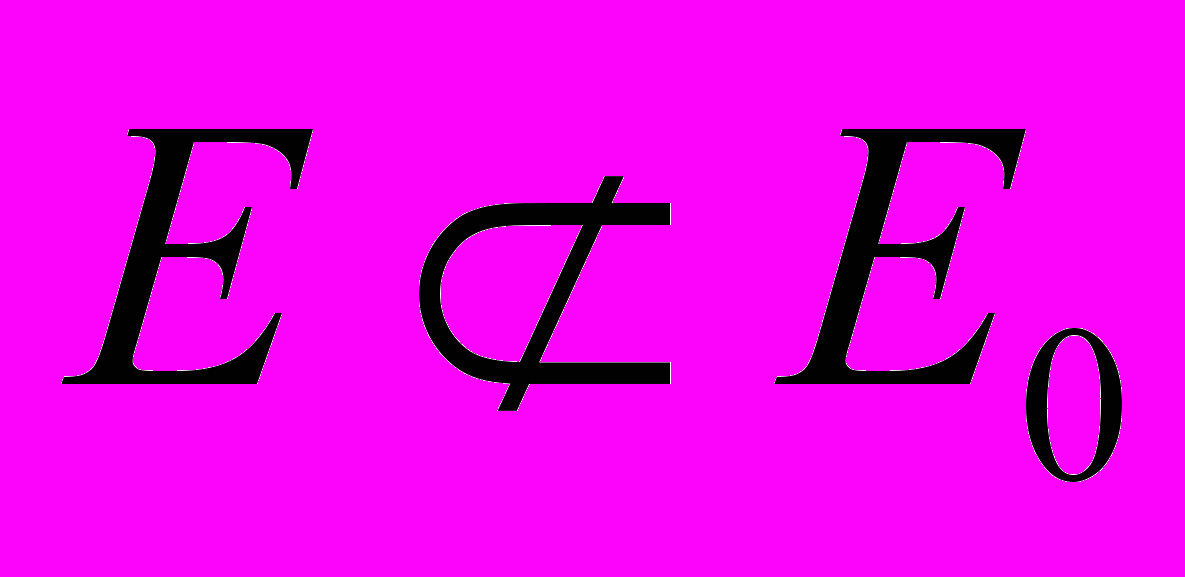). Используя также нормированную пространственную координату t_R=(T_R/T)t:

: .

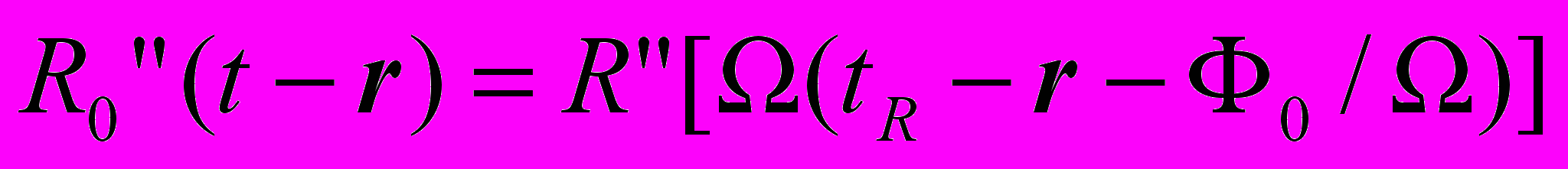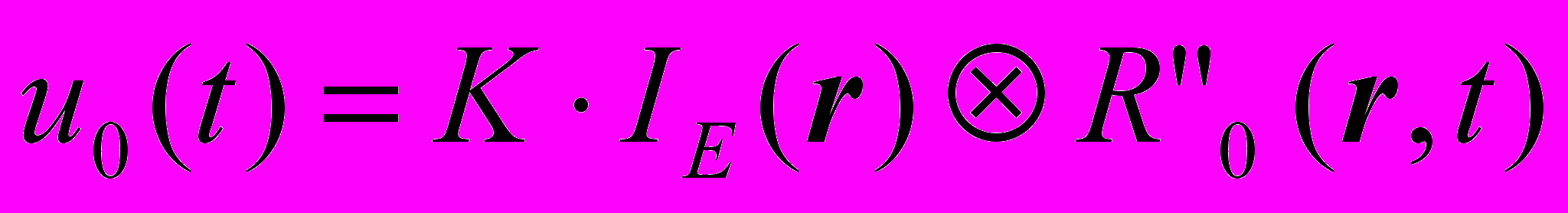Используя в свою очередь аппарат Фурье анализа, можно в последнем уравнении перейти к спектру Фурье:

,

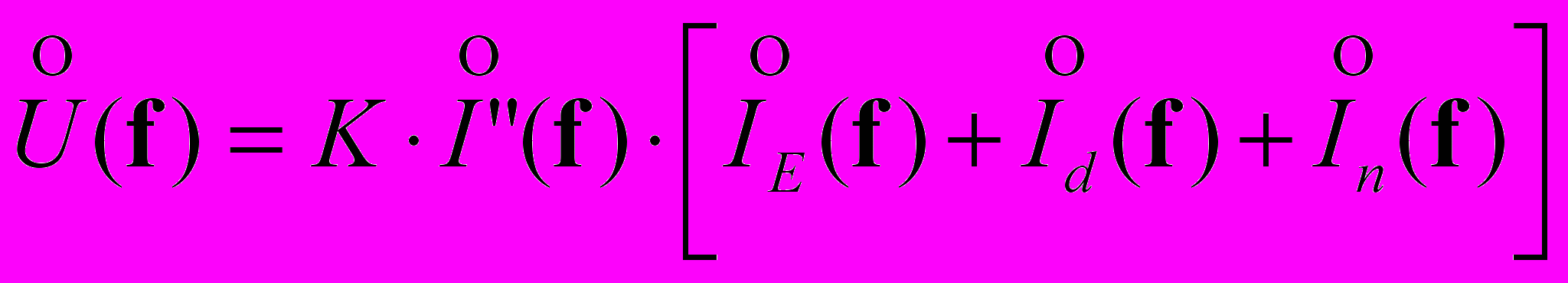где 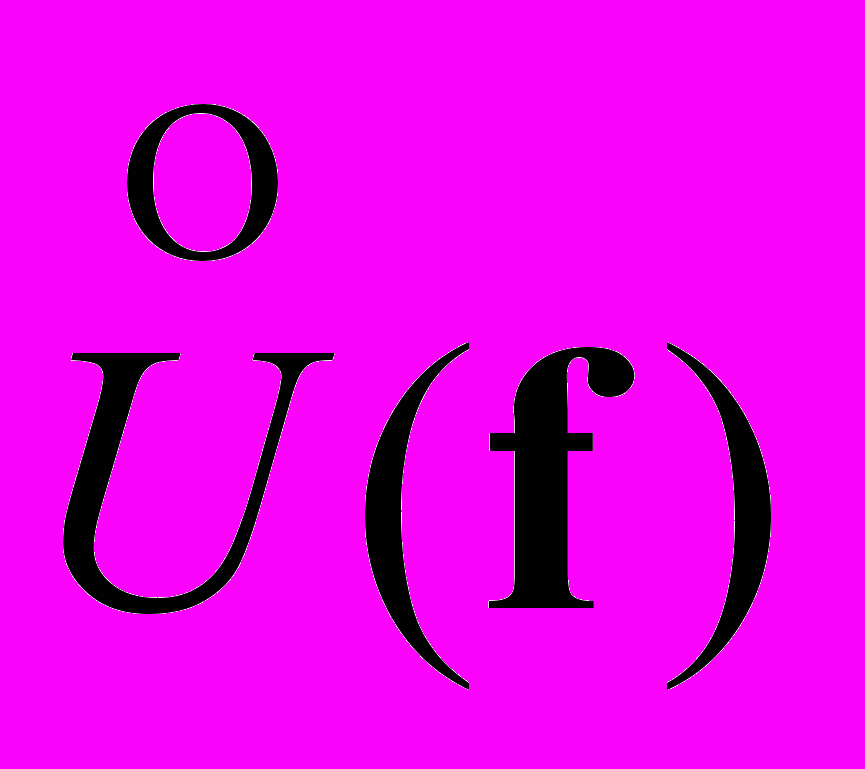, , 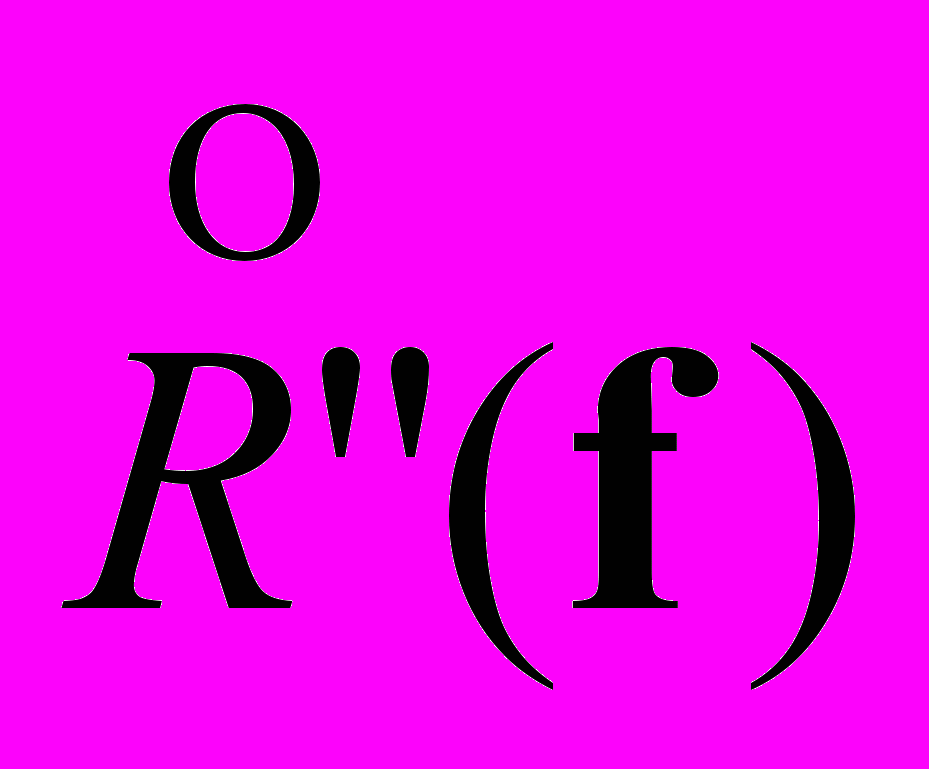, , 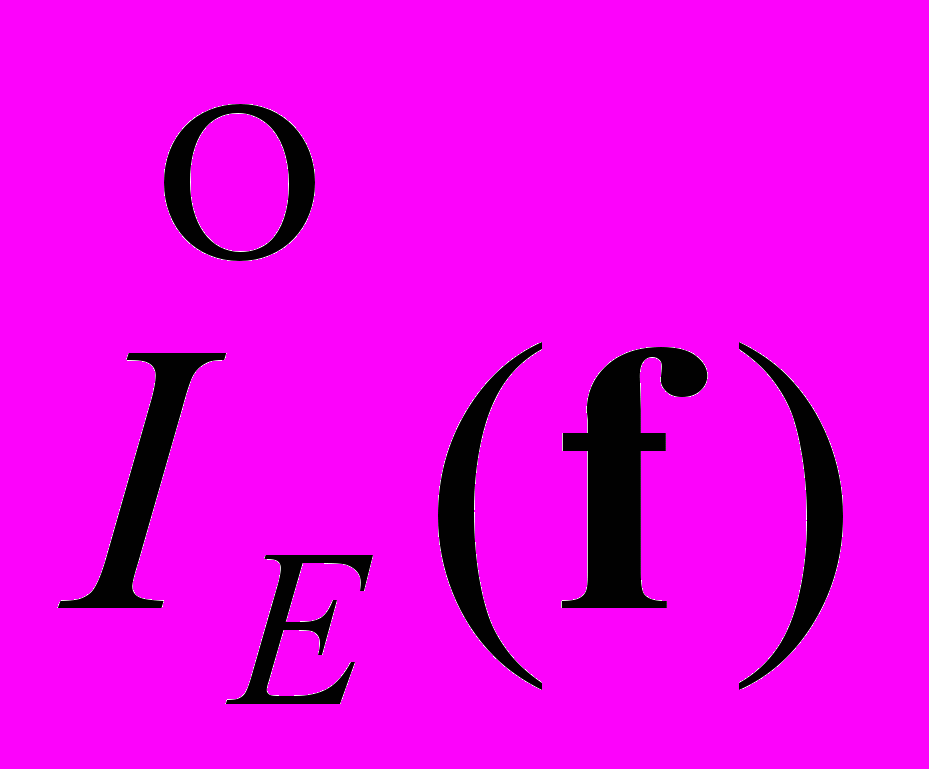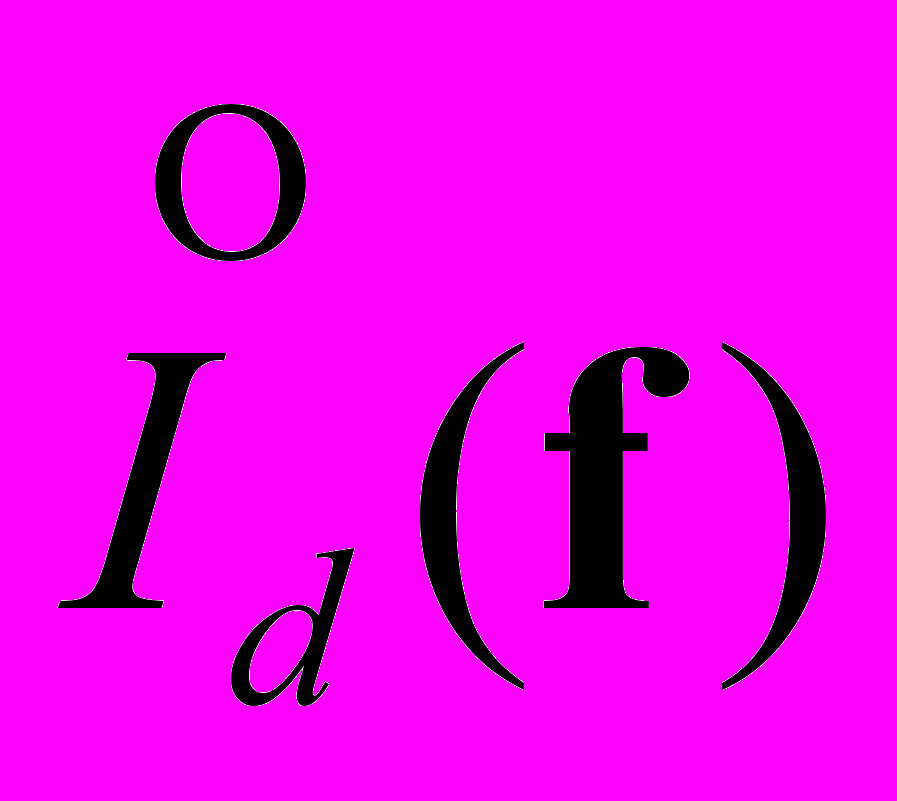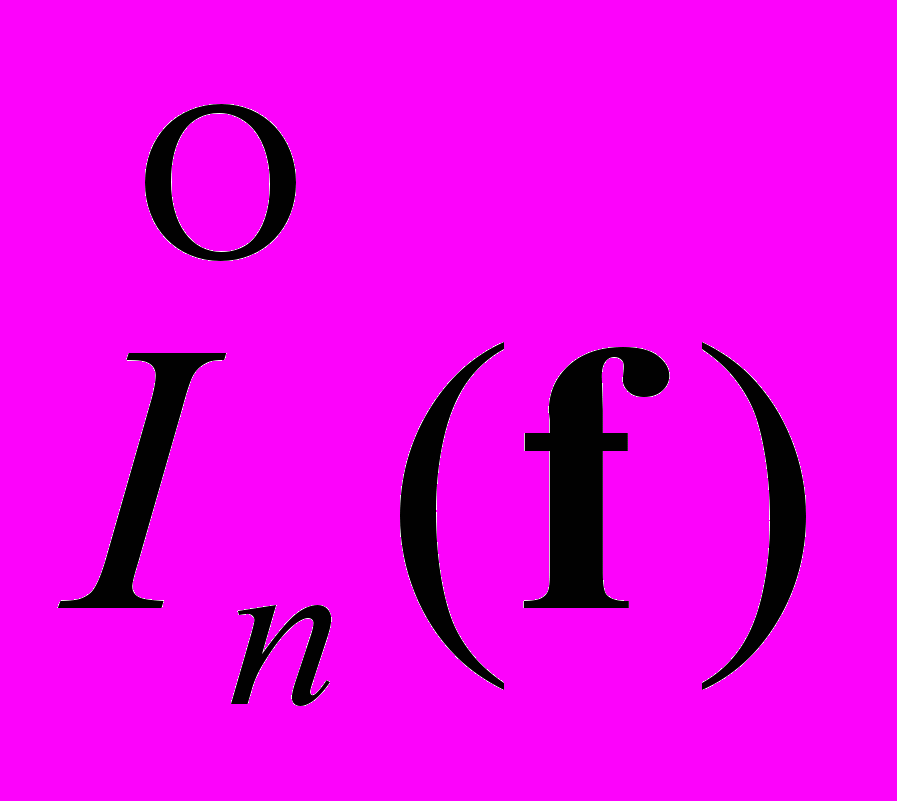- спектры Фурье выходного сигнала, функции растра, функции распределения освещенности, функции апертуры и функции шума соответственно. Это выражение показывает отображение пространственных частот распределения освещенности ( f ) во временные частоты с весовыми множителями растровой функции.

В то же время каждый член выражения является комплексной величиной, который определяется своей амплитудой и фазой: . С учетом необходимых условий представления периодических функций по системе ортогональных тригонометрических функций, указанное интегральное уравнение можно свести к системе линейно независимых интегральных уравнений. Исходное интегральное уравнение или эквивалентная ему система уравнений с математической точки зрения не имеет единственного решения, что согласуется с нашими физическими представлениями. Например, пространственное перемещение светового поля на величину кратную периоду растра, не изменяет фазовую характеристику выходного сигнала u(t) с одной стороны, с другой - различные поля могут давать один и тот же выходной сигнал.

Важным выводом является то, что эквивалентное рассмотренному ГР преобразование с периодической функцией растра можно осуществлять на растровой динамической апертуре фотоприемника E(r,t))=R(t,r). Из чисто физических соображений очевидно, что такие преобразования должны быть эквивалентными:

.

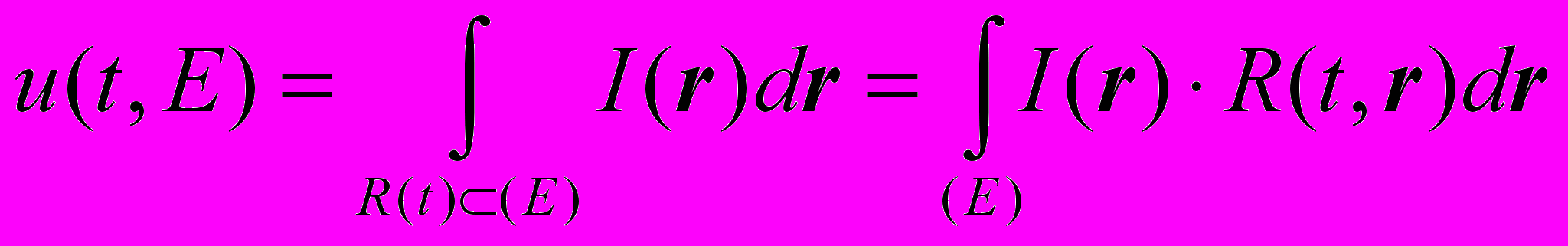Данный вид преобразования светового поля I (r) может быть использован для алгоритмической обработки сигналов, получаемых с матричного фотоприемника. В этом случае рассмотренная математическая модель будет иметь ряд специфических особенностей. Функция выходного сигнала u(t,E) будет представлять собой дискретный выборку значений 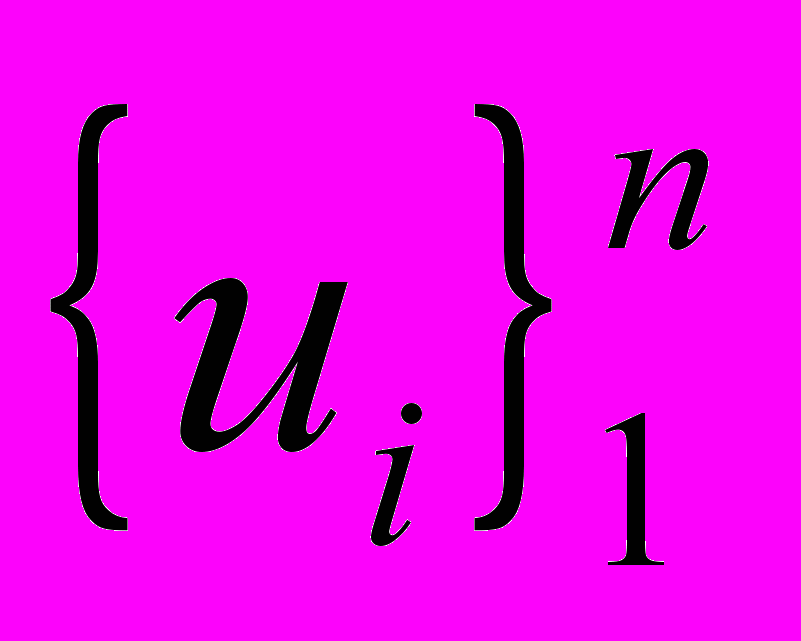относительно целочисленного параметра выборки i=1, 2, … n , который соотносится с моментами распределенного времени 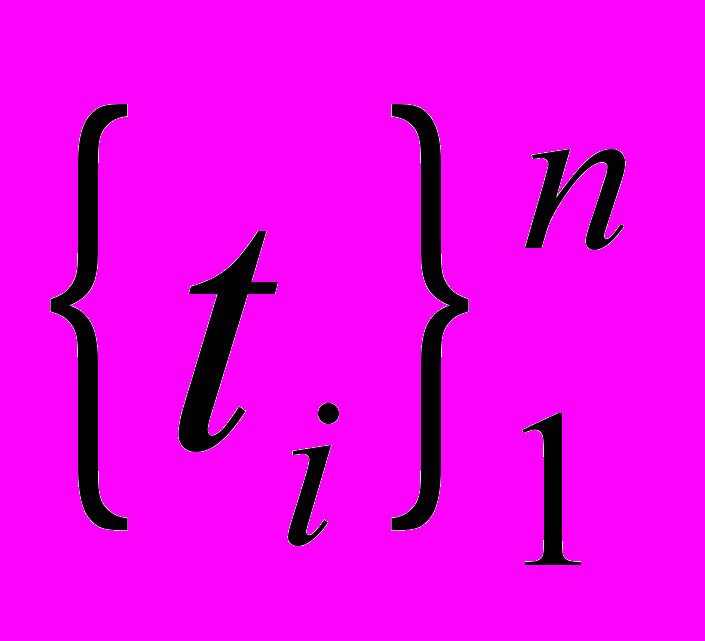. Выборка моментов распределенного времени t_i, может, как и раньше сопоставлена с любой временной шкалой реального времени.

Как можно заметить, в ГР методе функция растра инвариантна относительно способов ее реализации. Таким образом, аналогом ГР преобразования может быть достаточный набор фотоприемников матричного вида. Получаемый сигнал (временная выборка) должен быть группой (определяемой выбранной формой растровой функции) суперпозиций получаемых сигналов, реализованных алгоритмически с их элементов взятых с весовой функцией нормированной функции растра. Набор временной выборки сигналов образуют указанные суммы, в которых весовая функция (функция растра) последовательно алгоритмически сканируется (перемещается) по индексу группы i, который ассоциирован с параметром распределенного времени t_i :

.

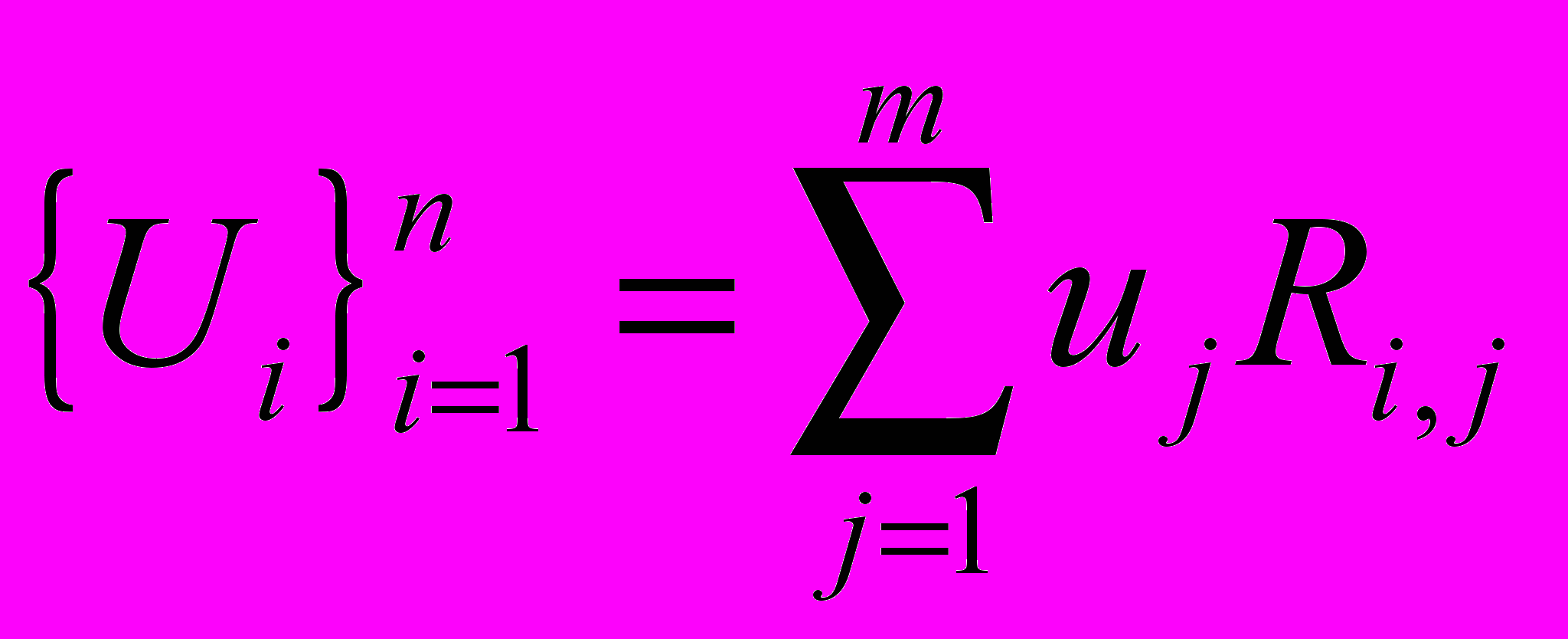В частности, можно представить следующую модельную функцию растра для дискретно-матричной реализации .

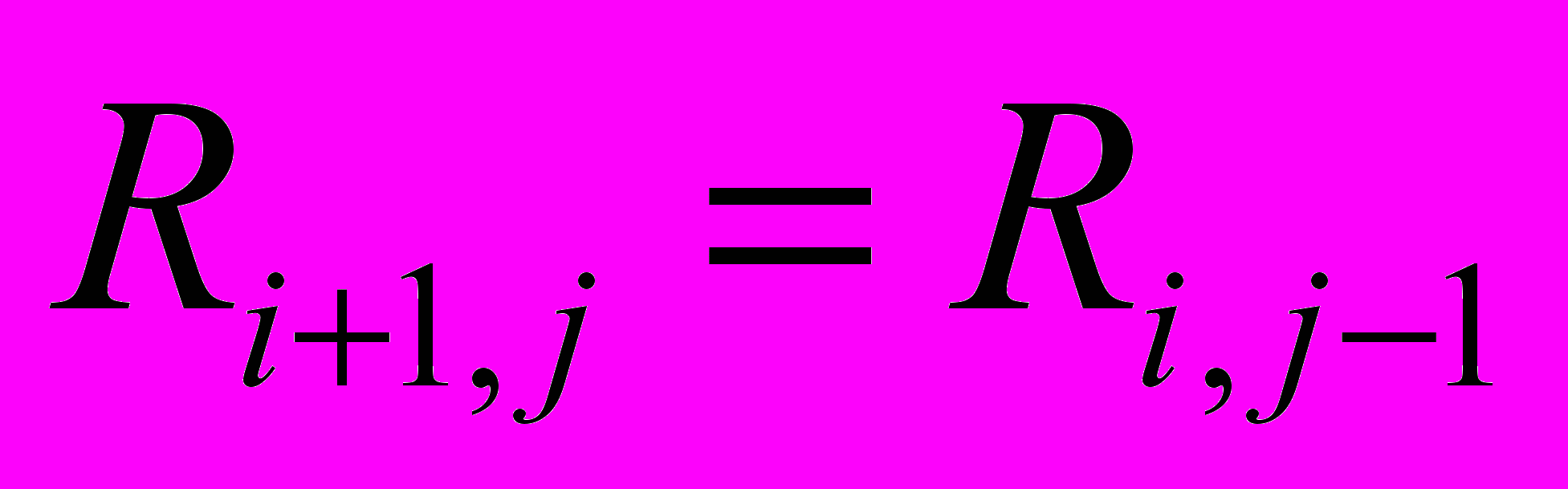Реализуя указанный подход на практике, мы можем иметь два случая. В первом случае мы можем обрабатывать, таким образом, единственное распределение освещенности (один кадр изображения). По своей сути это является одним из вариантов корреляционного анализа. В другом случае мы можем каждый раз при построении элемента выборки сигнала использовать новый кадр изображения, полученного в другой момент реального времени. Для приемника типа ПЗС – это является интегральным параметром по времени накопления заряда t и по площади элемента S_e: .

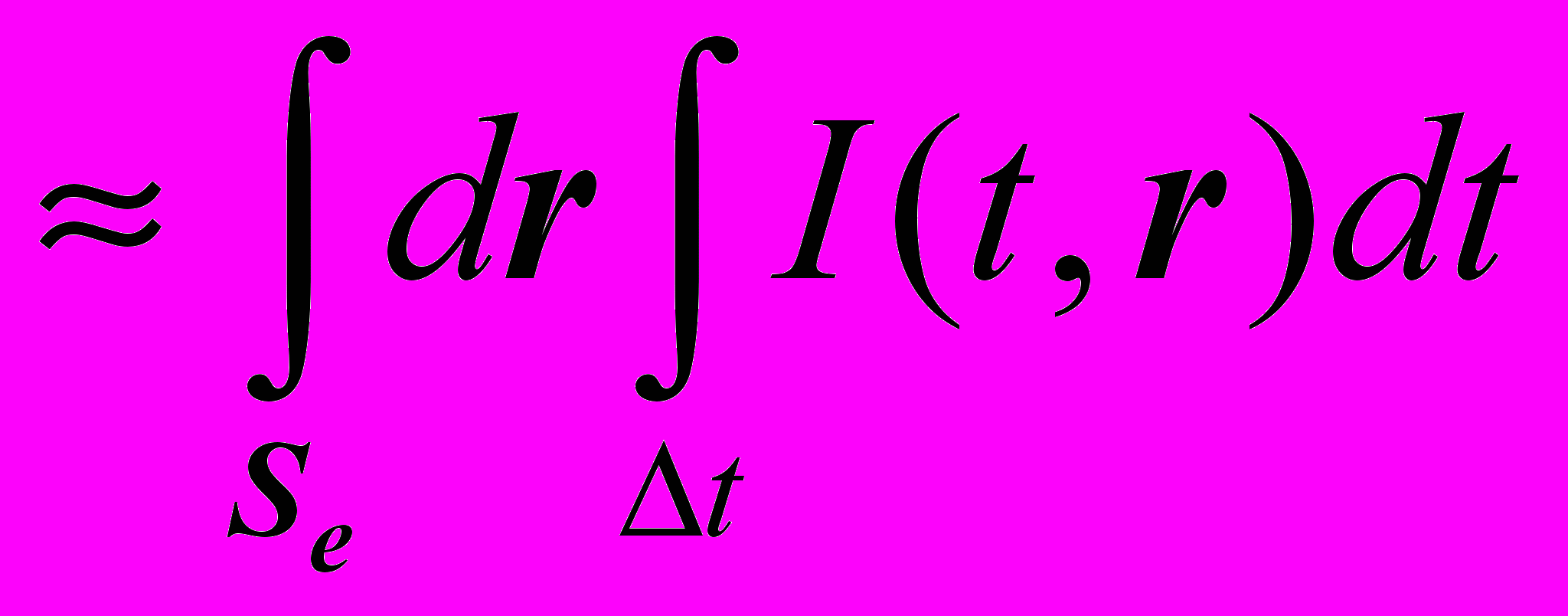Смоделированная таким образом дискретная выборка сигналов 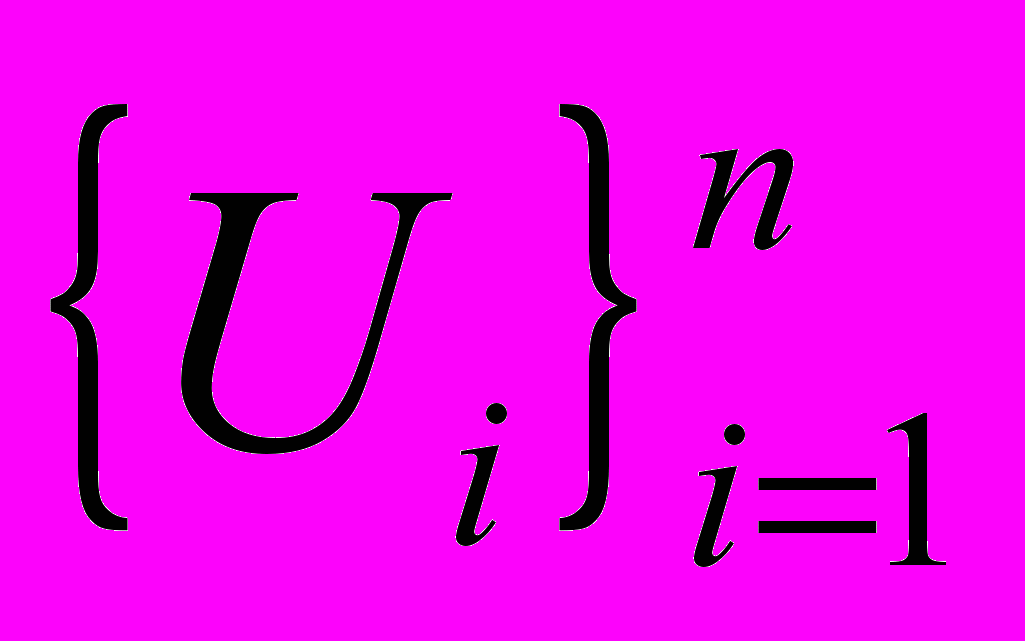является аналогом непрерывной периодической функции u(t,E) по распределенному времени или индексу выборки i. Для точечного источника единичной энергии на выходе имеем дискретную выходную функцию с параметром сдвига на группу элементов. Перемещение такого источника в пределе одного элемента не меняет фазы выходного сигнала. Так как погрешность равна одному элементу матричного фотоприемника, и ГР метод эквивалентен методу определения координаты матричным фотоприемником. Если взять сигнал из двух единичных точечных источников, расположенных на расстоянии равном половине периода матрицы, то ситуация принципиально изменится, погрешность фазового метода возрастает вдвое. Таким образом, если форма распределения освещенности перекрывает ряд элементов матричного фотоприемника, и выходной сигнал имеет уровни квантования, то ГР преобразование осуществляет математическую обработку согласно изложенным выше принципам.

Реализация изложенной выше математической модели требует помимо ввода и оцифровки изображения, компьютерную обработку данных с достаточно развитым интерфейсом пользователя. Опыт построения сервера OLE в среде Visual Studio (Basic), имеющий семейство свойств и методов ГР преобразования [2], и позволяющих производить обработку статических и динамических изображений, полученных с цифровых камер, показал крайнее неудобство в проведении измерений и виртуальных экспериментов.

Ранее проведенные исследования по автоматизации и повышению точности контроля различных оптических деталей с использованием решений фирмы NI показали полную адекватность указанных средств поставленной задачи контроля. Ранее уже успешно использовались аппаратные и программные средства фирмы NI [6] для контроля процесса формирования силикатных покрытий (фазово-растровый дилатометр [7]), технологический контроль внутреннего диаметра оптических капилляров [8]. Указанная эффективность достигалась за счет совмещения измерительного процесса, математической обработки, задание технологического режима и управление технологическим режимом с использованием единых аппаратно-программных средств.

В данной работе проводится дальнейшее исследования ГР метода для анализа картины интерференции типа колец Ньютона (двух координатная задача) на основе алгоритма обработки получаемой информации эллиптическим растром.

2. Результаты работы

Принципиальная схема установки, которая может быть использована как прототип автоматизированной системы для контроля оптических деталей (радиуса кривизны) приведена на рис. 1. Установка состоит из осветителя, включающего в себя источник света 1 и конденсор 2, светофильтра 3, блока двух оптических деталей: плоскопараллельной пластины 4, контролируемой выпукло – выпукло-плоской линзы 5, оптической проектирующей системы 7, видеокамеры наблюдения 8. Сигнал с видеокамеры вводится в компьютер 10.

Плоскопараллельная пластина 4 вместе с контролируемой оптической деталью 5 закрепляются в специальной регулировочной оправе, состоящей из фторопластового основания a и прижимных пластин b и c с другой стороны. Прижимная пластина b при помощи четырех регулировочных дифференциальных винтов (d, e, f, g) создает необходимое усилие прижатие деталей друг к другу P , и задают угол наклона пластины относительно плоскости основания, что в свою очередь определяет место ее контакта с выпуклой линзой.

Положение места контакта оптических деталей можно изменять с лицевой панели ВП, при помощи четырех шаговых двигателей 11, 12, 13, 14. Каждая пара шаговых двигателей (11 и 14), (12 и 13) расположенных по диагонали механического блока определяет свое диагональное направление перемещение места контакта оптических деталей. Причем один диагональный двигатель своим перемещением создает усилие прижатие, после чего второй шаговый двигатель – точно такое же перемещение на отпускание. Сжатие и отпускание должно происходить с некоторой задержкой, что обеспечивает более благоприятные условия для оптического контакта деталей. В силу низкой контрастности полос реализовать схему автоматического слежения затруднительно. Поэтому синхронно с перемещением места контакта по каждому ортогональному направлению происходит перемещение видеокамеры с помощью диагонально расположенных шаговых двигателей управляемых ВП. Добиться синхронности такого перемещения для каждой пары деталей можно путем подбора корректирующей функции. Однако, в реальных случаях будет наблюдаться уход места контакта из поля зрения видеокамеры, поэтому в ВП было предусмотрено ручное перемещение видеокамеры. Идеология открытого блок - диаграммного программирования позволяет намного проще и быстрее отработать алгоритм синхронизации для выбранной категории контролируемых деталей.

Полагая, что угол между направлением наблюдения равен углу падения лучей на поверхность относительно нормали, который можно определить из параметров эллиптичности интерференционных колец (d_y/d_x), всегда можно уточнить параметр cos ’:

.

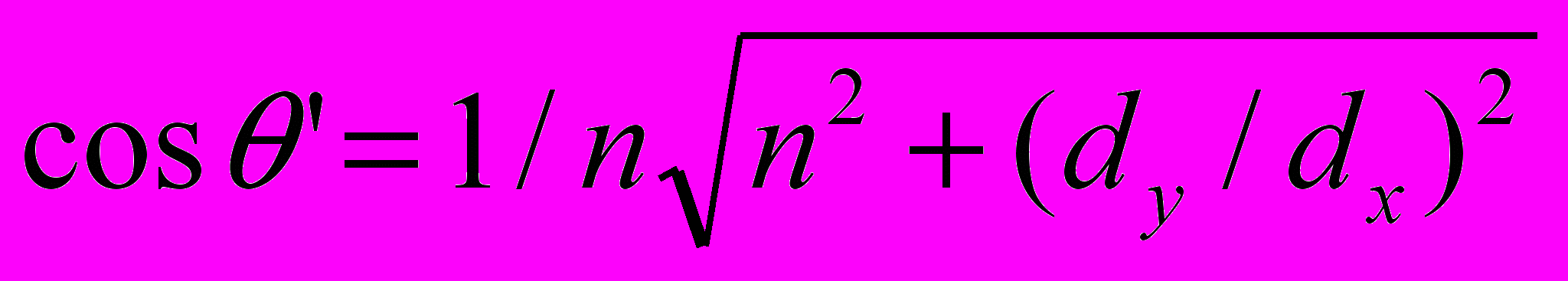Использование ГР метода обработки полученной информации, конструируя эллиптическую растровую функцию в цветовом пространстве RGB, позволяет в несколько раз повысить точность определения периода интерференционных полос. Пропорционально уменьшается погрешность определения радиуса интерференции.




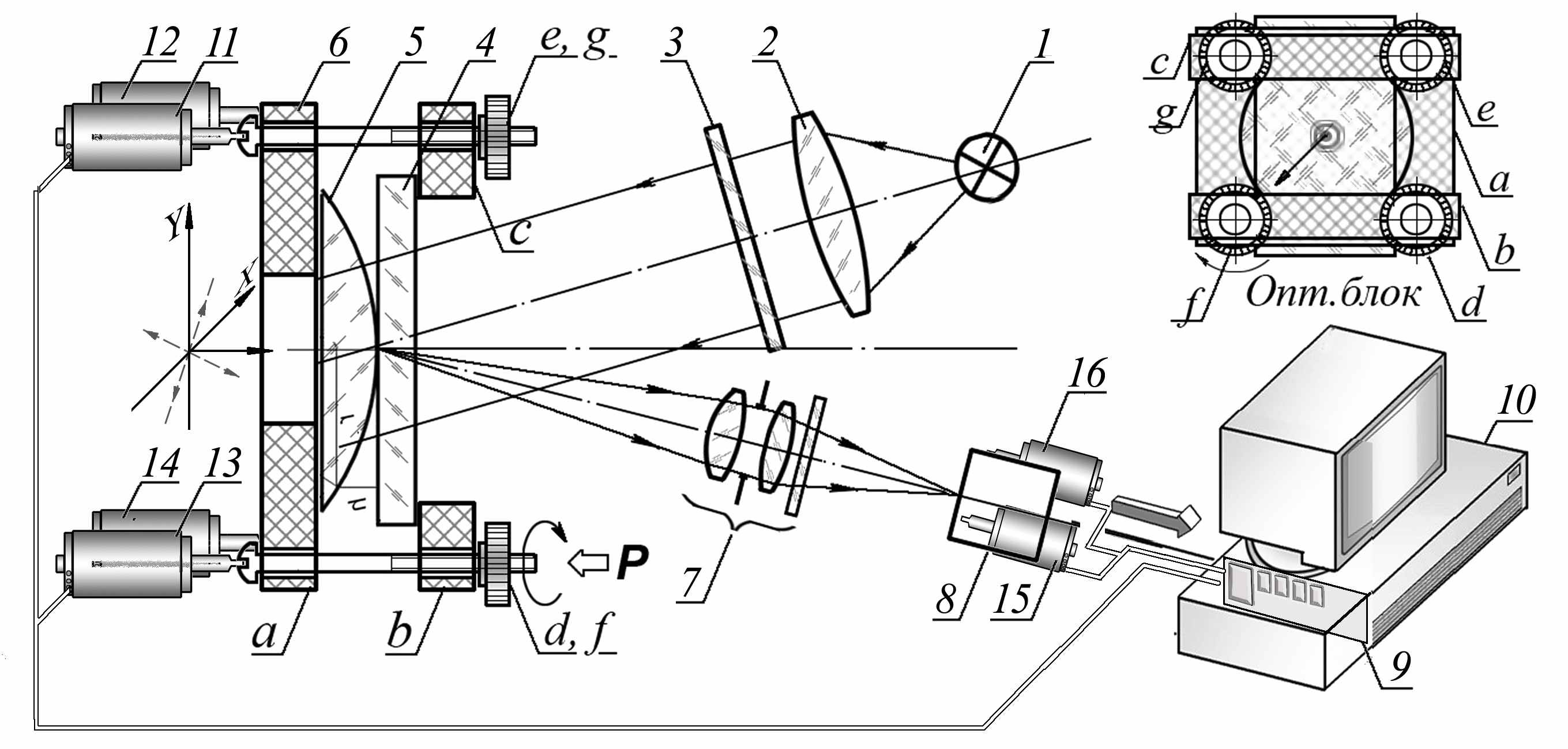
Рис. 1. Схема контроля оптических деталей:

1 – источник света; 2 – конденсор; 3 – светофильтр; 4 – плоскопараллельная пластина; 5 – контролируемая оптическая деталь; 6 – механический блок крепления оптических деталей; 7 – оптическая проектирующая система; 8 – видеокамера; 9 – плата NI; 10 – компьютер;

11, 12, 13, 14 – шаговые двигатели блока деталей; 15, 16 – шаговые двигатели видеокамеры

Для визуального наблюдения и получения с Web-камеры оцифрованного изображения калибровочного транспоранта и интерферограммы нами использовался ВП INVENTVision (рис.2). Достоинство указанной программы (ВП) заключается в отсутствии необходимости использовать специальные аппаратные средства NI по видеозахвату и возможность работы с широким набором недорогих Web камер. Указанный выше ВП, при небольшой доработки блок-диаграммы, позволяет сохранять массив полученных и оцифрованных данных на внешнем носителе, используемый для дальнейшей математической обработки.



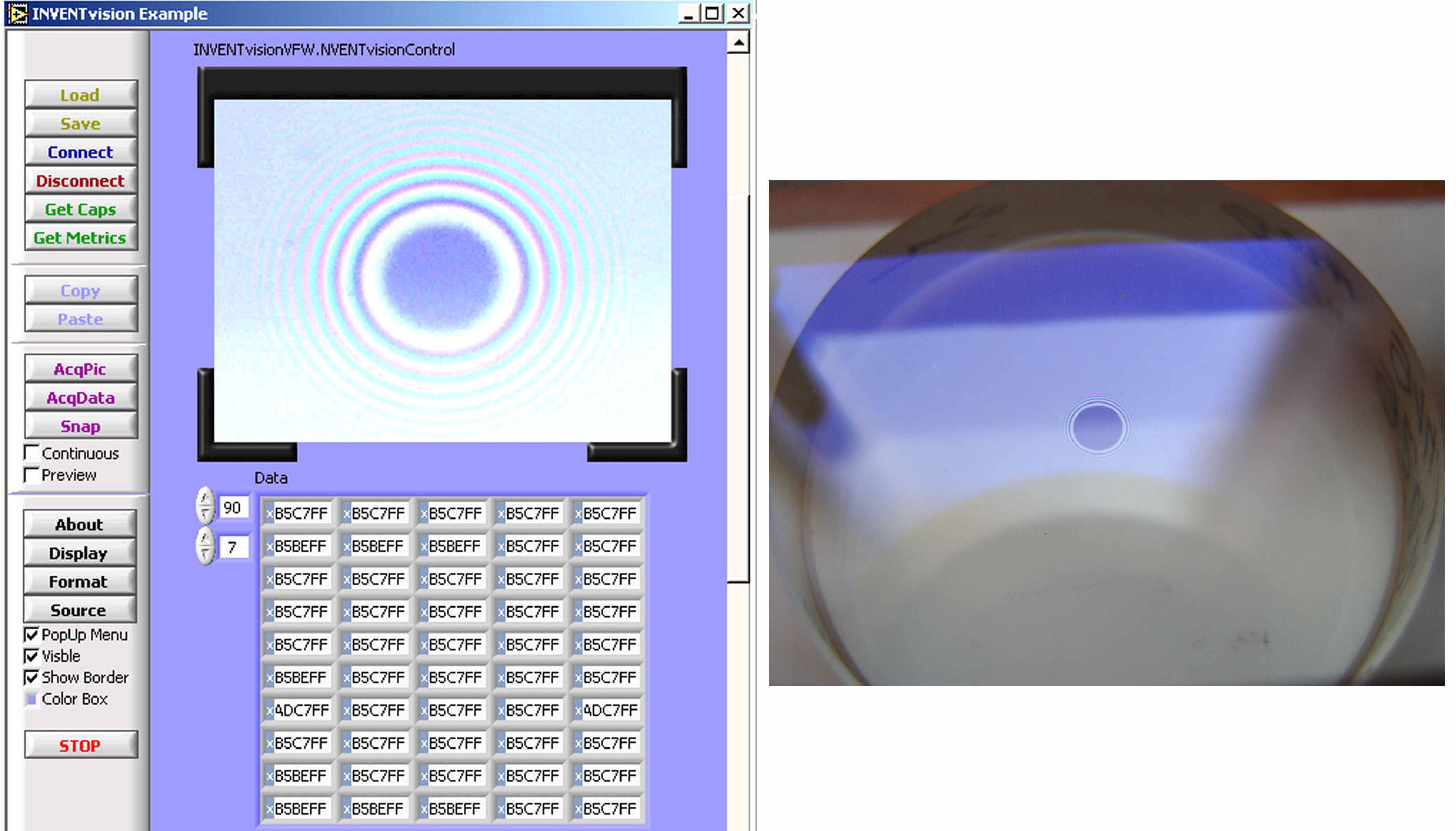
Рис. 2. Отображение колец Ньютона на лицевой панели ВП INVENTVision

Среда разработки ВП LabVIEW является идеальным инструментом для проведения виртуальных экспериментов. В нашем случае мы использовали ее для моделирования ГР преобразования информации, полученного с матричного фотоприемника. Радиус кривизны контролируемой детали был недостаточно велик (R₁=+920,4 мм, R₂=-914,1 мм), и в месте контакта наблюдалась явная деформация поверхности. Повышение точности измерения при ГР методе контроле позволил нам достаточно точно установить что радиус кривизны вместе контакта возрастает более чем в двое. Контроль по кольцам интерференции порядка выше третьего давал стабильно завышенное значение радиуса кривизны порядка 940 мм. Столь хорошее совпадение с калибровочным значением удивительно, и, отчасти можно отнести к простому совпадению. В фазово-растровом дилатометре [7] расчетная погрешность контроля составляла 10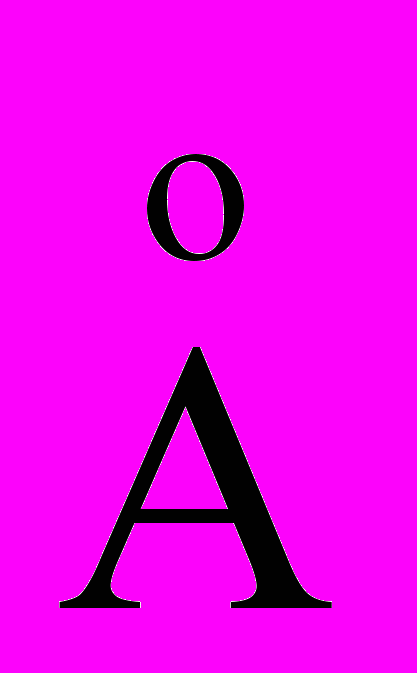, в то время как реальная погрешность была на два порядка выше.

Результаты данной работы были использованы в учебном процессе при проведении лабораторных работ по дисциплинам «Прикладная оптика» и «Компьютерные технологии в приборостроении». Использование одной темы лабораторной работы в двух дисциплинах, рассмотренной с различных сторон, показало положительный результат. Для визуализации математических моделей, описывающих интерференцию (кольца Ньютона) была создан ВП, позволяющий студентам проводить виртуальный эксперимент по моделированию идеальной картины колец Ньютона (рис.3). Виртуальный прибор позволял задавать длину волны  (L), радиус кривизны контролируемой оптической детали в месте контакта R (R), Интенсивности интерферирующих пучков I₁ I₂ (I1 и I2), выделять сечение картины интерференции n_y (NY). Полученные данные модели можно было просмотреть на лицевой пали ВП и сохранить в двухмерном массиве интенсивности 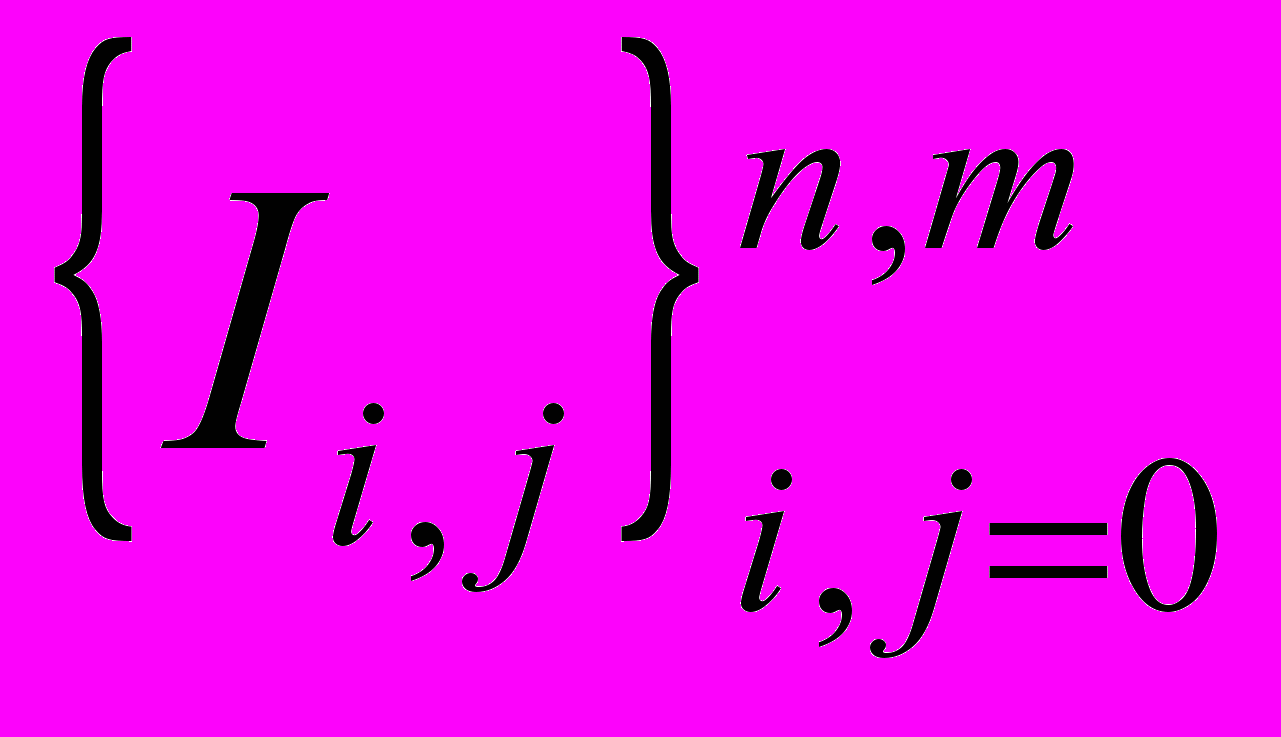(I).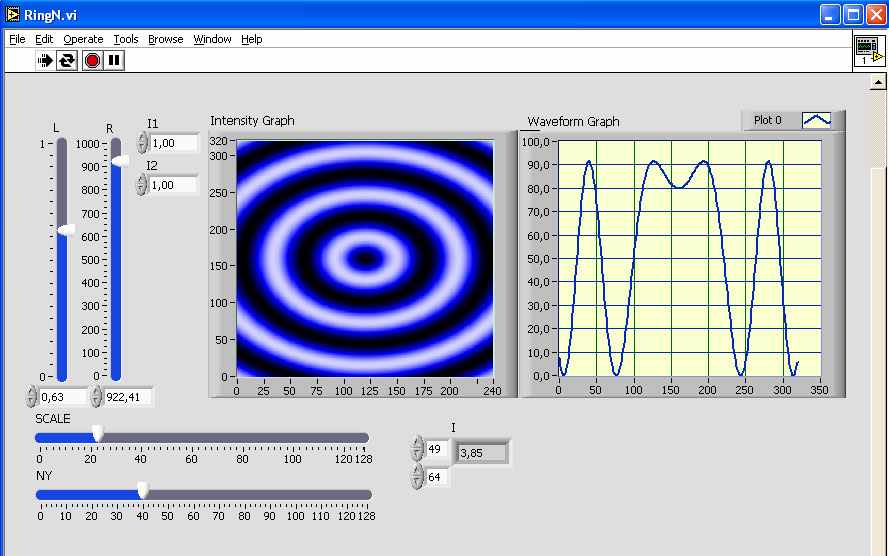





Рис. 3 Виртуальный прибор, моделирующий интерференцию колец Ньютона

Таким образом, использование виртуальных приборов в данном случае контроля дает значительные преимущества, так как позволяет легко задавать параметры работы механической и оптической регистрирующей системы для широкого диапазона параметров оптических деталей, а также в значительной степени повысить производительность и наглядность процесса контроля.

Результаты данной работы использованы в учебном процессе по дисциплинам «Прикладная оптика» и «Компьютерные технологии в приборостроении». Демонстрационные возможности позволяют также использовать результаты для курса «Экспериментальная физика». Особую ценность имеют результаты этой работы для студентов заочной формы обучения в удаленных УКП, так как позволяют полноценно восполнить лабораторный практикум при наличии мобильного комплекта оборудования.


3. Оборудование

Экспериментальные исследования проводились на персональных компьютерах (Intel PIII – PIV), с использованием Web- камеры (freenet i Phone: видеоформат 24-bit RGB, 300000 пикс. максимальное разрешение 640х480, USB- интерфейс, до 15 кадр/сек при разрешении 640х480, ручной фокус), универсальные платы сбора данных NI: PCI 6014.

Использовался механический блок двух оптических деталей: образцовая плоскопараллельная пластинка (0.2 интерференционной полосы), выпукло-вогнутая линза (R₁=+920,4 мм, R₂=-914,1 мм, D= 41 мм).


4. Преимущество технологии National Instruments

Использование технологий фирмы National Instruments позволило в значительной степени упростить аппаратную часть экспериментальной установки, которая в дальнейшем может служить прототипом технологической установки по контролю оптических деталей. Управление и проведение контроля при помощи лицевой панели виртуального прибора повысило производительность экспериментальных исследований, а в технологическом варианте должно привести к повышению производительности контроля, с одной стороны, с другой к повышению надежности, за счет уменьшения психологической нагрузки, не связанных с визуальным способом контроля или со многими рассредоточенными приборами. В значительной степени упростилось применение сложных математических моделей (ГР метод), используемы для обработки получаемой информации. Исходя из многогранности применения ГР метода для контроля различного вида изделий и общности используемого подхода появилась возможность создания пользовательских библиотек ВП для часто используемых функций математической модели, что повышает производительность разработки схем контроля для других видов изделий.

Технология виртуальных приборов и блок- диаграммного программирования в среде LabVIEW оказалась наиболее адекватна задачи проведения виртуальных экспериментов, которые позволили в достаточной мере провести исследование математической модели ГР метода контроля оптических изделий, произвести всесторонний метрологический анализ, произвести оптимальный выбор параметров контроля, осуществлять выбор параметров контроля. При этом имелись достаточные средства для визуализации процесса виртуального эксперимента или проводимого контроля.

Использование технологии National Instruments позволили повысит качественную сторону учебного процесса студентов приборостроительных специальностей по дисциплине «Прикладная оптика», которая в сочетании с дисциплиной «Компьютерные технологии в приборостроении» углубляет полученные знания специальных дисциплин и дает практические навыки использования современных направлений и решений в построении эффективной автоматизированных систем контроля в приборостроительной отрасли.


Литература:

1. М.Борн, Э.Вольф. Основы оптики, Изд. 2-е, Пер. с англ. – М.: Наука, 1973. – 719 с.
   
2. Ч.Вест. Голографическая интерферометрия: Пер. с англ. – М.: Мир, 1982. – 504 с.
   
3. В.Е.Махов, А.И.Потапов. Фазово-растровый метод неразрушающего контроля изделий. Сборник докладов VI Всероссийской научно-технической конференции «Неразрушающий контроль качества и диагностика материалов, конструкций, промышленных изделий и окружающей среды», СПб, СЗТУ, 2005. с.81-100.
   
4. В.Е.Махов, А.И.Потапов Гетеродинно-растровый метод контроля качества изделий. – АН СССР «Дефектоскопия», 1989, №10, с. 68-84.
   
5. Дж.Гудмен Введение в Фурье оптику. – М.: Мир, 1970. – 364 с.
   
6. В.Е.Махов, А.И.Потапов. Фазовый оптический метод и средства технологического контроля. Сборник докладов VI Всероссийской научно-технической конференции «Неразрушающий контроль качества и диагностика материалов, конструкций, промышленных изделий и окружающей среды», СПб, СЗТУ, 2005. с.117-134.
   
7. В.Е.Махов, А.И.Потапов. Способ определения температурной деформации образца и устройство для его осуществления. А.с. № 1392354, 13.04.88, бюллетень №16.
   
8. В.Е.Махов, А.И.Потапов Автоматизация гетеродинно-растрового контроля. Неразрушающий контроль и диагностика окружающей среды: Межвузов. сб., вып. 7. – СПб.: СЗТУ, 2003. – с.35-48.