Рабочая программа дисциплины Для студентов, обучающихся по направлению 080 100. 62 «Экономика»
| Вид материала | Рабочая программа |
- Учебно-методический комплекс для студентов факультета магистерской подготовки, обучающихся, 642.47kb.
- Рабочая программа учебной дисциплины Для студентов, обучающихся по направлению 080100., 600.17kb.
- Рабочая программа учебной дисциплины Для студентов, обучающихся по направлению 080100., 490.25kb.
- Кафедра «Денежно-кредитные отношения и монетарная политика», 11.89kb.
- Рабочая программа учебной дисциплины Для студентов, обучающихся по направлению 030200., 621.67kb.
- Рабочая программа дисциплины Для студентов Финуниверситета, обучающихся по направлению, 340.04kb.
- Рабочая программа учебной дисциплины Для студентов, обучающихся по направлению 040100., 630.28kb.
- Программа дисциплины Для студентов, обучающихся по направлению 080100. 68 «Экономика», 238.05kb.
- Программа дисциплины Для студентов, обучающихся по направлению 080100. 68 «Экономика», 483.4kb.
- Программа дисциплины Для студентов, обучающихся по направлению 080100. 68 «Экономика», 222.11kb.
1 2
ТЕМАТИКА ТЕОРЕТИКО-ПРАКТИЧЕСКИХ РАБОТ- История развития и формирования теории игр.
- Дж.фон Нейман – основоположник теории игр.
- Теория игр и принятие эффективных решений в финансово-экономической области.
- Выигрыш-функции игроков в антагонистической игре и их области определения. Примеры.
- Теоретико-множественное определение антагонистической игры. Примеры.
- Экономическая интерпретация максиминного и минимаксного принципов игры. Примеры.
- Задачи принятия решений. Методы.
- Векторная оптимизация. Многокритериальные задачи.
- Редуцирование игр методом разбиения платежной матрицы на подматрицы.
- Принцип доминирования стратегий игроков.
- Геометрическое решение игр.
- Решение игры методом Шепли-Сноу.
- Решение игры приближенным методом Брауна-Робинсон.
- Связь теории игр с линейным программированием.
- Основная теорема теории матричных игр – теорема существования решения в смешанных стратегиях Дж. Фон Неймана.
- Вклад Нобелевского лауреата Дж. Нэша в развитие теории игр.
- Вклад советских ученых в развитие теории игр.
31.Теоретико-игровые модели принятия решений в эколого–экономических системах.
32.Использование теории игр в математической экономике.
33.Теория игр в менеджменте.
ПЕРЕЧЕНЬ ВОПРОСОВ для подготовки к ЭКЗАМЕНУ
1. Задачи принятия решения.
2. Понятие о многокритериальной оптимизации.
3. Задачи теории игр в экономике, финансах и бизнесе.
4. Основные понятия и определения теории антагонистических игр.
5. Выигрыш-функция и матрица выигрышей. Чистые стратегии игроков. Соотношение между матрицами выигрышей игроков А и В в парной антагонистической игре с нулевой суммой выигрышей.
6. Максиминный и минимаксный принципы игроков. Показатели эффективности и неэффективности чистых стратегий игроков. Максимин и минимакс игры. Максиминные и минимаксные стратегии. Нижняя и верхняя цены игры в чистых стратегиях. Теорема о соотношениях между выигрышами игрока А, показателями эффективности и неэффективности стратегий, нижней и верхней ценами игры.
7. Устойчивые и неустойчивые игровые ситуации. Игровые ситуации, удовлетворительные для игроков, и их критерии.
8. Равновесная ситуация. Седловая точка выигрыш-функции и седловая точка матрицы игры. Свойства равнозначности и взаимозаменяемости седловых точек матрицы игры.
9. Нижняя и верхняя цены игры. Соотношение между ними. Цена игры в чистых стратегиях. Чистые оптимальные стратегии. Полное и частное решения игры в чистых стратегиях. Критерий существования цены игры в чистых стратегиях. Соотношения между множествами оптимальных и максиминных (минимаксных) стратегий.
10. Смешанные стратегии. Геометрическая интерпретация множества смешанных стратегий.
11. Определение выигрыш-функции в смешанных стратегиях; координатные и векторно-матричные формулы ее представления.
12. Определение и существование показателя эффективности смешанной стратегии игрока А относительно множеств смешанных и чистых стратегий игрока В.
13. Определение и существование показателя неэффективности смешанной стратегии игрока В относительно множеств смешанных и чистых стратегий игрока А.
14. Определения нижней и верхней цен игры в смешанных стратегиях и их существование.
15. Теорема о соотношении между нижней и верхней ценами игры в смешанных и чистых стратегиях.
16. Понятия выпуклого множества, выпуклой функции и седловых точек действительной функции двух векторных аргументов.
17. Свойства равнозначности и взаимозаменяемости седловых точек действительной функции двух векторных аргументов.
18. Критерий существования седловых точек действительной функции двух векторных аргументов.
19. Теорема о единственности точки экстремума строго вогнутой
(выпуклой) на выпуклом множестве функции.
20. Теорема о достаточных условиях существования седловых точек у непрерывной вогнуто-выпуклой на декартовом произведении выпуклых компактов функции.
21. Цена игры в смешанных стратегиях. Оптимальные смешанные стратегии. Полное и частное решения игры в смешанных стратегиях. Основная теорема теории игр Дж. фон Неймана.
22. Критерии оптимальных смешанных стратегий в терминах данной цены игры, выигрыш-функции и множеств смешанных стратегий игроков.
23. Критерии оптимальных смешанных стратегий в терминах данной цены игры, выигрыш-функции и множеств чистых стратегий игроков.
24. Геометрическая интерпретация множества оптимальных смешанных стратегий.
25. Критерий цены игры и оптимальных смешанных стратегий в терминах множеств смешанных стратегий игроков.
26. Критерий цены игры и оптимальных смешанных стратегий в терминах множеств чистых стратегий игроков.
27. Критерий цены игры и оптимальных смешанных стратегий в терминах выигрыш-функции и ее седловых точек.
28. Определение и теорема об активных стратегиях. Спектр стратегии. Определение и теорема о смесях активных чистых стратегий.
29. Принцип доминирования стратегий. Теорема и следствия о доминируемых стратегиях.
30. Принцип редуцирования матриц игры, основанный на разбиении ее на подматрицы с определенным свойством.
31. Изоморфное преобразования игры.
32. Зеркальный изоморфизм игры.
33. Аффинное преобразование игры.
34. Критерий седловой точки матрицы игры 22, основанный на принципе доминирования.
35. Критерий существования седловой точки в игре 22 в терминах пассивных стратегий.
36. Признак существования седловой точки в игре 22 в терминах сумм элементов главной и побочной диагоналей матрицы игры.
37. Теорема об аналитическом решении игры 22 без седловой точки в смешанных стратегиях и ее следствия для симметрической и двоякосимметрической матрицы игры.
38. Геометрический метод нахождения цены игры 22 и оптимальных стратегий игрока А.
39. Геометрический метод нахождения цены игры 22 и оптимальных стратегий игрока В.
40. Геометрический метод нахождения цены игры 2
и оптимальных стратегий игрока А. 41. Теорема об аналитическом методе нахождения цены игры 2
и оптимальных стратегий игрока А. 42. Теорема об аналитическом методе нахождения цены игры 2
и оптимальных стратегий игрока В. 43. Геометрический метод нахождения цены игры m2 и оптимальных стратегий игрока В.
44. Теорема об аналитическом методе нахождения цены игры m2 и оптимальных стратегий игрока В.
45. Принцип решения игры m n методом Шепли-Сноу. Теорема
Шепли-Сноу о крайних оптимальных стратегиях.
46. Алгоритм решения игры m n методом Шепли-Сноу.
47. Решение игры m n приближенным методом Брауна-Робинсон.
48. Теорема о сведении решения матричной игры к решению пары двойственных друг другу стандартных задач линейного программирования.
49. Определение и теорема о симметричной матричной игре.
50. Теорема о сведении решения пары взаимно двойственных задач линейного программирования к решению симметричной матричной игры.
УРОВЕНЬ ТРЕБОВАНИЙ И КРИТЕРИИ ОЦЕНОК
Оценка успеваемости студентов осуществляется по 100-балльной системе. Критерии, принятые на кафедре математического моделирования экономических процессов, и соответствующие им баллы по полусеместрам, представлены в табл.1.
Табл.1
Критерии и баллы по полусеместрам
-
№
п / п
Критерии
Баллы
1-я половина
семестра
2-я половина
семестра
1
Посещаемость практических занятий
20
10
2
Активность на практических занятиях
20
20
3
Контрольная работа
-
30
Всего по материалу практических занятий
40
60
4
Посещаемость лекций
10
20
5
Активность на лекциях
10
20
6
Теоретико-практическая работа
40
-
Всего по лекционному материалу
60
40
В 1-й половине семестра до аттестации студенты выполняют контрольную работу, а во 2-й половине семестра пишут и сдают теоретико-практическую работу (ТПР). Такое распределение с учетом предстоящего экзамена создает предпосылки равномерной во времени подготовки студентов по материалу лекционных и практических занятий.
Учет получаемых студентами баллов ведет преподаватель по следующим нормам.
Посещаемость занятий: При обучении по очной форме посещение студентами занятий обязательно. С другой стороны, присутствие студента на занятии дает возможность непосредственного контакта с преподавателем, что создает благоприятную обстановку для лучшего усвоения учебного материала. Поэтому посещаемость занятий включена в качестве одного из критериев оценки успеваемости студентов.
Активность на занятиях: Ответы студентов оцениваются в баллах следующим образом:
Табл.2
Ответы студентов в баллах
-
Качество ответов студентов
Баллы
отлично
5
хорошо
3
удовлетворительно
1
неудовлетворительно
0
Теоретико-практические работы проверяются лектором по нормативам составных частей работы, максимальные баллы по которым указаны в табл.3.
Табл.3
Максимальные баллы
по составным частям теоретико-практической работы
-
№
п / п
Составные части
теоретико-практической работы
Баллы
1.
План работы (содержание, оглавление)
3
2.
Введение (вступление)
6
3.
Теоретическая часть.
7
4.
Практическая часть.
7
5.
Заключение (выводы).
5
6.
Цитированная литература
4
7.
Собственные мысли
5
8.
Качество оформления
3
В С Е Г О
40
Аттестационные баллы каждого студента за 1-ю и 2-ю половины семестра образуются суммированием полученных им баллов по всем критериям в соответствующей половине семестра. Из табл.1 видно, что аттестационный балл каждого студента за каждую из половин семестра не может быть меньше 0 и больше 100.
Аттестационные баллы за каждую половину семестра конвертируются в 10-балльную систему следующим образом:
Табл.4
Конвертирование аттестационных баллов
-
Аттестационные баллы
0-50
0
51-55
1
56-60
2
61-65
3
66-70
4
71-75
5
76-80
6
81-85
7
86-90
8
91-95
9
96-100
10
Экзамен оценивается максимум в 80 баллов. Обозначим балл по экзамену
, 
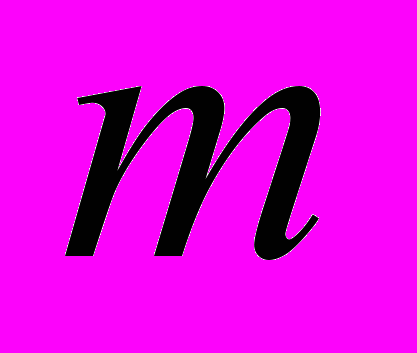.Распределение максимальных баллов по видам работы:
| № п/п | Вид отчетности | Баллы |
| 1. | Работа в семестре | 20 |
| 2. | Экзамен | 80 |
| | Итого: | 100 |
Итоговый балл студента, обозначим его через
, получается путем суммирования оценки за работу в семестре (равняется сумме двух k, полученных за 1-ю и 2-ю половины семестра) и оценки итоговых знаний в ходе экзамена m.Для выставления оценки в зачетную книжку, итоговые баллы конвертируются в пятибалльную оценку следующим образом:
Табл.5
Конвертирование итоговых баллов
в пятибалльную оценку-
Итоговые баллы,
Пятибалльная оценка
Цифрой
Прописью
0-50
2
неудовлетворительно
51-69
3
удовлетворительно
70-85
4
хорошо
86-100
5
отлично
Учебно-методическое
и информационное обеспечение дисциплины
Рекомендуемая литература
а) основная:
1. Бережная Е. В., Бережной В. И. Математические методы моделирования экономических систем: Учеб. пособие. - М.: Финансы и статистика, 2006.- 432 с.
2. Воробьев Н.Н. Теория игр: Лекции для экономистов-кибернетиков.- Л.: ЛГУ, 1974.
3. Моделирование рисковых ситуаций в экономике и бизнесе: Учеб. пос./ А.М.Дубров, Б.А.Лагоша, Е.Ю.Хрусталев, Т.П.Барановская; Под ред. Б.А.Лагоши .- М.: Финансы и статистика, 2003.
4. Исследование операций в экономике: Учеб. пос. / Под ред. Н.Ш.Кремера. - М.: ЮНИТИ, 2006.
5. Красс М.С., Чупрынов Б.П. Основы математики и ее приложения в экономическом образовании. - М.: ДЕЛО, 2006.
6. Красс М. С. Математика в экономике. Основы математики. - М.: ИД ФБК-ПРЕСС, 2005. - 472 с.
7. Лабскер Л. Г., Бабешко Л. О. Игровые методы в управлении экономикой и бизнесом: Учеб. пос. - М.: Дело, 2001. - 464 с.
8. Лабскер Л. Г. Теория критериев оптимальности и экономические решения: монография.- 2 изд., стер. - М.: КноРус, 2009.-744 с.
9. Ященко Н. А. Методические указания для самостоятельной работы студентов по разделу «Элементы теории игр» по дисциплине экономико-математическое моделирование. - М.: Финансовая академия при Правительстве РФ, 2006.
б) дополнительная:
1. Абчук В.А. Экономико-математические методы: Элементарная математика и логика. Методы исследования операций. - СПб.: Союз, 1999.
2. Бондарева О. Н. О теоретико-игровых моделях в экономике. - Л.: ЛГУ, 1974.
3. Васин А.А., Морозов В.В. Теория игр и модели математической экономики: Учебное пособие. — М.: МАКС Пресс, 2005. —272 с.
4. Горелик В.Д., Кононенко А.Ф. Теоретико-игровые модели принятия решений в эколого-экономических системах. - М.: Наука, 1982.
5. Давыдов Э.Г. Методы и модели теории антагонистических игр. - М.: МГУ, 1978.
6. Данилов Н.Н. Игровые модели принятия решений. - Кемерово: КГУ, 1981.
8. Дюбин Г.Н., Суздаль В.Г. Введение в прикладную теорию игр.- М.: Наука, 1981.
9. Лесик, А. И., Чистяков, Ю. Е. Теоретико-игровые модели взаимодействия экономических субъектов производственной системы. - М.: ВЦ РАН, 1994
10. Меньшиков И. С. Лекции по теории игр и математическому моделированию.-М.: Изд.: М3 Пресс, 2006.
12. Мулен Г. Теория игр с примерами из математической экономики.- М.: Мир, 1985.
13. Петросян Л.А., Зенкевич Н.А., Семина Е.А. Теория игр.- М.: Высшая школа, 1998.
14. Печерский С. Л., Беляева А. А. Теория игр для экономистов. Вводный курс. -СПб: изд-во ЕУСПб. 2001.
15. Подиновский В.В., Ногин В.Д. Парето-оптимальные решения многокритериальных задач. - М.: Наука, 1982.
16. Шикин Е.В., Чхартишвили А.Г. Математические методы и модели в управлении: Учебное пособие. - М.: Дело, 2004.
Перечень обучающих и контролирующих
компьютерных программ
Табличный процессор MS Excel.