Geum.ru

Рабочая программа дисциплины математика для студентов 1-2 курса для подготовки специалиста по специальности 060500 «Бухгалтерский учет и аудит»

Вид материалаРабочая программа

Содержание


Пояснительная записка.
Тематический план
Всего часов
Содержание учебной дисциплины
Тема 2.Элементы линейной и векторной алгебры.
Тема 3. Аналитическая геометрия на плоскости и в пространстве. Кривые 2
Тема 4. Введение в математический анализ. Функции. Пределы и непрерывность.
Тема 5. Дифференциальное исчисление. Производная. Приложения производной. Дифференциал функции.
II семестр
Тема 7. Определенный интеграл.
Тема 8. Несобственные интегралы.
Тема 10. Ряды. Числовые ряды. Степенные ряды.
Тема 11. Дифференциальные уравнения.
III семестр
Тема 14. Случайные события. Частота и вероятность.
Тема 15. Основные формулы для вычисления вероятностей.
Тема 16. Случайные величины.
Тема 17. Числовые характеристики случайных величин.
Тема 18. Основные законы распределения. Нормальный закон распределения.
Тема 19. Системы случайных величин. Корреляция и регрессия.
...
Полное содержание
Подобный материал:

АВТОНОМНАЯ НЕКОМЕРЧЕСКАЯ ОРГАНИЗАЦИЯ

МНОГОУРОВНЕВЫЙ ОБРАЗОВАТЕЛЬНЫЙ КОМПЛЕКС

ВОРОНЕЖСКИЙ ЭКОНОМИКО-ПРАВОВОЙ ИНСТИТУТ


Кафедра прикладной информатики и математики

РАБОЧАЯ ПРОГРАММА


дисциплины МАТЕМАТИКА

для студентов 1-2 курса


для подготовки специалиста

по специальности 060500

«Бухгалтерский учет и аудит»



Всего: 280 час.

Из них: 148 лекционных

122 практических


Форма отчетности: зачёт, экзамен, зачёт,

экзамен


По уч. плану 2007/2008 гг.
Составители: Колупанова Г.А.

Самсонова И.М.

Петрова Л.П.

Программа утверждена

На заседании кафедры


Протокол № _____ от ________


Зав.кафедрой ___Соломахин А.Н

Воронеж 2007

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА.


Программа составлена в соответствии с «Государственным образовательным стандартом высшего профессионального образования» по подготовке специалистов по направлению:

060500 – «Бухгалтерский а удит». При разработке программы были использованы следующие материалы:
    • «Примерная программа дисциплины «Математика»»/Гос. Комитет по РФ по Высшему образованию, М., 1996 г.;
    • «Взаимосвязь математических и экономических дисциплин»/Отчет рабочей группы УМО университетов, М., 1996 г.
    • Программы дисциплины «Математика» (МГУ, РЭА им. Плеханова, ГАУ им. Орджоникидзе);
    • Учебная и методическая литература по различным математическим дисциплинам.


Данная программа составлена для изучения блока математических дисциплин, которая является основой для изучения математических методов и моделей, эконометрики, прогнозирование и других математических спецкурсов в соответствии со специализацией.

Дисциплина «Математика» изучается студентом в течение 4-х семестров и включает следующие разделы:
    • общие математические дисциплины (элементы высшей алгебры, линейной и векторной алгебры, аналитической геометрии на плоскости и в пространстве);
    • математический анализ и дифференциальные уравнения;
    • теория вероятностей и математическая статистика;
    • исследование операций (задачи линейного и динамического программирования, сетевое планирование, задачи оптимизации, элементы теории игр и теории систем массового обслуживания).

Аудиторная нагрузка по обязательным курсам составляет 280 часов и включает лекции и практические занятия. Преподавание строится на сочетании аудиторных занятий и самостоятельной работы студентов.

В каждом семестре предусматривается проведение двух контрольных работ. При изучении математики для лучшего усвоения материала возможно проведение теоретических коллоквиумов.

По данному блоку дисциплин предусмотрено проведение двух зачётов по итогам 1-го и 3-го семестров, а также – экзамена по итогам 1-го и 2-го курса обучения. Одной из возможных форм контроля являются компьютерные тестирования.

Математическое образование следует рассматривать как одну из важнейших составляющих фундаментальной подготовки специалистов, так как математика является как элементом общей культуры, так и универсальным языком науки и основой для применения математических методов при решении экономических задач.

Особенностью данной программы является то, что она призвана дать студентам базовое, широкое , общее математическое образование, способствующее дальнейшему изучению экономических и прикладных математических дисциплин.

Дисциплина «Математика изучается параллельно с экономической теорией и другими фундаментальными экономическими дисциплинами, что позволяет активизировать освоение математических методов анализа экономических процессов и решения экономических задач.

Экономические примеры, иллюстрирующие применение основных математических понятий, обеспечивают понимание тех разделов экономических наук, развитие которых основывается на использовании математических моделей и методов из анализа.

Кроме того, изучение математических дисциплин способствует логическому мышлению, необходимому любому экономисту для того, чтобы четко разделить предпосылки анализа и полученные на их основе выводы, понимать и прослеживать причинно-следственные связи. В связи с этим, целью курса является ознакомление студентов с основами математического аппарата, необходимого для решения теоретических и практических задач, развитие логического мышления, выработки умения самостоятельного изучения математической литературы, умение сформулировать экономическую задачу на математическом языке и освоение навыков математического исследования прикладных экономических проблем.


ТЕМАТИЧЕСКИЙ ПЛАН



№
Наименование разделов и тем
Всего часов по учебному плану
В том числе аудиторных
Примечания

З/о

Всего часов по рабочему плану
Лекции
Практические занятия

Лекции
Практические занятия

1 семестр

1
Введение. Становление современной математики. Множества. Элементы высшей алгебры (комплексные числа).
16
8
4
4
1



2
Элементы линейной и векторной алгебры.

40
20
10
10
4
2

3
Аналитическая геометрия на плоскости и в пространстве. Кривые 2го порядка.
24
12
6
6
3
2

4
Введение в математический анализ. Пределы и непрерывность.
24
12
6
6
4
2

5
Дифференциальное исчисление. Производная. Приложения производной. Дифференциал функции.
32
16
8
8
4
2




Итого:
136
68
34
34
16
8

2 семестр

6
Неопределенный интеграл.
24
12
6
6
2
2

7
Определенный интеграл.
20
10
4
6
2
1

8
Несобственные интегралы.
8
4
2
2
2



9
Функции многих переменных.
24
12
6
6
2
1

10
Ряды. Числовые ряды. Степенные ряды.
24
12
6
6
4
2

11
Дифференциальные уравнения.
28
14
8
6
4
2




Итого:
128
64
32
32
16
8

3 семестр

12
Введение. Понятие о вероятности
2
1
1









13
Элементы комбинаторики.
8
4
2
2
2
-

14
Случайные события и операции над ними. Частота и вероятность.
10
5
3
2
2
2

15
Основные формулы для вычисления вероятностей.
16
8
4
4
2
2

16
Случайные величины.
12
6
2
4
1



17
Числовые характеристики случайных величин.
16
8
4
4
1
2

18
Основные законы распределения. Нормальный закон распределения.
8
4
2
2
2
2

19
Системы случайных величин. Корреляция и регрессия.
8
4
2
2
-
-

20
Закон больших чисел.
16
8
4
4
2
-

21
Математическая статистика. Генеральная совокупность и выборка..
16
8
4
4
1
-

22
Статистические методы оценки параметров.
16
8
4
4
1
-

23
Проверка статистических гипотез.
8
4
2
2
2
-




Итого:
136
68
34
34
16
8

4 семестр

24
Предмет дисциплины. Понятие модели.
8
4
2
2






25
Линейное программирование (ЛП).
44
22
14
8






26
Транспортная ЗЛП
16
8
4
4






27
Целочисленное программирование
4
2
2









28
Динамическое программирование
12
6
4
2






29
Элементы теории игр.
28
14
8
6






30
Элементы теории графов и сетевого планирования.
20
10
6
4






31
Элементы теории массового облуживания
16
8
4
4






32
Специальные экономико-математические модели
12
6
4
2









Итого:
160
80
48
32









Всего часов:
560
280
148
132
48
24


СОДЕРЖАНИЕ УЧЕБНОЙ ДИСЦИПЛИНЫ


I семестр


Тема 1. Введение. Становление высшей математики. Элементы высшей алгебры.

Роль и место математики в решении интеллектуальных задач в различных сферах человеческой деятельности. Геометрия Евклида как первая естественно-научная теория. Основные этапы развития и структура современной математики. Множества. Операции над множествами. Выпуклые множества и их свойства.

Комплексные числа. Арифметические операции над комплексными числами. Комплексная плоскость. Тригонометрическая и показательная формы комплексного числа. Многочлен в комплексной области. Теорема Безу. Основная теорема алгебры.


Тема 2.Элементы линейной и векторной алгебры.

Основные сведения о матрицах. Операции над матрицами. Определители квадратных матриц. Свойства определителей. Определители n-го порядка. Обратная матрица. Ранг матрицы. Способы вычисления ранга.

Системы линейных уравнений. Матричная запись системы. Решение системы n линейных уравнений с n независимыми переменными методом обратной матрицы. Правило Крамера. Система m линейных уравнений с n неизвестными. Метод Гаусса. Общее, частное, базисное решения системы. Фундаментальная система решений. Модель Леонтьева (балансовый анализ).

Системы координат на плоскости и в пространстве. Декартовы прямоугольные координаты. Преобразование координат. Трехмерное пространство. Векторы на плоскости и в пространстве. Линейные операции над векторами. Скалярное произведение векторов и его свойства.

Линейно независимые системы векторов. Базис. Разложение вектора по базису. Линейные операторы и действия над ними. Собственные векторы и собственные значения. Квадратичные формы. Линейная модель обмена (модель международной торговли).

Понятие евклидова пространства, метрического, нормированного пространств. Примеры экономических пространств.


Тема 3. Аналитическая геометрия на плоскости и в пространстве. Кривые 2го порядка.

Уравнение линии на плоскости. Общее уравнение прямой. Взаимное расположение 2-х прямых. Различные формы задания уравнения прямой. Расстояние от точки до прямой. Условия параллельности и перпендикулярности двух прямых.

Уравнение плоскости в пространстве. Взаимное расположение плоскостей. Уравнение прямой в пространстве. Способы задания прямой в пространстве.

Кривые второго порядка, их геометрические свойства и уравнения. Основные поверхности второго порядка.


Тема 4. Введение в математический анализ. Функции. Пределы и непрерывность.

Понятие функции. Основные свойства функций. Основные элементарные функции и их свойства. Понятие сложной и обратной функций. Неявные функции. Классификация функций. Применение функций в экономике. Интерполирование функций.

Числовые последовательности. Предел числовой последовательности и его свойства.

Предел функции на бесконечности и в точке. Односторонние пределы. Бесконечно малые и бесконечно большие функции. Сравнение бесконечно малых. Свойства функций, имеющих предел (основные теоремы о пределах).

1-й и 2-й замечательные пределы. Непрерывность функции в точке. Свойства функций, непрерывных в точке. Точки разрыва и их классификация. Свойства функций, непрерывных на отрезке. Непрерывность основных элементарных функций. Экономическое приложение – задача о непрерывном начислении процентов.


Тема 5. Дифференциальное исчисление. Производная. Приложения производной. Дифференциал функции.

Определение производной, ее геометрический и экономический смысл. Производная суммы, произведения и частного. Производная сложной функции. Производная обратной функции. Основные правила дифференцирования. Производные основных элементарных функций. Понятие производных высших порядков.

Приложения производной. Основные теоремы дифференциального исчисления. Правило Лопиталя. Условия возрастания и убывания функции. Точки экстремума. Необходимое условие экстремума. Достаточные признаки существования экстремума. Исследование функции на выпуклость и вогнутость. Точки перегиба. Асимптоты функции. Общая схема исследования функции и построение ее графика.

Дифференциал функции. Применение дифференциала в приближенных вычислениях. Дифференциалы высших порядков. Использование понятия производной в экономике. Приложение производной в экономической теории.


II семестр


Тема 6. Неопределенный интеграл.

Первообразная функции. Неопределенный интеграл и его основные свойства. Интегралы от основных элементарных функций. Замена переменной в неопределенном интеграле. Метод интегрирования по частям. Интегрирование рациональных и простейших иррациональных функций. Интегрирование тригонометрических функций.


Тема 7. Определенный интеграл.

Определенный интеграл, его геометрический и экономический смысл. Основные свойства определенного интеграла. Интеграл с переменным верхним пределом. Формула Ньютона-Лейбница. Интегрирование по частям и замена переменной в определенном интеграле. Приближенные методы интегрирования. Приложения определенного интеграла. Использование понятия определенного интеграла в экономике.


Тема 8. Несобственные интегралы.

Несобственные интегралы 1-го и 2-го рода. Признаки сходимости несобственных интегралов.


Тема 9. Функции многих переменных.

Функции многих переменных. Предел и непрерывность. Основные свойства непрерывных функций. Частные и полное приращения функции многих переменных. Понятие производной по направлению и градиента. Дифференцирование неявной и сложной функции. Частные производные и дифференциалы высших порядков функции многих переменных. Использование функций многих переменных в экономической теории. Экономические приложения: изокванты ПФ, кривые безразличия. Коэффициенты эластичности, предельная производительность труда. Экстремумы функции многих переменных. Необходимое условие локального экстремума. Достаточное условие локального экстремума. Условный экстремум функции многих переменных: теорема о разрешимости системы функциональных уравнений, метод множителей Лагранжа. Понятие о методе наименьших квадратов. Примеры решения экономических задач.


Тема 10. Ряды. Числовые ряды. Степенные ряды.

Определение числового ряда и его суммы. Необходимый признак сходимости числовых рядов. Гармонический ряд. Ряд с положительными членами. Достаточные признаки сходимости числового ряда (признак сравнения, признак Даламбера, интегральный признак Коши). Знакопеременные ряды. Абсолютная и условная сходимость. Понятие о функциональных рядах. Интервал и радиус сходимости степенного ряда. Разложение функции в степенные ряды (ряды Тейлора и Маклорена). Применение рядов в приближенных вычислениях.


Тема 11. Дифференциальные уравнения.

Динамические экономические задачи, приводящие к дифференциальным уравнениям. Дифференциальные уравнения 1-го порядка, общие понятия. Уравнения с разделяющимися переменными. Однородные и линейные уравнения 1-го порядка. Уравнения в полных дифференциалах. Задача Коши. Дифференциальные уравнения высших порядков. Дифференциальные уравнения 2-го порядка: 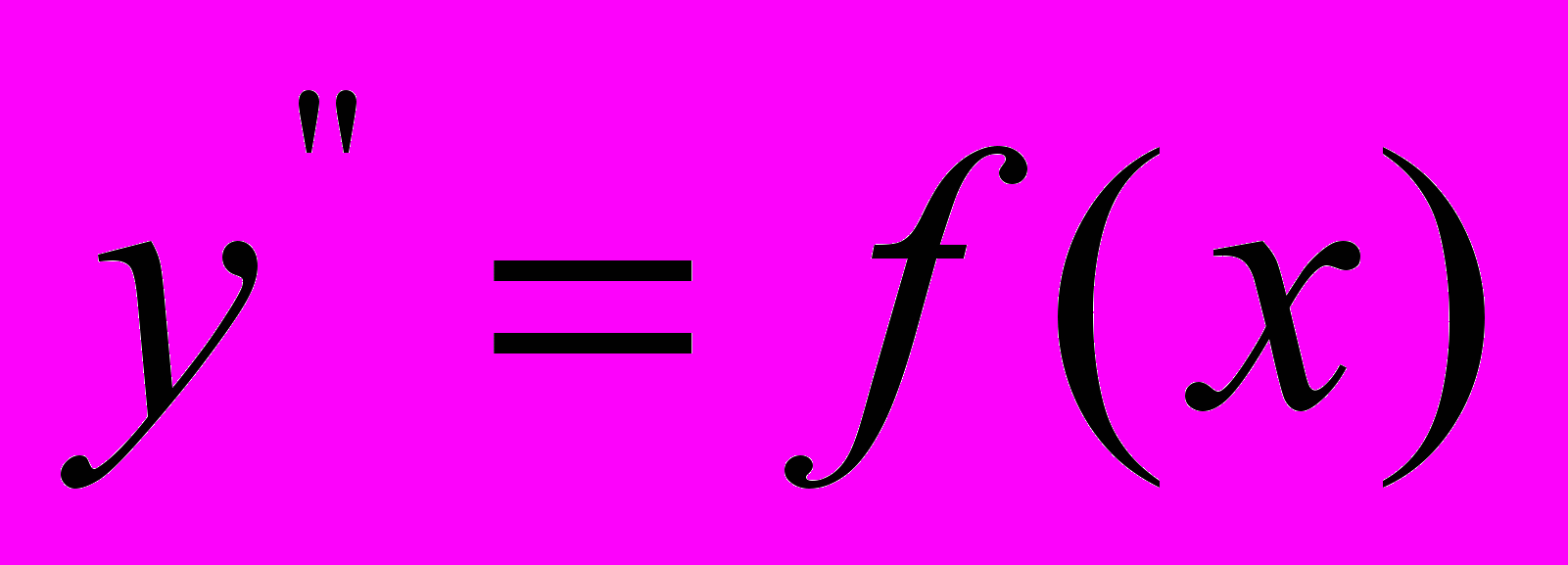, , 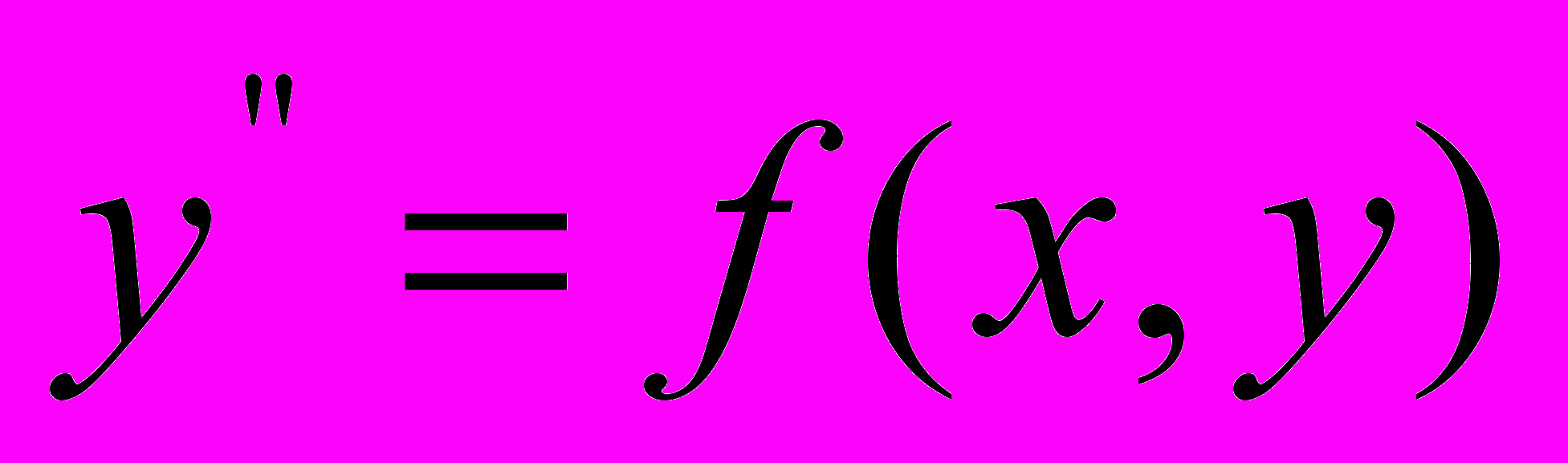, 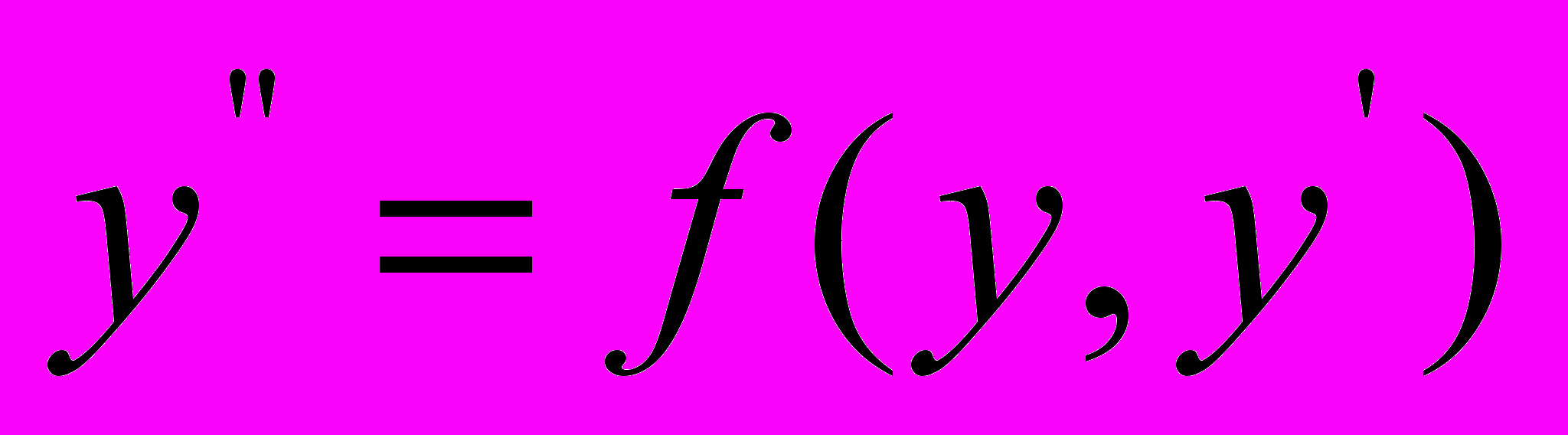методы их решения. Линейные дифференциальные уравнения (однородные, неоднородные, с постоянными коэффициентами). Приложение линейных дифференциальных уравнений к описанию линейных моделей в экономике. Понятие о разностных уравнениях и их применение при анализе динамических экономических процессов.


III семестр


Тема 12. Введение. Понятие о вероятности.

Предмет теории вероятностей. Необходимость применения вероятностных методов в экономике.


Тема 13. Элементы комбинаторики.

Общие правила комбинаторики. Выборка. Перестановки, сочетания, размещения без повторений и с повторениями.


Тема 14. Случайные события. Частота и вероятность.

Определение случайного события. Виды событий. Действия над событиями. Частота и вероятность. Классическое определение вероятности. Вычисление вероятностей с использованием комбинаторных схем.


Тема 15. Основные формулы для вычисления вероятностей.

Теоремы сложения вероятностей для совместных и несовместных событий. Условная вероятность. Теоремы умножения вероятностей для зависимых и независимых событий. Формула полной вероятности и формула Байеса. Повторение испытаний. Формула Бернулли.


Тема 16. Случайные величины.

Понятие случайной величины. Понятие распределения вероятностей случайных величин. Дискретные случайные величины и способы их задания. Ряд распределения дискретной случайной величины. Непрерывные случайные величины. Функция распределения случайной величины и ее свойства. Вероятность попадания на заданный интервал. Плотность распределения вероятностей и ее свойства.


Тема 17. Числовые характеристики случайных величин.

Числовые характеристики дискретных случайных величин: математическое ожидание, дисперсия, среднее квадратическое отклонение. Числовые характеристики непрерывных случайных величин: математическое ожидание, дисперсия, среднее квадратическое отклонение. Свойства числовых характеристик.


Тема 18. Основные законы распределения. Нормальный закон распределения.

Основные законы распределения дискретных случайных величин: биномиальное, пуассоновское, геометрическое. Основные законы распределения непрерывных случайных величин: равномерное, показательное нормальное распределения. Функция Лапласа и ее свойства. Вычисление вероятности попадания случайной величины, распределенной по нормальному закону, на заданный интервал. Правило трех .


Тема 19. Системы случайных величин. Корреляция и регрессия.

Многомерные случайные величины. Функция распределения систем случайных величин. Условные законы распределения. Числовые характеристики системы случайных величин. Коэффициент регрессии. Матрица ковариаций. Функции от случайных величин. Корреляции связи в экономике.


Тема 20. Закон больших чисел.

Понятие закона больших чисел и его место в изучении статистических закономерностей в экономке. Примеры действия закона больших чисел. Понятие сходимости по вероятности. Содержательных смысл предельных теорем теории вероятностей. Неравенство Чебышева. Теорема Маркова, Теорема Бернулли, Теорема Пуассона. Содержательный смысл центральной предельной теоремы. Предельные теоремы Муавра-Лапласа. Теорема Колмогорова. Теорема Ляпунова.


Тема 21. Математическая статистика. Генеральная совокупность и выборка.

Предмет математической статистики. Связь математической статистики с теорией вероятностей. Генеральная совокупность и выборка. Способы отбора. Выборочное распределение. Вариационный ряд, его характеристики и графическое изображение. Гистограмма. Полигон. Выборочный аналог функции распределения - и ее свойства. Числовые характеристики выборочного распределения: выборочное среднее, выборочная дисперсия, медиана.


Тема 22. Статистические методы оценки параметров.

Постановка задач. Классификация оценок. Свойства оценок: состоятельность, несмещенность, эффективность. Точечные методы оценки параметров распределения. Метод моментов. Метод максимального правдоподобия. Метод наименьших квадратов. Интервальное оценивание параметров распределения. Доверительный интервал.


Тема 23. Проверка статистических гипотез.

Описание гипотез. Простые и сложные гипотезы. Нулевая и конкурирующая гипотезы. Проверка гипотез о законах распределения. Проверка гипотез и доверительные интервалы. Проверка гипотез о равенстве дисперсий. Критерий согласия.


IV семестр


Тема 24. Предмет дисциплины. Понятие модели.

Понятие модели. Классификация моделей. Математическая модель.


Тема 25. Линейное программирование (ЛП).

Обзор областей применения ЛП. Построение математических моделей простейших экономических задач. Общая и основная задача линейного программирования (ЗЛП). Графический метод решения ЗЛП. Симплекс-метод решения ЗЛП. Построение опорных планов. Отыскание оптимального плана. Условия оптимальности. Симплекс-таблицы.

Двойственность в ЛП. Экономическая интерпретация двойственности. Составление двойственных задач. Нахождение решений с помощью теорем двойственности.


Тема 26. Транспортная (ТЗ) ЗЛП.

Закрытая и открытая транспортные задачи. Метод северо-западного угла, метод наименьших затрат. Метод потенциалов. Условия оптимальности.


Тема 27. Целочисленное программирование (ЦП).

Обзор методов ЦП: графический метод, метод отсечения (метод Гомори), метод ветвей и границ.


Тема 28. Динамическое программирование.

Основные понятия, постановка задачи. Геометрическая интерпретация ЗДП. Принцип поэтапного построения оптимального управления и рекуррентные соотношения Беллмана. Математическая теория оптимального управления.


Тема 29. Элементы теории игр.

Матричные игры. Кооперативные игры. Игры с природой.


Тема 30. Элементы теории графов и сетевого планирования.

Плоские графы. Эйлеровы графы. Гамильтоновы графы. Орграфы. Сетевые графики. Сети Петри.


Тема 31. Элементы теории массового облуживания (ТМО).

Марковские процессы. Задачи анализа замкнутых и разомкнутых систем массового обслуживания.

Тема 32. Экономико-математические модели

Функция полезности. Кривые безразличия. Функции спроса. Уравнение Слуцкого. Кривые «доход-потребление», кривые «цены-потребление». Коэффициенты эластичности. Материальные балансы. Функции выпуска продукции. Производственные функции затрат ресурсов. Модели поведения фирмы в условиях совершенной и несовершенной конкуренции. Модели общего экономического равновесия. Модель Эрроу-Гурвица. Статистическая и динамическая модель межотраслевого баланса.Общие модели развития экономики. Модель Солоу.

ТЕМЫ ПРАКТИЧЕСКИХ ЗАНЯТИЙ


I семестр


Тема 1. Множества. Элементы высшей алгебры – 4 часа.

Занятие № 1. Операции над множествами. Числовые множества. Модуль действительного числа. [1], [5].

Занятие № 2. Комплексные числа. Геометрический смысл комплексного числа. Тригонометрическая и показательная форма комплексного числа. Операции над комплексными числами. Формула Муавра. Извлечение корня. [1], [5].


Тема 2. Элементы линейной и векторной алгебры - 10 часов.

Занятие № 3. Действия над матрицами. Вычисление определений n-го порядка («обнуление», разложение по строке (столбцу). [1], [5].

Занятие № 4. Нахождение обратной матрицы. Нахождение ранга матрицы. Решение экономических задач с использованием матриц. [1], [5].

Занятие № 5. Решение систем линейных уравнений тремя методами (Метод Крамера, метод обратной матрицы, метод Гаусса). [1], [5].

Занятие № 7. Векторы. Линейные операции над векторами. Разложение вектора по базису. Вычисление скалярного, векторного, смешанного производства. Нахождение собственных векторов и собственных значений матрицы. [1], [5].

Занятие № 8. Модель Леонтьева межотраслевого баланса. Линейная модель обмена (модуль международной торговли). [1], [5]


Тема 3. Аналитическая геометрия на плоскости и в пространстве.

Кривые 2го порядка - 6 часов

Занятия № 9, 10. Решение задач на прямую плоскость (уравнение, условие параллельности, перпендикулярности, расстояние от точки до прямой). [1], [5].

Занятие № 11. Кривые 2-го порядка. [1], [5].


Тема 4. Введение в математический анализ. Пределы и непрерывность – 6 часов

Занятие № 12. Вычисление пределов числовых последовательностей. [1], [5].

Занятие № 13. Вычисление пределов функций. 1-й и 2-й замечательные пределы. [1], [5].

Занятие № 14. Исследование функций на непрерывность. [1], [5].

Тема 5. Дифференциальное исчисление. Производная. Приложения


производной. Дифференциал функции – 6 часов

Занятие № 15. Нахождение производных сумм разности произведения, частного, сложных функций. [1], [5].

Занятие № 16. Построение графиков функций, используя общую схему исследования функций. [1], [5].

Занятие № 17. Решение экономических задач, используя понятие производной. [1], [5].


II семестр


Тема 6. Неопределенный интеграл – 6 часов

Занятие № 18. Неопределенный интеграл и его свойства. Интегрирование методом разложения. Замена переменной в неопределенном интеграле. [1], [5].

Занятие № 19. Метод интегрирования по частям. Интегрирование рациональных функций. [1], [5].

Занятие № 20. Интегрирование иррациональных функций, тригонометрических функций. [1], [5].


Тема 7. Определенный интеграл – 6 часов

Занятие № 21. Формула Ньютона-Лейбница. Замена переменной в определенном интеграле, интегрирование по частям. [1], [5].

Занятие № 22. Приближенные методы интегрирования. [1], [5].

Занятие № 23. Приложение определенного интеграла. Использование определенного интеграла. Использование определенного интеграла в экономике. [1], [5].


Тема 8. Несобственные интегралы – 2 часа

Занятие № 24. Несобственный интеграл 1-го и 2-го рода. Признаки сходимости. [1], [5].


Тема 9. Функции многих переменных – 6 часов

Занятие № 25. Область определения ФНП. График. Линии уровня. [1], [5].

Занятие № 26. Частные производные. Производные по направлению. Градиент. Частные производные высших порядков. [1], [5].

Занятие № 27. Экстремумы функции дву4х переменных. Необходимое условие экстремума. Достаточное условие экстремума. Наибольшее и наименьшее значение функции. [1], [5].


Тема 10. Ряды. Числовые ряды. Степенные ряды – 6 часов

Занятие № 28. Признаки сходимости рядов с положительными членами. [1], [5].

Занятие № 29.Знакопеременные ряды. Теорема Лейбница. [1], [5].

Занятие № 30. Разложение функций в степенные ряды. Применение рядов в приближенных вычислениях. [1], [5].


Тема 11. Дифференциальные уравнения – 6 часов

Занятие № 31. Уравнение с разделяющими переменными. Однородные уравнения. [1], [5].

Занятие № 32. Линейные дифференциальные уравнения 1-го порядка. [1], [5].

Занятие № 33. Линейные дифференциальные уравнения 2-го порядка с постоянными коэффициентами. [1], [5].

III семестр


Тема 13. Элементы комбинаторики. -2 часа

Занятие № 34. Элементы комбинаторики. [2], [4], [5].


Тема 14. Случайные события и операции над ними. Частота и вероятность. -2 час

Занятие №35. Вычисление вероятностей по классической формуле (подсчет) с использованием комбинаторных схем. [2], [4], [5].


Тема 15. Основные формулы для вычисления вероятностей. – 4 часа

Занятие № 36. Теоремы сложения и умножения вероятностей. Условная вероятность. Формула полной вероятности, формула Байеса. [2], [4], [5].

Занятие № 37. Повторение испытаний. Формула Бернулли. [2], [4], [5].


Тема 16. Случайные величины. -4 часа

Занятие № 38. Дискретные случайные величины. Ряд распределения. [2], [4], [5].

Занятие № 39. Непрерывные случайные величины. Функция распределения. Плотность распределения. Вероятность попадания на заданный интервал. [2], [4], [5].


Тема 17. Числовые характеристики случайных величин. – 4 часа

Занятие № 40. Математическое ожидание и дисперсия дискретных случайных величин. [2], [4], [5].

Занятие № 41. Математическое ожидание и дисперсия непрерывных случайных величин. [2], [4], [5].


Тема 18. Основные законы распределения. Нормальный закон распределения – 4 часа

Занятие №42. Основные законы распределение. Равномерный, показательный, нормальный. [2], [4], [5].

Занятие № 43. Нормальное распределение. Функция Лапласа. Правило трех . [2], [4], [5].


Тема 20. Системы случайных величин. Корреляция и регрессия. – 4 часа.

Занятие № 44. Закон распределения системы двух случайных величин. [2], [4], [5].

Занятие № 45. Корреляция и регрессия. [2], [4], [5].


Тема 21. Математическая статистика. Генеральная совокупность и выборка.-4 часа

Занятие № 46-47. Генеральная совокупность и выборка. Числовые характеристики выборочного распределения. [2], [4], [5].


Тема 22. Статистические методы оценки параметров. -4 часа

Занятие № 48-49. Статистические методы оценки параметров. Метод наименьших квадратов. Доверительный интервал. [2], [4], [5].


Тема 23. Проверка статистических гипотез. -2 часа

Занятие № 50. Проверка статистических гипотез. [2], [4], [5].


IV семестр


Тема 24. Предмет дисциплины. Понятие модели. -2 часа

Занятие №51 Построение математических моделей простейших экономических задач. [3], [5].


Тема 25. Линейное программирование (ЛП).-8 часа

Занятие №52 Графический метод решения ЗЛП. [3], [5].

Занятие №53-54. Симплекс-метод решения ЗЛП. Симплекс-таблицы. [3], [5].

Занятие №55. Двойственность в ЛП. Составление двойственных задач. Нахождение решений с помощью теорем двойственности. [3], [5].


Тема 26. Транспортная ЗЛП – 4 часа

Занятие № 56-57. Решение транспортных задач. [3], [5].


Тема 28. Динамическое программирование -2 часа

Занятие №58. Построение оптимального управления с помощью рекуррентных соотношений Беллмана. [3], [5].


Тема 29. Элементы теории игр. – 6 час

Занятие № 59 Матричные игры. [3], [5].

Занятие № 60 Кооперативные игры. [3], [5].

Занятие № 61. Игры с природой[3], [5].


Тема 30. Элементы теории графов и сетевого планирования.- 4 часа

Занятие № 62 Плоские графы. Эйлеровы графы. Гамильтоновы графы. Орграфы. [3], [5].

Занятие № 63. Сетевые графики. [3], [5].


Тема 31. Марковские процессы. Задачи анализа замкнутых и разомкнутых систем массового обслуживания. – 4 часа

Занятие № 64. Марковские процессы. [3], [5].

Занятие № 65. Задачи анализа замкнутых и разомкнутых систем массового обслуживания.


Тема 32. Специальные экономико-математические модели – 2часа

Занятие № 66. Модель Леонтьева. [3], [5].


Темы практических занятий (З/о)


Установочная сессия

Занятие № 1. Матрицы и определители. Решение систем линейных уравнений – 2 часа, [1], [5].

Занятие № 2. Элементы аналитической геометрии – 2 часа, [1], [5].

Занятие № 3. Последовательности. Предел последовательности. Предел функций – 2 часа, [1], [5].

Занятие № 4. Дифференциальное исчисление. Исследование функций – 2 часа, [1], [5].


1 семестр

Занятие № 1. Неопределенный интеграл – 2 часа, [1], [5].

Занятие № 2. Определенный интеграл. Функции нескольких переменных – 2 часа, [1], [5].

Занятие № 3. Ряды. Числовые ряды. Степенные ряды – 2 часа, [1], [5].

Занятие № 4. Дифференциальные уравнения – 2 часа, [1], [5].


2 семестр

Занятие № 1. Основные понятия теории вероятностей – 2 часа. [2], [4], [5].

Занятие № 2. Основные теоремы теории вероятностей – 2 часа. [2], [4], [5].

Занятие № 3. Числовые характеристики случайных величин – 2 часа. [2], [4], [5].

Занятие № 4. Основные законы распределения случайных величин – 2 часа. [2], [4], [5].


Вопросы к зачету (1 семестр)

  1. Общее понятие матрицы. Определение квадратной, треугольной, диагональной, единичной матриц.
  2. Определитель и его свойства.
  3. Схемы вычисления определителей матриц второго и третьего порядка.
  4. Обратная матрица. Методы её вычисления.
  5. Связь обратимости матрицы со значением её определителя. Свойства обратной матрицы.
  6. Определение решения системы линейных уравнений с постоянными коэффициентами. Эквивалентные системы уравнений.
  7. Совместная, несовместная, определённая и неопределённая система.
  8. Методы решения систем.
  9. Ранг матрицы его связь с разрешимостью системы линейных уравнений с постоянными коэффициентами.
  10. Линейная зависимость и независимость строк (столбцов) матрицы. Связь с рангом матрицы числа линейно независимых её строк (столбцов).
  11. Собственные значения и собственные вектора квадратной матрицы.
  12. Определение ортогональной, симметричной и приводимой к диагональному виду матрицы.
  13. Квадратичная форма и её канонический вид. Приводимость квадратичной формы к каноническому виду.
  14. Определённость знака квадратичной формы. Критерии определённости знака квадратичной формы.
  15. Уравнения прямой на плоскости.
  16. Признак параллельности и перпендикулярности двух прямых на плоскости. Расстояние от точки до прямой.
  17. Общее уравнение кривой второго порядка на плоскости. Канонические уравнения окружности, эллипса, гиперболы, параболы. Основные характеристики этих кривых.
  18. Предел функции. Бесконечно большие и бесконечно малые величины их свойства.
  19. Первый и второй замечательные пределы.
  20. Раскрытие неопределённостей , , ?
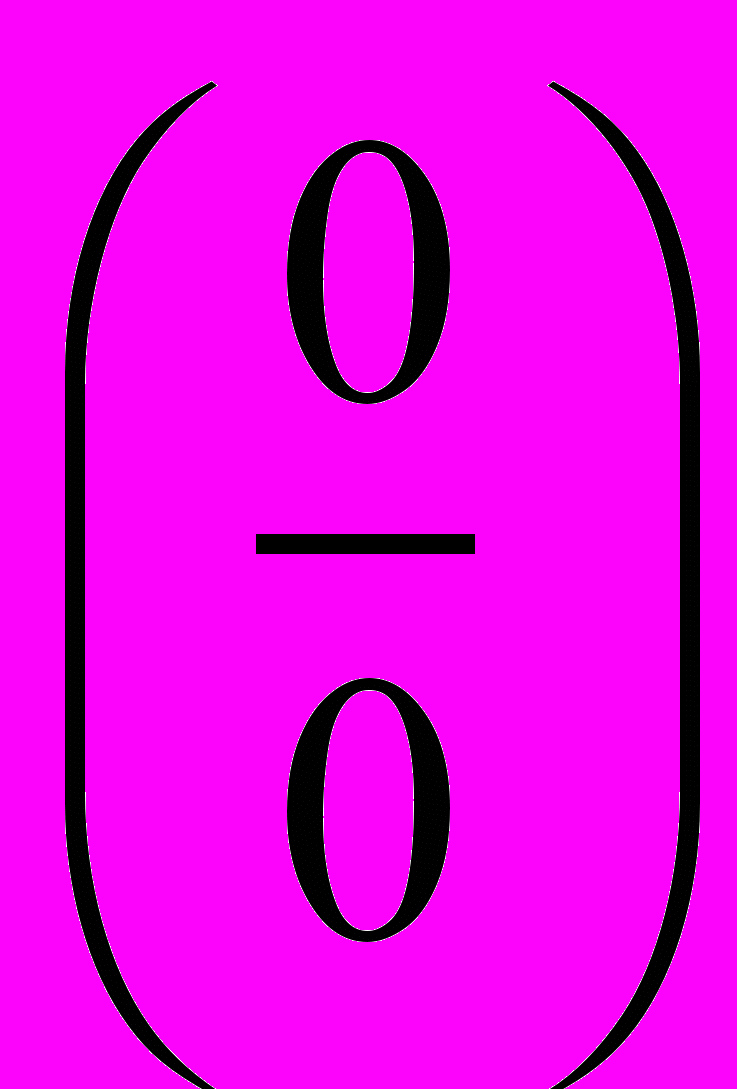  21. Односторонние пределы, их связь с двусторонним пределом.
  22. Теоремы о неравенствах в пределе.
  23. Определение непрерывности функции в точке и на промежутке. Свойства непрерывных функций.
  24. Точки разрыва функции и их классификация.
  25. Определение производной функции в точке и дифференцируемости функции на промежутке, основные правила дифференцирования.
  26. Теорема о связи дифференцируемости и непрерывности функции.
  27. Теорема о достаточном условии монотонности функции.
  28. Определение выпуклости функции на промежутке и точки перегиба графика функции. Теорема о достаточном условии выпуклости функции.
  29. Экстремум и критические точки функции. Теоремы об экстремуме дифференцируемой функции.
  30. Асимптоты графика функции. Теоремы о вертикальной, горизонтальной и наклонной асимптотах.



Вопросы к экзамену (2 семестр)

  1. Определение первообразной функции. Теорема о числе первообразных и о связи между ними.
  2. Определение неопределённого интеграла и его свойства.
  3. Основные методы интегрирования. Интегрирование разложением.
  4. Метод интегрирования по частям.
  5. Интегрирование заменой переменных.
  6. Разложение рациональных дробей
  7. Интегрирование рациональных дробей.
  8. Интегрирование тригонометрических функций.
  9. Интегрирование иррациональных выражений.
  10. Определение и основные свойства определённого интеграла.
  11. Теорема о вычислении площади фигуры, заключённой между графиками двух функций на .
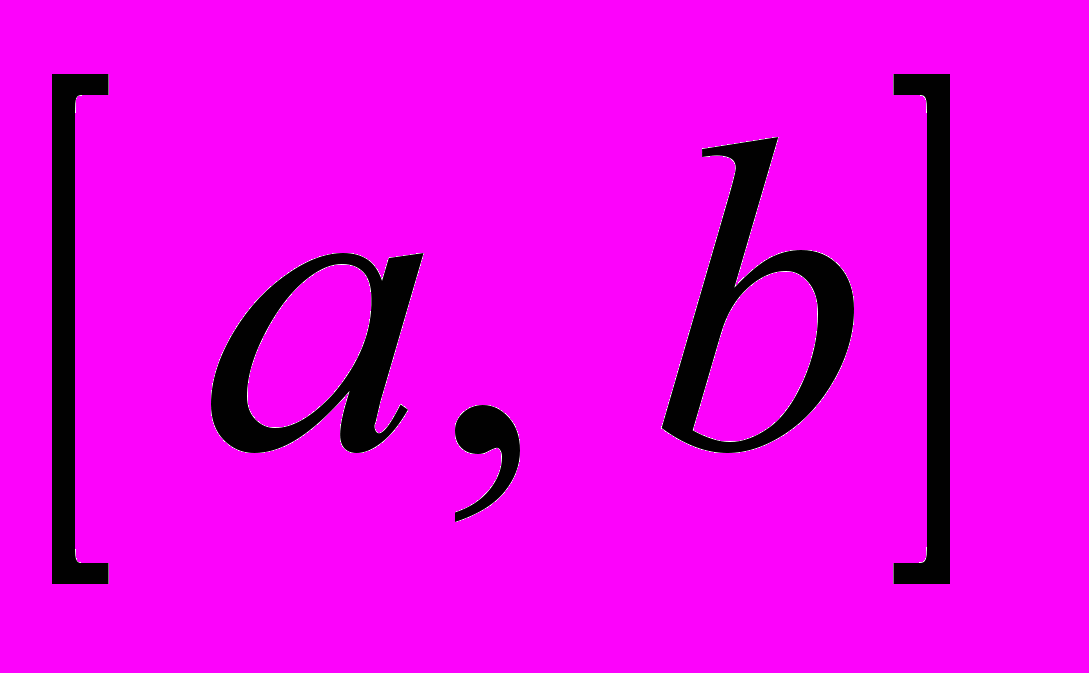  12. Вычисление объёмов тел вращения и длин дуг плоских кривых.
  13. Несобственные интегралы функций на неограниченном промежутке.
  14. Несобственные интегралы от неограниченных функций.
  15. Сходимость несобственных интегралов. Признаки сходимость.
  16. Дифференциальные уравнения (ДУ), порядок ДУ, начальное условие для ДУ, задача Коши.
  17. Дифференциальных уравнения интегрируемого типа.
  18. Определение уравнения с разделяющимися переменными и его решение.
  19. Определение однородного уравнения и его решение.
  20. Определение линейного уравнения и уравнения Бернулли, их решения.
  21. ДУ допускающие понижение порядка.
  22. Определение линейных ДУ с постоянными коэффициентами. Характеристические уравнения. Однородное и неоднородное ДУ второго порядка.
  23. Связь общего решения однородного линейного ДУ с постоянными коэффициентами с решениями характеристического.
  24. Метод неопределённых коэффициентов.
  25. Метод вариации произвольных постоянных.
  26. Определение ряда, сходящегося ряда, суммы ряда.
  27. Специальные примеры числовых рядов и их сходимость.
  28. Знакоположительные ряды и признаки их сходимости.
  29. Знакопеременные ряды и признаки их сходимости.
  30. Функциональные ряды и область его сходимости.
  31. Степенные ряды. Радиус их сходимости. Формулы вычисления радиуса сходимости.
  32. Разложение функций в ряд Маклорена и Тейлора.



Вопросы к зачету (3 семестр)

  1. Предмет теории вероятностей.
  2. Элементы комбинаторики. Перестановки, сочетания, размещения без повторений и с повторениями.
  3. События и операции над ними.
  4. Классическое, статистическое и геометрическое определение вероятности.
  5. Теоремы сложения вероятностей для совместных и несовместных событий.
  6. Условная вероятность. Теоремы умножения вероятностей.
  7. Формула полной вероятности и формула Байеса.
  8. Повторение испытаний. Формула Бернулли.
  9. Понятие случайной величины. Распределения вероятностей случайных величин.
  10. Дискретные случайные величины. Функция распределения и плотность вероятностей.
  11. Непрерывные случайные величины. Функция распределения и плотность вероятностей.
  12. Математическое ожидание и дисперсия дискретных и непрерывных случайных величин.
  13. Равномерное распределение и распределение Пуассона.
  14. Нормальное распределение.
  15. Локальная и интегральная теорема Лапласа.
  16. Геометрическое распределение. Показательное распределение.
  17. Система случайных величин. Функция распределения систем СВ.
  18. Числовые характеристики системы СВ. Коэффициент корреляции. Коэффициент регрессии.
  19. Закон больших чисел.
  20. Статистическое описание результатов наблюдений.
  21. Графические представления выборки.
  22. Точечные оценки параметров распределения.
  23. Метод максимального правдоподобия.
  24. Метод наименьших квадратов.
  25. Интервальное оценивание параметров распределения.
  26. Проверка статистических гипотез.
  27. Проверка гипотез о законах распределения.
  28. Проверка гипотез о равенстве и дисперсий.


Вопросы к экзамену (4 семестр)

  1. Постановка задачи линейного программирования (ЗЛП). Общая и основная ЗЛП.
  2. Понятие модели. Классификация моделей. Экономико-математическая модель.
  3. Задача о составлении рациона питания.
  4. Геометрический метод решения ЗЛП.
  5. Симплексный метод (пошаговый) решения ЗЛП. Пример. Критерий оптимальности.
  6. Симплекс-таблицы. Критерий оптимальности.
  7. Метод искусственного базиса.
  8. Обзор экономических задач, сводящихся к ЗЛП.
  9. Двойственные задачи. Экономическая интерпретация.
  10. Свойства взаимно-двойственных задач. Алгоритм составления двойственных задач.
  11. Теоремы двойственности.
  12. Нахождение решения ЗЛП с помощью теорем двойственности.
  13. Транспортная задача. (ТЗ). Основные понятия. Закрытая и открытая модели ТЗ.
  14. ТЗ. Нахождение первого опорного решения методом «северо-западного угла» (на примере).
  15. ТЗ. Нахождение первого опорного решения методом «наименьших затрат» (на примере).
  16. ТЗ. Метод потенциалов. Критерий оптимальности.
  17. ТЗ. Алгоритм решения ТЗ. Критерий оптимальности.
  18. Целочисленное программирование (ЦП). Методы решения ЗЦП.
  19. Динамическое программирование (ДП). Основные понятия.
  20. ДП. Принцип оптимальности. Уравнения Беллмана.
  21. ДП. Решение задачи об оптимальности распределении ресурсов между двумя отраслями производства на несколько лет.
  22. ДП. Решение задачи определения оптимальной траектории.
  23. Игра как модель конфликтной ситуации. Виды игр.
  24. Понятие стратегии. Матрица игры. Пример.
  25. Верхняя цена игры, нижняя цена игры, седловая точка. Примеры.
  26. Принцип «минимакса». Минимаксная, максимальная стратегии.
  27. Решение игры в смешанных стратегиях.
  28. Основная теорема теории. Упрощение игры.
  29. Геометрический метод решения игры 2x2, 2xn, mx2.
  30. Игры «с природой». Матрица рисков.
  31. Основные критерии принятия решений в условиях неопределенности. Пример.
  32. Основные понятия теории графов.
  33. Матрицы, задающие графы.
  34. Эйлеровы и гамильтоновы графы.
  35. Применение графов в решении экономических задач: построение коммуникационной сети минимальной длины, задача определения кратчайшего пути, задача определения максимального потока.
  36. Сетевая модель. Построение сетевого графика.
  37. Системы массового обслуживания (СМО). Основные понятия.
  38. Случайные процессы. Марковский процесс. Потоки событий.
  39. Уравнения Колмогорова. Процесс «рождения-гибели».
  40. Экономические задачи, сводящиеся к марковским цепям.
  41. Производственные функции. Функция полезности.
  42. Моделирование спроса и предложения. Паутинообразная модель рынка.
  43. Понятие эластичности. Балансовые модели (модель Леонтьева).



Основная литература
  1. Кремер Н. Ш., Путко Б. А., Тришин И. М., Фридман М. Н. Высшая математика для экономистов. – М., Банки и биржи. ЮНИТИ, 1997.
  2. Кремер Н.Ш Теория вероятностей и математическая статистика. Учебник для вузов.-М.: ЮНИТА-ДАНА,2001
  3. Исследование операций в экономике: Учебн. пособие для вузов / Н.Ш.Кремер, Б.А. Путко, И.М.Тришин, М.Н.Фридман; Под ред. Проф. Н.Ш Кремера.- М.:ЮНИТИ,2001.-407с.
  4. Гмурман В. Е. Руководство к решению задач по теории вероятностей и математической статистике. – М., Высшая школа, 1979.
  5. Ермаков Р.К. и др. Сборник задач по высшей математике для экономистов. – М. ИНФРА-М, 2001.
  6. О.В.Авсеева, О.Н.Дикарева. Теория вероятностей и математическая статистика. Учебное пособие.- Воронеж, ВЭПИ,2007.
  7. О.Н.Дикарева, Г.А.Колупанова, Т.А.Самохина. Элементы теории множеств, линейной алгебры, аналитической геометрии, дифференцирование и исследование функций одной переменной. Методические указания- Воронеж, ВЭПИ, 2007.



Дополнительная литература
  1. Гмурман В. Е. Теория вероятностей и математическая статистика. – М., Высшая школа, 1972
  2. Красс А. С. Математика для экономических специальностей. – М., ЮНИТИ, 1998.
  3. Ермаков Р.К. и др. Общий курс высшей математики для экономистов. – М. ИНФРА-М, 2001.
  4. Бутузов В. Ф. И др. Математический анализ в вопросах и задачах. – М., Высшая школа. 1993.
  1. Давнис В. В., Дихачева Л. Н., Эйтингон В. Н. Модели макроэкономического равновесия. – Воронеж, Изд-во ВГУ, 1995.
  2. Коршунова Н. И., Пискунова В. С. Математика в экономике. – М. Вита Пресс, 1996.
  3. Лихолетов И. И., Мацкевич И. П. Руководство по решению задач по высшей математике, теории вероятностей и математической статистике. – Минск, Высшая школа, 1969.
  4. А. С. Солодовников, В. А. Юаюайцев, А. В. Брашлов. Математика в экономике. ч. I, ч. II, М., Финансы и статистика, 1999.
  5. П. Е. Данко, А. Г. Попов, Т. Я. Кожевникова. Высшая математика в упражнениях и задачах, ч. I, ч. II, М.,- Высшая школа, 1980.