Geum.ru

Вопросы к экзамену по дисциплине «Математика» для студентов

Вид материалаВопросы к экзамену
Подобный материал:
Теоретические вопросы к экзамену по дисциплине « Математика» для студентов
  1. курса очной формы обучения. ( 1 семестр )
  1. Вектора и действия над ними.
  2. Действия над векторами заданными в базисе.
  3. Уравнение прямой с угловым коэффициентом.
  4. Уравнение прямой, проходящей через точку в данном направлении.
  5. Уравнение прямой, проходящей через две точки.
  6. Общее уравнение прямой и его исследование.
  7. Угол между прямыми.
  8. Общее уравнение плоскости.
  9. Матрица. Действие над матрицами.
  10. Минор, алгебраическое дополнение. Ранг матрицы.
  11. Определитель. Свойства определителей.
  12. Способы вычисление определителей.
  13. Обратная матрица, нахождение обратной матрицы.
  14. Теорема Крамера.
  15. Метод Гаусса. Метод Жордано-Гаусса. Сходство и различие.
  16. Матричный способ решения систем линейных уравнений.
  17. В каком случае вектора называются линейно зависимыми и в каком – линейно -независимыми?
  18. Что называется базисом на прямой, на плоскости и в пространстве ?
  19. Формулы деления отрезка в данном отношении.
  20. Что называется векторным произведением двух векторов?
  21. Что называется смешанным произведением трех векторов?
  22. Уравнение плоскости, проходящей через три точки?
  23. Как вычисляются углы между двумя плоскостями и между прямой и плоскостью?
  24. Каковы канонические уравнения эллипса, гиперболы и параболы?
  25. Что называется комплексным числом? Как изображаются?
  26. Какие действия производятся над комплексными числами?
  27. Что называется алгебраической, тригонометрической и показательной формами записи комплексного числа?
  28. Что называется модулем и аргументом комплексного числа?
  29. Формула Муавра.
  30. Собственные значения и собственные векторы линейных операторов.


Математика 1 курс 1 семестр


1,. Вычислить определитель по формуле Сарруса


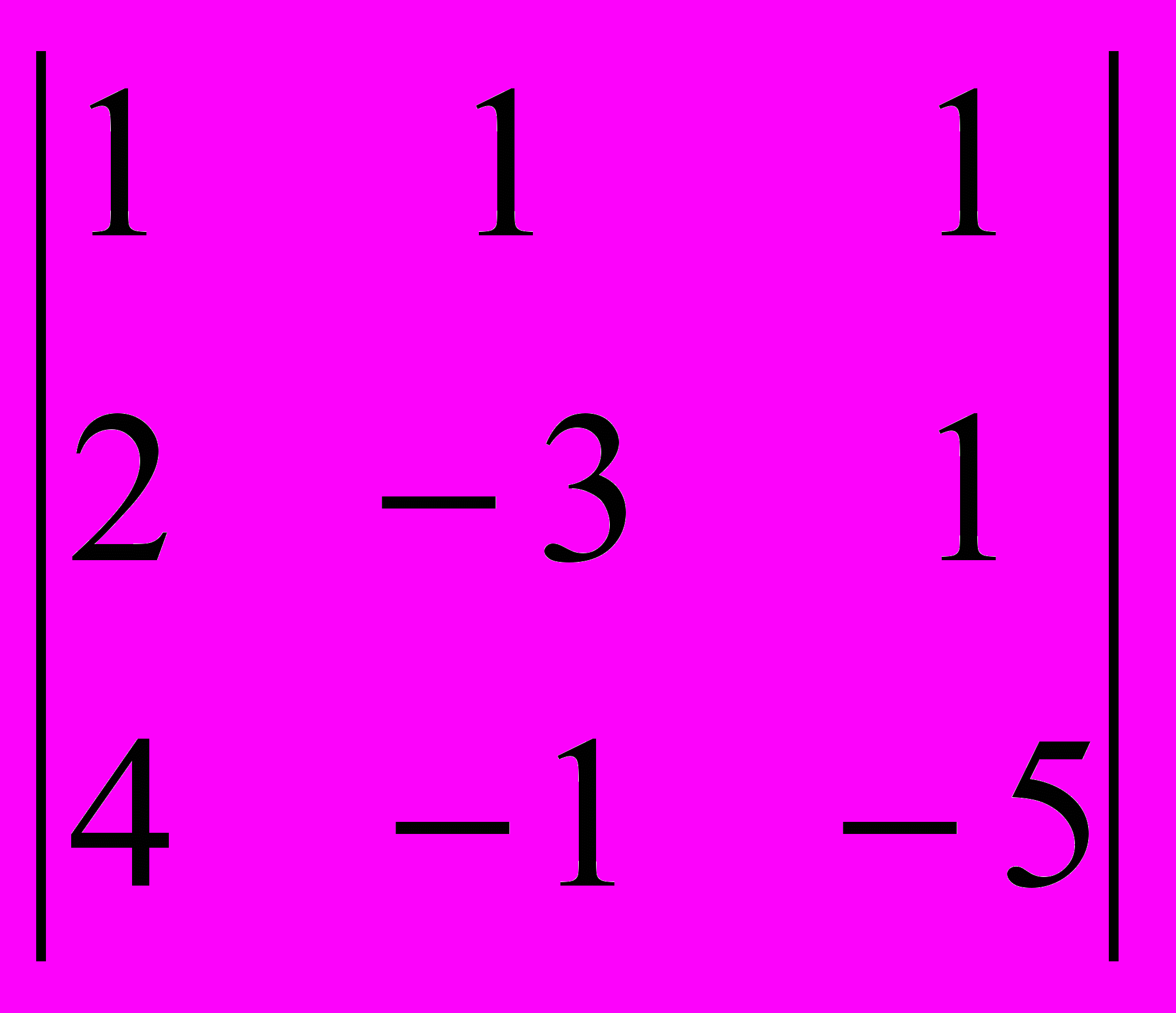
2. Вычислить определитель по формуле Лапласа:

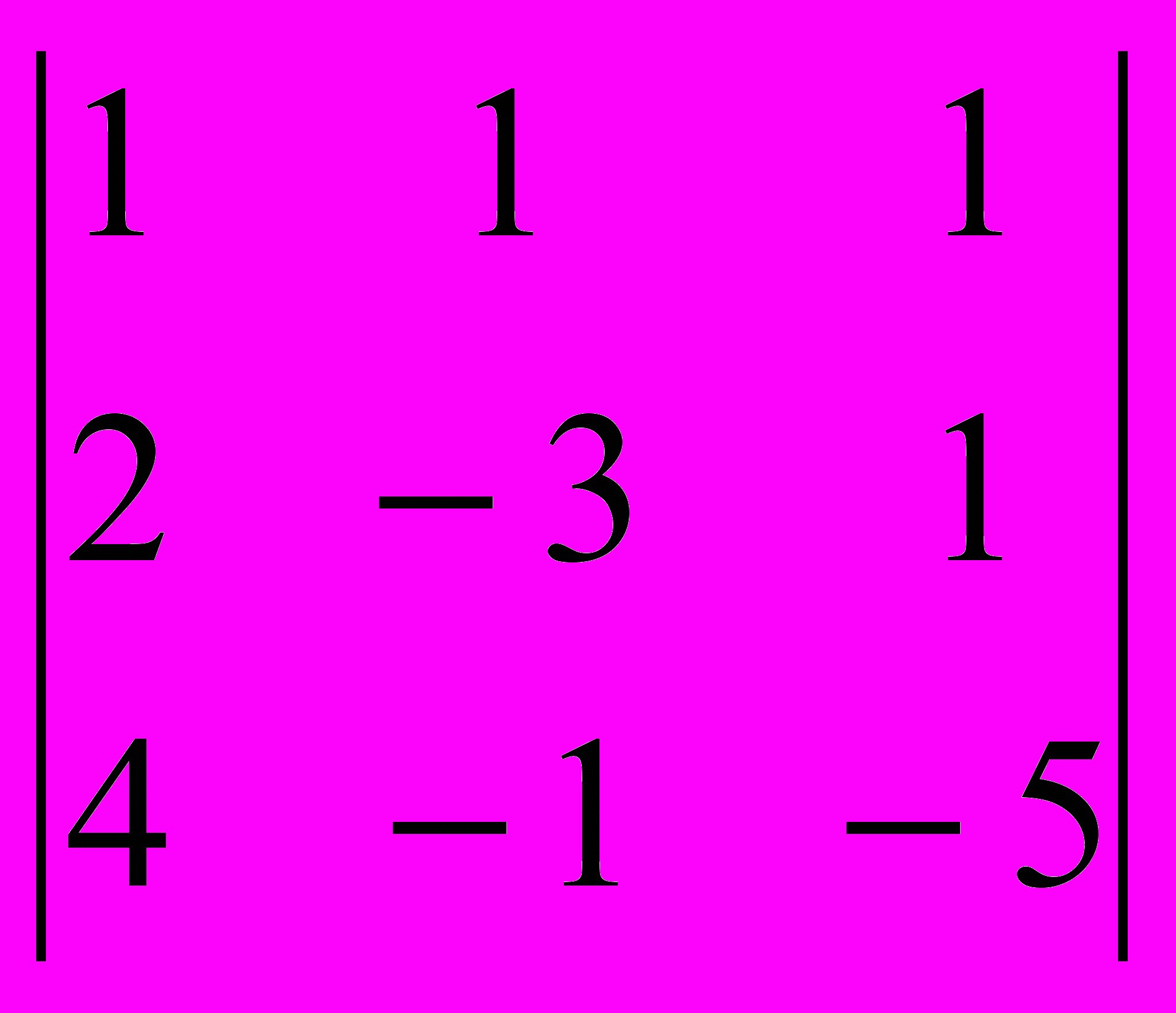
3. Найти обратную матрицу A-1,если A =

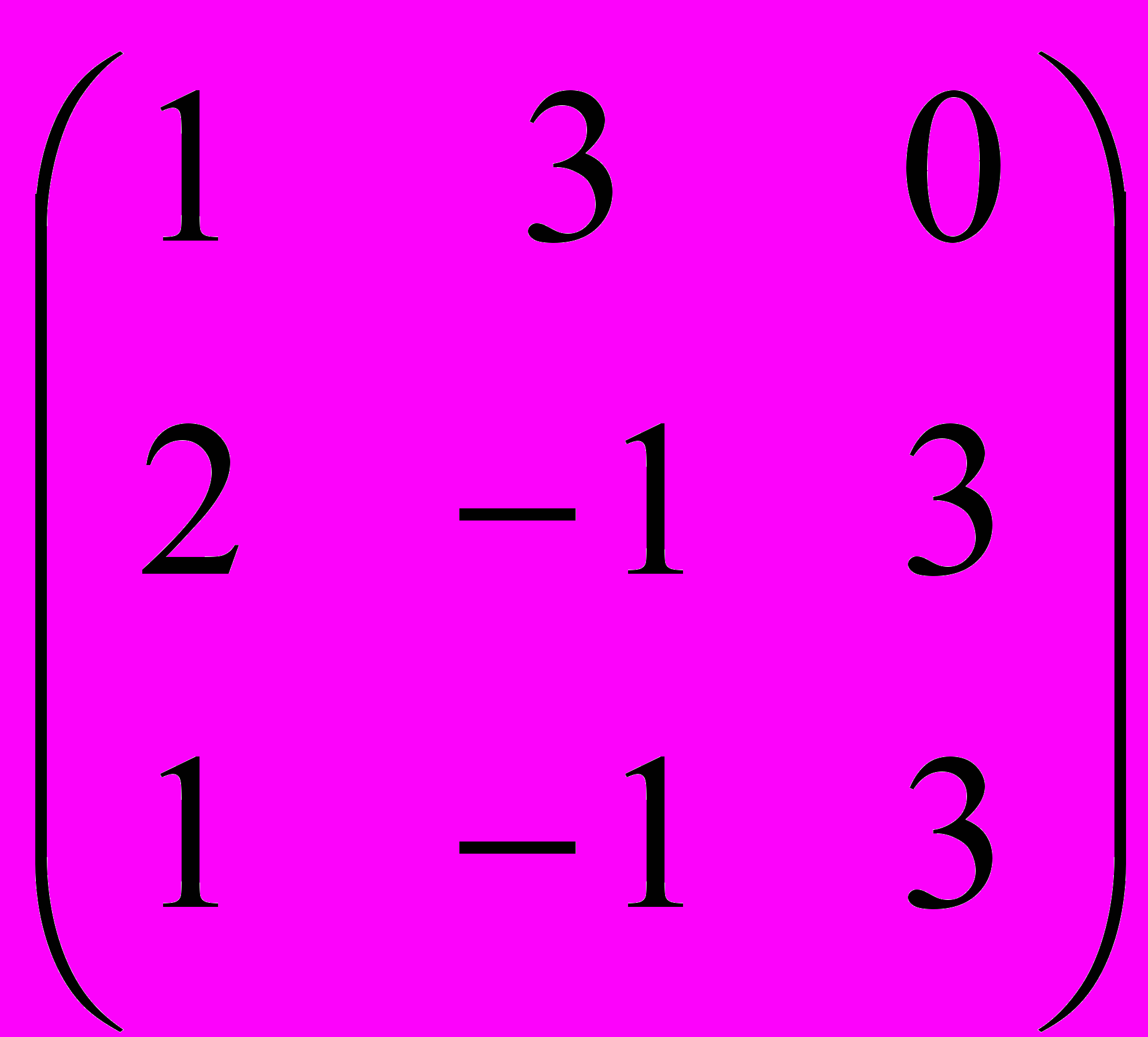
4. Решить систему методом Гаусса:


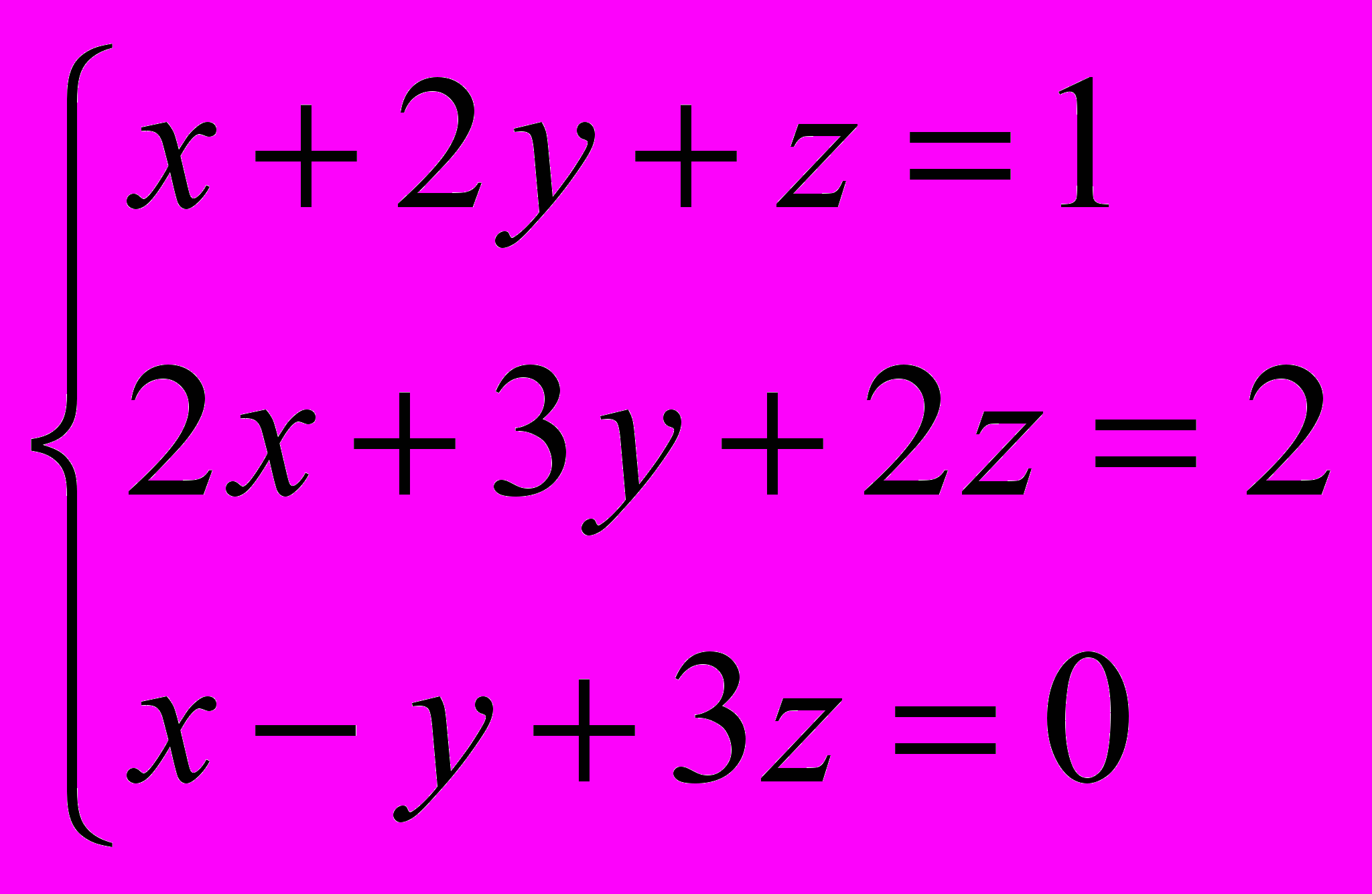
5. Решить систему методом Крамера:

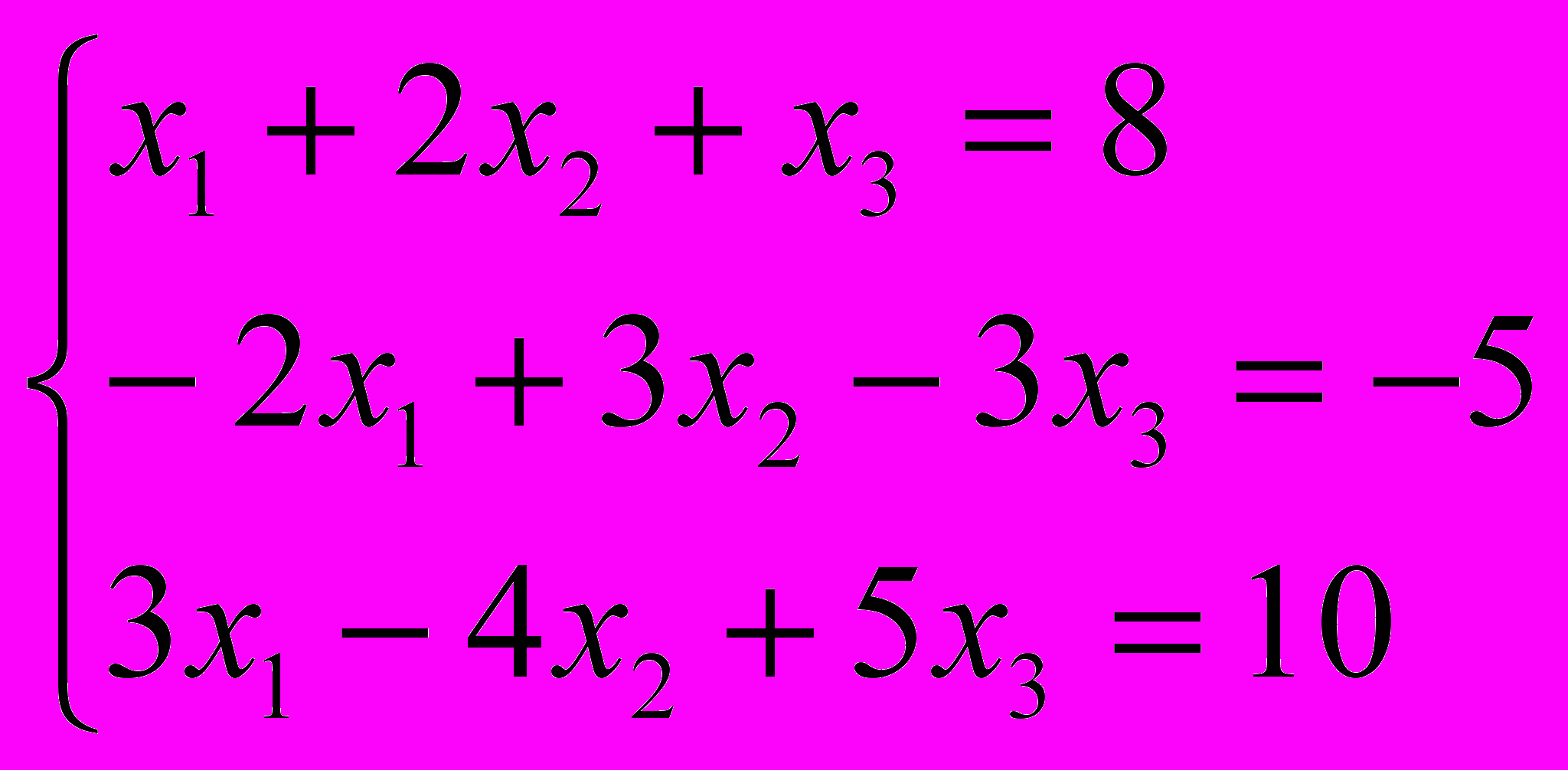
6. Найти сумму матриц A + B, если A = , B =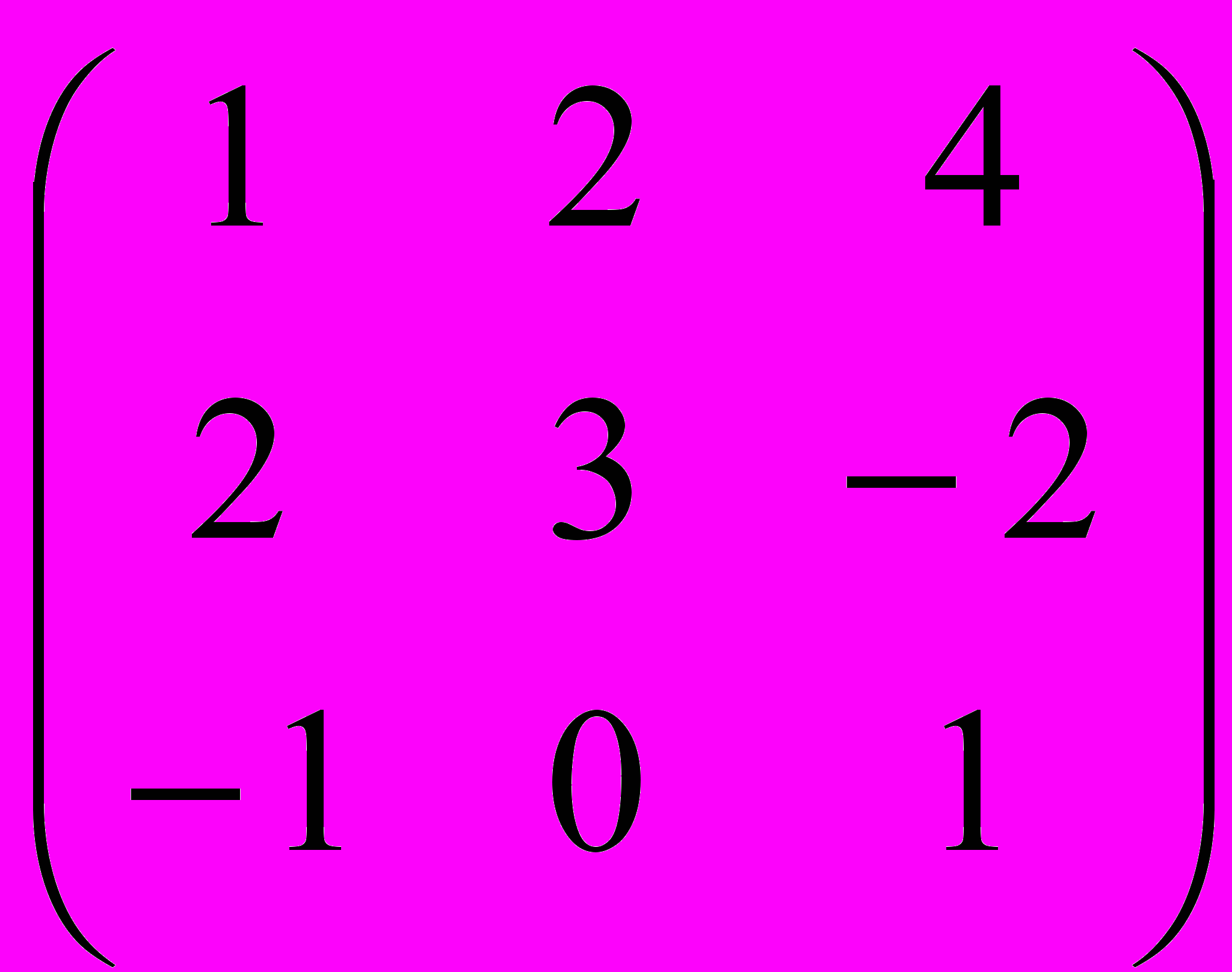

7. Вычислить:

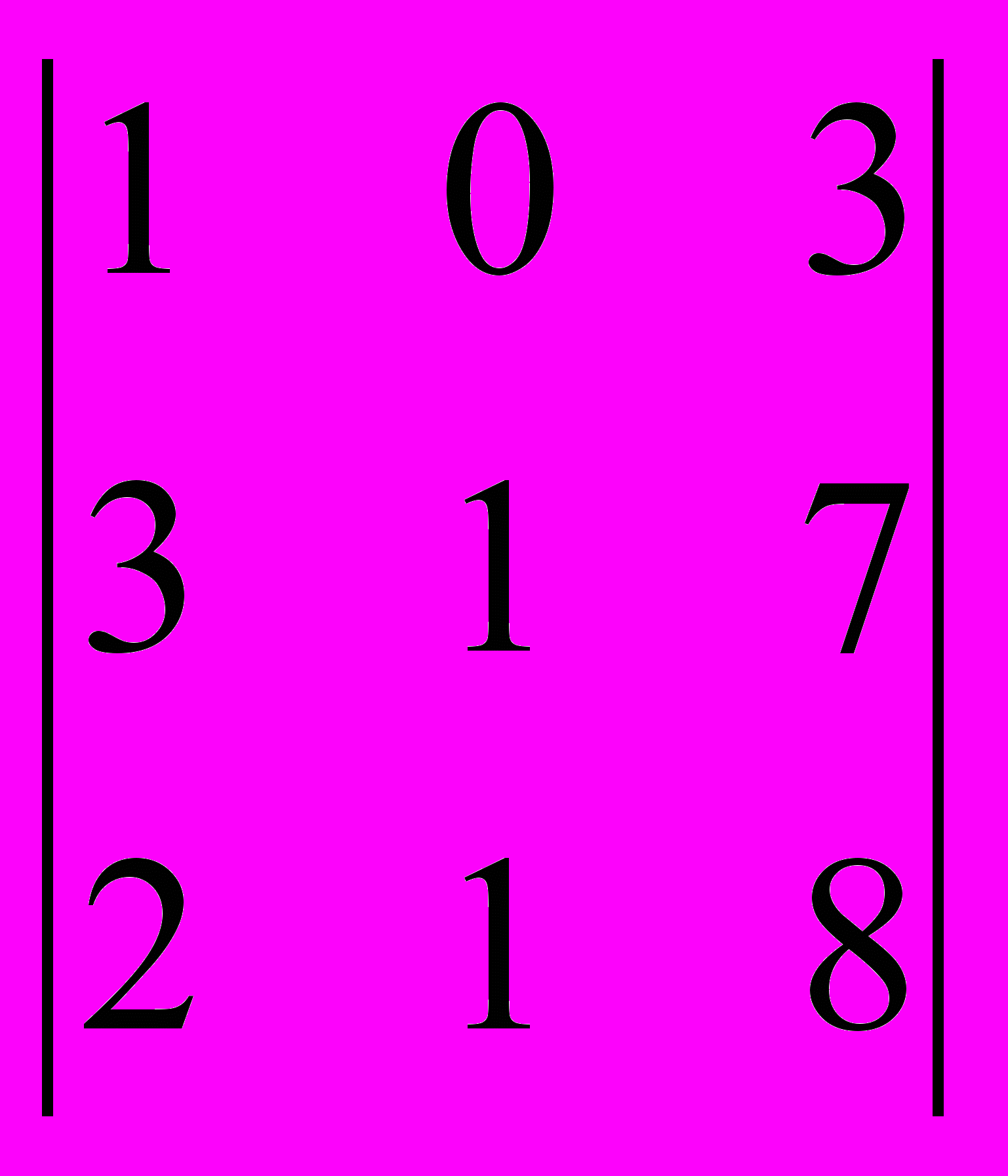
8. Найти матрицу В-1, если B =

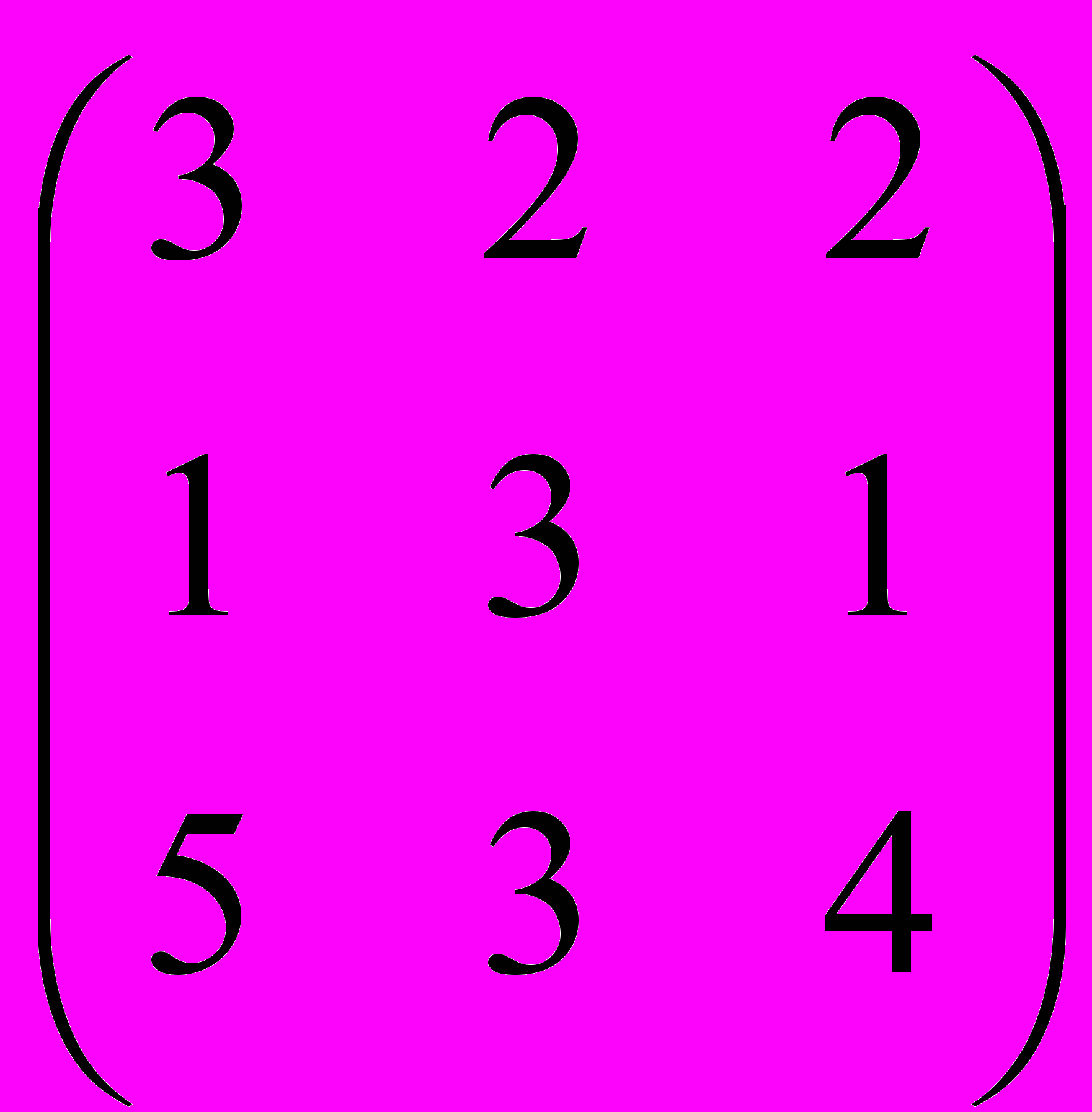
9. Найти матрицу: C = 2A – B, где A =, B =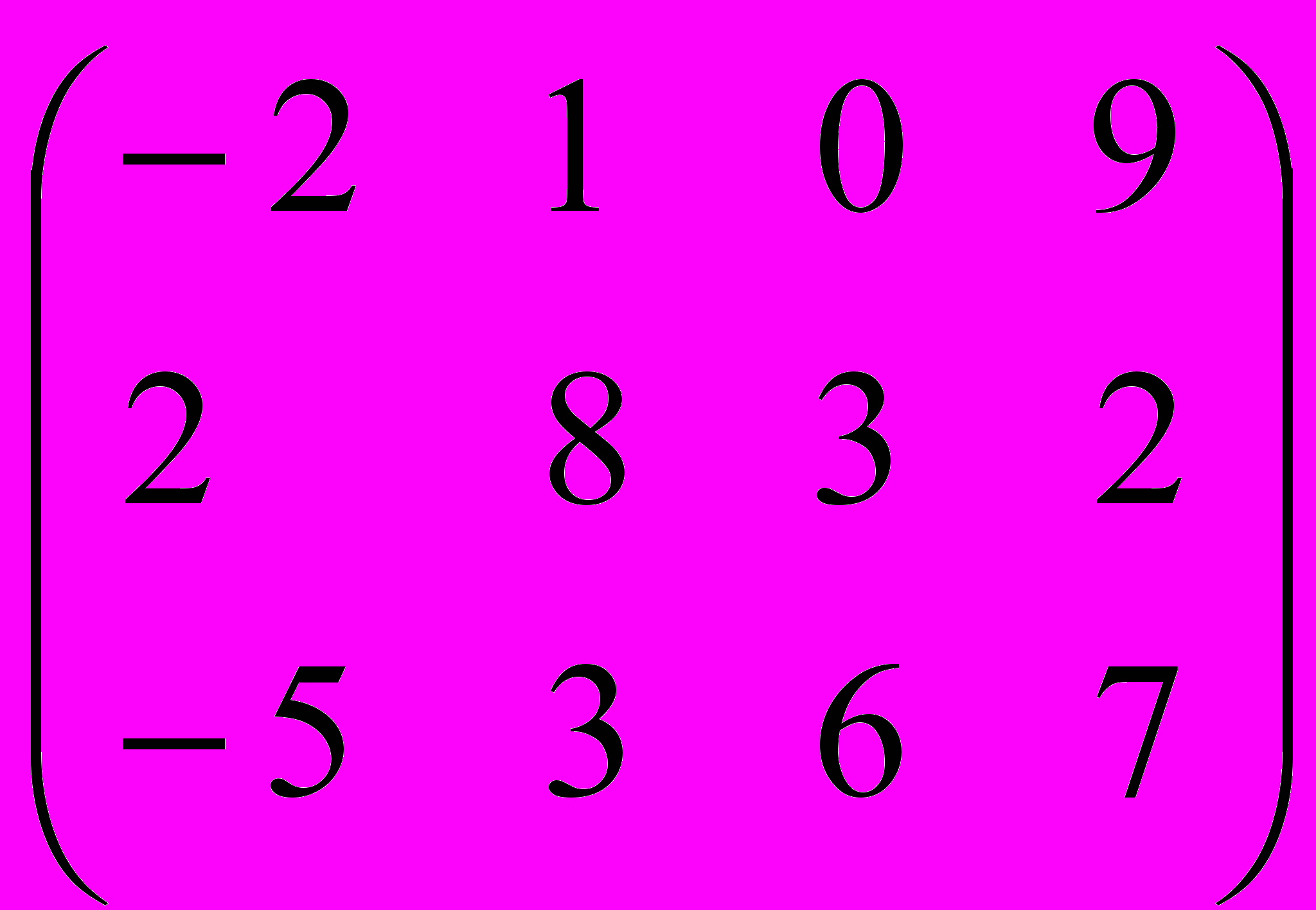

10. Найти A-1, если А =

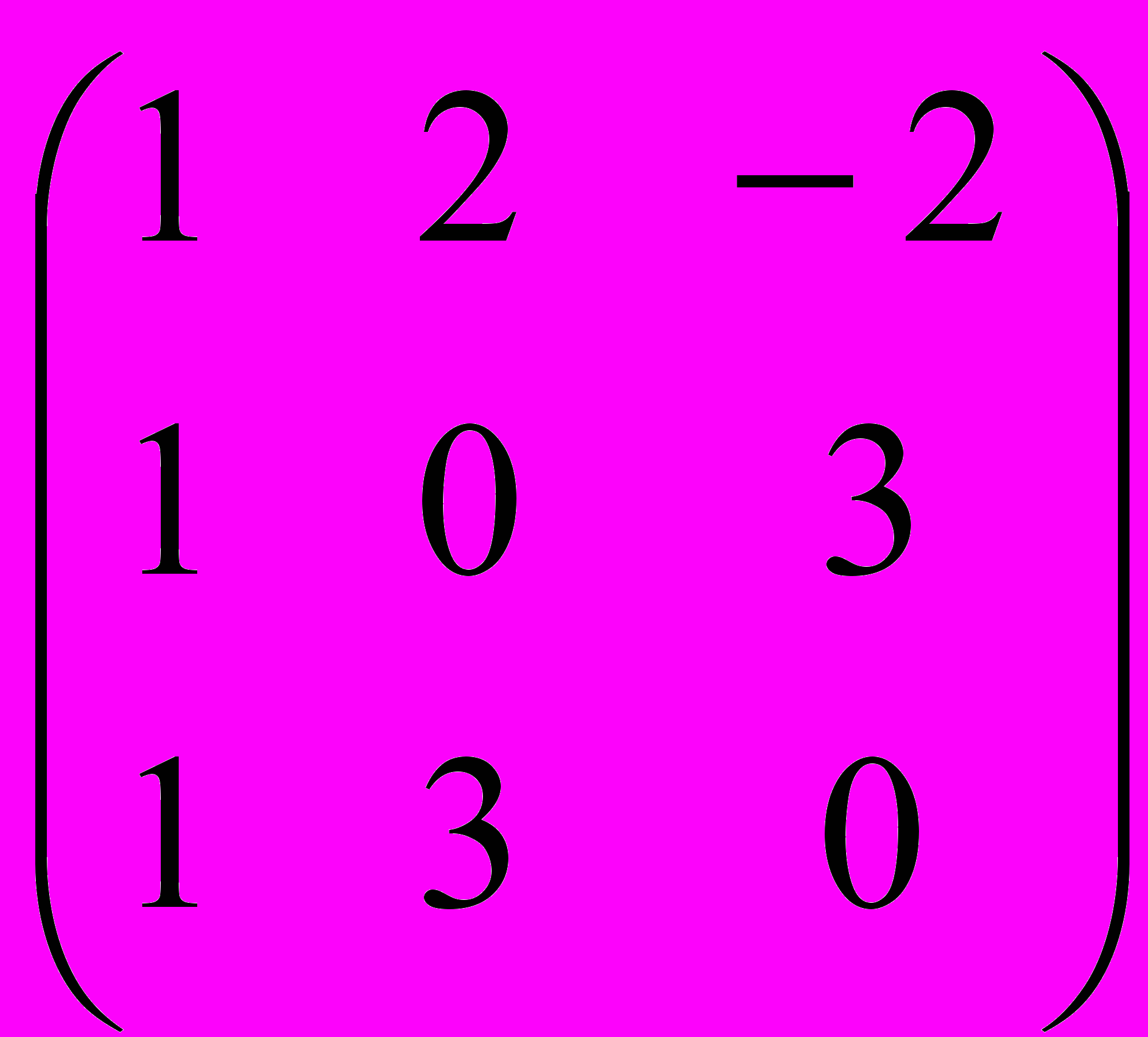
11. Найти алгебраическое дополнение А21 матрицы


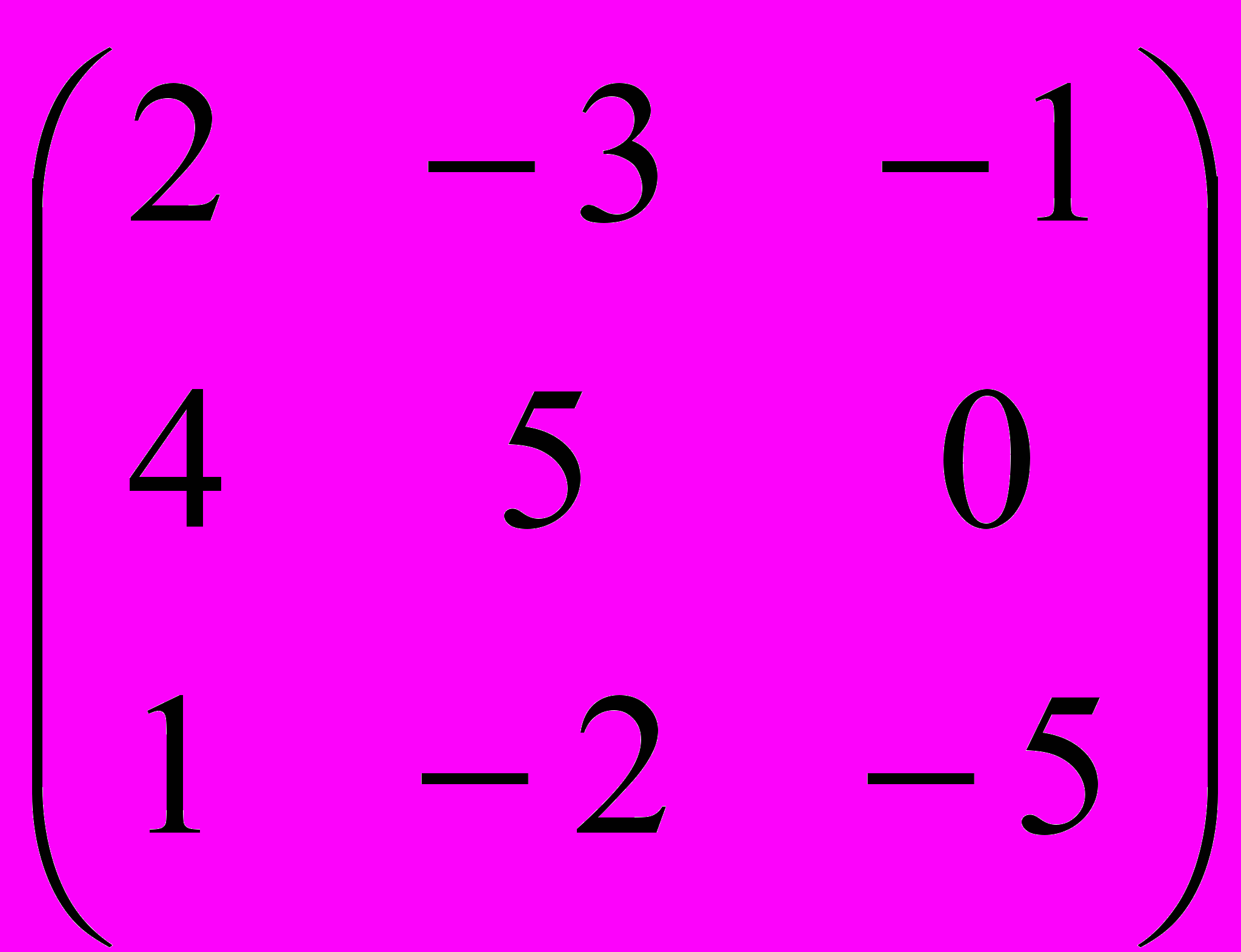
12. Найти С = А В , если A = , B =

13. Вычислить определитель по формуле Лапласа

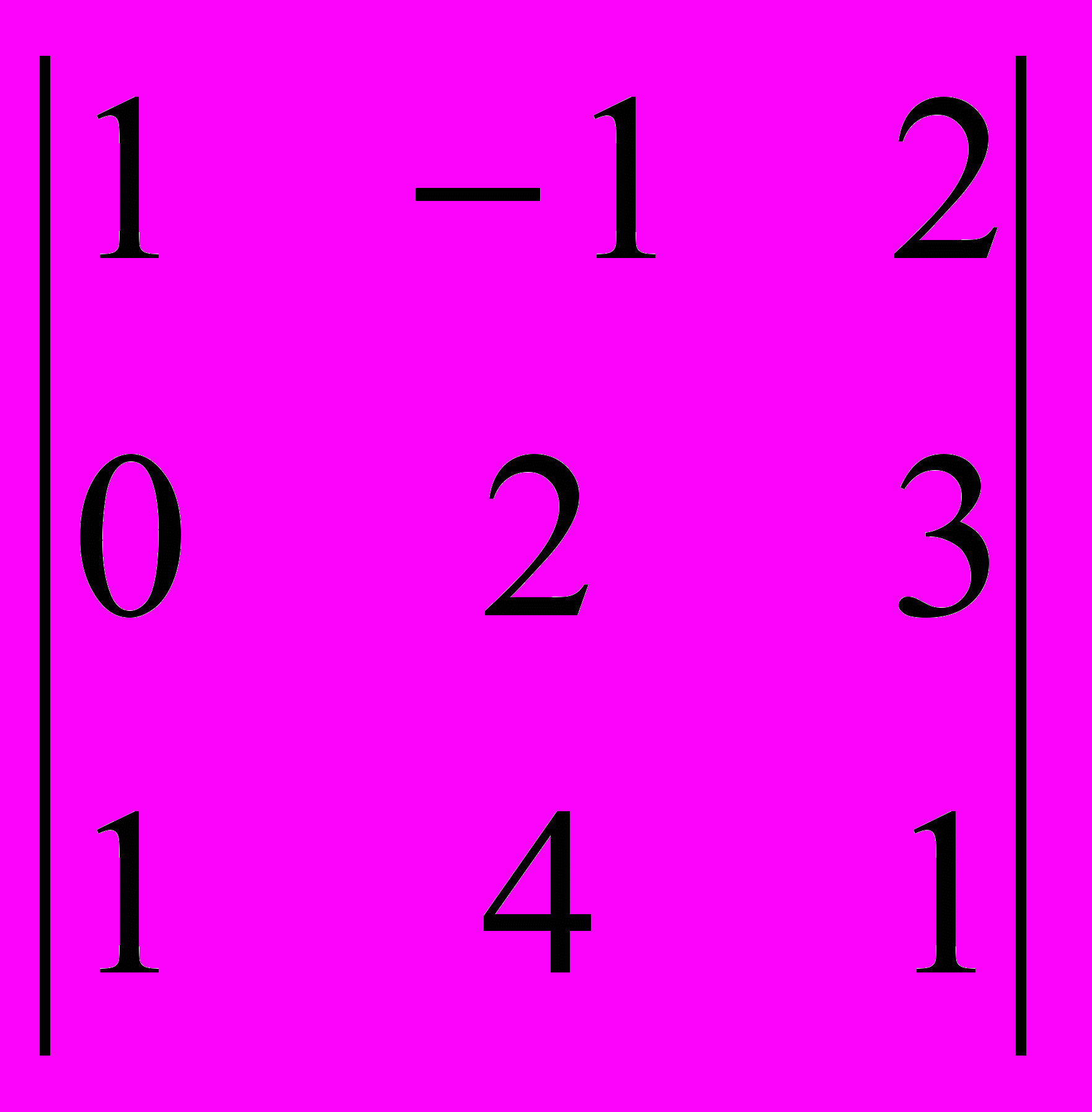
14. Найти уравнение высоты AD в АВС, если А (-2;0), В (2;4), С (4;0)


15. Через точку N(2;-1;-3) провести плоскость, параллельную плоскости 5x – 4y + 6z – 3 = 0

16. Составить уравнение плоскости, перпендикулярной вектору n = (2;-1;4) и проходящей через точку М0 (5;2;-3)

17. Составить уравнение прямой, проходящей через точку М (2;3) перпендикулярно прямой 5x – 4y – 20 = 0

18. Найти расстояние от точки М0(3;4;-7) до плоскости 2x – y + 2z – 9 = 0

19. Найти угол между прямыми 5x – 12y – 16 = 0 и 3x + 4y – 12 = 0

20. Найти угол С в треугольнике АВС, если А (-2;0), В (2;4), С (4;0)


21. Перпендикулярны ли прямые 3x – 4y + 12 = 0 и 4x – 3y – 6 = 0

22. Дан АВС, А (-2;0), В(2;4), С(4;0). Составить уравнение медианы АЕ и найти её длину.

23. Найти угол между плоскостями: 4x – 10y + z – 3 = 0 и -11x + 8y + 7z + 5 = 0


24. Перпендикулярны ли прямые 4x + 5y – 8 = 0 и 3x – 2y + 4 = 0

-- 25. Вычислить: (-1+i)8

26. Выполнить действие :

27. Представить число в тригонометрической форме: -1+i

29. Представить число в показательной форме:

31. Дано комплексное число z = 1+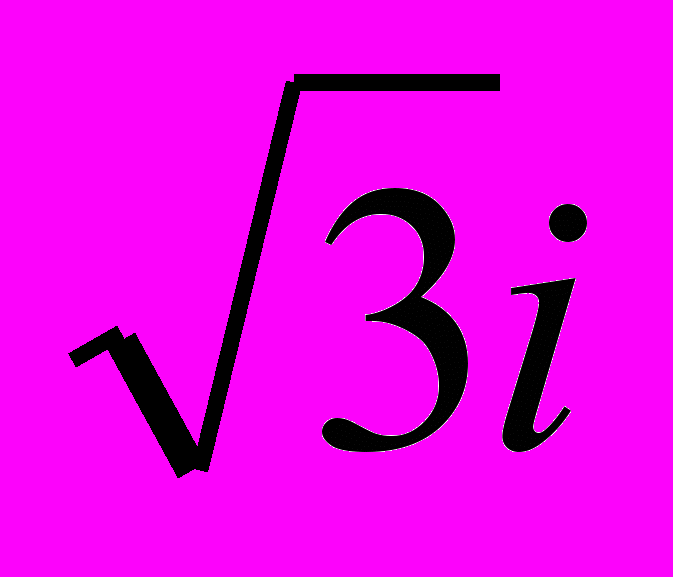. Выполнить действие .

Формы контроля знаний студентов в рамках рейтинговой системы оценки успеваемости



Модуль
Тематический план
Формы контроля
Балл

Следящий
Текущий



Матрицы, определители и системы уравнений.


12л+11пз
1,2.Матрицы и определители. (лекция)
конспект



2

3,4,5.Системы линейных уравнений: матричный способ, теорема Крамера, метод Жордано – Гаусса . (лекция)
конспект



3

6. Балансовая модель Леонтьева. (лекция)
конспект



1

1,2. Действия над матрицами и определителями. Сам. раб.(п/з 1,2 )
Фронтальный опрос



4+8

3,4,5.Решение систем линейных уравнений. (п/з 3,4,5)

Фронтальный опрос



6

6. Решение систем линейных уравнений. (п/з 6)
Фронтальный опрос



2







Решение задач межотраслевого баланса.


2

Рубежный контроль - самостоятельная работа (пз – 6)
8



Элементы аналитической геометрии.

12л+11пз
7,8,9.Векторы. Действия над вектора

ми. Декартовы координаты. Базис. Действия над векторами в базисе. Нелинейные операции над векторами. (лекция)
конспект





3

9. Линейные операторы. Собственные векторы. (лекция)
конспект



1

10,11,12.Уравнение прямой линии. Плоскость. Линии второго порядка.

(лекция)
конспект
Реферат:

Бюджетная линия


3+2

13. Комплексные числа. ( лекция)
конспект



2

14. Квадратичные формы. (лекция)
конспект



1

15. Системы линейных неравенств. (лекция)
конспект



1

16. Линейные задачи оптимизации. (лекция)
конспект



1

7. Действие над векторами. (п/з 7)
Фронтальный опрос



2

8. Собственные векторы линейных операторов. (п/з 8)
Фронтальный опрос



2

9. Прямая линия. (п/з 9)
Фронтальный опрос



2

10. Плоскость. . (п/з 10)
Фронтальный опрос



2

11. Линии второго порядка. . (п/з 11)
Фронтальный опрос



2

12. Решение задач. Сам. раб. (п/з 12)
Фронтальный опрос



2+8

13. Комплексные числа. (п/з 13)
Фронтальный опрос



2

14. Решение задач. Сам. раб. (п/з 14)
Фронтальный опрос



2+8

15. Системы линейных неравенств. (п/з 15
Фронтальный опрос



2

16. Линейные задачи оптимизации. (п/з 16)
Фронтальный опрос



2




Домашняя самостоятельная работа
14