Курсовая работа по дисциплине «Анализ хозяйственной деятельности предприятия» на тему

Вид материала

Курсовая

Содержание 1.2. Методы анализа хозяйственной деятельности Классические методы экономического анализа Факторный анализ на основе жестко детерминированных моделей Традиционные методы экономической статистики Метод группировки данных Регрессионный анализ Кластерный анализ Дисперсионный анализ

Подобный материал:

• Курсовая работа по дисциплине «Анализ и диагностика производственно-финансовой деятельности, 121.56kb.
• Курсовая работа на тему: Анализ и диагностика финансово хозяйственной деятельности, 735.02kb.
• Курсовая работа по дисциплине: Анализ и диагностика финансово-хозяйственной деятельности, 383.65kb.
• Курсовая работа по предмету «экономический анализ» на тему: «анализ хозяйственной деятельности, 943.07kb.
• Методические указания по выполнению курсовой работы на тему: «Анализ финансового состояния, 145.73kb.
• Методические указания по написанию курсовой работы по дисциплине «комплексный экономический, 102.6kb.
• Курсовая работа по дисциплине «Экономический анализ», 660.88kb.
• Курсовая работа по дисциплине «Финансы предприятий» на тему «Анализ использования прибыли, 355.67kb.
• Методические рекомендации по выполнению дипломной работы на тему «Анализ финансово-хозяйственной, 286.86kb.
• Рабочая программа по дисциплине "Анализ и диагностика финансово-хозяйственной деятельности, 159.79kb.

1.2. Методы анализа хозяйственной деятельности

Сравнение в анализе финансово-хозяйственной деятельности

Сравнение - это действие, посредством которого устанавливается сходство и различие явлений объективной действительности. С помощью этого метода решаются следующие основные задачи:

выявление причинно-следственных связей между явлениями;

проведение доказательств или опровержений;

классификация и систематизация явлений.

Сравнение может быть качественным ("вчера было теплее") и количественным (20 всегда больше, чем 10).

Процедура сравнения в АФХД включает несколько этапов: выбор сравниваемых объектов; выбор вида сравнения (динамическое, пространственное, по отношению к плановым значениям); выбор шкал сравнения и степени значимости различий; выбор числа признаков, по которым должно производиться сравнение; выбор вида признаков, а также определение критериев их существенности и несущественности; выбор базы сравнения.

Классические методы экономического анализа

Балансовый метод

Этот метод применяется при изучении соотношения двух групп взаимосвязанных показателей, итоги которых должны быть равны между собой. Своим названием он обязан бухгалтерскому балансу, который был одним из первых исторических примеров увязки большого числа экономических показателей двумя равными итоговыми суммами. Особенно широко распространено использование метода при анализе правильности размещения и использования хозяйственных средств и источников их формирования. Прием балансовой увязки используется также при изучении функциональных аддитивных связей, в частности, при анализе товарного баланса, а также для проверки полноты и правильности произведенных расчетов в факторном анализе: общее изменение результативного показателя должно равняться сумме изменений за счет отдельных факторов.

Факторный анализ на основе жестко детерминированных моделей

Одним из основных понятий в экономическом анализе является понятие фактора (от лат. factor - делающий, производящий). В экономических исследованиях под фактором понимают условия, необходимые для проведения данного хозяйственного процесса, а также причину, движущую силу этого процесса, определяющую его характер или одну из основных черт. На результаты хозяйственной деятельности оказывает влияние множество факторов, находящихся во взаимной связи, зависимости и обусловленности.

Любой хозяйственный процесс складывается под влиянием разнообразных факторов. Знание этих факторов и умение управлять ими позволяет воздействовать на изменение показателей эффективности деятельности предприятия.

Наиболее распространенным видом анализа в хозяйственной практике является детерминированный факторный анализ, т.е. анализ зависимостей между показателями с помощью жестко детерминированных факторных моделей.

Основным результатом детерминированного факторного анализа является разложение прироста результативного показателя, обусловленного совместным влиянием или изменением факторных признаков, на сумму частных приростов результативного показателя, любой из которых обусловлен изменением только одного фактора.

Жестко детерминированный факторный анализ в АФХД используется для решения нескольких типовых задач. Приемы решения этих задач разработаны достаточно давно и имеют стандартную форму. Рассмотрим типовые задачи факторного анализа и способы их решения.

Задача 1 формулируется как задача оценки влияния абсолютного изменения любого фактора на абсолютное изменение результативного показателя. Это основная задача детерминированного факторного анализа, а ее общая постановка такова.

Пусть у = f(x₁, x₂, ..., x_n) - жестко детерминированная модель, характеризующая изменение результативного показателя у от факторов {х_i}. Пусть у получил приращение Δу за анализируемый период (например, в динамике или по сравнению с планом). Требуется определить, какой частью Δу обязано приращению каждого аргумента, т.е. представить его в следующем виде:


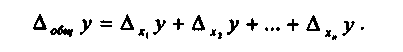(1.2.1)

Где Δу – изменение результативного показателя;

х_{i –} фактор.

Для решения этой задачи в экономическом анализе разработан ряд специфических методов (иногда их называют приемами). Основными из них являются методы цепных подстановок и арифметических разниц, а также метод выявления изолированного влияния факторов. [4, c.66]

Традиционные методы экономической статистики

Метод средних величин

В любой совокупности экономических явлений или субъектов наблюдаются различия между отдельными единицами этой совокупности. Одновременно с этими различиями существует и нечто общее, что объединяет совокупность и позволяет отнести все рассматриваемые субъекты и явления к одному классу. Например, все рабочие одного цеха, выполняющие одну и ту же работу, выполняют ее по-разному, с разной производительностью. Однако, несмотря на некоторые индивидуальные различия, можно определить среднюю выработку или среднюю производительность на одного рабочего по цеху. Можно усреднить рентабельность предприятия за несколько последовательных кварталов, получив величину средней рентабельности, и т.п.

Роль средних величин, таким образом, заключается в обобщении, т.е. замене множества индивидуальных значений признака средней величиной, характеризующей всю совокупность явлений. Средняя величина обобщает качественно однородные значения признака и, следовательно, является типической характеристикой признака в данной совокупности. Например, средний товарооборот на одного работающего является типической характеристикой торговой сети города. [9,c.18]

Метод группировки данных

Группировка - это расчленение совокупности данных на группы с целью изучения ее структуры или взаимосвязей между компонентами. В процессе группировки единицы совокупности распределяются по группам в соответствии со следующим принципом: различие между единицами, отнесенными к одной группе, должно быть меньше, чем различие между единицами, отнесенными к разным группам.

При оформлении результатов группировки в таблице признак-результат размещается в сказуемом, группировочные признаки, рассматриваемые в качестве факторных, размещаются в подлежащем таблицы.

Выбрать один признак в качестве группировочного зачастую бывает достаточно трудно. Анализ по нескольким признакам довольно трудоемок и обладает принципиальным недостатком - размыванием совокупности, поскольку даже комбинация двух признаков при попытке разбить совокупность на три или четыре категории дает шесть или восемь подгрупп. В некоторых из них оказывается одно-два наблюдения, что недостаточно для подготовки обоснованных выводов об этих подгруппах. Избежать этого недостатка позволяют методы многомерных группировок. Широкое распространение они получили благодаря использованию вычислительной техники при расчетах. При анализе деятельности отдельных предприятий методы многомерной группировки используют нечасто из-за их сложности, более распространены они при социологических и экономических исследованиях отраслей и регионов. Наиболее разработанным методом многомерной классификации является кластерный анализ. [6,c.89]


Современные математико-статистические методы

Корреляционный анализ

Корреляционный анализ есть метод установления связи и измерения ее тесноты между наблюдениями, которые можно считать случайными и выбранными из совокупности, распределенной по многомерному нормальному закону.

Корреляционной связью называется такая статистическая связь, при которой различным значениям одной переменной соответствуют разные средние значения другой. Возникать корреляционная связь может несколькими путями. Важнейший из них - причинная зависимость вариации результативного признака от изменения факторного. Кроме того, такой вид связи может наблюдаться между двумя следствиями одной причины. Основной особенностью корреляционного анализа следует признать то, что он устанавливает лишь факт наличия связи и степень ее тесноты, не вскрывая ее причин.

В статистике теснота связи может определяться с помощью различных коэффициентов (Фехнера, Пирсона, коэффициента ассоциации и т.д.), а в анализе хозяйственной деятельности чаще используется линейный коэффициент корреляции.

Регрессионный анализ

Регрессионный анализ - это метод установления аналитического выражения стохастической зависимости между исследуемыми признаками. Уравнение регрессии показывает, как в среднем изменяется у при изменении любого из x_i, и имеет вид:


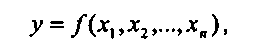(1.2.2)


где у - зависимая переменная (она всегда одна);

х_i - независимые переменные (факторы) (их может быть несколько).

Если независимая переменная одна - это простой регрессионный анализ. Если же их несколько (п 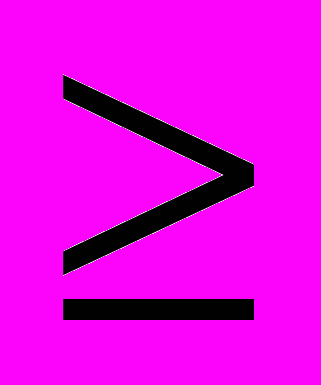2), то такой анализ называется многофакторным.

В ходе регрессионного анализа решаются две основные задачи:

• построение уравнения регрессии, т.е. нахождение вида зависимости между результатным показателем и независимыми факторами x₁, x₂, …, x_n.
  

• оценка значимости полученного уравнения, т.е. определение того, насколько выбранные факторные признаки объясняют вариацию признака у.
  

Применяется регрессионный анализ главным образом для планирования, а также для разработки нормативной базы.

В отличие от корреляционного анализа, который только отвечает на вопрос, существует ли связь между анализируемыми признаками, регрессионный анализ дает и ее формализованное выражение. Кроме того, если корреляционный анализ изучает любую взаимосвязь факторов, то регрессионный - одностороннюю зависимость, т.е. связь, показывающую, каким образом изменение факторных признаков влияет на признак результативный.

Кластерный анализ

Кластерный анализ - один из методов многомерного анализа, предназначенный для группировки (кластеризации) совокупности, элементы которой характеризуются многими признаками. Значения каждого из признаков служат координатами каждой единицы изучаемой совокупности в многомерном пространстве признаков. Каждое наблюдение, характеризующееся значениями нескольких показателей, можно представить как точку в пространстве этих показателей, значения которых рассматриваются как координаты в многомерном пространстве.

Так же как и процедуры регрессионного анализа, процедура кластеризации достаточно трудоемка, ее целесообразно выполнять на компьютере.

Дисперсионный анализ

Дисперсионный анализ - это статистический метод, позволяющий подтвердить или опровергнуть гипотезу о том, что две выборки данных относятся к одной генеральной совокупности. Применительно к анализу деятельности предприятия можно сказать, что дисперсионный анализ позволяет определить, к одной и той же совокупности данных или нет относятся группы разных наблюдений. [2,с.92]