Программа алгоритм, записанный на языке программирования, служащий для выполнения каких-либо действий. Транслятор
| Вид материала | Программа |
- Автор программы И. В. Баркова Ф. И. О., Педагога дополнительного образования; квалификационная, 224.25kb.
- Игра ) Имя известного ученого, в честь которого названа самая популярная программа, 21.91kb.
- Программа элективного курса «Программирование на языке Pascal» 10 класс, 63.48kb.
- Алгоритмизация и программирование. Языки программирования высокого уровня. Технологии, 57.23kb.
- Краткий курс лекций "Основы программирования на языке Паскаль" Основные понятия, 265.68kb.
- Тема : Обработка массива (написать программу из 10-15 строк на языке программирования, 361.29kb.
- Данная инструкция содержит описание и порядок действий для самостоятельного подключения, 280.92kb.
- Урок математики во 2-м классе по теме: Порядок действий. Алгоритм, 63.65kb.
- Программа дополнительного образования муниципального общеобразовательного учреждения, 214.64kb.
- Перечень вопросов по медицинской информатике к контрольной работе №2 для студентов, 84.61kb.
Вычитание
Пример. Вычтем единицу из чисел 102, 108 и 1016


Пример. Вычтем единицу из чисел 1002, 1008 и 10016.


Деление
Деление в любой позиционной системе счисления производится по тем же правилам, как и деление углом в десятичной системе. В двоичной системе деление выполняется особенно просто, ведь очередная цифра частного может быть только нулем или единицей.
Пример. Разделим число 30 на число 6.


Ответ: 30 : 6 = 510 = 1012 = 58.
Пример. Разделим число 5865 на число 115.

Восьмеричная: 133518 :1638

Ответ: 5865 : 115 = 5110 = 1100112 = 638.
Проверка. Преобразуем полученные частные к десятичному виду:
1100112 = 25 + 24 + 21 + 20 = 51; 638 = 6 . 81 + 3 . 80 = 51.
Пример. Разделим число 35 на число 14.


Восьмеричная: 438 : 168

Ответ: 35 : 14 = 2,510 = 10,12 = 2,48.
Проверка. Преобразуем полученные частные к десятичному виду:
10,12 = 21 + 2 -1 = 2,5;
2,48 = 2 . 80 + 4 . 8-1 = 2,5.
Перевод из двоичной системы счисления в четверичную, восьмеричную,
шестнадцатеричную и обратно.
Двоичная система, удобная для компьютеров (потому, что она имеет ряд преимуществ перед другими системами: для ее реализации нужны технические устройства с двумя устойчивыми состояниями (есть ток — нет тока, намагничен — не намагничен и т.п.), а не, например, с десятью, — как в десятичной; представление информации посредством только двух состояний надежно и помехоустойчиво; возможно применение аппарата булевой алгебры для выполнения логических преобразований информации; двоичная арифметика намного проще десятичной. Недостаток двоичной системы — быстрый рост числа разрядов, необходимых для записи чисел), для человека неудобна из-за ее громоздкости и непривычной записи.
Перевод чисел из десятичной системы в двоичную и наоборот выполняет машина. Однако, чтобы профессионально использовать компьютер, следует научиться понимать слово машины. Для этого и разработаны восьмеричная и шестнадцатеричная системы.
Числа в этих системах читаются почти так же легко, как десятичные, требуют соответственно в три (восьмеричная) и в четыре (шестнадцатеричная) раза меньше разрядов, чем в двоичной системе (ведь числа 8 и 16 — соответственно, третья и четвертая степени числа 2).
Перевод восьмеричных и шестнадцатеричных чисел в двоичную систему очень прост: достаточно каждую цифру заменить эквивалентной ей двоичной триадой (тройкой цифр) или тетрадой (четверкой цифр).
Например:

Чтобы перевести число из двоичной системы в восьмеричную или шестнадцатеричную, его нужно разбить влево и вправо от запятой на триады (для восьмеричной) или тетрады (для шестнадцатеричной) и каждую такую группу заменить соответствующей восьмеричной (шестнадцатеричной) цифрой.
 С
ССводная таблица переводов целых чисел из одной системы счисления в другую.
Рассмотрим только те системы счисления, которые применяются в компьютерах — десятичную, двоичную, восьмеричную и шестнадцатеричную. Для определенности возьмем произвольное десятичное число, например 46, и для него выполним все возможные последовательные переводы из одной системы счисления в другую. Порядок переводов определим в соответствии с рисунком:

На этом рисунке использованы следующие обозначения:
- в кружках записаны основания систем счисления;
- стрелки указывают направление перевода;
- номер рядом со стрелкой означает порядковый номер соответствующего примера в сводной таблице.
Например:
 означает перевод из двоичной системы в шестнадцатеричную, имеющий в таблице порядковый номер 6.
означает перевод из двоичной системы в шестнадцатеричную, имеющий в таблице порядковый номер 6. 

Контрольная работа по системам счисления.
Задание: Написать программу позволяющую перевести число из любой системы счисления, в любую другую. Для хорошо успевающих учеников вплоть до шестнадцатеричной системы и позволяющей вводить число, содержащее до 200 символов.
Графический режим работы.
Помимо модуля CRT, который позволяет улучшать вывод на экран. Но как уже говорилось это не единственная библиотека, сегодня мы начнем знакомиться с новой библиотекой, которая позволяет работать с графическим режимом дисплея. В этом режиме любое изображение на экране синтезируется на множество мельчайших элементов, называемых пикселями. Каждый пиксель представляет собой светящуюся точку таких размеров, при которых промежутки между соседними пикселями отсутствуют. Если группа смежных пикселей светятся, то они воспринимаются не как совокупность отдельных точек, а как сплошной участок. Таким образом, на экране дисплея может быть синтезировано любое графическое изображение.
В графическом режиме экран разделяется прямоугольной сеткой, каждый элемент которой имеет свои координаты. Левый верхний угол экрана имеет координаты (0;0). Значение левой координаты (Х) увеличивается в горизонтальном направлении слева направо. Значение правой координаты (У) увеличивается в вертикальном направлении сверху вниз.
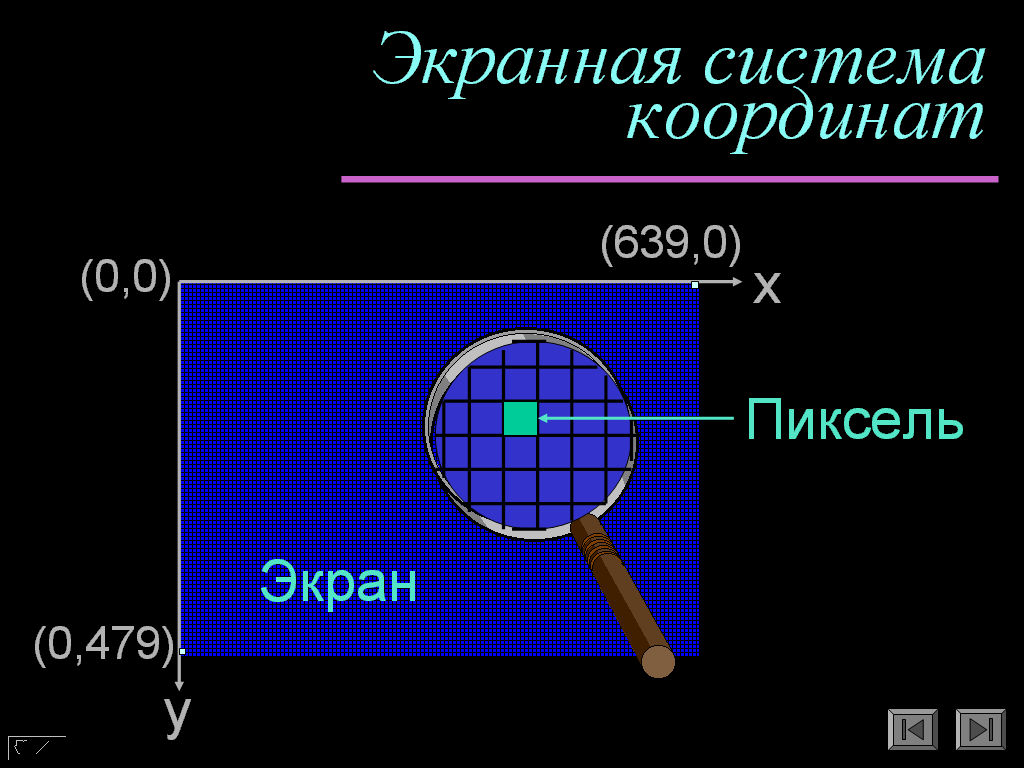
Графическому режиму как и текстовому, присуще понятие текущего указателя. Текущий указатель в любой момент времени может находится в любой точке экрана с координатами (х;у). Его местонахождение отображается курсором, но в графическом режиме курсор не виден.
Инициализация (включение) графического режима
InitGraph (gd, gm, p);
где gd – переменная типа integer, которая указывает на используемый тип графического драйвера; gm – переменная типа integer устанавливающая разрешение экрана; p – строковая константа, указывающая путь к драйверу.
Драйвер – это программа обеспечивающая работу отдельного устройства, в данном случае графического адаптера, который в свою очередь позволяет реализовать графический режим.
В нашем случае gd=9 всегда.
Что касается разрешения то возможны такие варианты значений которые принимает переменная gm:
gm=0 - низкое (640x200)
gm=1 - среднее (640x350)
gm=2 - высокое (640x480)
Ну а путь к драйверу на наших машинах выглядит следующим образом: ‘c:\trans\bp\bgi’
Выключение графического режима
CIoseGraph;
Изображение точек
PutPixel (x, y, c);
где х и у – координаты точки, а с – это цвет которым будет изображена точка (номера цветов аналогичны номерам цветам в модуле crt).
Пример: Нарисовать точку зеленого цвета в центре экрана
Program Primer;
Uses Graph;
Var Gd, Gm : Integer;
Begin
Gd:=9; Gm:=2;
InitGraph(Gd,Gm,’c:\trans\bp\bgi’);
PutPixel(320,240,2);
Readln;
CloseGraph;
End.
Задание:
- Изобразить точку в центре экрана при низком разрешении экрана.
- Изобразить на экране звездное небо.
- Изобразить на экране разноцветное звездное небо.
- Изобразить звездное небо на четверти экрана.
- Изобразить звездное небо в центре экрана.
Изображение линий.
Цвет линии
SetColor (c);
где с – цвет которым будет изображена линия или текст.
Стиль линии
SetLineStyle (s, p, t);
где s – стиль лини; p – шаблон линии; t – толщина линии.
П
 еременная s может принимать следующие значения:
еременная s может принимать следующие значения:0
1
2
3
4 Определяется шаблоном
Переменная t принимает следующие значения:
1 - Тонкая
3 - Толстая
Переменная p может иметь любое значение если стиль линии не шаблон (т.е. если s<>4).
Отрезок прямой линии
Line (x1,y1, x2,y2);
где x1,y1- начальные координаты прямой линии; x2,y2 – координаты конца линии.
Отрезок до точки
LineTo (x,y);
где линия рисуется от точки в который находится указатель в данный момент; х, у – координаты указателя после выполнения команды, т.е. линия рисуется до точки с координатами х, у.
Данную команду удобно использовать при рисовании ломанных линий.
Перемещение текущего указателя в точку с координатами (x,y)
MoveTo (x,y);
Отрезок (вектор)
LineRel (dx, dy);
где линия рисуется от точки в который находится указатель в данный момент; а конечные координаты отрезка формируются следующим образом: к текущим координатам х и у прибавляются соответственно dx и dy.
Задания:
- Построить желтый треугольник, вершинами которого являются следующие точки (200;100), (300;100), (250; 10).
- Нарисовать домик.
- Нарисовать лесенку, если с клавиатуры задаются следующие параметры: а – ширина ступеньки, b – высота ступеньки, с – количество ступенек.
- Нарисовать лесенку если помимо вышеуказанных параметров задается еще начало и направление лесенки.
Самостоятельная работа: Нарисовать куб. (Оценивается на «5» - если нижняя левая вершина куба, а также длина его ребра задается с клавиатуры, на «4» - если изобразили отталкиваясь от исходных данных: вершина имеет координаты (100; 400), длина ребра 200).
Контур прямоугольника
Rectangle(x1,y1,x2,y2);
x1,y1,x2,y2 – координаты противоположных не смежных вершин прямоугольника.
Окружность
Circle (x, y, r);
где x, y – координата центра окружности, а r – радиус окружности.
Дуга окружности
Arc (x,y,nu,ku,r);
где x,y – координаты центра окружности, r – радиус окружности, nu – начальный угол с которого начинается рисование дуги, ku – конечный угол, переменные nu,ku – измеряются в градусах.
Дуга эллипса
Ellipse(x,y,nu,ku,rx,ry);
где x,y – координаты центра эллипса, rx,ry – радиусы эллипса соответственно по оси х и по оси у, nu – начальный угол с которого начинается рисование дуги, ku – конечный угол, переменные nu,ku – измеряются в градусах.
Например для того чтобы нарисовать полный эллипс необходимо выполнить такую команду: Ellipse(x,y,0,360,rx,ry);
Задание: Изобразить на экране какую–нибудь смешную рожицу.
Закрашенные фигуры
Стиль заполнения фигуры
SetFillStyle (s, c);
где s – стиль заполнения фигуры, c – номер активного цвета.
Виды стилей заполнения:
0 - сплошная закраска фоновым цветом
1 - сплошная закраска активным цветом
9 - закраска пикселей в шахматном порядке
12 - пользовательский стиль
2 3 4 5 6 7 8 10 11

Закрашенный прямоугольник
Bar (x1,y1, x2,y2);
x1,y1,x2,y2 – координаты противоположных не смежных вершин прямоугольника.
Параллелепипед
Bar3d(x1,y1,x2,y2,d,t);
x1,y1,x2,y2 – координаты противоположных не смежных вершин передней грани параллелепипеда, d – ширина боковой грани, t - Верхняя грань(True (TopOn) – есть, False (TopOff) – нет).
Закрашенный эллипс
FillEllipse (x,y,Rx,Ry);
где x,y – координаты центра эллипса, Rx,Ry – радиусы эллипса соответственно по оси х и по оси у.
Закрашенный сектор круга
PieSlice (x,y,nu,ku,r);
где x,y – координаты центра круга, r – радиус круга, nu – начальный угол с которого начинается рисование сектора круга, ku – конечный угол, переменные nu,ku – измеряются в градусах.
Закрашенный сектор эллипса
Sector(x,y,nu,ku,rx,ry);
где x,y – координаты центра эллипса, rx,ry – радиусы эллипса соответственно по оси х и по оси у, nu – начальный угол с которого начинается рисование сектора эллипса, ku – конечный угол, переменные nu,ku – измеряются в градусах.
Закраска произвольной фигуры
FloodFill (x,y, b);
где x,y - координаты внутренней точки; b – номер цвета границы.
Задание на оценку: Разукрасить нарисованную ранее рожицу.
Вывод текста в графике
Стиль текста
SetTextStyle(s, d, r)
где s – стиль текста, d – направление, r – размер.
стиль: 0 – побитовый направление: 0 - горизонтально (®) размер: 1..10
1 – тройной 1 - вертикально ()
2 – малый
3 – гротесковый
4 – готический
Вывод текста
OutTextXY(x, y,s)
где, x, y – координаты, s – текст (тип - string).
Выравнивание текста
SetTextJustify(h, v)
где h - выравнивание по горизонтали, v - выравнивание по вертикали.
Выравнивание текста относительно точки привязки
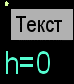

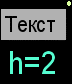



Преобразование чисел в текст
Str ( x, s )
где x – исходное число, s - строка (текст) - тип - string
Ширина строки - Функция
TextWidth (S)
где S – строка (ширина в пикселях)
Высота строки - Функция
TextHeight(S)
где S – строка (высота в пикселях)
Задание:
- Заполнить экран квадратами, если сторона квадрата задается с клавиатуры и если полный квадрат на экране не убирается его выводить не нужно совсем.
- Нарисовать шахматную доску, если координаты верхнего левого угла и сторона квадрата задаются с клавиатуры.
Самостоятельная работа заполнить экран окружностями, так чтобы не полные окружности на экран не выводились, если радиус задается с клавиатуры.
Задачи:
- Нарисовать снеговика так, чтобы в центре каждой окружности стоял его порядковый номер, они были разноцветными, и радиус каждой последующей окружности на одну четверть меньше предыдущей, количество окружностей, радиус большей, а также ее центр задавались с клавиатуры.
- Нарисовать наклонную шахматную доску.
Самостоятельная работа вложенные окружности, причем если просто вложенные окружности то оценка четыре, если еще симметричные им то тогда пять.
Зачет по текстовому режиму.
Задачи:
- Написать программу, которая сообщает пользователю: «Я умею рисовать отрезок». Запрашивает: «Введите координаты начала и конца отрезка» и рисует отрезок с соответствующими координатами.
- Построить рисунок лодочки.
- Написать программу, которая рисует концентрические окружности.
- Нарисуйте радугу, т.е. разноцветные дуги концентрических окружностей опирающихся на нижнюю границу экрана.
- Написать программу, которая запрашивает координаты центра окружности, ее радиус и рисует закрашенный круг, соответствующий введенным величинам.
- Написать программу, которая рисует лучи исходящие из левого нижнего угла экрана.
- В верхнем левом углу экрана нарисовать солнышко.
- Написать программу, которая рисует произвольную ломанную линию.
- Написать программу, рисующую произвольный бегущий отрезок.
- Написать программу, которая рисует эллипсы.
- Составить программу построения квадрата. На одном из его оснований построить равносторонний треугольник со сторонами произвольной длины.
- Построить ромб со стороной А и острым углом х.
- Изобразите на экране движение точки по окружности.
- «Нарисуйте» часы и «заставьте их «ходить».
- Составить программу построения отрезка штриховой прямой линии, ограниченного точками с координатами А(X,Y) B(X,Y). Размеры штриха и интервала между штрихами возьмите равными. Исходные данные: значения координат точек и размер штриха введите с клавиатуры.
- Изобразите на экране таяние горящей свечи.
- Составить программу рисования спирали.
- Составить программу вычерчивания графиков следующих функций:
а) y=sinx б) y=tgx в) y=cosx г) y=ax+b д) y=ex е) y=logx
- Нарисуйте горизонтальные(вертикальные) линии длиной L располагая их по всей плоскости экрана на расстоянии d.
- Расчертите на клеточки со стороной a весь экран.
-
в )
)
б)
Нарисуйте :
а
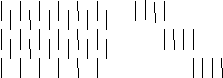 )
) д
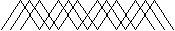 )
)г
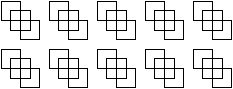 )
)е



 )
)ж
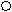









 )
)9 класс.
Организация движения в Turbo Pascal.
Алгоритм организации движения:
- Задать начальную точку привязки.
- Нарисовать фигуру относительно этой точки привязки.
- Сделать задержку.
- Стереть нарисованную фигуру, то есть нарисовать ее фоновым цветом.
- Изменить начальные координаты точки привязки.
- Проверка окончания движения, если движение еще не закончено то выполняем пункт 2.
Пример: На экране прямая по которой движется точка. (от левого края до правого).
Задачи:
- На экране по прямой двигается точка от левого края до правого и обратно, до тех пор, пока не будет нажата какая-либо клавиша.
- Даны две прямые, по которым двигаются две точки с разными скоростями.
Самостоятельная работа дан прямоугольный контур, по которому двигается точка (координаты противоположных не смежных вершин прямоугольника задаются с клавиатуры).
Задачи:
- Два мячика двигаются по экрану (один сверху вниз, другой слева направо).
- Две рожицы двигаются по экрану (одна веселая, другая грустная).
- Бильярдный шарик двигается по экрану.
- Броуновское движение.
Управление движением.
Пример: движение шарика только при нажатии стрелок.
Задачи:
- Шарик двигается, а при нажатии различных клавиш изменяется его направление. скорость, радиус и т.д.
Движение по окружности.
Подпрограммы.
В практике программирования часто встречаются задачи, в которых по ходу выполнения программы приходится производить одни и те же действия или вычисления, но при различных исходных данных. Чтобы исключить повторение одинаковых операторов и сделать тем самым программу проще и понятнее, можно выделить эти повторяющиеся действия в самостоятельную часть программы, которая может быть использована многократно по мере необходимости.
Автономная часть программы, реализующая определенный алгоритм и допускающая обращение к ней из различных частей общей программы, называется подпрограммой.
Подпрограммы оформляются в виде замкнутых участков программы, имеющих четко обозначенные вход и выход.
Обращение к подпрограмме осуществляется из основной программы через заголовок подпрограммы. При вызове подпрограммы работа основной программы приостанавливается, и начинает выполняться вызванная подпрограмма. Она обрабатывает данные, переданные ей из основной программы, или просто выполняет заданную последовательность действий. По завершении выполнения подпрограммы основная программа продолжает выполнятся с того места, где прервалось ее действие.
Передача данных из основной программы в подпрограмму (входные данные) и возврат результата выполнения подпрограммы осуществляется с помощью параметров.
Параметры - это данные, которые передаются вызываемой подпрограмме и используются последней в качестве входной и (или) выходной информации.
Использование подпрограмм позволяет реализовать один из самых прогрессивных методов программирования - структурное программирование.
Процедура в Паскале
и ее формат.
Любая программа может содержать несколько процедур и функций. Процедуры и функции объявляются в разделе описания вслед за пределом описания переменных.
Процедура - это независимая часть программы, которую можно вызывать по имени для выполнения определенных действий.
Структура процедуры имеет вид :
Procedure имя(список формальных параметров);
(* раздел описаний *)
begin
(* раздел операторов *)
end;
Первая строка описания называется заголовком процедуры, а раздел операторов называется телом процедуры.
В заголовке указывается служебное слово PROCEDURE, за которым следуют имя процедуры и список формальных параметров, заключенные в круглые скобки (если такие имеются). В списке перечисляются имена формальных параметров и их тип. Имя параметра отделяется от типа двоеточием, а параметры друг от друга - точкой с запятой. Если несколько формальных параметров имеют одинаковый тип, тогда их можно перечислить через запятую, а затем указать тип.
Тело процедуры заключается в операторные скобки BEGIN и END, причем после END ставится точка с запятой.
Раздел описаний процедуры подобен программе и состоит из разделов меток, констант, типов, переменных и , в свою очередь, процедур и функций.
Процедура вызывается по ее имени :
имя(список фактических параметров);
Формальные параметры - параметры, определенные в заголовке процедуры.
Фактические параметры - выражения, задающие конкретные значения при обращении к процедуре.
При обращении к процедуре ее формальные параметры замещаются фактическими, переданными из основной программы.
Фактические параметры - это параметры, которые передаются процедуре при ее вызове.
Количество и тип формальных и фактических параметров должны в точности совпадать.
Формальные параметры описываются в заголовке процедуры и определяют тип и место подстановки фактических параметров. Формальные параметры делятся на два вида: параметры-переменные и параметры-значения.
Параметры-переменные отличаются тем, что передними стоит служебное слово Var. Они используются тогда, когда необходимо, чтобы изменения значений формальных параметров в теле процедуры приводили к изменению соответствующих фактических параметров.
Параметры-значения отличаются тем, что перед ними слово Var не ставится. Внутри процедуры можно производить любые действия с параметрами-значениями, но все изменения никак не отражаются на значениях соответствующих фактических параметров, то есть какими они были до вызова процедуры, такими же и останутся после завершения ее работы.
Все переменные программы делятся на глобальные и локальные. Глобальные переменные объявляются в разделе описаний основной программы. Локальные переменные объявляются в процедурах и функциях. Таким образом, локальные переменные «живут» только во время работы подпрограммы.
Пример. Составить программу для вычисления аn : целые числа а и n (n>=0) вводятся с клавиатуры. ( составить процедуру для вычисления степени целого числа).
Program ex;
var a, n : integer;
s: longint;
Procedure Degree(x,y : integer; var st : longint);
var i : integer;
begin
st:=1;
for i:=1 to y do st:=st*x;
end;
{ начало основной программы}
begin
writeln(‘введите два числа - основание и показатель степени’);
readln(a,n);
Degree(a,n,s); { обращение к процедуре }
writeln(‘Результат ’,s);
end.
Процедура названа именем Degree. В скобках записан список формальных параметров, то есть перечислены переменные с указанием их типа. Используем три параметра: первый - основание степени, то есть число, которое надо возвести в степень; второй - показатель степени, третий - результат. Первые два формальных параметра - параметры значения, третий - параметр-переменная, и перед ним указано слово var. Все они описаны как целые (x и y - переменные типа integer, st - Longint, так как степенная функция быстро возрастает).
После заголовка процедуры идут разделы описаний. В нашем примере имеется только раздел описания переменных, в котором описывается одна переменная i (счетчик цикла).
Далее идет тело процедуры. Оно начинается служебным словом Begin и заканчивается служебным словом End, после которого стоит точка с запятой (в конце программы после последнего End ставится точка). В теле процедуры вычисляется степень числа x с помощью цикла For.
В программе процедуры и функции описываются после раздела описания переменных программы, но до начала ее основной части, то есть до Begin , начинающего эту часть программы.
!!!! Процедура вызывается как оператор, состоящий из имени процедуры. В круглых скобках записываются фактические параметры. В нашем примере формальные параметры x, y и st принимают значения фактических параметров a, n и s соответственно. После завершения работы процедуры переменные a и n сохранят те же значения, что и при вызове, а s получит новое значение.
Пример 2 : Используя процедуру для вычисления степени числа, найти значение выражения : y=a4x4 + a3x3 + a2x2 + a1x + a0
program ex2;
var a: array[0..4] of integer;
i, x: integer;
y,s: longint;
Procedure Degree(xx,n : integer; var st : longint);
var i : integer;
begin
st:=1;
for i:=1 to n do st:=st*xx;
end;
{ начало основной программы}
begin
write(‘введите значение переменной х ‘); readln(x);
writeln(‘введите массив коэффициентов’);
for i:=0 to 4 do begin write(‘a[‘,i,’]=’); readln(a[i]); end;
y:=a[0];
for i:=1 to 4 do
begin
Degree(x,i,s); y:=y+a[i]*s;
end;
writeln(‘y=’,y);
end.
Пример 3. Просуммировать различные части массива.
Program sumir;
var a: array [1..100] of integer; sa1, sa2,sa3 : integer;
n,l,t : integer;
procedure summa(a:array [1..100] of integer; k,m :integer; var s:integer);
var i:integer;
begin
s:=0;
for i:=k to m do s:=s+a[i];
end;
BEGIN
for t:=1 to 100 do
begin
write(‘введите очередной элемент массива ‘);
readln(a[i]);
end;
summa(a,10,20,sa1);
summa(a, n , l , sa2);
summa(a, n,n+3,sa3);
end.
Задачи:
- Составить программу, в результате которой величина А меняется значением с величиной В, а величина С - с величиной D. (Определить процедуру, осуществляющую обмен значениями двух переменных величин)
- Даны стороны двух треугольников. Найти сумму их периметров и сумму их площадей. (Определить процедуру для расчета периметра и площади треугольника по его сторонам.)
- Даны основания и высоты двух равнобедренных трапеций. Найти сумму их периметров и сумму их площадей (Определить процедуру для расчета периметра и площади равнобедренной трапеции по ее основаниям и высоте)
- Написать рекурсивную процедуру для вывода на экран цифр натурального числа в обратном порядке.
- Написать рекурсивную процедуру для ввода с клавиатуры последовательности чисел и вывода ее на экран в обратном порядке (окончание последовательности - при вводе нуля).
- Написать рекурсивную процедуру перевода натурального числа из десятичной системы счисления в двоичную.
