Программа алгоритм, записанный на языке программирования, служащий для выполнения каких-либо действий. Транслятор
| Вид материала | Программа |
- Автор программы И. В. Баркова Ф. И. О., Педагога дополнительного образования; квалификационная, 224.25kb.
- Игра ) Имя известного ученого, в честь которого названа самая популярная программа, 21.91kb.
- Программа элективного курса «Программирование на языке Pascal» 10 класс, 63.48kb.
- Алгоритмизация и программирование. Языки программирования высокого уровня. Технологии, 57.23kb.
- Краткий курс лекций "Основы программирования на языке Паскаль" Основные понятия, 265.68kb.
- Тема : Обработка массива (написать программу из 10-15 строк на языке программирования, 361.29kb.
- Данная инструкция содержит описание и порядок действий для самостоятельного подключения, 280.92kb.
- Урок математики во 2-м классе по теме: Порядок действий. Алгоритм, 63.65kb.
- Программа дополнительного образования муниципального общеобразовательного учреждения, 214.64kb.
- Перечень вопросов по медицинской информатике к контрольной работе №2 для студентов, 84.61kb.
Функции
Заголовок функции состоит из слова Function, за которым указывается имя функции, затем в круглых скобках записывается список формальных параметров, далее ставится двоеточие и указывается тип результата функции.
В теле функции обязательно должен быть хотя бы один оператор присваивания, в левой части которого стоит имя функции, а в правой - ее значение. Иначе значение функции не будет определено.
Таким образом, общий вид описания функции следующий :
Function Имя[(список формальных параметров)]:Тип результата
описательная часть
Begin
тело функции, в которой обязательно должно быть
присваивание Имя_функции:=значение
End;
Пример 1 Составить программу, подсчитывающую число сочетаний без повторения из n элементов по k. Число сочетания без повторения вычисляется по формуле
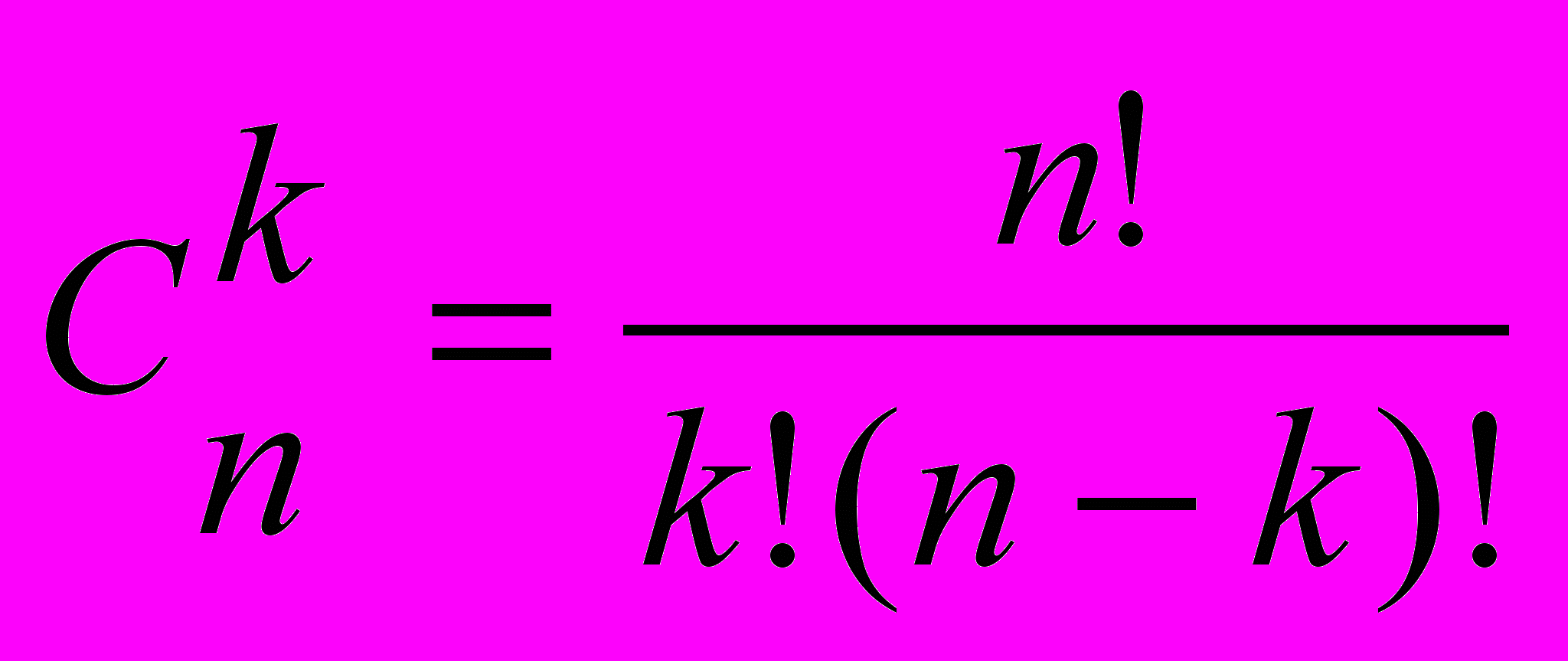
Обозначим через n и k переменные для хранения введенных чисел; С - переменную для хранения результата.
Воспользуемся функцией для вычисления факториала числа n. (n!=1*2*..*n)
program sochet;
var n,k : integer;
a1,a2,a3,c : lohgint;
Function factorial(n:integer):longint;
var i: integer;
rez : longint;
begin
rez:=1;
for i:=1 to n do rez:=rez*i;
factorial:=rez;
end;
begin
writeln(‘ ввод n и k :’); readln(n,k);
a1:=factorial(n); { вычисление n!}
a2:=factorial(k); { вычисление k!}
a3:=factorial(n-k); {вычисление (n-k)!}
c:=a1 div (a2*a3); { результат}
writeln(‘результат=’,c) ;
end.
Первая строка в описании функции - это ее заголовок. Служебное слово Function (функция) указывает на то, что именем factorial названа функция. В скобках записан список формальных параметров функции, состоящий из одной переменной целого типа. Далее в заголовке указан тип значения функции. В данном примере результат функции factorial - длинное целое число.
За заголовком функции следует описательная часть функции, которая, как у программы, может состоять из разделов описания переменных, констант, типов. В данном примере есть переменные i (счетчик цикла) rez (для накопления значения факториала).
Далее идет раздел операторов (тело функции).
В тексте программы описания функций всегда следуют за разделом описания переменных и до начала основной части, как и описания процедур.
Пусть n=5, k=3. Когда в программе встречается оператор a1:=factorial(n), выполняются следующие действия:
- выделяется память для переменных, описанных в функции factorial;
- формальному параметру присваивается значение фактического: n:=n (n=5);
- выполняется функция, вычисляется факториал числа 5;
- значение функции передается в место обращения к этой функции, то есть присваивается переменной a1;
- в операторах a2:=factorial(k) a3:=factorial(n-k) еще дважды вызывается функция factorial с параметрами k=3 n-k=2.
Функция - это самостоятельная часть программы, имеющая собственные переменные, которым отводится отдельное место в памяти ЭВМ. Этим объясняется тот факт, что переменные с одинаковыми именами, используемые в функции и в основной программе, являются разными ( переменная n основной программы и параметр n функции). При выполнении программы машина «не путает» имена этих переменных, т.к. области их действия не совпадают.
Пример 2 : Написать функцию, подсчитывающую количество цифр натурального числа. Используя ее, определить, в каком из двух данных чисел больше цифр.
Program chisla;
Var n1, n2 : longint;
k1, k2 : byte;
Function kol(x : longint): byte;
var k: byte;
begin
k:=0;
While x<>0 do
begin
Inc(k);
x:=x div 10;
end;
kol:=k;
end;
BEGIN
writeln(‘Введите два числа’); readln(n1, n2);
k1:=kol(n1);
k2:=kol(n2);
if k1=k2 Then writeln(‘одинаковое количество цифр’)
else if k1>k2 Then Writeln(‘в первом числе цифр больше’)
else writeln(‘во втором числе цифр больше’)
END.
Задачи:
- Рассчитать значение х, определив и использовав функцию :
-
а)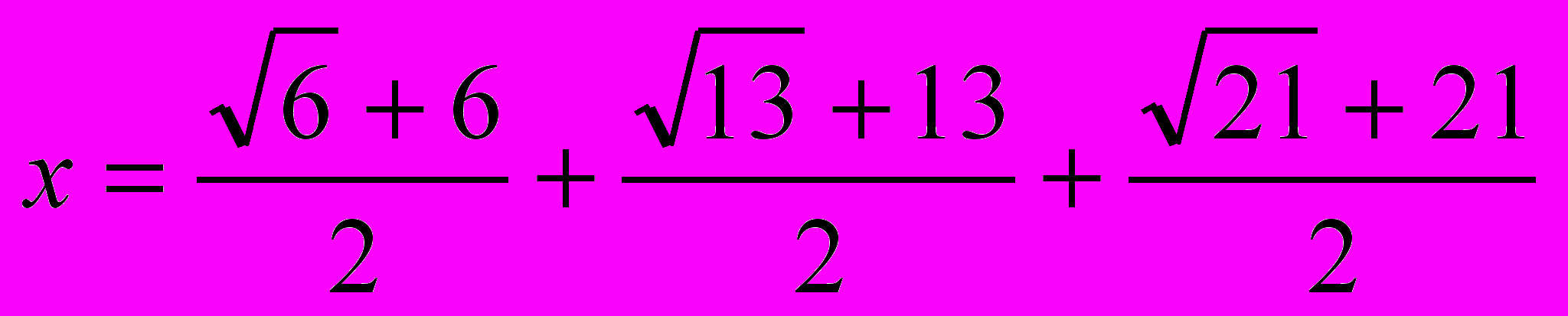
г)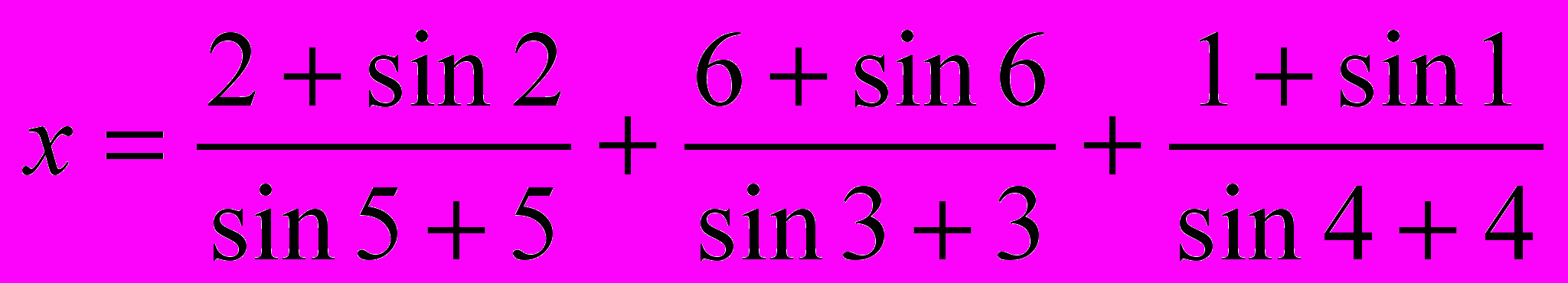
б)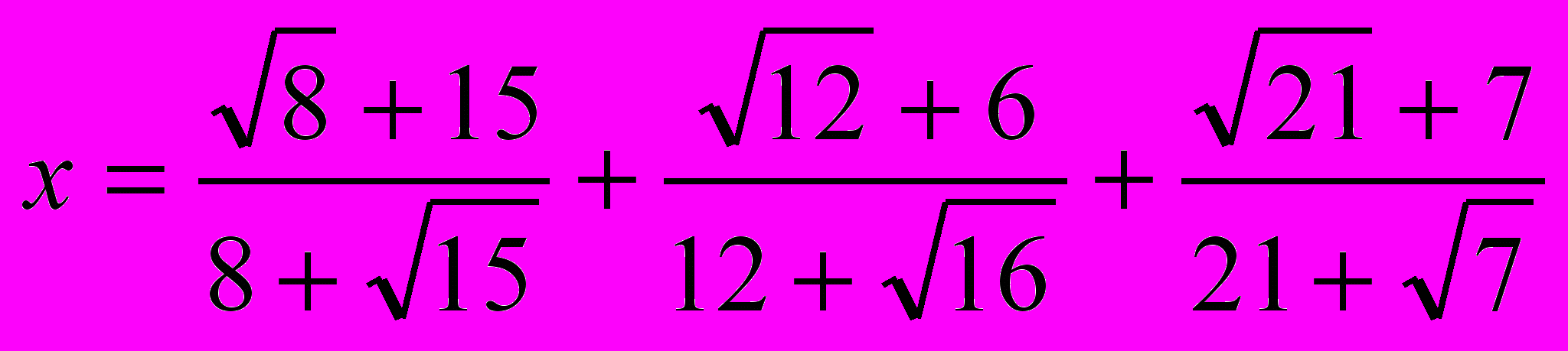
д)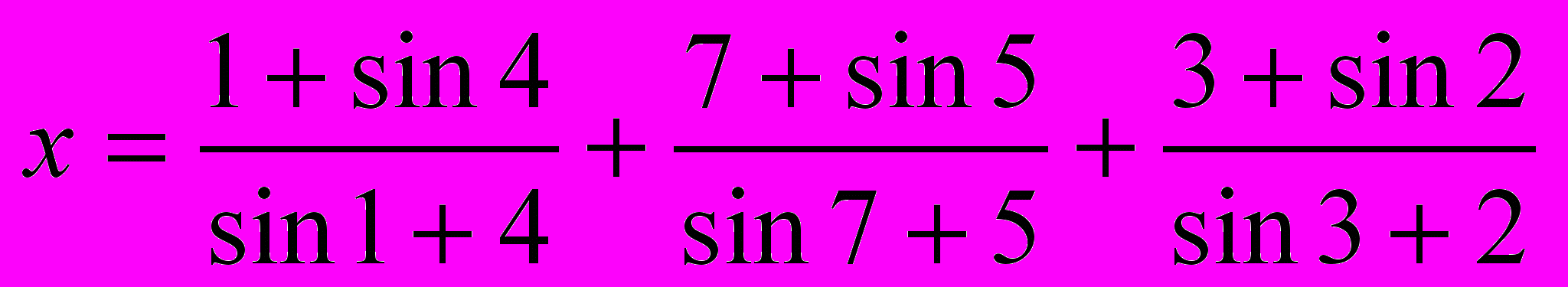
в)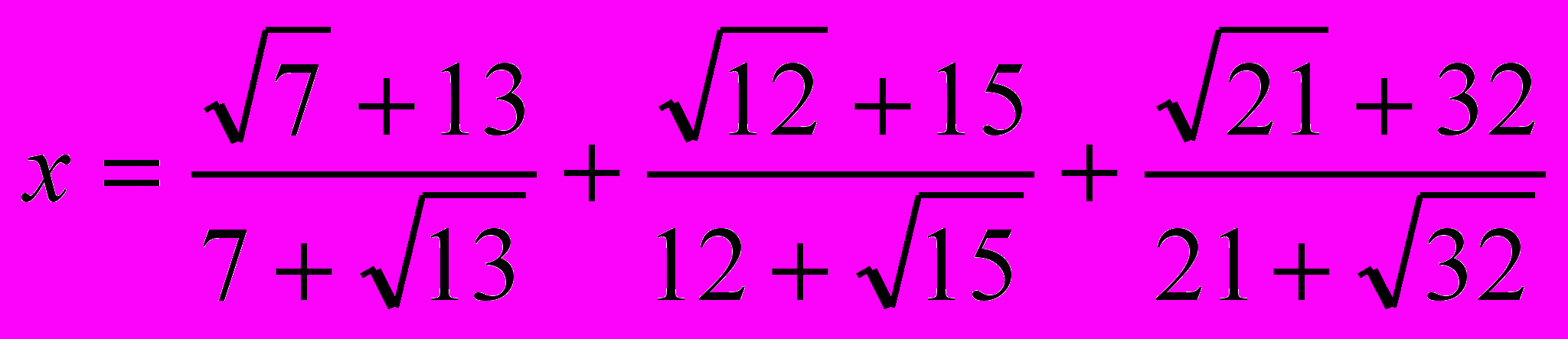
е)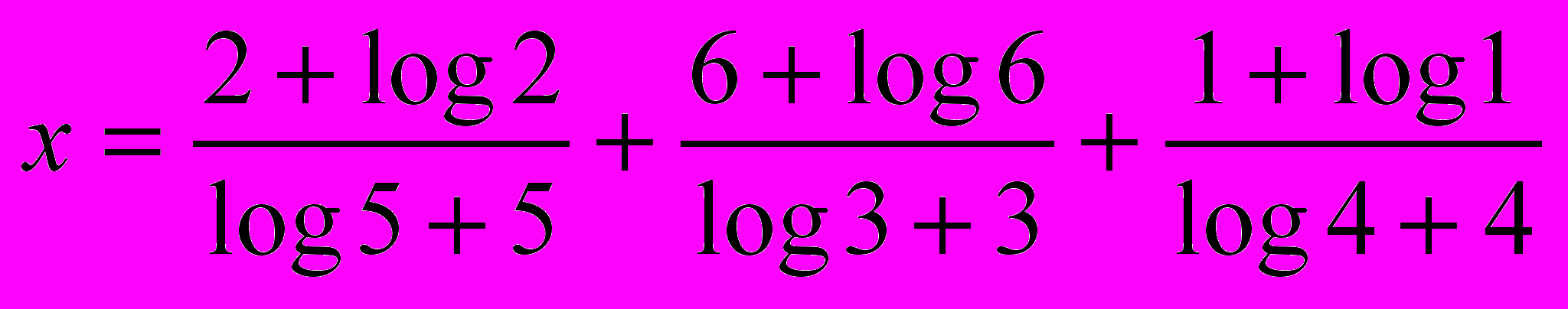
- Определить значение
а) z=max(a,2b)*max(2a-b,b) б) z=min(a,3b)*min(2a-b,b)
где max(x,y), min(x,y) - максимум и минимум из чисел x,y
При решении:1) не использовать функцию max, min.
2) определить и использовать функцию max,min.
- Даны основания и высоты двух равнобедренных трапеций. Найти сумму их периметров. (Определить функцию для расчета периметра равнобедренной трапеции по ее основаниям м высоте.)
- Даны три квадратных уравнения ax2 + bx + c = 0, bx2 + ax + c = 0, cx2 + ax + + b = 0. Сколько из них имеют вещественные корни ? (Определить функцию, позволяющую распознавать наличие вещественных корней в квадратном уравнении.)
- Найти периметр треугольника, заданного координатами своих вершин. (Определить функцию для расчета отрезка по координатам его вершин)
- Даны вещественные числа a, b, c, d, e, f, g.
| Н  айти площадь пятиугольника, изображенного на рисунке. (Определить функцию для расчета площади треугольника по трем сторонам.) айти площадь пятиугольника, изображенного на рисунке. (Определить функцию для расчета площади треугольника по трем сторонам.) | е g d a f b с |
- Даны вещественные числа x1, y1, x2, y2,... x5, y5.Найти площадь пятиугольника (см 10.6) вершины которого имеют координаты (x1, y1), (x2, y2), ...( x5, y5). (Определить функцию для расчета площади треугольника по координатам его вершин).
- Даны две последовательности целых чисел : а1, а2,... а8, и b1, b2, ... b8. Найти количество четных чисел в первой из них и количество нечетных вол второй. (Определить функцию, позволяющую распознавать четные числа.)
- Найти значение выражения (2*5! + 3*8!)/(6! + 4!), где n! функция.
- Даны два натуральных числа. Выяснить, в каком из них сумма цифр больше.(сумма цифр - функция).
- Даны n различных чисел. Определить максимальное из них. (Определить функцию, находящую максимум из двух различных чисел.)
- Найти НОД(a,b,c)=НОД(НОД(a,b),c). (где НОД(a,b) - функция.)
- Даны n натуральных чисел. Найти их НОД. (где НОД(a,b) - функция.)
- Написать рекурсивную функцию :
а) вычисления суммы цифр натурального числа;
б) вычисления количества цифр натурального числа.
- Даны первый член и разность арифметической прогрессии. Написать рекурсивную функцию для нахождения :
а) n-го члена прогрессии; б) суммы n первых членов прогрессии.
- Даны первый член и знаменатель геометрической прогрессии. Написать рекурсивную функцию для нахождения :
а) n-го члена прогрессии; б) суммы n первых членов прогрессии.
Построение графиков функций и диаграмм.
Для начала работы, немного упростим задачу. А именно, договоримся, что функция задана явно, то есть все наши функции имеют следующий вид y = f(x). И пока мы будем брать только такие функции которые не имеют точек разрыва в исследуемой области определения. Грубо говоря, на рассматриваемой области не должен вычисляться корень из отрицательного числа и не должно выполняться деление на ноль.
Ниже приведен простейший алгоритм, который должен в принципе работать для задачи построения графиков:
Для все Х от ЛГ до ПГ делать
Вычислить y=f(x)
Построить точку с координатами (x,y)
Для реальной задачи этот алгоритм работать не будет, по следующим причинам:
- Он не учитывает, то, как устроена система координат компьютерного монитора. (Начало координат в левом верхнем углу и y растет вниз).
- Он не учитывает, что экран монитора имеет ограниченные размеры и если значения функции будут слишком велики или слишком велика будет область, на которой требуется график, то значительной части графика мы просто не увидим.
- Если наоборот значения функции будут малы или область построения будет мала, то мы увидим все, но получившаяся картинка будет слишком мала по своим размерам.
Попробуем учесть указанные моменты.
Все эти проблемы можно решить одним махом, если функцию нарисовать в том же масштабе, что и экран монитора. Это очень просто. Пусть, мы желаем просмотреть картинку которая очень мала, например она может быть нарисована в прямоугольнике который в 1000 раз меньше экрана монитора, тогда её перед тем как выводить необходимо увеличить в 1000 раз. Если же она наоборот в 1000 раз больше, то перед выводом её надо в 1000 раз уменьшить.
Выше описано преобразование подобия, но это преобразование ещё не полностью описывает положение картинки на экране. Мало, чтобы картинка совпадала с экраном монитора размерами, ещё необходимо, чтобы совпадали координаты.
Но после того как исходная область будет увеличена, она все равно будет находиться за пределами экрана для отображения. А это означает, что после преобразования подобия необходимо осуществить ещё параллельный перенос. После преобразования подобия вектор переноса останется прежним, если преобразование проводить так, чтобы левый нижний угол исходной области остался на месте.
И последнее, что нужно сделать – это учесть особенное расположение начала системы координат на экране монитора компьютера. Для этого изображение необходимо перевернуть, тогда на экране оно останется прежним.
Итак, мы изложили все, что необходимо на языке геометрических преобразований, но так как язык программирования не умеет работать с понятиями геометрии, и ему необходимы алгебраические выражения, то далее мы рассмотрим каким образом всё вышесказанное записать на языке алгебры.
Введём обозначения:
Left – левая граница исходной области.
Right – правая граница исходной области.
Down – нижняя граница исходной области.
Up – верхняя граница исходной области.
Размеры экрана монитора величина фиксированная. Но для общности примем для них буквенные обозначения:
Long_x – размер по горизонтали
Long_y – размер по вертикали
x, y – значения до выполнения преобразований
x’, y’ – значения после выполнения преобразований
Тогда преобразование подобия запишется следующим образом:
x’ = x/(Right - Left)*Long_x y’ = y/(Up - Down)*Long_y
Преобразование переноса запишем так:
x’’ = x’ – Left y’’ = y’ – Down
И наконец преобразование “отображения сверху вниз” запишется так:
x’’’ = x’’ y’’’ = Long_y – y’’
А сейчас объединим все три преобразования в одно:
