Курс экономической теории учебник Издание 4-е, дополненное и переработанное Под общей редакцией проф. Чепурина М. Н
| Вид материала | Учебник |
- Учебник 3-е издание, переработанное и дополненное, 10138.23kb.
- Учебник издание пятое, переработанное и дополненное проспект москва 2001 Том 3 удк, 11230.01kb.
- Учебник издание пятое, переработанное и дополненное проспект москва 2001 Том 3 удк, 11433.24kb.
- Учебник. 3-е издание, переработанное и дополненное, 10586.44kb.
- Курс экономической теории: учебник / Под ред. М. Н. Чепурина, Е. А. Киселевой. Киров:, 204.91kb.
- С. С. Экономическая теория : Краткий курс. Владос 2010 Бесовский Л. Е. Фомичева, 26.91kb.
- Учебник 2-е издание, 4260.56kb.
- К. С. Гаджиев введение в политическую науку издание второе, переработанное и дополненное, 7545.88kb.
- В. Д. Аракина издание четвертое, переработанное и дополненное Допущено Министерством, 2717.43kb.
- В. И. Кузищина издание третье, переработанное и дополненное рекомендовано Министерством, 5438.98kb.
Неоклассические модели экономического роста строятся на базе производственной функции и основаны на предпосылках полной занятости, гибкости цен на всех рынках, а также полной взаимозаменяемости факторов производства. Попытки исследовать, в какой степени качество факторов производства и различные пропорции в их сочетании воздействуют на экономический рост, привели к созданию модели производственной функции Кобба-Дугласа. Рассмотрим эту модель подробнее.
Производственная функция Кобба-Дугласа и ее свойства
Функция Кобба-Дугласа получена в результате математического преобразования простейшей производственной функции У= F(L, К) в такую модель, которая показывает, какой долей совокупного продукта вознаграждается участвующий в его создании фактор производства. Она имеет следующий вид:

Функция Кобба-Дугласа - модель с двумя переменными факторами производства. Параметр А - коэффициент, отражающий уровень технологической производительности и в краткосрочном периоде он не изменяется. Показатели а и j3 - коэффициенты эластичности объема выпуска (К) по фактору производства, т. е. по капиталу К и труду L соответственно. При этом, если каждый из факторов оплачивается в соответствии со своим предельным продуктом, то а и /3 показывают доли капитала и труда в совокупном доходе. Иными словами, если цена капитала равна предельному продукту капитала, а цена труда равна предельному продукту труда, то параметры а и /3 определяют пропорцию, в которой труд и капитал получают свое вознаграждение за созданный продукт, т. е. долю капитала в доходе aY и долю труда в доходе /3Y. Так как /3= 1 - α, то а + /3 = 1, из чего следует, что мы имеем дело с постоянной отдачей от масштаба. Интересно рассмотреть эмпирические значения параметров функции Кобба-Дугласа: А = 1,1; а = 1/4; /J = 3/4. Следова-
Экономический рост 567
тельно, доля капитала в национальном доходе составляет 25%, а доля труда - 75%.
В поисках путей наибольшей эффективности производства нас всегда должна интересовать предельная производительность участвующих в нем факторов', с помощью которой определяется оптимальный объем используемых ресурсов. Предельный продукт капитала МРК пропорционален отношению доли капитала в доходе к объему использованного капитала: МРк = аУ/ К. Аналогично определяется и предельная производительность труда: MPL =/3Y/L.
Рассмотрим свойства производственной функции Кобба-Дугласа.
Первое свойство - постоянство отдачи от масштаба - описывается формулой F(nK,nL) = п А К°ЬВ и означает, что если увеличить использование капитала и труда в n раз, то объем совокупного выпуска, или объем дохода, возрастет в такое же число раз.
Второе важное свойство функции Кобба-Дугласа связано с изменением предельной производительности факторов. Например, если привлечь в производство дополнительное количество капитала К, а труд L использовать в прежнем объеме, то, при прочих равных условиях, предельная производительность труда MPL увеличится, а предельная производительность возросшего объема капитала МРк снизится. Если же увеличить количество труда, при прочих равных условиях, то его предельная производительность снизится, а предельная производительность капитала возрастет. Вывод: нарушение пропорции между трудом и капиталом при заданной технологии приводит к отклонению от оптимального объема производства, т. е. к неэффективности производства.
Однако, если мы увеличим параметр Л, например, внедрив более производительную технологию, то получим одновременное повышение МРк и MPV что является условием интенсивного экономического роста.
Третье свойство производственной функции Кобба-Дугласа ~ постоянство отношения дохода от труда к доходу от капитала (Р/а), т. е. постоянство соотношения долей капитала и труда в национальном продукте.
Исследования американского сенатора и экономиста Пола Дугласа показали, что в Соединенных Штатах за сорок лет (с 1948 по 1989 гг.) соотношение р/а колебалось в пределах между 2 и З2, в результате чего оплата
1 Предельная производительность капитала и труда представляют собой производные фун
кции Кобба-Дугласа: МРК = аА К"-' U5 ; MPL - j&4 К" £""' . В функции Кобба-Дугласа МРК
пропорциональна средней производительности капитала Y/K , a MPL пропорциональна сред
ней производительности труда Y/L.
2 Мэнкью Г. Макроэкономика. М. 1994. С. 113.
568
Глава 25
труда в 2-3 раза превышала вознаграждение капитала.1 Можно предположить, что постоянные рамки колебания соотношения |3/а заданы технологически. Колебания /5/а внутри этих рамок могут быть объяснены отклонением в соотношении / и S, так как вряд ли заработная плата, шкала налогообложения и нормы амортизации почти ежегодно могли претерпевать значительные изменения.
Макроэкономическое равенство /= 5 лежит в основе механизма экономического роста еще одной неоклассической модели, которая также базируется на производственной функции. Она называется моделью роста Со-лоу, по имени американского экономиста, лауреата Нобелевской премии Роберта Солоу.
Модель роста Солоу
Цель данной модели - ответить на три важных вопроса экономической политики: как добиться высоких и стабильных темпов роста, как одновременно с этим найти максимальный объем потребления и какое влияние на экономический рост оказывает увеличение населения и внедрение новых технологий.
Построение модели. Разделив двухфакторную производственную функцию Y = F(K,L) на количество труда L, мы получим производственную функцию для одного человека: у =f(k), где к = K/L - уровень капиталовооруженности единицы труда. Доход предстает как функция только одного фактора - капиталовооруженности. Такая единичная производственная функция изображена на рис. 25.2.
В данной функции предельная производительность капитала МР измеряется постоянно меняющимся углом наклона кривой у =/(к) и показывает прирост выпуска, если капиталовооруженность работника возрастет на 1 единицу, т. е. МРК = f(k + /) -f(k).
В модели Солоу спрос на продукцию предъявляется со стороны потребителей и инвесторов. Производственные блага в условиях равновесия полностью инвестируются (S = /), не оставляя места накоплению товарно-материальных запасов. Помня о макроэкономическом равенстве Y = С + I, выпуск одного работника можно записать в виде у = с + i ; функцию потребления как с = (l-s)y = (l-s)f(k)2, а функцию инвестиций на одного ра-
1 В понятие вознаграждение капитала, или доход на капитал, включается совокупная не
распределенная прибыль корпораций (т. е. прибыль ча вычетом налогов, амортизационных
отчислений и рентных платежей). Под вознаграждением труда, или доходом на труд, подразу
мевается лишь заработная плата. Во избежание искажений из данной модели исключен доход
собственников, так как это доход смешанного типа.
2 s - норма сбережения в доходе, a (1-s) - норма потребления в доходе.
Экономический рост 569
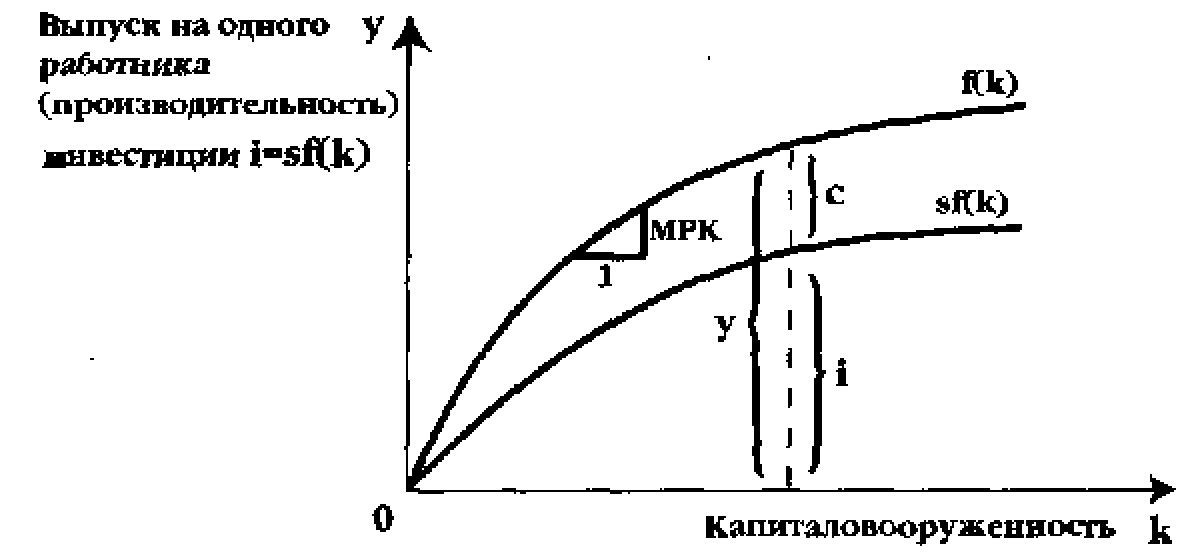
Рис. 25.2. Производственная функция у = f (к)
Данная функция построена из расчета на одного работника и характеризуется понижающейся предельной производительностью капитала МРХ
ботника как i = sy = s f(k). Графически размер потребления и инвестиций при каждом уровне капиталовооруженности изображены на рис. 25.2. Линией sf{k) обозначена функция инвестиций. Расстояние между функциями f(k) и sf(k) определяет объем потребления. На этом основании функция потребления выглядит как c=f(k) - Щк).
Важное место в модели Солоу занимает рассмотрение движения капитальных запасов, величина которых составляет разницу между размером инвестиций и объемом выбытия капитала: Дк =/- 6к , где 6 - норма выбытия капитала (или норма амортизации) и является константой, а 6к - объем выбытия капитала.
В ходе производства ежегодно пополняются капитальные запасы, независимо от того, с каким объемом капитала экономика начинает развиваться. Однако прирост капитала идет затухающими темпами. Это объясняется уже рассмотренным выше снижением предельной производительности капитала МРК, происходящей по мере увеличения капиталовооруженности одного работника. Но при наращивании капиталовооруженности растет и объем выбытия капитала. С ростом производства разница между инвестициями и объемом выбытия будет уменьшаться до тех пор, пока эти величины не выровняются между собой. Когда Дк = 0, производство, инвестиции и выбытие капитала не могут продолжать свой рост и останавливаются на определенном устойчивом уровне. Экономика достигает равновесия. Уровень капиталовооруженности, при котором Дк = 0, называется устойчивым уровнем капиталовооруженности (к*) и характеризует состояние равновесия экономики, отличающееся устойчивостью инвестиций и выбытия капитала, неизменностью объема производства. В условиях равновесия sf(k*) -бк* = 0 или sf(k*) = бк*.
570
Глава 25
Эта формула дает возможность вычислить устойчивый уровень капиталовооруженности (к*), не прибегая к длительным подсчетам ежегодного прироста капитала и производства за ряд лет. Из пропорции к*// (к*) = s/6 видно, что к* =f(k*) s/6.
Устойчивый уровень капиталовооруженности можно найти и с помощью графического анализа. На рис. 25.3 пересечение графика инвестиций sf(k) и графика выбытия капитала 8к как раз и будет соответствовать к*.
Величину к* можно найти, опустив перпендикуляр на ось абсцисс из точки пересечения графика инвестиций и графика выбытия капитала, чему соответствует равенство sf(k)= 6к.
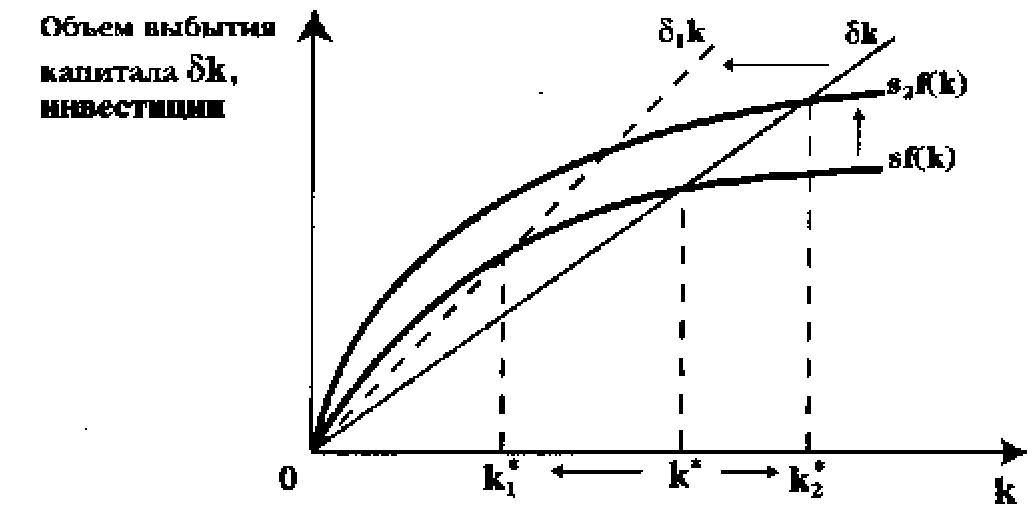
Капиталовооруженность
Рис. 25.3. Устойчивый уровень капиталовооруженности к*
Для уяснения работы модели Солоу нужно иметь в виду, что при необходимости государственная политика может повлиять на уровень к*, воздействуя на норму сбережения s или на норму амортизационных отчислений б, от величины которой зависит скорость обновления капитала. Например, политика ускоренной амортизации на рис. 25.3 выразится в смещении графика бк до уровня &,к. При этом устойчивый уровень капиталовооруженности сократится до к* 1 Увеличение нормы сбережений s до s2 наоборот, приведет к повышению равновесного уровня капиталовооруженности до k*2 в результате смещения графика инвестиций до уровня s2 f(k).
Модель Солоу показывает, что большему объему инвестиций, а значит, и более высокой норме сбережений в национальном доходе {при условии выполнения равенства S = I), соответствует наибольший доход на душу населения. Это статистически подтверждено исследованиями многих экономистов. Так, к странам с наибольшим годовым доходом на душу населения (по состоянию на 1993 г., в долл. США) относятся Великобритания (14660
Экономический рост
571
долл.), Франция (5130 долл.), Германия (16420 долл.), Италия (14670 долл.), США (21530 долл.), Япония (17710 долл.).1 В этой группе стран на протяжении трех десятилетий разница между средними объемами инвестиций и сбережений была минимальной (0,1% от ВВП), а норма сбережений - наиболее высокой (23% от ВВП) по сравнению с аналогичными показателями в странах с более низкими доходами. В странах со средним уровнем дохода сберегалось от 20% до 22% от ВВП, а в странах с низким уровнем дохода на душу населения - от 10% до 19% от ВВП.2
Модель Солоу помогает ответить на очень важный вопрос, от которого зависит успех макроэкономической политики правительства: как в стране достичь максимального уровня потребления при заданных темпах экономического роста? Условие, при котором достигается максимальный уровень потребления, американский экономист Э.Фелпс в работе «Басня для тех, кто занимается ростом» (1961 г.) назвал золотым правилом накопления.
В соответствии с золотым правилом, уровень потребления будет самым высоким при достижении наибольшей разницы между объемом выпуска f(k*) и объемом выбытия Ък* в условиях устойчивого уровня капиталовооруженности, когда &к* равен объему инвестиций. Поэтому потребление по золотому правилу называется устойчивым уровнем потребления:
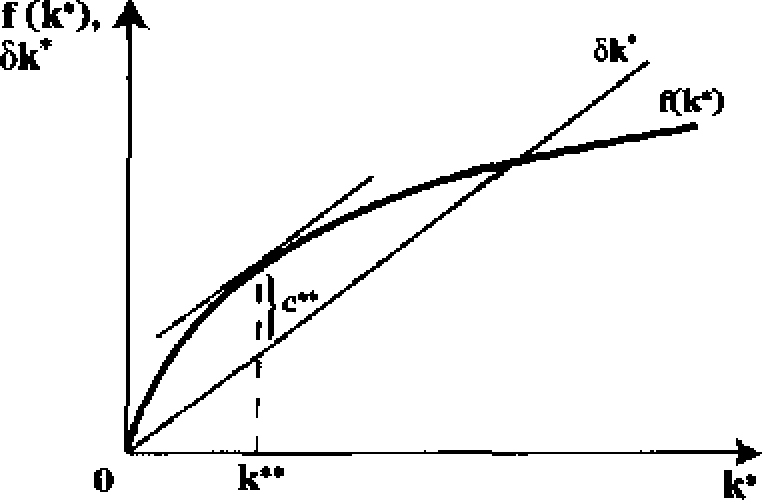
с** =Л**) " °к (5)
Запас капитала, обеспечивающий устойчивое состояние при таком потреблении, называется золотым уровнем накопления капитала (к**). На рис. 25.4 показано, как можно найти с** и к** графическим способом.
Рис. 25,4. Золотой уровень потребления с** и золотой уровень накопления капитала к**
Итак, максимального уровня потребления с** можно достичь только при золотом уровне накопления капитала к**. Такой уровень накопления капитала возможен только при выполнении условия МРК — 8. Это и есть само золотое правило: максимальный уровень потребления с** достигается только при
МРК = 5 (6)
'Гайдар Е. Аномалии экономического роста. М. 1997. С. 37. 2Там же. С. 25.
572
Глава 25
Действительно, если имеющийся устойчивый запас капитала превышает золотой уровень к**, то при дальнейшем росте капитала его предельный продукт будет меньше нормы выбытия, что снизит уровень потребления. В противном случае рост капитала вызовет повышение потребления, так как МР превысит норму выбытия. Следовательно, золотое правило, т. е. равенства МРК = б, является условием достижения максимального уровня потребления при заданных темпах экономического роста.
Таким образом, для поддержания максимального потребления необходимо, чтобы чистая производительность капитала (МРК - б), т. е. предельный продукт капитала, оставшийся после амортизационных отчислений, была равна темпу прироста производства.
Рассмотрим, как модифицируется золотое правило, если в модель Со-лоу последовательно ввести условие роста населения и технического прогресса.
Рост населения влияет на капиталовооруженность так же, как и норма выбытия, то есть уменьшает запасы капитала. Действительно, с ростом L снижается и уровень капиталовооруженности k = K/L, и выпуск на одного работника у = f(k)= Y/L. Если в модель Солоу ввести показатель темпа роста населения л, то уровень инвестиций, необходимый для компенсации выбытия капитала и роста населения, должен быть равен (Ь + п) к. Прежний объем капитала распределяется между возросшим количеством работников. Это объясняет снижение устойчивого уровня капиталовооруженности: s f(k) = (б + п) к, что проиллюстрировано на рис. 25.5а. Так же снизится и устойчивый максимальный уровень потребления: с** =f(K*) - (б + п) к*, который с учетом роста населения будет достигаться при таком устойчивом уровне накопления к**, который возможен только при МРК = б + п. Итак, максимизирующее уровень потребления золотое правило с учетом роста населения описывается равенством:
МРк=Ь + п (7)
Поэтому для достижения максимального уровня потребления необходимо, чтобы чистый предельный продукт капитала (МРК- б) был равен темпу прироста населения. Таким образом, по модели Солоу страна с быстро растущими темпами населения будет иметь более низкий устойчивый уровень капиталовооруженности и более низкий доход на душу населения.
Воздействие технического прогресса на экономику связано, прежде всего, с приростом эффективности труда (E), идущего постоянным темпом g. Тогда общее количество единиц труда составит L Е и с учетом роста населения будет расти темпом n+g. В этом случае к = K/(LE) - количество капитала на единицу труда с постоянной эффективностью, а у = Y/(LE) -объем производства на единицу труда с постоянной эффективностью.
Экономический рост
573
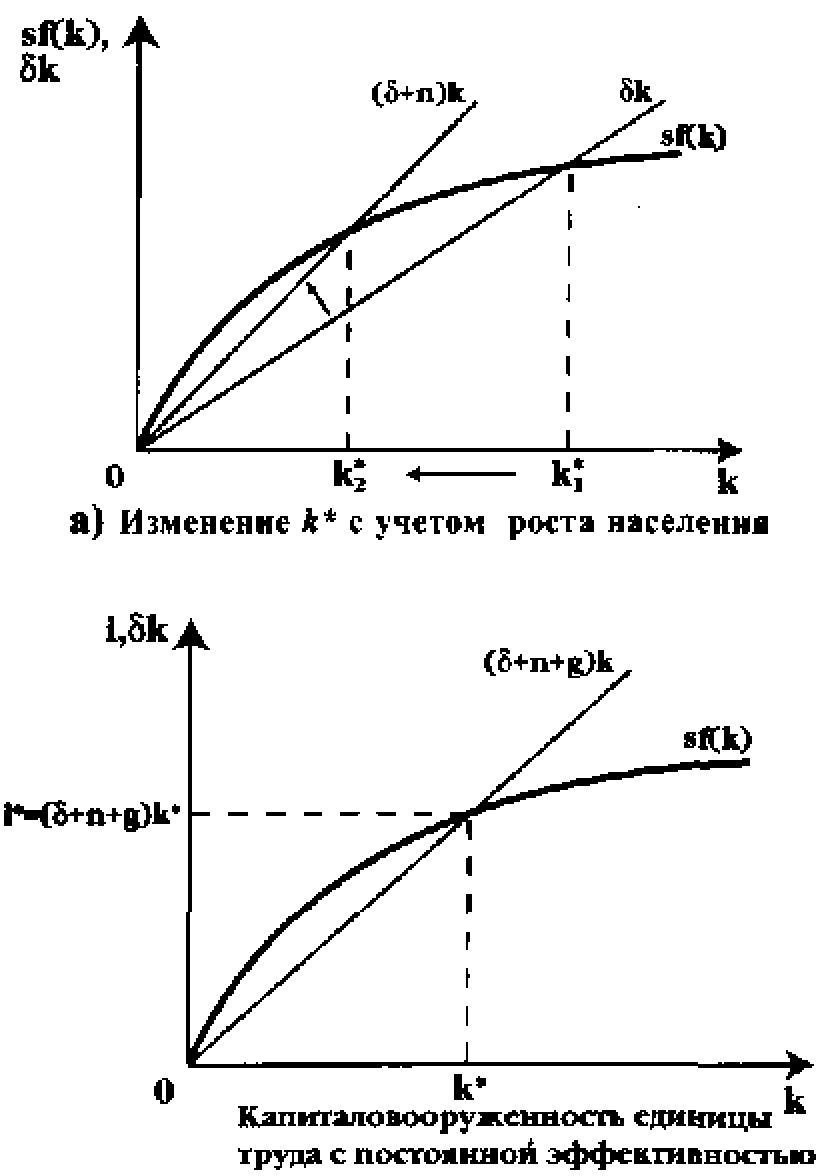
б) к* с учетом роста населения и технического прогресса
Рис. 25.5. Устойчивый уровень капиталовооруженности с учетом параметров роста населения и технического прогресса
Технический прогресс вызывает прирост эффективности труда с постоянным темпом g. Следовательно, выпуск на одного работника также растет с темпом g.
Прирост запасов капитала с ростом технического прогресса снизится: Ak = sf(k ) - (6 + п + g)k. Устойчивый уровень капиталовооруженности к* будет достигнут, когда инвестиции полностью смогут компенсировать уменьшение к из-за выбытия капитала, роста населения и технического прогресса: яДй)=(8 + п + g)k. При равновесии к* будет отражать устойчивый уровень капиталовооруженности единицы труда с постоянной эффективностью (см. рис. 25.56). Соответственно, устойчивый уровень потребления составит: с** =f(k*) - (5 + я + g) k*. Итак, максимальный устойчивый уровень потребления гарантируется таким объемом накопления к**, который достигается при выполнении золотого правила с учетом роста населения и технического прогресса:
574
Глава 25
МРК = 6 + п +g (8)
Так как выпуск на одного работника в устойчивом состоянии растет темпом g, то валовой выпуск растет темпом n + g. Именно этому темпу выпуска должен соответствовать чистый предельный продукт капитала, чтобы достичь максимального объема потребления в устойчивом состоянии экономики, т. е. МРК - 5 = » + g.
Модель Солоу показывает, что увеличение сбережений приводит в краткосрочном плане к увеличению капитальных запасов и объему производства. Но это происходит только до момента достижения равновесного состояния экономики при устойчивом уровне капиталовооруженности. В долгосрочном плане рост производства зависит от темпа технического прогресса. Только этот экзогенный фактор может поддержать непрерывный рост производства, а значит, и рост потребления.
§ 4. Неокейнсианские модели экономического роста
В неокейнсианских моделях экономический рост исследуется с помощью инструментов и методов анализа кейнсианской школы, примененных к динамическим процессам. Напомним, что под динамическим равновесием понимается равенство темпов прироста совокупного спроса и совокупного предложения. Поэтому модели, исследующие достижение и характер такого равенства, называются динамическими.
Необходимо отличать временные лаги от понятий кратко- и долгосрочного периода. В динамических моделях, в отличие от статических, критерием кратко- или долгосрочности периода является изменение технологии производства. Краткосрочный динамический период характеризуется неизменностью технологии, которая может сохраняться в предыдущем, текущем и будущем периодах (t1 , t и t) при варьирующихся темпах реального ВВП. Соответственно, в долгосрочном динамическом плане меняется сам технологический уровень производства.1
Модель динамического равновесия Домара
Модель динамического равновесия американского экономиста Е.Дома-ра2 основана на производственной функции, факторы которой не являются взаимозаменяемыми. Каковы предпосылки данной модели? Во-первых, из-
1 В неокейнсианских моделях экономического роста предпосылки и методы кеннсианско-
го анализа экономики в краткосрочном плане используются в более широких рамках, но это
оправдано тем, что для динамических моделей неизменность технологии растущего произ
водства является признаком краткосрочного периода.
2 Любопытно заметить, что американский экономист Евсей Домар был выходцем из России.
Экономический рост
575
менения спроса и предложения рассматриваются только на реальном рынке, находящемся в состоянии равновесия. Во-вторых, избыток предложения труда и постоянство относительных затрат факторов производства позволяют расширять производство без изменения цен. В-третьих, при неизменной технологии (т. е. в краткосрочном динамическом плане) прирост инвестиций рассматривается в качестве единственного фактора роста совокупного спроса и совокупного предложения, а предельная производительность ресурсов, прежде всего капитала, - величина постоянная.
В модели Домара совокупный спрос в текущем периоде (t) изменяется по кейнсианскому сценарию, т. е. в результате мультипликационного эффекта увеличения инвестиций в том же (текущем) периоде:
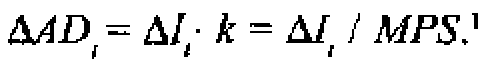
Процесс увеличения совокупного предложения в текущем периоде &AS распадается на два этапа. В предшествующем периоде (/-1) происходит рост инвестиций А/ , который и создает в начале текущего периода (t) приращение капитала АК1; как непосредственный источник роста совокупного предложения. Таким образом, прирост совокупного предложения в текущем периоде составит: AASt— аАК — оА1 , где СТ - предельная производительность капитала (AY/AK) = const по условию.2
Условием равновесного экономического роста в текущем периоде является достижение одинаковых темпов изменения совокупного спроса и совокупного предложения, измеряемых в темпах прироста: AADt = AASt = AY IY
Подставив
в
равенство AAD, = AASt формулы этих величин, получим
о MPS
All MPS = Ш.,, или Ы. I Л/
-,., —,'—,., - — (9)
Например, если норма сбережения равна 20%, или 0,2, а предельная производительность капитала равна 0,3, то равновесный темп экономического роста будет наблюдаться при темпах роста инвестиций, составляющих 0,2 х 0,3 = 0,06 или 6% в год.
Итак, мы выявили критерий достижения равновесного экономического роста: инвестиции в период t должны расти темпами, равными произведению нормы сбережений на величину предельной производительности капитала.
При соблюдении изложенных выше предпосылок модели краткосрочного динамического равновесия: S = I; (MPS, a, KIL ) = const, темп прироста
1 При небольшой разнице в долгосрочном плане среднюю норму сбережений APS (или s) условно можно приравнять к величине предельной склонности к сбережению MPS.
2Следует заметить, что одни и те же буквы у разных экономистов могут означать различные экономические категории. См. список сокращений в конце учебника.
576
Глава 25
предложения труда AL/L,л должен быть равен темпу прироста капитала (Kt / Kt-1, который, в свою очередь, равен темпу прироста инвестиций и совокупного продукта:
Л/ / М =ДГ / Y = АК / К = ALI L = aMPS (10)
Мы получили расширенное условие динамического равновесия в модели экономического роста Домара.
Однако для того, чтобы поддерживалось такое динамическое равновесие, необходимо выполнение условия, которое в экономической литературе получило название «парадокс Домара». Парадокс заключается в том, что при постоянно растущем объеме производственного капитала недостаточное инвестирование приводит к перепроизводству продукции (хотя, на первый взгляд, сокращение инвестиций должно бы привести к недопроизводству). Действительно, если Д1( - const или Д1( < АК, , обнаруживается перепроизводство продукции, так как совокупный спрос отклоняется в сторону превышения, а совокупное предложение - в сторону занижения своего равновесного значения. Иными словами, если рост инвестиций отстает от роста капитала, то можно говорить об относительном сокращении инвестиций в составе совокупного спроса, что и вызывает снижение темпов роста AD. Таким образом, для поддержания равновесного темпа роста на постоянном уровне необходимо от периода к периоду увеличивать прирост инвестиций для полной загрузки растущих производственных мощностей (К). Следовательно, существует темп роста, гарантирующий полное использование производственного потенциала. Такой темп роста, обеспечивающий полную занятость капитала, называется гарантированным1 и является равновесным.
Очевидно, что равновесный темп роста очень неустойчив и во многом зависит от инвестиционной политики правительства, которое (в краткосрочном для динамической модели плане) регулирует и норму сбережений, и объем инвестиционных потоков в экономику. В долгосрочном динамическом плане научно-техническая политика правительства способна повлиять и на предельную производительность капитала. Однако следует иметь в виду, что очень сложно воздействовать на национальную норму сбережений посредством экономической политики по сравнению с воздействием на нормы амортизационных отчислений, устанавливающихся административным способом. Нельзя заставить людей больше или меньше сберегать: величина MPS определяется множеством факторов, включая институциональные и психологические.
Первым понятие гарантированного темпа роста ввел английский экономист Р.Харрод. Е.Домар проводил свои исследования позже и пришел к модели гарантированного темпа роста независимо от Харрода.
Экономический рост 577
Например, в условиях современной России из-за низкой степени доверия к банковской системе реализация равенства S = I весьма сомнительна. Большая часть сбережений хранится на руках у населения, а не в кредитных учреждениях, что серьезно осложняет задачу превращения сбережений населения в инвестиции.
Модель экономического роста Харрода
В конце 30-х гг. нашего века английский экономист Рой Ф. Харрод, которого Кейнс провозгласил продолжателем своих научных идей, создает динамическую модель1 экономического роста. Он исследует, каким образом в процессе роста происходит взаимодействие капитала, рабочей силы и величины дохода на душу населения. Первый вопрос, который ставит Харрод, сводится к следующему: как должен изменяться объем капитала, чтобы соответствовать росту остальных названных элементов при постоянной процентной ставке.
При условии, что население растет в геометрической прогрессии, а уровень технического развития и процентной ставки остается неизменным, спрос на капитал, по утверждению Харрода, будет расти в той же пропорции, что и население. Достижение равновесного объема производства возможно, если норма сбережения s и отношение величины используемого капитала к объему дохода K/Y (коэффициент капитала, или капиталоемкость) постоянны. Харрод полагает, что при соблюдении этих условий для обеспечения экономического роста необходимо, чтобы норма сбережения была равна произведению капиталоемкости и прироста населения в текущем периоде. Если изменить условия, зафиксировав движение населения и учитывать непрерывное развитие технического прогресса, то для обеспечения экономического роста потребуется такая же норма сбережения (так как технический прогресс выражается в сбережении труда или капитала).
Таким образом, увеличение численности населения и поступательное движение технического прогресса являются естественными условиями экономического роста.
Методом исследования и систематизации факторов экономического роста в модели Харрода является основное уравнение:
GxC = s, (10)
где G = AYt/Ytл - рост (growth) выпуска продукции за единичный период, измеряемый в темпах прироста; С =AK/AY, - предельная капиталоемкость, выражающая количество капитальных благ, фактически произведен-
1 Модель Харрода была создана им раньше модели Домара. Сходство выводов и допущений этих двух независимых моделей позволило дать им общее название: модель Харрода-Домара.
37
578
Глава 25
ных ex-post за каждый период, деленное на прирост продукции за тот же период1; s = S/Y - предполагавшаяся норма сбережения (Харрод считает, что «вероятную величину сбережения» ex-ante лучше всего выразить как сберегаемую часть совокупного дохода)2. Основное уравнение определяет, какой должна быть норма сбережения для достижения экономического роста.
Следует отметить, что AKt =Itlи поэтому величину С можно выразить как1ы,/ДУ((т. е. как акселератор). Подставив в формулу (] 0) значения ее величин, получим AYt/Ytl X I tl/AY= St/Ytl при условии, что сбережения осуществляются и расходуются на капиталовложения (инвестиции) в рамках одного временного периода. Сократив левую часть равенства на AYt, получим IJY= St_, /Yt_, т. e. I = S: инвестиции ex-post равны сбережениям ex-ante (инвестиции, фактически осуществленные в данный период, совпали с ранее планировавшимися на этот период сбережениями), что является важным условием динамического равновесия.
Основное уравнение (10) выражает фактический темп роста, наблюдающийся как при подъеме, так и при рецессии.
Для характеристики условий стабильного поступательного экономического роста (при нейтральности3 технического прогресса и при неизменной процентной ставке) Харрод использует формулу:
G.xC=S, (И)
где Cw - темп роста, гарантирующий полную занятость растущего капитала, при котором производители из периода в период остаются в положении равновесия (т. е. G - линия предпринимательского равновесия). Так Харрод вводит понятие гарантированного (warranted) темпа роста.
С. - это требуемая (required) предельная капиталоемкость, выражающая, в отличие от фактического показателя предельной капиталоемкости С, потребность в добавочном капитале для выпуска добавочной продукции.4
Итак, для поддержания стабильного и равновесного роста необходима такая норма сбережений, величина которой равна произведению показате-
1 Харрод Р. К теории экономической динамики. Классики кейнсианства. T.I. M., 1997.
С. 112.
2 Харрод Р. К теории экономической динамики. Классики кейнсианства. T.I. M.. 1997.
С. 113.
s Нейтральным Харрод считает технический прогресс, т. е. «поток ичобретении, оставляющих без изменения ту пропорцию, в которой совокупный продукт распределяется между трудом и капиталом при постоянной процентной ставке». Это объясняется тем, что эффекты от изобретений, требующих увеличения капитальных затрат, и от изобретений, снижающих затраты капитала, уравновешиваются.
4 Харрод трактует С, как «предельную величину, выражающую потребность в новом капитале для сохранения такого выпуска продукции, который должен удовлетворить потребительский спрос, возникающий из предельного добавочного дохода потребителей» {Харрод Р. К теории экономической динамики. Классики кейнсианства. Т. 1. М. 1997. С. 117).
Экономический рост
579
ля гарантированного темпа роста и требуемой для его обеспечения предельной капиталоемкости.
Между уравнениями (10) и (11) существует определенная связь, основанная на том, что, если растет G, то уменьшается значение С (разумеется, при условии, что норма сбережения s постоянна). Следовательно, если фактический темп роста превышает гарантированный (G > Gw ), то значение показателя фактической предельной капиталоемкости становится ниже требуемой (С < Сr). Это говорит о том, что фактических товарно-материальных запасов и оборудования становится недостаточно и предприниматели увеличивают свои заказы. Если же фактический рост меньше гарантированного (G < Gw) то С > Сr, и предприниматели будут сокращать инвестиции, что приведет к дальнейшему снижению совокупного спроса и увеличению избыточных производственных мощностей. Таким образом, Харрод обосновывает крайнюю неустойчивость рассматриваемой им системы, получившую в экономической науке название «балансирование на лезвии ножа» (knife edge). Отклонение от равенства G = Gw приводит к нарастанию из периода в период центробежных сил, углубляющих этот дисбаланс и приводящих все к большему расхождению между совокупным спросом и совокупным предложением.
Однако рост G имеет естественные ограничители в виде темпов роста населения и темпа технического прогресса. Харрод вводит понятие естественного темпа роста GN учитывающий эти естественные условия экономического роста. GN- это темп роста, при котором полностью используется растущее предложение труда. Он характеризует такую линию развития, которая обеспечивает равновесие на рынке труда. Если фактический темп роста G равен GN то экономика развивается в условиях полной занятости. Таким образом, GN - это верхний предел фактического темпа роста G.
Харрод исследует связь между G, Gw и GN с помощью уравнений:
GNCr = s или GNCr <>S (12)
Иными словами, идеальные условия для поддержания стабильных равновесных темпов экономического роста выражаются в равенстве:
GwCr = s = GNCr1 (13)
Однако основная проблема заключается в отклонении от равновесия (когда GNCr <> s), порождающем расхождение между Gw и GN что обусловливает хроническую безработицу. Другая важная проблема, которая рассматривалась выше - отклонение фактического темпа роста от гарантиро-1 Такое равенство допустимо при больших величинах Сr и выполняется в долгосрочном плане.
37*
580
Глава 25
ванного (G от Gn ), что лежит, по мнению Харрода, в основе промышленного цикла.
Соотношение GN G и GW имеет решающее значение для определения тенденций экономической конъюнктуры. Харрод считает, что тенденции бума или кризиса определяются не величиной Gw , а степенью отклонения от нее. Подведем итоги рассматриваемой проблемы:
- Если G > Gw или GN > Gw, то возникает тенденция к развитию бума. Действительно, недостаточность в капитале вызывает повышение спроса на капитал и способствует росту инвестиций.
- Если GN < Gw, то и G, ограниченный уровнем GN в среднем должен быть ниже G , что подталкивает экономику к депрессии. Это обстоятельство Харрод считает парадоксальным. Ведь на первый взгляд может показаться, что более быстрое развитие экономики, превышающее темпы, заданные естественными условиями, должно привести к буму.
Интересно заметить, что, по мнению Харрода, этот «парадокс» касается основного противоречия между кейнсианской и классической школами. Сбережения в экономике могут играть как положительную, так и отрицательную роль в зависимости от соотношения между GN и Gw. До тех пор, пока GN > GW, сбережения «добродетельны». Когда же GN
Таким образом, политика государства, стимулирующая экономический рост, должна опираться на корректирующую (сдерживающую или стимулирующую) инвестиционную политику, на регулирование баланса между сбережениями и инвестициями. Государственное регулирование также должно стремиться к минимизации отклонения между гарантированным и естественным темпом роста. Однако для поддержания равновесного темпа роста и сохранения уровня полной занятости необходимо поступательное снижение процентной ставки (а не снижение уровня заработной платы, как считают классики). В рыночной системе процентная ставка неизбежно колеблется, и поддержание ее на стабильно низком уровне, по мнению кеЙн-сианцев, - долгосрочная задача экономической политики.
§ 5. Научно-технический прогресс (НТП) как внешний фактор
экономического роста. Оценка вклада НТП
в экономический рост в динамических моделях
Как подсчитать тот вклад в прирост совокупного продукта, который дает улучшение качества капитала и труда за счет внедрения результатов научно-технического прогресса? Ведь исследования экономистов показывают, что суммарный прирост капитала и труда на 1% приводит к большему, чем на 1% , приросту совокупного дохода.
Экономический рост
5 81
Попытку подсчитать темп экономического роста с учетом фактора технического прогресса сделал голландский экономист Ян Тинберген, лауреат Нобелевской премии по экономике. Он усовершенствовал функцию Кобба-Дугласа, введя в нее показатель темпа технического прогресса:
Y = AK"LGn, (14)
где r - темп технического прогресса, а е - основание натурального логарифма.
Однако слишком трудно выявить и тем более подсчитать вклад технического прогресса в экономический рост. Во-первых, технический прогресс - весьма долгосрочный фактор, его сложно наблюдать в кратко и среднесрочных отрезках времени. Во-вторых, технический прогресс, как внешний фактор экономического роста, проявляется в большей степени неявно и опосредованно, через улучшение качества производственных факторов. Поэтому более плодотворными оказались попытки ученых подсчитать вклад технического прогресса в рост производства, прибегая к остаточным методам.
Рассмотрим два подхода к определению вклада технического прогресса, использующих остаточные методы. Это теоретический подход, воплощенный в модели «остаток Солоу», и подход, используемый в фундаментальной науке, который мы назовем «остатком Денисона».
Весьма показательно демонстрирует вклад технического прогресса в экономический рост модель, основанная на функции Кобба-Дугласа. Принцип расчета предельно прост: если из общего прироста совокупного дохода Гвычесть ту его часть, которая образовалась за счет прироста капитала К и прироста труда L, то станет очевидным, что оставшаяся часть совокупного дохода создана за счет фактора технического прогресса. Как найти эти величины?
Известно, что прирост капитала на АК увеличит производство на МРАК. Аналогично расширение фактора труда на &L приведет к расширению объема производства на величину МР. ■ AL. Соответственно, при одновременном изменении этих двух факторов прирост совокупного продукта составит: AY = МРК-АК + MPL-M. Однако экономический рост измеряется в темпах прироста. Учитывая, что доля капитала в произведенном продукте выражается как а= MPK-&K/Y, а доля труда, как j3 = MP&JL/Y, что соответствует показателям а и (3 в производственной функции Кобба-Дугласа, мы можем записать функцию темпов прироста производства в следующем виде: AY/Y = a-AKIK + ptd.IL.
Для того, чтобы учесть фактор технического прогресса, представим производственную функцию, как Y = A F(K, L). Фактор А обозначает технологический уровень производства, который определяет совокупную произво-
582 Глава 25
дительность факторов Kи L. Теперь в нашу динамическую функцию экономического роста можно добавить вклад прироста совокупной производительности факторов АА/А и функция примет вид:
AY/Y= аАК/К + /ЗА L/L+ АА/А
Таким образом, мы получаем возможность оценить долю технического прогресса в приросте объема производства (АА/А) остаточным методом:
АА/А = AY/Y - аАК/К - /3AL/L (Ц)
Показатель АА/А в экономической теории называется остатком Солоу и является мерой участия технического прогресса в экономическом росте.
Большой вклад в исследование роли технического прогресса внес американский, ученый Эдвард Ф.Денисон. В упомянутой выше работе «Исследование различий в темпах экономического роста» (1967 г.) ему удалось подсчитать величину остаточного фактора экономического роста, включающую в себя все факторы, которые влияют на экономический рост помимо труда, капитала и земли. В таблице 25.2 показано, какая доля экономического роста обеспечена остаточными факторами (выражены в темпах прироста).
Таблица 25.2
Мера влияния остаточных факторов, включая прогресс знаний, на темпы роста национального дохода (НД) (в процентных пунктах)
| Годы | 1950-1962 г г . | 1950-1955 гг. | 1955-1962 гг. | |||
| | темпы роста | Темпы роста | темпы роста | |||
| Страна, Регион США | НД 3,32 | остаточного фактора 0,76 | НД 4,23 | остаточного фактора 0,76 | НД 2,67 | остаточного фактора 0,76 |
| СевероЗападная Европа | 4,78 | 1,30 | 5,68 | 1,77 | 4,11 | 0,99 |
| Франция | 4,92 | 1,51 | 4,77 | 1,48 | 5,03 | 1,56 |
| ФРГ | 7,26 | 1,56 | 9,93 | 2,55 | 5,59 | 0,87 |
| Англия | 2,29 | 0,79 | 2,32 | 0,70 | 2,27 | 0,87 |
| Италия | 5,96 | 1,65 | 6,30 | 2,12 | 5,71 | 1,30 |
Источник: Денисон Э. Исследование различий в темпах экономического роста. М.,1971. Составлено по таблицам 20-1,21-1, 21-9, 21-11, 21-17, 21-19.
Экономический рост 583
Вполне очевидно, что остаток Солоу и остаточный фактор Денисона (или остаток Денисона) - суть один и тот же показатель, учитывающий фактор технического прогресса. Из таблицы 25.2 видно, что увеличение остатка Денисона сопровождается ростом темпов национального дохода. Представленные в таблице данные делятся на два периода: послевоенный (1950-1955 гг.) - восстановительный для пострадавших стран, и период с восстановленной экономикой (1955-1960 гг.). Страны с наибольшими разрушениями - Италия и ФРГ - демонстрируют наивысшие темпы роста НД в восстановительном периоде. В период с нормальным функционированием экономики темпы роста НД, естественно, замедляются, но остаются сравнительно высокими, так как страны Европы пытались ликвидировать технологический разрыв с США и повышать эффективность производства, перенимая опыт лидера.
Итак, рассмотрев влияние научно-технического прогресса на экономический рост, можно сделать следующие выводы.
Воплощенный, т. е. материализованный технический прогресс - важный внешний фактор интенсивного экономического роста, который можно оценить как степень улучшения качества капитала, его производительности. Невоплощенный, т. е. нематериализованный технический прогресс, включающий в себя прогресс знаний (производственных и управленческих), очень сложно выделить и оценить отдельно от других факторов, повышающих производительность на единицу затрат. Очевидно, оценить этот фактор можно, используя остаточные методы, например, в виде остатка Солоу или остатка Денисона.
Для проведения эффективной политики стимулирования экономического роста необходимо давать реалистичную оценку темпов изменения национального дохода в соответствии со следующими принципами. Наиболее высокие темпы национального дохода характерны для перехода страны к более высокому уровню экономического развития, осуществляемому в виде скачка в производственных и организационных технологиях. Этому периоду предшествует стадия с низкими темпами роста национального дохода, а возможно, и отрицательными, что отражает потребность экономики в этом скачке. После осуществления перехода к более высокому уровню экономического развития и распространения новой производственно-управленческой технологии как доминирующей, темпы национального дохода замедляются и стабилизируются. В странах, правительство которых в политике стимулирования роста национального дохода делает ставку на повышение производительности, прежде всего, с помощью прогресса знаний и технологий, высокие темпы будут обеспечиваться преимущественно за счет уве-
584
Глава 25
личения так называемого остаточного фактора. Следует помнить, что высокие темпы характерны только для промежуточного, переходного периода к более высокому уровню производства. В условиях нормального режима работы экономики нельзя ставить задачу сохранения высоких темпов роста. Цель экономической политики в этот период должна смениться на поддержание более умеренных, но стабильных темпов. Необходимо изменить и способ достижения этой цели: перенести акценты с мер активизации внешних факторов экономического роста на внутренние факторы (совокупный спрос и совокупное предложение). Соответственно, основными инструментами достижения этой цели послужат стимулирующая кредитная или бюджетно-налоговая политика, воздействие на уровень занятости, поддержание необходимого баланса между сбережениями и инвестициями.
Основные понятия:
Экономический рост Темпы экономического роста Экстенсивный экономический рост Интенсивный экономический рост Факторы экономического роста Нематериализованный технический прогресс Материализованный технический прогресс Производственная функция Кобба-Дугласа Модель роста Солоу Золотое правило Динамическое равновесие Модель Домара Парадокс Домара Модель Харрода Гарантированный темп роста Естественный темп роста Остаток Солоу Остаток Денисона
economic growth
economic growth rate
extensive economic growth
intensive economic growth
economic growth factors
disembodied technical
progress
embodied technical
progress
Cobb-Douglas production
function
Solow growth model
golden rule
dynamic equilibrium
Domar model
Domar paradox
Harrod model
warranted rate of growth
natural rate of growth
Solow residual
Denison residual
585
