Geum.ru

Вестник Брянского государственного технического университета. 2009. №3(23) Управление, вычислительная техника и информатика

Вид материалаДокументы
Подобный материал:

Вестник Брянского государственного технического университета. 2009. № 3(23)

Управление, вычислительная техника


и информатика


УДК 681.5.09


И.Г.Горюнов, Н.К.Жиганов


Принятие решений ситуационного управления
в автоматизированных системах массового обслуживания


Рассмотрены вопросы повышения производительности автоматизированных систем массового обслуживания путем применения ситуационного управления, вопросы оценки рисков принятия ошибочных решений о коррекции значений параметров алгоритма ситуационного управления в процессе функционирования системы массового обслуживания.


Ключевые слова: принятие решений, ситуационное управление, автоматизированные системы массового обслуживания, имитационные эксперименты.


Ситуационное управление (СУпр) процессом массового обслуживания применяется к отдельному классу систем массового обслуживания (СМО) с конечным временем старения (ожидания) заявок, часто встречающемуся на практике. Характерной особенностью СМО, относящихся к данному классу, является то, что качество их функционирования определяется ценностью заявок в момент завершения их обслуживания. При этом ценность каждой заявки, поступающей в СМО, снижается по мере пребывания в системе, причем заявка полностью обесценивается за конечный интервал времени. Для определения величины ценности заявке присваивают функцию старения, которая по условию должна быть невозрастающей от времени пребывания заявки в системе и падать до нуля за конечный промежуток времени [1].

Одним из элементов СУпр является возможность отказа в обслуживании заявки. При выборе очередного управляющего воздействия, связанного с отказами в обслуживании, проверяются следующие условия [2]:

1) из всех заявок одного типа, находящихся на одном месте в очереди СМО, в первую очередь должна быть отброшена заявка с наибольшим числом фаз дообслуживания;

2) из всех заявок одного типа с одинаковым числом фаз дообслуживания в первую очередь должна быть отброшена самая старая заявка.

В большинстве реальных СМО встречается явление пробок, т.е. ситуаций, когда поступившая в очередь или уже частично обслуженная заявка ввиду внешних условий временно не может дальше обслуживаться, что создает очередь заявок, которые вынуждены ожидать дообслуживания текущей.

Следовательно, для повышения эффективности функционирования таких СМО необходимо учитывать состояние заявки и условия пребывания в этом состоянии (в частности, время, в течение которого заявка находится в этом состоянии).

Типовыми примерами СМО, относящихся к данному виду, являются автоматизированные системы банковских расчетов (АСБР), осуществляющие перевод платежей со счетов отправителей на счета получателей в течение ограниченного интервала времени, а также информационно-сервисные системы нефтедобывающего комплекса (ИССНК). В АСБР простои, отказы и задержки в обслуживании приводят к значительным материальным затратам участников расчетов, а в нефтедобывающих комплексах - к снижению производительности и уровня безопасности технологических процессов.

С математической точки зрения поступление заявки (электронного платежного сообщения в АСБР или заявки на сервисную операцию в ИССНК), ее пребывание и обслуживание являются случайными процессами. Соответственно поступление заявок и их пребывание в автоматизированной системе массового обслуживания (АСМО) описываются с помощью вероятностных законов распределения значений случайных величин (величины интервала поступления, времени пребывания в очереди и обслуживания).

Для АСМО характерна ситуация, когда только увеличением мощности ее аппаратно-программного комплекса не удается повысить производительность (которая выражается в количестве обслуженных и отброшенных заявок относительно общего числа поступивших за интервал времени), так как после некоторого порогового значения увеличения мощности аппаратно-программного комплекса СМО задержки и отказы в обслуживании заявок будут определяться прежде всего внешними условиями, препятствующими обслуживанию. Например, в АСБР обслуживание ЭС (перевод денежных средств со счета плательщика на счет получателя) может быть остановлено в случае возникновения условия недостаточности средств на счете плательщика.

Следовательно, одним из возможных способов решения задачи повышения производительности СМО в условиях, когда полезная вычислительная мощность ее аппаратно-программного комплекса уже максимально увеличена, является оптимизация технологического регламента функционирования СМО. В ходе оптимизации осуществляется динамическая коррекция значений параметров алгоритма СУпр в процессе функционирования СМО.

Перед непосредственной коррекцией значений параметров алгоритма СУпр должен быть осуществлен предварительный поиск оптимального набора значений параметров, т.е. поиск оптимальной стратегии управления процессом обслуживания, минимизирующей средние потери ЭС в единицу времени при заданном ограничении на число состояний СМО.

Данная задача сводится к задаче поиска оптимальной стратегии для управляемого полумарковского процесса, поскольку моменты принятия решений совпадают с моментами вложения марковской цепи. Для нахождения оптимальной стратегии на практике часто используются итерационные схемы Джевелла и Швейцера [1], основанные на методе динамического программирования и предназначенные для оптимизации управляемых полумарковских процессов без переоценки с бесконечным горизонтом планирования. Необходимым условием применимости этих схем является условие эргодичности вложенной однородной марковской цепи для любой стратегии управления, а также конечная величина длительности шагов [1].

Авторами была разработана имитационная модель функционирования АСБР в виде многоканальной СМО с отказами и однородным стохастическим входным потоком заявокбслуживаемой заявки (т.е. анияективности функционирования таких СМО необходимо использовать так называем.

Значения параметров СМО и суммарного входного потока заявок, использованных при имитационных экспериментах:

1. Суммарная интенсивность входных потоков заявок: 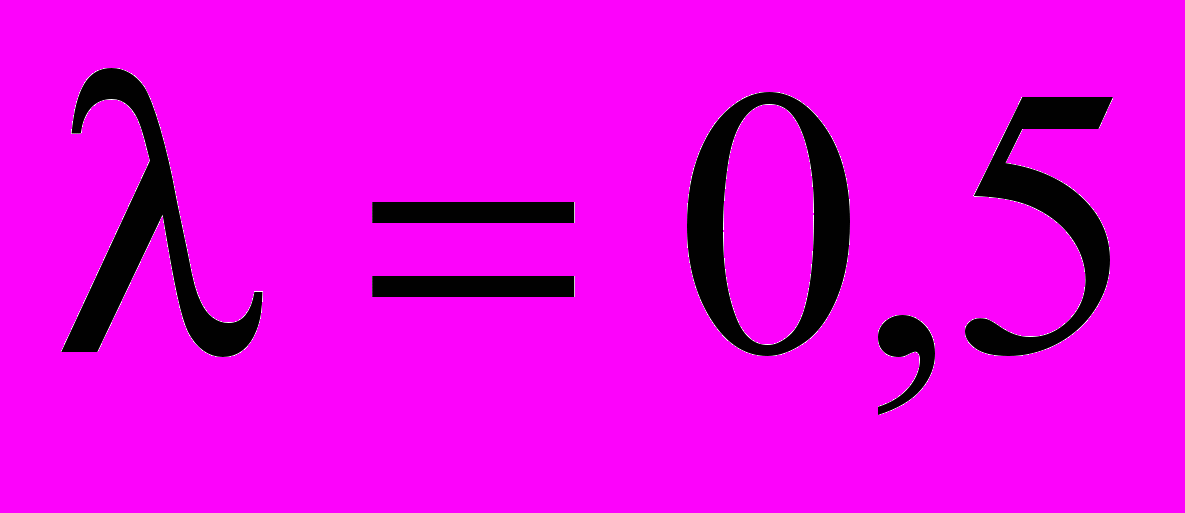заявки в секунду.

2. Среднее время обслуживания заявок приборами: 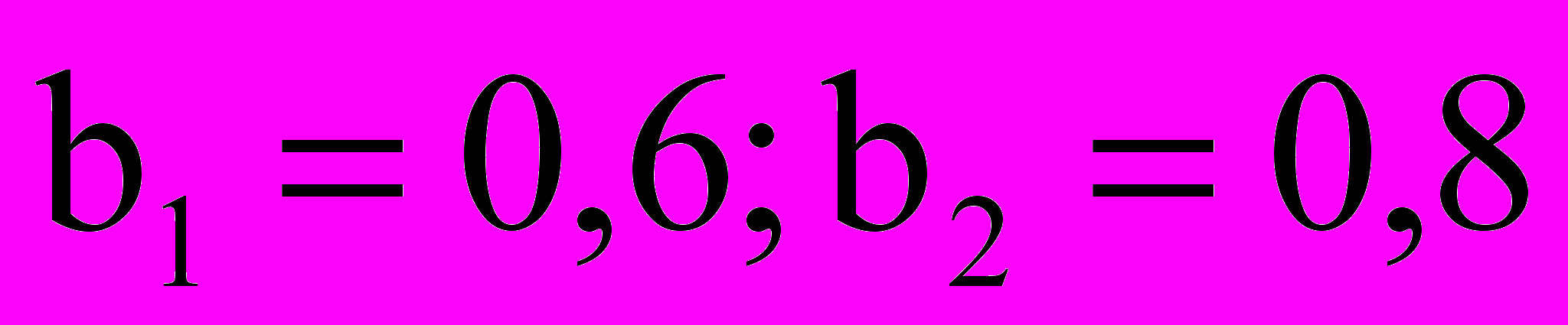заявки в секунду.

3. Интервал считывания значений параметров функционирования СМО: 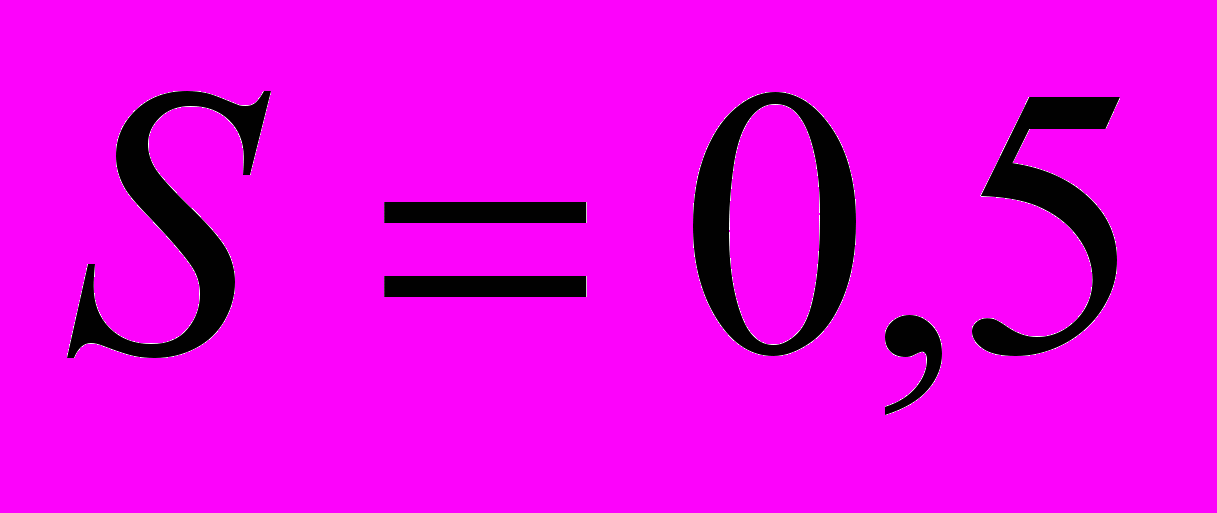мин.

4. Допустимое время обслуживания ЭС: Tобсл = 5 мин.

5. Число циклов моделирования: 1000.

6. Временной интервал моделирования: 3 ч.

С
mx, ЭС/мин
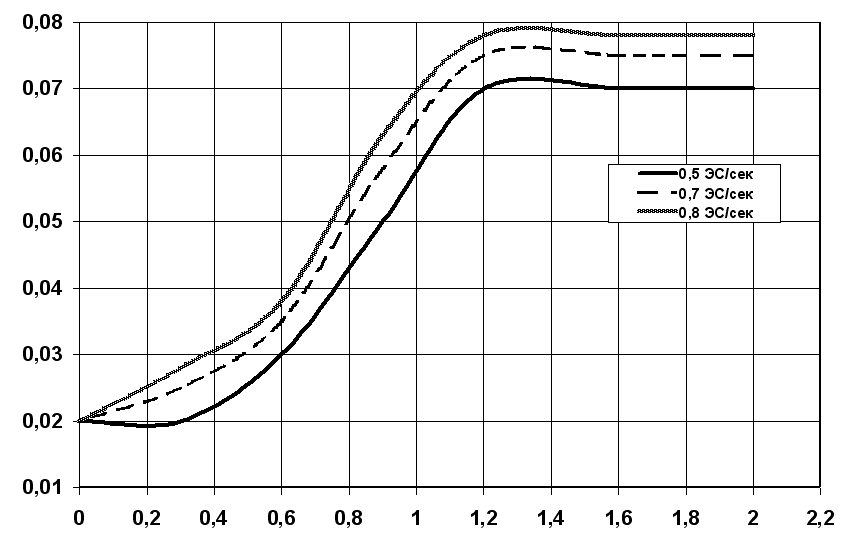
использованием данной модели проводились имитационные эксперименты, в ходе которых были получены зависимости статистических параметров закона распределения интенсивности отказов в обслуживании ЭС от параметров СУпр (рис. 1, 2).

А
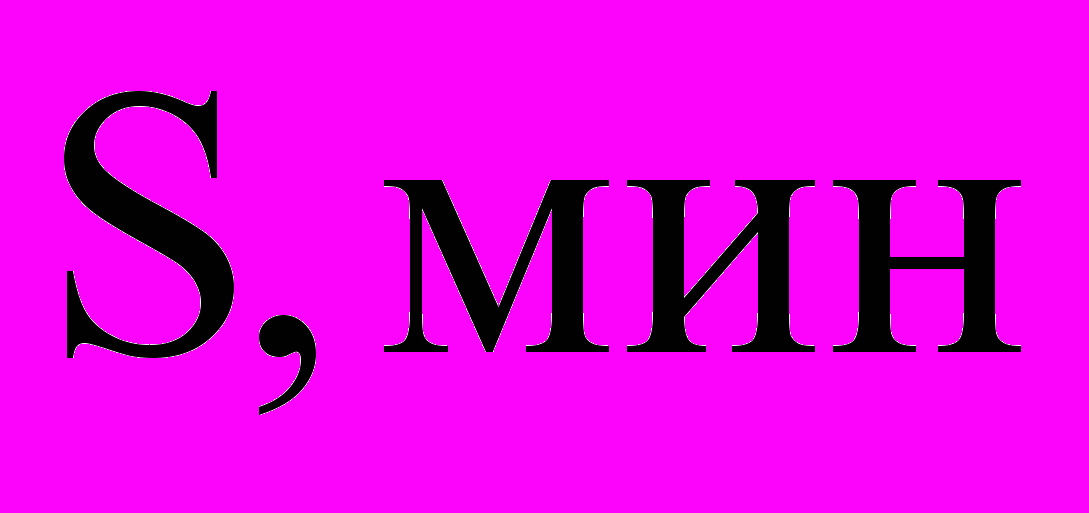
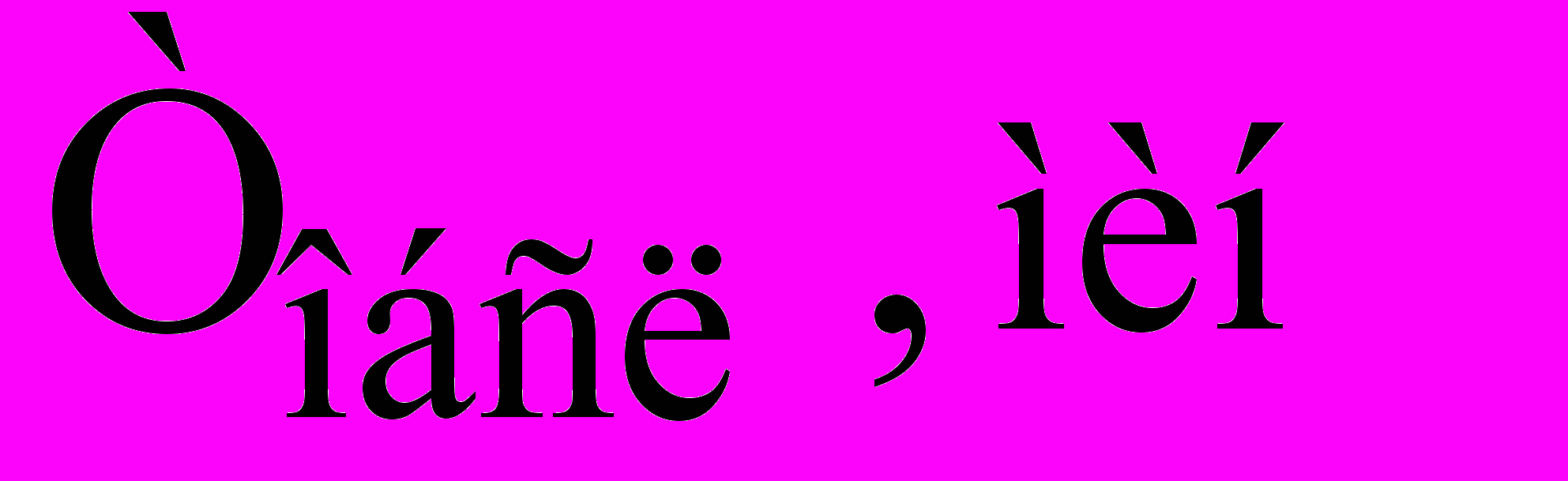
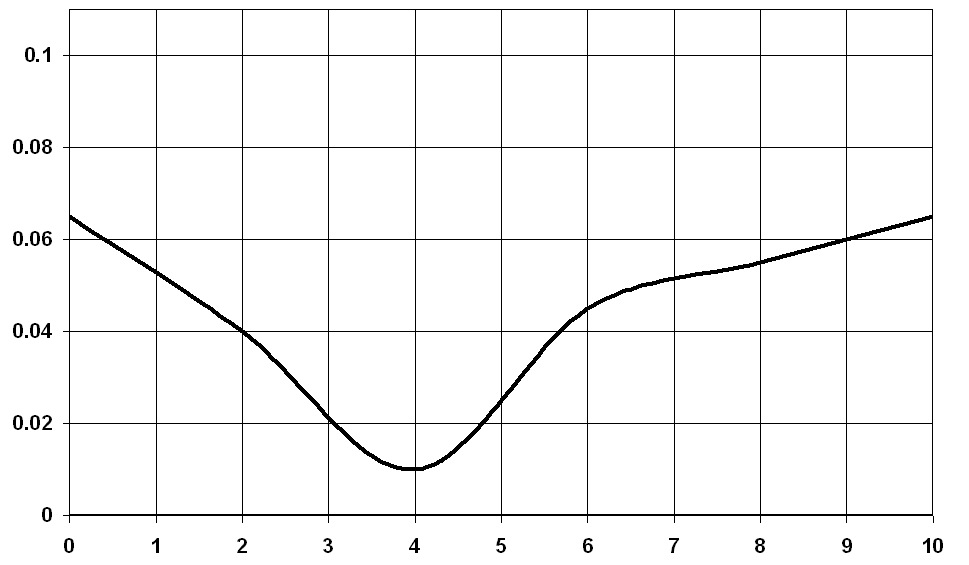
Рис. 1. Зависимость математического ожидания величины интенсивности отказов 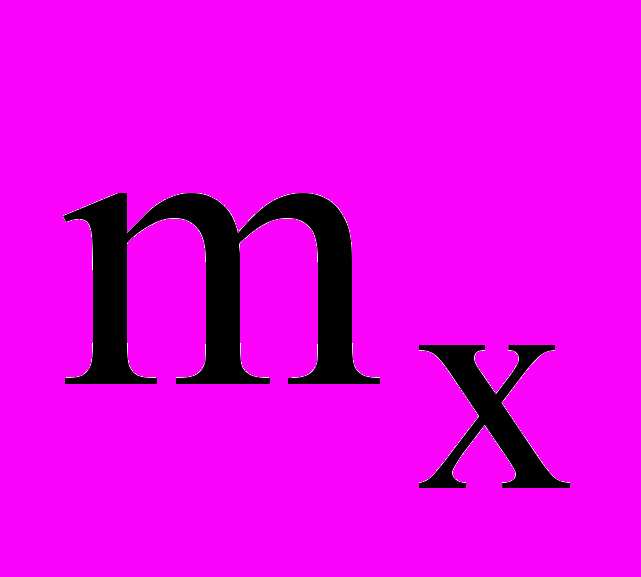от величины интервала считывания значений параметров функционирования СМО (интервала наблюдения) 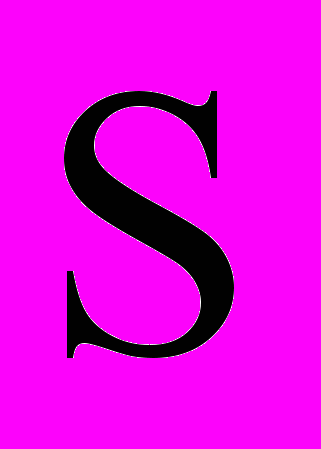при различной интенсивности поступления ЭС: - 0,5 ЭС/с; - - - - - 0,7 ЭС/с; - 0,8 ЭС/с


S, мин

mx ЭС/мин
нализ результатов имитационных экспериментов с принятыми характеристиками функционирования СМО (результаты частично приведены на рис. 1 и 2) показал, что статистические параметры закона распределения интенсивности отказов f(x) (математическое ожидание mx и среднеквадратическое отклонение x интенсивности отказов в обслуживании ЭС) меняются в зависимости от параметров СМО (количество обслуживающих приборов, длина очереди), интенсивности входной нагрузки, а также параметров СУпр (интерв
Тобсл/мин
ал наблюдения за СМО, допустимое время обслуживания Э
Рис. 2. Зависимость математического ожидания величины интенсивности отказов 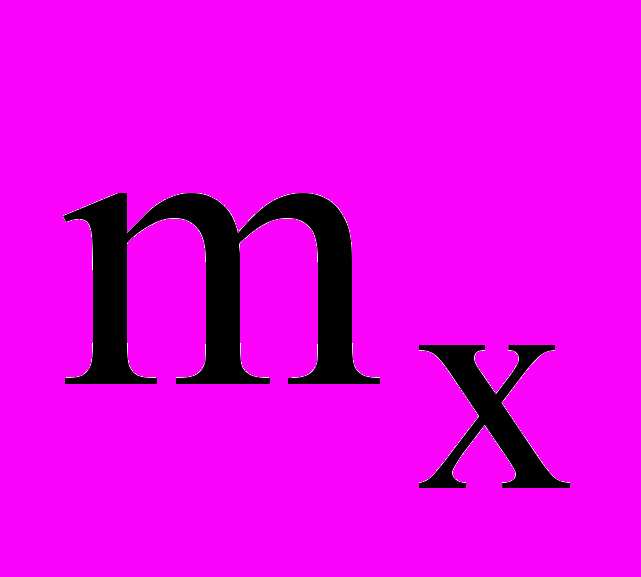от величины допустимого времени обслуживания ЭС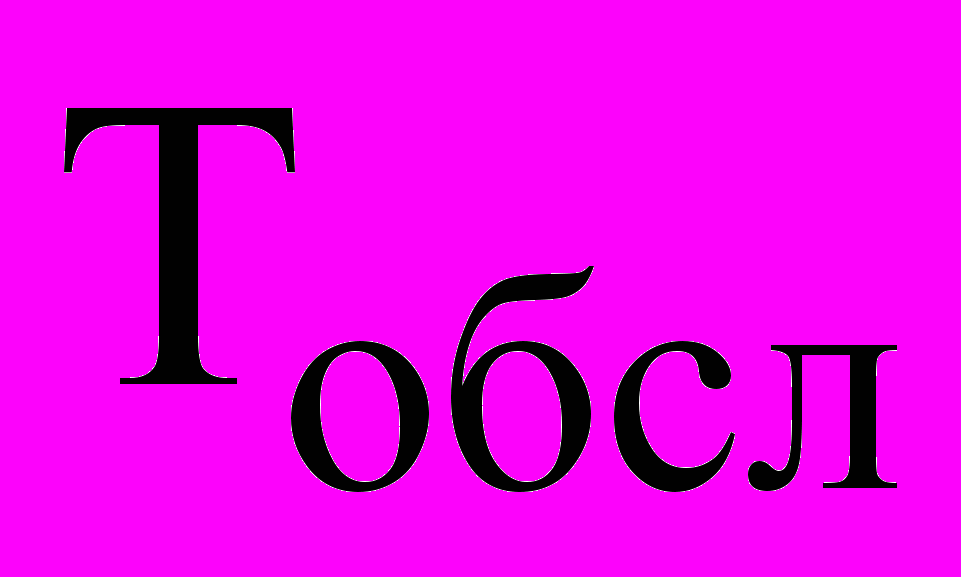

С и т.д.).

Результаты определения статистических параметров закона распределения интенсивности отказов в обслуживании ЭС (при заданных при моделировании исходных данных по характеристикам СМО) могут быть представлены в виде функций двух переменных – интенсивности суммарного входного потока (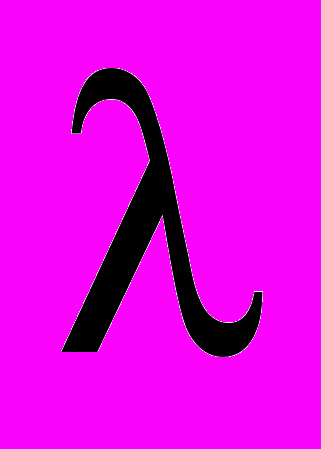) и интервала считывания значений параметров функционирования СМО (S):

mx (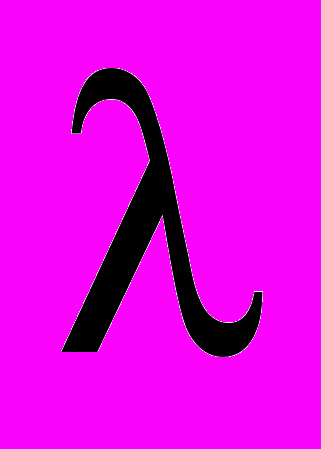, S), x(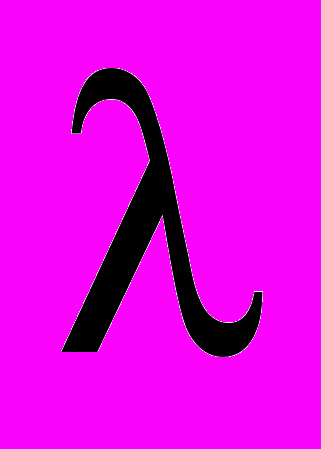, S).

Полиномиальная аппроксимация данных функций имеет следующий вид (размерность статистических характеристик - ЭС, интенсивности суммарного входного потока - ЭС/с, интервала наблюдения - мин):

mx = 347,1 + 50,79 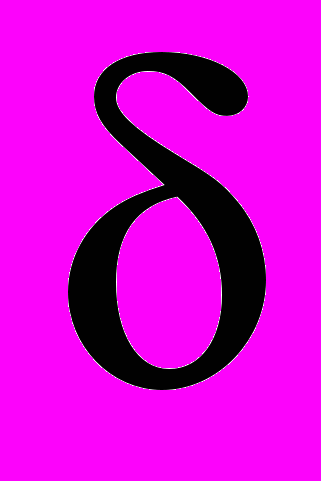+ 140,53 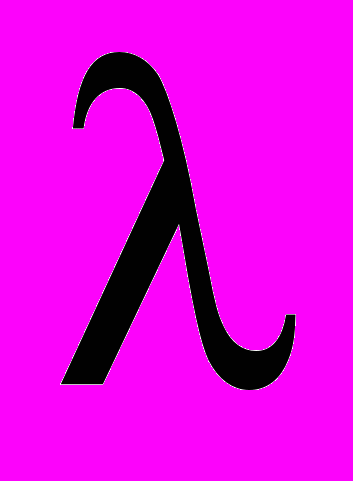+ 2,59 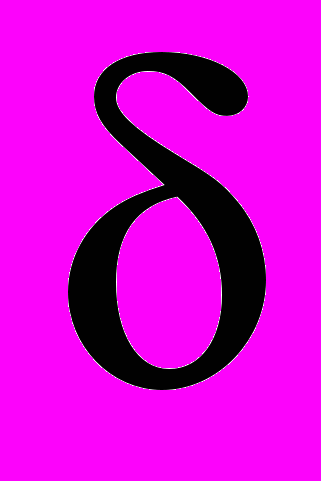2 - 4,92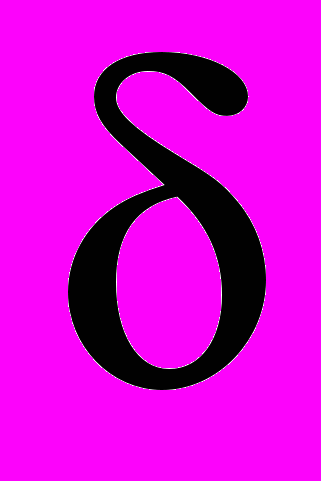 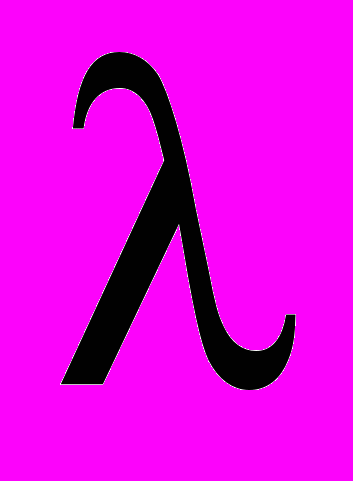- 14,5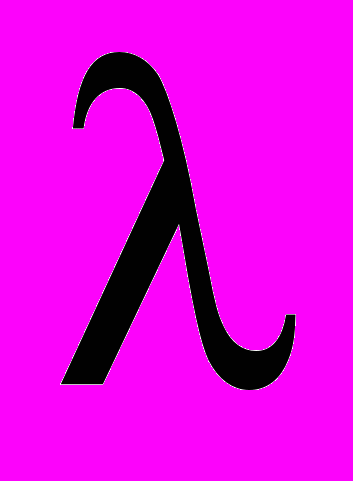22 ;

x= 180,73+81,11 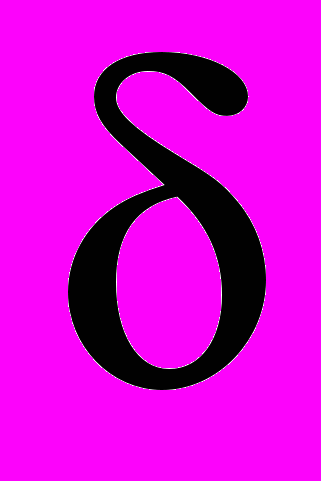+ 11,83 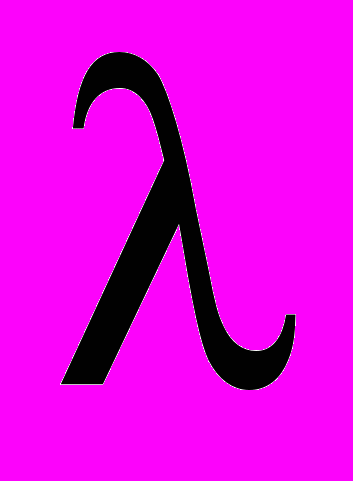- 2,23 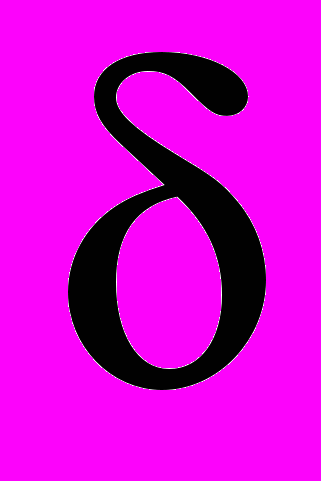2 - 4,05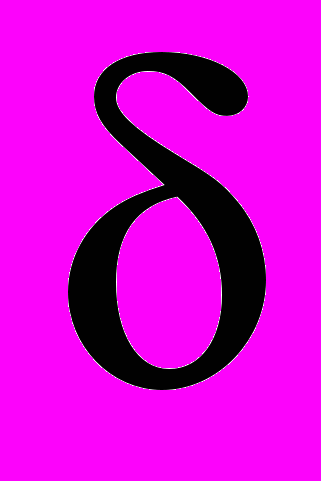 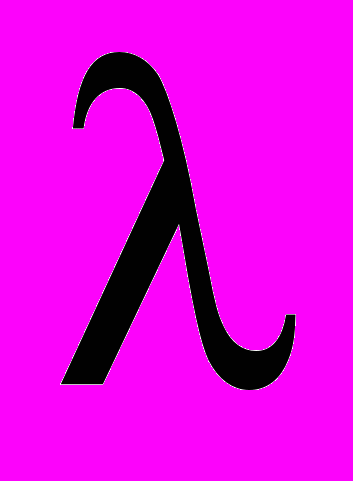- 1,8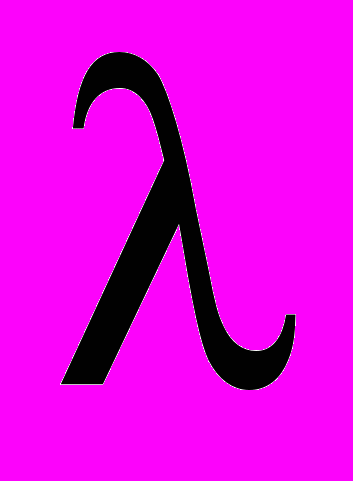22.

Очевидно, что для СМО с характеристиками, отличными от принятых при моделировании, параметры закона распределения интенсивности отказов в обслуживании ЭС f(x) будут иными.

Анализ значений параметров функционирования исследуемой СМО, полученных в результате имитационного моделирования для различных значений параметров СУпр, а также входной нагрузки позволил авторам предположить о нормальном виде распределения f(x).

Для проверки данного предположения была осуществлена статистическая проверка гипотез о законах распределения случайной величины. Необходимое число реализаций для статистической оценки параметров исследуемого распределения определялось для значений доверительной вероятности, равной 0,95, и доверительного интервала, равного 0,05, по каждому из статистических параметров с последующим выбором наибольшего числа необходимых реализаций, которое составило 10000.

Оценка согласованности полученного закона распределения с нормальным проводилась по критерию согласия 2 Пирсона и дала положительный результат.

Таким образом, плотность распределения интенсивности отказов в обслуживании ЭС f(x) в общем виде может быть представлена как

,

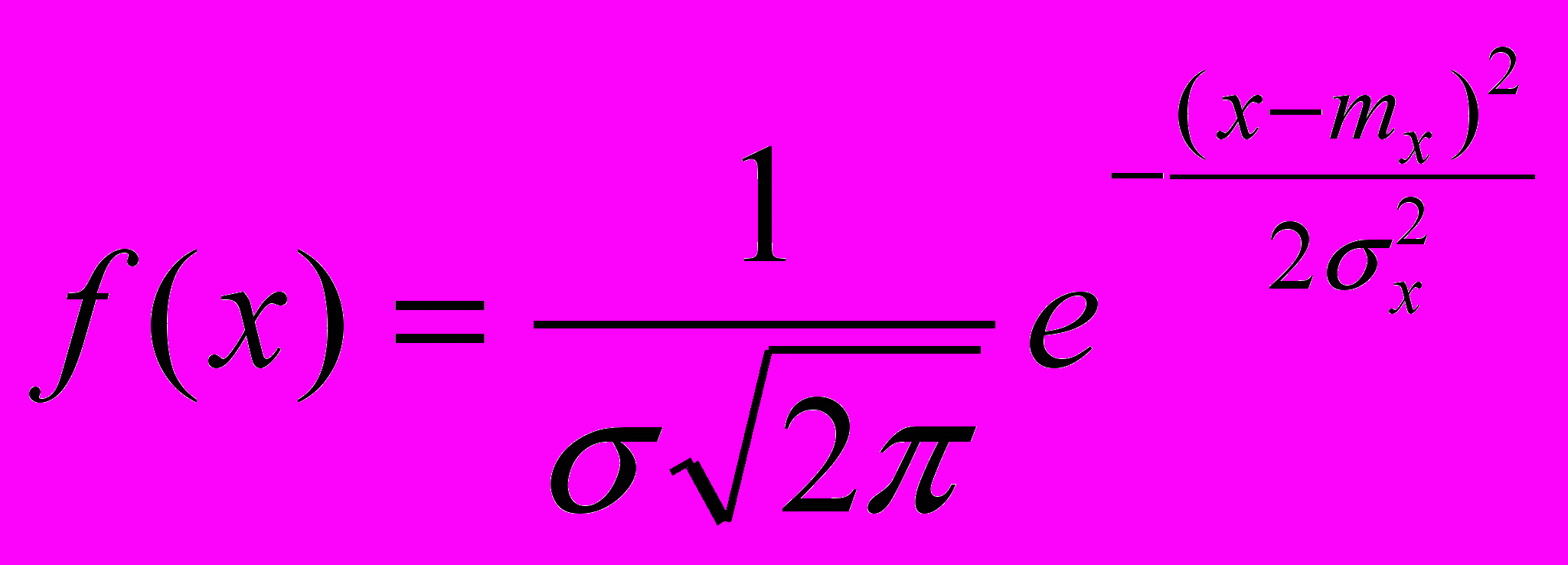где mx – математическое ожидание интенсивности отказов;  – среднеквадратическое отклонение интенсивности отказов.

Реальные условия функционирования СМО, в том числе и АСБР, характеризуются изменением интенсивности входной нагрузки в течение цикла функционирования СМО, а также изменением параметров самой СМО. Следовательно, значения параметров алгоритма СУпр, заданные на момент начала цикла функционирования СМО и обеспечивающие наименьшее число отказов при обслуживании заявок с использованием СУпр (так называемой управляемой дисциплины обслуживания), к моменту завершения цикла функционирования СМО могут обеспечивать даже большее число отказов, чем при обслуживании заявок в порядке поступления (дисциплина FIFO).

Таким образом, существует необходимость адаптировать параметры СУпр к изменяющимся входной нагрузке и параметрам СМО (например, в случае плановой замены или неисправности одного из приборов, изменения требований технологического регламента).

Важным моментом является то, что параметры алгоритма СУпр адаптируются путем настройки программного обеспечения СМО, осуществляющего СУпр (в рассматриваемом примере - прикладного и системного программного обеспечения АСБР), и/или изменения конфигурации аппаратного комплекса СМО. Различные изменения конфигурации аппаратно-программного обеспечения СМО требуют временных затрат и не всегда могут быть осуществимы по техническим и организационным причинам.

Авторы предлагают подход, при котором перед непосредственной коррекцией алгоритма СУпр оценивается риск принятия ошибочного решения о необходимости коррекции и делается вывод о целесообразности такого решения.

Информация о приросте процента отказов в обслуживании ЭС может служить основой для инициализации процесса принятия решения о необходимости коррекции алгоритма СУпр.

Решение о коррекции алгоритма СУпр может быть принято при двух взаимоисключающих условиях:
    1. коррекция СУпр действительно необходима;
    2. коррекция СУпр не приведет к повышению эффективности МО, а в некоторых случаях (из-за временных затрат на изменение конфигурации СМО) при коррекции СУпр может наблюдаться и снижение эффективности обслуживания, выражающееся в росте количества отказов в обслуживании.

Следовательно, возможны следующие ситуации совмещения случайных событий «Условие» и «Принятое решение»:
  1. Принято решение о коррекции алгоритма СУпр при действительной необходимости коррекции - ситуация R1R1 (принятие правильного решения).
  2. Принято решение о коррекции алгоритма СУпр при действительном отсутствии данной необходимости: - ситуация R1R0 (принятие неправильного решения).
  3. Принято решение об отсутствии необходимости коррекции алгоритма СУпр при действительной необходимости - ситуация R0R1 (принятие неправильного решения).
  4. Принято решение об отсутствии необходимости коррекции алгоритма СУпр при действительном отсутствии необходимости - ситуация R0R0 (принятие правильного решения).

Перечисленным ситуациям соответствуют четыре вероятности совмещения событий, сумма которых равна единице:

.

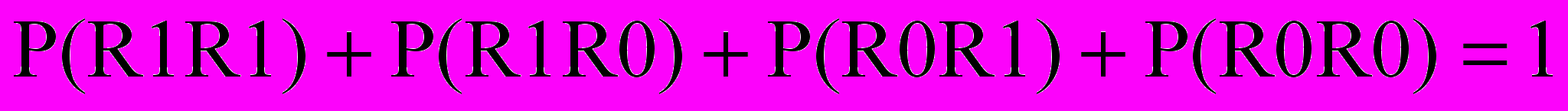В дальнейшем будем использовать обозначения:

P(R1R1) = W11, P(R1R0) = W10, P(R0R1) = W01, P(R0R0) = W00.

Данные вероятности характеризуют достоверность принимаемых решений о необходимости коррекции параметров алгоритма СУпр.

В соответствии с предлагаемым подходом к решению задачи оценки рисков при коррекции параметров алгоритма СУпр в процессе функционирования СМО с заданной периодичностью S измеряется текущая интенсивность отказов в обслуживании заявок, рассчитывается прирост процента отказов и вычисляются вероятности принятия правильных решений о целесообразности или нецелесообразности коррекции алгоритма СУпр (зависят от S и 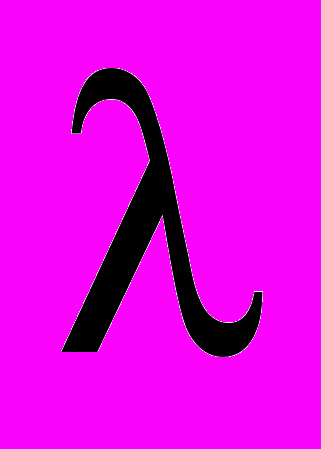) по следующим формулам:

;

,

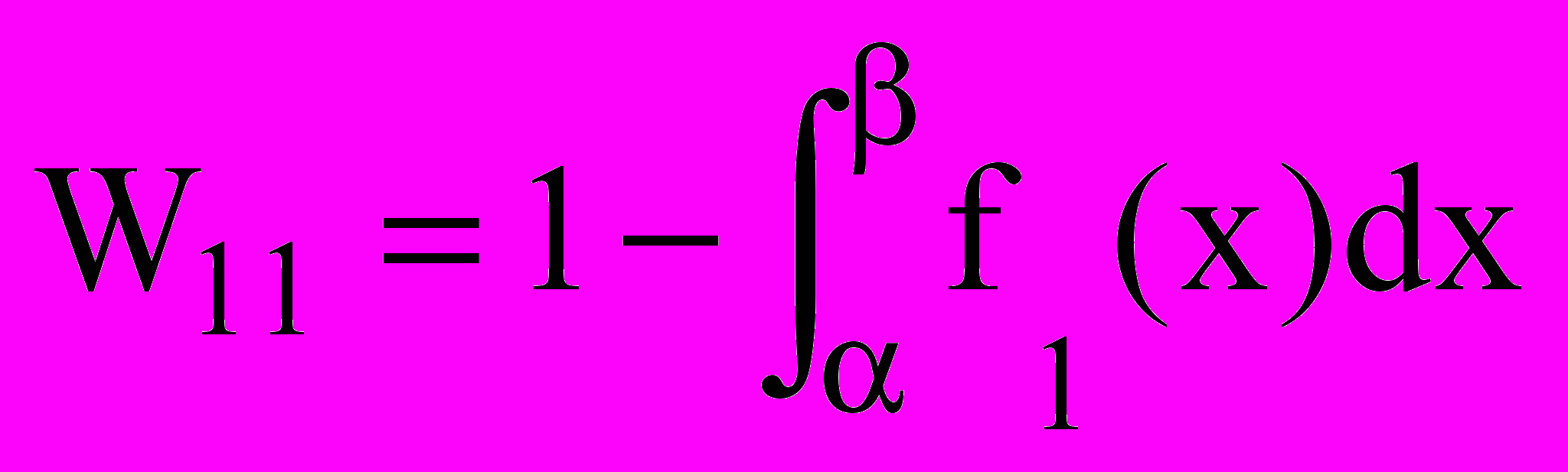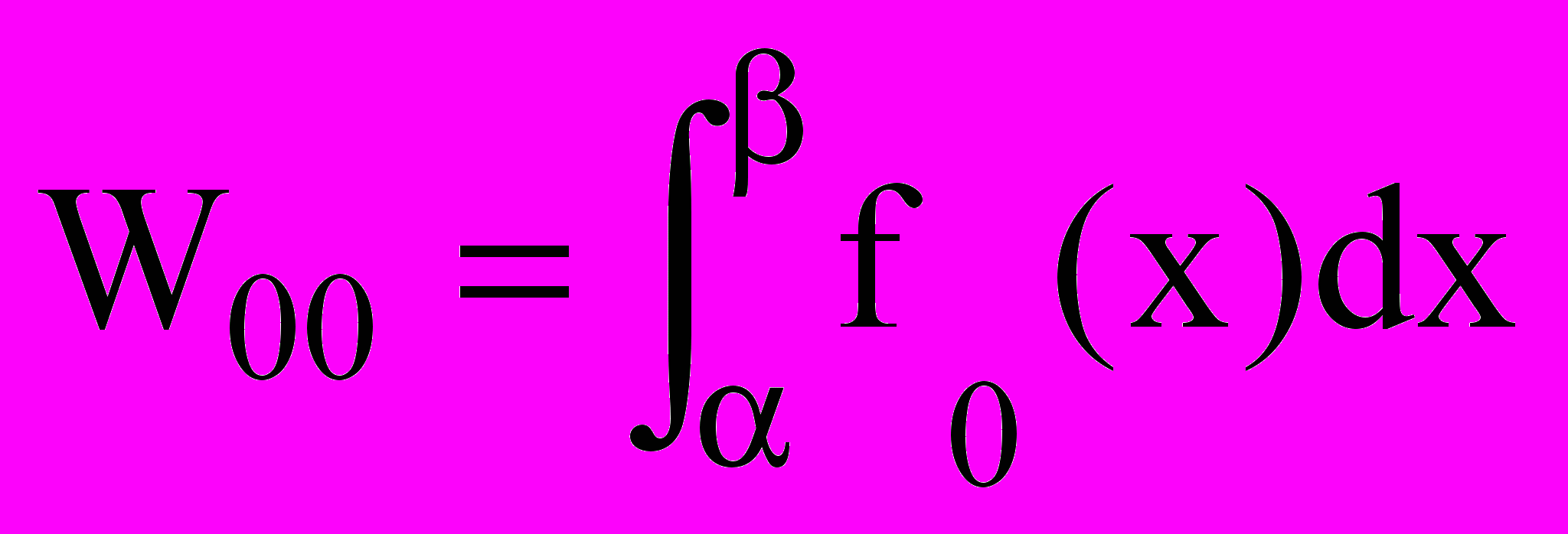где 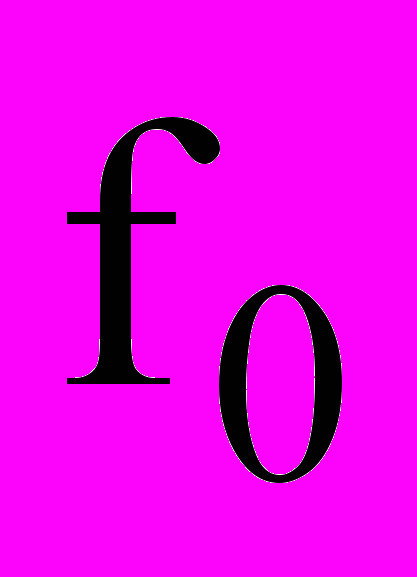- закон распределения интенсивности отказов при использовании дисциплины FIFO, - закон распределения интенсивности отказов при использовании СУпр, 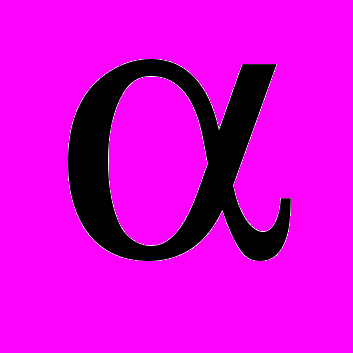и - граничные значения интенсивности отказов в обслуживании заявок.

В качестве среды имитационного моделирования, а также для реализации некоторых функций принятия решений и поиска рационального варианта СУпр используется пакет прикладных программ MatLab.

Специальный Cи-интерфейс пакета MatLab (технология C Engine MatLab) позволяет использовать функции пакета во внешнем приложении, реализующем модель АСБР как АСМО. В качестве языка программирования при реализации модели использовался язык Cи++.

С
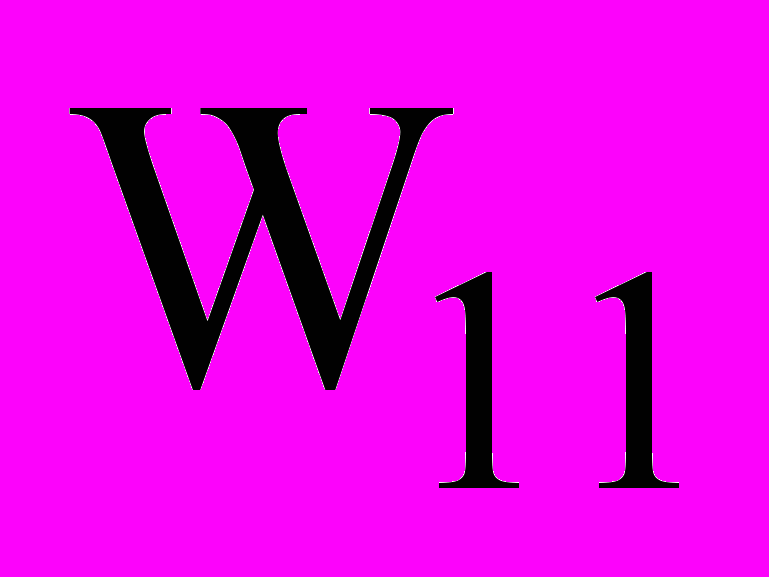
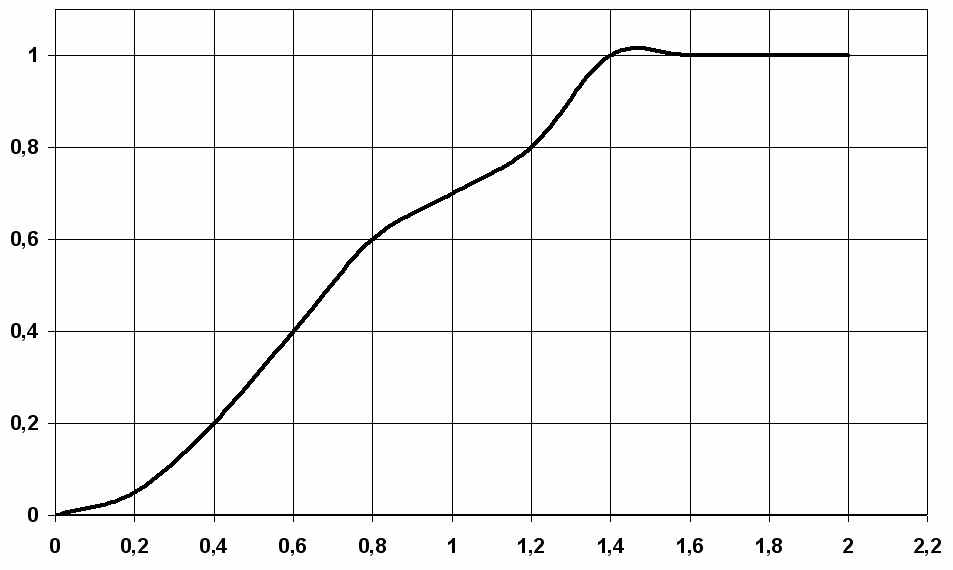
Рис. 3. Зависимость вероятности принятия правильного решения от интенсивности входного потока ЭС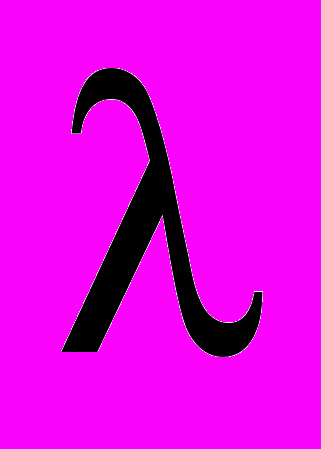

помощью разработанной модели функционирования АСБР и программных средств принятия решений ситуационного управления были получены зависимость значений вероятности принятия правильного решения о целесообразности коррекции алгоритма СУпр W11 от интенсивности входного потока 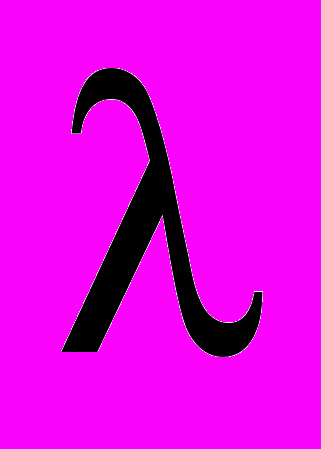, а также результаты применения описанного подхода в виде зависимости относительного прироста математического ожидания числа обслуженных заявок Mобсл от значений вероятности принятия правильного решения W11 (рис. 3 и 4).

Р
W11
еализация в управляемых СМО описанного подхода, рассмотренного на п
λ, ЭС/с
римере применения в АСБР, позволит повысить эффективность массового обслуживания заявок благодаря преодолению эффекта пробок в АСМО, вызванных внешними условиями (характеристиками текущей входной нагрузки), в оперативном режиме, а также снизить число случаев принятия ошибочных решений о коррекции значений параметров алгоритма СУпр, приводящих к потере производительности СМО.

Д
W11

ΔМобсл, %

Рис. 4. Зависимость прироста процента обслуженных заявок 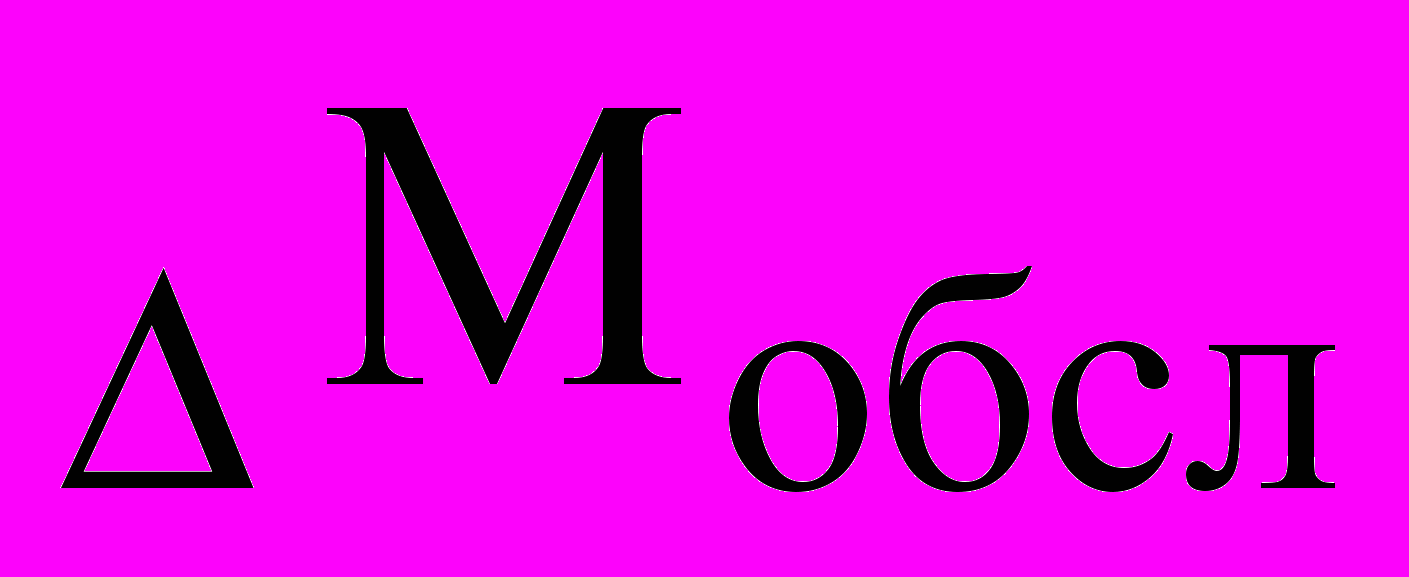(относительно общего числа поступивших) от вероятности принятия правильного решения о коррекции алгоритма СУпр

альнейшие исследования авторов в данной области направлены на доработку и развитие изложенного подхода и соответствующих программных средств, а также на учет прогнозной информации о входном потоке заявок в АСМО при принятии решений о коррекции значений параметров алгоритма СУпр.


Список литературы

      1. Бурлаков, М.В. Ситуационное обслуживание заявок с конечным временем старения / М.В.Бурлаков. – Киев: АН УССР, 1984.
      2. Бурлаков, М.В Ситуационное управление заявками в СМО / М.В. Бурлаков. – Киев: Наукова думка, 1991.



Материал поступил в редколлегию 28.04.09.