Методическая разработка доцента Широковой О. А. по теме: Компьютерное математическое моделирование в экономике

Вид материала

Методическая разработка

Содержание Оптимизационные модели. Графическое решение задачи об оптимальном плане производства. Сервис, Параметры Поиск решения Задача 2. Производство столов и тумбочек Схема перевозок стали Матрица питательности Транспортная задача – склады и потребители. Сервис, Поиск решения Задача о диете – корма для животных. Задачи для самостоятельного решения Задача о бензине Задача о мебельном цехе Гнездо хищника Экспедиция «Северный полюс» Дешевый кузов Дневной рацион – задача о диете Авиапредприятие – транспортная задача. Нефтеперерабатывающий завод

Подобный материал:

• Сборник статей Разработка дипломного проекта для транспортных специальностей, 44.28kb.
• Программа дисциплины Компьютерное моделирование в экономике и менеджменте для направления, 192.72kb.
• Математическое и компьютерное моделирование динамического состояния систем передачи, 388.39kb.
• Аннатационная программа дисциплины интегральные преобразования и операционное исчисление, 30.41kb.
• Аннатационная программа дисциплины стохастический анализ направление подготовки 010200., 38.6kb.
• Программа дисциплины имитационное моделирование в экономике для направления 080100., 228.47kb.
• В. И. Широковой по теме: Совершенствование основ закон, 88.6kb.
• Е. Е. Гетманова компьютерное моделирование нелинейных колебаний, 81.56kb.
• Методическая разработка может представлять собой, 78.78kb.
• Муниципальное Образовательное Учреждение лицей №23 г. Сочи методическая разработка, 233.75kb.

Методическая разработка доцента Широковой О. А. по теме:

Компьютерное математическое моделирование в экономике.


Экономика может быть по праву отнесена к одной из труднейших (и интереснейших) наук, так как, изучая ее, в идеальном случае исследователь, помимо всего прочего, должен понять, как функционирует каждая ее часть.

Так же, как всякая наука, экономика должна уметь давать ответы на некоторые основные вопросы, ставящие перед ней: что производить? Где производить? Какова цена продукции? Какова зарплата лиц, занятых в производстве? Как соизмерить настоящие и будущие издержки? и т.п.

С чего начинать исследование? Прежде всего, нужно четко выделить факторы, которые существенно влияют на принимаемые решения.

Выбрав определенную программу деятельности экономической системы, теоретически мы воздействуем на всю экономическую систему, практически же – лишь на очень малую часть ее. Соответственно при выделении факторов, влияющих на принимаемые решения нужно учитывать те из них влияние которых наиболее ощутимо.

Для моделирования экономики применяют не одну модель, а систему моделей. В этой системе есть модели, описывающие разные стороны экономики. Есть модели экономики страны, есть модели экономических явлений на отдельном предприятии или даже модель одного экономического события. При составлении модели экономики сложного объекта производят так называемое агрегирование. При этом ряд родственных параметров объединяют в один параметр, тем самым общее количество параметров уменьшается. На этом этапе важную роль играют опыт и интуиция. В качестве параметров можно выбрать не все характеристики, а наиболее важные.

Известно, насколько важно для решения экономических задач планирование – как при рыночной, так и при плановой экономике. Обычно для решения экономической проблемы существует много способов (стратегий). Отнюдь не равноценных по затратам финансов, людских ресурсов, времени исполнения, а также по достигаемым результатам. Наилучший из способов по отношению к выбранному критерию (критериям) называют оптимальным .

Мы рассмотрим лишь один из разделов – оптимальное планирование – и внутри него одну из моделей, так называемое, линейное программирование. Это связано с относительной простотой и ясностью как содержательной постановки соответствующих задач, так и методов решения. О таких интересных, но более сложных проблемах, как выпуклое программирование, динамическое программирование, мы лишь упомянем. Отметим еще, что термин «программирование» в названии этих разделов теории оптимального планирования весьма условен, связан с историческими обстоятельствами и к программированию в общепринятом сейчас смысле прямого отношения не имеет.

Оптимизационные модели.


Изучаемый процесс описывается математической моделью М, т.е. имеется совокупность соотношений, связывающих некоторые параметры, определяющие ход процесса. Из множества всех этих параметров 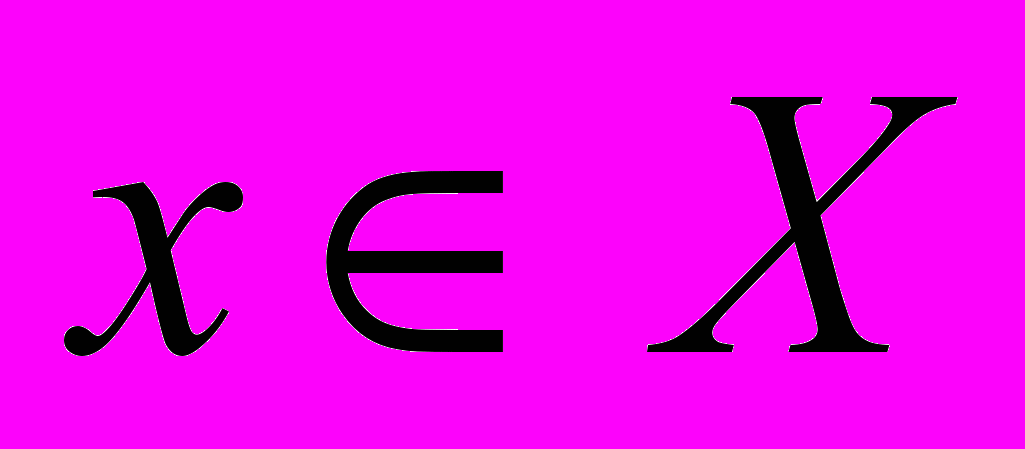будем выделять множество переменных управления , т.е. значения этих переменных в распоряжении того, кто управляет процессом.

Поскольку можно количественно оценить результат каждого действия, каждого управления, то это значит, что известна функция Ф (целевая функция), сопоставляющая каждому возможному в данной модели управлению число Ф(u).

Целенаправленная деятельность, как правило, предполагает наилучшее её использование, т.е. в зависимости от целей управления нас будет интересовать такое допустимое управление , на котором достигается либо максимальное значение 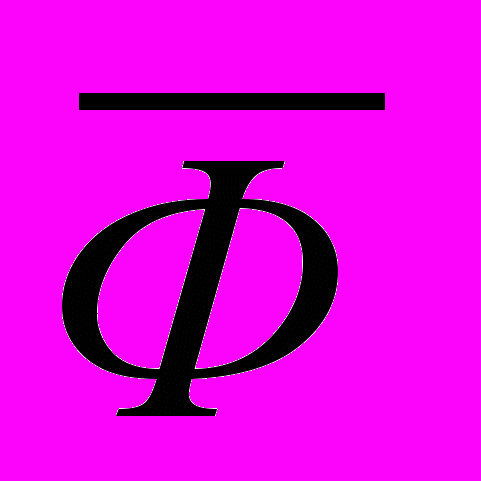(u):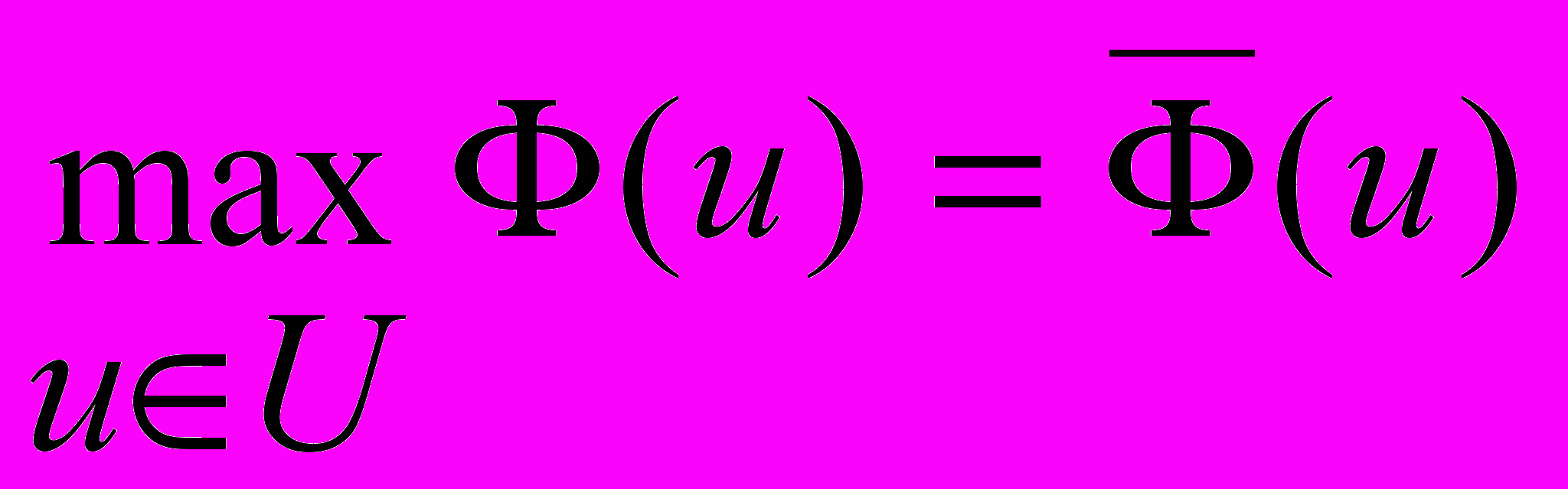

,

либо минимальное значение Ф(u):

.

Задачи такого типа носят название экстремальных или оптимизационных задач.

В зависимости от вида модели M и функции Ф(u) используются различные методы для решения соответствующих оптимизационных задач.

Познакомимся с этими методами на конкретных примерах.

Приведем примеры экономических задач линейного программирования.

Задача 1.

На некотором предприятии могут выпускать изделия двух видов (например, мотоциклы и велосипеды). В силу ограниченности возможностей сборочного цеха в нем могут собирать за день либо 25 мотоциклов (если не собирать вообще велосипеды), либо 100 велосипедов (если не собирать вообще мотоциклы), либо какую-нибудь комбинацию тех и других, определяемую приемлемыми трудозатратами. Склад может принять не более 70 изделий любого вида в сутки. Известно, что мотоцикл стоит в два раза дороже велосипеда. Требуется найти такой план выпуска продукции, который обеспечил бы предприятию наибольшую выручку.

Такого рода задачи возникают повседневно в огромном количестве, но в реальности число изделий гораздо больше двух, да и дополнительных условий тоже больше. Решить подобную задачу путем перебора всех мыслимых вариантов часто невозможно даже на ЭВМ. В нашем случае задача легко решается графически (геометрически).

Обозначим число выпускаемых за день мотоциклов х, велосипедов – у.

Переменные х и у называются поисковыми переменными.

Пусть τ₁ – время (в часах), уходящее на производство одного мотоцикла, а τ₂ – одного велосипеда. Из условия задачи следует, что τ₁=4τ₂. Если завод работает круглосуточно, то, очевидно, при одновременном выпуске обоих изделий

τ₁^.х + τ₂^.у ≤ 24,

или

4τ₂^.х + τ₂^.у ≤ 24, 4х + у ≤ .




Но - число максимально производимых велосипедов в сутки, оно равно 100. Итак, возможности производства определяют условие

4х + у ≤ 100.

Еще одно условие – ограниченная емкость склада:

x + у ≤ 70

Обозначим цену мотоцикла а₁ (руб.), цену велосипеда – а₂(руб.). По условию

а₁ = 2а₂. Общая цена дневной продукции

S= a₁^.x + a₂^.y = 2a₂^.x + a₂^.y = a₂^. (2x + y).

Поскольку a₂ – заданная положительная константа, то наибольшего значения следует добиваться от величины f = (2x + y).

Итак, учитывая все условия задачи, приходим к ее математической модели: среди неотрицательных целочисленных решений системы линейных неравенств




(1)



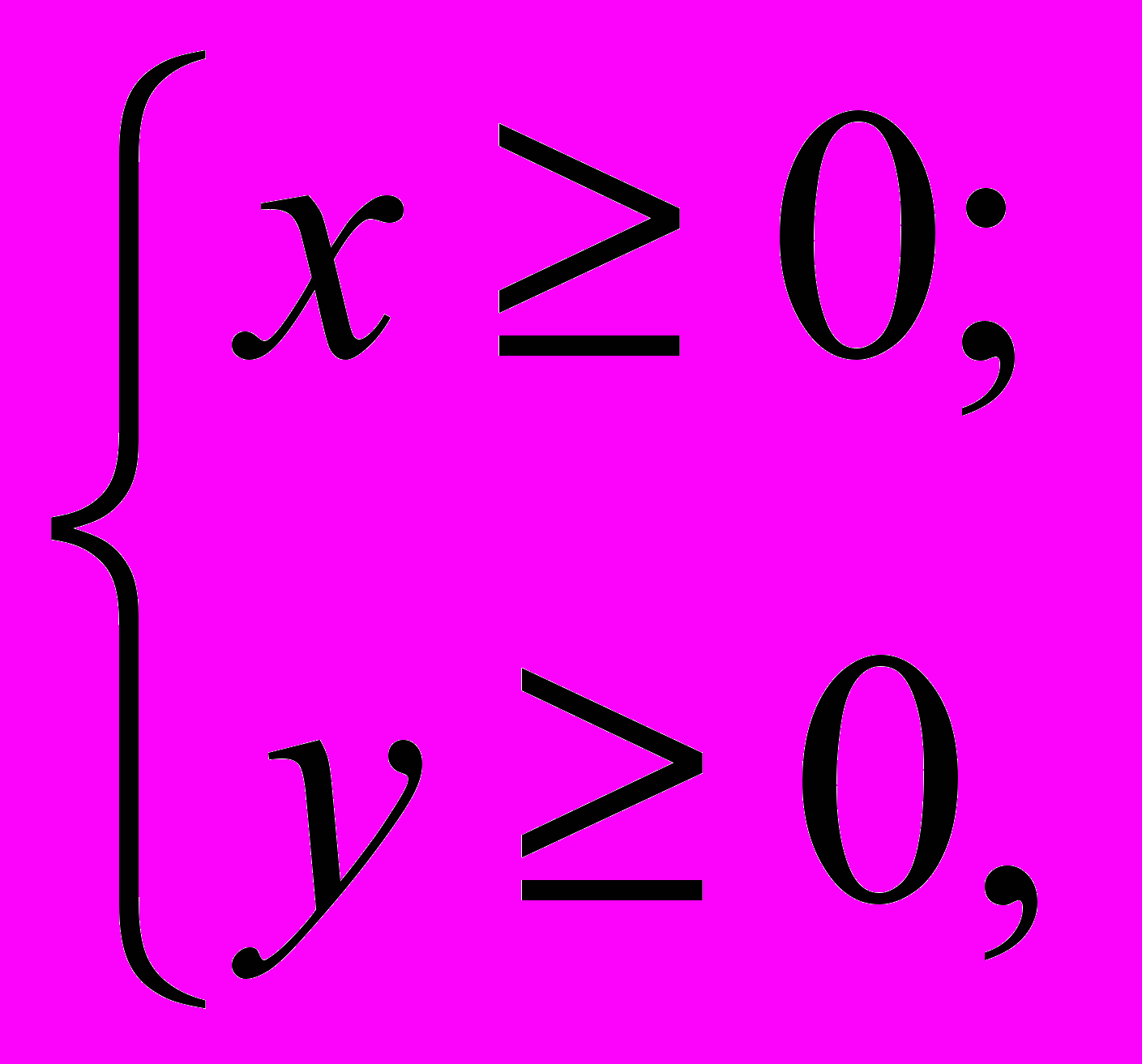
найти такое, которое соответствует максимуму линейной функции

f = (2x + y). (2)

Функция (2) называется целевой функцией.

Проще всего решить эту задачу чисто геометрически.


Геометрический метод решения ЗЛП


Если система ограничений ЗЛП представлена в виде системы линейных неравенств с двумя переменными, то такая задача может быть решена геометрически. Этот метод решения представляет большой интерес, поскольку он наглядно раскрывает сущность задач линейного программирования.

Геометрический метод предполагает последовательное выполнение ряда шагов:

1. сформулировать ЗЛП,
   
2. построить на плоскости прямые, уравнения которых получаются в результате замены в ограничениях знаков неравенств на знаки точных равенств,
   
3. найти полуплоскости, определяемые каждым из ограничений задачи,
   
4. найти область допустимых решений (допустимых планов),
   
5. построить прямую, соответствующую целевой функции,
   
6. перемещать построенную прямую параллельно самой себе в направлении увеличения (при максимизации) или уменьшения (при минимизации) определяющей ее константы,
   
7. определить координаты точки максимума (или минимума) функции. Координаты этой точки – есть искомый оптимальный план (оптимальное решение).
   

Итак ЗЛП сформулирована. Построим на плоскости (х,у) прямые, уравнения которых получаются в результате замены в ограничениях знаков неравенств на знаки точных равенств:

4x+y =100 или y =100 -4x – на рисунке это линия с координатами (0,100) и (25,0),

x+y= 70 или x+y= 70 – на рисунке это линия с координатами (0,70) и (70,0),

x=0 – на рисунке это линия, совпадающая с осью ОУ,

y=0 – на рисунке это линия, совпадающая с осью ОX.

Найдем полуплоскости, определяемые каждым ограничением системы линейных неравенств (1).

В результате построим на плоскости (х,у) область, соответствующую неравенствам (1). Эта область выделена жирной линией. Это область допустимых планов – четырехугольник OABC. Всякая точка области удовлетворяет неравенствам (1).

Построим прямую (2x+y)=С, соответствующую целевой функции при заданном значении константы С=40. На рисунке это линия с координатами (0,40) и (20,0). Построим также прямые f = (2x+y)=С при С=80 и С=120. Давая большее значение константе С, мы прямую как-бы перемещаем вверх параллельно самой себе. Все три прямые параллельны (на рисунке – это тонкие линии). Они называются линиями уровня целевой функции. Это семейство прямых, удовлетворяющих уравнению f = (2x+y)=С с разными значениями константы С.

Вполне очевидно, что наибольшему возможному значению f, совместному с условиями (1), соответствует одна из этих линий, соприкасающаяся с областью М в точке В .





Графическое решение задачи об оптимальном плане производства.


Этой линии соответствует значение f =80. Линия правее хоть и соответствует большему значению f , но не имеет общих точек с М, левее – соответствует меньшим значениям f. Координаты точки В(10,60) - искомый оптимальный план производства. Таким образом, x=10, y=60.

Отметим, что нам повезло, т.к. решение (х,у) оказалась целочисленным. Если бы прямые



пересеклись в точке с нецелочисленными координатами, мы бы столкнулись со значительными проблемами. Еще больше их было бы, если бы переменных было три и более (завод выпускал три или более видов продукции).


Решение с помощью MS Excel


Итак, ЗЛП сформулирована: среди неотрицательных целочисленных решений системы линейных неравенств




(1)



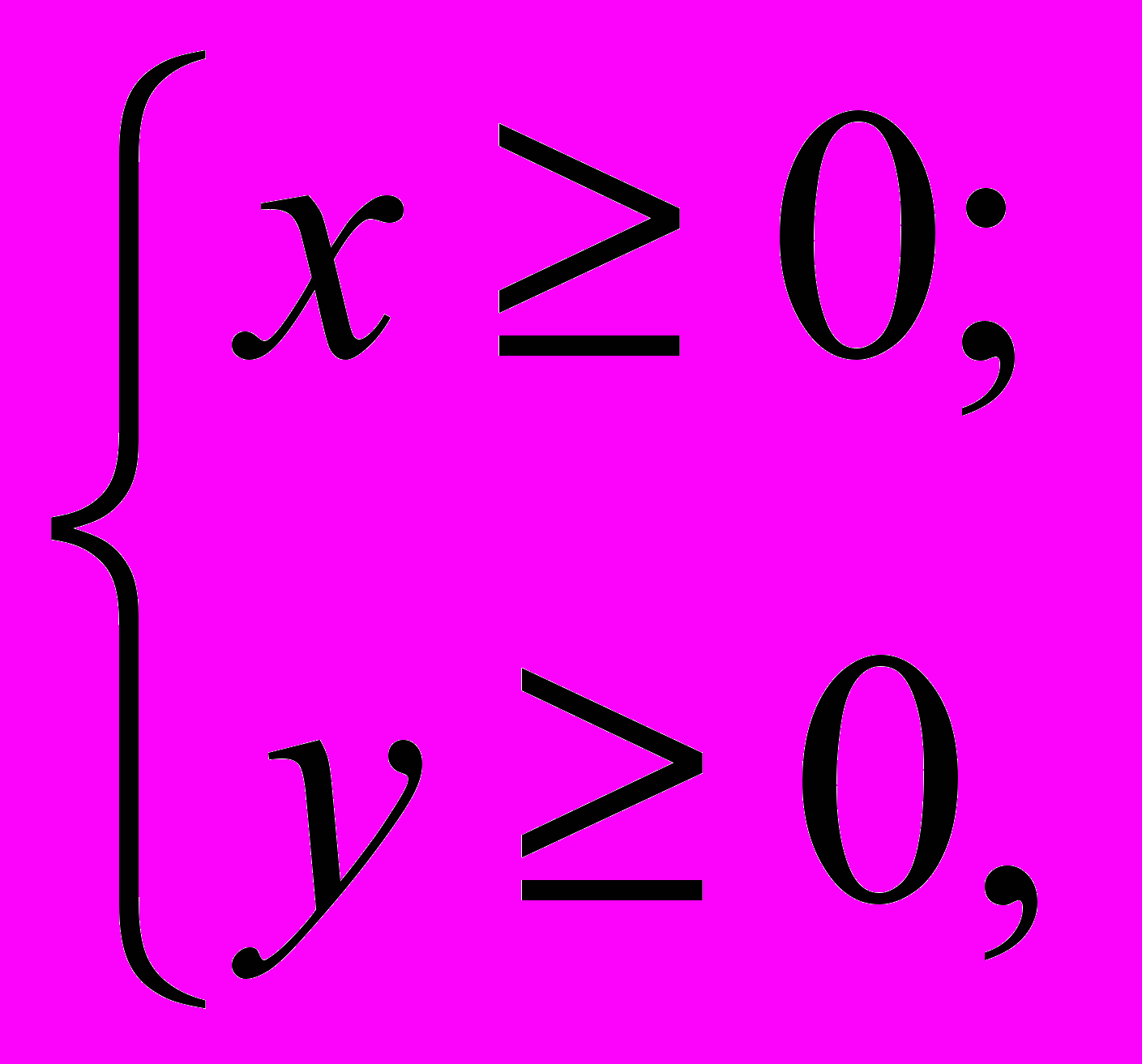
найти такое, которое соответствует максимуму линейной функции

f = (2x + y).

В качестве начальной точки (т.е. начальных значений поисковых переменных) можно взять: x=0, y=0, т. к. эти значения удовлетворяют системе неравенств (1). .

Задача решается с помощью табличного процессора MS Excel. Это облегчает не только расчеты технико-экономических коэффициентов и других данных, но и дает в дальнейшем возможность автоматического обновления информации в экономико-математической модели.

Вся разработанная информация сводится в развернутую экономико-математическую модель и заносится в рабочий лист MS Excel (рис 1).





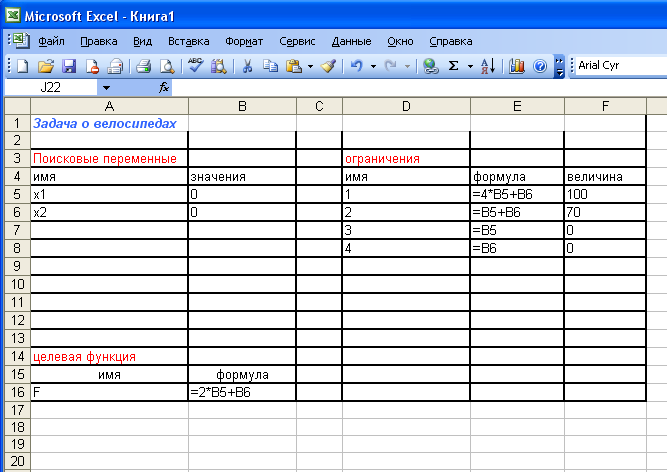
Рис.1. Расположение данных задачи “задача о велосипедном заводе”

в ячейках рабочего листа ЭТ Excel (формулы).


Данные в модель рекомендуется заносить в виде ссылок на ячейки с соответствующей информацией в расчетных рабочих листах или рабочих листах с исходными сведениями.

В ячейках В5:В6 находятся начальные значения поисковых переменных x, y. В эти же ячейки после решения задачи будут помещены оптимальные значения поисковых переменных. В ячейке В16 находится формула вычисления значения целевой функции. В эту же ячейку после решения задачи будет помещено максимальное значение этой функции. В ячейках Е5:Е8 расположены формулы левых частей ограничений.

Чтобы вывести на экран содержимое ячеек в виде формул, а не отображаемых значений этих формул, необходимо выполнить команду Сервис, Параметры, выбрать вкладку “Вид”, установить опцию формулы в окне “Параметры окна”.

После размещения данных следует выполнить команду Сервис, Поиск решения и в открывшемся диалоговом окне “поиск решения” задать расположение исходных данных в таблице (рис.2.).




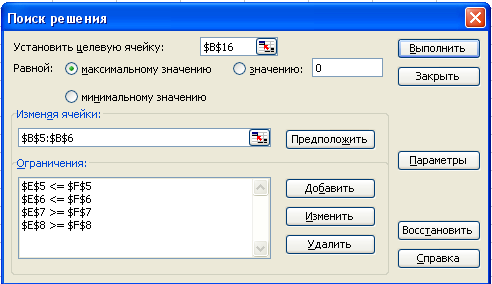
Рис.2. Диалоговое окно “Поиск решения”.


Порядок работы в диалоговом окне “Поиск решения”.

1. Укажите ячейку В16, содержащую формулу целевой функции, в поле ввода Установить целевую ячейку.
   
2. В группе Равной установите опцию Максимальному значению, чтобы максимизировать целевую функцию.
   
3. В поле ввода Изменяя ячейки введите диапазон ячеек В5:В6, посредством изменения значений которых будет достигнуто оптимальное значение целевой функции.
   
4. Чтобы добавить ограничения задачи, щелкните на кнопке Добавить. Появится диалоговое окно “Добавление ограничения”(рис.3.).
   

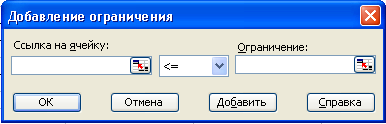
Рис.3. Диалоговое окно “Добавление ограничения”.


Ограничения следует добавлять по очереди: 1,2,3,4, для этого:

• В поле ввода Ссылка на ячейку введите имя ячейки, содержащей формулу текущего ограничения;
  
• В соседнем поле введите “>=” в раскрывающемся списке;
  
• Введите предельное значение в последнее окно ввода;
  
• Щелкните на кнопке Добавить, чтобы ввести следующее ограничение, или на кнопке ОК, чтобы вернуться в диалоговое окно “Поиск решения”. Созданные ограничения появятся в списке Ограничения.
  

Замечание: ввод ограничений 3,4 можно выполнить, задав диапазон Е7:Е8, т.к. они имеют равные правые части и знаки отношений.

Для изменения и удаления ограничений в списке Ограничения диалогового окна Поиск решения укажите ограничение, которое требуется изменить или удалить. Выберите команду Изменить и внесите изменения либо нажмите кнопку Удалить.

5. В диалоговом окне “ Поиск решения” щелкните на кнопке Выполнить, чтобы произвести поиск решения. Когда решение будет найдено, появится диалоговое окно “Результаты поиска решения” (рис.6.). Установите опцию сохранить найденное решение, чтобы сохранить предлагаемое решение, или опцию Восстановить исходное значение, чтобы вернуться к исходным данным. Щелкните на кнопке ОК.
   

Рис.6. Диалоговое окно “Результаты поиска решения”.


На рабочем листе появится результат оптимизации: при х=10, у=60 максимальная прибыль F=80.




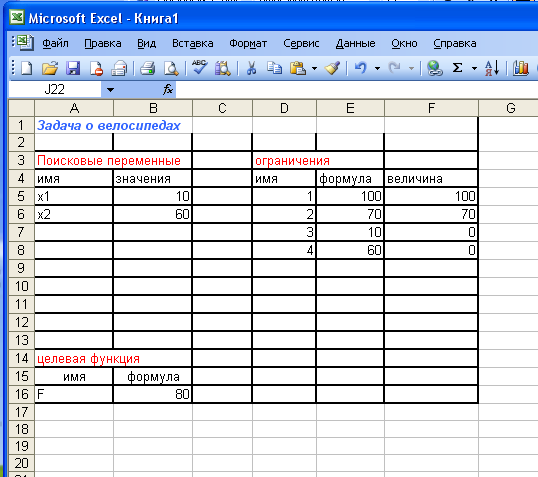
ЭТ Excel позволяет представить результаты поиска решения в форме отчета. Для этого в диалоговом окне “Результаты поиска решения” следует указать тип отчета из списка Тип отчета. Выберем опцию Результаты. Отчет будет создан на отдельном рабочем листе




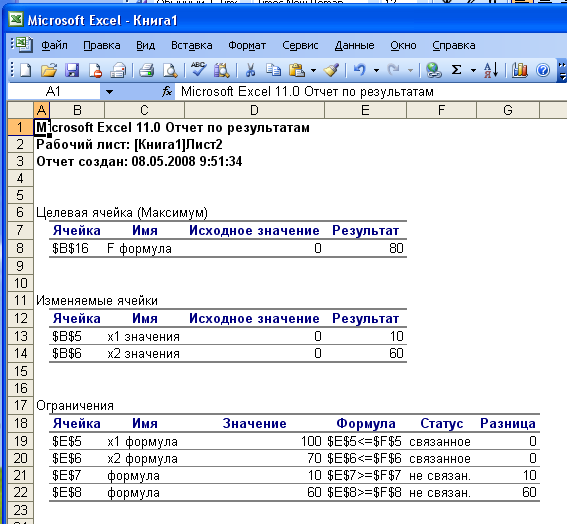
Задача 2. Производство столов и тумбочек

В мастерской освоили производство столов и тумбочек для торговой сети. Для их изготовления имеется 2 вида древесины. Первого вида – 72 м. куб, второго вида – 56 м. куб. На каждое изделие требуется:

	Виды древесины (м. куб)
	1	2
стол	0.18	0.08
тумбочка	0.09	0.28

Цена тумбочки – 0.7 у.е., стола – 1.1 у.е. Сколько нужно выпускать столов и тумбочек, чтобы мастерская получила максимальную прибыль?

Решение.

Пусть х –количество столов; у - количество тумбочек.

Целевая функция:

1.1х+0.7у –> max

Ограничения:

0.18х+0.09у=<72

0.08x+0.28y=<56

x>=0

y>=0

x, y – целые


Вся разработанная информация сводится в развернутую экономико-математическую модель и заносится в рабочий лист MS Excel




Результаты:




Транспортная задача.

Некий продукт (например, сталь) вырабатывается на m заводах Р₁,Р₂,...,Р_m, причем ежемесячная выработка составляет а₁,а₂,…,а_m тонн, соответственно. Пусть эту сталь надо доставить на предприятия Q₁,Q₂,…,Q_k (всего k) , причем b₁,b₂,…,b_k – ежемесячная потребность этих предприятий. Наконец, пусть задана стоимость c_ij перевозки одной тонны стали с завода P_i на предприятие Q_j . Естественно считать, что общее производство стали равно суммарной потребности в ней:

а₁+а₂+…+а_m = b₁+b₂+…+b_k . (1)

Необходимо составить план перевозок, при котором

1. 
   была бы точно удовлетворена потребность в стали предприятий Q₁,Q₂,…,Q_k;
   
2. Была бы вывезена вся сталь с заводов Р₁,Р₂,...,Р_m;
   
3. Общая стоимость перевозок была бы наименьшей.
   

Обозначим через x_ij количество стали (в тоннах), предназначенной к отправке с завода P_i на предприятие Q_j . План перевозок состоит из (m^.k) неотрицательных чисел x_ij (i = 1,2,…,m; j = 1,2,…,k).

Схема перевозок стали

	вQ1	в Q2	в Q3	…	в Qk	Отправлено
Из Р1	x11	x12	x13	…	x1k	a1
Из Р2	x21	x22	x23	…	x2k	a2
. . .	. . .	. . .	. . .	… … …	. . .	. . .
Из Рm	xm1	xm2	xm3	…	xmk	am
Привезено	b1	b2	b3	…	bk

Первое условие примет вид




(2)


Второе условие примет вид



(3)


Поскольку стоимость перевозки одной тонны из P_i в Q_j равна c_ij , то общая стоимость S всех перевозок равна

S = c₁₁ x₁₁+c₁₂x₁₂+ … +c_1kx_1k+c₂₁x₂₁+c₂₂x₂₂+ … +c_2kx_2k+ … +

+c_m1x_m1+c_m2x_m2+ … +c_mkx_mk (4)

Таким образом, мы приходим к следующей чисто математической задаче: дана система m+k линейных алгебраических уравнений (2), (3) с (m·k) неизвестными (обычно m^.k>>m+k) и линейная функция (4). Требуется среди всех неотрицательных решений данной системы 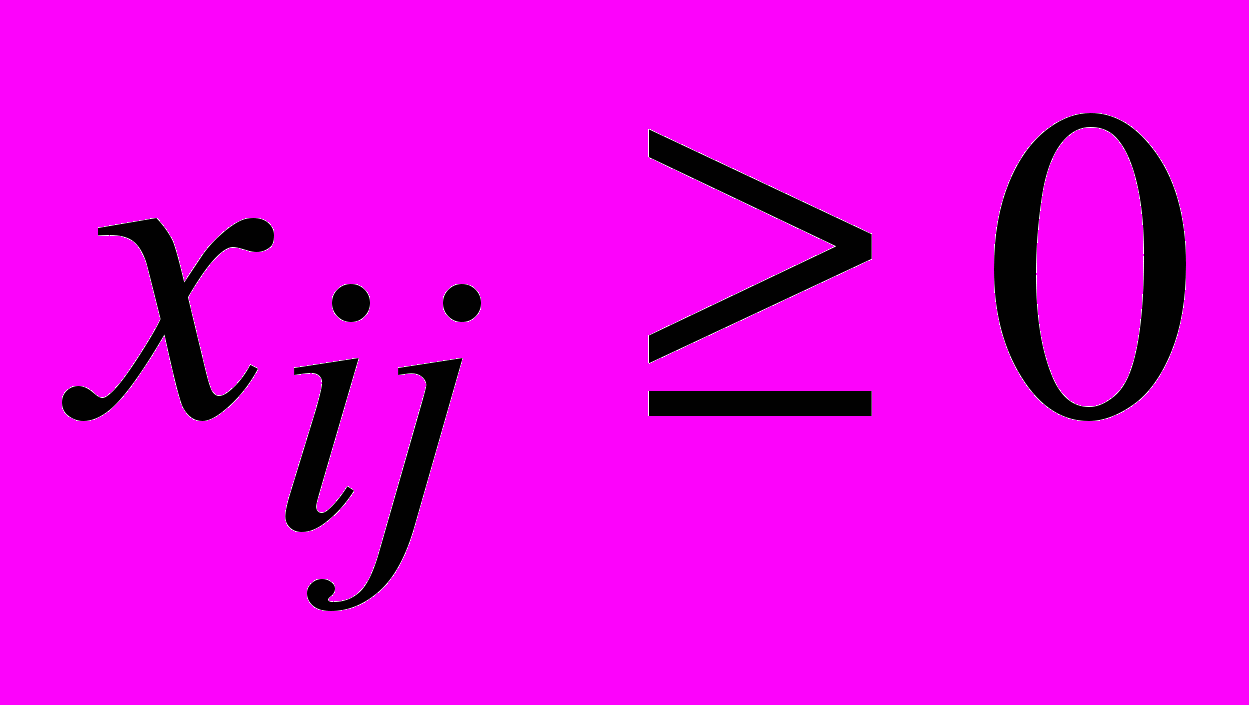найти такое, при котором функция S достигает наименьшего значения (минимизируется): .

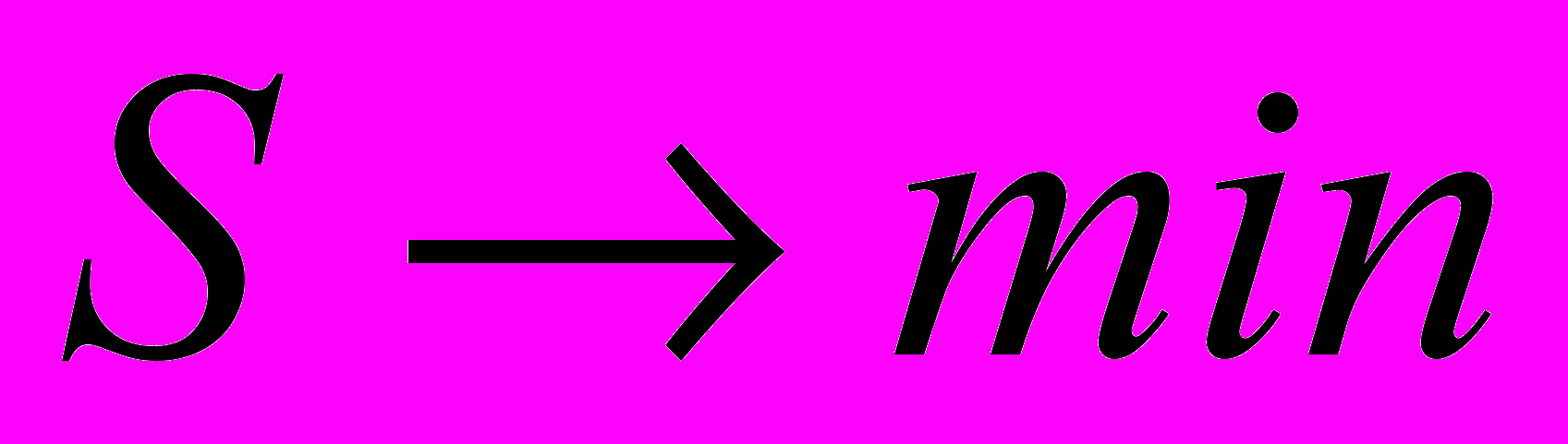Практическое значение этой задачи огромно, её умелое решение в масштабах страны могло бы экономить ежегодно огромные средства.

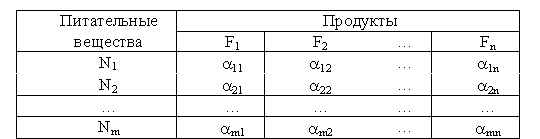
Задача о диете. Пусть у врача-диетолога имеется n различных продуктов F₁,F₂, … ,F_n, из которых надо составить диету с учетом их питательности. Пусть для нормального питания человеку необходимо m веществ N₁,N₂, … ,N_m. Предположим, что за месяц каждому человеку необходимо g₁ кг вещества N₁, g₂ кг вещества N₂, … , g_m кг вещества N_m. Для составления диеты необходимо знать содержание питательных веществ в каждом продукте. Обозначим через a_ij количество i-го питательного вещества, содержащегося в одном килограмме j-го продукта. Всю эту информацию представляют в виде, так называемой, матрицы питательности.

Матрица питательности

g₁

g₂


g_m


Предположим, что диетолог уже выбрал диету, т.е. определил, что человек должен за месяц потреблять h₁ кг продукта F₁ , … ,h_n кг продукта F_n. Полное количество питательного вещества N₁ будет

η₁α₁₁ + η₂α₁₂ + … +η_nα_1n.

По условию требуется, чтобы его, по крайней мере, хватило

η₁α₁₁ + η₂α₁₂ + … +η_nα_1n ≥γ₁.

Точно то же и для остальных веществ. В целом

η₁α_i1 + η₂α_i2 + … +η_nα_in ≥γ_i. (i = 1,2,…,m). (5)


Эти условия определяют наличие минимума необходимых питательных веществ.

Диета, для которой выполнены условия (5) – допустимая диета. Предположим, что из всех допустимых диет должна быть выбрана самая дешевая. Пусть π_i – цена 1 кг продукта F_i. Полная стоимость диеты, очевидно,

S = π₁η₁ + π₂η₂ + … + π_n η_n. (6)

Таким образом, мы пришли к задаче: найти неотрицательное решение η₁, … , η_n системы неравенств (5), минимизирующее выражение (6): .

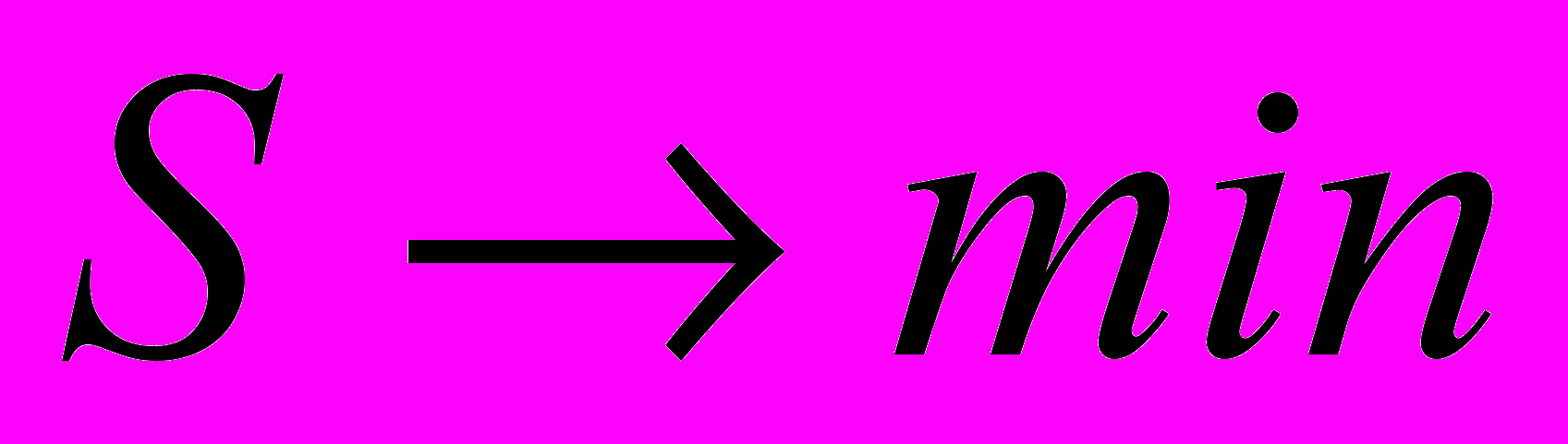В задачах линейного программирования имеется нечто общее. Каждая из них требует нахождения наиболее выгодного варианта в определенной экономической ситуации. С чисто математической стороны в каждой задаче требуется найти значение нескольких неизвестных так, чтобы

1. 
   все эти значения были неотрицательны;
   
2. удовлетворяли системе линейных уравнений или линейных неравенств;
   
3. при этих значениях некоторая линейная функция имела бы минимум (или максимум).
   

Таким образом, линейное программирование – это математическая дисциплина, изучающая методы нахождения экстремального значения линейной функции нескольких переменных при условии, что последние удовлетворяют конечному числу линейных уравнений и неравенств.

Запишем это с помощью формул: дана система линейных уравнений и неравенств





(7)


и линейная функция

f = c₁x₁ + c₂x₂ + … +c_nx_n (8)

Требуется найти такое неотрицательное решение

х₁ ³ 0, х₂ ³ 0, … ,х_n ³ 0, (9)

системы (7), чтобы целевая функция f принимала наименьшее (или наибольшее) значение.

Условия (7) называются ограничениями данной задачи, а функция f –целевой функцией.


Транспортная задача – склады и потребители.


Имеется два склада готовой продукции и три потребителя этой продукции А1, А2, А3. Склад 1 располагает 10000 единиц продукции, а склад 2 – 5000 единиц продукции. Потребителям нужно соответственно А1 –4000 единиц. А2 –8000 единиц. А3 –3000 единиц. В таблице отражена стоимость доставки единицы продукции от складов к потребителям:

	А1	А2	А3
Склад 1	3	3	2
Склад 2	6	5	1

Составить такой план перевозок, который соответствует минимальной суммарной стоимости.


Исходный план перевозок:

x1	x2	x3	<=10000
y1	y2	y3	<=5000

=4000 =8000 =3000


Матрица стоимости:

3	3	2
6	5	1

Целевая функция:

F = 3* x1+ 3*x2+ 2*x3+ 6*y1+5* y2+ 1*y3;


Ограничения задачи:

x1 + x2 + x3 <=10000;

y1 + y2 + y3 <=5000;

x1 + y1 =4000;

x2 + y2 =8000;

x3 + y3 =3000;


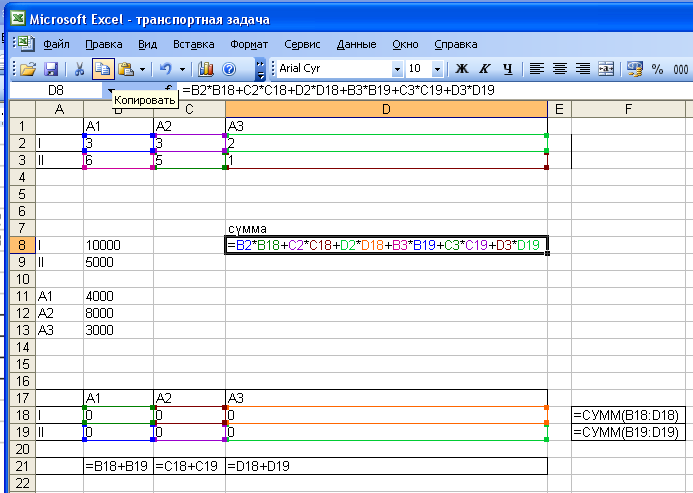
Вся разработанная информация сводится в развернутую экономико-математическую модель и заносится на рабочий лист MS Excel

В ячейках В2:D3 находится матрица стоимости.

В ячейках В18:D19 находятся начальные значения поисковых переменных x1, x2, x3, y1, y2, y3. В эти же ячейки после решения задачи будут помещены оптимальные значения поисковых переменных.

В ячейке D8 находится формула вычисления значения целевой функции:


= B2*B18+C2*C18+D2*D18+B3*B19+ C3*C19 +D3*D19


В эту же ячейку после решения задачи будет помещено минимальное значение этой функции.

В ячейках B8:B13 расположены значения правых частей ограничений.

В ячейках F18: F19 расположены формулы левых частей двух первых ограничений.

В ячейках B21:D21 расположены формулы левых частей трех последних ограничений.





После размещения данных следует выполнить команду Сервис, Поиск решения и в открывшемся диалоговом окне “поиск решения” задать расположение исходных данных в таблице с ограничениями:


F18<=B8

F19<=B9

B21=B11

C21=B12

D21=B13

B18= целое

C18= целое

D18= целое

B19= целое

C19= целое

D19= целое

B18:D19>=0

Диалоговое окно “Поиска решения”.




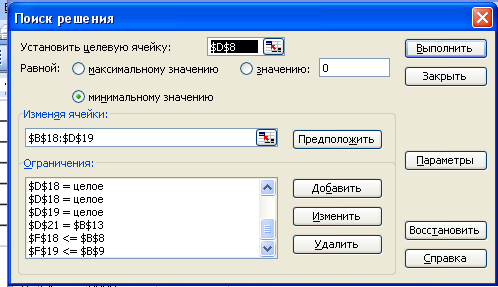
Результат:





Получим план перевозок:

4000	6000	0
0	2000	3000

Целевая функция: F =43000.


Задача о диете – корма для животных.

Для откорма животных на ферме в их еженедельный рацион необходимо включать не менее 33 единиц питательного вещества А, 23 единицы питательного вещества В и 12 единиц питательного вещества С. Для откорма используются три вида кормов. Данные о содержании питательных веществ и стоимость одной весовой единицы каждого из кормов даны в таблице:

	А	В	С	Стоимость одной весовой единицы.
В одной весовой ед. корма 1	4ед.	3 ед.	1 ед.	20 коп.
В одной весовой ед. корма 2	3 ед.	2 ед.	1 ед.	20 коп.
В одной весовой ед. корма 3	2ед.	1 ед.	2ед.	10 коп.

Составить наиболее дешевый рацион, при котором каждое животное получало бы необходимые количества питательных веществ А, В, С.

Решение

Выберем поисковые переменные:

x₁ – кол-во весовых единиц корма 1,

x₂ – кол-во весовых единиц корма 2,

x₃ – кол-во весовых единиц корма 3.

Ограничения:




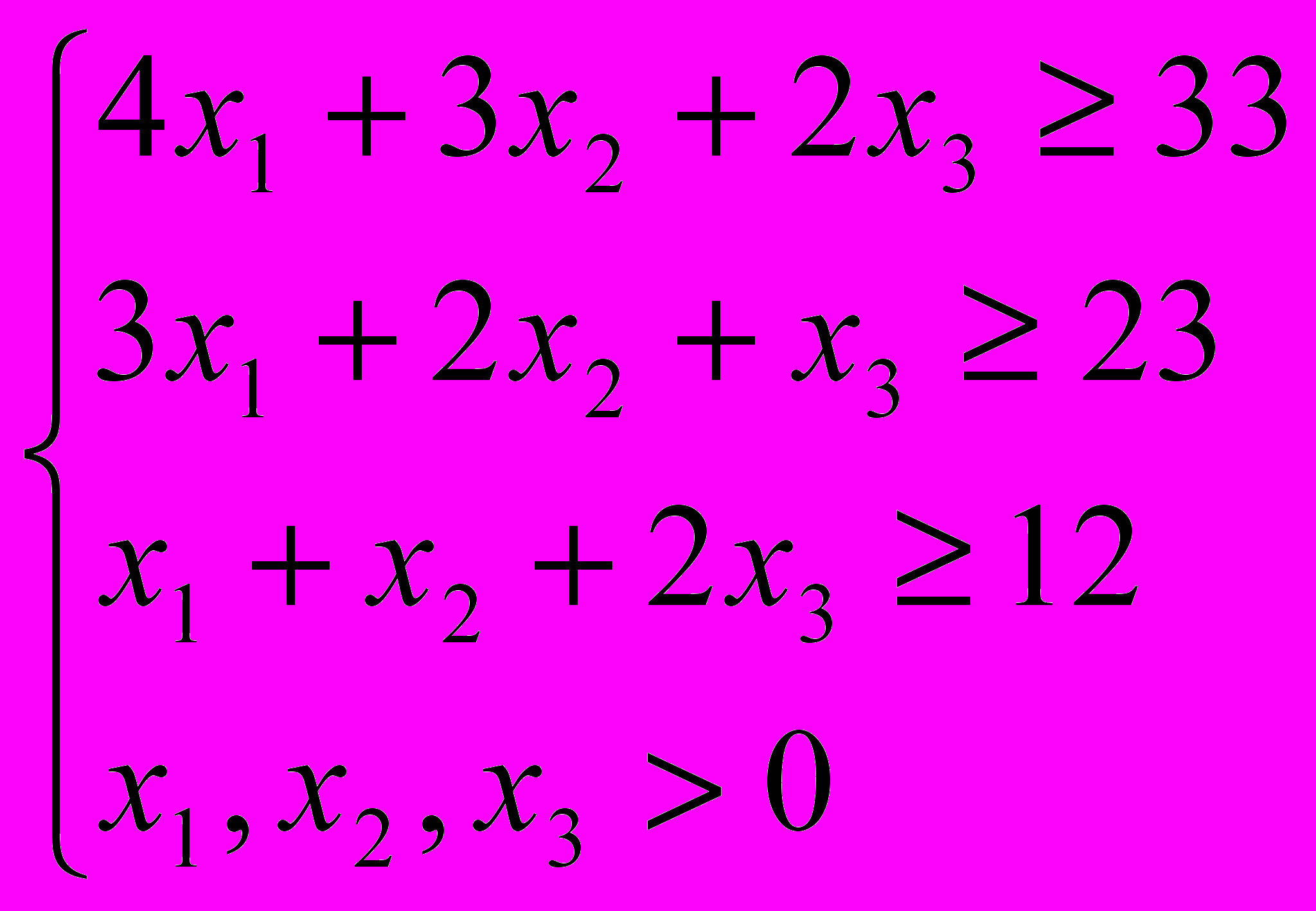
Целевая функция:




Поскольку поисковые переменные должны удовлетворять ограничениям, то в качестве начального плана выберем:

x₁ =12 ,

x₂ =0,

x₃ =0 .

Расположение данных задачи планирования на рабочем листе ЭТ Excel. (формулы).




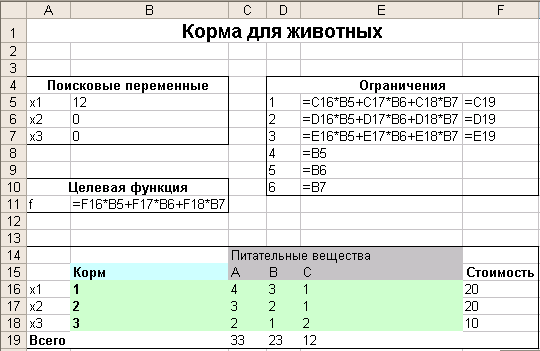
Результаты на рабочем листе ЭТ Excel.




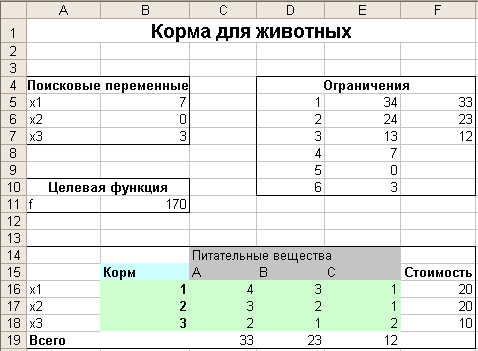
Ниже приведен отчет о результатах оптимизации





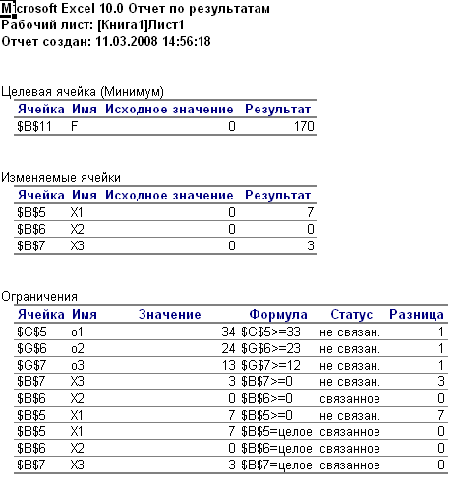
Задачи для самостоятельного решения


Смесь

Необходимо составить наиболее дешевую смесь из трех веществ. В состав смеси должно входить не менее 6 единиц химического вещества А, не менее 8 единиц вещества В и не менее 12 единиц вещества С. Имеется 3 вида продуктов, содержащих эти химические вещества в следующих пропорциях:

	А	В	С	Стоимость
I	2	1	3	2руб.
II	1	2	4	3руб.
III	3	1.5	2	2.5руб.

Задача о сырье


Имеется три вида сырья -А, В , С, которые используются для производства двух видов продуктов- I и II. В распоряжении находится 500 единиц сырья А, 750 единиц сырья В и 200 единиц сырья С.Продукт I состоит из 1 единицы сырья А и 2 единиц сырья В. Продукт II состоит из 2 единиц сырья А,1 единицы сырья В и 1 единицы сырья С. Доход от производства одной единицы продукта I составляет 4 руб.,а от одной единицы продукта II -5 руб. Сколько единиц каждого продукта нужно производить, чтобы максимализировать прибыль?


Задача о бензине

На нефтеперерабатывающем заводе имеется три вида сырья: алкилата – 1000 литров, крекинг-бензина – 1500 литров, бензина прямой перегонки – 800 литров, Это сырье используется для производства двух видов бензина- I и II. Бензин I состоит из 1 единицы алкилата, 2 единиц крекинг-бензина и 2 единиц бензина прямой перегонки. Бензин II состоит из 2 единиц алкилата ,1 единицы крекинг-бензина и 1 единицы бензина прямой перегонки. Сколько литров каждого вида бензина I и II нужно производить, чтобы максимизировать прибыль, если доход от производства одного литра бензина I составляет 35 рублей, а от одного литра бензина II -50 рублей?


Задача о мебельном цехе

Мебельный цех получает ежедневно 40 досок первого сорта и 19 второго сорта. Цех выпускает столы и стулья, при этом на изготовление стола требуется 4 доски первого сорта и одна доска второго сорта, а на изготовление стула – 1 доска первого и одна доска второго. Прибыль же от стола составляет 8 руб., а от стула – 6 руб. Какой план работы будет наиболее выгоден этому цеху.

Гнездо хищника

Гнездо хищника находится в точке А, а два потенциальных источника пищи хищника в точках В и С. Время, необходимое хищнику для того, чтобы добраться до участков В и С и возвратиться с единицей добычи, равно 2 и 3 минутам соответственно. В точке В хищник затрачивает на поимку единицы добычи х1 2 минуты, а в точке С – 1 минуту, чтобы поймать единицу добычи х2. Энергетическая эффективность единицы х1 оценивается в 25 Дж, а единицы х2 в 30 Дж. На путь из гнезда в любой из участков и обратно хищник может затрачивать не более 120 минут в сутки и на поиск жертв он может тратить не более 80 минут в сутки. Определить максимальную энергетическую эффективность хищника при поимке добыч х1 и х2.


Экспедиция «Северный полюс»

Участник экспедиции «Северный полюс» укладывает рюкзак и ему требуется решить, какие положить продукты. В его распоряжении имеются мясо мука, сухое молоко и сахар. В рюкзаке для продуктов осталось лишь 45 дм3, и нужно, чтобы суммарная масса продуктов не превосходила 35 кг. Врач экспедиции рекомендовал, чтобы мясо по массе было больше муки по крайней мере в два раза, муки не меньше молока, а молока по крайней мере в восемь раз больше, чем сахара. Сколько и каких продуктов нужно положить в рюкзак с тем, чтобы суммарная калорийность продуктов была наибольшей? Характеристики продуктов приведены в таблице.

Характеристики	Продуктов
	Мясо	Мука	Молоко	Сахар
Объем (дм3/кг) Калорийность(ккал/кг)	1 1500	1,5 5000	2 5000	1 4000

Дешевый кузов

Перед проектировщиками автомобиля поставлена задача сконструировать самый дешевый кузов, используя листовой металл, стекло и пластмассу. Основные характеристики материалов, их стоимости представлены в таблице. Общая поверхность кузова (вместе с дверьми и окнами)должна составить 14м2; из них не менее 4 м2 и не более 5м2 следует отвести под стекло. Масса кузова не должна превышать 150 кг. Сколько металла, стекла и пластмассы должен использовать наилучший проект?

Характеристики	Материалы
	металл	стекло	пластмасса
стоимость (руб/м2) масса (кг/м2)	25 10	20 15	40 3

Звероферма

Звероферма выращивает черно-бурых лисиц и песцов. На звероферме имеется 100 000 клеток. В одной клетке могут жить либо 2 лисицы, либо 1 песец. По плану на ферме должно быть не менее 3000 лис и не менее 6000 песцов. В одни сутки каждой лисе необходимо выдавать 4 единицы корма, а каждому песцу 5 единиц. Ферма ежедневно может иметь не более 200 000 единиц корма. От реализации одной шкурки лисицы ферма получает прибыль в 10 руб., а от песца 5 руб. Какое количество лисиц и песцов нужно держать на ферме, чтобы получить наибольшую прибыль?

Дневной рацион – задача о диете

Для поддержания жизнедеятельности человеку ежедневно необходимо потреблять не менее 118г белков, 56г жиров, 500г углеводов, 8г минеральных солей. Количество питательных веществ, содержащихся в 1 кг каждого вида потребляемых продуктов, а также цены 1кг каждого из этих продуктов  приведены в следующих таблицах: 

 

Питательные вещества	Содержание питательных веществ в 1 кг продуктов (г)
	Мясо	Рыба	Молоко	Масло	Сыр	Крупа	Картофель
Белки	180	190	30	10	260	130	21
Жиры	20	3	40	865	310	30	2
Углеводы	_	_	50	6	20	650	200
Минеральные соли	9	10	7	12	60	20	10

 

Цена за 1 кг продуктов (руб.)
Мясо	Рыба	Молоко	Масло	Сыр	Крупа	Картофель
31,8	21	4,28	25,4	32,9	6,5	3,1

 

Составить дневной рацион, содержащий не менее минимальной суточной нормы потребности человека в необходимых питательных веществах, так, чтобы общая стоимость продуктов была минимальной.


Авиапредприятие – транспортная задача.

Авиапредприятию необходимо решить, какое количество топлива следует закупить у трех поставщиков, если имеют место следующие ограничения:

1. заправка самолетов осуществляется в 4х аэропортах;
   
2. нефтяные заводы имеют возможности поставок – 2,5 миллиона литров, 5 миллионов литров и 6 миллионов литров соответственно;
   
3. распределение топлива по аэропортам осуществляется в следующих количествах – 1 миллион литров, 2 миллиона литров, 3 миллиона литров и 4 миллиона литров.
   

Составить модель оптимального прикрепления поставщиков, если стоимость доставки 1000 литров топлива задается таблицей

	I поставщик	II поставщик	III поставщик
1 аэропорт	12	9	10	1 млн литров
2 аэропорт	10	11	14	2 млн литров
3 аэропорт	8	11	13	3 млн литров
4 аэропорт	11	13	9	4 млн литров
	2,5 млн литров	5 млн литров	6 млн литров

Нефтеперерабатывающий завод


Нефтеперерабатывающий завод получает 4 полуфабриката: алкилата 400 литров, крекинга бензина – 250 литров, бензина прямой перегонки – 350 литров, изопентана – 300 литров. В результате смешивания этих четырех компонентов в отношении 2:3:5:2 образуется бензин А, стоимостью 120 руб за литр, в отношении 3:2:2:1 – бензин В – стоимостью 100 руб за литр, в отношении 2:2:1:3 – бензин С – стоимостью 150 руб за 1 литр. Определить такой план смешивания компонентов, при котором будет достигнута максимальная стоимость всей продукции, причём завод доложен выпустить бензина А не менее 400 литров, бензина В – не менее 100 литров, бензина С - не менее 100 литров.

Ограничения


Целевая функция

F=120*x₁ + 100*x₂ + 150*x₃