Преобразования в 3D пространстве

Вид материала

Документы

Подобный материал:

• «упаковать», 279.17kb.
• Лекция Преобразования типов Преобразования типов. Преобразования внутри арифметического, 236.75kb.
• Линия тождественных преобразований Практическое занятие №1 Тождественные преобразования, 55.72kb.
• Лекция Удаление невидимых линий и поверхностей (продолжение), 83.28kb.
• Программа по курсу: практикум по трёхмерной машинной графике (базовый) по направлению:, 91.42kb.
• Гранта: «Внешняя политика России на постсоветском пространстве: проблемы и тенденции, 68.45kb.
• Некорректные задачи геофизики. План лекций. Лекция I. Функциональные пространства., 64.34kb.
• 5. 11. Как упростить логическую формулу?, 21.9kb.
• Экономическая интеграция на пространстве СНГ, 218.96kb.
• План: Преобразования в восстановительный период (1949-1952 гг.). Пять секторов экономики, 28.1kb.

Преобразования в 3D пространстве

Смещение

Не забывайте, что все операции проходят в однородных координатах. Отличие преобразований в 3D от 2D в том, что добавлена третья координата по оси 0z.

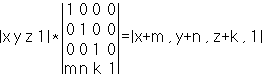
Масштабирование

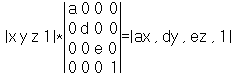
Общее полное масштабирование

Вращение вокруг оси x на угол

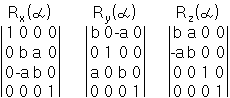
где a=sin; b=cos




Вращение тела вокруг собственной оси

• Перемещение в начало координат
  
• Вращение
  
• Перемещение обратно
  

V=SRS^-1

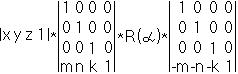
Зеркалирование

Вращение тела вокруг произвольной оси проходящей через точку (0,0,0) на угол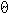

Это не базовая операция. Ее можно получить из выше названных операций и поэтому запоминать её совсем не нужно.

-угол наклона относительно ОХ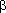

- угол наклона относительно ОY

  - угол наклона относительно ОZ

n₁ = cos
n₂ = cos
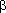
n₃ = cos