Игра «Морской бой» игры-алгоритмы глава Поиск закономерностей в математических играх > Сумма чисел или инвариант виртуальный «угадыватель» мыслей
| Вид материала | Закон |
- «Морской бой» интеллектуально-творческая игра, 144.52kb.
- Урок игра «Морской бой», 61.3kb.
- Морской бой. Интеллектуальная игра по русскому языку для 3 класса правила, 154.16kb.
- Конкурс Место проведения Кол-во баллов, 691.22kb.
- Интеллектуальная игра «Морской бой», 271.42kb.
- Игра «Морской бой» по информатике Возрастная группа (класс), 16.68kb.
- Первый. Предмет и история юридической статистики 7 Глава, 5134.73kb.
- «Численные методы в химии» Общая трудоёмкость дисциплины составляет, 22.46kb.
- Круг чтения в 6 классе, 21.78kb.
- Тема игры : «Лесные чудеса», 73.19kb.
ОКРУЖНАЯ НАУЧНАЯ КОНФЕРЕНЦИЯ УЧАЩИХСЯ
СЕКЦИЯ “Математика”
Поиск беспроигрышных стратегий в математических играх
Автор: Некрылов Леонид Сергеевич
учащийся 8 класса
МОУ Герасимовская СОШ
Научный руководитель: Остапенко Нина Устиновна
учитель математики
Нефтегорск, 2009
Оглавление
Введение ....................................................................................................................... 3
Глава 1. Математические игры и головоломки ……………………………………. 4
1.1. Игра «Крестики-нолики» …………………………………………………… 4
1.2. Игры с дыркой или «пятнашки» …………………………………………… 5
1.3. Игра НИМ и другие аналогичные игры …………………………………… 7
1.4.Игра «Морской бой» ………………………………………………………… 9
1.5. Игры-алгоритмы ……………………………………………………………. 10
Глава 2. Поиск закономерностей в математических играх ……………………… 12
2.1. Сумма чисел или инвариант ………………………………………………. 12
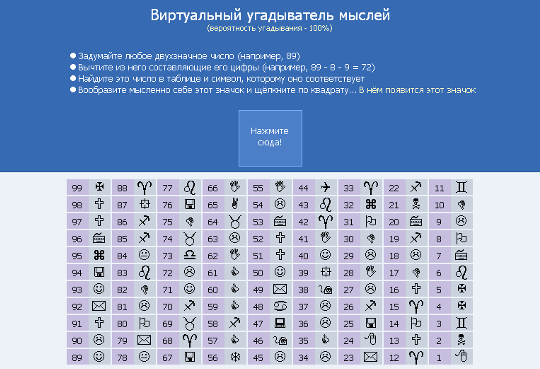
2.2. Виртуальный «угадыватель» мыслей …………………………………….. 17
Заключение …………………………………………………………………………. 18
Список литературы ………………………………………………………………… 19
Приложения …........................................................................................................... 20
Приложение 1 ….................................................................................................. 20
Приложение 2 …………………………………………………………………. 21
Приложение 3 ………………………………………………………………… 21
Приложение 4 ………………………………………………………………… 22
Приложение 5 ………………………………………………………………… 24
Приложение 6 ………………………………………………………………… 24
Введение
Часто, играя дома с родными во всем знакомую игру «Крестики-нолики», я оказывался победителем. Я пробовал по-разному начинать игру, и результат оказывался для меня одинаковым – все время выигрывал. Тогда я решил выяснить, существует ли выигрышная стратегия в эту игру или мои победы оказываются случайными результатами? Подойдя к учителю математики, я задал мучивший меня вопросе. Нина Устиновна ответила, что есть выигрышная стратегия и не только в игру «Крестики-нолики», но и в другие известные игры, а разобраться в них помогут знания математики.
Так у меня появилась цель исследования: экспериментально доказать существование выигрышных стратегий.
Задачи исследования:
Изучить литературу, описывающую математические игры и головоломки.
- Провести экспериментальную работу с одноклассниками по выявлению действия беспроигрышной стратегии.
- Объяснить математические закономерности, использующиеся в беспроигрышной стратегии.
- Найти практическое применение моему исследованию.
Объектом исследования является поиск математических закономерностей.
Предмет исследования – беспроигрышные стратегии.
Исходя из цели исследования, выдвинута следующая гипотеза: если знать математические закономерности, можно разработать беспроигрышную стратегию.
В своей работе я использовал экспериментальные методы и их математическую обработку.
Считаю выбранную мной тему очень интересной и актуальной, так как это позволяет посмотреть на математику по-новому - это не только примеры и задачи, но и занимательные игры и фокусы, которые будут интересны многим людям.
Глава 1. Математические игры и головоломки
Простейшие математические игры часто используют как задачи, в которых нужно найти выигрышную стратегию, либо одно положение перевести в другое. Иногда задачи бывают весьма простыми, когда они решаются известными методами, такими как инвариант и раскраска, но есть весьма простые, но до сих пор неразрешённые задачи, связанные с математическими играми.
1.1.Игра «Крестики-нолики»
Все знают эту игру: на маленьком поле - 3×3 – двое игроков по очереди ставят свои значки, один – крестики, другой – нолики. Тот, кто первым построит ряд из трех значков по горизонтали, вертикали или диагонали, выиграл.
Эта игра быстро надоедает, поскольку вскоре игроки начинают понимать, как свести партию вничью. Но идея хороша, и существует множество вариаций на тему простейших крестиков-ноликов, куда более интересных. Даже на доске 3×3 игру можно усложнить, например, разрешив каждому из игроков ставить любой значок, крестик или нолик. Правда, в такой игре побеждает (т.е. собирает ряд из трех каких-нибудь одинаковых значков) тот, кто ходит первым. Как только игроки найдут выигрышную стратегию, игра теряет свою прелесть.
Игра «три в ряд» относится к категории конечных, детерминированных, переборных, стратегических игр двух лиц с полной информацией. Легко обнаружить, что при правильной игре партия заканчивается вничью. Собственно, исход игры решается уже на первом ходу. У крестиков три принципиально различных начала — пойти в угол, в центр и в боковую
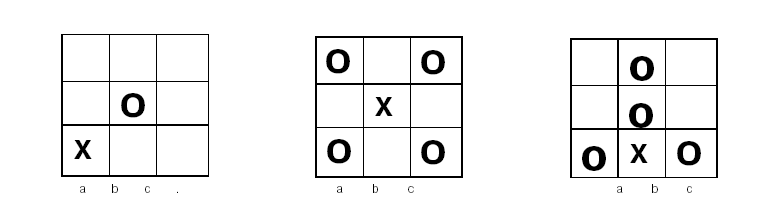
клетку (рис. ….). На рисунке показаны правильные ответы ноликов в каждом из этих случаев. Как мы видим, самый опасный «дебют» крестиков — в угловую клетку. Из возможных ответов ноликов лишь один спасает положение, и неопытный игрок вряд ли изберет его. Пусть, скажем, в ответ на ход al нолики пойдут b1. Тогда следует ход аЗ с угрозой закончить игру по вертикали «а». У ноликов единственный ответ а2, на что следует решающий ход сЗ с «вилкой», то есть двойным ударом на b2 и bЗ. Следующим ходом крестики выигрывают. Вилкой заканчивается партия и в других вариантах
Но самые интересные – крестики-нолики на бесконечном поле. Разумеется, поле – это обычный тетрадный листок в клетку, но его вполне хватает. Здесь нужно выстроить в ряд (по вертикали, горизонтали или диагонали) пять своих значков. Правда, и в этой игре крестики, ходящие первыми, имеют преимущество, но оно не так очевидно, как в играх на маленьких полях.
1.2.Игры с дыркой или «пятнашки»
До изобретения кубика Рубика для многих людей знакомство с головоломками начиналось с «пятнашек» - так часто называют известную игру «15».
С пятнашек начинается история игр с дыркой – головоломок, в которых фишки перемещаются по игровому полю за счёт того, что одно из мест на поле свободно. У «пятнашек» есть множество родственников, которые как раз и образовывают целый раздел этих головоломок.
Игру «15» придумал в 70-х годах 19 века прославленный американский изобретатель головоломок Сэмюель Ллойд. Время появления его игрушки и известного всем кубика Рубика разделяют ровно 100 лет. Любопытно, что возраст обоих изобретателей, когда они придумали свои знаменитые головоломки, был одинаков – не многим больше тридцати. До «пятнашек» никакая другая головоломка таким успехом не пользовалась.
Великий Марк Твен, будучи современником Ллойда и свидетелем всеобщего ажиотажа вокруг игры «15», включил в свою сатирическую повесть «Американский претендент» изложений сообщения, якобы преданного агентством «Ассошиэйтед пресс», в котором говорилась, что «за последние несколько недель вошла в моду новая игрушка – головоломка…и что от Атлантического океана до Тихого всё населения Соединённых Штатов прекратило работу и занимается только этой игрушкой; что в связи с этим вся деловая жизнь в стране замерла, ибо судьи, адвокаты, взломщики, священники, воры, торговцы, рабочие, убийцы, женщины, дети, грудные младенцы,- словом, все с утра до ночи заняты одним-единственным высокоинтеллектуальным и сложным делом… что веселья и радость покинули народ, - на смену им пришли озабоченность, задумчивость, тревога, лица у всех вытянулись, на них появились отчаяние и морщины- следы прожитых лет и пережитых трудностей, а вместе с ними и более печальные признаки, указывающие на умственную не полноценность и начинающиеся помешательство; что в восьми городах день и ночь работают фабрики, и всё же до сих пор не удалось удовлетворить спрос на головоломку».
Вскоре после своего появления на свет коробочка с цифрами 15 на крышке пересекла океан, быстро распространилась во всех европейских странах и получила новое имя «такен». Изобретателю посчастливилось найти ту неуловимую меру сложности, когда головоломка решалась без труда почти всеми и в то же время требовала определённой сообразительности, благодаря чему каждый мог получить удовольствие от сознания своего высокого интеллектуального уровня.
Первому успеху головоломки в немалой степени способствовало и напечатанное в газетах объявление о призе в 1000$ за решение следующей задачи: исходной позиции фишки располагается по порядку номеров, за исключением двух последних, которые переставлены местами друг с другом; передвигая по одной фишки, но не вынимая фишки из коробочки, нужно поменять местами номера 15 и 14 так, чтобы все фишки стояли по порядку номеров, а первый нижний угол был свободен.
Помещая это объявление, Ллойд знал, что ничем не рискует, так как предлагает неразрешимую задачу. Эта задача ещё сыграла с изобретателем злую шутку, когда он пытался запатентовать свою игру, - ему сказали, что нельзя запатентовать игру, не имеющую решения.
Секрет игры «15»
Не всегда можно головоломку перевести из одного состояния в другое, - запрещены такие переходы, при которых нарушаются те или другие законы сохранения. Есть такой закон и в игре «15». Чтобы объяснить его, мысленно заполним пустое место с фишкой с номером «16». Тогда каждый ход – сдвиг фишки – будет состоять в том, что эта фишка меняется местами с фишкой «16». Операцию, при которой какие-то две фишки (не обязательно соседние) меняются местами, так и назовем – обменом; математический термин для таких операций – транспозиция. Очевидно, что из любой расстановки16 фишек можно не более чем за 15 обменов получить правильную позицию – обозначим ее S – и вообще любую другую расстановку, при этих обменах не запрещается вынимать фишки из коробки. Например, можно сначала поставить на свое место фишку 1, обменяв её с той фишкой, которая это место занимает, затем точно так же поставить на место фишку 2 и т.д. Последними мы обменяем фишки 15 и 16- при этом сразу обе встанут правильно. Конечно, не исключено, что по ходу дела какие- то фишки автоматически попадут на свои места, и их трогать не придется, при этом число обменов окажется меньше 15. Можно расставлять фишки по этой же системе, но в другом порядке, скажем 16, 15, 14,… или совсем иначе. И тогда число обменов может оказаться другим. Однако каким бы способом ни выбирать последовательность обменов, превращающую одну заданную расстановку фишек в другую, четность числа обменов в этой последовательности всегда буде одной и той же.
Это очень важное и неочевидное докажем ниже. Оно позволяет дать следующее определение: расстановка называется четной, если ее можно превратить в правильную позицию. С помощью четного числа обменов, и нечетной в противном случае. В математике обычно говорят не «расстановка», а «перестановка»; к этому мы еще вернемся. Сама правильная расстановка S всегда четная, а ловушка Ллойда - нечетная. Но почему они не переводятся друг в друга?
Как выше уже указано, каждый ход в игре «15» можно рассматривать как обмен фишки с одной из соседних. Следовательно, при каждом ходе четность расстановки 16 фишек меняется: если до хода расстановку можно было упорядочить за N обменов, то после него- за N+1 обменов( взяв этот ход назад), а числа N и N+1- разной четности. В обеих расстановках классической задачи Ллойда дырка ( или фишка 16) расположена одинаково. Если бы мы сумели одну расстановку перевести в другую, то фишка 16 должна была совершить столько же ходов вверх, сколько вниз, и столько же ходов вправо, сколько влево, иначе она не вернулась бы назад. Поэтому мы сделали бы четное число ходов, а так как при каждом ходе четность расстановки меняется, в начале и в конце она была бы одинаковой. Но позиция S и L, как мы видели. Имеют разную четность.
1.3. Игра НИМ и другие аналогичные игры
Существует несколько игр, в которых двое играющих A и B, руководствуясь определёнными правилами, по очереди вынимают то или иное число фишек из одной или нескольких кучек – побеждает тот, кто берёт последнюю фишку. Простейшая такая игра – это игра с одной кучкой фишек, и сделать ход в ней – значит взять из кучки любое число фишек от 1 до m включительно. Многие подобные игры поддаются исследованию с помощью числа Шпрага-Гранди G(C). Пустой позиции O, не содержащей фишек, отвечает G(O)=0. Комбинацию кучек, состоящих соответственно из x, y, … фишек, обозначим C=(x, y, …) и предположим, что допустимые ходы переводят C в другие комбинации: D, E, … Тогда G(C) есть наименьшее неотрицательное число, отличное от G(D), G(E), … Это позволяет по индукции определить G(C) для любой комбинации C, разрешённой правилами игры. Так, в упомянутой задаче G(x)=x mod (m+1).
Если G(C)>0, то игрок, делающий следующий ход, допустим, это игрок A, может обеспечить себе выигрыш, если ему удастся перейти к «безопасной» комбинации S с G(S)=0. Действительно, по определению G(S) в этом случае либо S – пустая позиция, и тогда A уже выиграл, либо B следующим ходом должен перейти к «опасной» позиции U с G(U)>0 – и тогда всё повторяется снова. Такая игра после конечного числа ходов заканчивается победой A.
К подобным играм относится ним. Имеется произвольное число кучек фишек, и игроки по очереди выбирают одну какую-то кучку и вынимают из неё любое число фишек (но хотя бы одну обязательно).
Более общий случай представляет игра Мура, которую также можно назвать k-ним. Правила её те же, что и в обычном ниме (1-ним), но здесь разрешается брать фишки из любого количества кучек, не превосходящего k.
Ещё одна подобная игра – Кегли. В ней фишки разложены в ряд, и при каждом ходе убирается одна какая-либо фишка или две соседние. При этом ряд может разбиться на два меньших ряда. Выигрывает тот, кто возьмёт последнюю фишку. Обобщённая вариация этой игры известна под именем игры Витхоффа.
Есть интересная вариация игры ним под названием «звёздный ним». Она довольно проста, но стратегия в ней видна не сразу. Играют в эту игру на звездообразной фигуре, изображённой на рис. 1, слева. Поставьте по одной фишке на каждую из девяти вершин звезды. Игроки A и B делают ходы по очереди, снимая при каждом ходе либо одну, либо две фишки, соединённые отрезком прямой. Тот, кто снимает последнюю фишку, выигрывает.
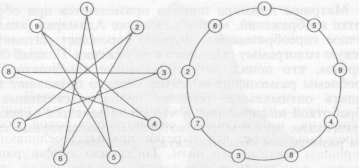
рис. 1
Звёздный ним (слева) и выигрышная стратегия для него (справа)
У игрока B при игре в «звёздный ним» есть выигрышная стратегия, использующая симметрию игровой доски (вообще, выигрышные стратегии многих математических игр строятся на этом). Представим, что отрезки прямых, соединяющих вершины звезды, - это нити. Тогда всю конфигурацию можно развернуть в окружность, топологически эквивалентную нитяной звезде. Если A снимает с окружности одну фишку, то B снимает две фишки с противоположного участка окружности. Если A берёт две фишки, то B снимает с противоположного участка окружности одну фишку. В обоих случаях на окружности остаются две группы из трёх фишек. Какую бы фишку (или какие бы фишки) ни взял A из одной группы, B берёт соответствующую фишку (или фишки) из другой группы. Ясно, что последняя фишка достанется игроку B.
1.4.Игра «Морской бой»
Вряд ли можно найти человека, который ни разу в жизни не играл в «морской бой». Несмотря на внешнюю простоту, эта популярная игра и ее различные модификации содержат немало тонкостей.
В классическом варианте морского боя каждый из двух игроков рисует на клетчатом листе бумаги две доски размером 10х10. На одной из них он расставляет свои корабли, а на второй стремится угадать расположение кораблей противника. В состав флотилии входят десять кораблей: один линкор (корабль 4х1), два крейсера (3х1), три эсминца (2х1) и четыре катера (1х1). Корабли могут занимать любые поля доски, но не должны касаться друг друга ни сторонами, ни углами.
После размещения флота игроки начинают по очереди стрелять по неприятельским кораблям, то есть называть поля доски — аЗ, с7, к9 и т. д. (по аналогии с шахматами горизонтали доски обозначаются числами от 1 до 10, а вертикали — латинскими буквами от а до k). После каждого выстрела игрок получает от партнера следующую информацию: «попал», если выстрел пришелся на поле с кораблем, «потопил», если это последнее поле корабля (по другим полям, занятым им, попадание произошло раньше), и наконец, «промах», если поле пустое. В первых двух случаях игрок получает право на дополнительный выстрел, и так до первого промаха, после чего очередь хода передается партнеру. Победителем становится игрок, которому первому удается потопить все десять кораблей противника.
Если говорить об искусстве игры, то возникают два вопроса: 1) как производить выстрелы, чтобы повысить вероятность попадания в неприятельские корабли, и 2) как расставить свои собственные корабли, чтобы противнику было трудно их потопить.
Предположим, что мы хотим попасть в неприятельский линкор. Если мы будем стрелять последовательно сначала по полям первой горизонтали (слева направо), затем, по полям второй горизонтали и т. д., то не исключено, что попадем в него только на 97-м ходу (если он занимает поля с g 10 по k10). Однако если мы будем наносить удары только по полям, обозначенным крестиками на рис. 2, то при этом наверняка попадем в линкор не позднее 24-го хода (24 крестика следуют друг за другом через три поля вдоль каждой вертикали и горизонтали).
Рис. 2
Рассмотрим теперь более общий случай. Предположим, что на доске nxn расположен один-единственный корабль kх1(к-мино). Совокупность выстрелов, гарантирующих нам попадание в этот корабль, назовем стратегией. Стратегию, содержащую минимальное число выстрелов, назовем оптимальной; число выстрелов в ней обозначим через s (n, k).
Очевидно, s (4, 4) =4; cдвигая все выстрелы на четыре поля по вертикали и горизонтали, получаем семь стратегий на доске 10X10. Однако только одна из них является оптимальной (рис. 2), причем s (10,4) =24.
Ясно, что для попадания в корабль kх1, расположенный на доске nxn, выстрелы должны отстоять друг от друга на k полей по вертикали и на столько же по горизонтали.
Это означает, что на каждой вертикали и на каждой горизонтали доски содержится примерно по
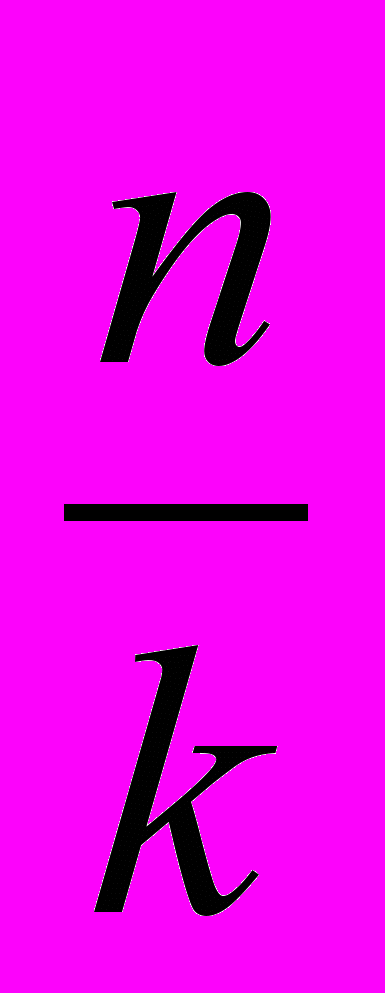выстрелов оптимальной стратегии, и получаем приближенную формулу
Опытные игроки обычно поступают следующим образом. Сначала, пользуясь стратегией на рис. 2, обнаруживают единственный линкор противника. Когда с ним покончено, начинают поиски крейсеров. Теперь удары наносятся не через 4 поля по вертикали или горизонтали, а через три. Потопив оба крейсера, переходят к эсминцам. Когда на доске остаются одни катера, то удары по всем его свободным полям можно наносить в произвольном порядке.
1.5. Игры-алгоритмы
Среди школьников очень популярными являются игры на угадывание задуманных чисел. Дело здесь, конечно же, не в угадывании задуманного числа, а в решении конкретной задачи. Причем в таких играх развиваются навыки быстрого устного счета, что является одной из составляющей математической компетентности.
Я хотел бы привести одну из таких игр. Возьмем числа от 1 до 12 и расположим их по кругу. Пусть кто-либо задумает число из круга. Затем нужно на этом круге указать любое число, а мысленно прибавить к нему 12. Получившееся число громко объявить присутствующим. Пусть потом задумавший считает про себя от задуманного числа, притрагиваясь сначала к указанному числу, а потом к каждому следующему числу по кругу в обратном порядке, и пусть считает до сказанного числа. Когда он досчитает до него, последовательно притрагиваясь к цифрам, то остановится как раз на задуманном числе.
Глава 2. Поиск закономерностей в математических играх
В процессе поиска и обработки теоретической информации по беспроигрышным стратегиям я стал задумываться над некоторыми математическими закономерностями, используемыми в них. Так родилась идея самому придумать игру с беспроигрышной стратегией, полезной не только для развития математической компетентности, но и для применения в своей учебной деятельности.
2.1. Сумма чисел или инвариант
Однажды на уроке математики нам продиктовали ряд цифр: 1, 2, 3, 4 и предложили составить из него все возможные суммы. У меня получились такие примеры:
1+234=235 4+123=127 214+3=217
2+134=136 432+1=433 21+34=55
3+124=127 321+4=325 14+23=37 и т.д.
От нечего делать я придумал себе игру: начал искать суммы цифр всех полученных ответов. Во всех случаях результат был один и тот же: получалось число 10.
Например, 2+3+5=10, 4+3+3=10, 3+7=10, 5+5=10 и т.д.
Дальше мне пришло в голову найти сумму исходных цифр (продиктованных учителем): 1+2+3+4=10.
Я заинтересовался этой закономерностью и стал ее проверять на больших числах.
2.1.1. Исследование сумм цифр,
составляющих запись четырехзначных и пятизначных чисел.
Я проверил замеченную мной закономерность на четырехзначных и пятизначных числах. Приведу примеры работы с двумя такими числами: 52963 и 12345.
- Число 52963
Сумма цифр, его составляющих равна: 5 + 2 + 9 + 6 + 3 + = 25, а 2 + 5 = 7.
Я начал составлять все возможные суммы цифр, составляющих число 52963 и сразу находить суммы цифр полученных ответов:
52 + 96 + 3 = 151 1 + 5 + 1 = 7
369 + 52 = 421 4 + 2 + 1 + = 7 и т.д.
- Число 12345
Сумма цифр, его составляющих равна: 1 + 2 + 3 + 4 + 5 = 15, а 1 + 5 = 6
Я начал составлять все возможные суммы цифр, составляющих число 12345 и сразу находить суммы цифр полученных ответов:
123 + 45 = 168 1 + 6 + 8 = 15 1 + 5 = 6
1352 + 4 = 1356 1 + 3 + 5 + 6 = 15 1 + 5 = 6 и т.д.
Я доказал, что замеченная мною закономерность «срабатывает» для четырехзначных и пятизначных чисел. (На самом деле я сделал намного больше вычислений, подтверждающих мой вывод, а в работе привел только некоторые из них.)
2. 1. 2. Исследование сумм цифр, составляющих шестизначные числа.
Затем я проверил замеченную мной закономерность на 10 шестизначных числах.
Приведу результаты работы с двумя такими числами: 548769 и 269751.
- Число 548769
Как всегда, сначала я нашел сумму цифр, составляющих это число.
5 + 4 + 8 + 7 + 6 + 9 = 39 3 + 9 = 12 1 + 2 = 3.
Затем я опять начал составлять возможные суммы: 54 + 87 + 69 = 210, а 2 + 1 = 3
769 + 485 = 1254, а 1 + 2 + 5 + 4 = 12, а 1 + 2 = 3
Я составлял все возможные суммы из цифр, составляющих число 548769. Окончательная сумма цифр всех полученных ответов всегда равнялась 3.
- Число 269751
Сумма цифр, составляющих данное число: 2 + 6 + 9 + 7 + 5 + 1 = 30, 3 + 0 = 3
Некоторые из сумм цифр, составляющих это число и суммы цифр ответов:
961 + 257 = 1218 1 + 2 + 1 + 8 = 12 1 + 2 = 3
157 + 269 = 426 4 + 2 + 6 = 12 1 + 2 = 3 и т.д.
Вывод: я доказал, что замеченная мною закономерность «срабатывает» для четырехзначных, пятизначных и шестизначных чисел.
2.1.3. Исследование сумм цифр, составляющих запись семизначных чисел.
Я проверил замеченную мной закономерность на 10 семизначных числах. Приведу результаты работы с двумя такими числами: 1234567 и 9786543.
- Число 1234567
Как всегда, сначала я нашел сумму цифр, составляющих это число.
1 + 2 + 3 + 4 + 5 + 6 + 7 = 28 2 + 8 = 10 1 + 0 = 1
Затем я опять начал составлять возможные суммы:
76 + 54 + 32 + 1 = 163 1 + 6 + 3 = 10 1 + 0 = 1
345712 + 6 = 345718 3 + 4 + 5 + 7 + 1 + 8 = 28 2 + 8 = 10 1 + 0 = 1
- Число 9876543
Сумма цифр, составляющих это число: 9 + 8 + 7 + 6 + 5 + 4 + 3 = 42 4 + 2 =6
Приведу некоторые из сумм, составленных из цифр этого числа и суммы цифр ответов:
9876 + 543 = 10419 1 + 0 + 4 + 1 + 9 = 15 1 + 5 = 6
9753 + 468 = 10221 1 + 0 + 2 + 2 + 1 = 6
Вывод: теперь я доказал, что замеченная мною закономерность «срабатывает» для четырехзначных, пятизначных, шестизначных и семизначных чисел.
2.1.4. Исследование сумм цифр,
составляющих запись восьмизначных и девятизначных чисел
Я проверил замеченную мной закономерность на 10 восьмизначных числах и 10 девятизначных числах.
Приведу результаты работы с двумя такими числами: 12345678 и 978265143.
- Число 12345678
Сумма цифр числа: 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 = 36 3 + 6 = 9
Некоторые из сумм, составленных из цифр этого числа и суммы цифр ответов:
1245 + 6378 = 7623 7 + 6 + 2 + 3 = 18 1 + 8 = 9
37 + 82 + 46 + 15 = 180 1 + 8 + 0 = 9
- Число 978265143
Сумма цифр числа: 9 + 7 + 8 + 2 + 6 + 5 + 1 + 4 + 3 = 45 4 + 5 = 9
Некоторые из возможных сумм, составленных из цифр этого числа и суммы цифр ответов:
9782 + 65143 = 74925 7 + 4 + 9 + 2 + 5 = 27 2 + 7 = 9
341 + 562 + 879 = 1782 1 + 7 + 8 + 2 = 18 1 + 8 = 9
Вывод: замеченная мною закономерность «срабатывает» для четырехзначных, пятизначных, шестизначных, семизначных, восьмизначных и девятизначных чисел.
2.1.5. Исследование сумм цифр чисел,
в записи которых есть цифра 0 и повторяющиеся цифры.
Я проверил, сработает ли открытая мною закономерность для чисел, в запись которых входят цифры 0 и повторяющиеся цифры. Свое предположение я проверил на 10 таких числах. Приведу только 2 числа.
- Число 79805014
Сумма цифр числа: 7 + 9 + 8 + 0 + 5 + 0 + 1 + 4 = 34 3 + 4 = 7
Некоторые из сумм, составленных из цифр этого числа и суммы цифр ответов:
79 + 80 + 50 + 14 = 223 2 + 2 + 3 = 7
7854 + 1009 = 8863 8 + 8 + 6 + 3 = 25 2 + 5 = 7
- Число 79797979
Сумма цифр числа: 7 + 9 + 7 + 9 + 7 + 9 + 7 + 9 = 64 6 + 4 = 10 1 + 0 = 1
Некоторые из сумм, составленных из цифр этого числа и суммы цифр ответов:
9797 + 7979 = 17776 1 + 7 + 7 + 7 + 6 = 28 2 + 8 = 10 1 + 0 = 1
97 + 79 + 97 + 79 = 352 3 + 5 + 2 = 10 1 + 0 = 1
7977 + 7999 = 15976 1 + 5 + 9 + 7 + 6 = 28 2 + 8 = 10 1 + 0 = 1
Из проведенного мной исследования я могу сделать такой вывод:
Замеченная мною закономерность распространяется на любые числа.
2.1.6. Практическое применение открытой мной закономерности
Мне стало интересно, а как использовать мое открытие на практике.
1. Еще работая над темой исследования, я понял, что знание открытой мной закономерности очень полезно на уроках математики. Теперь любой пример на сложение я проверяю не вычитанием, а при помощи «своего» закона.
Например, 5896 + 4561 = 10457
5 + 8 + 9 + 6 = 28 2 + 8 = 10 1 + 0 = 1
4 + 5 + 6 + 1 = 16 1 + 6 = 7
1 + 0 + 4 + 5 + 7 = 17 1 + 7 = 8
Проверка: 1 + 7 = 8 8 = 8
Пример решен верно.
А вот другой пример: 368 + 405 = 783
7 + 8 + 3 = 18 1 + 18 = 9
3 + 6 + 8 = 17 1 + 7 = 8 4 + 0 + 5 = 9
Проверка: 8 + 9 = 17 1 + 7 = 8 8 = 9
Пример решен не верно. Нужно искать ошибку в вычислениях.
2. Это очень интересная игра. Я так увлекся замеченной мною закономерностью, что стал проверять ее на десятках номерах телефонов из справочника, номерах денег и т.д. (Что бы я ни делал, закономерность оставалась в силе.) Теперь мне всегда есть чем заняться в поездках, очередях и просто если скучно.
3. Каждый покупатель при помощи открытой мной закономерности может быстро узнать, не обсчитали ли его. Для этого надо только, чтоб на всех ценниках штучного товара рядом с его ценой указывали сумму цифр его цены (приложение I)
4. Я проверил закономерность на примерах из тетрадей моих одноклассников. Этот эксперимент тоже доказал правомерность моего открытия. Кроме того, я предложил учителю свой упрошенный способ проверки примеров на сложение.
Чтобы проверить, правильно ли решен пример, теперь достаточно найти сумму всех цифр слагаемых и сумму цифр найденного ответа. Если обе эти суммы равны, то пример решен правильно (приложение 2)
Кроме того, из статьи И.С. Тебляшкина [5] я узнал, как быстро можно проверить примеры на деление любого числа на 9 (с остатком и без) (приложение 3).
Мне удалось обобщить весь наработанный мной материал и разработать методические рекомендации по быстрой проверке навыков ребят в делении с остатком и сложении столбиком. Эти рекомендации апробированы на моих одноклассниках. Я разработал брошюру (приложение 4) для учителя математики начальной школы и предложил провести ряд работ на проверку вычислительных навыков учащихся. Пономарева Ольга Николаевна провела такие работы и сравнила время проверки работ с использованием и без использования моего метода. Результат оказался более чем хорошим: учитель сэкономил 40% своего времени. Например, в 3 классе, чтобы апробировать мой экспресс – метод, провели такую самостоятельную работу: первому варианту предложили разделить на 9 числа – варианты набора цифр 1,2,3,4,5, а второму ряду – варианты набора цифр 5,6,7,8.
Учитывая, что у первого варианта в остатке всегда должно быть число 6,
(1+2+3+4+5=15 1+5=6),
а у второго ряда – число 8 (5+6+7+8=26 2+6=8), самостоятельная была проверена учителем всего за 4 минуты.
Затем ребятам был открыт секрет самопроверки примеров на деление любого числа на 9.
5. Основываясь на открытой мной закономерности, я придумал свой математический фокус. Приведу простейший его пример. (приложение 5)
Перед вами ряд цифр: 1234.
Составьте из него любое двухзначное число.
Составьте теперь другое двухзначное число из оставшихся цифр. Сложите оба задуманных вами числа.
Сложите между собой все цифры полученного вами ответа. Если у вас вышло двузначное число, найдите сумму его цифр еще раз.
У вас получилось число 1?
6. Я очень хочу понять, как можно использовать открытую мной закономерность в математике и что эта закономерность нам дает. Я обращался за помощью к знакомому, сведущему в вопросах математики. Знакомый ответил, что я пока ничего в его объяснении не пойму, т.к. знаний одной только арифметики для этого не достаточно. Он только сказал мне, что число, которое я каждый раз нахожу, называется инвариантом. Из «Иллюстрированного энциклопедического словаря» я узнал: «Инвариант – это величина, не изменяющаяся при тех или иных преобразованиях» [2].
В статье того же И.Тебляшкина я прочитал, что в основе открытой мной закономерности лежат основные свойства нумерологического числа. [5]. Я не очень понял такое объяснение, но из «Справочника по элементарной математике» узнал о системах нумерации у разных народов [4], а из «Энциклопедии для девочек и мальчиков» узнал, что нумерологические числа применяются при составлении гороскопов. [7].
2.2. Виртуальный «угадыватель» мыслей
Изучив замеченную мною закономерность, я решил предложить еще один эффектный фокус – угадыватель мыслей. В этом мне помог Интернет.
Во время поиска информации в сети я случайно наткнулся на программу с угадыванием чисел (Приложение 6). В этом фокусе нужно было задумать двухзначное число, вычесть из него составляющие его цифры. Найти получившееся число в таблице и сосредоточится на знаке, который соответствует полученному числу. После этого программа выдает именно тот знак, на котором я сосредоточился. Стопроцентное угадывание было во всех случаях моей игры! Мне стало очень интересно. Но так как в магию компьютера я не верю, то начал искать математические закономерности. И после долгих поисков я все-таки заметил определенную закономерность: какое бы двухзначное число я не выбирал, результат последовательного вычитания всех чисел всегда будет числом, кратным 9. Остальное оказалось не сложным: в таблице напротив чисел, кратных 9, всегда стоит один и тот же значок.
С этим «фокусом» я выступил на школьной научно-практической конференции. Ни один человек, включая наших учителей, не смогли отгадать секрет моего «фокуса»
III. Заключение
Задачи, которые я поставил вначале своего исследования, я решил. Мне пришлось исследовать различные суммы цифр, находить суммы цифр полученных ответов. К сожалению, моих знаний пока не достаточно, чтобы понять объяснения, данные мне со страниц журнала. Кроме того, как я ни старался, мне не удалось вывести формулу «моей» закономерности. Я понял главное: устный счет – очень полезный навык. Несмотря на то, что у нас давно наступила эпоха калькуляторов, устный счет не перестает преподносить нам новые сюрпризы. И одно из доказательств тому – это мое исследование.
Из своего исследования я делаю такой вывод:
математику нужно знать и любить, тогда в математике можно увидеть много необычного, увлекательного.
Что еще мне хочется сделать ещё?
а) Я мечтаю создать программу, чтобы исследовать изученные закономерности при помощи компьютера. Я хочу, чтобы компьютер сам перебирал все возможные варианты сумм и вычислял их.
б) Я узнал, что игры и фокусы, подобные тем, что придумал я, придумывали еще математики Древней Греции десятки веков назад. Я хочу изучить математические игры древних греков.
в) Полученные закономерности позволяют мне предположить, что существуют выигрышные стратегии в игре с лотереями. В дальнейшем я хочу отыскать эти закономерности.
IV. Литература
Горденко Г. Закономерность гармонична? [Из цикла «Математические досуги»] // Наука и жизнь. - 2006. № 9. - с. 66.
- Иллюстрированный энциклопедический словарь, издательство «ТЕРРА», Москва, 1998 год.
- Ниходовский А. Игра с числами. [Из цикла «Математические досуги»] // Наука и жизнь. -2006. №3. - с. 45.
- Справочник по элементарной математике, издательство «Большая Медведица», Москва, 1998 год.
- Тебляшкин И. Серьезные игры с числами. [Из цикла «Математические досуги»] // Наука и жизнь. - 2006. № 6. - с. 65.
- Энциклопедический словарь юного математика, издательство «Педагогика», Москва, 1985 год.
- Энциклопедия для девочек, издательство «Основа - Астарта», Киев, 1995 год.
V. ПРИЛОЖЕНИЯ
П
риложение 18 + 7 = 15, 1 + 5 = 6
Если на каждый чек штучного товара дополнительно нанести рядом с ценой значение суммы цифр цены, покупателю будет гораздо легче проверить, не обсчитали ли его.
Например, мной приобретено:
Масло подсолнечное - 58 руб., сумма цифр цены 5 + 8 = 13 1 + 3 = 4
Печенье «Каравай» - 45 руб., сумма цифр цены 4 + 5 = 9
Хлеб - 12 рублей, сумма цифр цены 1 + 2 = 3
Минеральную воду - 16 рублей, сумма цифр цены 1 + 6 = 7
Шоколад по цене 21 рублей, сумма цифр цены 2 + 1 = 3
Подсчитывать устно, на какую сумму мной приобретено продуктов, не очень легко: 58 + 45 + 12 + 16 + 21 = 152
А вот складывать суммы цифр цены, то есть однозначные числа, гораздо легче:
4 + 9 + 3 + 7 + 3 = 26 2 + 6 = 8
Продавец сказал уплатить 153 рубля.
1 + 5 + 3 = 9
9 не равно 8
Ясно, что продавец ошибся.
Приложение 2
Способ самопроверки примера на сложение.
Конечная сумма всех цифр слагаемых всегда равна конечной сумме всех цифр найденного ответа.Конечная сумма цифр слагаемых:
3 + 5 + 2 + 6 + 4 + 5 + 1 = 26 2 + 6 = 8
Конечная сумма всех цифр ответа:
3 + 9 + 7 + 7 = 26 2 + 6 = 8, 8 = 8
Самостоятельная работа по теме «Сложение в столбик» была проверена учителем при помощи моего экспресс-метода.
Первому ряду предложили составить примеры на сложение из набора цифр
2, 3, 4, 5, 8, 9, 0, 0, а второму ряду – из набора цифр 1, 1, 6, 7, 7, 8, 9, 0.
Учитывая, что у первого ряда сумма цифр каждого из полученных ответов должна составить 4: (2 + 3 + 4 + 5 + 8 + 9 + 0 + 0 = 31 3 + 1 = 4),
а у второго ряда – 3: (1 + 1 + 6 + 7 + 7 + 8 + 9 + 0 = 39 3 + 9 = 12 1 + 2 = 3),
самостоятельная была проверена учителем гораздо быстрее.
Приложение 3
Конечная сумма цифр делимого:
9 + 5 + 6 + 7 + 8 = 35 3 + 5 = 8
Конечная сумма цифр числа – это всегда остаток от деления этого числа на 9.
А в случае, если конечная сумма цифр числа равна 9, число делится на 9 без остатка.
Самостоятельная работа по теме «Деление с остатком» была проверена учителем при помощи моего экспресс-метода.
Первому ряду предложили разделить на 9 числа – варианты набора цифр 1,2,3,4,5,
а второму ряду – варианты набора цифр 5,6,7,8.
Учитывая, что у первого ряда в остатке должно быть число 6 (1 + 2 + 3 + 4 + 5 = 15 1 + 5 = 6),
а у второго ряда – число 8 (5 + 6 + 7 + 8 = 26 2 + 6 = 8),
самостоятельная была проверена учителем всего за 4 минуты.
Приложение 4
В помощь учителю.
Методические разработки по экспресс - проверке навыков ребят в сложении столбиком и делении с остатком.
(для учителей 2-5 классов)
Меня восхищают терпение и выдержка наших учителей. Даже моя мама иногда может сказать мне: «У меня сегодня ни на что нет сил и настроения. Лёня, давай ты сегодня все будешь делать самостоятельно». И я понимаю, что у нее есть на это право. А вот у учителей сказать нам, что они устали, права нет совсем. Есть силы или их давно уже нет, устали они, или болеют, а на урок идти надо. И проводить каждый урок нужно на совесть, как выражаются сами учителя, с полной отдачей. Да еще потом проверить все тетрадки нужно! Я предлагаю экспресс- методы проведения самостоятельных работ по некоторым темам математики, которые могут минимизировать труд учителя.
1.Как быстро проверить навыки сложения чисел в столбик.
Эта работа основана на таком «секрете»: Конечная сумма цифр всех слагаемых всегда равна сумме цифр полученного результата сложения.
Цель работы: проверка навыка сложения чисел в столбик.
Время, необходимое для проведения работы: 20 минут.
План проведения самостоятельной работы:
Продиктовать ребятам любую комбинацию цифр, лучше – неповторяющихся, и без нулей, чтобы избежать путаницы.
- Предложить составить как можно больше примеров на сложение из продиктованных цифр, при этом соблюдая следующие условия:
- в каждом примере должны участвовать все заданные цифры,
- все цифры должны участвовать только один раз (или, если они повторяются в записи учителя, должны повторяться столько раз, сколько они повторяются у учителя.
3. Проверить работы ребят. Для этого достаточно найти конечную сумму (нумерологическое число) продиктованных цифр. Затем нужно только находить конечную сумму всех полученных ребятами ответов и сравнивать ее с суммой исходных цифр. Если числа совпали – пример решен верно. Если суммы не совпали, значит, проверяемый допустил одну из двух ошибок:
- решил неверно пример, значит, не в полной мере освоил сложение в столбик,
- по невнимательности составил неправильно пример на сложение, значит, проверяемый не смог сконцентрировать внимание на поставленной задаче.
Например:
- Комбинация цифр 171268.
Конечная сумма цифр числа: 1+7+1+2+6+8=25 2+5=7
Некоторые из возможных сумм, составленных из цифр этого набора цифр и суммы цифр ответов:
1712+68=1780, 1+7+8+0=16, 1+6=7, 7=7 – пример решен верно.
862+171=1033, 1+0+3+3=7, 7=7 - пример решен верно.
711+682=1383, 1+3+8+3=15, 1+5=6, 6 не равно 7 – допущена ошибка в вычислениях.
Кроме того, если ребята будут знать, что конечная сумма цифр всех слагаемых всегда равна сумме цифр полученного результата сложения, они всегда смогут более внимательно и очень быстро проверять все примеры на сложение.
Проверено на себе и на моих одноклассниках!
2. Как быстро проверить навыки деления чисел с остатком.
Эта работа основана на таком «секрете»: Конечная сумма цифр числа – это всегда остаток от деления этого числа на 9. А в случае, если конечная сумма цифр числа равна 9, число делится на 9 без остатка.
Цель работы: проверка навыка деления чисел с остатком.
Время, необходимое для проведения работы: 20 минут.
План проведения самостоятельной работы:
Продиктовать ребятам любую комбинацию цифр.
- Предложить составить как можно больше чисел из этой комбинации цифр и разделить столбиком каждое число на 9. Условие: каждая цифра в составленном ребятами числе должна встречаться столько раз, сколько она встречается в исходном, т.е. продиктованном учителем, наборе цифр.
- Проверить работы ребят. Для этого достаточно найти конечную сумму (нумерологическое число) продиктованных цифр и сравнивать ее со значением полученного при делении остатка. Если конечная сумма исходных цифр и значение остатка совпали – пример решен верно.
Приложение 5
Фокус «Загадка суммы цифр»
Перед вами ряд цифр: 2, 3, 4, 5, 6, 7.
Составьте из него любое трехзначное число.
Составьте теперь другое трехзначное число из оставшихся цифр.
Сложите оба задуманных вами числа.
Сложите между собой все цифры полученного вами ответа. Если у вас вышло двухзначное число, найдите сумму его цифр еще раз.
У вас получилось число 9?
Приложение 6
